- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Лекция 4. Преобразование объектов презентация
Содержание
- 1. Лекция 4. Преобразование объектов
- 2. Преобразование объектов Пусть любая точка, принадлежащая определенному
- 3. Аффинные преобразования объектов на плоскости Аффинные преобразования
- 4. Аффинные преобразования объектов на плоскости 1. Сдвиг В матричной форме: Обратное преобразование:
- 5. Аффинные преобразования объектов на плоскости 2. Растяжение-сжатие (масштабирование) В матричной форме: Обратное преобразование:
- 6. Аффинные преобразования объектов на плоскости 3. Поворот В матричной форме: Обратное преобразование:
- 7. Трехмерные аффинные преобразования объектов В общем виде
- 8. Трехмерные аффинные преобразования объектов . 1. Сдвиг
- 9. Трехмерные аффинные преобразования объектов . 3. Повороты
- 10. Трехмерные аффинные преобразования объектов . Поворот вокруг
- 11. Связь преобразований объектов и координат . Движение
- 12. Связь преобразований объектов и координат . 1.
- 13. Связь преобразований объектов и координат . Преобразования в матричной форме:
Слайд 2Преобразование объектов
Пусть любая точка, принадлежащая определенному объекту, имеет координаты (k1, k2,
Тогда преобразование объекта можно определить как изменение положения точек объекта. Новое положение точки пространства соответствует новым значениям координат (m1, m2, …, mn)
Соотношение между старыми и новыми координатами для всех точек объекта
(m1, m2, …, mn) = F(k1, k2, …, kn)
и будет определять преобразование объекта, где F – функция преобразования
Слайд 3Аффинные преобразования объектов на плоскости
Аффинные преобразования объектов на плоскости описывается формулой:
где
Рассмотрим частные случаи аффинного преобразования
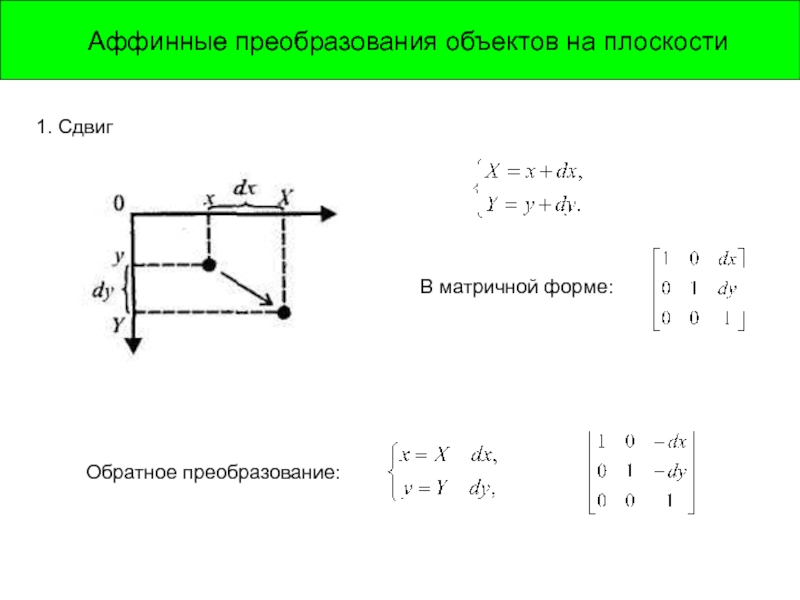
Слайд 4Аффинные преобразования объектов на плоскости
1. Сдвиг
В матричной форме:
Обратное преобразование:
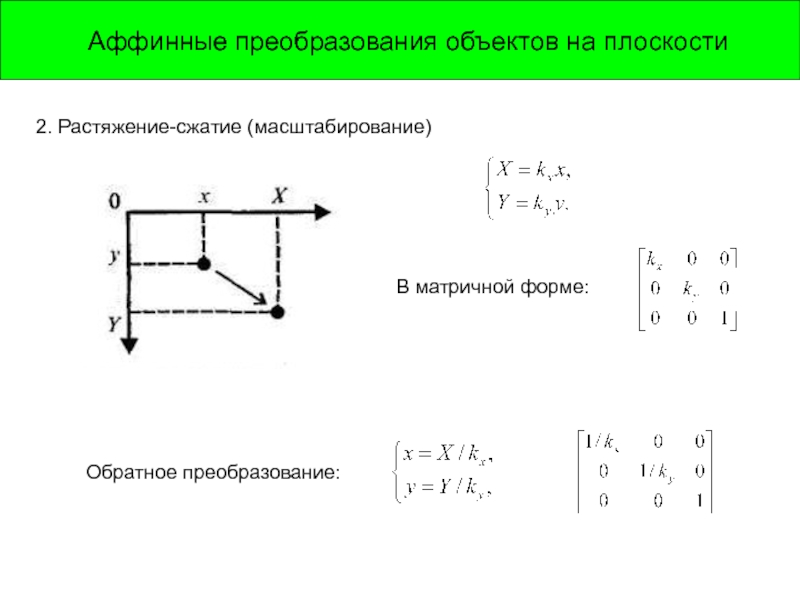
Слайд 5Аффинные преобразования объектов на плоскости
2. Растяжение-сжатие (масштабирование)
В матричной форме:
Обратное преобразование:
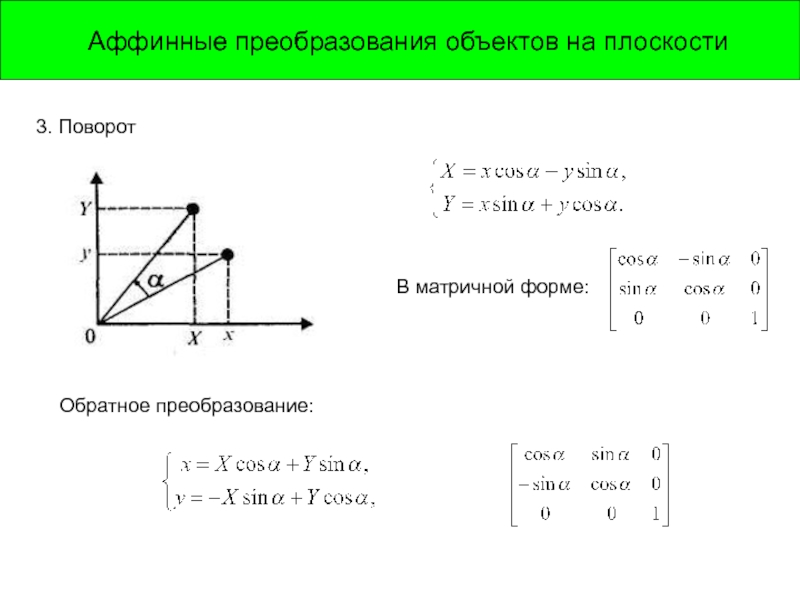
Слайд 6Аффинные преобразования объектов на плоскости
3. Поворот
В матричной форме:
Обратное преобразование:
Слайд 7Трехмерные аффинные преобразования объектов
В общем виде записываются
где A, B, …, N
В матричном виде
.
Слайд 8Трехмерные аффинные преобразования объектов
.
1. Сдвиг объектов на dx, dy, dz:
2. Растяжение/сжатие
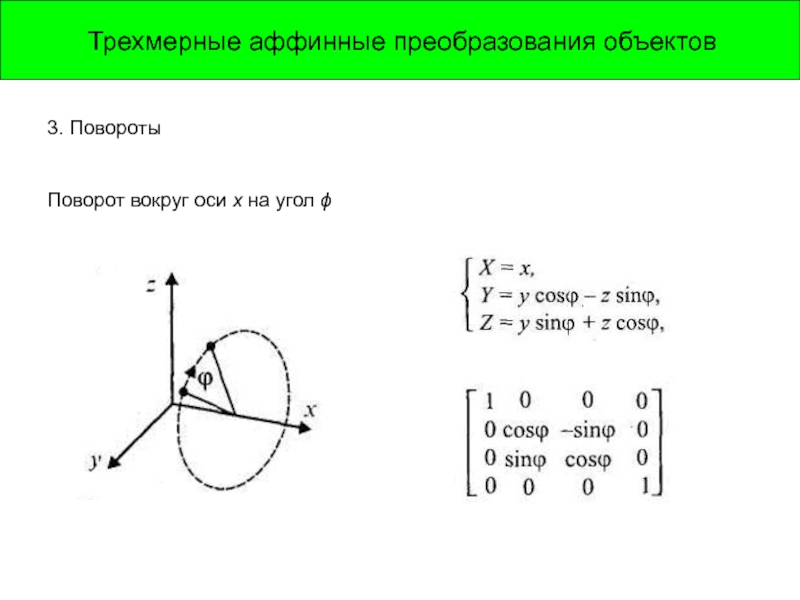
Слайд 10Трехмерные аффинные преобразования объектов
.
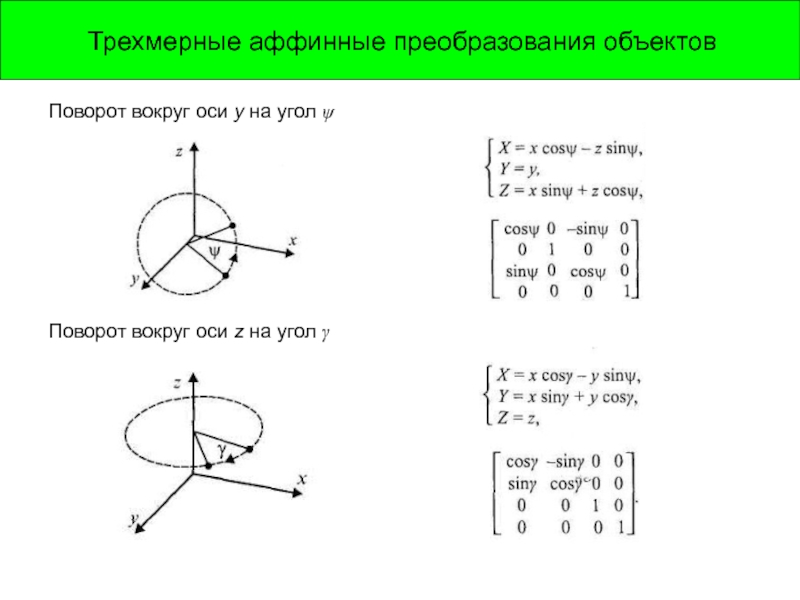
Поворот вокруг оси y на угол ψ
Поворот вокруг
Слайд 11Связь преобразований объектов и координат
.
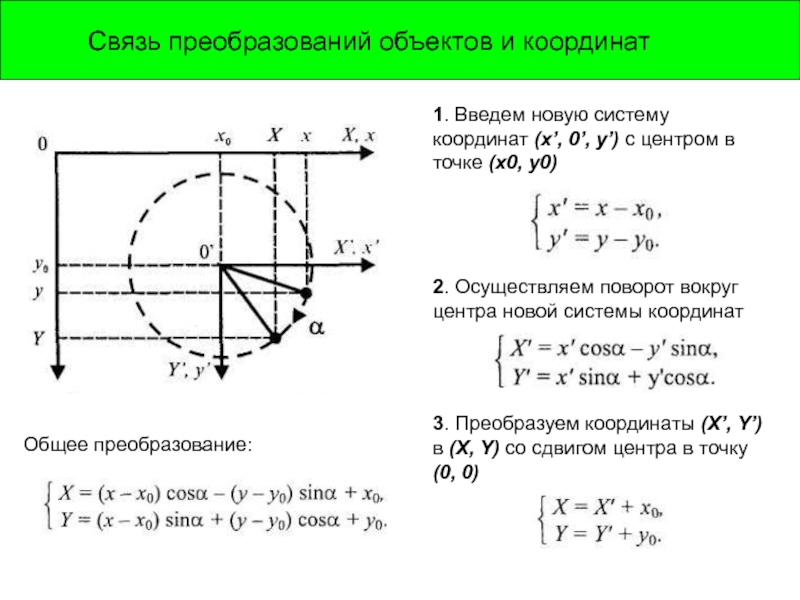
Движение объектов можно рассматривать как движение в
Пусть необходимо получить функцию расчета координат (X, Y) = F(x, y) для поворота вокруг точки с координатами (x0, y0) на угол α
Слайд 12Связь преобразований объектов и координат
.
1. Введем новую систему координат (х’, 0’,
2. Осуществляем поворот вокруг центра новой системы координат
3. Преобразуем координаты (X’, Y’) в (X, Y) со сдвигом центра в точку (0, 0)
Общее преобразование: