- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Криптография. Симметричные алгоритмы шифрования презентация
Содержание
- 1. Криптография. Симметричные алгоритмы шифрования
- 2. Криптография. Симметричные алгоритмы шифрования. Введение. Терминология.
- 3. Введение Проблема защиты информации путем ее
- 4. Введение Первоначально письменность сама по себе
- 5. Введение С широким распространением письменности криптография
- 6. Введение Бурное развитие криптографические системы получили
- 7. Актуальность использования криптографических методов в информационных системах
- 8. Актуальность использования криптографических методов в информационных системах
- 9. КРИПТОЛОГИЯ - занимается проблемой защиты информации путем
- 10. Направления криптологии Криптография. Криптоанализ.
- 11. ЦЕЛЬ КРИПТОГРАФИИ Криптография занимается поиском и исследованием
- 12. ЦЕЛЬ КРИПТОАНАЛИЗА - исследование возможности расшифровывания информации без знания ключей.
- 13. РАЗДЕЛЫ КРИПТОГРАФИИ 1. Симметричные криптосистемы. 2. Криптосистемы
- 14. Основные направления использования криптографических методов Передача
- 15. Алфавиты, используемые в современных ИС Алфавит
- 16. ШИФРОВАНИЕ - преобразовательный процесс: исходный текст, который
- 17. ДЕШИФРОВАНИЕ - обратный шифрованию процесс. На основе ключа шифрованный текст преобразуется в исходный.
- 18. КЛЮЧ - информация, необходимая для шифрования и
- 19. Виды криптосистем Симметричные. Асимметричные (другие названия: несимметричные или системы с открытым ключом).
- 20. СИММЕТРИЧНЫЕ КРИПТОСИСТЕМЫ - для шифрования, и для дешифрования используется один и тот же ключ.
- 21. СИСТЕМЫ С ОТКРЫТЫМ КЛЮЧОМ - используются два
- 22. ПОТОКОВЫЕ АЛГОРИТМЫ В потоковых алгоритмах способ шифрования отдельного символа не зависит от соседних символов.
- 23. БЛОКОВЫЕ АЛГОРИТМЫ В блоковых алгоритмах сообщение разбивается
- 24. ЭЛЕКТРОННАЯ (ЦИФРОВАЯ) ПОДПИСЬ - присоединяемое к тексту
- 25. КРИПТОСТОЙКОСТЬ - характеристика шифра, определяющая его стойкость к дешифрованию без знания ключа (т.е. криптоанализу).
- 26. Показатели криптостойкости Количество всех возможных ключей.
- 27. Слабые ключи ключи, которые предсказуемо преобразуют некоторый
- 28. Шифр Шифром называют пару: алгоритм и
- 29. Метод грубой силы Метод «грубой силы» предполагает перебор всех возможных ключей.
- 30. Криптостойкий алгоритм Алгоритм называют криптостойким, если не
- 31. Симметричные криптосистемы Прежде, чем начать использовать
- 32. Базовые классы симметричных криптосистем Алгоритмы подстановки
- 33. Моноалфавитные подстановки - это наиболее простой вид
- 34. Алгоритм Цезаря Самый древний алгоритм, предложенный
- 35. Алгоритм Цезаря Идея состоит в следующем:
- 36. Алгоритм замены полиалфавитный Усложнить шифр можно,
- 37. Алгоритм замены полиалфавитный Очевидно, что во
- 38. Пример алгоритма замены полиалфавитного Пусть дан
- 39. Пример алгоритма замены полиалфавитного Пусть дан
- 40. Алгоритм замены с большим ключом Для
- 41. Алгоритм замены с большим ключом Можно
- 42. Проблемы использования алгоритма с большим ключом
- 43. Проблемы использования алгоритма с большим ключом
- 44. Алгоритм замены с большим ключом Так,
- 45. Схема с одноразовым блокнотом - применяет
- 46. Пример алгоритма замены Пример 1. Пусть
- 47. Пример алгоритма замены Пример 1. Пусть
- 48. Пример алгоритма замены Пример 2. Пусть
- 49. Пример алгоритма замены Коды «з» -
- 50. Пример алгоритма замены Коды «з» -
- 51. Пример алгоритма замены После «з» вторая
- 52. Пример алгоритма замены Т.к. здесь результат
- 53. Перестановки - несложный метод криптографического преобразования, заключающийся
- 54. Перестановки Блоки информации (байты, биты, более крупные
- 55. Ключ алгоритма перестановки - множество пар переставляемых символом. Часто его задают в виде таблицы перемешивания.
- 56. Пример алгоритма перестановки Правило перестановок зададим
- 57. Пример алгоритма перестановки Покажем результат шифрования
- 58. Гаммирование - представляет собой преобразование исходного текста,
- 59. Гаммирование В случае если последовательность является истинно
- 60. Гаммирование Гаммирование является также широко применяемым криптографическим
- 61. Принцип шифрования гаммированием - заключается в генерации
- 62. Принцип дешифрования при гаммировании - сводится к
- 63. Гамма шифра Полученный зашифрованный текст является
- 64. Гамма шифра Фактически же, если период
- 65. Недостатки метода гаммирования 1. Метод гаммирования
- 66. Недостатки метода гаммирования 2. Если гамма
- 67. Недостатки метода гаммирования Злоумышленник может сделать
- 68. Виды гаммирования битовое гаммирование; гаммирование в
- 69. Битовое гаммирование - исходный текст
- 70. Гаммирование в общем виде -
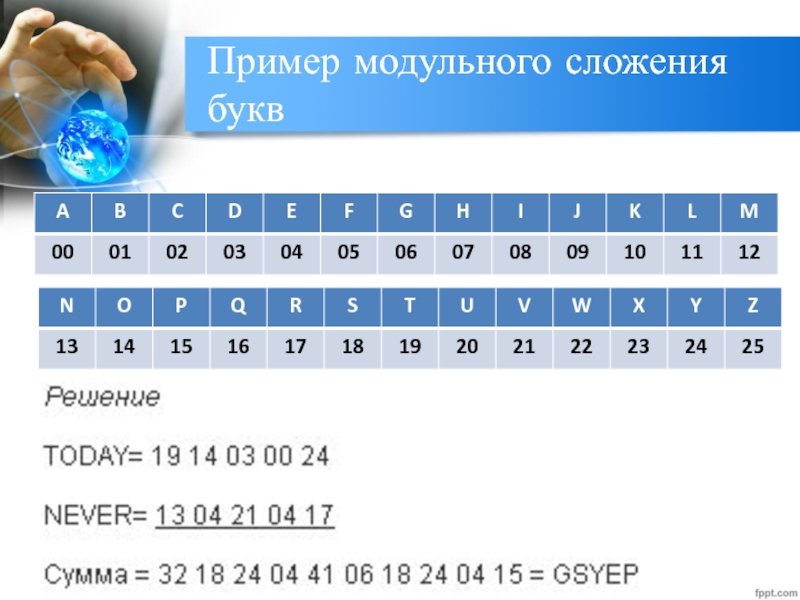
- 71. Пример модульного сложения букв
- 72. Пример модульного вычитания букв
- 73. Пример гаммирования в общем виде Пусть
- 74. Пример гаммирования в общем виде Пусть
- 75. Благодарим за внимание!
Слайд 1Криптография. Симметричные алгоритмы шифрования.
ИНФОРМАЦИОННАЯ БЕЗОПАСНОСТЬ И ЗАЩИТА ИНФОРМАЦИИ
Слайд 2Криптография. Симметричные алгоритмы шифрования.
Введение.
Терминология.
Симметричные криптосистемы.
Алгоритм Цезаря.
Алгоритм замены полиалфавитный.
Алгоритм замены с большим
Перестановки.
Гаммирование.
Слайд 3Введение
Проблема защиты информации путем ее преобразования, исключающего ее прочтение посторонним лицом,
Слайд 4Введение
Первоначально письменность сама по себе была криптографической системой, так как в
Слайд 5Введение
С широким распространением письменности криптография стала формироваться как самостоятельная наука. Первые
Слайд 6Введение
Бурное развитие криптографические системы получили в годы первой и второй мировых
Слайд 7Актуальность использования криптографических методов в информационных системах
Расширилось использование компьютерных сетей, в
Слайд 8Актуальность использования криптографических методов в информационных системах
2. появление новых мощных компьютеров,
Слайд 9КРИПТОЛОГИЯ
- занимается проблемой защиты информации путем ее преобразования (kryptos - тайный,
Слайд 11ЦЕЛЬ КРИПТОГРАФИИ
Криптография занимается поиском и исследованием математических методов преобразования информации с
Слайд 13РАЗДЕЛЫ КРИПТОГРАФИИ
1. Симметричные криптосистемы.
2. Криптосистемы с открытым ключом.
3. Системы электронной подписи.
4.
Слайд 14Основные направления использования криптографических методов
Передача конфиденциальной информации по каналам связи (например,
Установление подлинности передаваемых сообщений.
Хранение информации (документов, баз данных) на носителях в зашифрованном виде.
Слайд 15Алфавиты, используемые в современных ИС
Алфавит Z33 – 33 буквы русского алфавита
Алфавит Z256 – символы, входящие в стандартные коды ASCII и КОИ-8.
Алфавит Z2 – {0,1}.
Восьмеричный алфавит.
Шестнадцатеричный алфавит.
Слайд 16ШИФРОВАНИЕ
- преобразовательный процесс: исходный текст, который носит также название открытого текста,
Слайд 17ДЕШИФРОВАНИЕ
- обратный шифрованию процесс. На основе ключа шифрованный текст преобразуется в
Слайд 18КЛЮЧ
- информация, необходимая для шифрования и дешифрования текстов. Обычно ключ представляет
Слайд 19Виды криптосистем
Симметричные.
Асимметричные (другие названия: несимметричные или системы с открытым ключом).
Слайд 20СИММЕТРИЧНЫЕ КРИПТОСИСТЕМЫ
- для шифрования, и для дешифрования используется один и тот
Слайд 21СИСТЕМЫ С ОТКРЫТЫМ КЛЮЧОМ
- используются два ключа - открытый и закрытый
Слайд 22ПОТОКОВЫЕ АЛГОРИТМЫ
В потоковых алгоритмах способ шифрования отдельного символа не зависит от
Слайд 23БЛОКОВЫЕ АЛГОРИТМЫ
В блоковых алгоритмах сообщение разбивается на блоки, в которых способ
Слайд 24ЭЛЕКТРОННАЯ (ЦИФРОВАЯ) ПОДПИСЬ
- присоединяемое к тексту его криптографическое преобразование, которое позволяет
Слайд 25КРИПТОСТОЙКОСТЬ
- характеристика шифра, определяющая его стойкость к дешифрованию без знания ключа
Слайд 26Показатели криптостойкости
Количество всех возможных ключей.
Среднее время, необходимое для криптоанализа.
Слайд 27Слабые ключи
ключи, которые предсказуемо преобразуют некоторый текст (или множество текстов).
Примеры
Слайд 28Шифр
Шифром называют пару: алгоритм и ключ.
Эффективность шифрования зависит от сохранения тайны
Слайд 30Криптостойкий алгоритм
Алгоритм называют криптостойким, если не существует способов вскрытия зашифрованного текста
Слайд 31Симметричные криптосистемы
Прежде, чем начать использовать систему, необходимо получить общий секретный ключ
Слайд 32Базовые классы симметричных криптосистем
Алгоритмы подстановки или замены.
Алгоритмы перестановки.
Алгоритмы гаммирования.
Слайд 33Моноалфавитные подстановки
- это наиболее простой вид преобразований, заключающийся в замене символов
Слайд 34Алгоритм Цезаря
Самый древний алгоритм, предложенный Юлием Цезарем.
В настоящее время не
Слайд 35Алгоритм Цезаря
Идея состоит в следующем: задан алфавит и задан шаг (целое
Слайд 36Алгоритм замены полиалфавитный
Усложнить шифр можно, используя не один, а несколько алфавитов.
Слайд 37Алгоритм замены полиалфавитный
Очевидно, что во всех алфавитах должны быть все символы
Слайд 38Пример алгоритма замены полиалфавитного
Пусть дан первый алфавит «аяздкв бмл», второй «яозеадивлкн»
третий «аколд кмзв».
Пусть алфавиты используются по очереди. Шаг равен 5.
Исходный текст «задавака».
Тогда результат шифрования:
Слайд 39Пример алгоритма замены полиалфавитного
Пусть дан первый алфавит «аяздкв бмл», второй «яозеадивлкн»
третий «аколд кмзв».
Пусть алфавиты используются по очереди. Шаг равен 5.
Исходный текст «задавака».
Тогда результат шифрования: «бквво лк».
Слайд 40Алгоритм замены с большим ключом
Для обеспечения высокой криптостойкости требуется использование больших
Слайд 41Алгоритм замены с большим ключом
Можно говорить здесь о криптосистеме с одноразовым
Слайд 42Проблемы использования алгоритма с большим ключом
Этот способ неудобен для практического применения.
Слайд 43Проблемы использования алгоритма с большим ключом
Чем больше ключ, тем проблематичнее передача.
Слайд 44Алгоритм замены с большим ключом
Так, например, криптокарта Forteza, используемая агентами национальной
Слайд 45Схема с одноразовым блокнотом
- применяет алгоритм Диффи-Хэлмана для генерации очередного секретного
Слайд 46Пример алгоритма замены
Пример 1. Пусть дан алфавит
«аяздкв бмл».
Ключ, то
Исходный текст «задавака».
Тогда результат шифрования:
Слайд 47Пример алгоритма замены
Пример 1. Пусть дан алфавит
«аяздкв бмл».
Ключ, то
Исходный текст «задавака».
Тогда результат шифрования: «дв бб мя».
Слайд 48Пример алгоритма замены
Пример 2. Пусть дан алфавит «аяздкв бмл». Задан ключ,
Слайд 49Пример алгоритма замены
Коды «з» - 231, «а» - 224, «д» -
Тогда результат шифрования:
Слайд 50Пример алгоритма замены
Коды «з» - 231, «а» - 224, «д» -
Тогда результат шифрования: «ккякякмк».
Слайд 51Пример алгоритма замены
После «з» вторая буква «к».
Код буквы «а» 224.
четвертая буква после «а» - «к».
3. Код буквы «д» 228.
228 mod 10 = 8.
восьмая буква после «д» - «я».
4. ……..
Слайд 52Пример алгоритма замены
Т.к. здесь результат шифрования зависим от исходного текста, то
Слайд 53Перестановки
- несложный метод криптографического преобразования, заключающийся в перестановке местами символов исходного
Слайд 54Перестановки
Блоки информации (байты, биты, более крупные единицы) не изменяются сами по
Слайд 55Ключ алгоритма перестановки
- множество пар переставляемых символом. Часто его задают в
Слайд 56Пример алгоритма перестановки
Правило перестановок зададим следующее: первый символ исходного текста меняется
Слайд 57Пример алгоритма перестановки
Покажем результат шифрования по шагам: 1 буква меняется местами
Слайд 58Гаммирование
- представляет собой преобразование исходного текста, при котором символы исходного текста
Слайд 59Гаммирование
В случае если последовательность является истинно случайной (например, снятой с физического
Слайд 60Гаммирование
Гаммирование является также широко применяемым криптографическим преобразованием. На самом деле граница
Слайд 61Принцип шифрования гаммированием
- заключается в генерации гаммы шифра и наложении полученной
Слайд 62Принцип дешифрования при гаммировании
- сводится к повторной генерации гаммы шифра при
Слайд 63Гамма шифра
Полученный зашифрованный текст является достаточно трудным для раскрытия в том
Слайд 64Гамма шифра
Фактически же, если период гаммы превышает длину всего зашифрованного текста
Слайд 65Недостатки метода гаммирования
1. Метод гаммирования становится бессильным, если злоумышленнику становится известен
Слайд 66Недостатки метода гаммирования
2. Если гамма получена в результате работы генератора псевдослучайных
Слайд 67Недостатки метода гаммирования
Злоумышленник может сделать предположение о содержании исходного текста. Так,
Слайд 69Битовое гаммирование
- исходный текст складывается с гаммой при помощи операции
Слайд 73Пример гаммирования в общем виде
Пусть дан алфавит «абюя 123». В этом
а13
ю2ю
Слайд 74Пример гаммирования в общем виде
Пусть дан алфавит «абюя 123». В этом
а13 -> юяб
ю2ю