Дисциплина:
«Компьютерная инженерная графика»
Тема занятия:
«Введение в начертательную геометрию»
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Компьютерная инженерная графика. Тема занятия: Введение в начертательную геометрию презентация
Содержание
- 1. Компьютерная инженерная графика. Тема занятия: Введение в начертательную геометрию
- 2. Проецирование Проецирование – получение изображения на плоскости
- 3. Метод центрального проецирования Суть метода В
- 4. Метод центрального проецирования Примеры Центральное проецировании линии Центральное проецирование поверхности
- 5. Метод параллельного проецирования Суть метода Центр проецирования
- 6. Метод Монжа При проецировании на одну плоскость
- 7. Метод Монжа Чтобы получить плоский чертеж, состоящий
- 8. Геометрические элементы предмета точка — бесконечно малая
- 9. Точка в ортогональной системе двух плоскостей проекций
- 10. Точка в ортогональной системе трех плоскостей проекций
- 11. Взаимное расположение точек На рисунке представлены точки
- 12. Прямая линия. Положение прямой линии относительно плоскостей
- 13. Прямая линия. Положение прямой линии относительно плоскостей
- 14. Прямая линия. Положение прямой линии относительно плоскостей
- 15. Прямая линия. Положение прямой линии относительно плоскостей
- 16. Прямая линия. Положение прямой линии относительно плоскостей
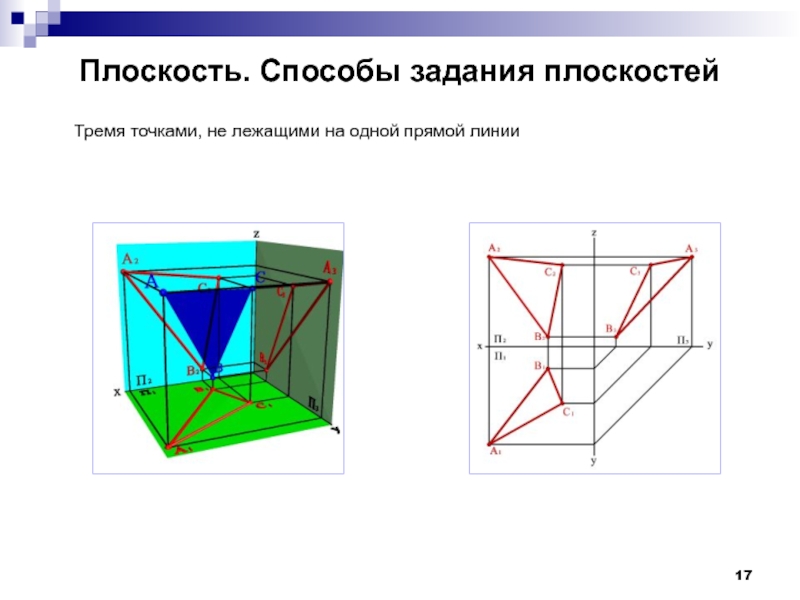
- 17. Плоскость. Способы задания плоскостей Тремя точками, не лежащими на одной прямой линии
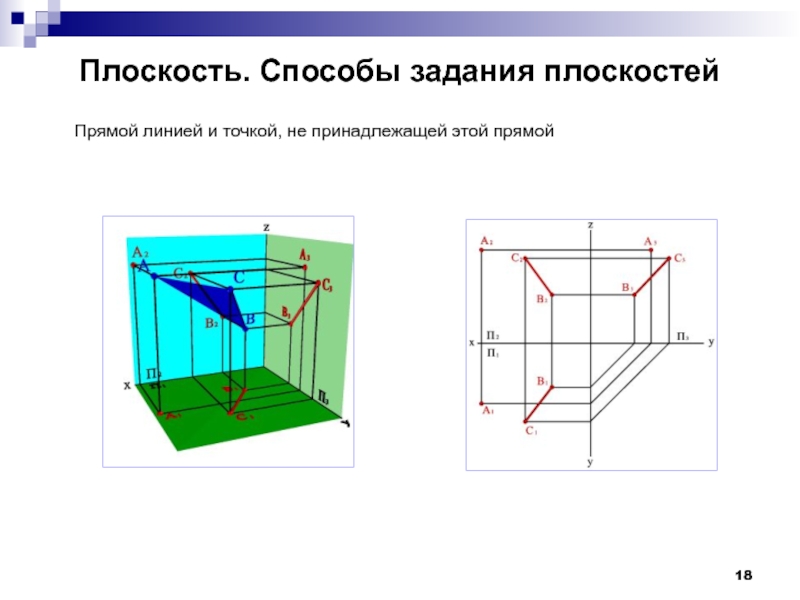
- 18. Плоскость. Способы задания плоскостей Прямой линией и точкой, не принадлежащей этой прямой
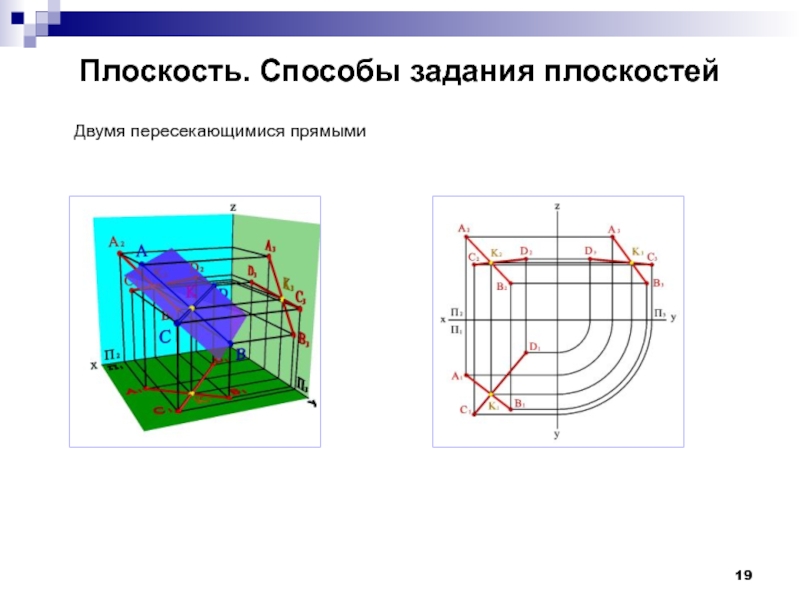
- 19. Плоскость. Способы задания плоскостей Двумя пересекающимися прямыми
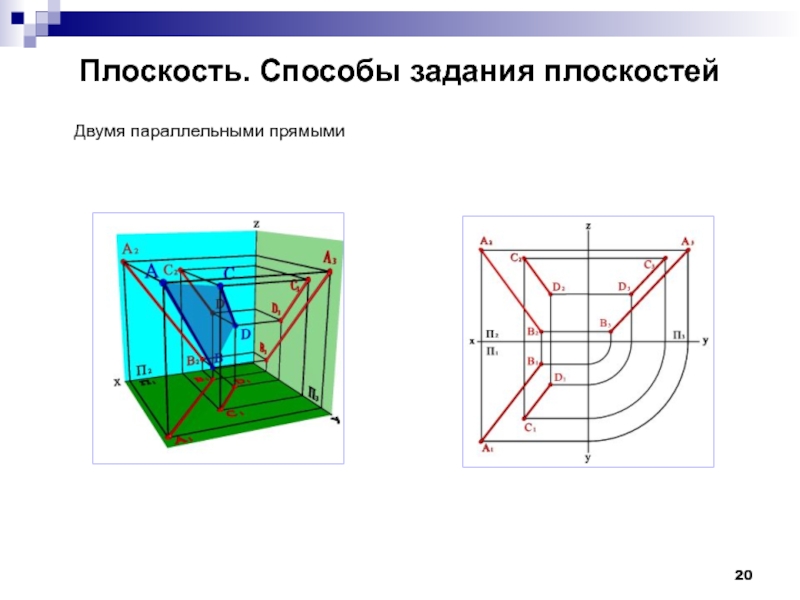
- 20. Плоскость. Способы задания плоскостей Двумя параллельными прямыми
- 21. Положение плоскости относительно плоскостей проекций Профильная плоскость
- 22. Способы преобразования чертежа Использование частных положений прямых
- 23. Способы преобразования чертежа. Метод вращения вокруг оси,
- 24. Способы преобразования чертежа. Метод замены плоскостей проекций
- 25. Дополнительная информация Более подробно ознакомиться с материалом
- 26. Задание По координатам пяти точек необходимо построить
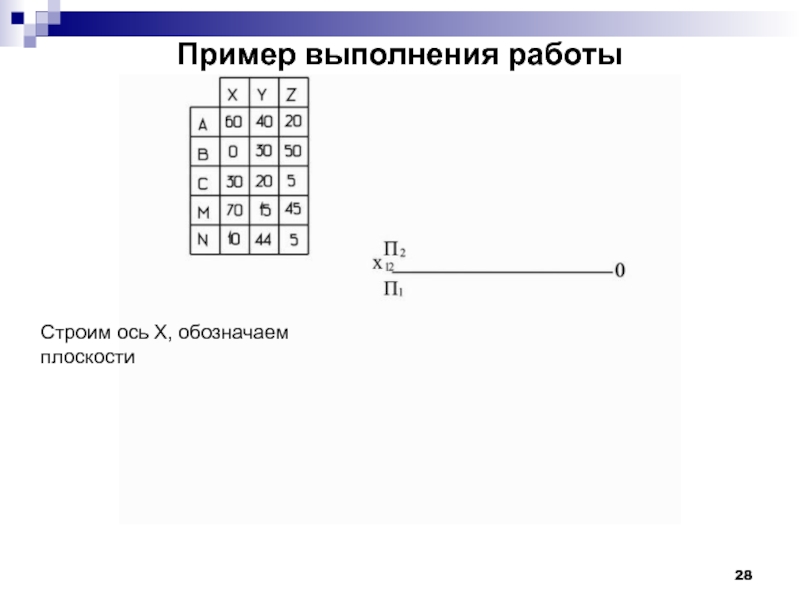
- 27. Пример выполнения работы Даны координаты точек
- 28. Пример выполнения работы Строим ось Х, обозначаем плоскости
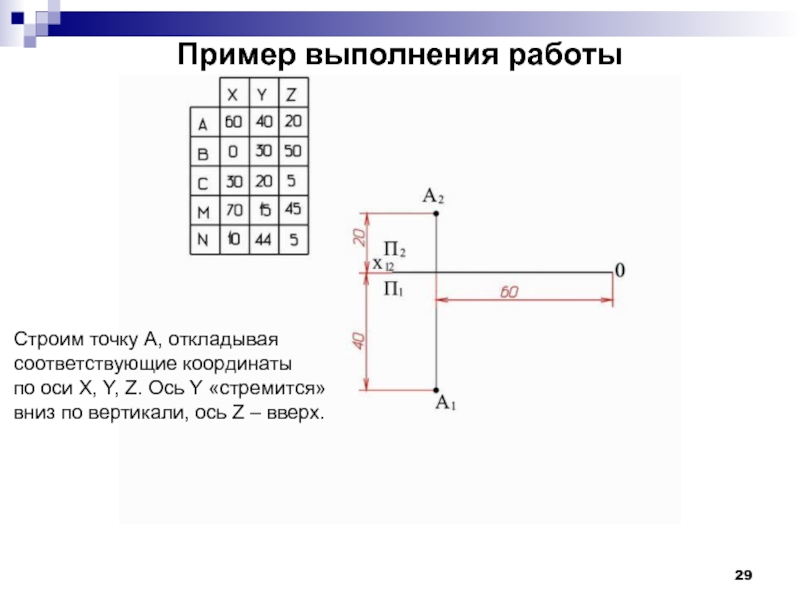
- 29. Пример выполнения работы Строим точку А, откладывая
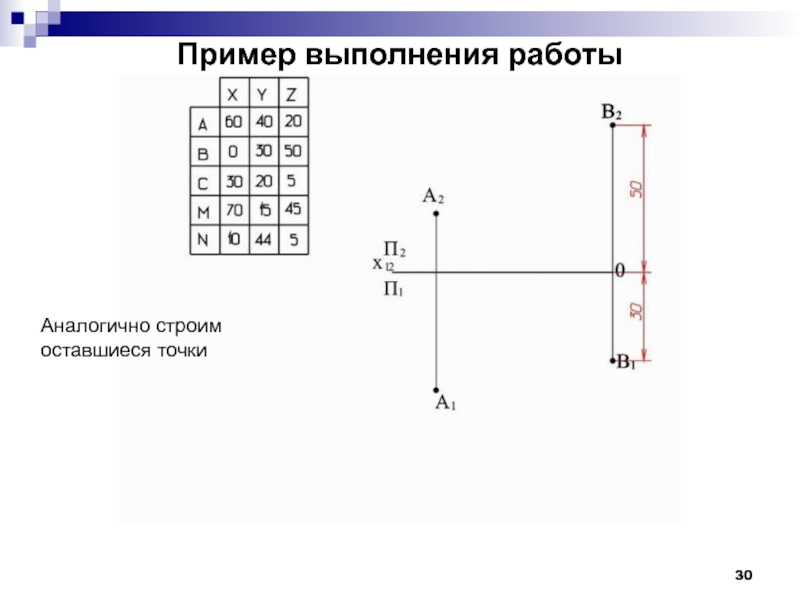
- 30. Пример выполнения работы Аналогично строим оставшиеся точки
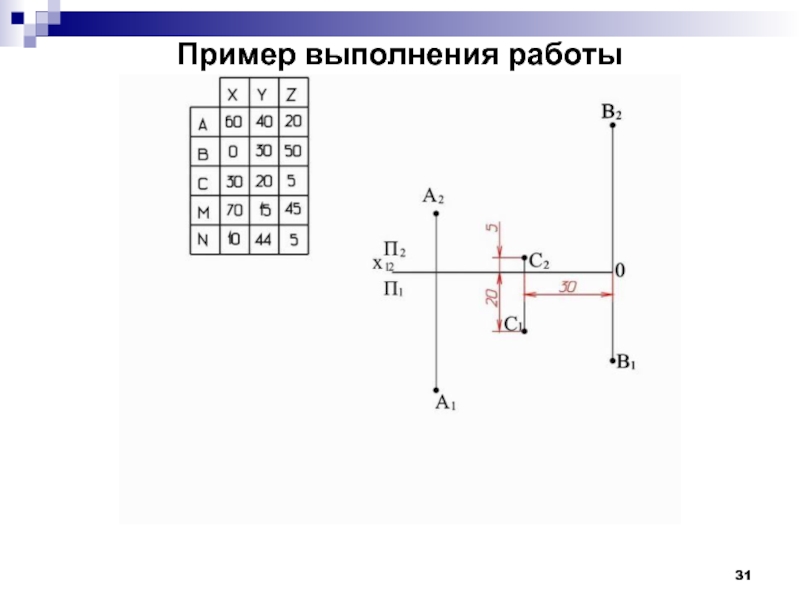
- 31. Пример выполнения работы
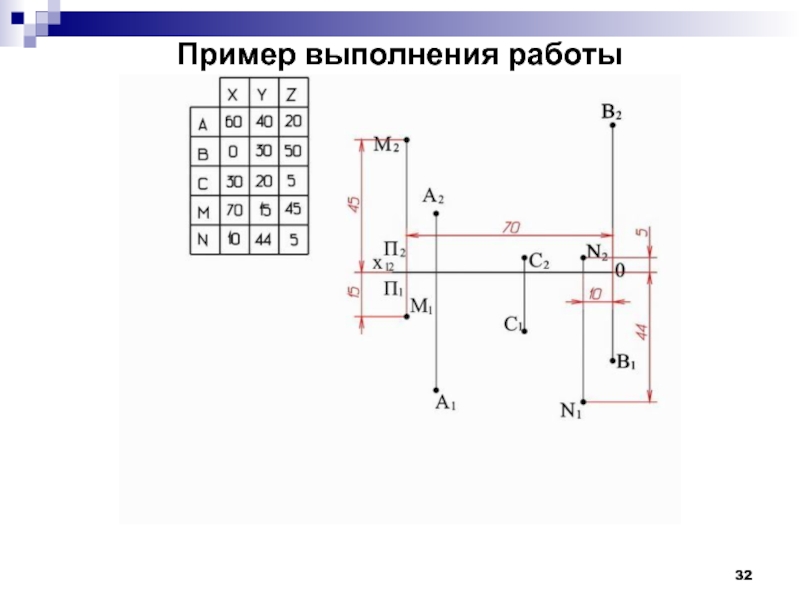
- 32. Пример выполнения работы
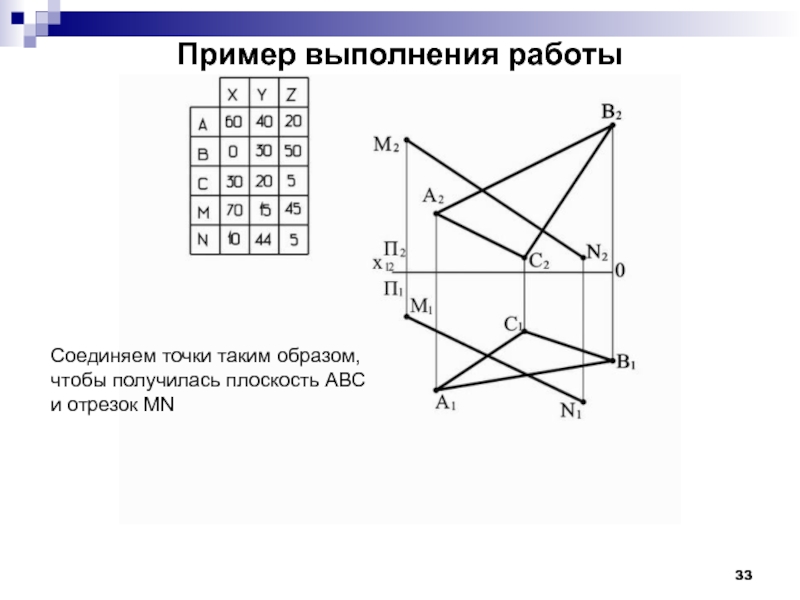
- 33. Пример выполнения работы Соединяем точки таким образом,
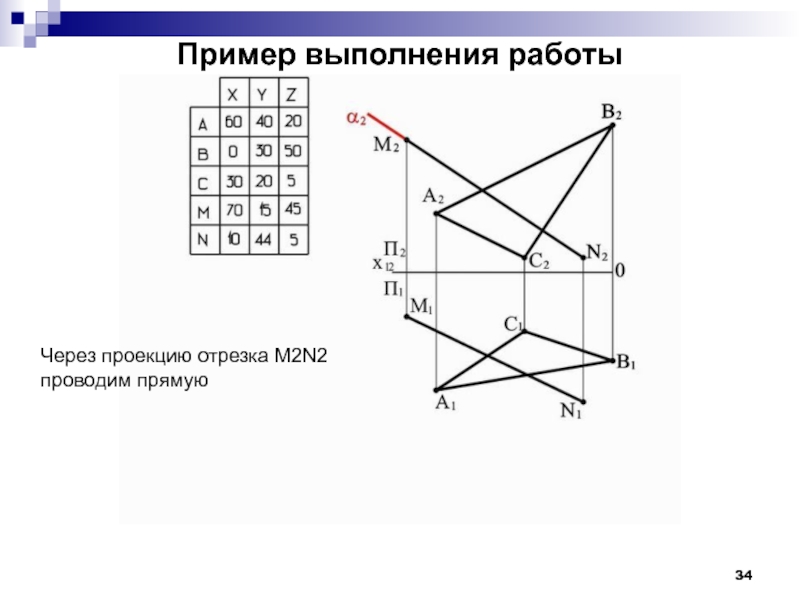
- 34. Пример выполнения работы Через проекцию отрезка M2N2 проводим прямую
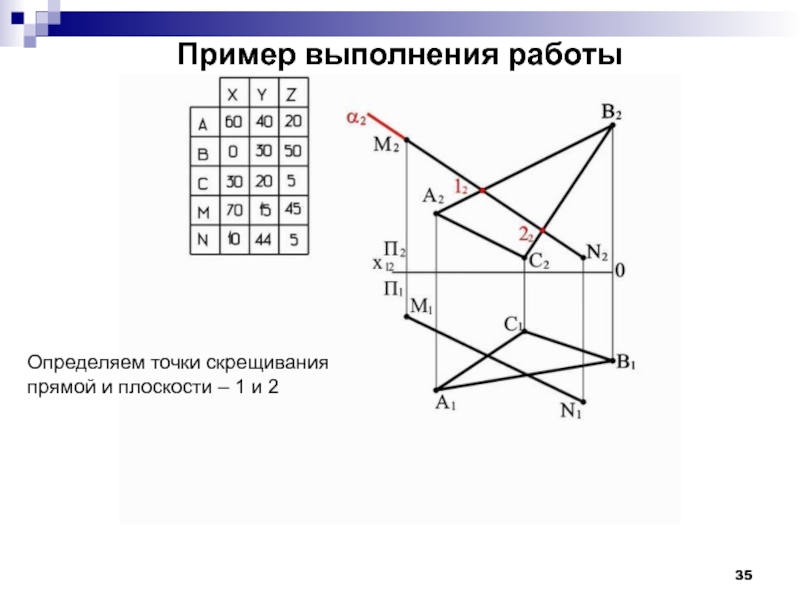
- 35. Пример выполнения работы Определяем точки скрещивания прямой и плоскости – 1 и 2
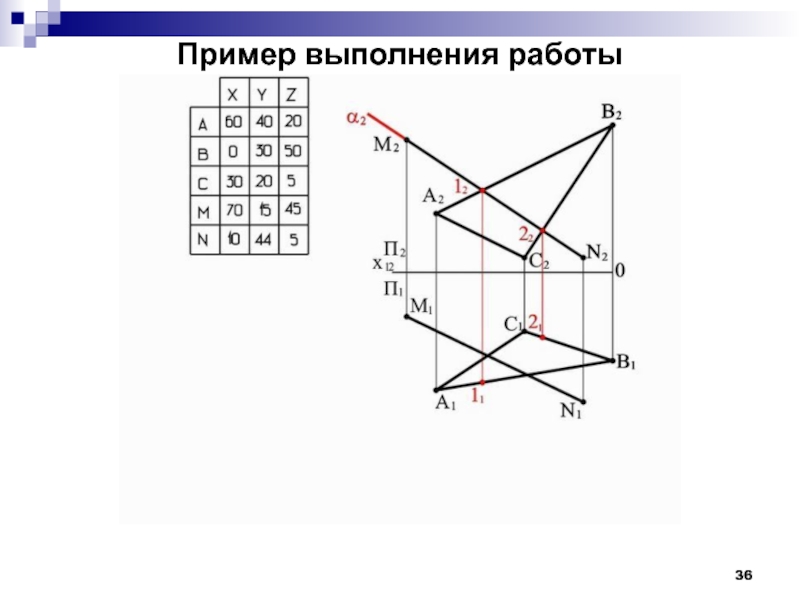
- 36. Пример выполнения работы
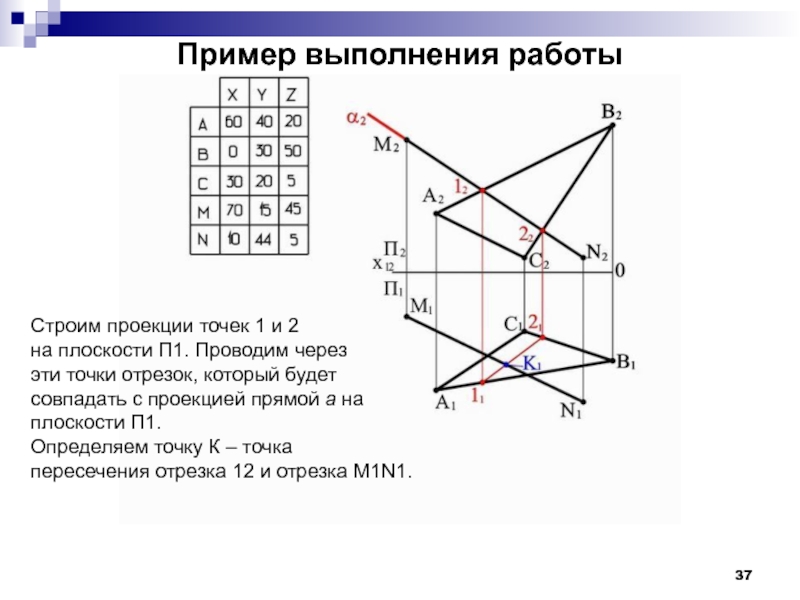
- 37. Пример выполнения работы Строим проекции точек 1
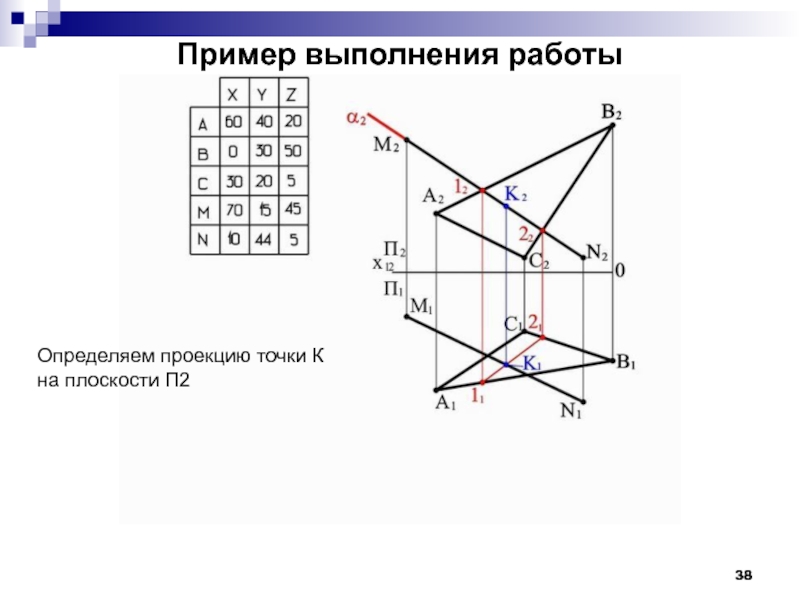
- 38. Пример выполнения работы Определяем проекцию точки К на плоскости П2
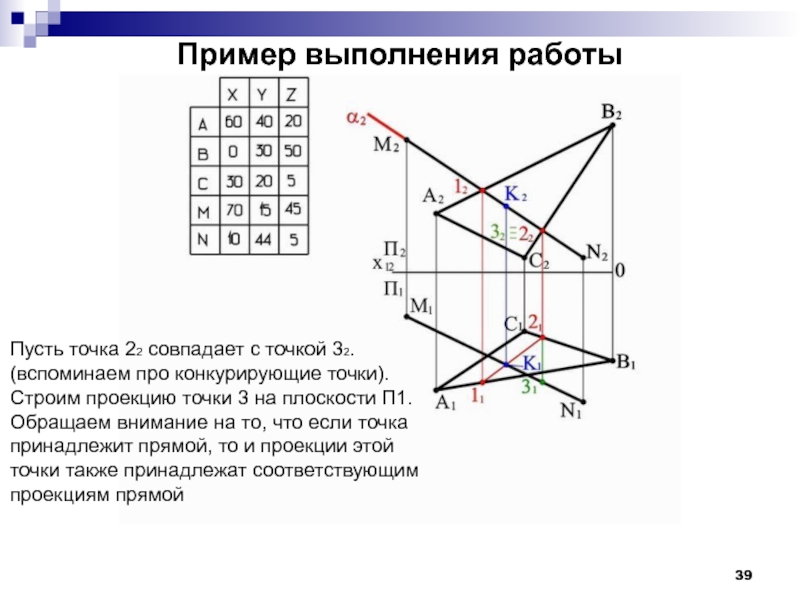
- 39. Пример выполнения работы Пусть точка 22 совпадает
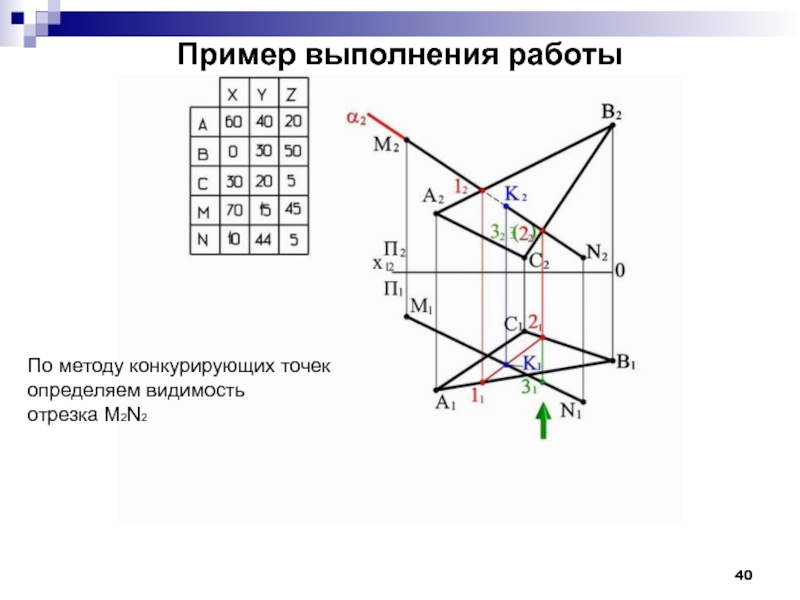
- 40. Пример выполнения работы По методу конкурирующих точек определяем видимость отрезка M2N2
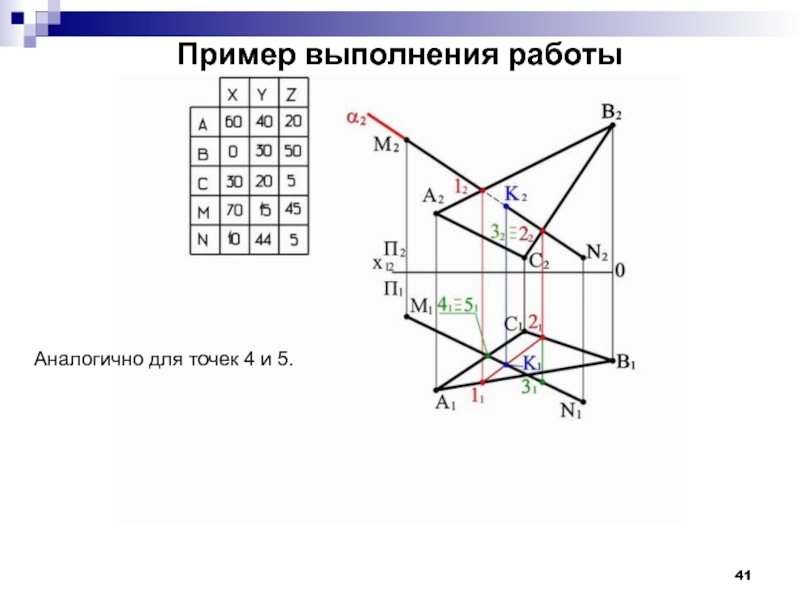
- 41. Пример выполнения работы Аналогично для точек 4 и 5.
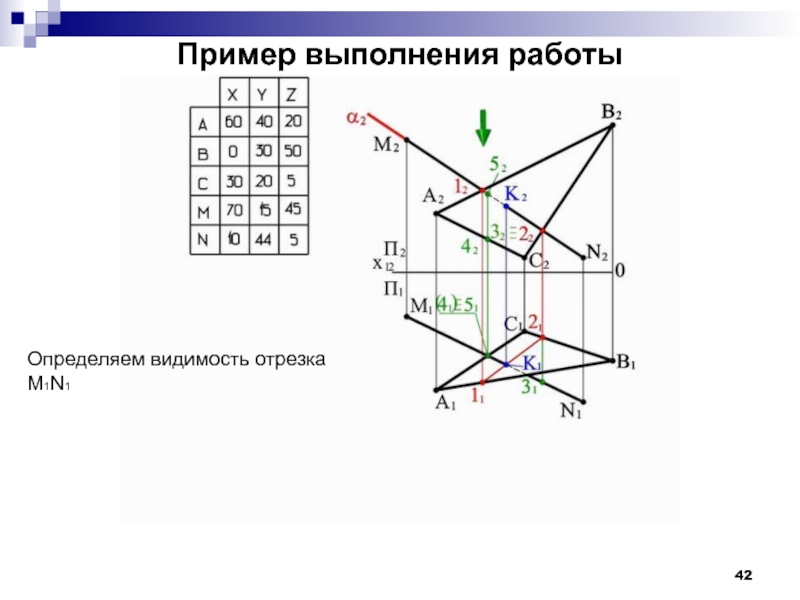
- 42. Пример выполнения работы Определяем видимость отрезка M1N1
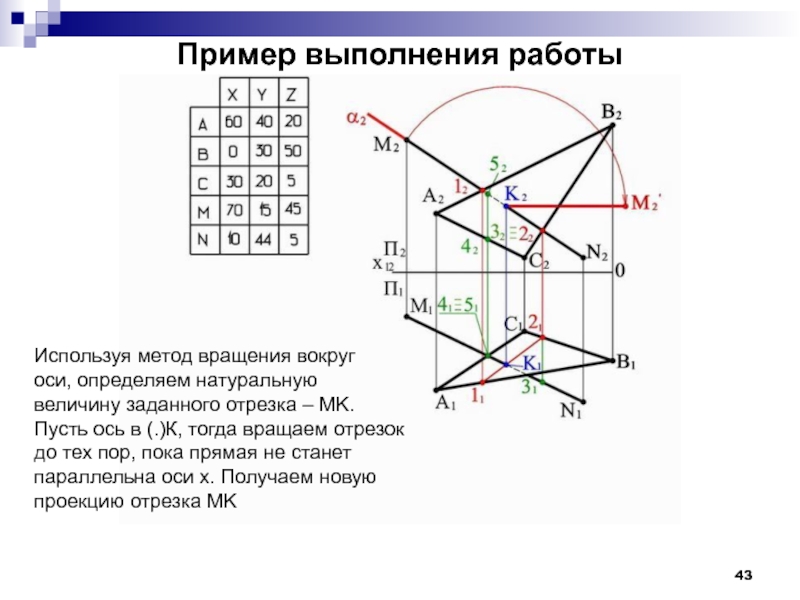
- 43. Пример выполнения работы Используя метод вращения вокруг
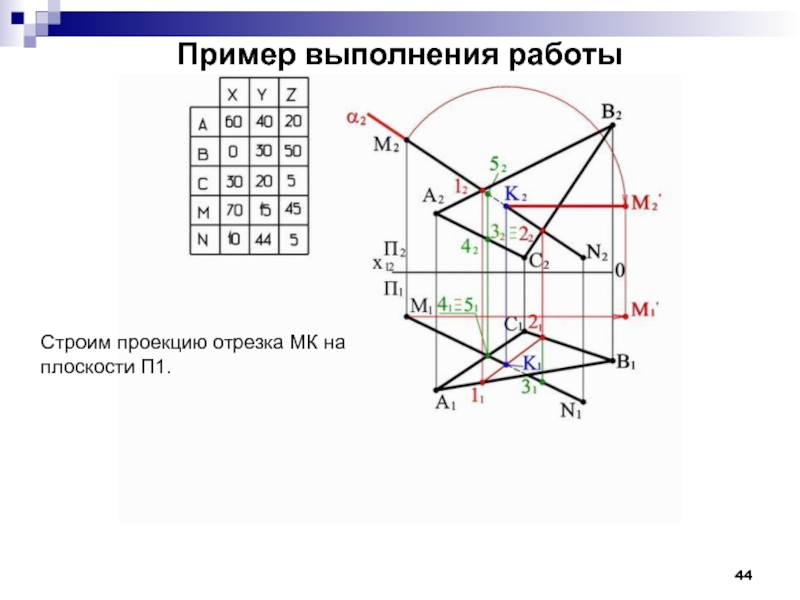
- 44. Пример выполнения работы Строим проекцию отрезка МК на плоскости П1.
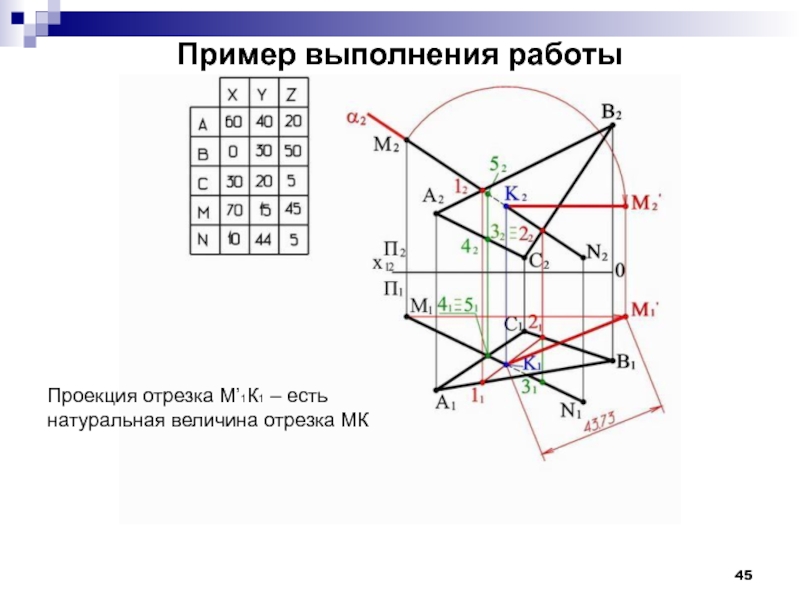
- 45. Пример выполнения работы Проекция отрезка М’1К1 – есть натуральная величина отрезка МК
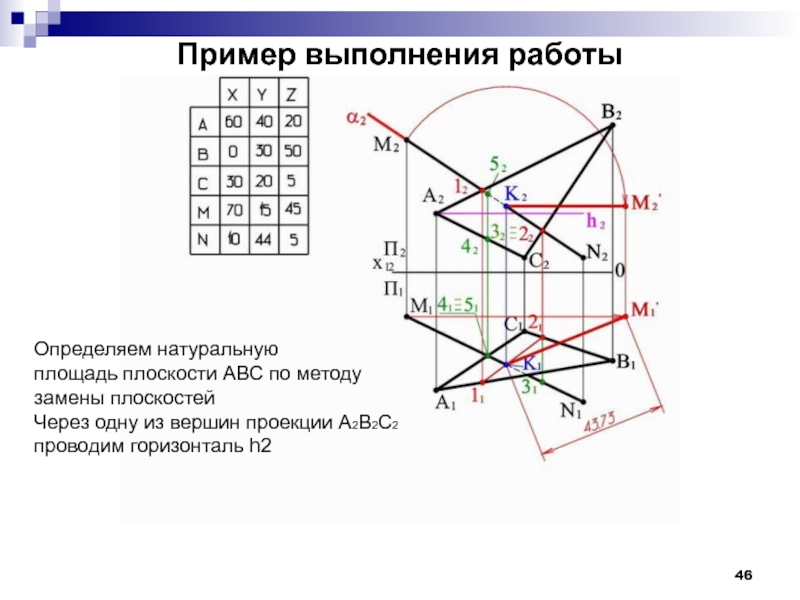
- 46. Пример выполнения работы Определяем натуральную площадь
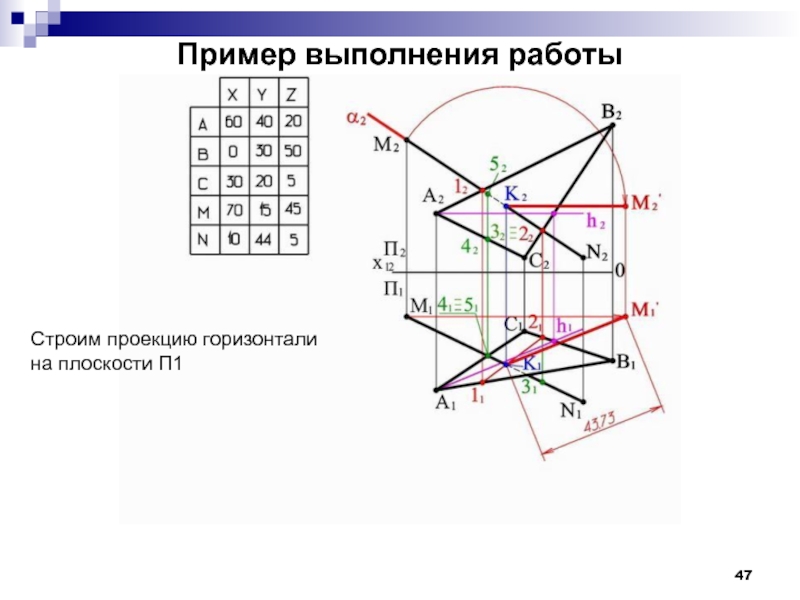
- 47. Пример выполнения работы Строим проекцию горизонтали на плоскости П1
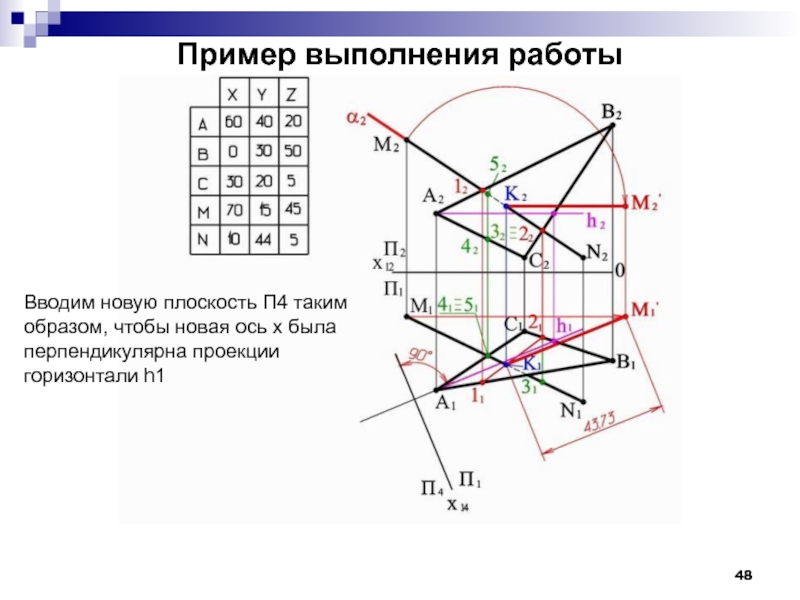
- 48. Пример выполнения работы Вводим новую плоскость П4
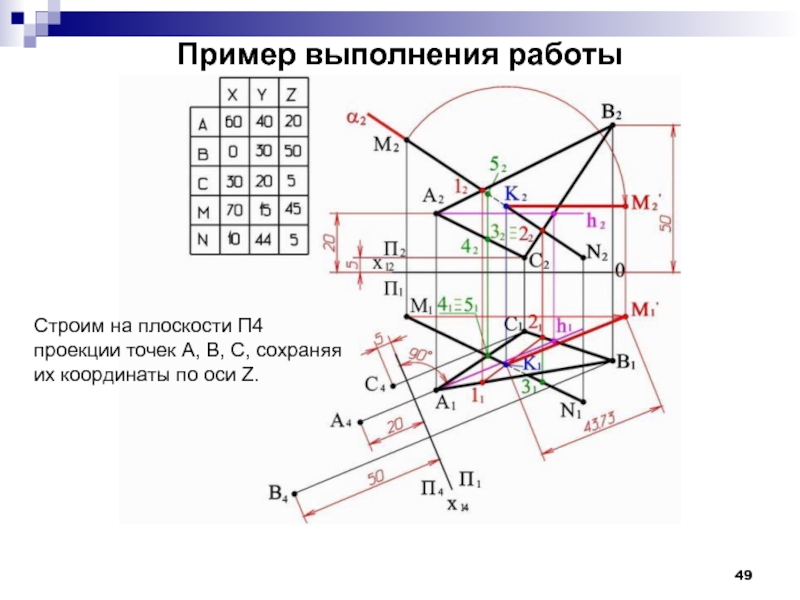
- 49. Пример выполнения работы Строим на плоскости П4
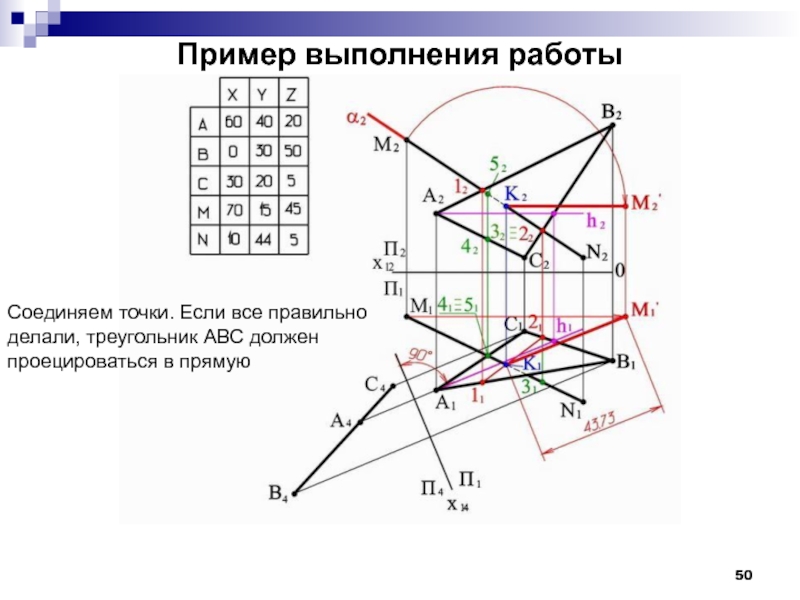
- 50. Пример выполнения работы Соединяем точки. Если все
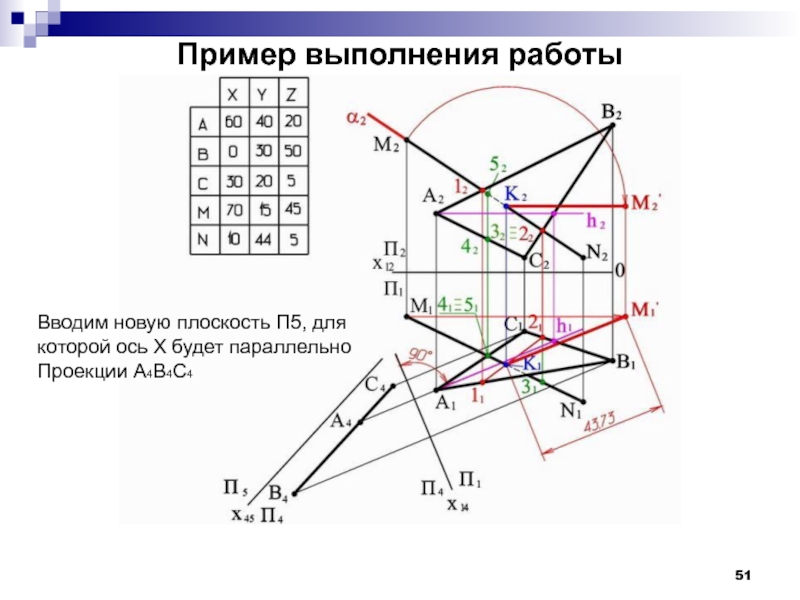
- 51. Пример выполнения работы Вводим новую плоскость П5,
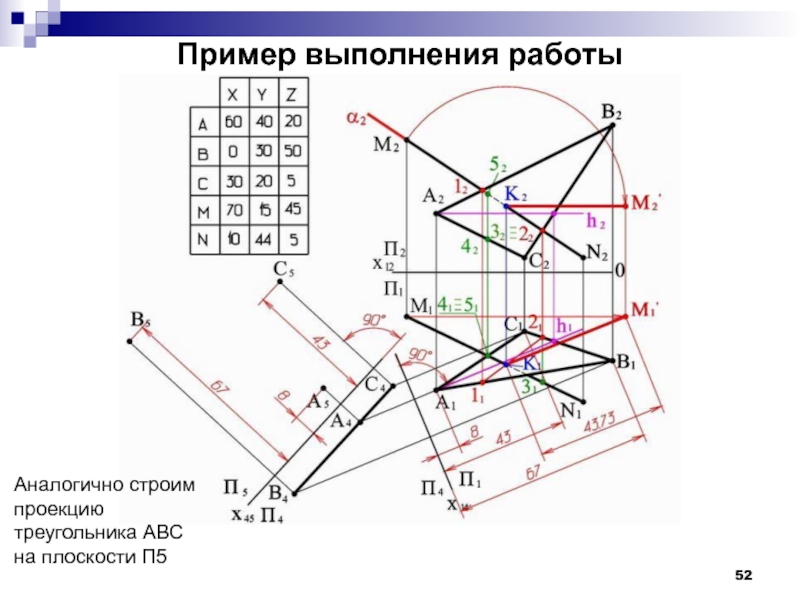
- 52. Пример выполнения работы Аналогично строим проекцию треугольника АВС на плоскости П5
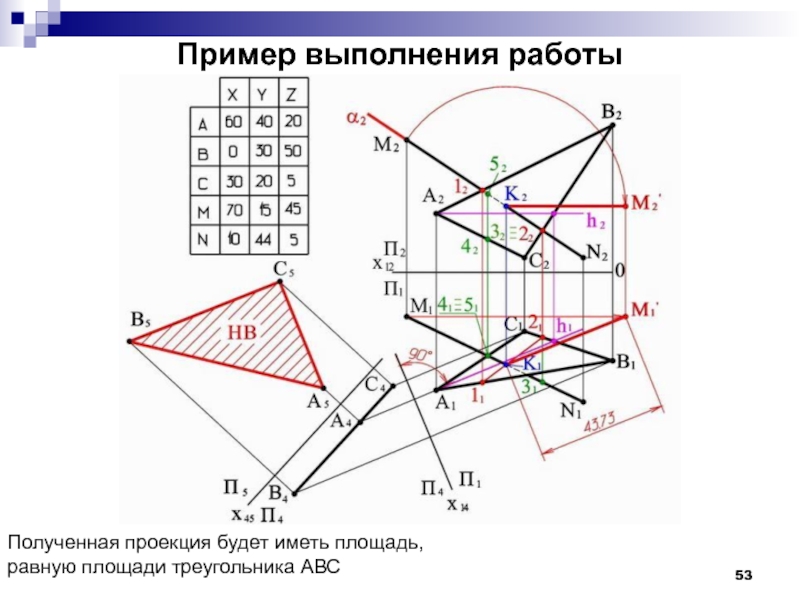
- 53. Пример выполнения работы Полученная проекция будет иметь площадь, равную площади треугольника АВС
Слайд 1САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
ИНФОРМАЦИОННЫХ ТЕХНОЛОГИЙ, МЕХАНИКИ И ОПТИКИ
КАФЕДРА ПРИКЛАДНОЙ И КОМПЬЮТЕРНОЙ ОПТИКИ
Санкт-Петербург,
Слайд 2Проецирование
Проецирование – получение изображения на плоскости с помощью
проецирующих лучей (световых
исходящих из определенной точки пространства (центра
проецирования), проходящих через точки изображаемого
предмета и отображаемых на плоскости в виде точек и
линий
Плоскость, на которую проецируют предмет, называется плоскостью проекций
В зависимости от направления проецирующих лучей по отношению к плоскости проекций выделяют два метода проецирования: центральное и параллельное.
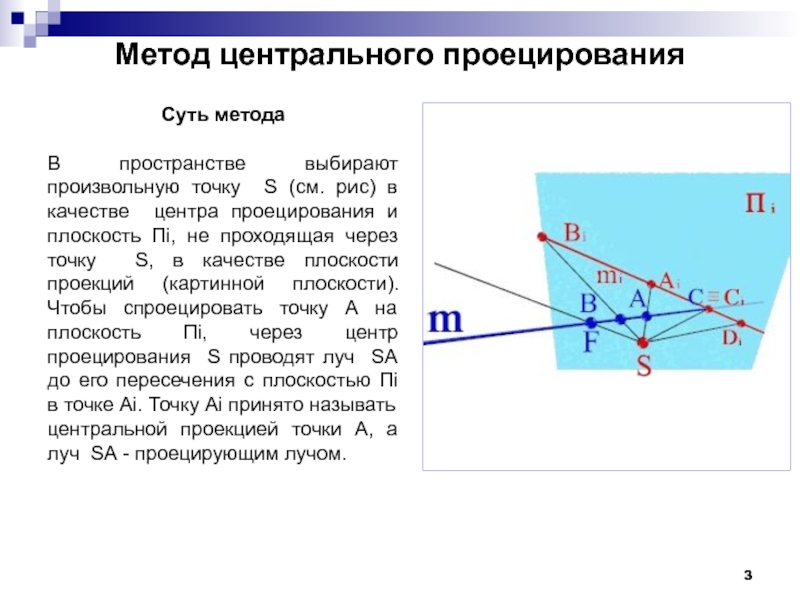
Слайд 3Метод центрального проецирования
Суть метода
В пространстве выбирают произвольную точку S (см. рис)
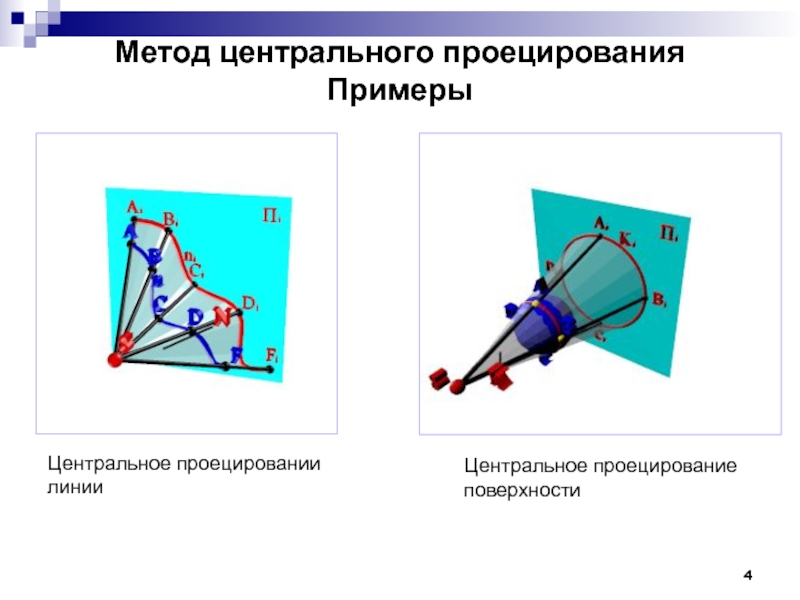
Слайд 4Метод центрального проецирования
Примеры
Центральное проецировании
линии
Центральное проецирование
поверхности
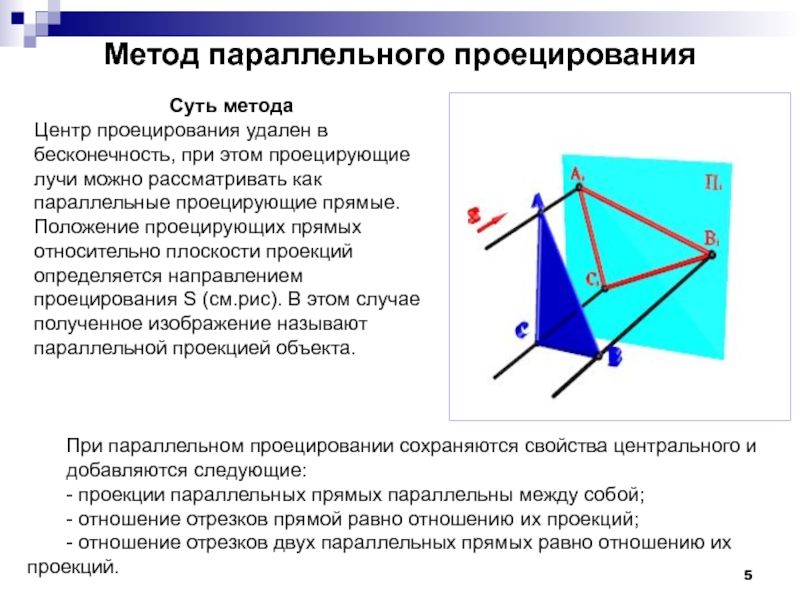
Слайд 5Метод параллельного проецирования
Суть метода
Центр проецирования удален в бесконечность, при этом проецирующие
При параллельном проецировании сохраняются свойства центрального и
добавляются следующие:
- проекции параллельных прямых параллельны между собой;
- отношение отрезков прямой равно отношению их проекций;
- отношение отрезков двух параллельных прямых равно отношению их проекций.
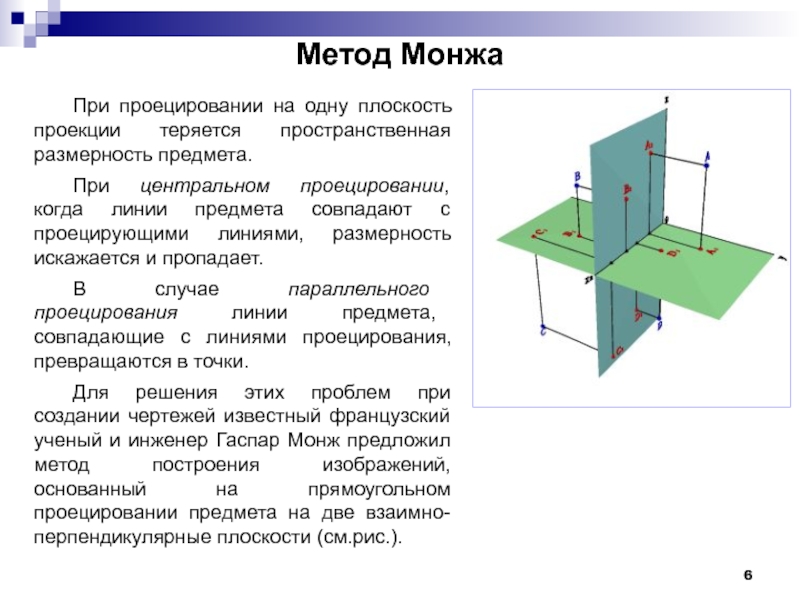
Слайд 6Метод Монжа
При проецировании на одну плоскость проекции теряется пространственная размерность предмета.
При центральном проецировании, когда линии предмета совпадают с проецирующими линиями, размерность искажается и пропадает.
В случае параллельного проецирования линии предмета, совпадающие с линиями проецирования, превращаются в точки.
Для решения этих проблем при создании чертежей известный французский ученый и инженер Гаспар Монж предложил метод построения изображений, основанный на прямоугольном проецировании предмета на две взаимно-перпендикулярные плоскости (см.рис.).
Слайд 7Метод Монжа
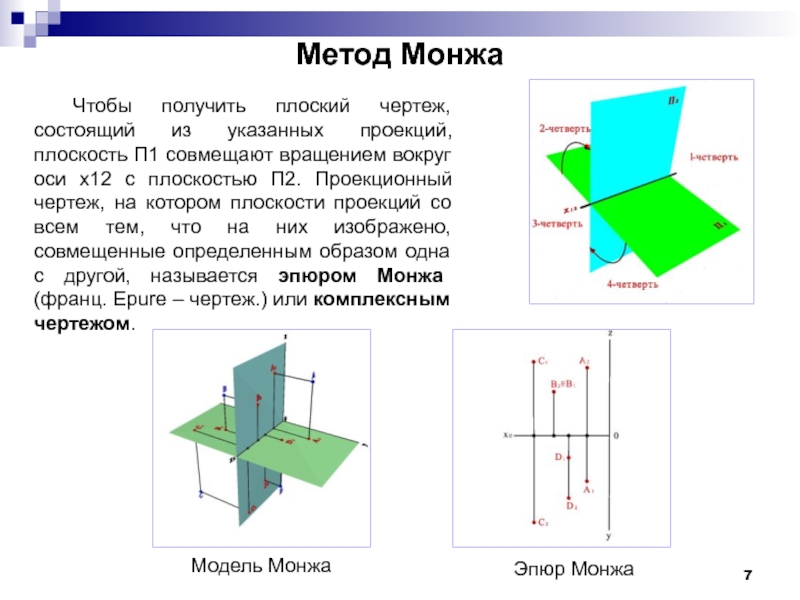
Чтобы получить плоский чертеж, состоящий из указанных проекций, плоскость П1
Эпюр Монжа
Модель Монжа
Слайд 8Геометрические элементы предмета
точка — бесконечно малая величина, не имеющая размера и
линия, состоящая из последовательности бесчисленного множества точек, не имеющих размера и подчиняющихся определенному закону распространения в пространстве;
поверхность, частным случаем которой является плоскость, состоящая из совокупности множества точек, размещенных в пространстве по определенному закону распределения и не имеющая толщины.
Слайд 9Точка в ортогональной системе двух плоскостей проекций
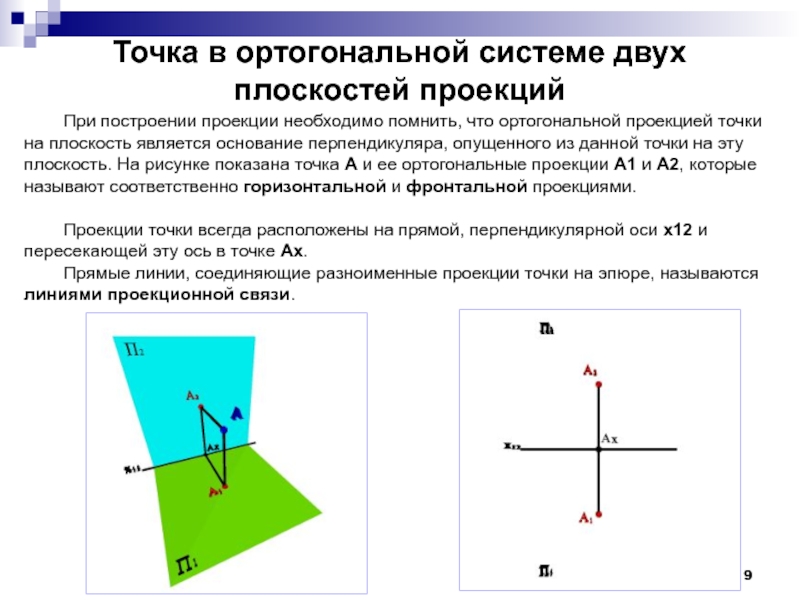
При построении проекции необходимо помнить,
Проекции точки всегда расположены на прямой, перпендикулярной оси x12 и пересекающей эту ось в точке Аx.
Прямые линии, соединяющие разноименные проекции точки на эпюре, называются линиями проекционной связи.
Слайд 10Точка в ортогональной системе трех плоскостей проекций
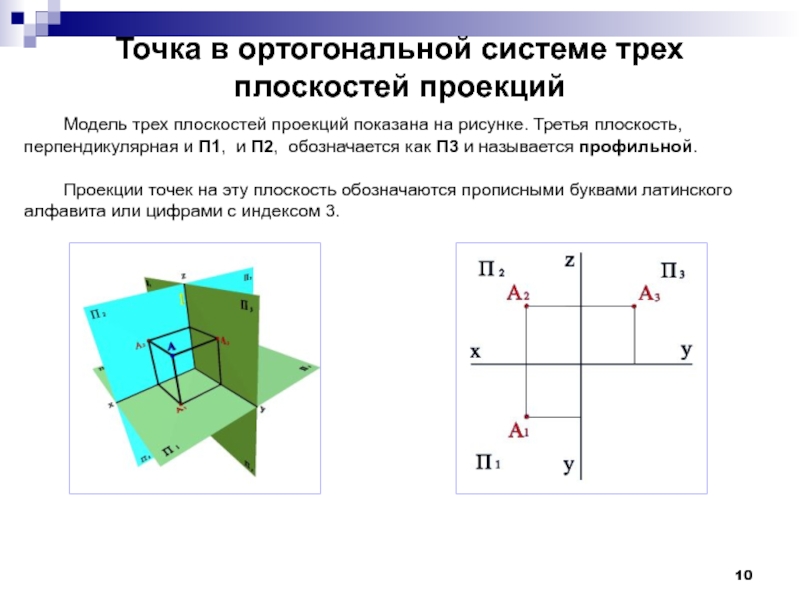
Модель трех плоскостей проекций показана
Проекции точек на эту плоскость обозначаются прописными буквами латинского алфавита или цифрами с индексом 3.
Слайд 11Взаимное расположение точек
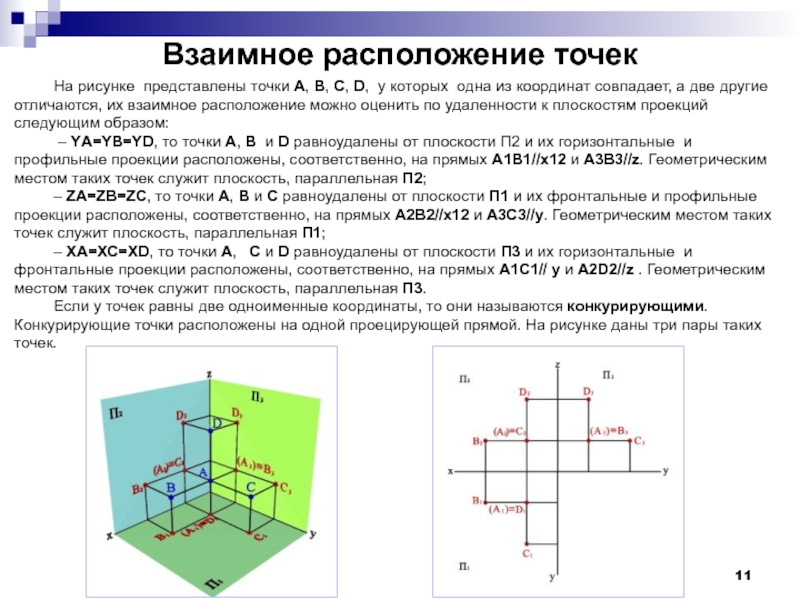
На рисунке представлены точки А, В, С, D, у
– YА=YВ=YD, то точки А, В и D равноудалены от плоскости П2 и их горизонтальные и профильные проекции расположены, соответственно, на прямых А1В1//x12 и А3В3//z. Геометрическим местом таких точек служит плоскость, параллельная П2;
– ZА=ZВ=ZС, то точки А, В и С равноудалены от плоскости П1 и их фронтальные и профильные проекции расположены, соответственно, на прямых А2В2//x12 и А3С3//y. Геометрическим местом таких точек служит плоскость, параллельная П1;
– XА=XC=XD, то точки А, C и D равноудалены от плоскости П3 и их горизонтальные и фронтальные проекции расположены, соответственно, на прямых А1C1// y и А2D2//z . Геометрическим местом таких точек служит плоскость, параллельная П3.
Если у точек равны две одноименные координаты, то они называются конкурирующими. Конкурирующие точки расположены на одной проецирующей прямой. На рисунке даны три пары таких точек.
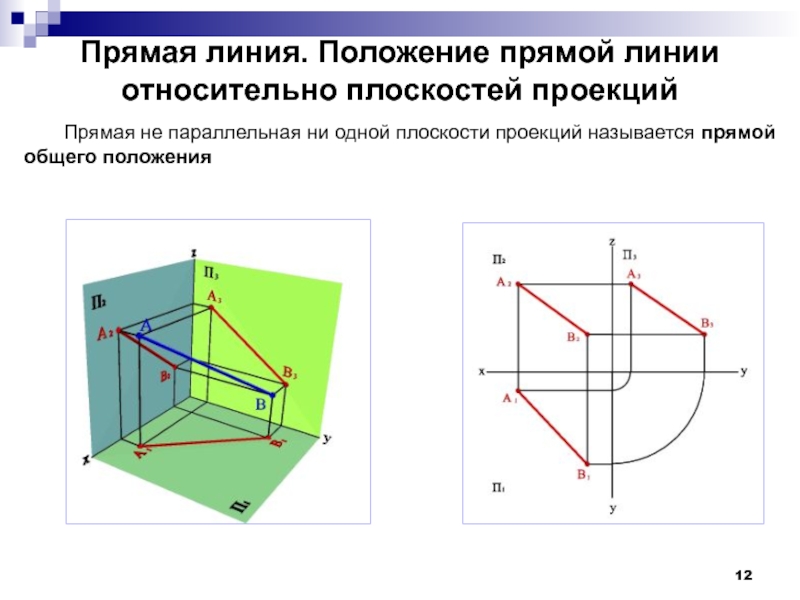
Слайд 12Прямая линия. Положение прямой линии относительно плоскостей проекций
Прямая не параллельная ни
Слайд 13Прямая линия. Положение прямой линии относительно плоскостей проекций
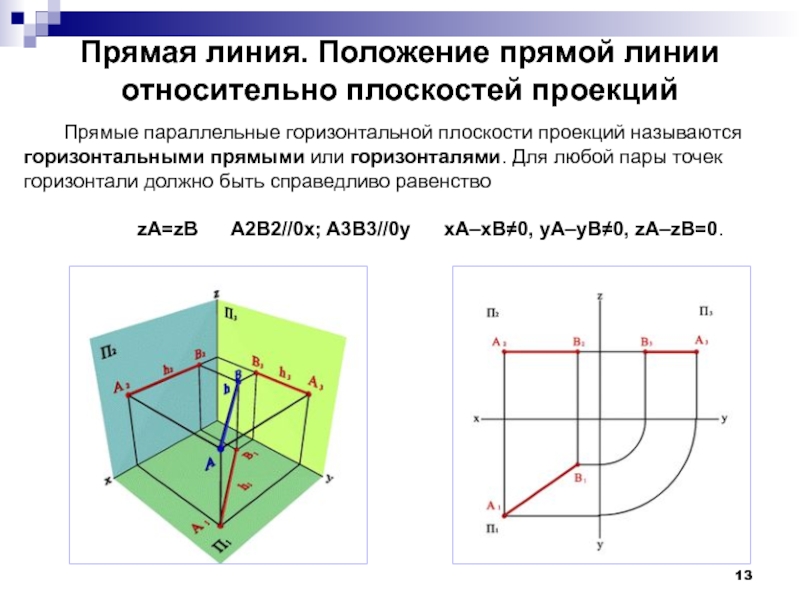
Прямые параллельные горизонтальной плоскости
zA=zB A2B2//0x; A3B3//0y xA–xB≠0, yA–yB≠0, zA–zB=0.
Слайд 14Прямая линия. Положение прямой линии относительно плоскостей проекций
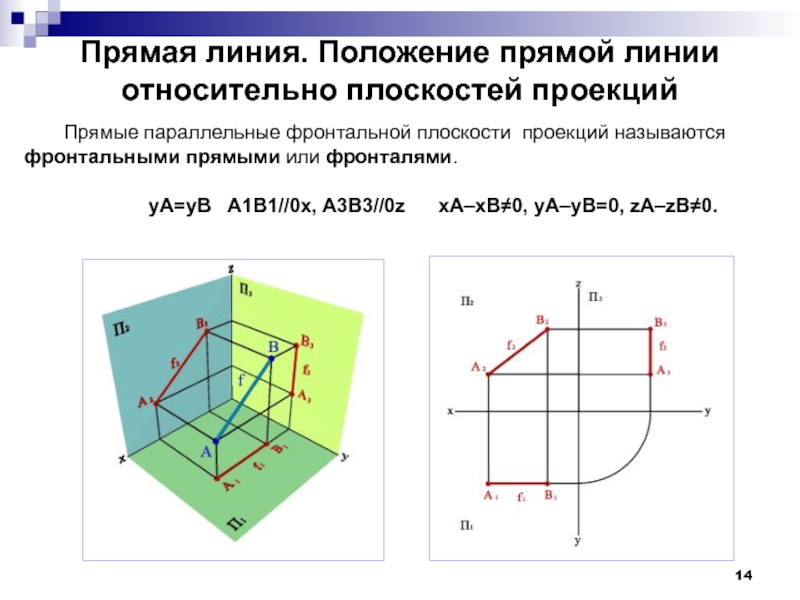
Прямые параллельные фронтальной плоскости
yA=yB A1B1//0x, A3B3//0z xA–xB≠0, yA–yB=0, zA–zB≠0.
Слайд 15Прямая линия. Положение прямой линии относительно плоскостей проекций
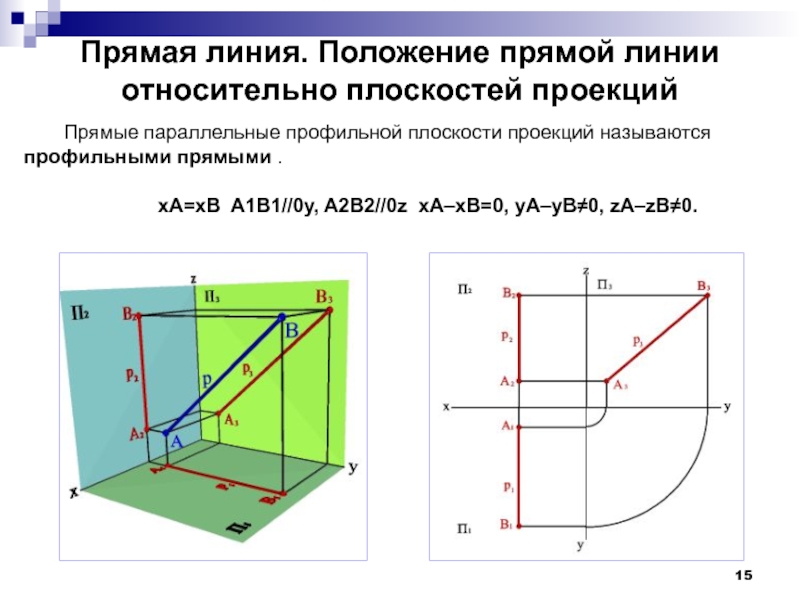
Прямые параллельные профильной плоскости
xA=xB A1B1//0y, A2B2//0z xA–xB=0, yA–yB≠0, zA–zB≠0.
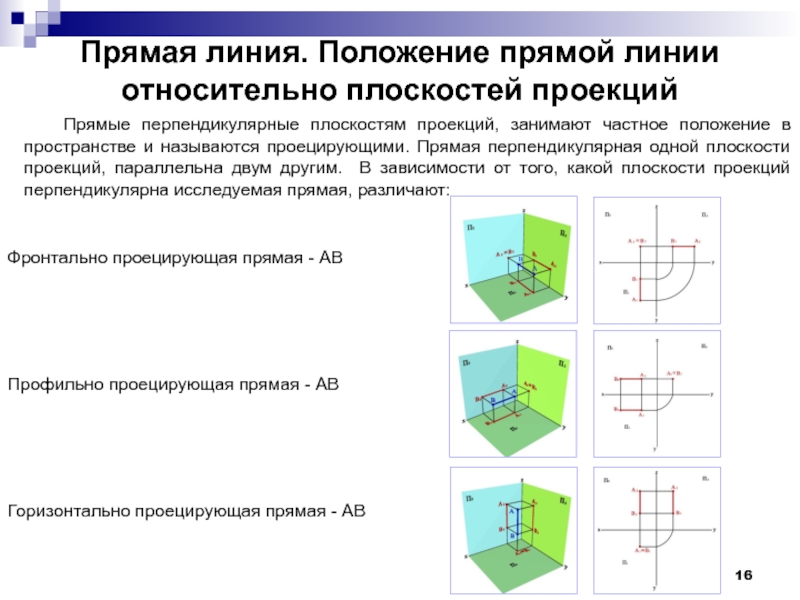
Слайд 16Прямая линия. Положение прямой линии относительно плоскостей проекций
Прямые перпендикулярные плоскостям проекций,
Фронтально проецирующая прямая - АВ
Профильно проецирующая прямая - АВ
Горизонтально проецирующая прямая - АВ
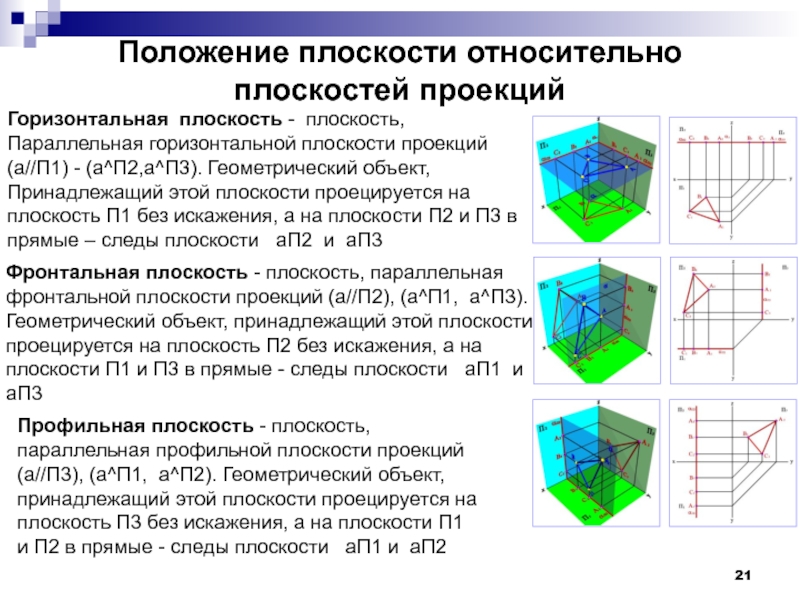
Слайд 21Положение плоскости относительно плоскостей проекций
Профильная плоскость - плоскость,
параллельная профильной плоскости
(a//П3), (a^П1, a^П2). Геометрический объект,
принадлежащий этой плоскости проецируется на
плоскость П3 без искажения, а на плоскости П1
и П2 в прямые - следы плоскости aП1 и aП2
Горизонтальная плоскость - плоскость,
Параллельная горизонтальной плоскости проекций
(a//П1) - (a^П2,a^П3). Геометрический объект,
Принадлежащий этой плоскости проецируется на
плоскость П1 без искажения, а на плоскости П2 и П3 в
прямые – следы плоскости aП2 и aП3
Фронтальная плоскость - плоскость, параллельная
фронтальной плоскости проекций (a//П2), (a^П1, a^П3).
Геометрический объект, принадлежащий этой плоскости
проецируется на плоскость П2 без искажения, а на
плоскости П1 и П3 в прямые - следы плоскости aП1 и
aП3
Слайд 22Способы преобразования чертежа
Использование частных положений прямых линий и плоских фигур относительно
плоскостей проекций значительно упрощает построение чертежа и позволяет
отобразить натуральные размеры прямых линий, плоских фигур, расположенных
на одной плоскости проекций, и расстояний между ними. Для такого
преобразования чертежа используют:
1). Введение дополнительных плоскостей проекций таким образом, чтобы прямая
линия или плоская фигура, не изменяя своего положения в пространстве,
оказалась в каком-либо частном положении в новой системе плоскостей
проекций — способ перемены плоскостей проекций;
2). Изменение положения прямой линии или плоской фигуры посредством
поворота вокруг некоторой оси таким образом, чтобы прямая или плоская фигура
оказалась в частном положении относительно неизменной системы плоскостей
проекций — способ вращения.
Преобразование чертежа (для достижения необходимого результата) при
определении натуральных размеров отрезков и углов может осуществляться
многократно одним или разными способами.
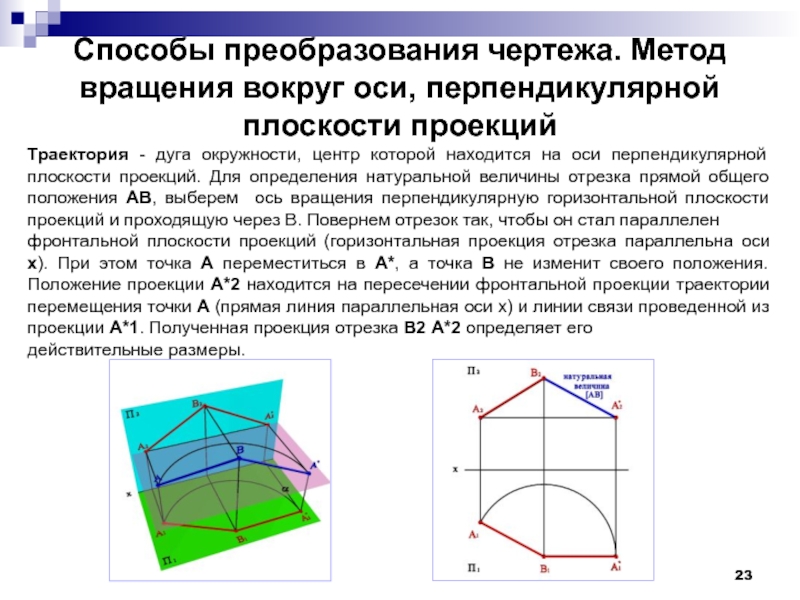
Слайд 23Способы преобразования чертежа. Метод вращения вокруг оси, перпендикулярной плоскости проекций
Траектория -
фронтальной плоскости проекций (горизонтальная проекция отрезка параллельна оси x). При этом точка А переместиться в А*, а точка В не изменит своего положения. Положение проекции А*2 находится на пересечении фронтальной проекции траектории перемещения точки А (прямая линия параллельная оси x) и линии связи проведенной из проекции А*1. Полученная проекция отрезка В2 А*2 определяет его
действительные размеры.
Слайд 24Способы преобразования чертежа. Метод замены плоскостей проекций
Изменение взаимного положения изучаемого объекта
Для решения некоторых задач может потребоваться двойная замены плоскостей проекций. Последовательный переход от одной системы плоскостей проекций к другой необходимо осуществлять, выполняя следующее правило: расстояние от новой проекции точки до новой оси должно равняться расстоянию от заменяемой проекции точки до заменяемой оси.
Выберем новую плоскость проекций П4, параллельно отрезку АВ и перпендикулярно плоскости П1. Введением новой плоскости, переходим из системы плоскостей П1П2 в систему П1П4 , причем в новой системе плоскостей проекция отрезка А4 В4 будет натуральной величиной отрезка АВ.
Слайд 25Дополнительная информация
Более подробно ознакомиться с материалом можно:
В.М. Дягтерев, В.П. Затыльникова. Инженерная
Главы 1-4 (стр. 3-36)
2. Мультимедийный учебник по начертательной геометрии
Слайд 26Задание
По координатам пяти точек необходимо построить комплексный чертеж треугольника АВС и
Слайд 29Пример выполнения работы
Строим точку А, откладывая
соответствующие координаты
по оси Х, Y, Z.
вниз по вертикали, ось Z – вверх.
Слайд 33Пример выполнения работы
Соединяем точки таким образом,
чтобы получилась плоскость АВС
и
Слайд 37Пример выполнения работы
Строим проекции точек 1 и 2
на плоскости П1.
эти точки отрезок, который будет
совпадать с проекцией прямой a на
плоскости П1.
Определяем точку К – точка
пересечения отрезка 12 и отрезка M1N1.
Слайд 39Пример выполнения работы
Пусть точка 22 совпадает с точкой 32.
(вспоминаем про конкурирующие
Строим проекцию точки 3 на плоскости П1.
Обращаем внимание на то, что если точка
принадлежит прямой, то и проекции этой
точки также принадлежат соответствующим
проекциям прямой
Слайд 43Пример выполнения работы
Используя метод вращения вокруг
оси, определяем натуральную
величину заданного
Пусть ось в (.)К, тогда вращаем отрезок
до тех пор, пока прямая не станет
параллельна оси х. Получаем новую
проекцию отрезка MK
Слайд 46Пример выполнения работы
Определяем натуральную
площадь плоскости АВС по методу
замены плоскостей
Через
проводим горизонталь h2
Слайд 48Пример выполнения работы
Вводим новую плоскость П4 таким
образом, чтобы новая ось
перпендикулярна проекции
горизонтали h1
Слайд 49Пример выполнения работы
Строим на плоскости П4
проекции точек А, В, С,
их координаты по оси Z.
Слайд 50Пример выполнения работы
Соединяем точки. Если все правильно
делали, треугольник АВС должен
проецироваться в прямую
Слайд 51Пример выполнения работы
Вводим новую плоскость П5, для
которой ось Х будет
Проекции А4В4С4