- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Комп’ютерна логіка (частина 1) презентация
Содержание
- 1. Комп’ютерна логіка (частина 1)
- 2. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка
- 3. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка
- 4. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка
- 5. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка
- 6. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка
- 7. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка
- 8. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка
- 9. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка
- 10. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка
- 11. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка
- 12. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка
- 13. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка
- 14. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка
- 15. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка
- 16. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка
- 17. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Робочий журнал
- 18. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка
- 19. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Віртуальне Навчальне Середовище - ВНС
- 20. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Тема у ВНС
- 21. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Білет семестрової контрольної роботи
- 22. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка
- 23. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка
- 24. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка
- 25. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка
- 26. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка
- 27. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка
- 28. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка
- 29. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка
- 30. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка
- 31. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка
- 32. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка
- 33. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка
- 34. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка
- 35. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Застосування придбаних навичок в проектуванні.
- 36. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Вбудовані ЕОМ
- 37. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка
- 38. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Комірки
- 39. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка
- 40. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка
- 41. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка
- 42. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка
- 43. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка
- 44. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка
- 45. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка
- 46. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка
- 47. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Комп’ютерна логіка і „Комп’ютерна інженерія”
- 48. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка
- 49. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка
- 50. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка
- 51. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Таблиця множення
- 52. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка
- 53. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка
- 54. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Математичні основи – математичні константи
- 55. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка
- 56. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Системи числення
- 57. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Позиційні системи числення
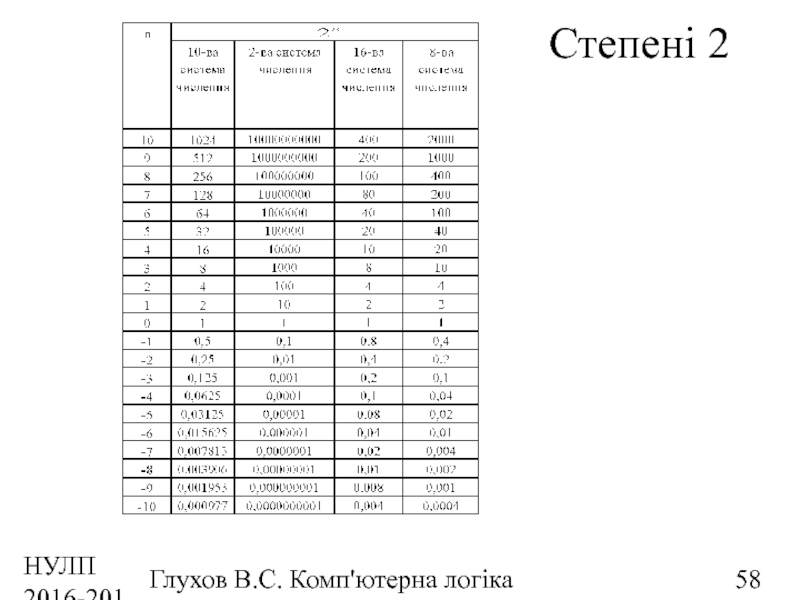
- 58. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Степені 2
- 59. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка
- 60. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Основи електроніки Транзистори – біполярні та польові
- 61. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка
- 62. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка
- 63. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Матерія
- 64. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка
- 65. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка
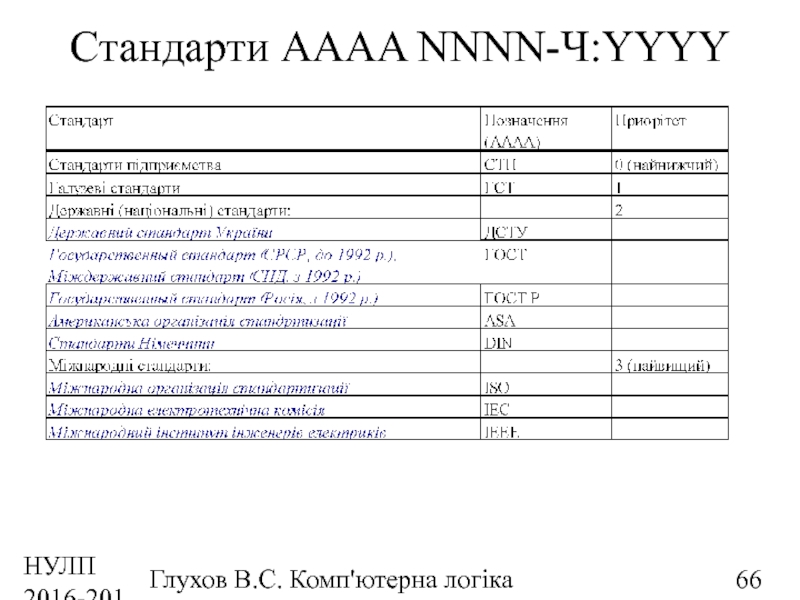
- 66. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Стандарти AAAA NNNN-Ч:YYYY
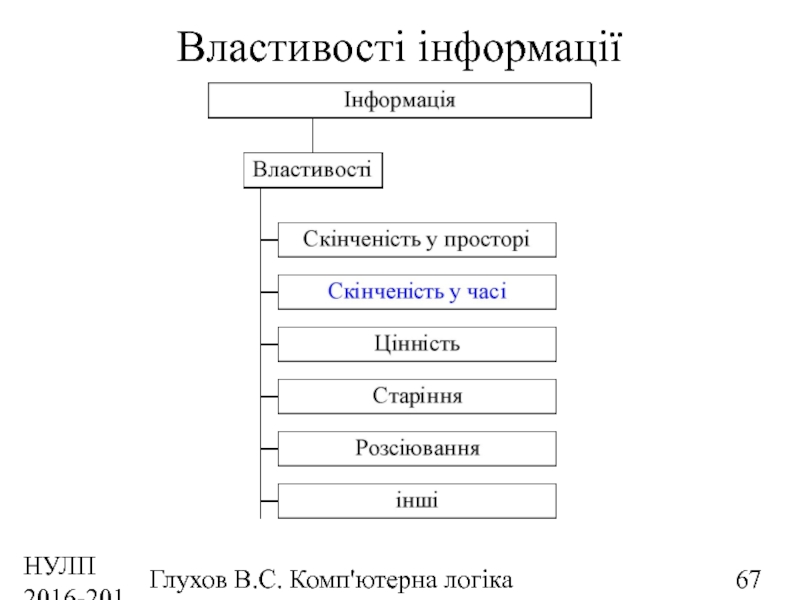
- 67. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Властивості інформації
- 68. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка
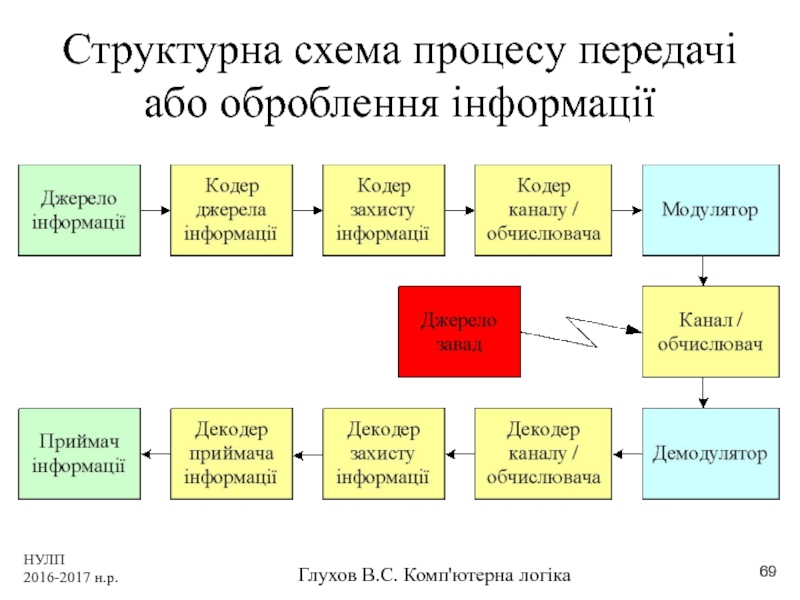
- 69. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Структурна схема процесу передачі або оброблення інформації
- 70. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка
- 71. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Баланс швидкостей
- 72. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка
- 73. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка
- 74. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка
- 75. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка
- 76. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка
- 77. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Порівняння аналогових та цифрових методів обробки інформації
- 78. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка
- 79. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка
- 80. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка
- 81. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка
- 82. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка
- 83. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка
- 84. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка
- 85. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка
- 86. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка
- 87. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Переваги кодування двома символами Просто Надійно
- 88. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка
- 89. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Параметри імпульсу
- 90. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка
- 91. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка
- 92. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Числа з фіксованою комою
- 93. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Порядок байтів
- 94. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Числа з рухомою комою. Стандарт IEEE-754
- 95. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Кодова таблиця КОИ-7
- 96. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Кодова таблиця KOI-8U
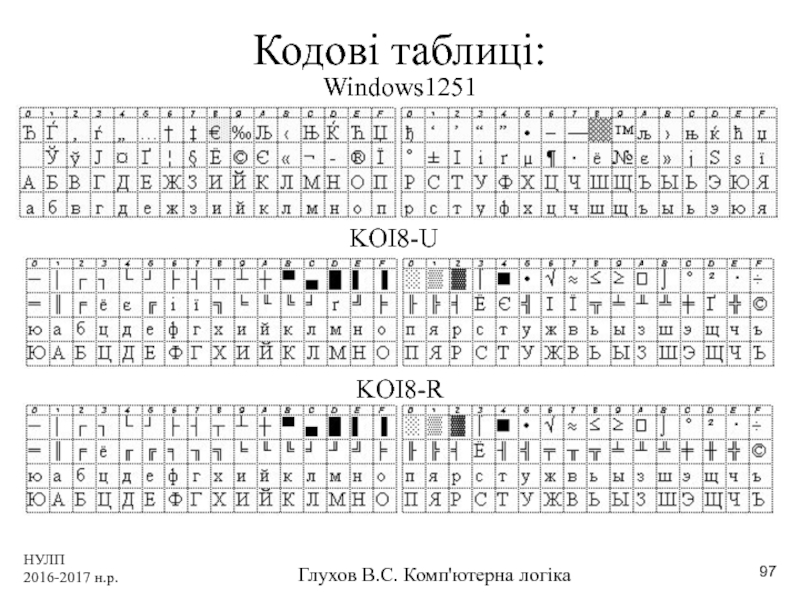
- 97. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Кодові таблиці: Windows1251 KOI8-U KOI8-R
- 98. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Структура кодів UTF-8 (Unicode Transformation Formats )
- 99. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Кодування зображень. Матричні та векторні формати
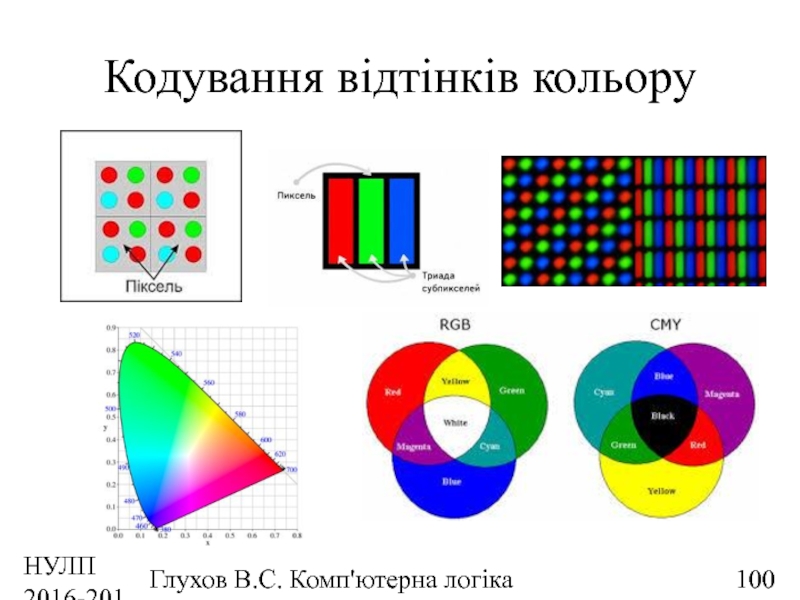
- 100. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Кодування відтінків кольору
- 101. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Кількість кольорів
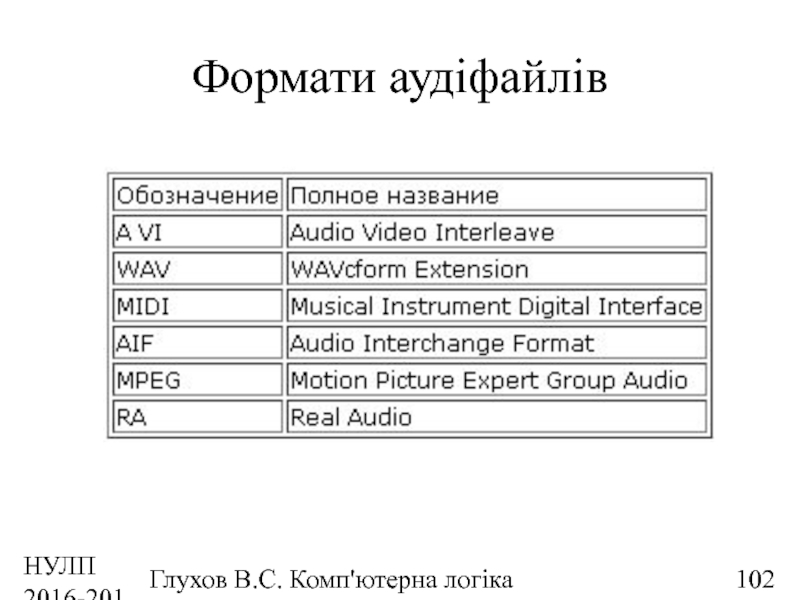
- 102. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Формати аудіфайлів
- 103. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Міри інформації Структурні Семантичні Статистичні Інші
- 104. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка
- 105. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка
- 106. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка
- 107. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка
- 108. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка
- 109. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка
- 110. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка
- 111. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка
- 112. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка
- 113. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка
- 114. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка
- 115. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка
- 116. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка
- 117. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка
- 118. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка
- 119. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка
- 120. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка 3. Статистична міра, Клод Шеннон, 1948, США
- 121. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка
- 122. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка
- 123. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Залежність ентропії двох подій від їх імовірності
- 124. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Кількість отриманої інформації I = Hпочаткове – Hкінцеве
- 125. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка
- 126. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Абетка Морзе
- 127. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Послідовний та паралельний спосіб передачі інформації
- 128. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Способи оброблення даних
- 129. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Послідовний та паралельний способи опрацювання даних
- 130. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Опрацювання даних з використанням зворотних зв’язків
- 131. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Опрацювання даних в ієрархічних структурах
- 132. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка
- 133. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Загальна схема криптографічної системи
- 134. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Перемішування
- 135. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка
- 136. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Контроль на парність / непарність
- 137. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка
- 138. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка
- 139. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Контроль виконання операцій. Числовий контроль за модулем
- 140. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка SerDes
- 141. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Строб (вказівник, спрацьовувати)
- 142. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка
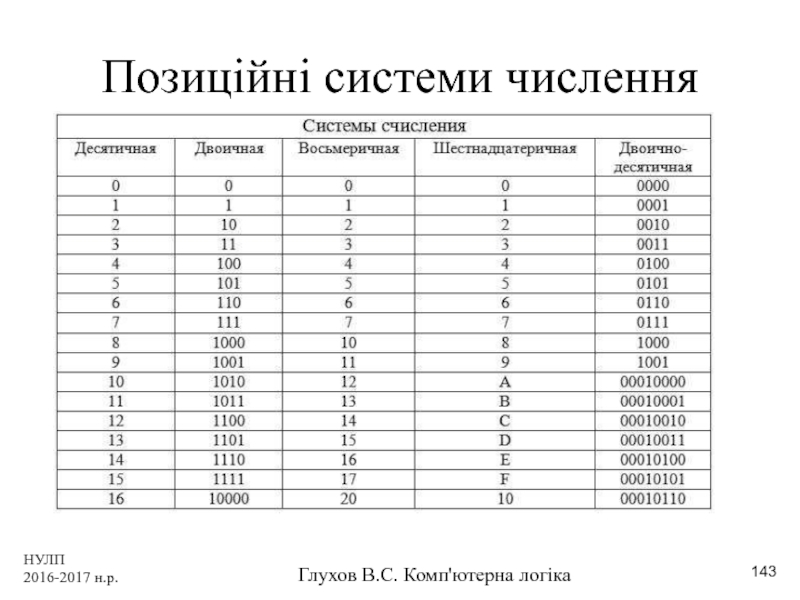
- 143. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Позиційні системи числення
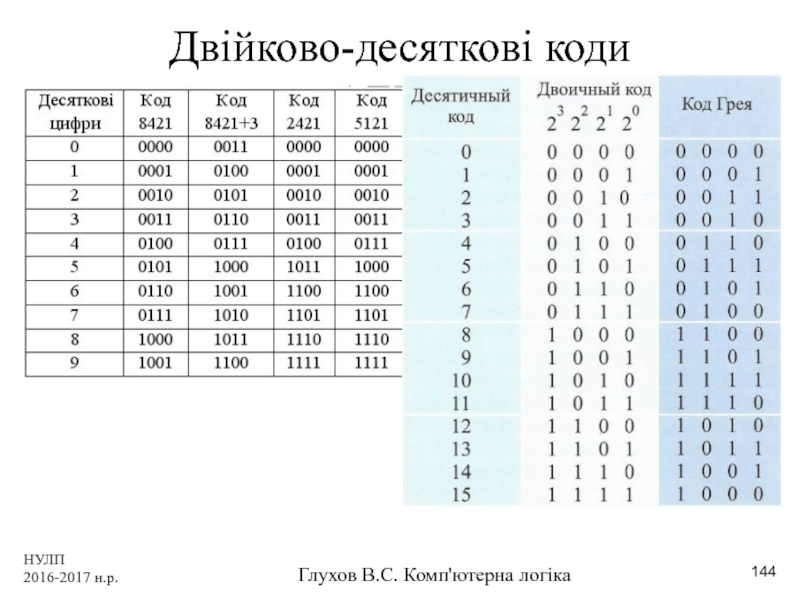
- 144. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Двійково-десяткові коди
- 145. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Двійково-десяткові коди
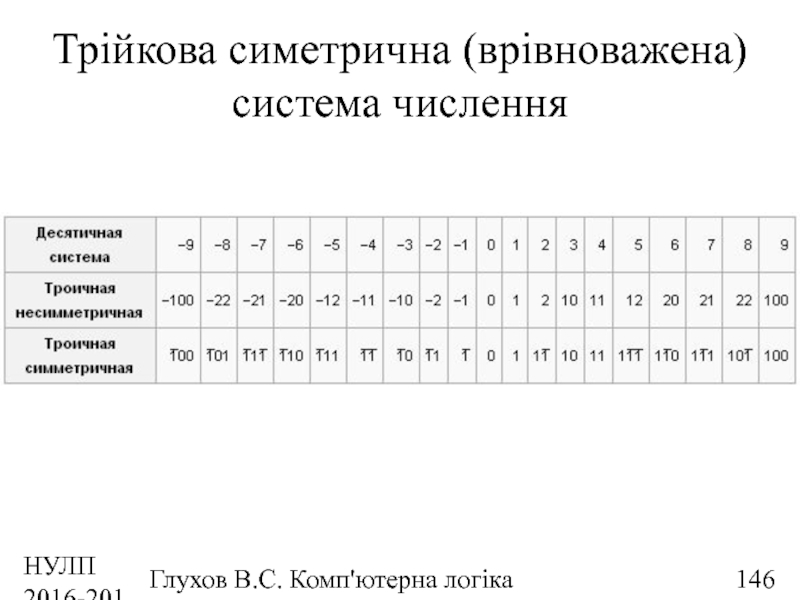
- 146. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Трійкова симетрична (врівноважена) система числення
- 147. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка
- 148. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Система залишкових класів
- 149. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Поля Галуа
- 150. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Сусідній код (код Грея)
- 151. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Сусідні коди
- 152. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Карти Карно
- 153. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Скручування карти Карно по вертикалі
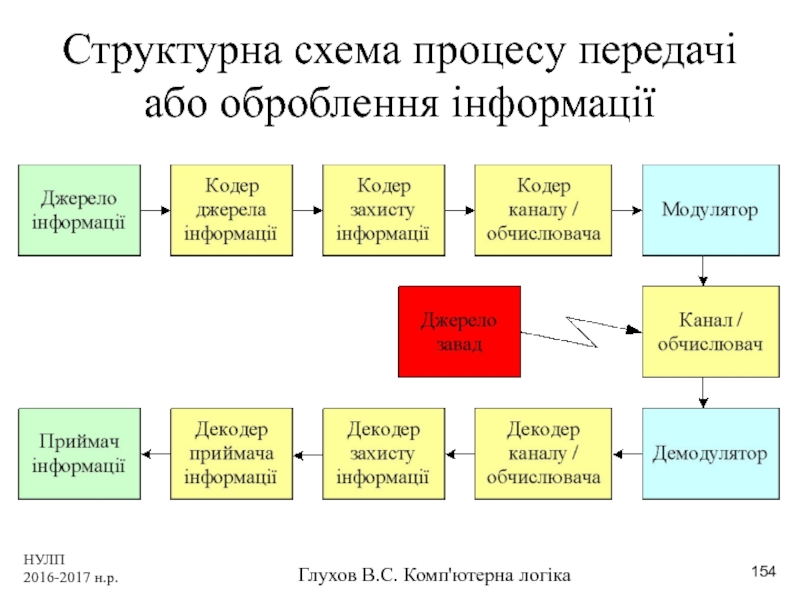
- 154. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Структурна схема процесу передачі або оброблення інформації
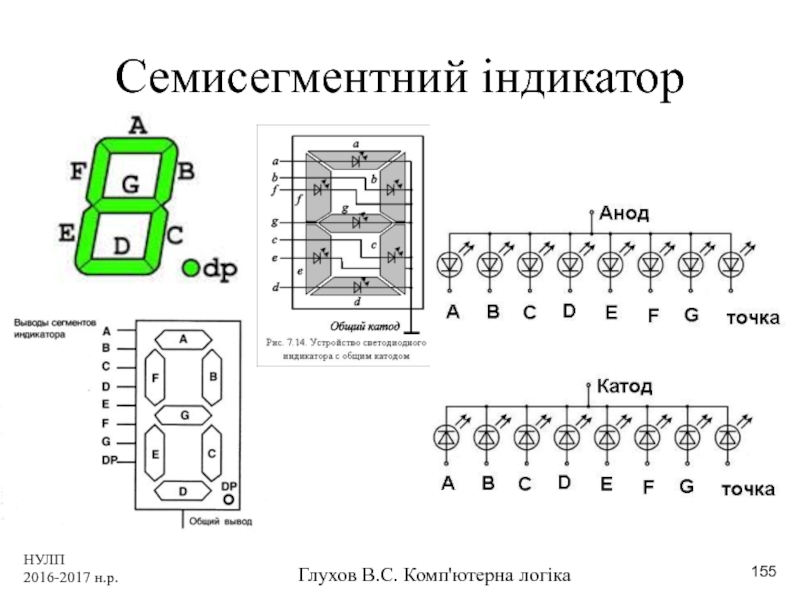
- 155. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Семисегментний індикатор
- 156. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка
- 157. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка
- 158. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка
- 159. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка
- 160. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка
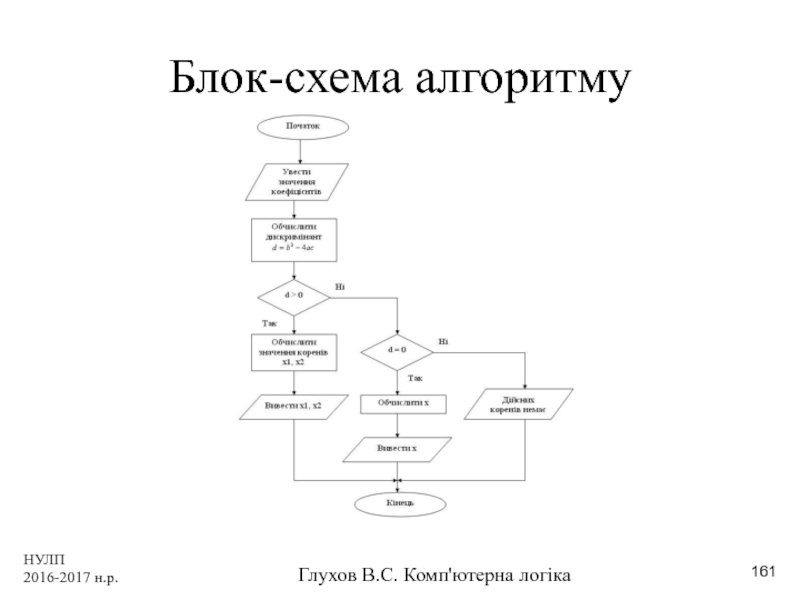
- 161. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Блок-схема алгоритму
- 162. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка
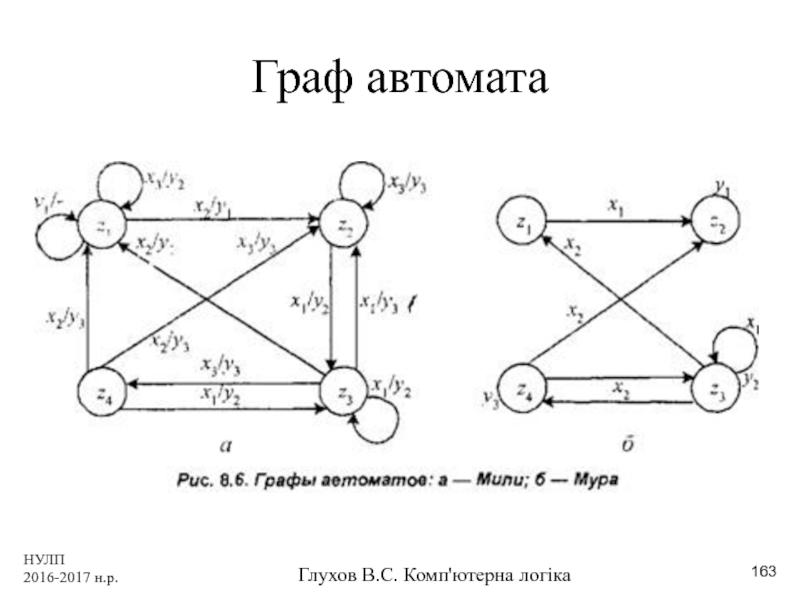
- 163. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Граф автомата
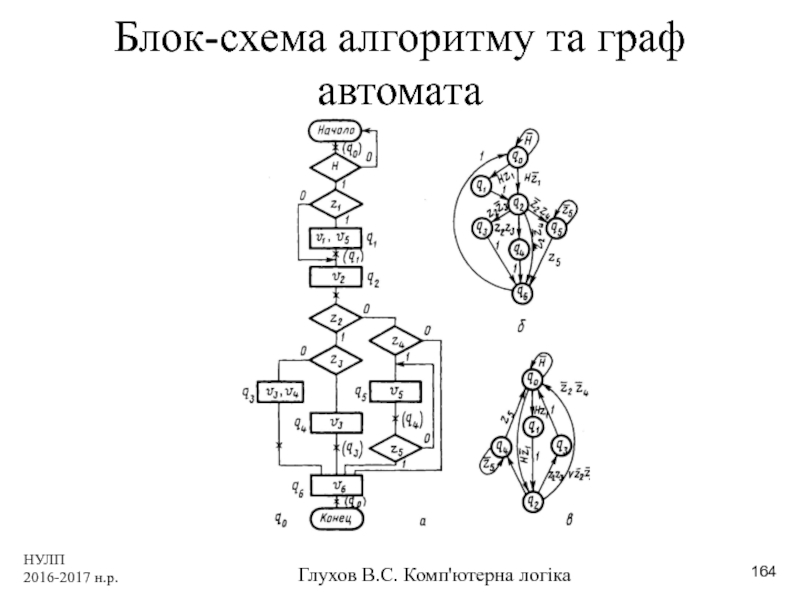
- 164. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Блок-схема алгоритму та граф автомата
- 165. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Таблиці переходів та виходів автомата Мура
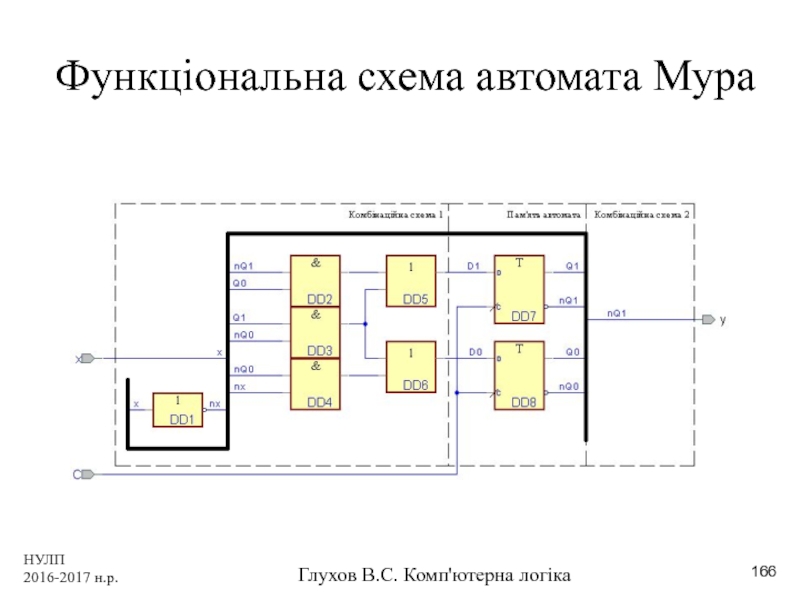
- 166. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Функціональна схема автомата Мура
- 167. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Часова діаграма роботи автомата Мура
- 168. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка
- 169. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка
- 170. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка
- 171. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка
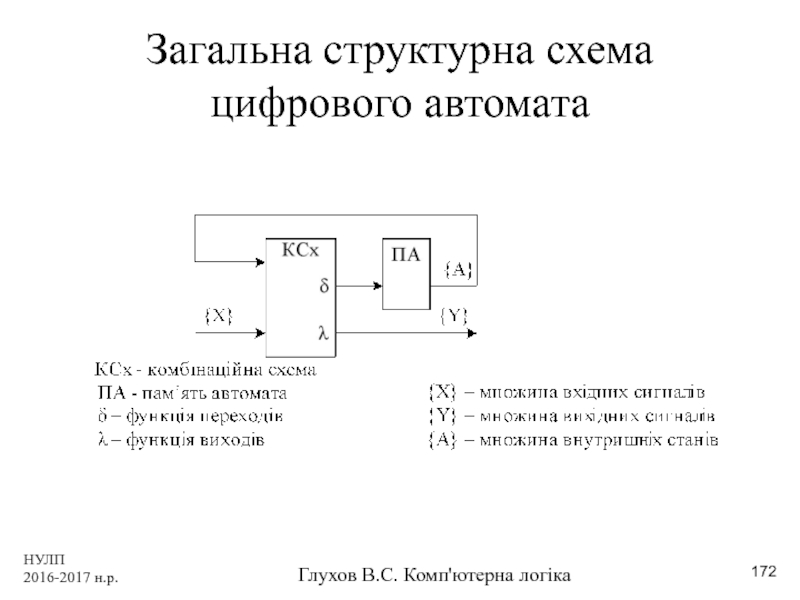
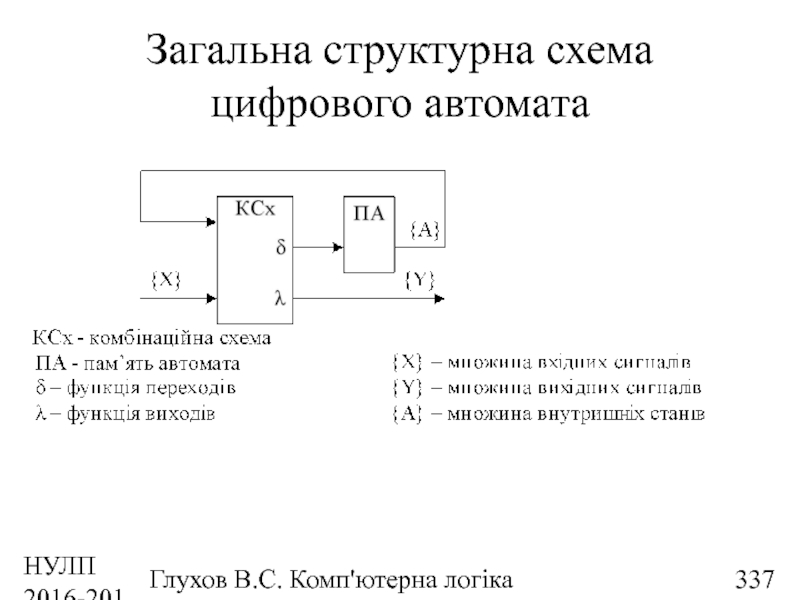
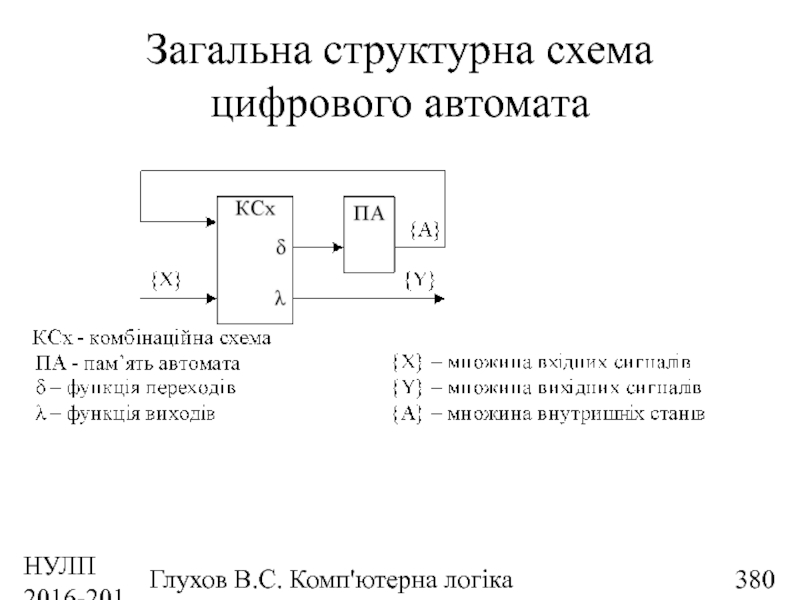
- 172. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Загальна структурна схема цифрового автомата
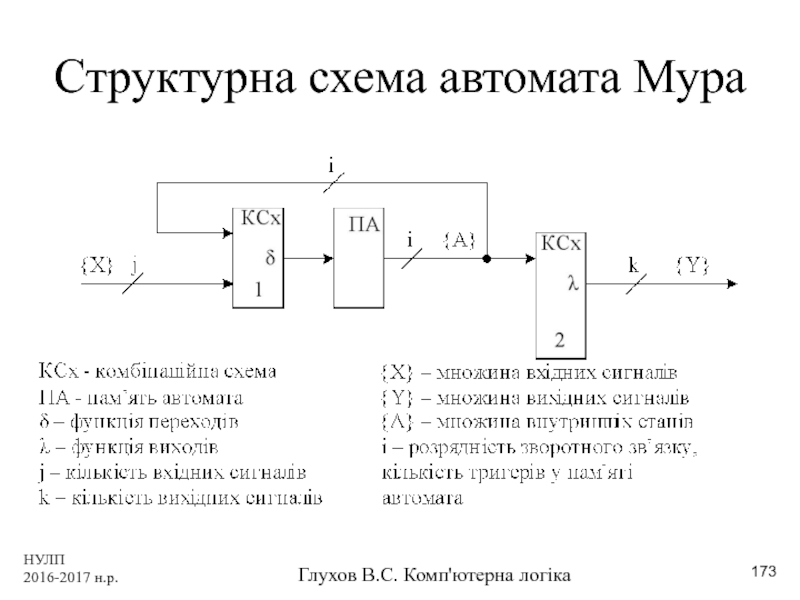
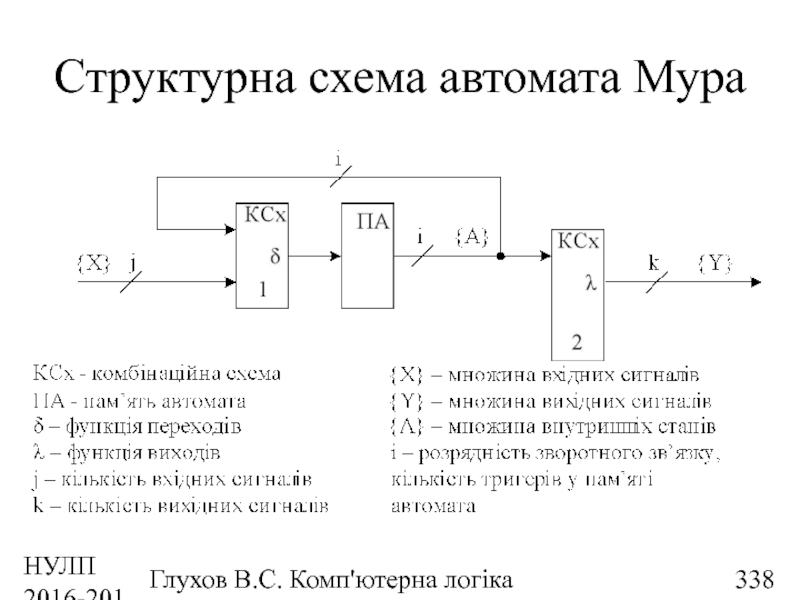
- 173. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Структурна схема автомата Мура
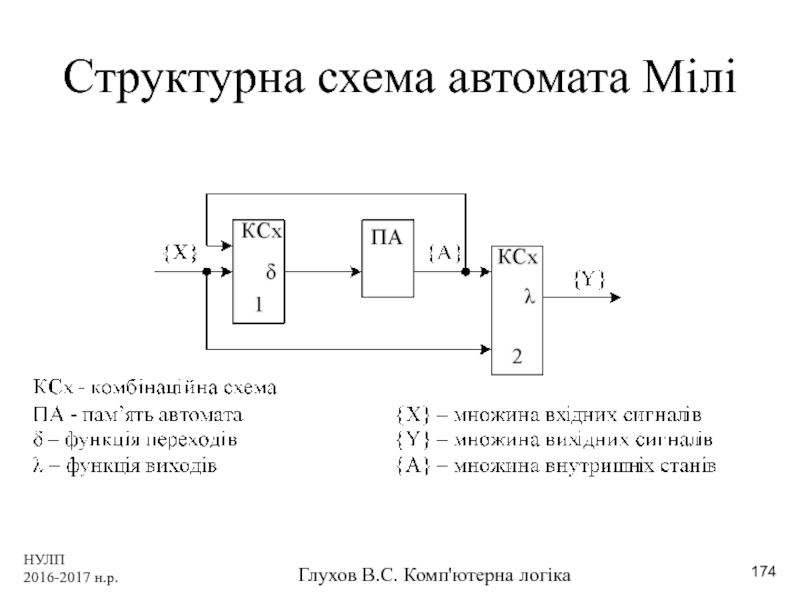
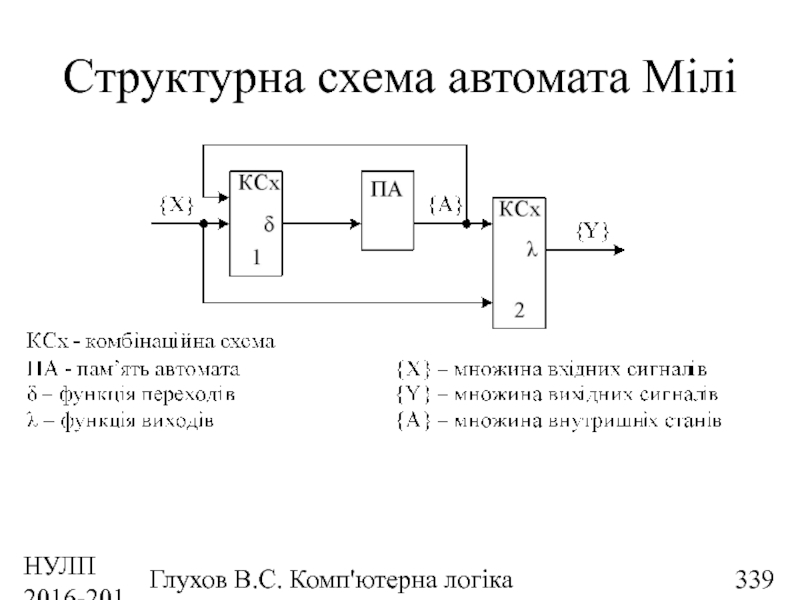
- 174. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Структурна схема автомата Мілі
- 175. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка
- 176. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка
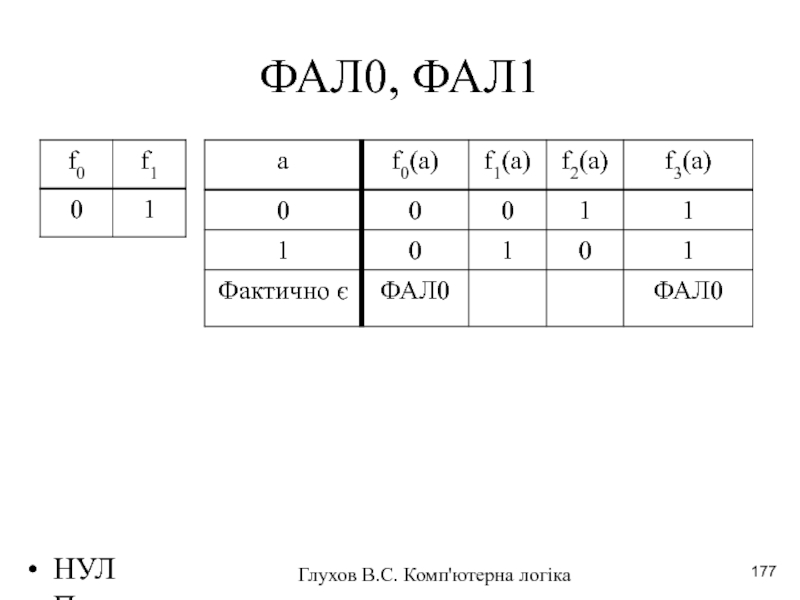
- 177. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка ФАЛ0, ФАЛ1
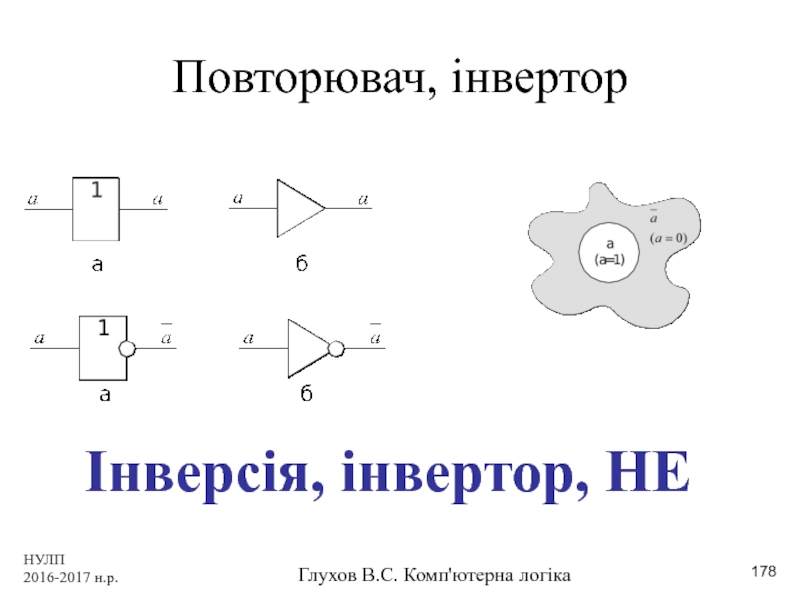
- 178. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Повторювач, інвертор Інверсія, інвертор, НЕ
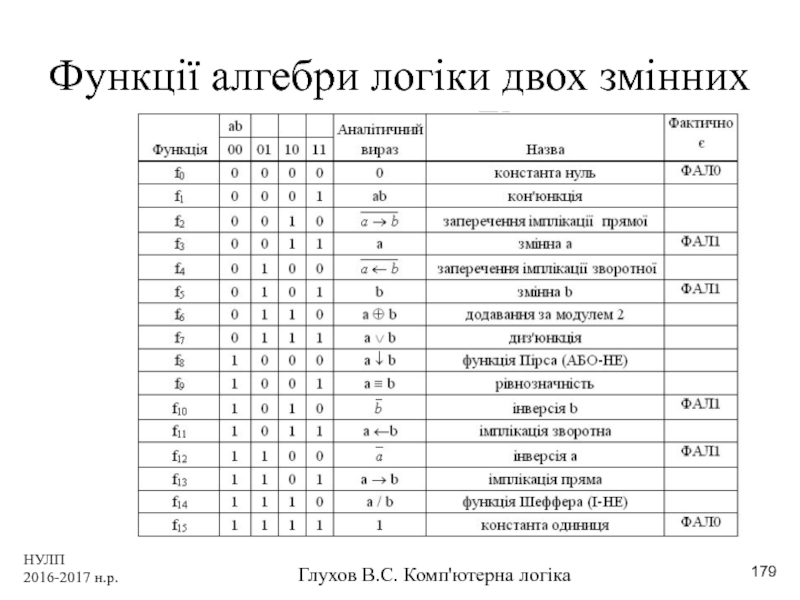
- 179. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Функції алгебри логіки двох змінних
- 180. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка
- 181. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка
- 182. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка
- 183. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка
- 184. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Виключне АБО (XOR)
- 185. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Рівнозначність (еквівалентність)
- 186. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Імплікація (пряма)
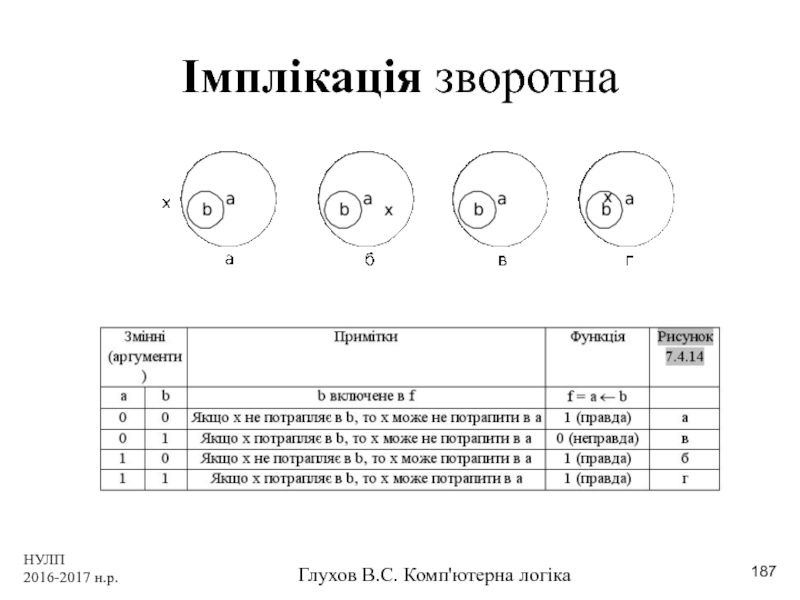
- 187. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Імплікація зворотна
- 188. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Заперечення імплікації (прямої) Заперечення зворотної імплікації
- 189. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка
- 190. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка
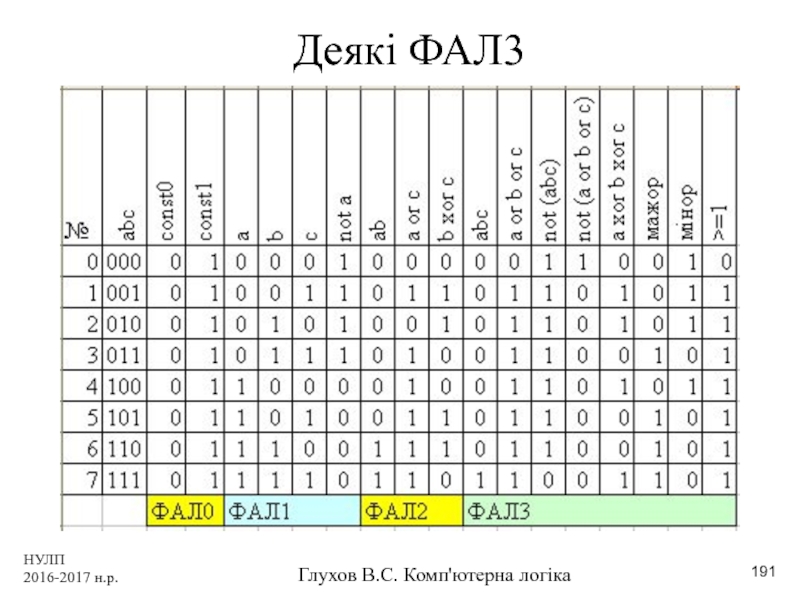
- 191. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Деякі ФАЛ3
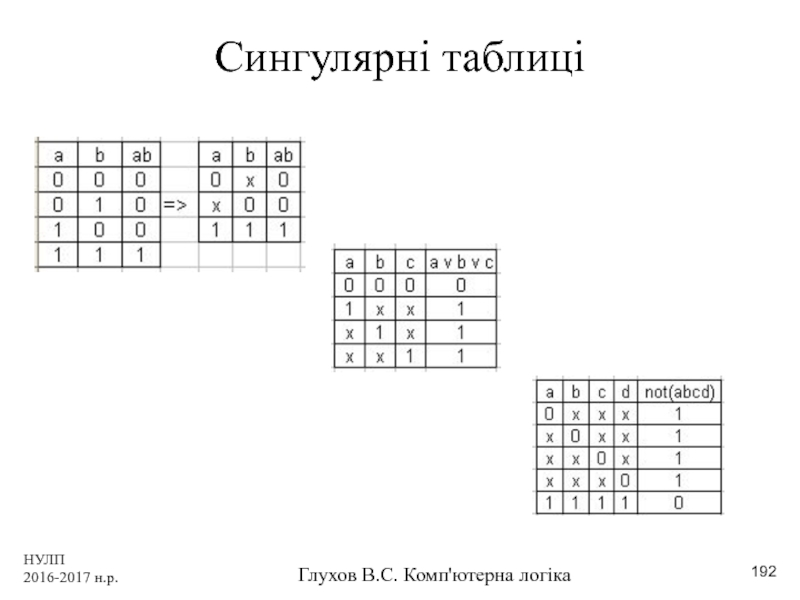
- 192. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Сингулярні таблиці
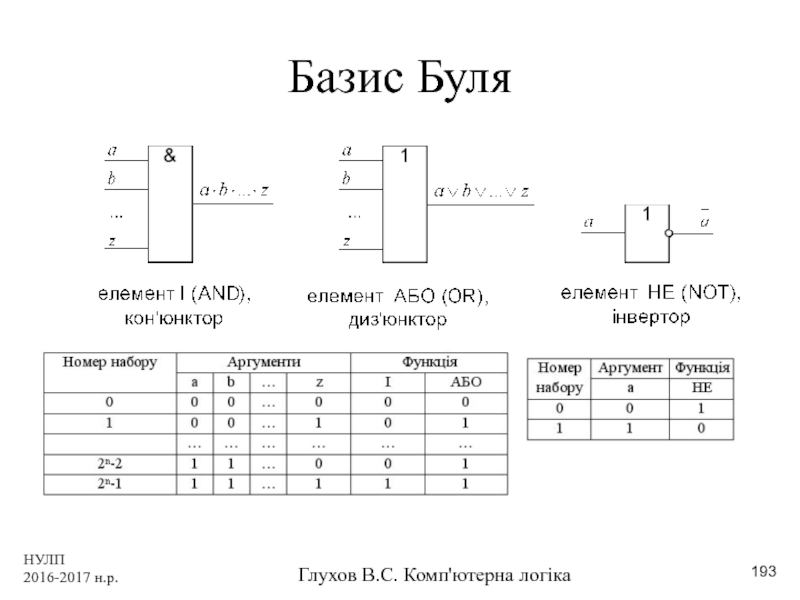
- 193. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Базис Буля
- 194. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка
- 195. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка
- 196. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Повторювач, інвертор Інверсія, інвертор, НЕ
- 197. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка
- 198. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка
- 199. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Використання базису з 2-х ФАЛ: (І, НЕ)
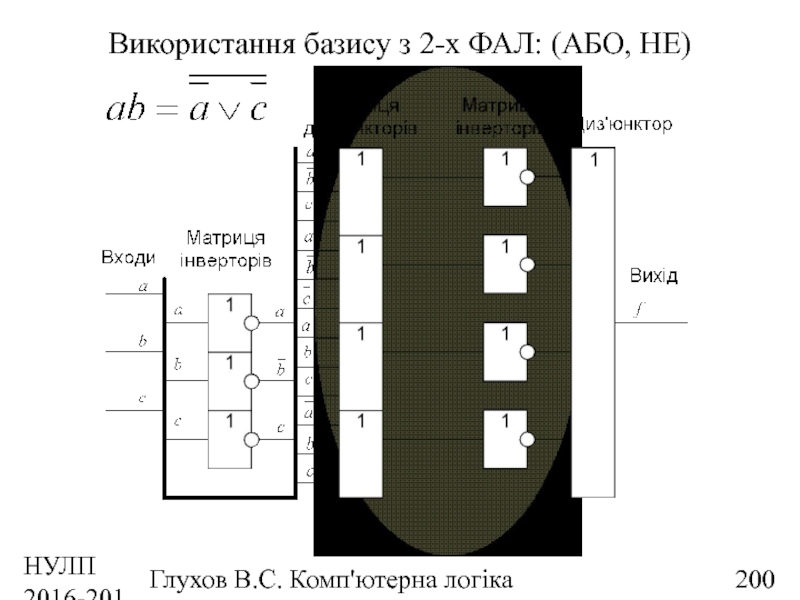
- 200. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Використання базису з 2-х ФАЛ: (АБО, НЕ)
- 201. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Основні правила виконання операцій у базисі Буля
- 202. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка
- 203. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка
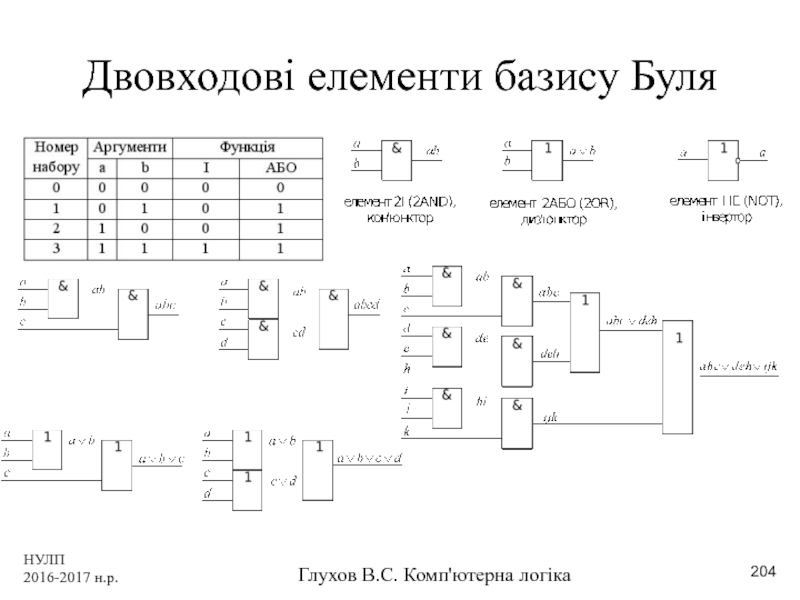
- 204. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Двовходові елементи базису Буля
- 205. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка
- 206. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Монобазис І-НЕ (NAND)
- 207. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка
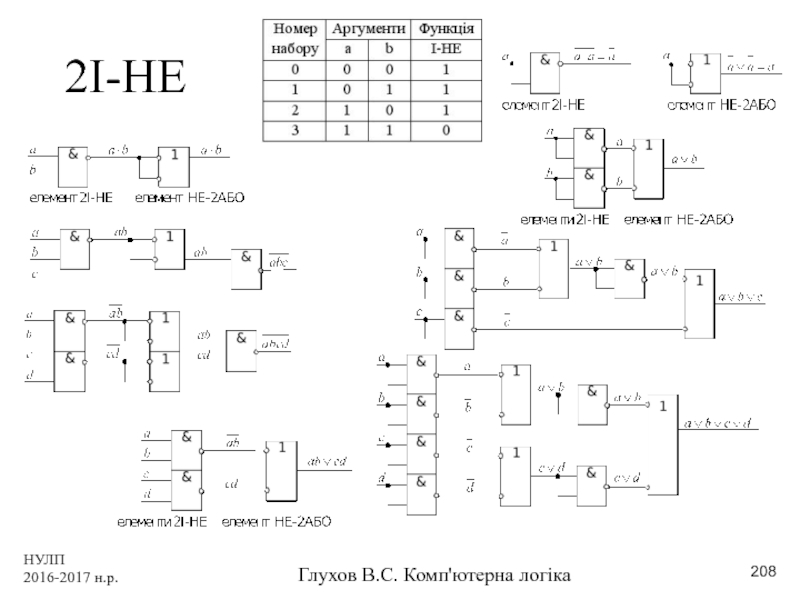
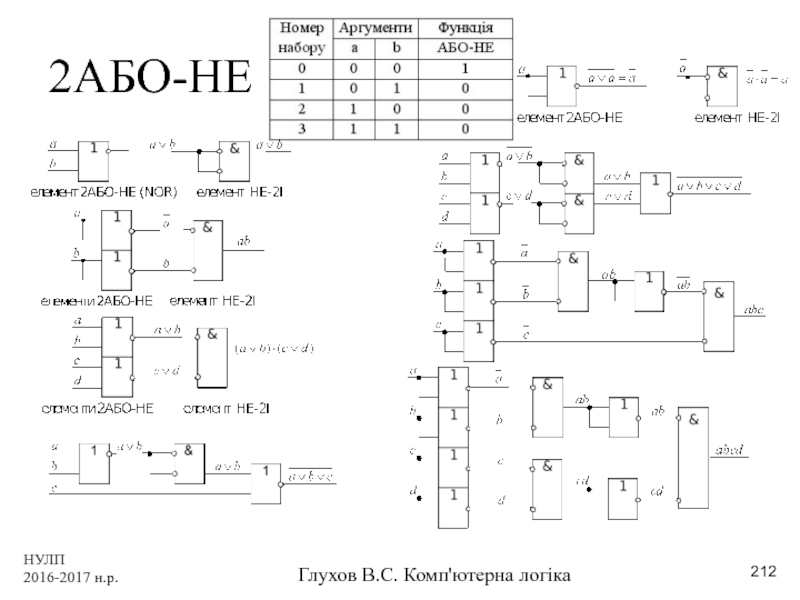
- 208. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка 2І-НЕ
- 209. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка
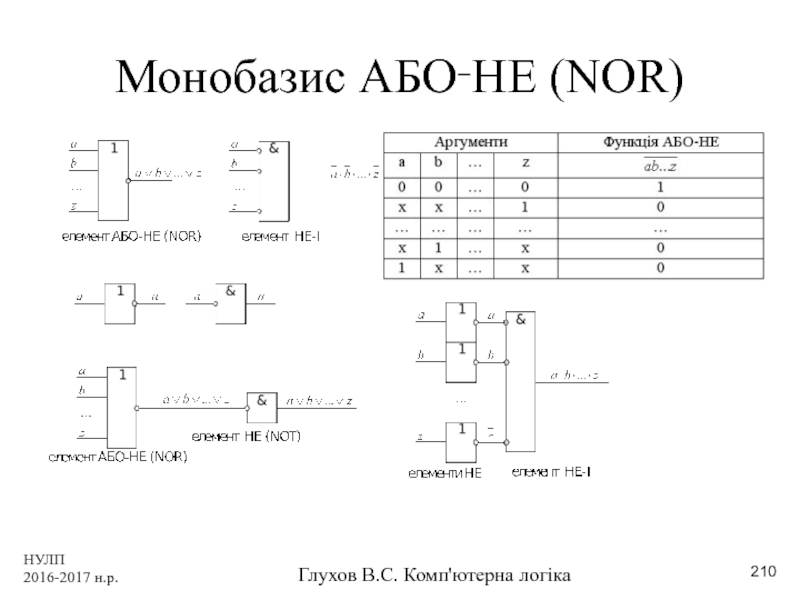
- 210. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Монобазис АБО‑НЕ (NOR)
- 211. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка
- 212. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка
- 213. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка
- 214. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Схеми елементів монобазисів на КМОН-транзисторах
- 215. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка
- 216. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка
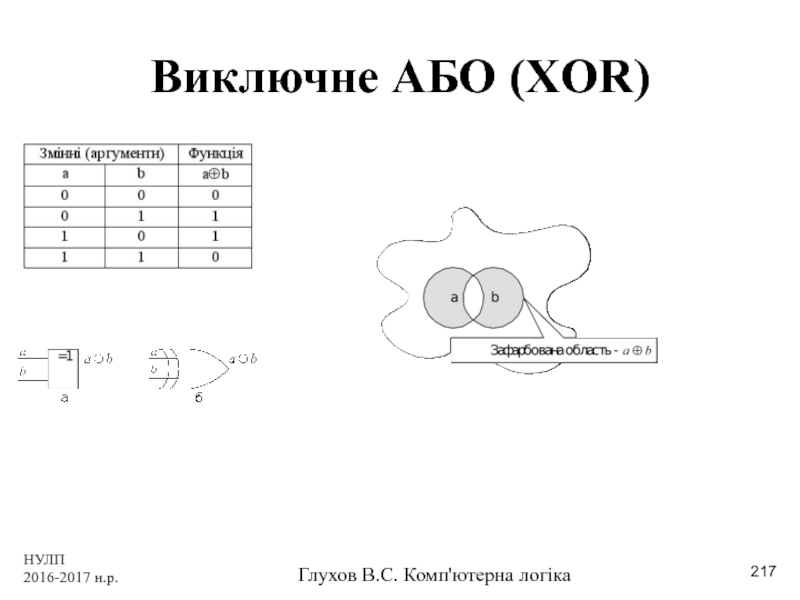
- 217. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Виключне АБО (XOR)
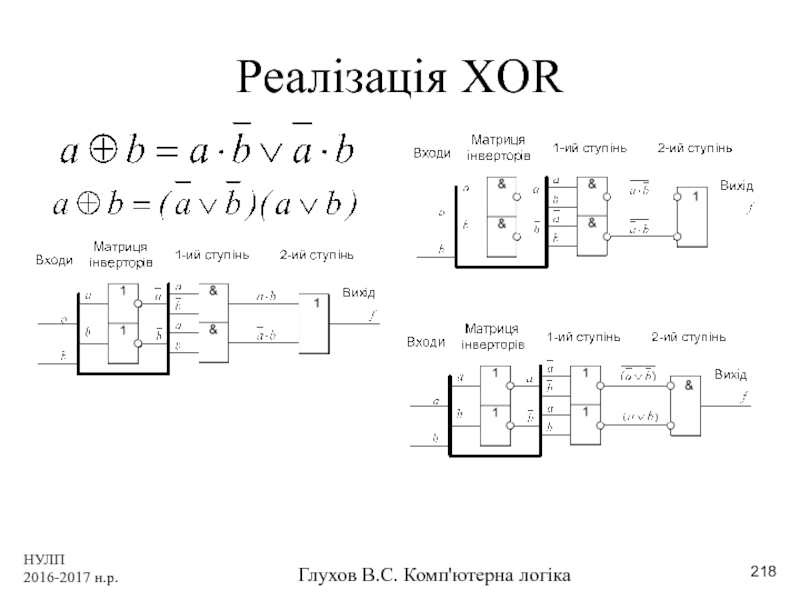
- 218. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Реалізація XOR
- 219. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка
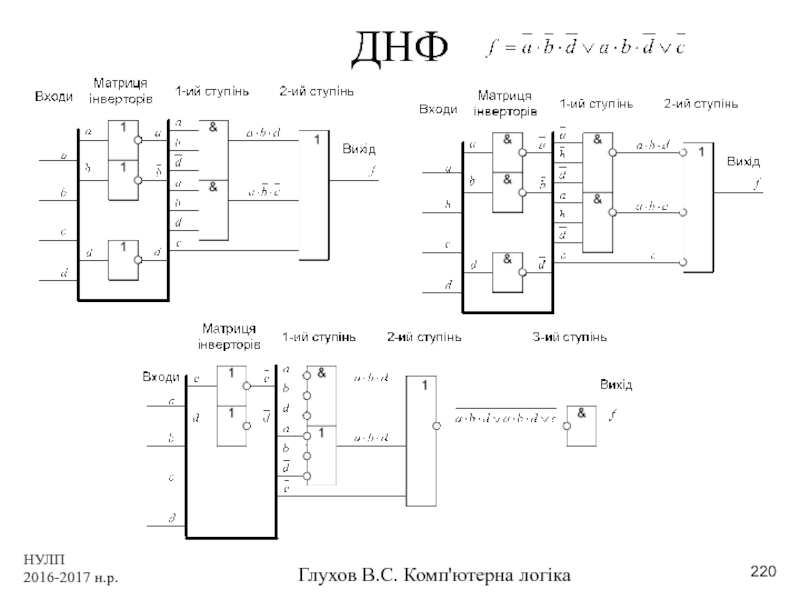
- 220. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка ДНФ
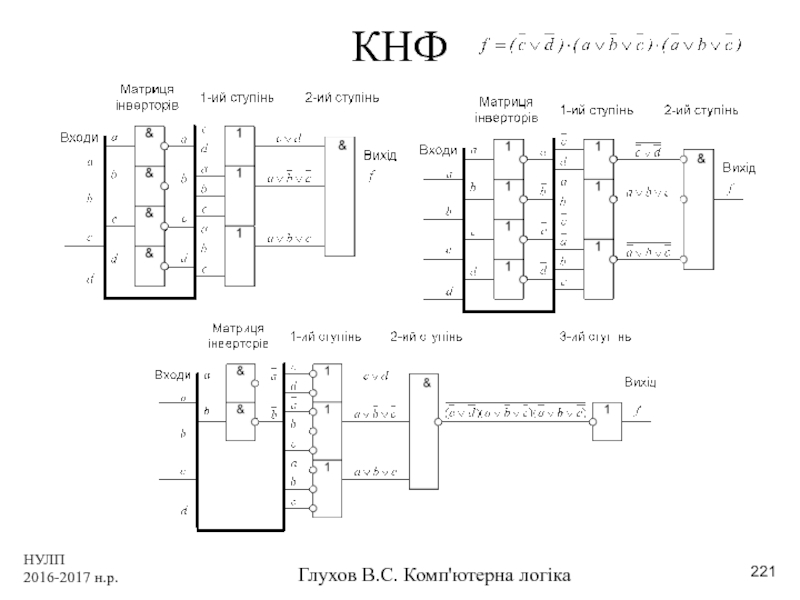
- 221. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка КНФ
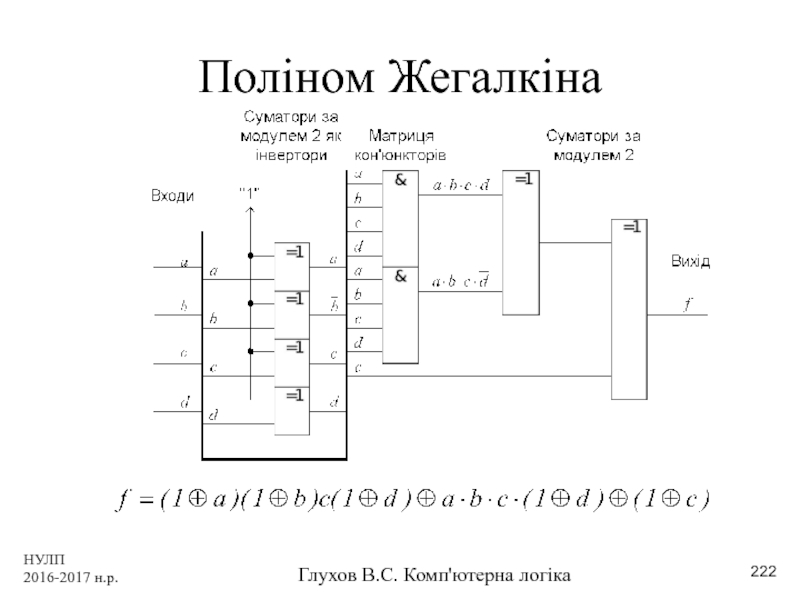
- 222. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Поліном Жегалкіна
- 223. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка
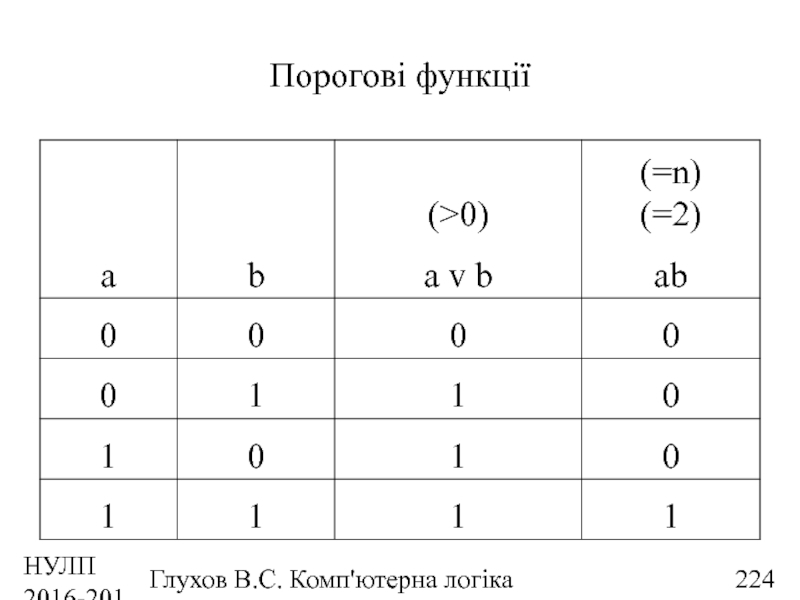
- 224. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Порогові функції
- 225. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка
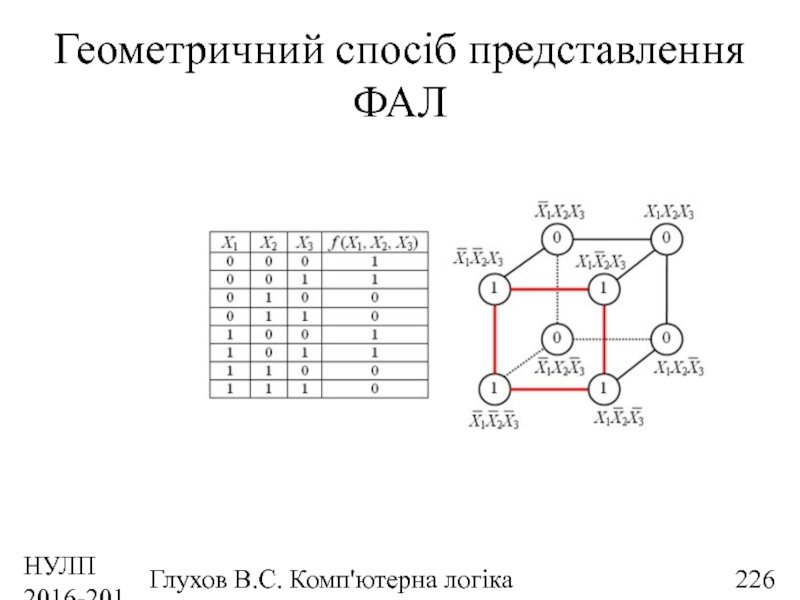
- 226. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Геометричний спосіб представлення ФАЛ
- 227. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка
- 228. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка
- 229. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка
- 230. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка
- 231. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка
- 232. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка
- 233. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка
- 234. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка
- 235. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка
- 236. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка
- 237. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка
- 238. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Еврістичний
- 239. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка
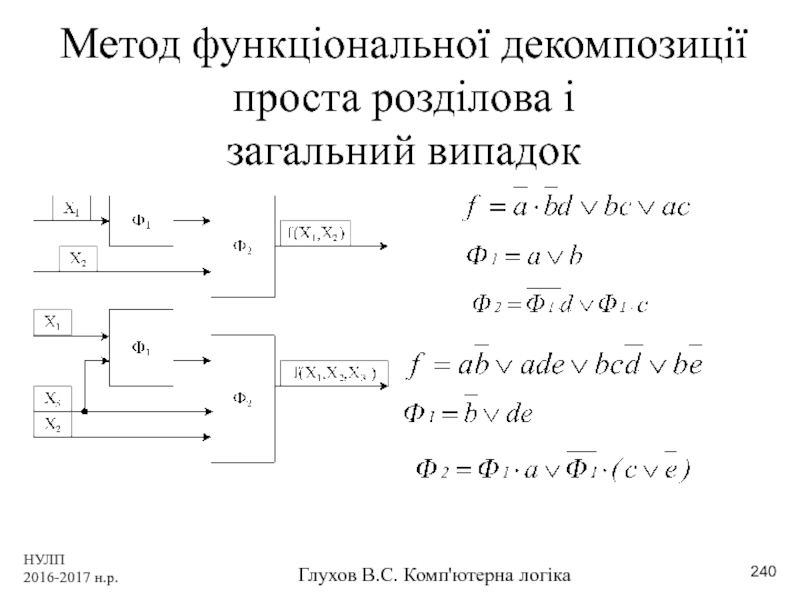
- 240. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка
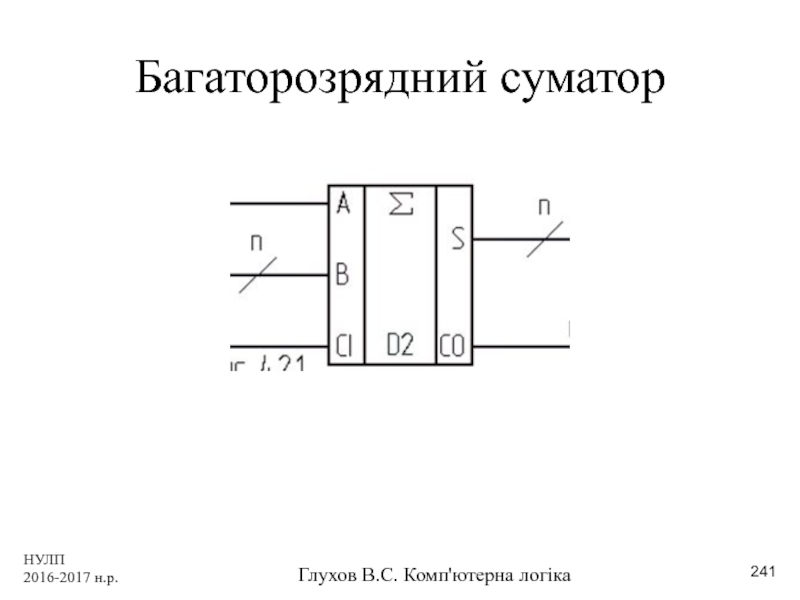
- 241. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Багаторозрядний суматор
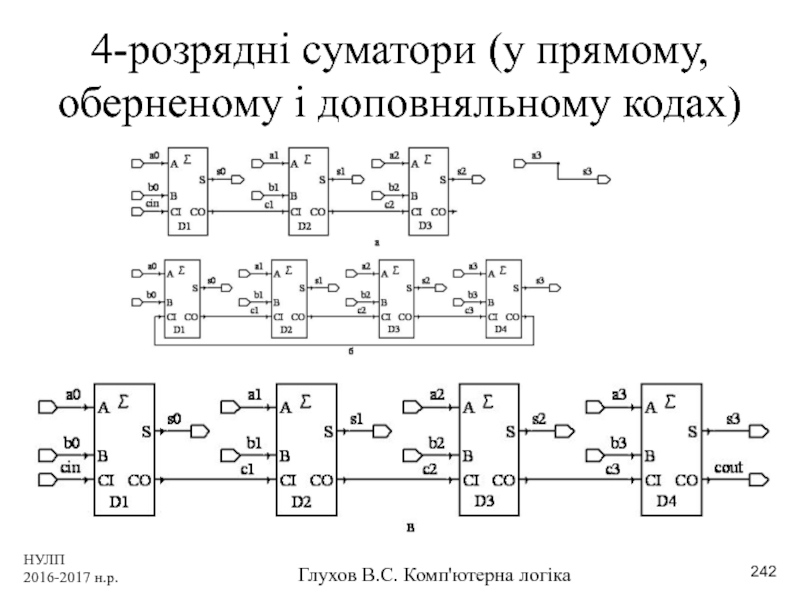
- 242. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка 4-розрядні суматори (у прямому, оберненому і доповняльному кодах)
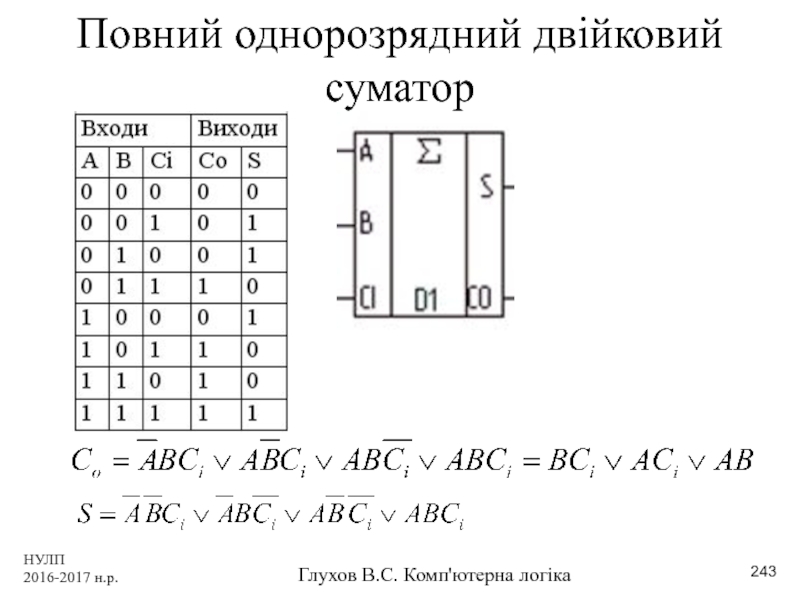
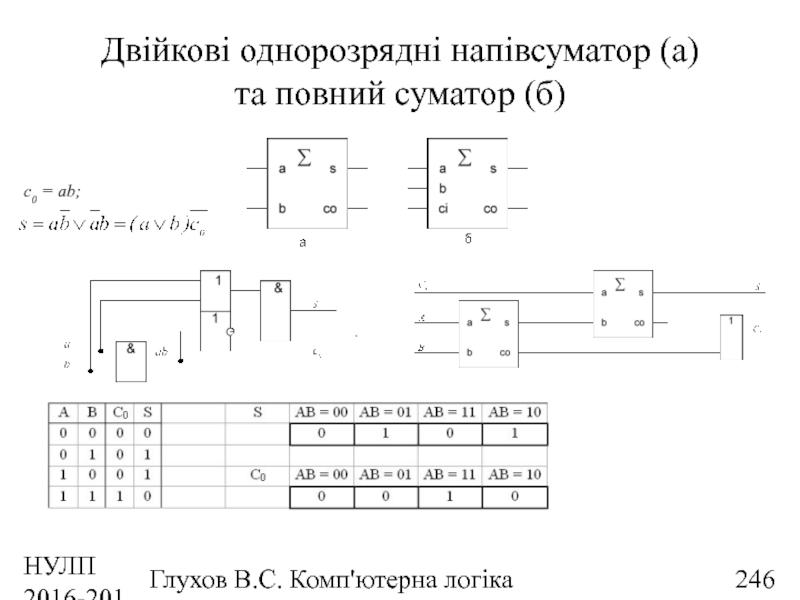
- 243. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Повний однорозрядний двійковий суматор
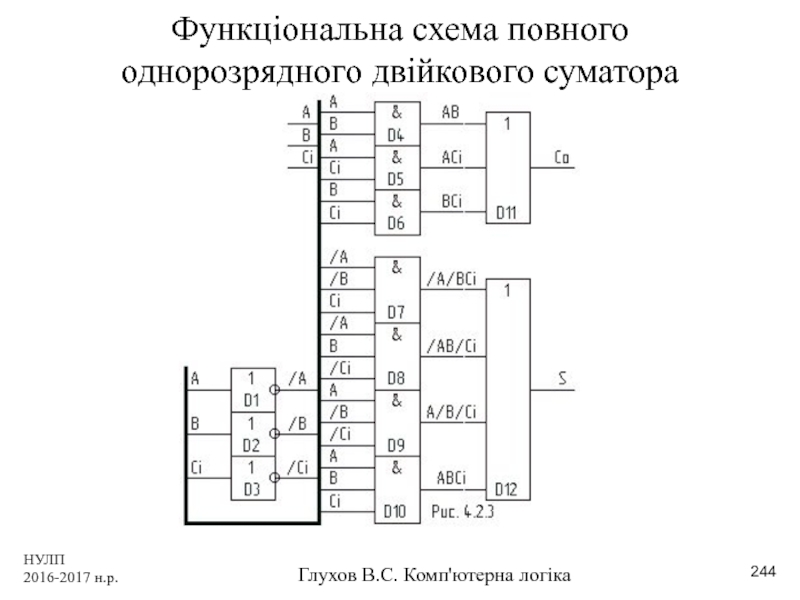
- 244. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Функціональна схема повного однорозрядного двійкового суматора
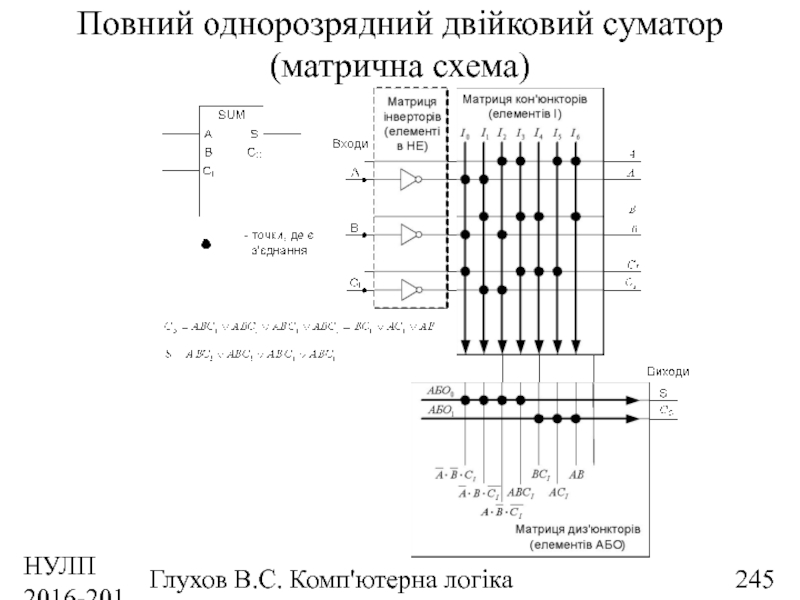
- 245. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Повний однорозрядний двійковий суматор (матрична схема)
- 246. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка
- 247. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка
- 248. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка
- 249. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка
- 250. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка
- 251. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка
- 252. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка
- 253. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка
- 254. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка
- 255. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка
- 256. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка
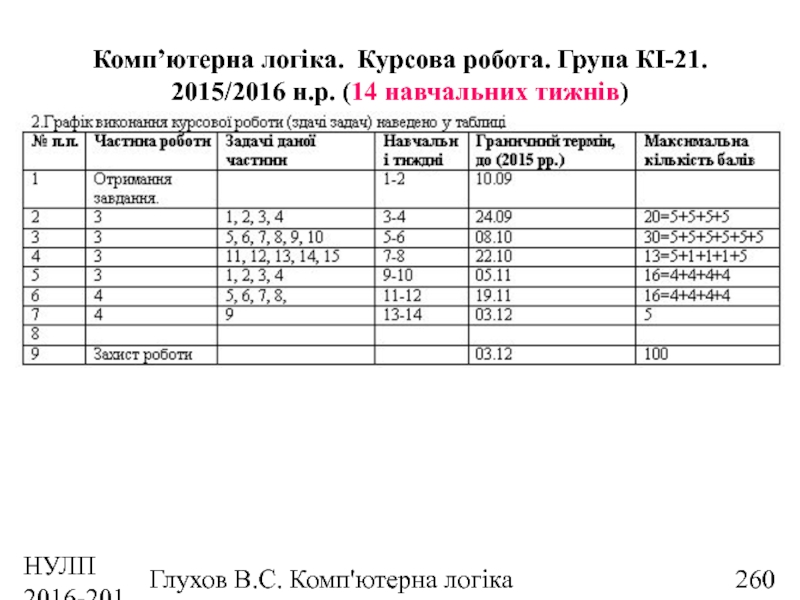
- 257. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Курсова робота
- 258. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Використання результатів 2-ої частини
- 259. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Вимоги до оформлення курсової роботи
- 260. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка
- 261. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Оцінювання курсової роботи
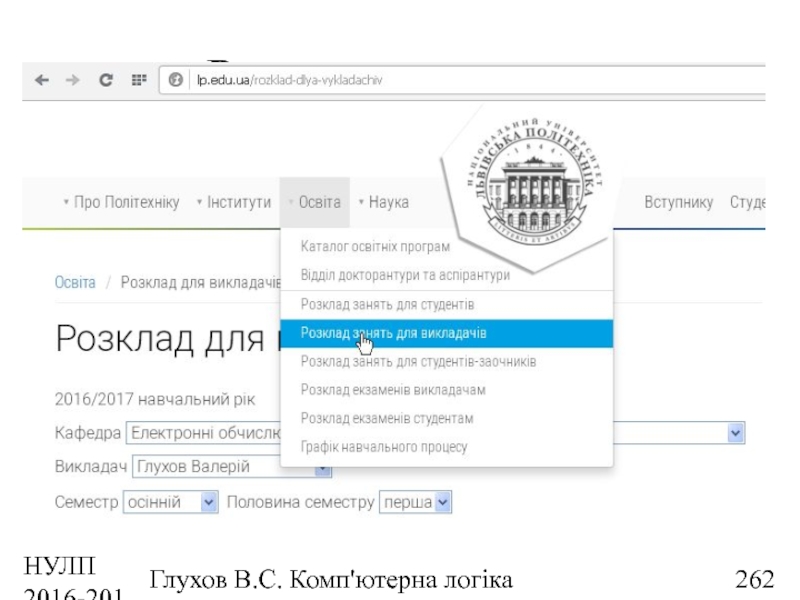
- 262. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Розклад викладача
- 263. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка
- 264. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Завдання на курсову роботу
- 265. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Віртуальне навчальне середовище
- 266. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка ВНС, Комп’ютерна логіка, ч.2
- 267. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Екзаменаційний білет
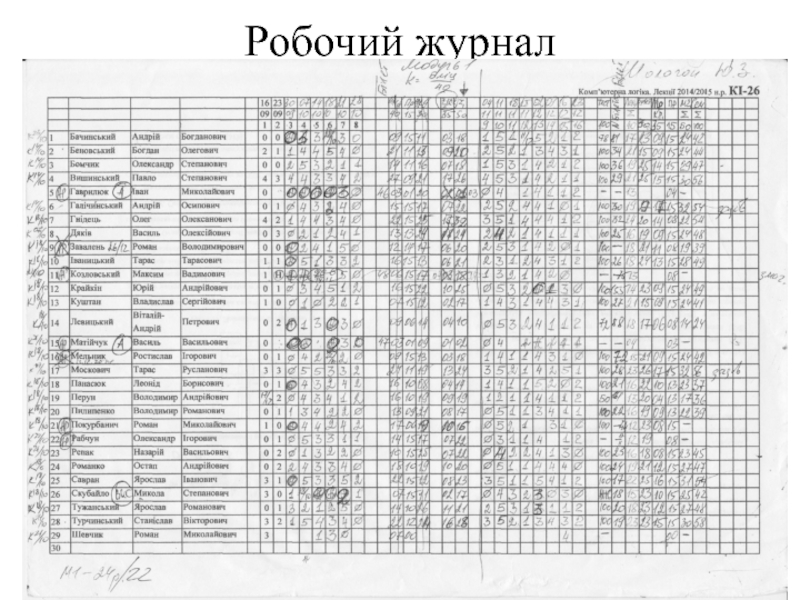
- 268. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Робочий журнал
- 269. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка
- 270. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Газорозрядні індикатори
- 271. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Дешифратор “3 у 8”
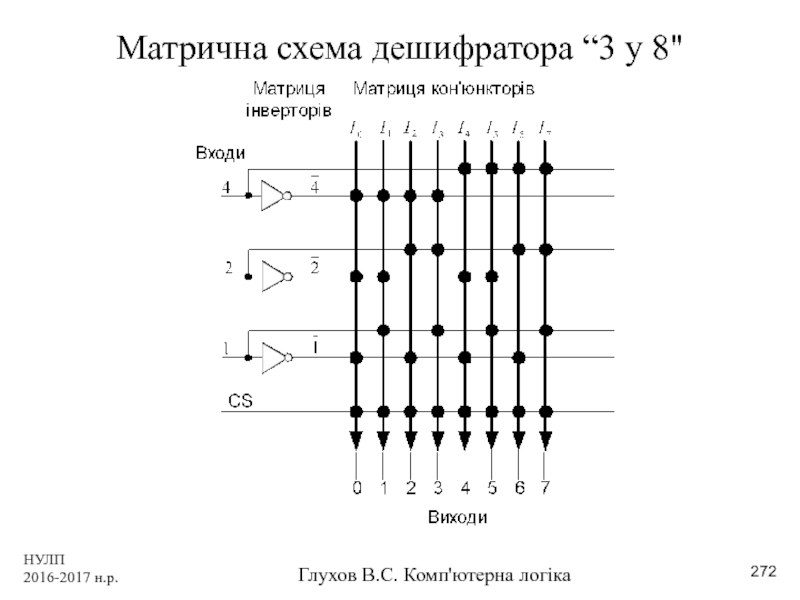
- 272. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Матрична схема дешифратора “3 у 8"
- 273. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка
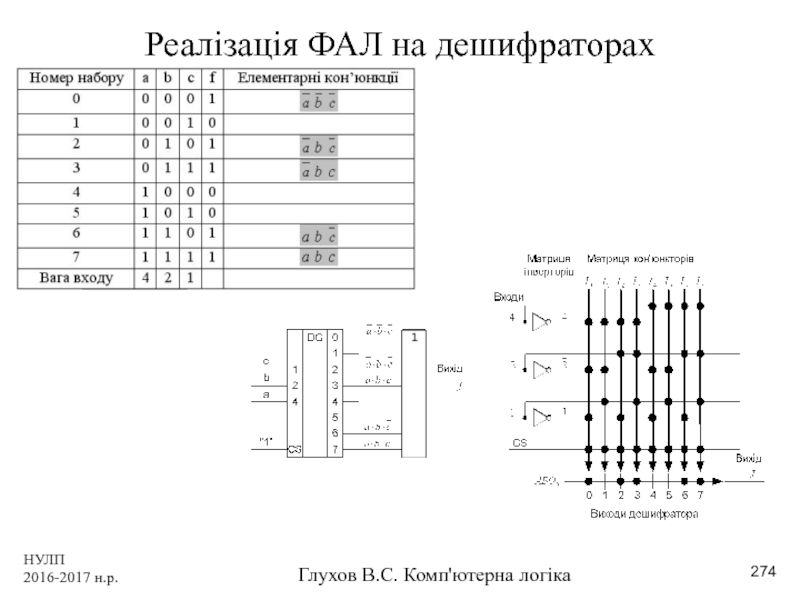
- 274. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Реалізація ФАЛ на дешифраторах
- 275. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка
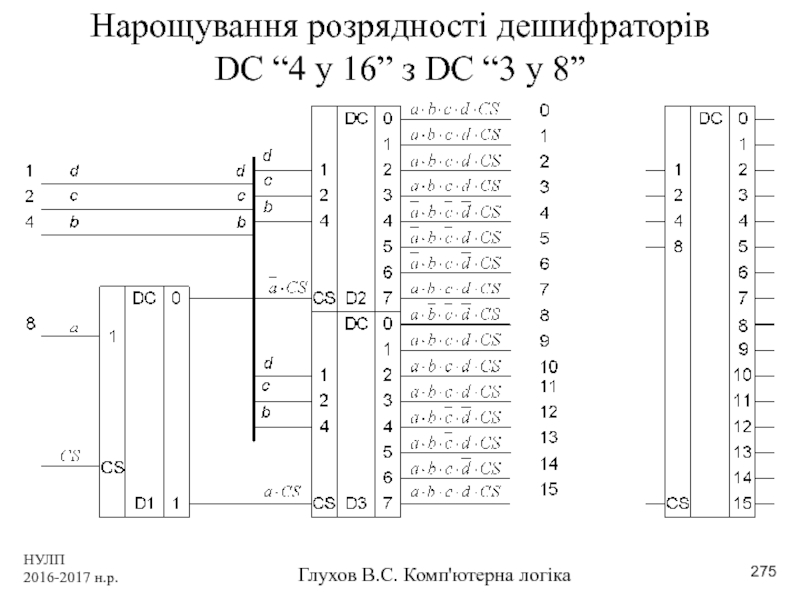
- 276. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка
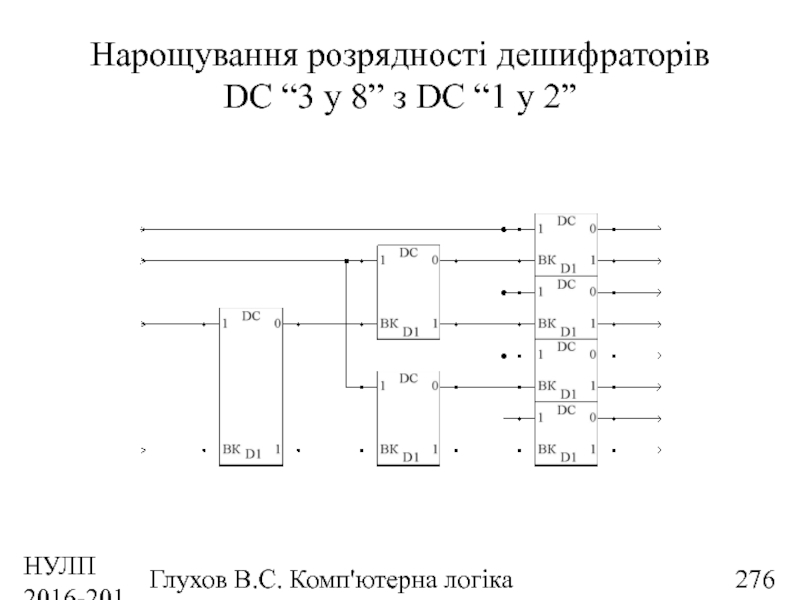
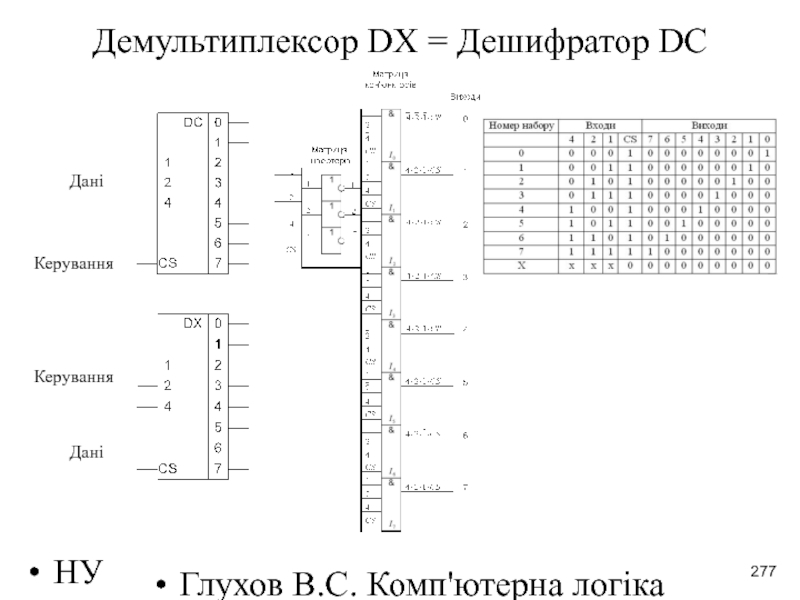
- 277. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка
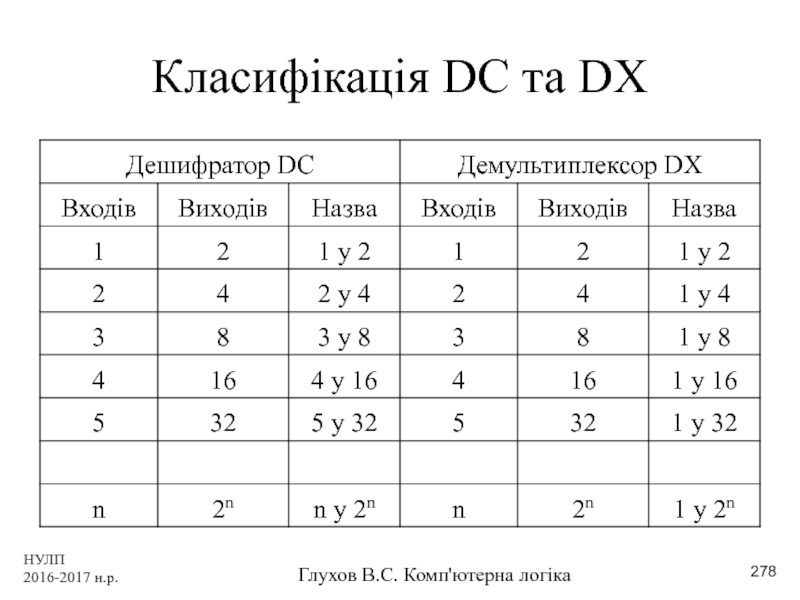
- 278. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Класифікація DC та DX
- 279. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Мультиплексор 8 в 1
- 280. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка
- 281. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Реалізація ФАЛ на мультиплексорах
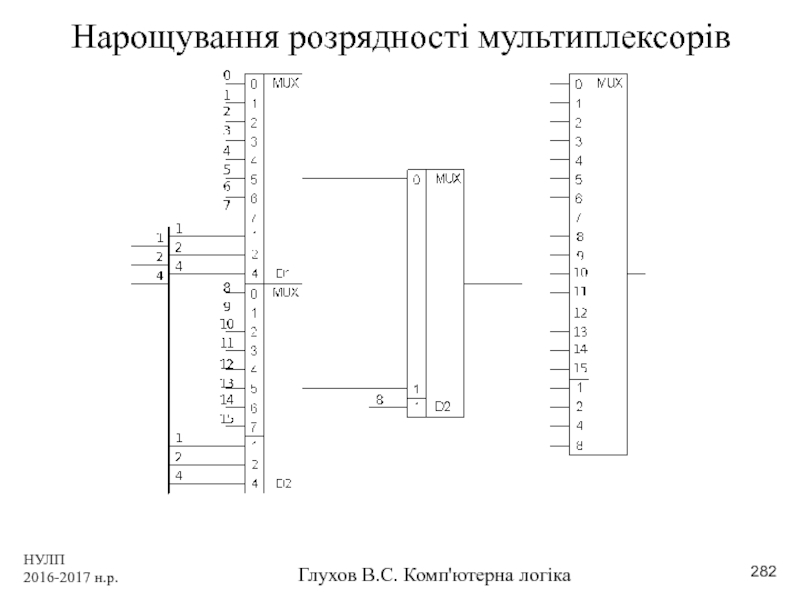
- 282. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Нарощування розрядності мультиплексорів
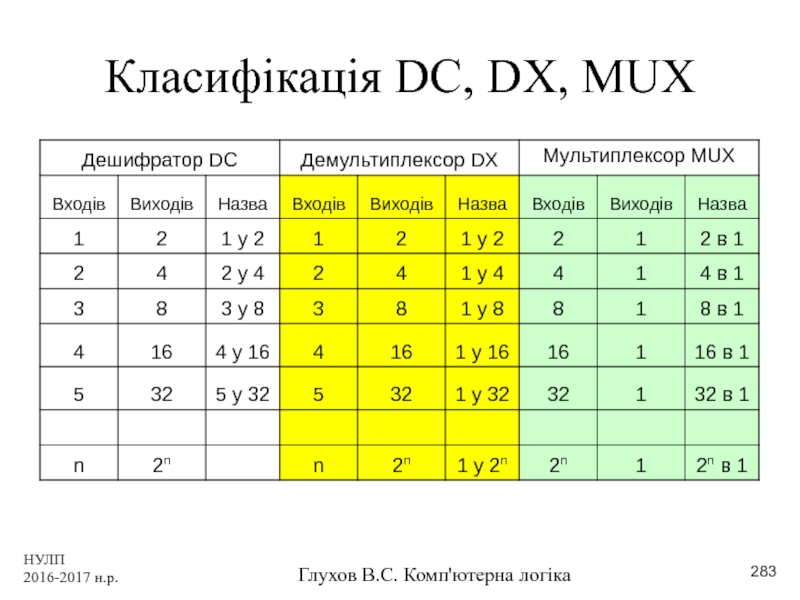
- 283. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Класифікація DC, DX, MUX
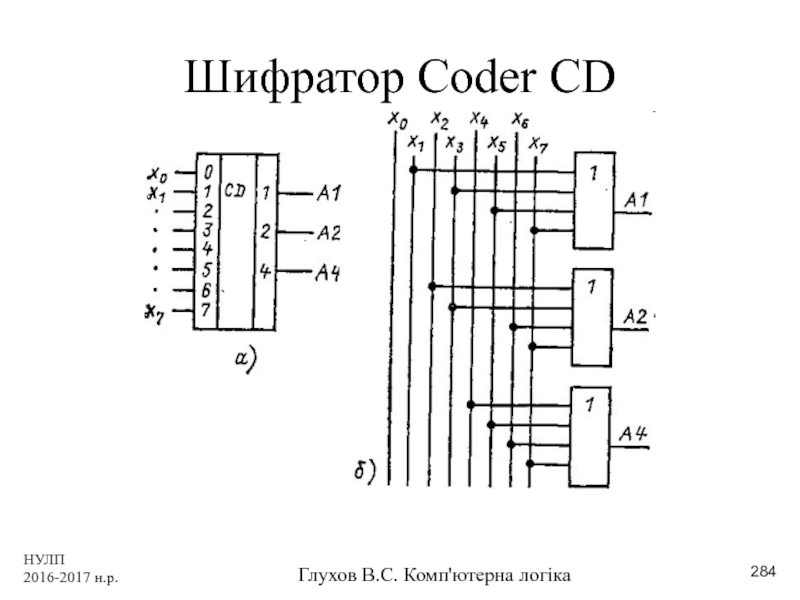
- 284. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Шифратор Coder CD
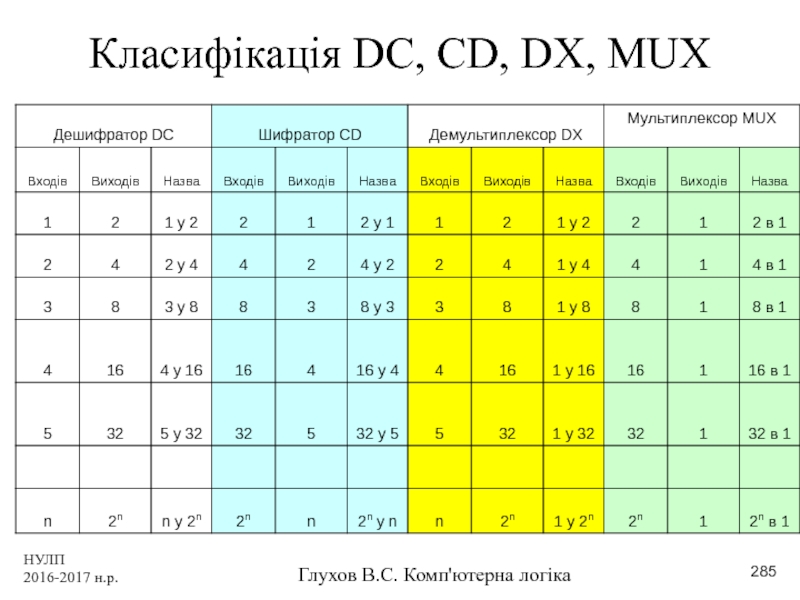
- 285. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Класифікація DC, CD, DX, MUX
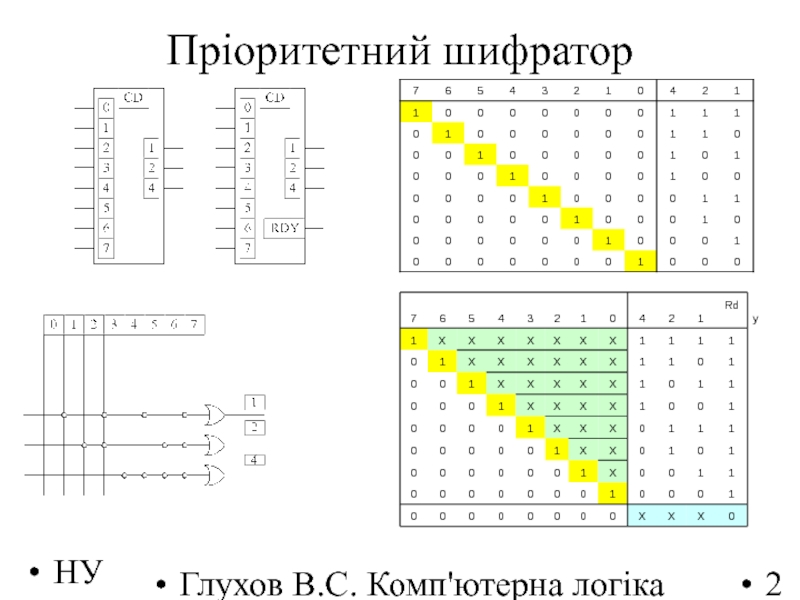
- 286. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Пріоритетний шифратор
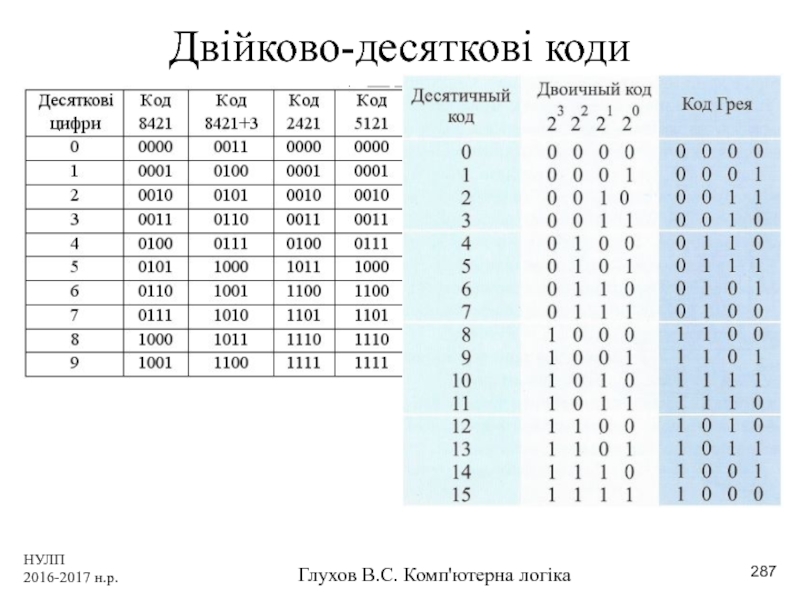
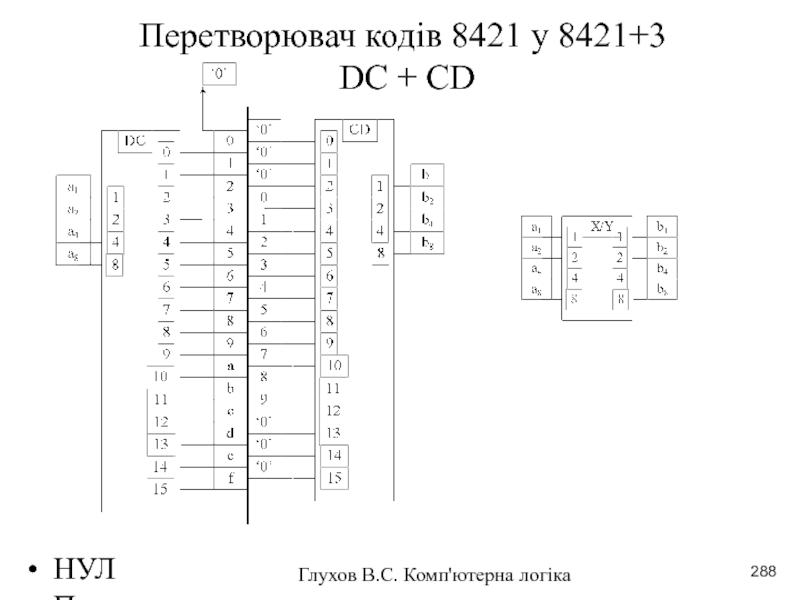
- 287. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Двійково-десяткові коди
- 288. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка
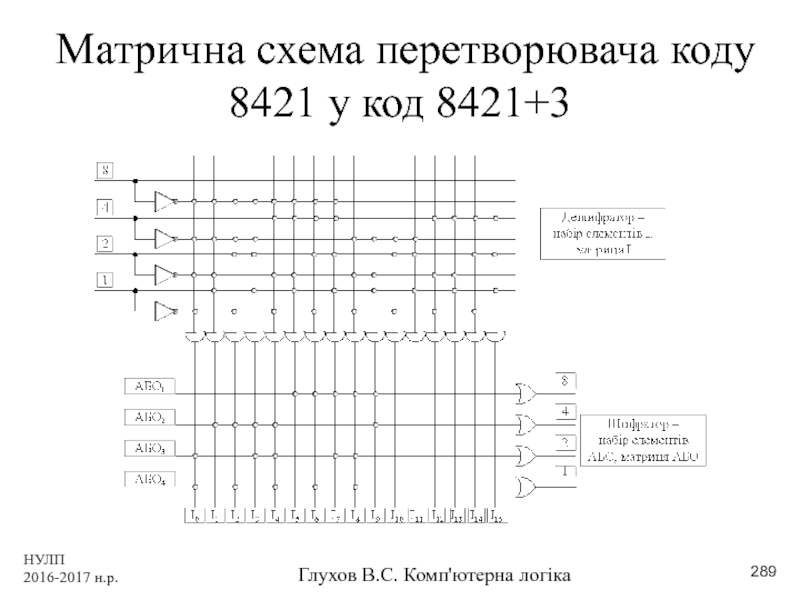
- 289. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Матрична схема перетворювача коду 8421 у код 8421+3
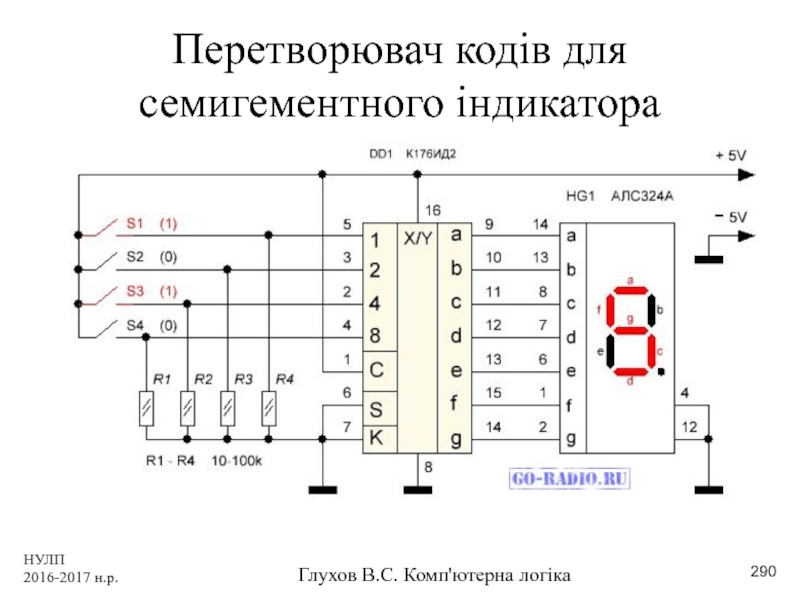
- 290. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Перетворювач кодів для семигементного індикатора
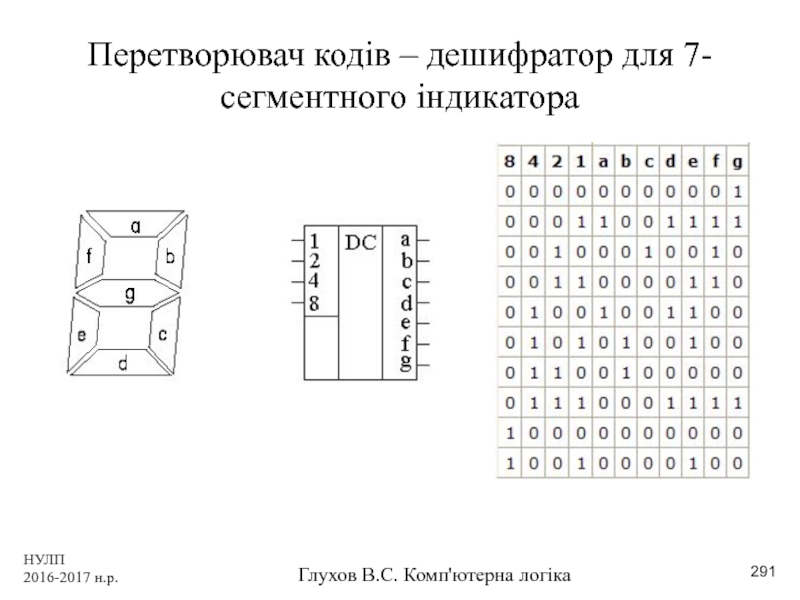
- 291. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Перетворювач кодів – дешифратор для 7-сегментного індикатора
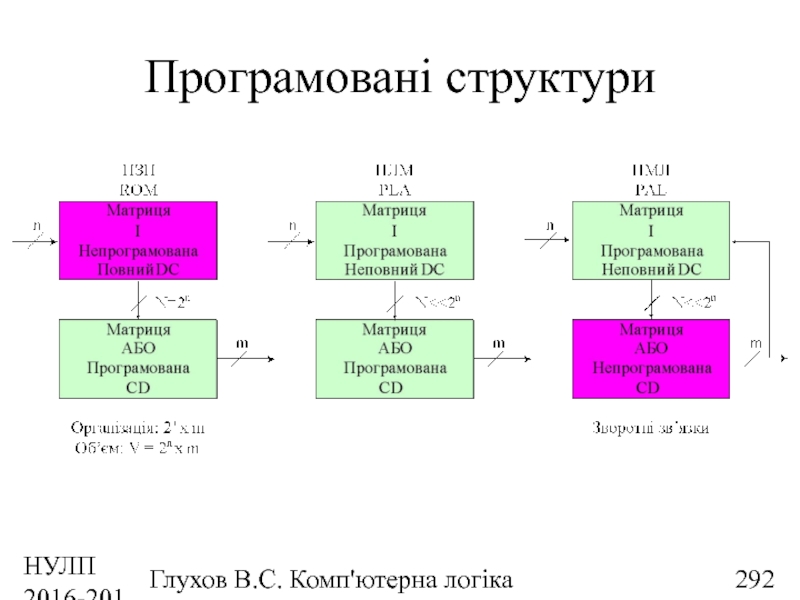
- 292. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Програмовані структури
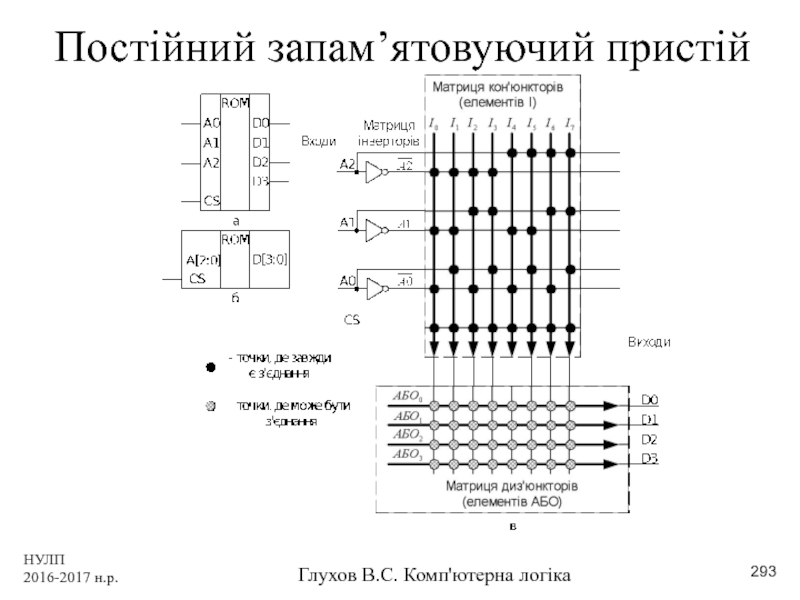
- 293. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Постійний запам’ятовуючий пристій
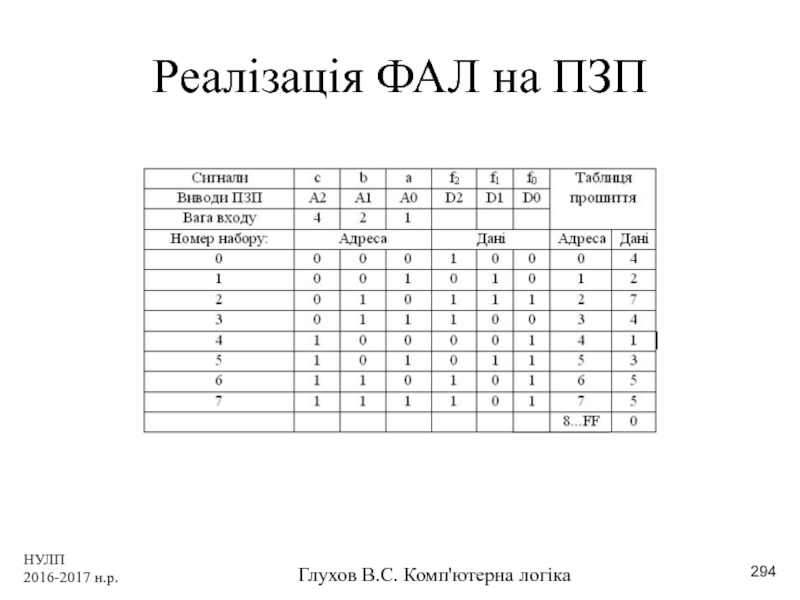
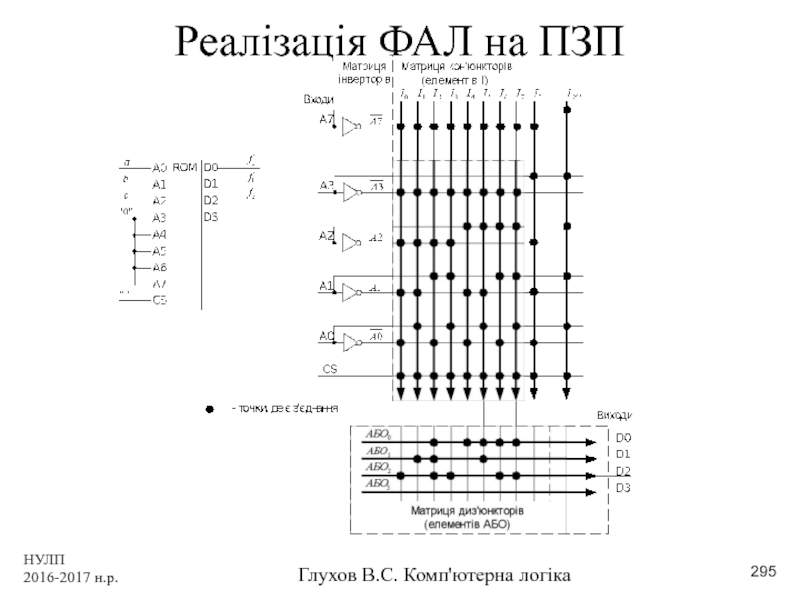
- 294. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Реалізація ФАЛ на ПЗП
- 295. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Реалізація ФАЛ на ПЗП
- 296. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка
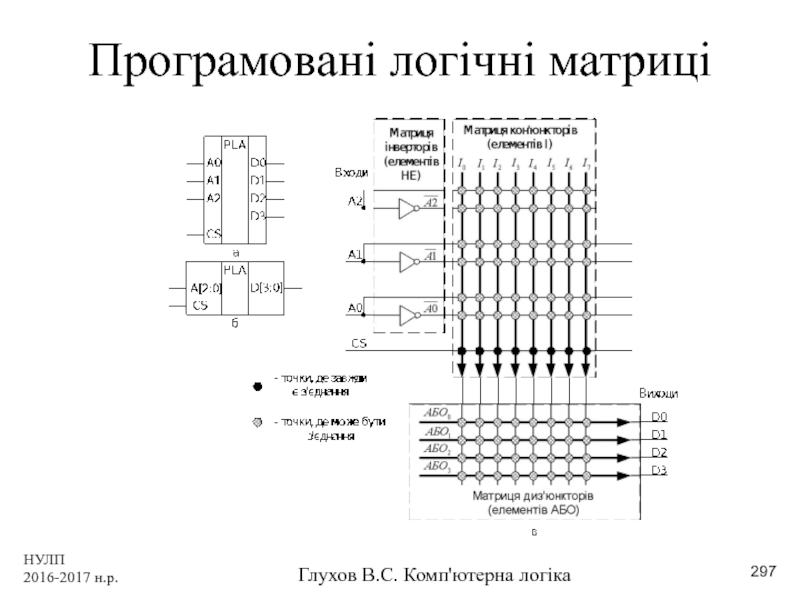
- 297. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Програмовані логічні матриці
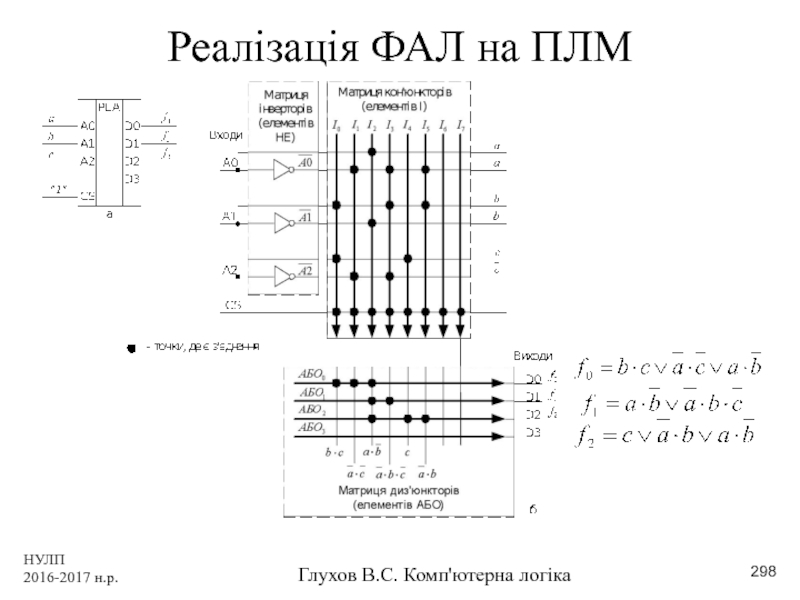
- 298. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Реалізація ФАЛ на ПЛМ
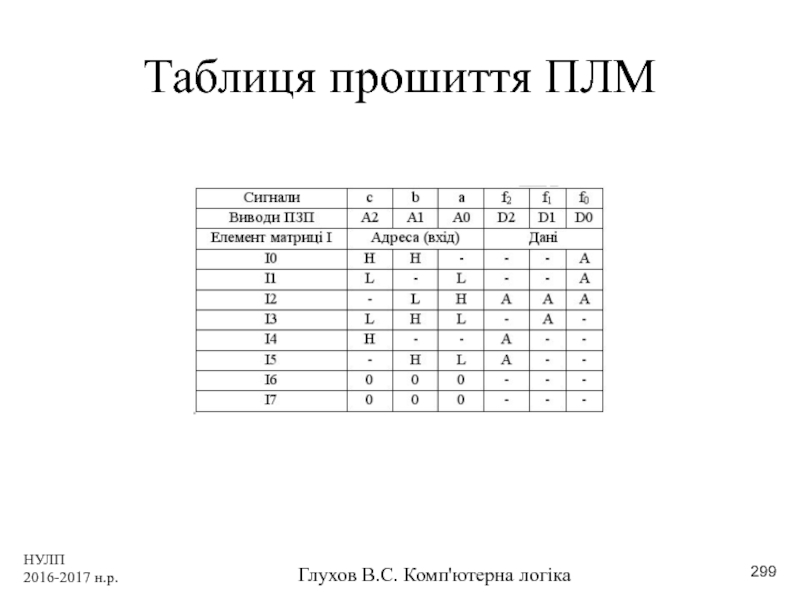
- 299. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Таблиця прошиття ПЛМ
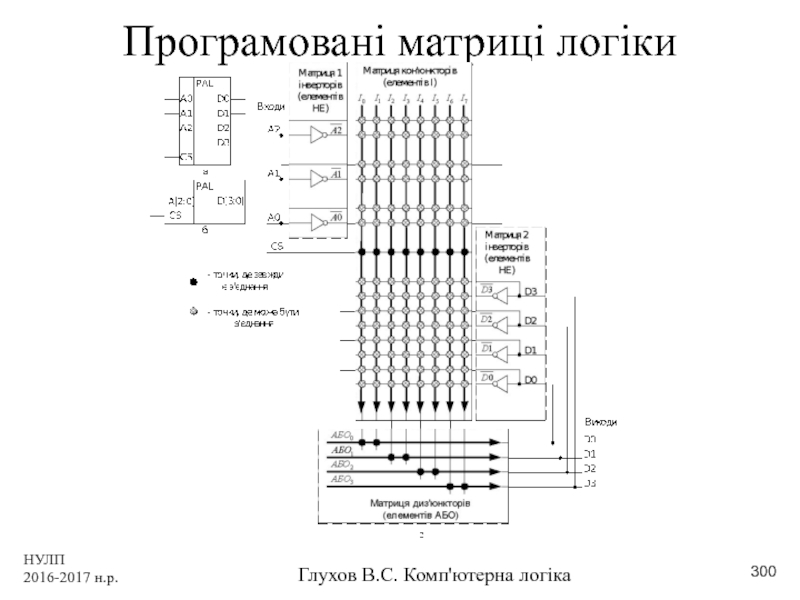
- 300. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Програмовані матриці логіки
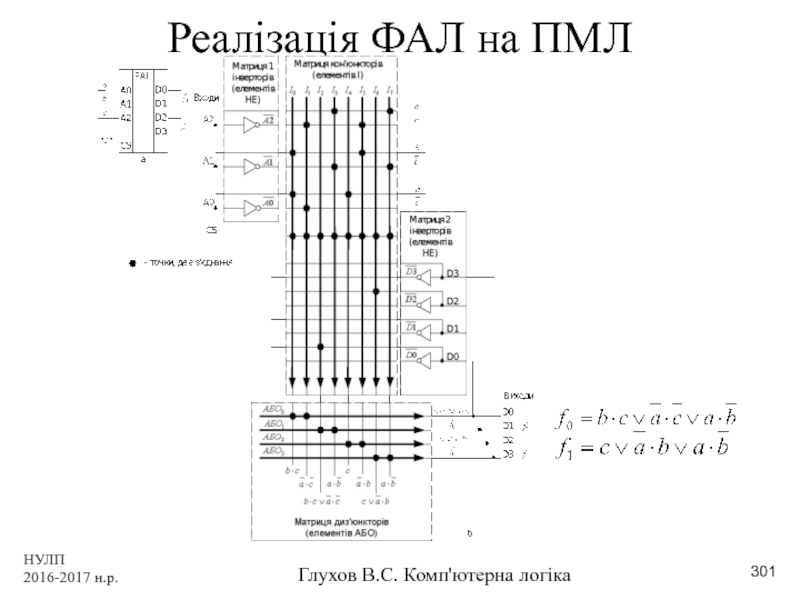
- 301. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Реалізація ФАЛ на ПМЛ
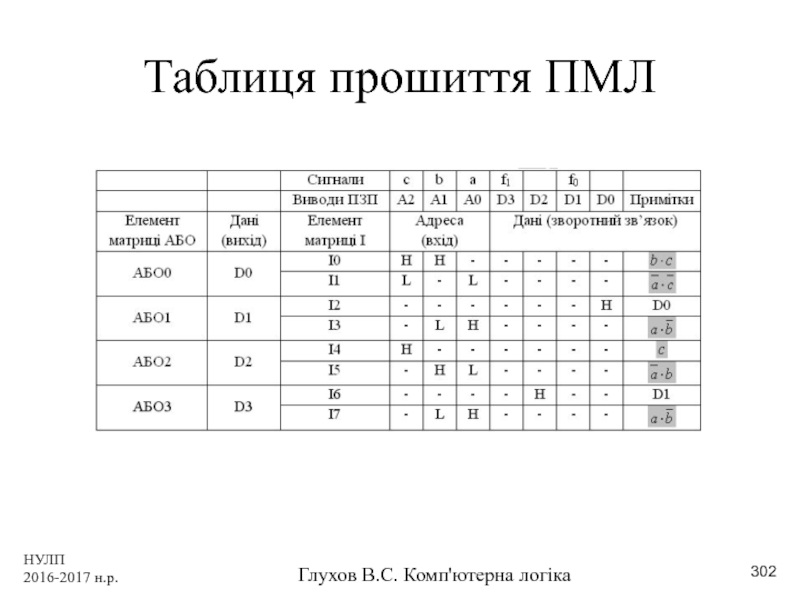
- 302. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Таблиця прошиття ПМЛ
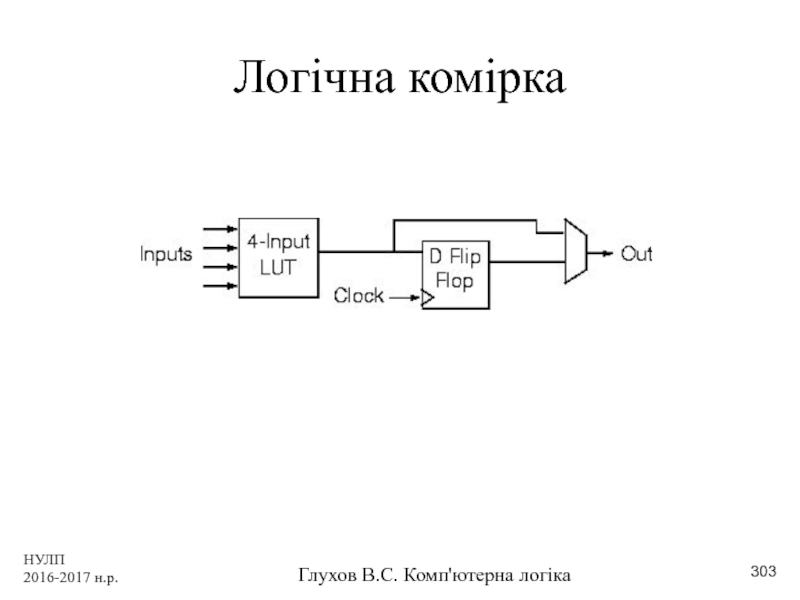
- 303. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Логічна комірка
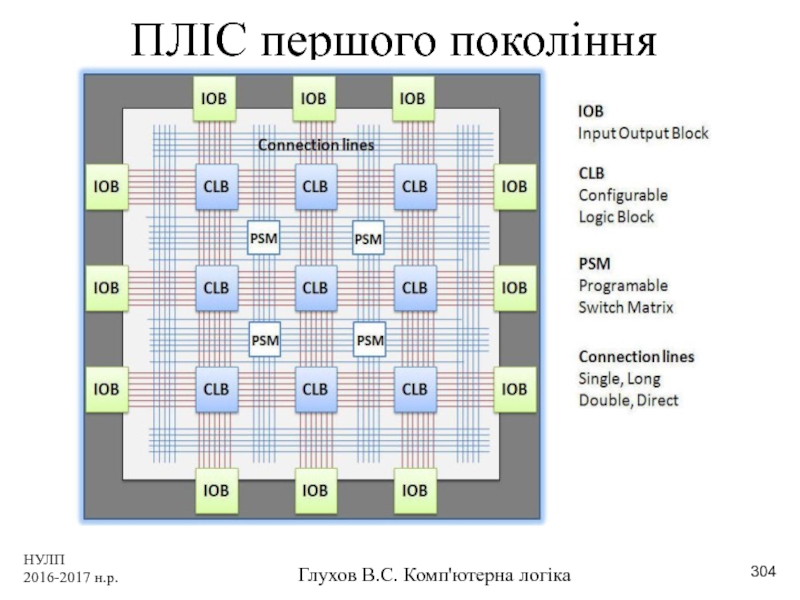
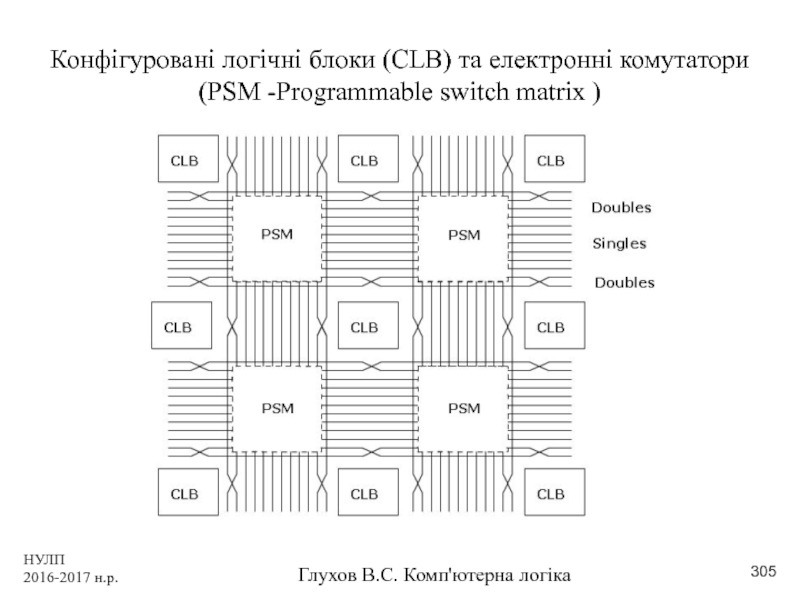
- 304. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка ПЛІС першого покоління
- 305. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка
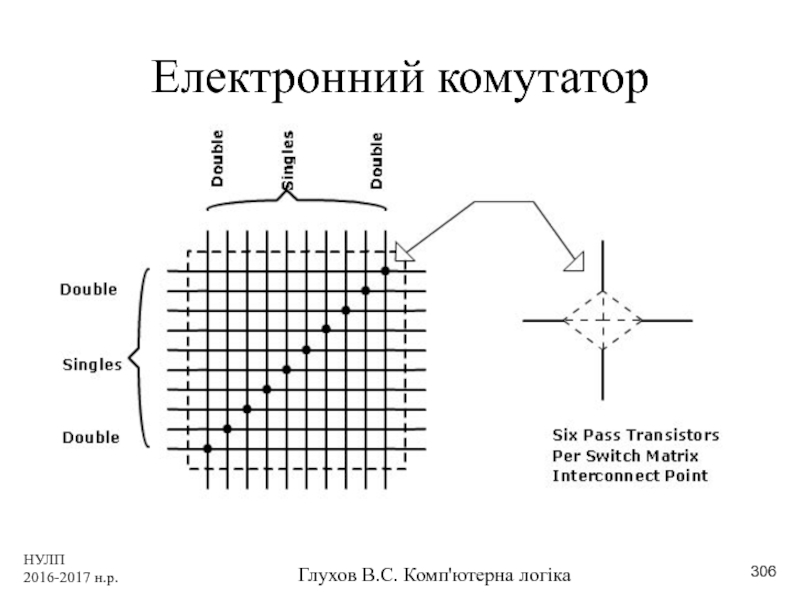
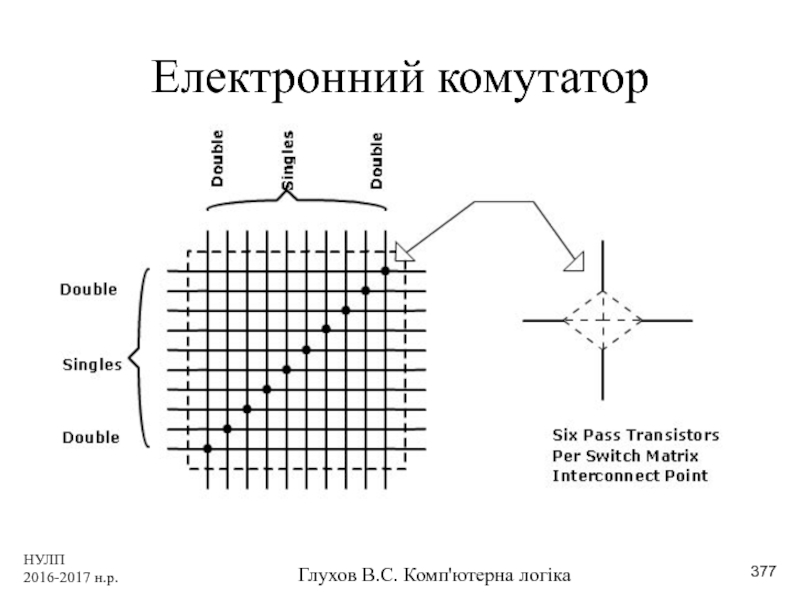
- 306. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Електронний комутатор
- 307. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка
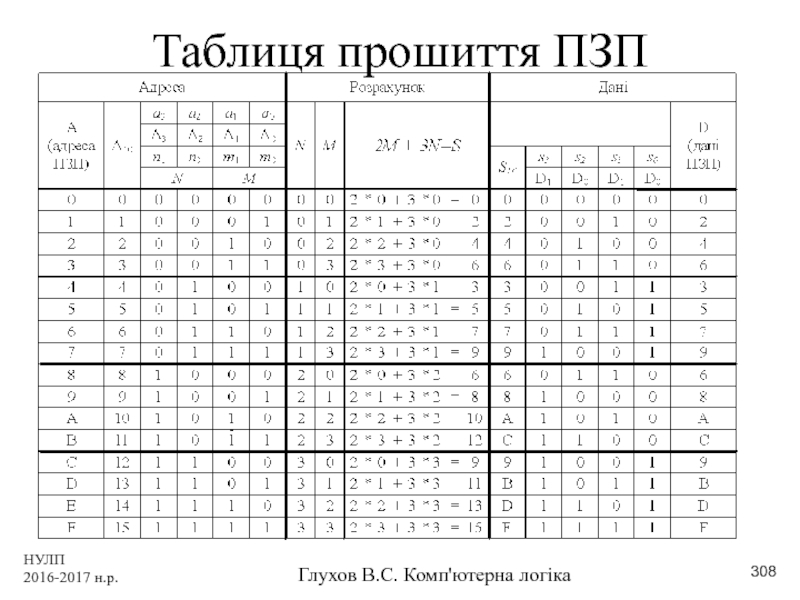
- 308. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Таблиця прошиття ПЗП
- 309. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Пам’ять перших комп’ютерів
- 310. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка
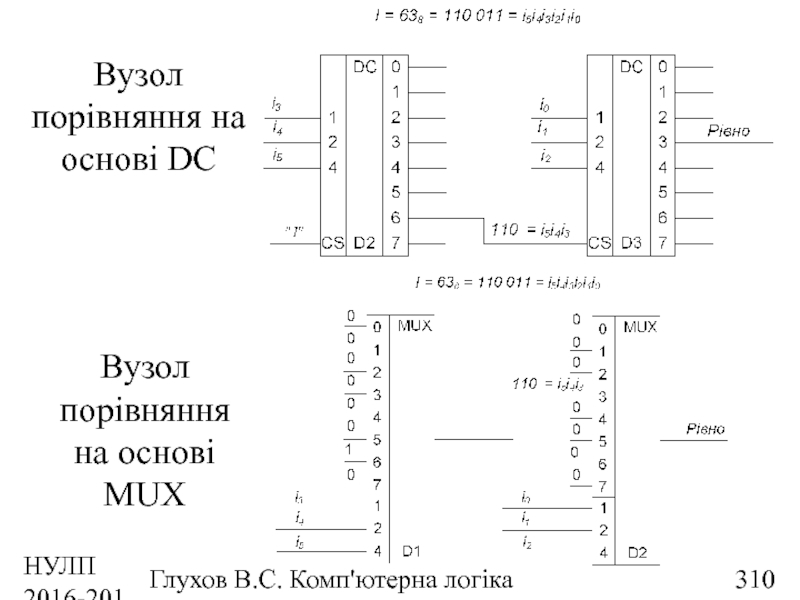
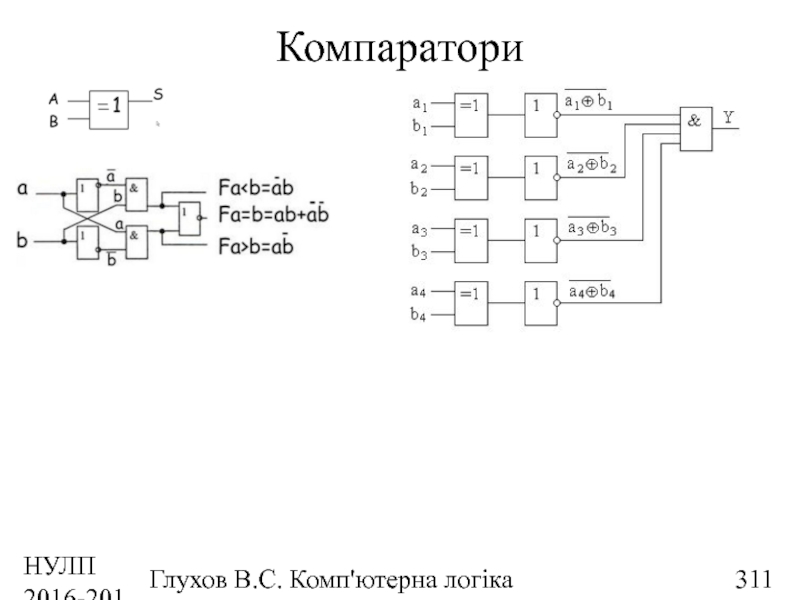
- 311. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Компаратори
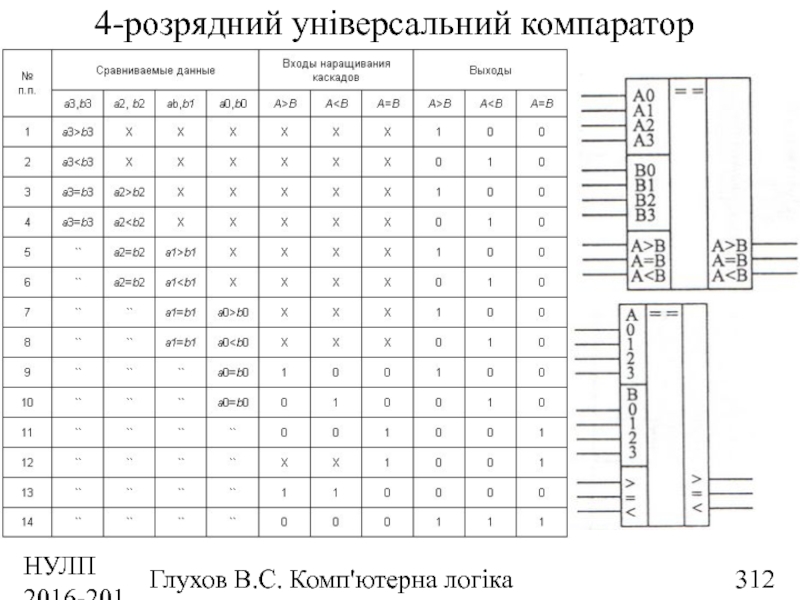
- 312. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка 4-розрядний універсальний компаратор
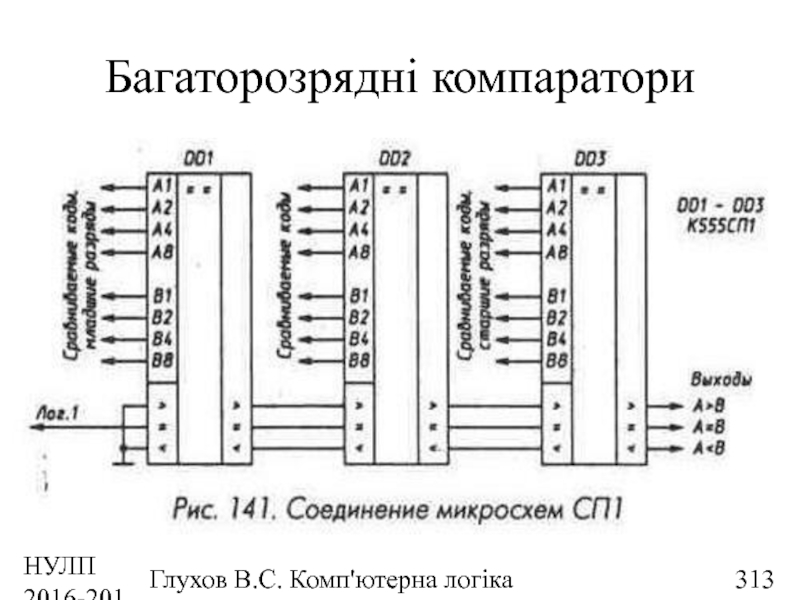
- 313. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Багаторозрядні компаратори
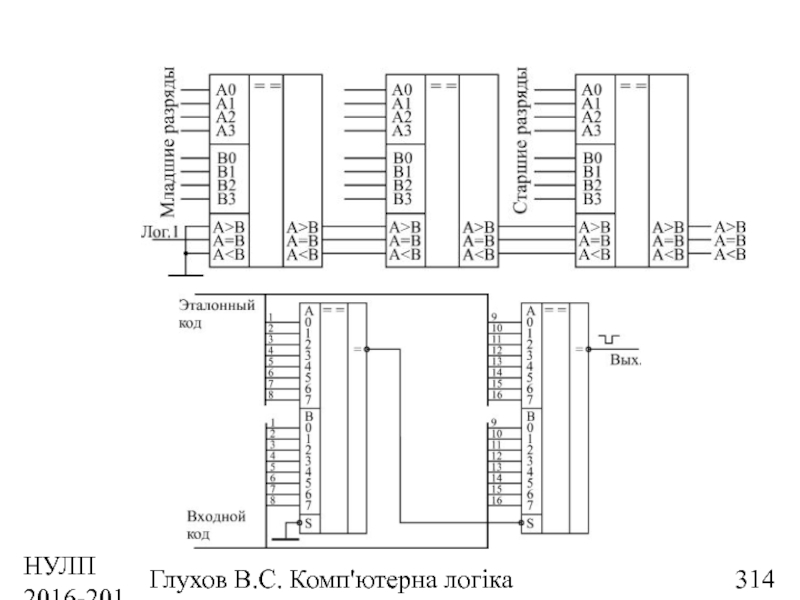
- 314. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка
- 315. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Неповні дешифратори
- 316. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка
- 317. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка
- 318. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Дешифратор діапазону кодів 04B8F ...1Е3А4
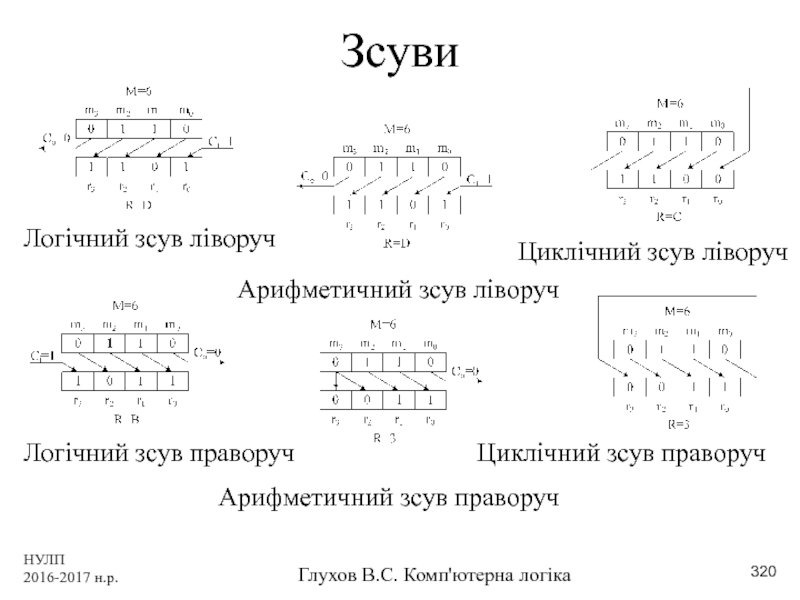
- 319. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Логічні операції над числами
- 320. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка
- 321. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Двійковий суматор з наскрізним (послідовним) переносом
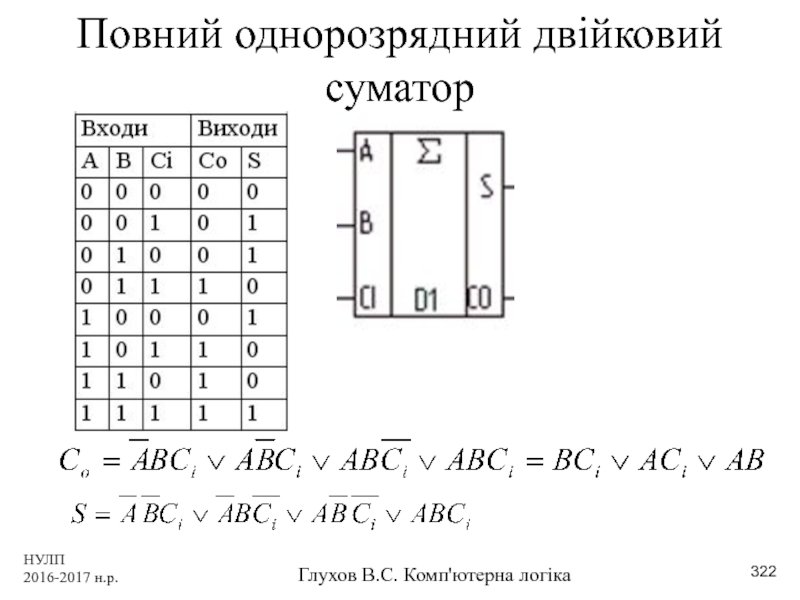
- 322. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Повний однорозрядний двійковий суматор
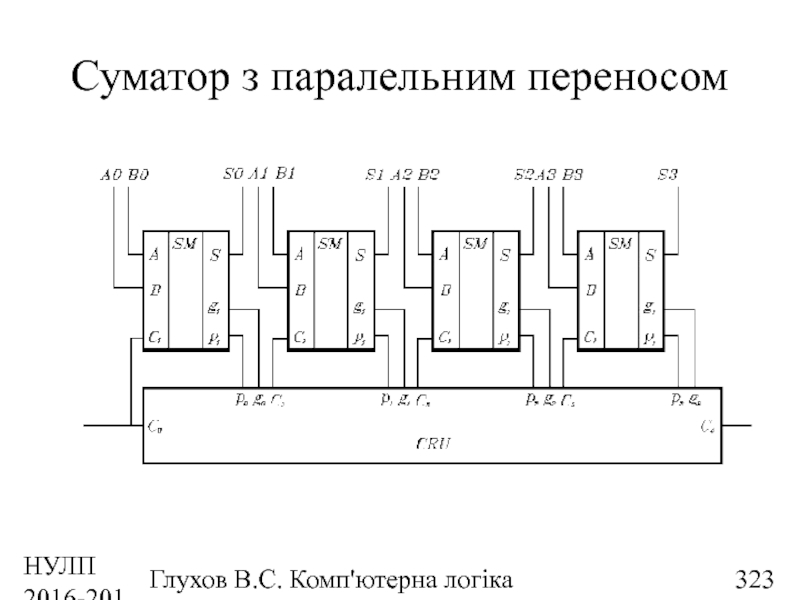
- 323. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Суматор з паралельним переносом
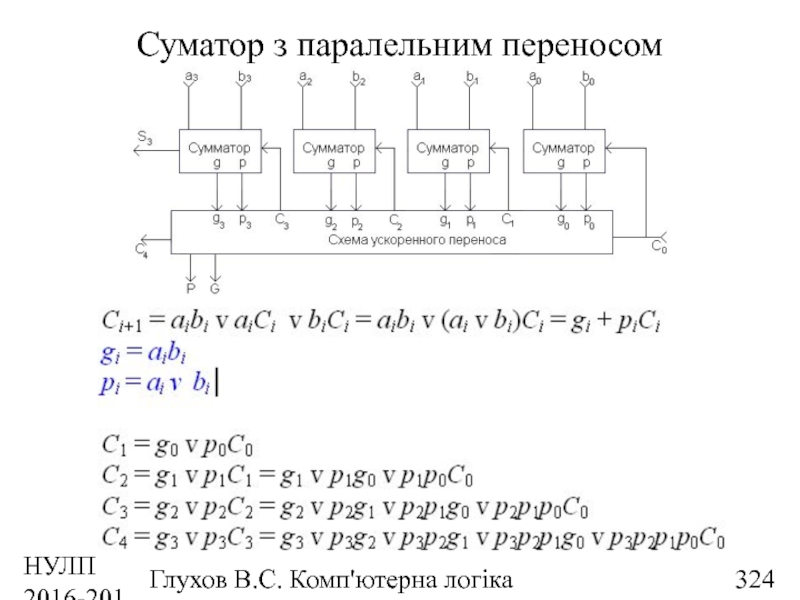
- 324. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Суматор з паралельним переносом
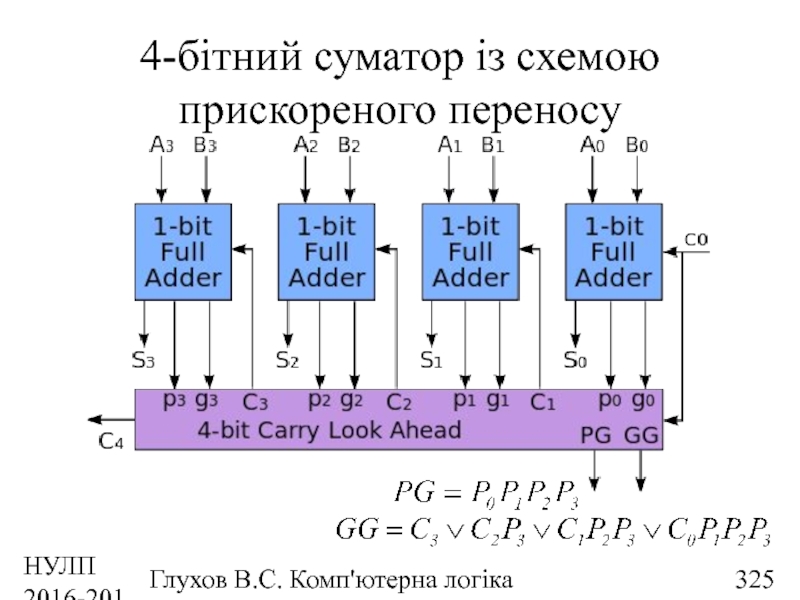
- 325. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка 4-бітний суматор із схемою прискореного переносу
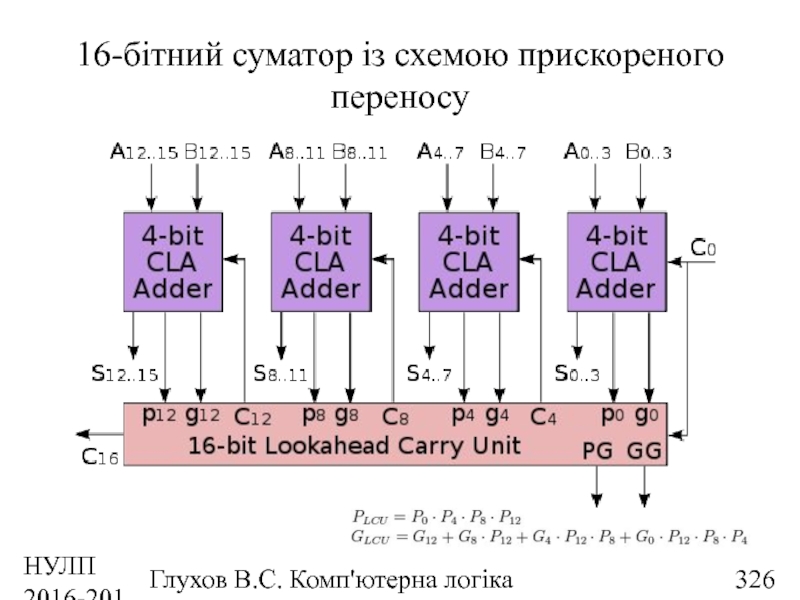
- 326. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка 16-бітний суматор із схемою прискореного переносу
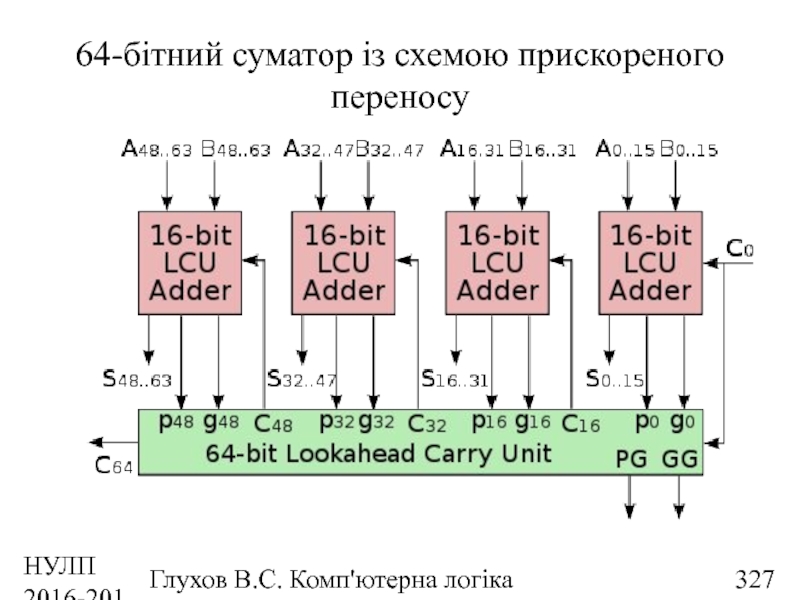
- 327. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка 64-бітний суматор із схемою прискореного переносу
- 328. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка
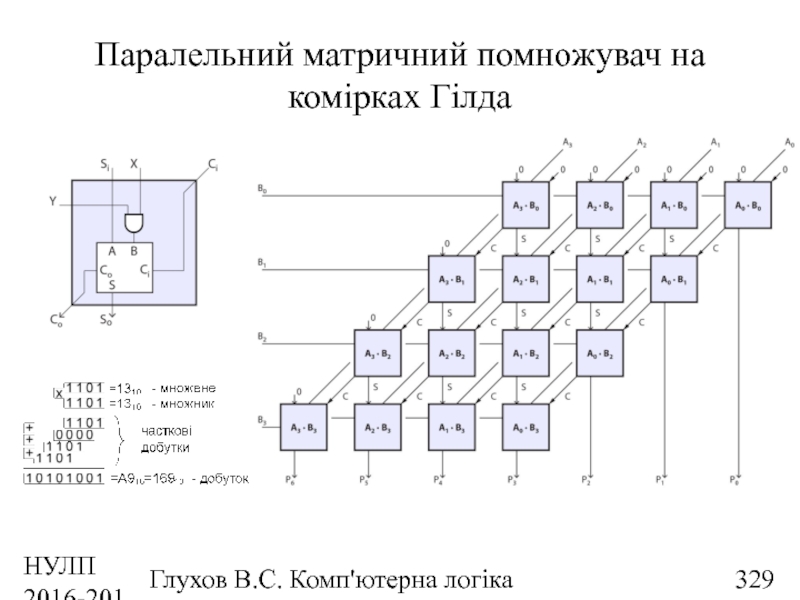
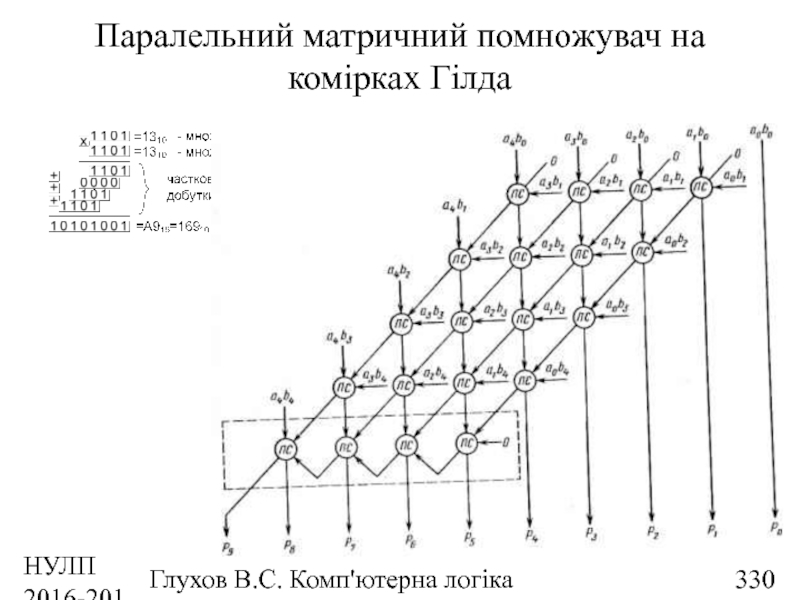
- 329. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Паралельний матричний помножувач на комірках Гілда
- 330. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Паралельний матричний помножувач на комірках Гілда
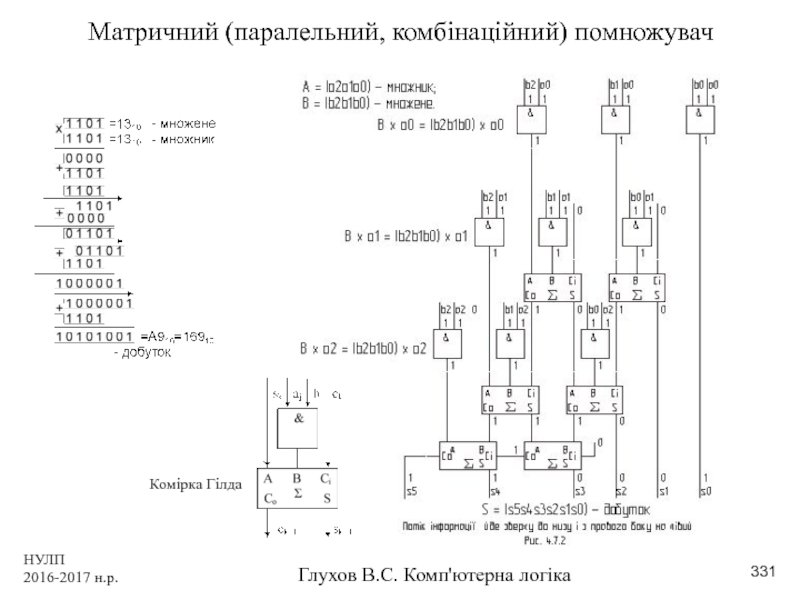
- 331. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Матричний (паралельний, комбінаційний) помножувач Комірка Гілда
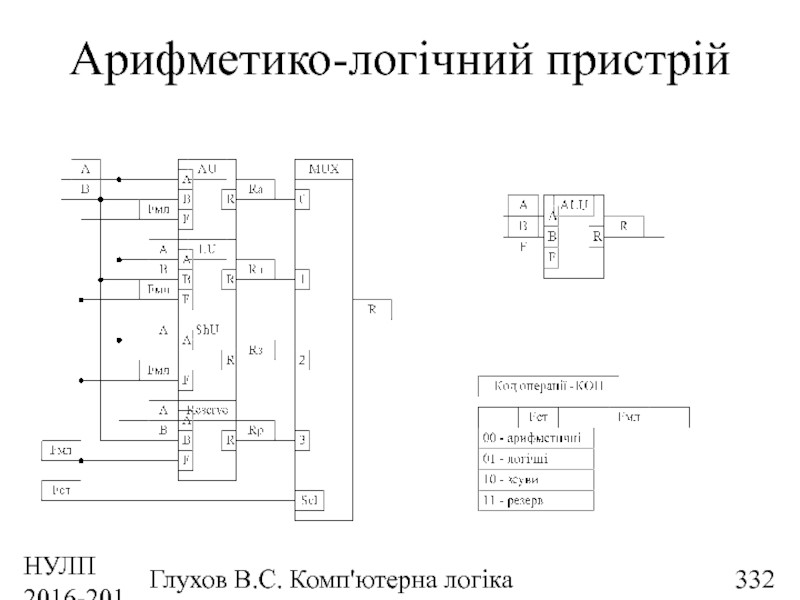
- 332. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Арифметико-логічний пристрій
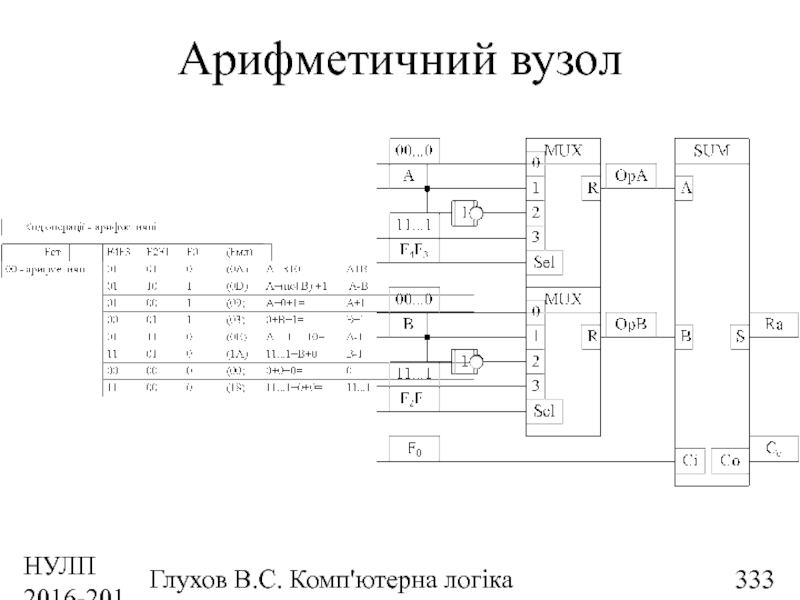
- 333. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Арифметичний вузол
- 334. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Логічний вузол
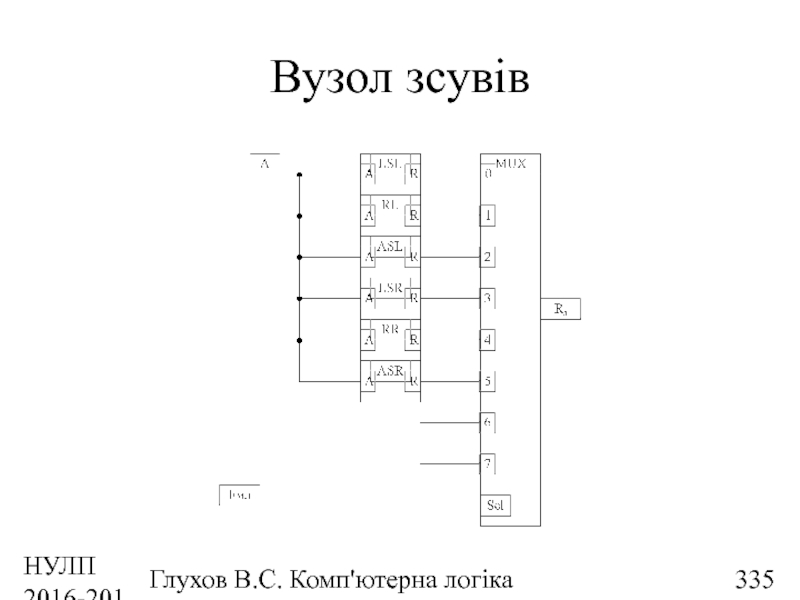
- 335. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Вузол зсувів
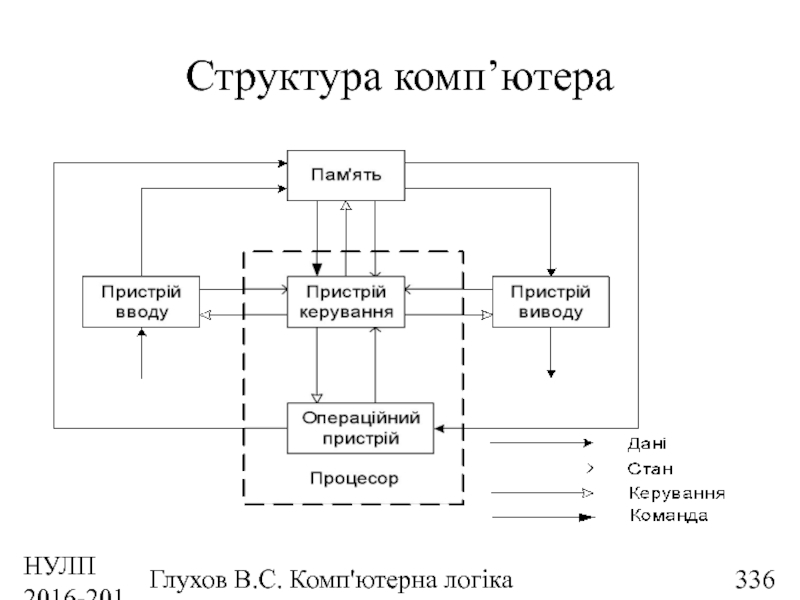
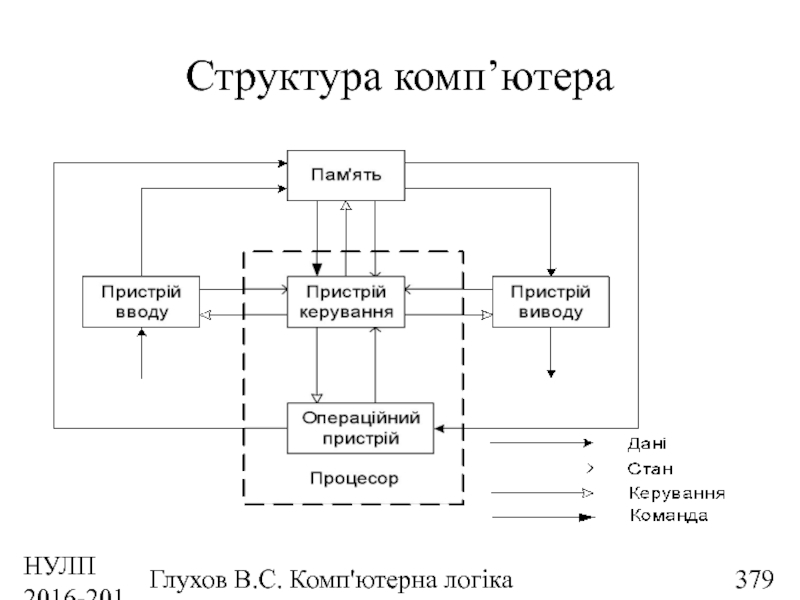
- 336. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Структура комп’ютера
- 337. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Загальна структурна схема цифрового автомата
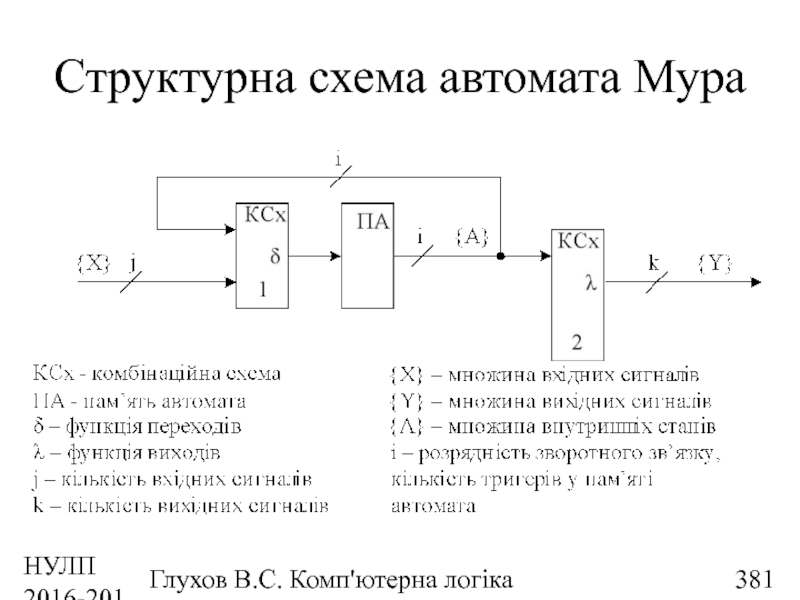
- 338. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Структурна схема автомата Мура
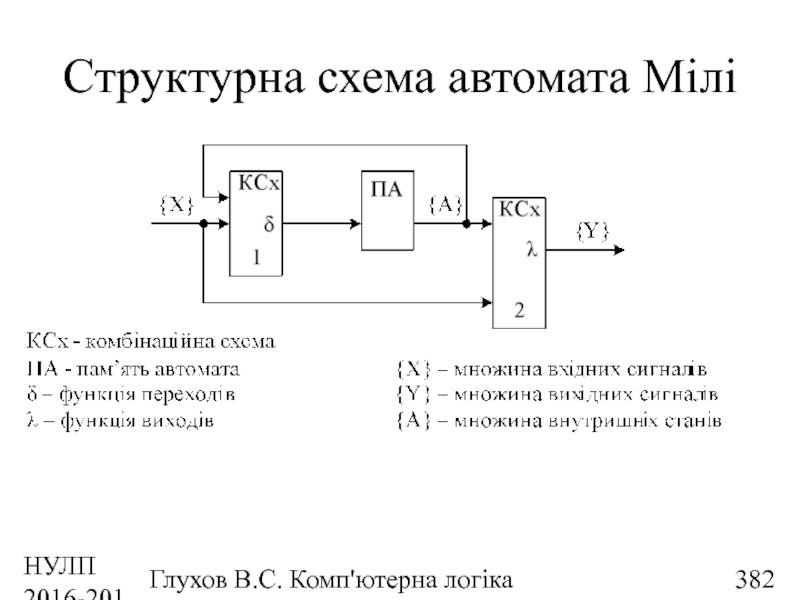
- 339. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Структурна схема автомата Мілі
- 340. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка
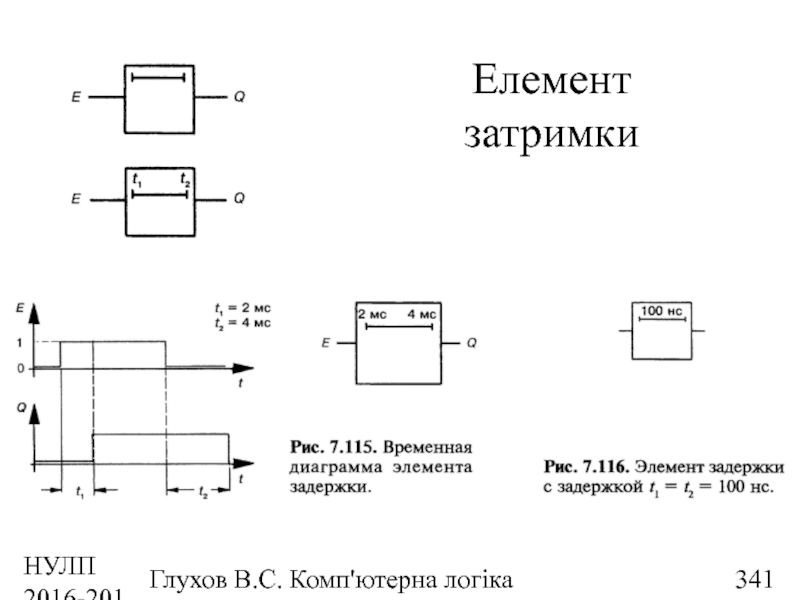
- 341. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Елемент затримки
- 342. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Часові ФАЛ 1-, 2- та 3-го роду
- 343. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка
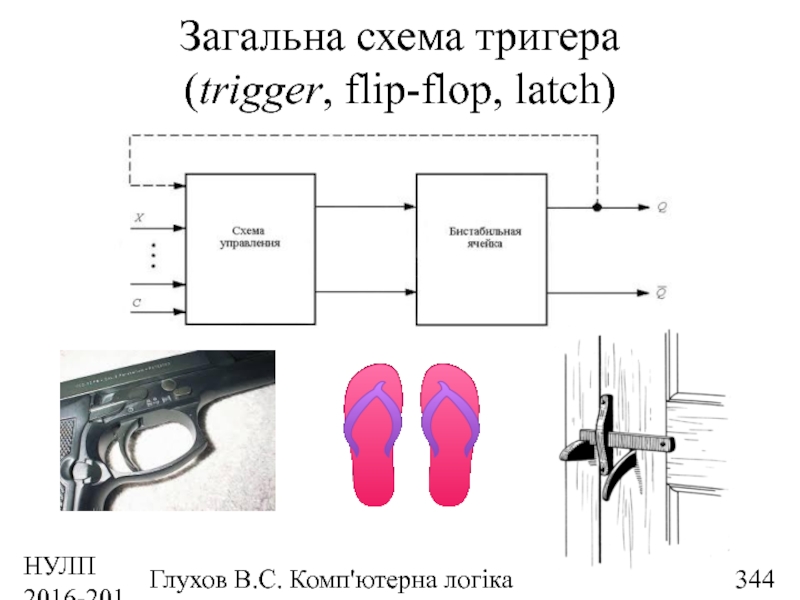
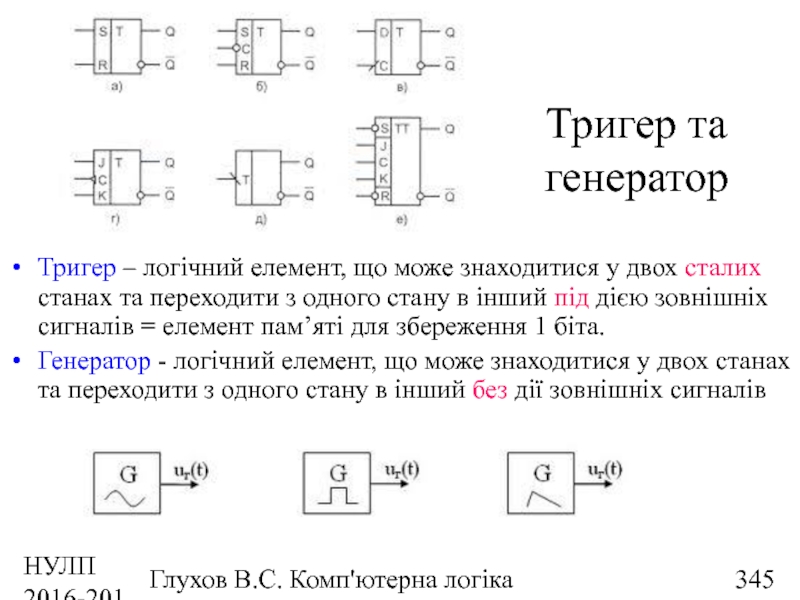
- 344. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Загальна схема тригера (trigger, flip-flop, latch)
- 345. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка
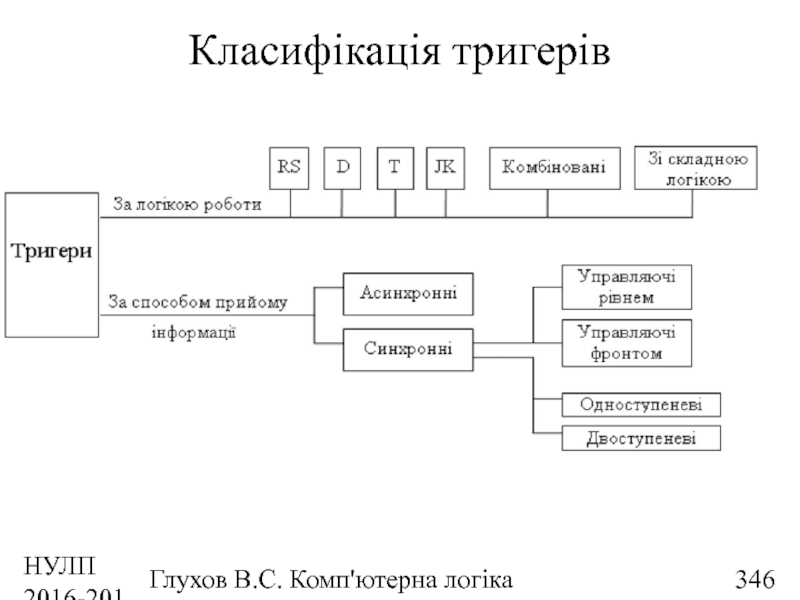
- 346. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Класифікація тригерів
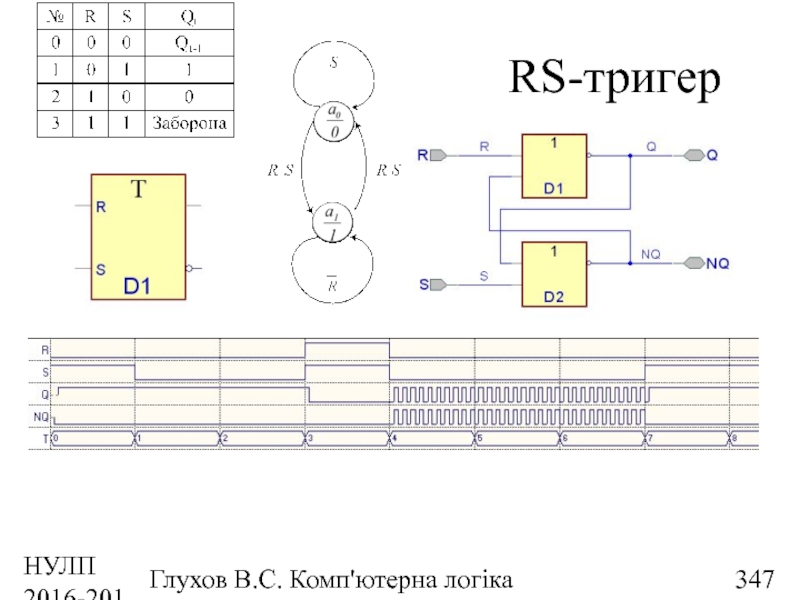
- 347. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка RS-тригер
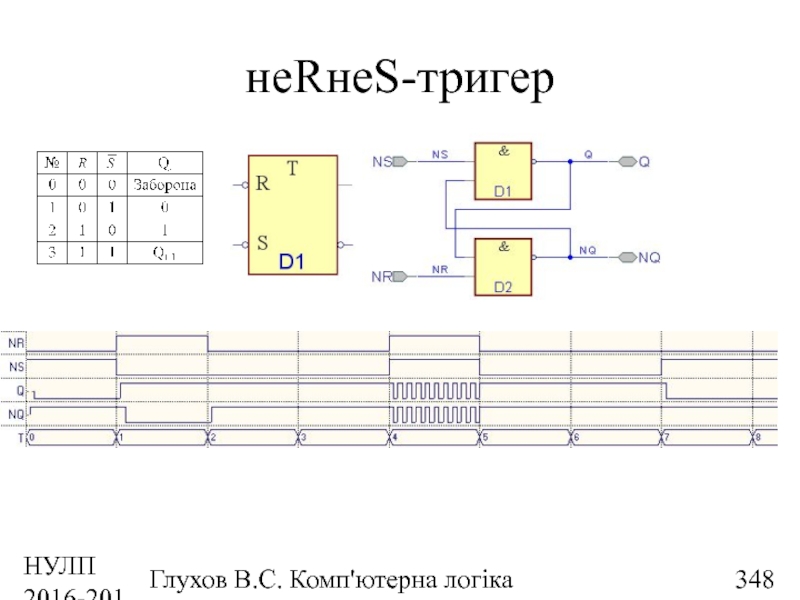
- 348. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка неRнеS-тригер
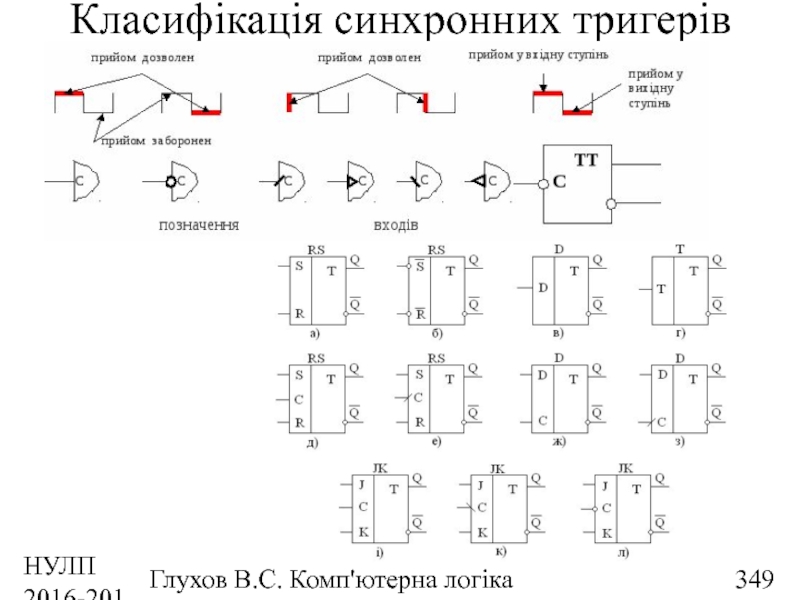
- 349. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Класифікація синхронних тригерів
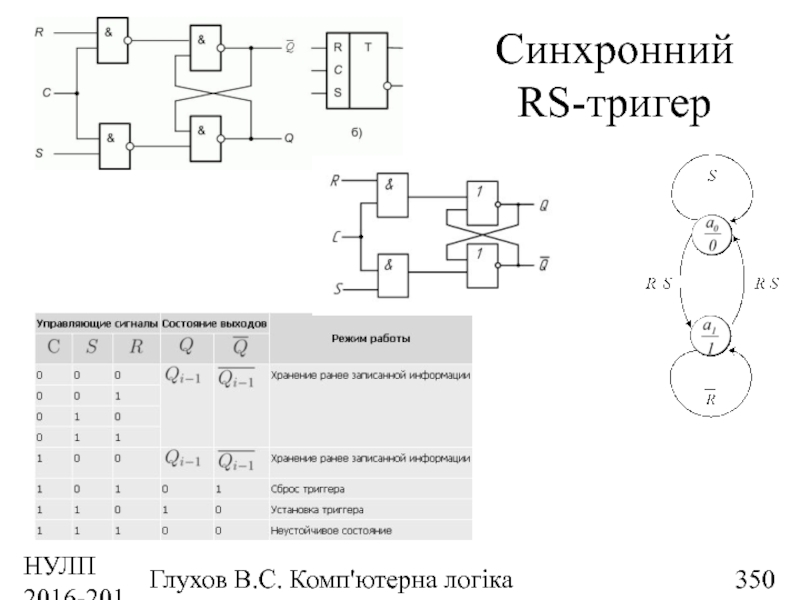
- 350. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Синхронний RS-тригер
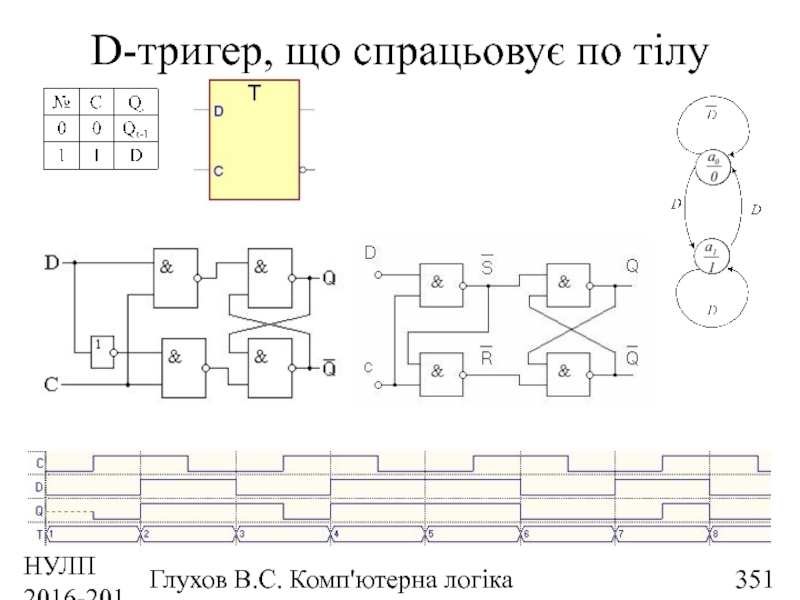
- 351. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка D-тригер, що спрацьовує по тілу
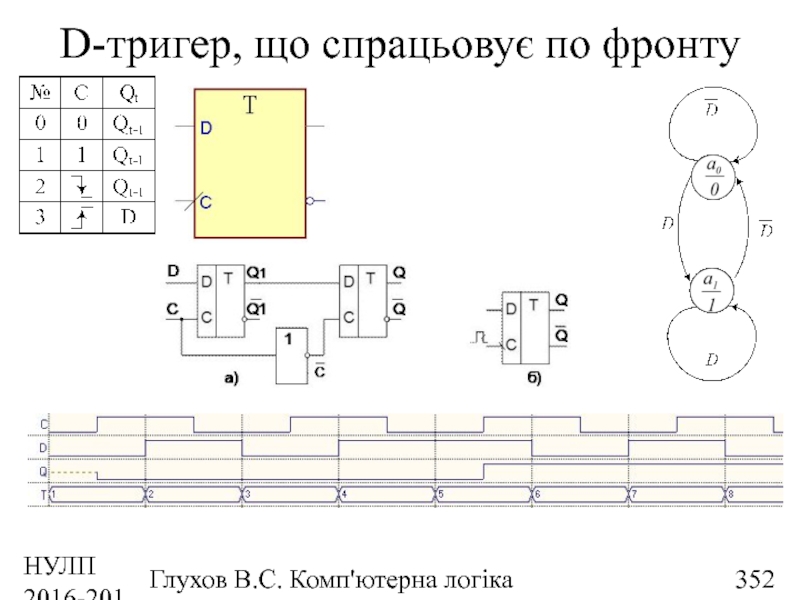
- 352. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка D-тригер, що спрацьовує по фронту
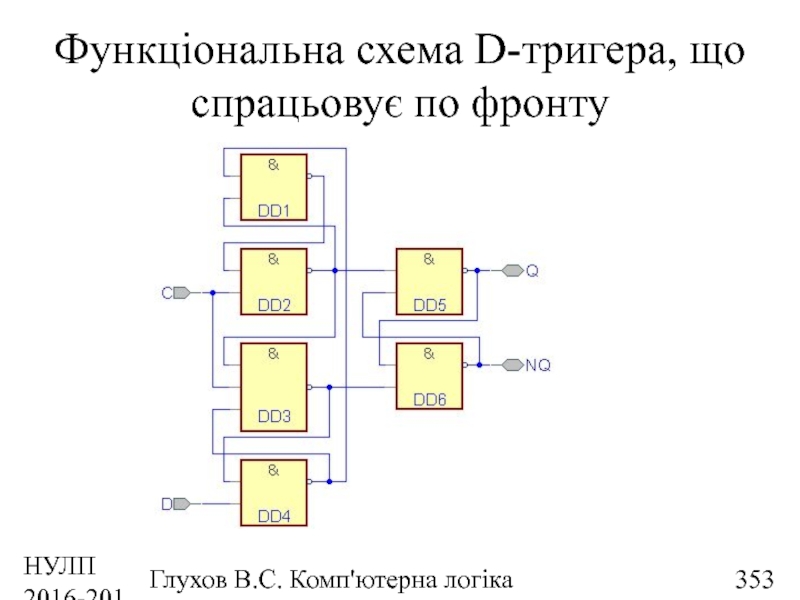
- 353. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Функціональна схема D-тригера, що спрацьовує по фронту
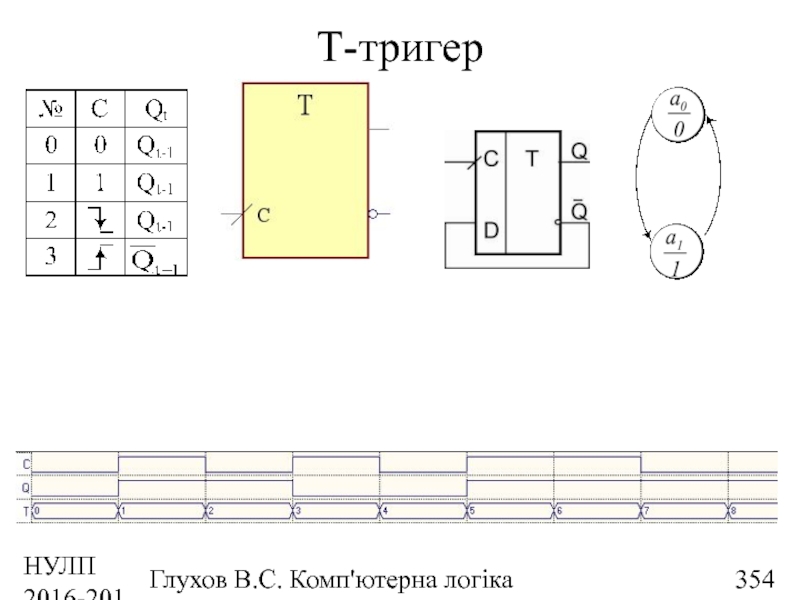
- 354. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Т-тригер
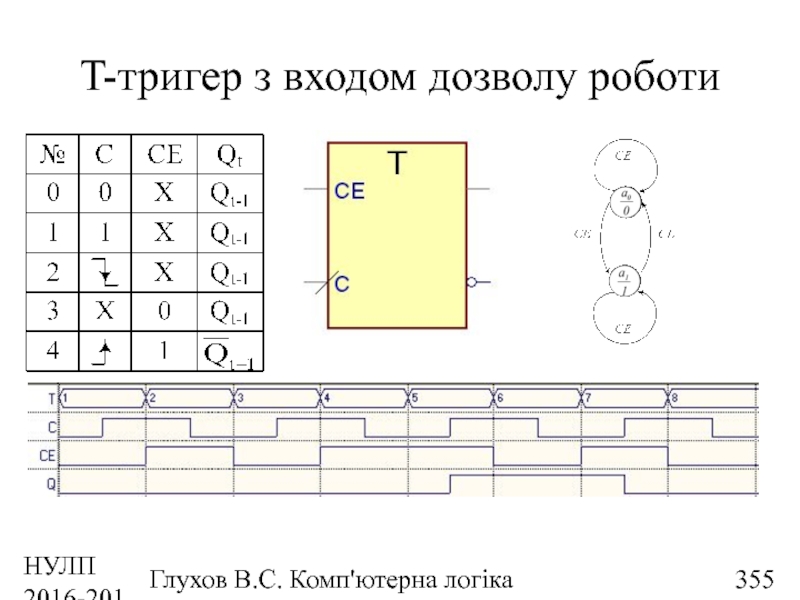
- 355. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка T-тригер з входом дозволу роботи
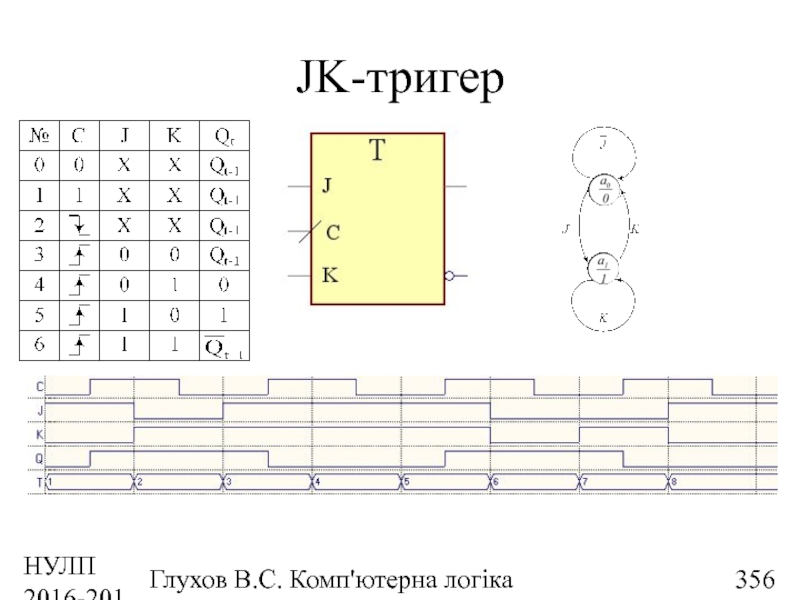
- 356. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка JK-тригер
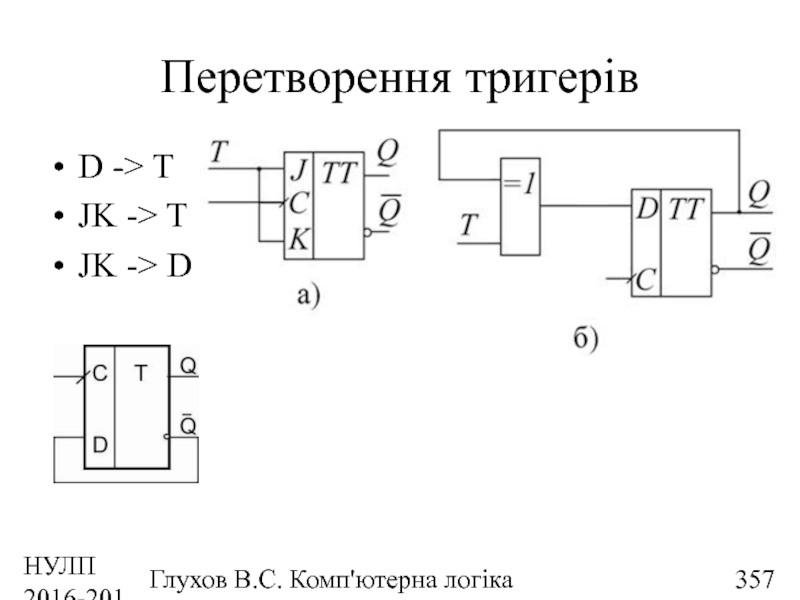
- 357. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка
- 358. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка
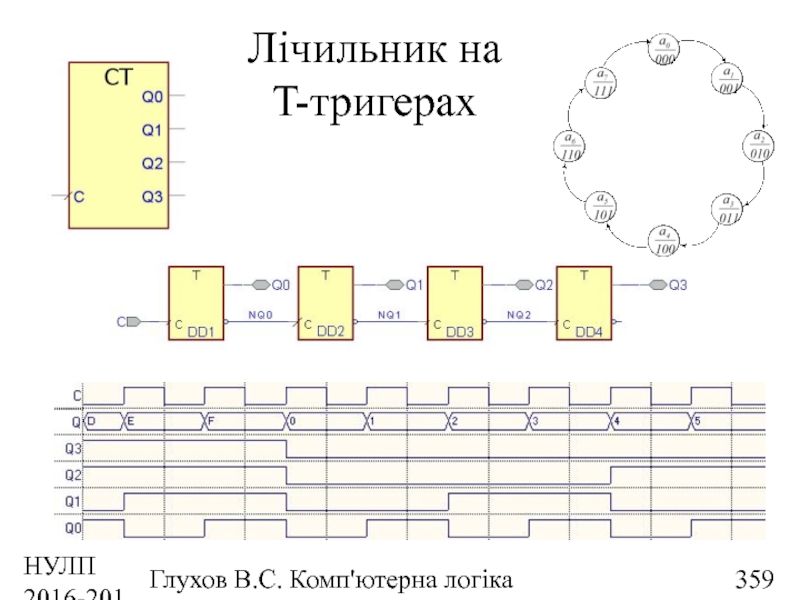
- 359. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Лічильник на T-тригерах
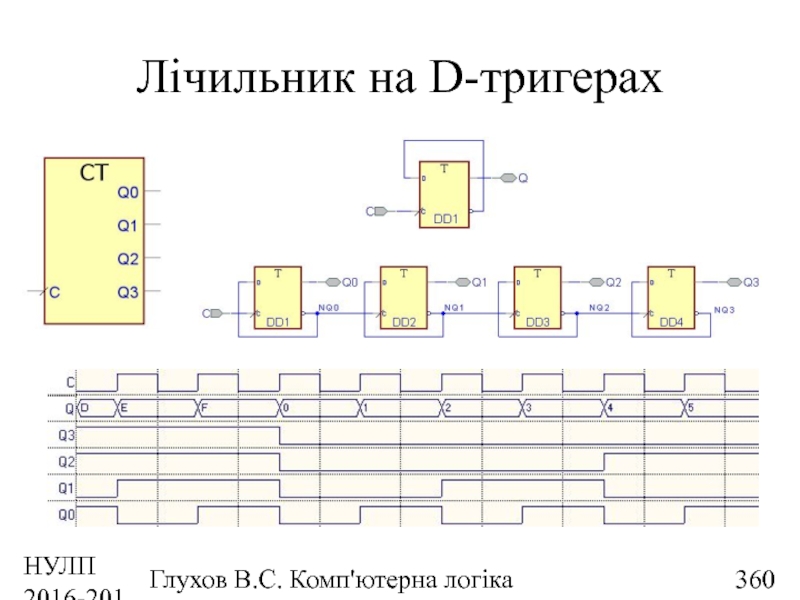
- 360. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Лічильник на D-тригерах
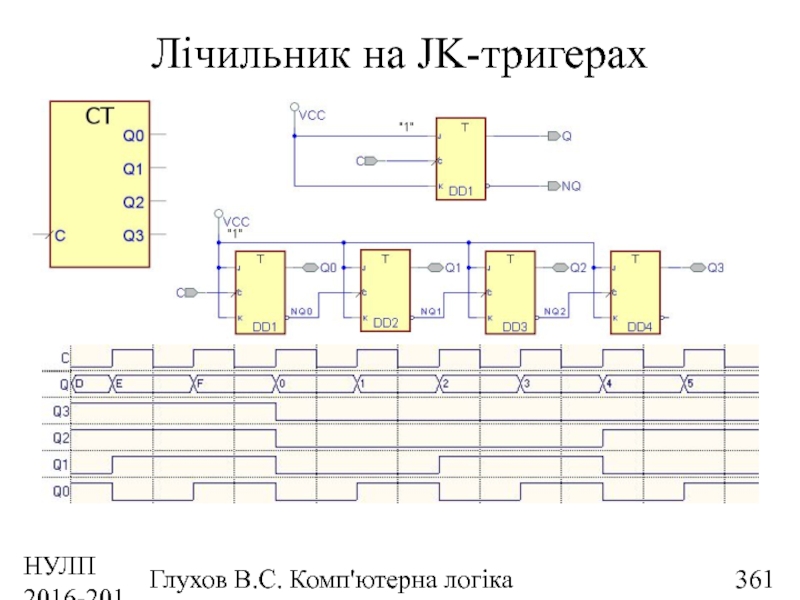
- 361. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Лічильник на JK-тригерах
- 362. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка
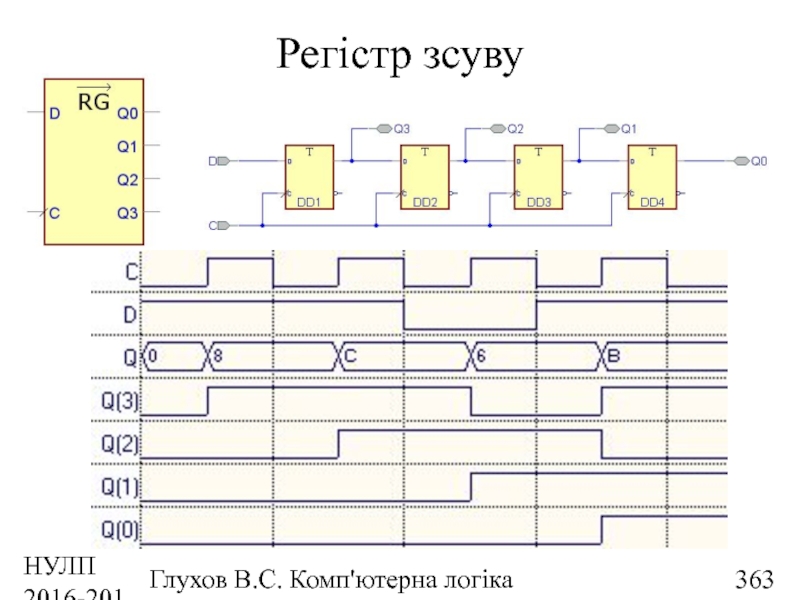
- 363. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Регістр зсуву
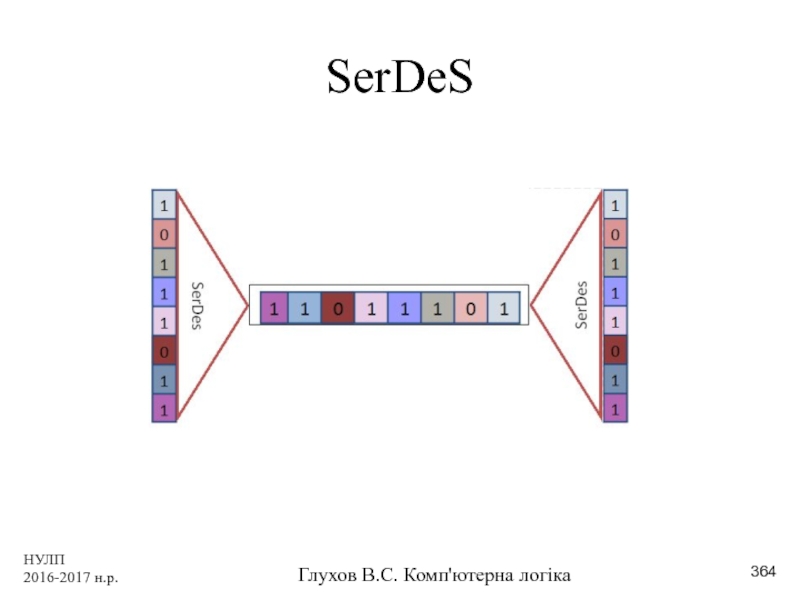
- 364. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка SerDeS
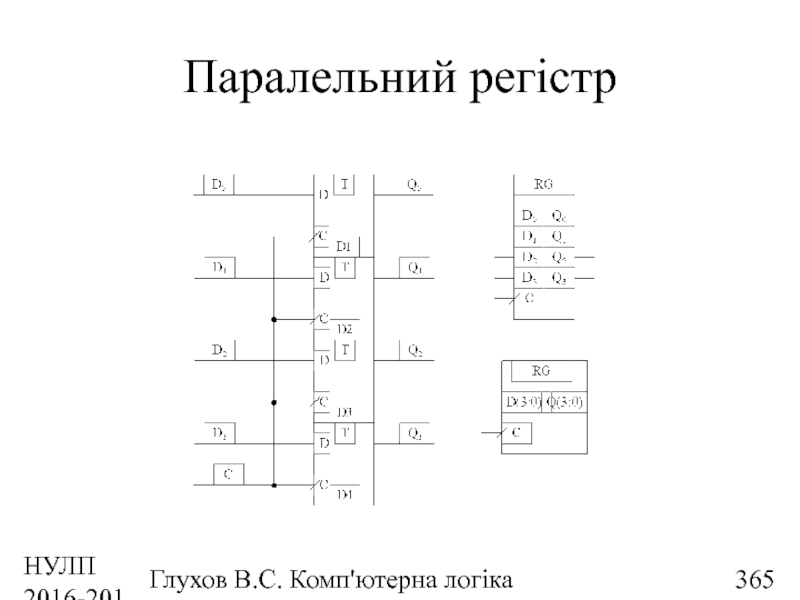
- 365. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Паралельний регістр
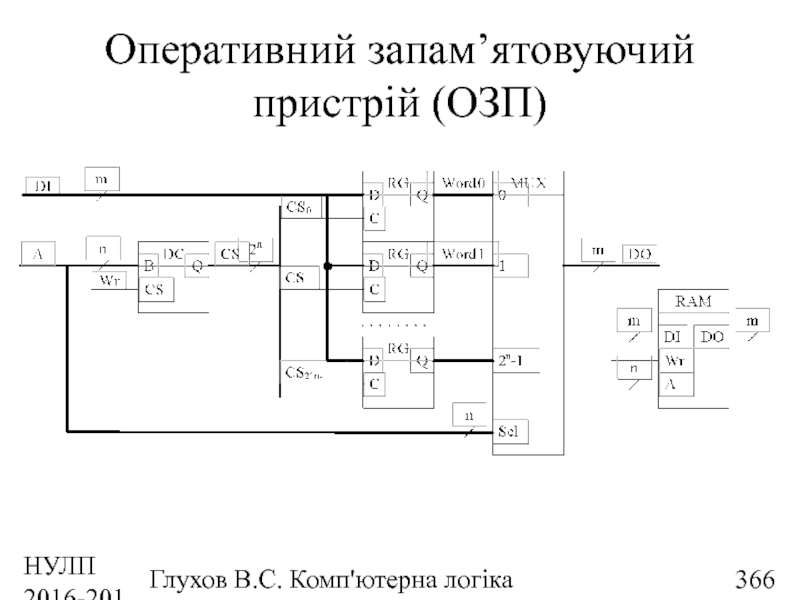
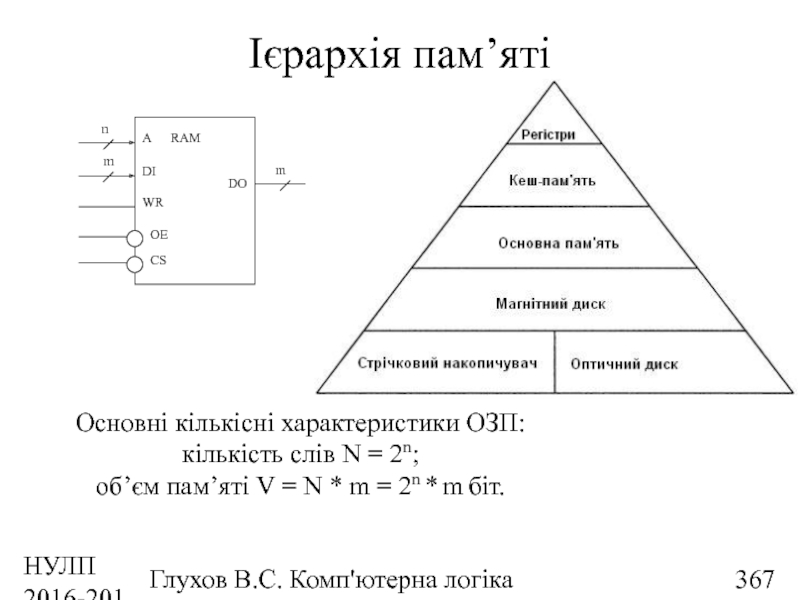
- 366. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Оперативний запам’ятовуючий пристрій (ОЗП)
- 367. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка
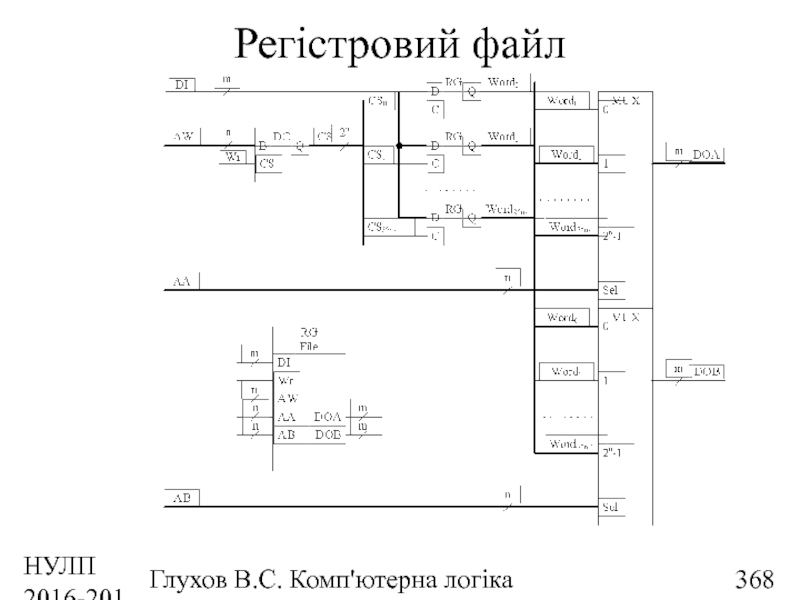
- 368. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Регістровий файл
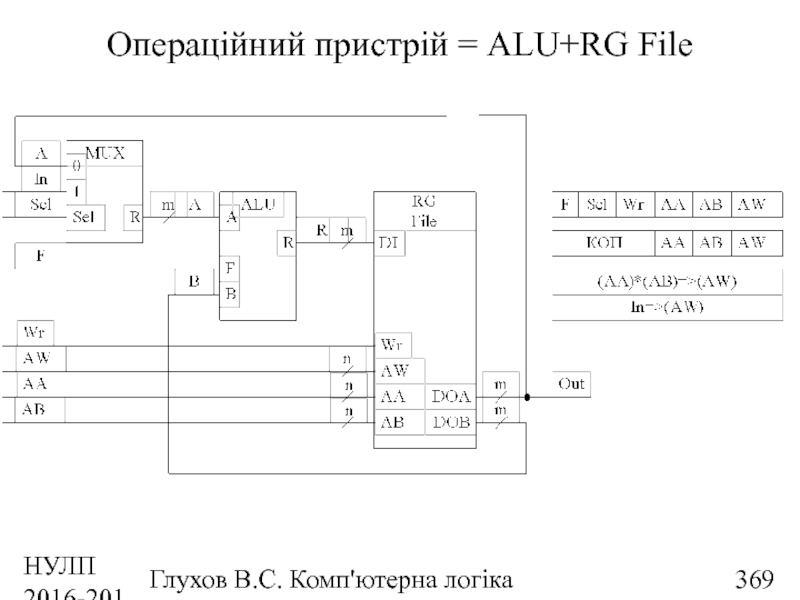
- 369. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Операційний пристрій = ALU+RG File
- 370. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Структура комп’ютера
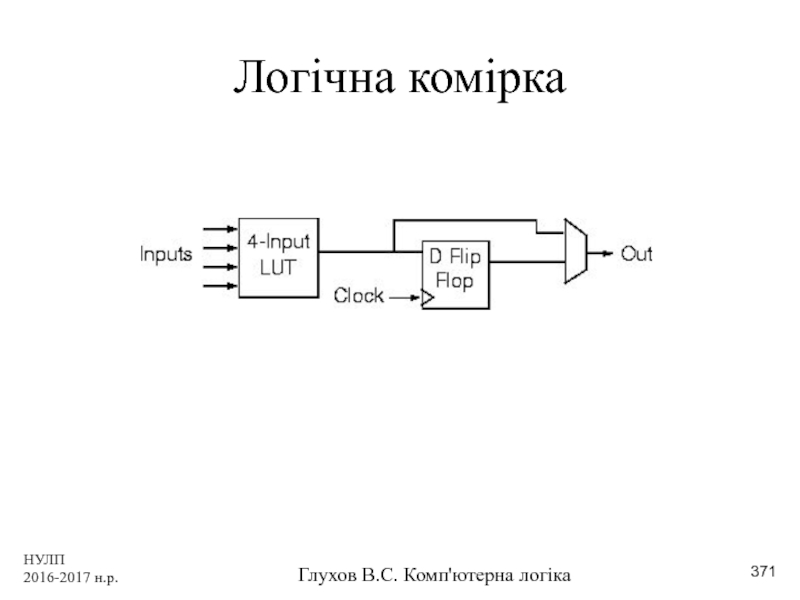
- 371. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Логічна комірка
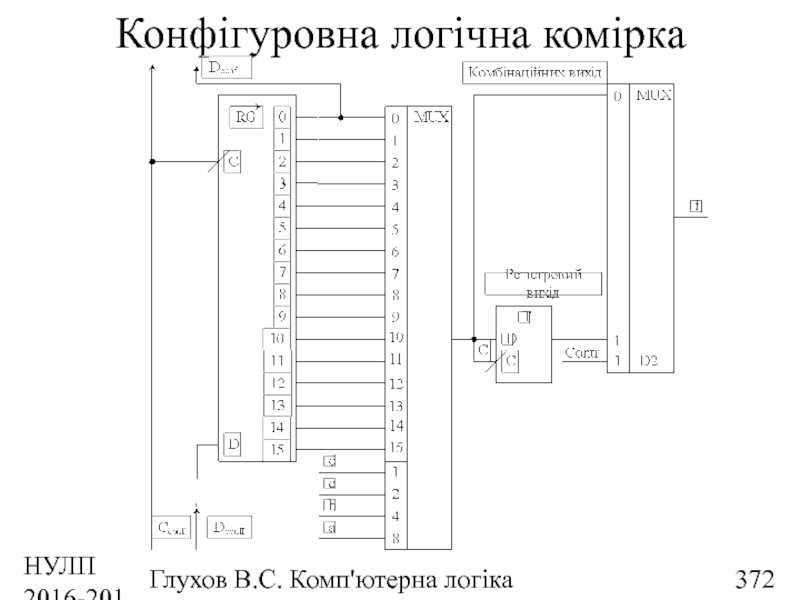
- 372. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Конфігуровна логічна комірка
- 373. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Логічні комірки в складі Slice
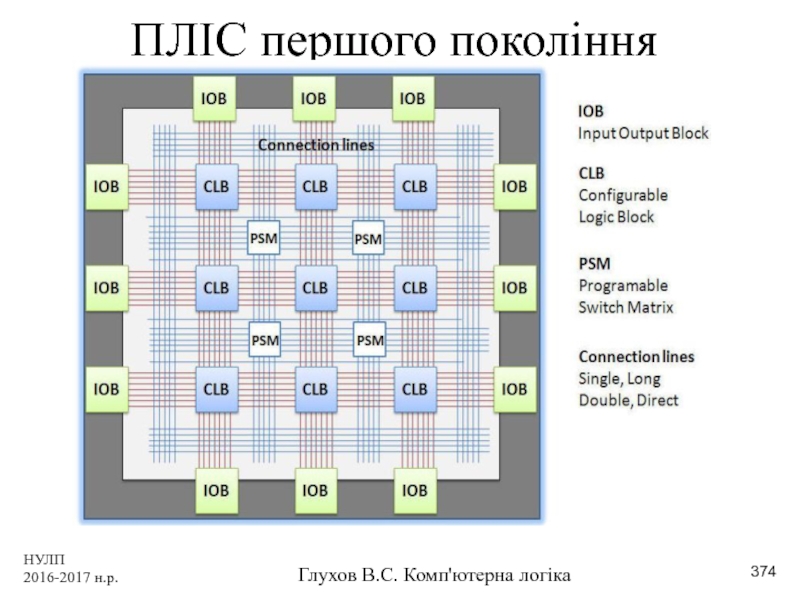
- 374. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка ПЛІС першого покоління
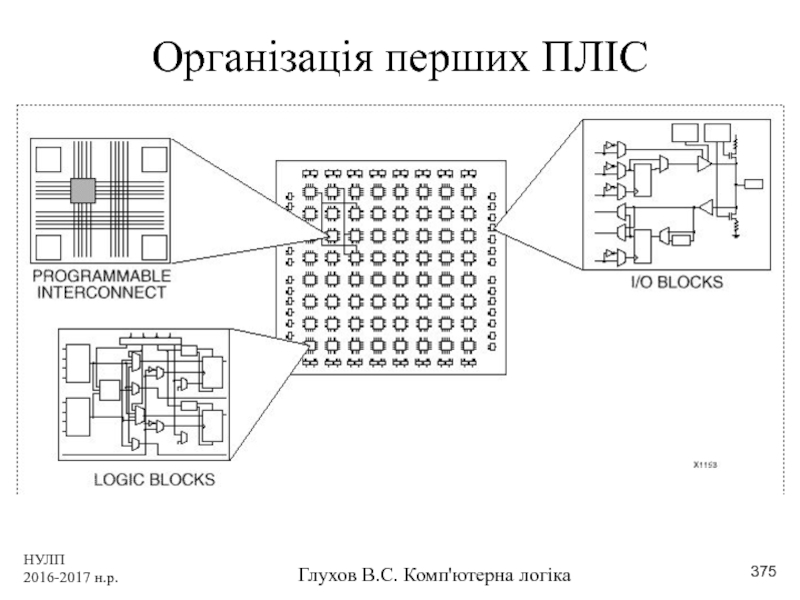
- 375. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Організація перших ПЛІС
- 376. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка
- 377. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Електронний комутатор
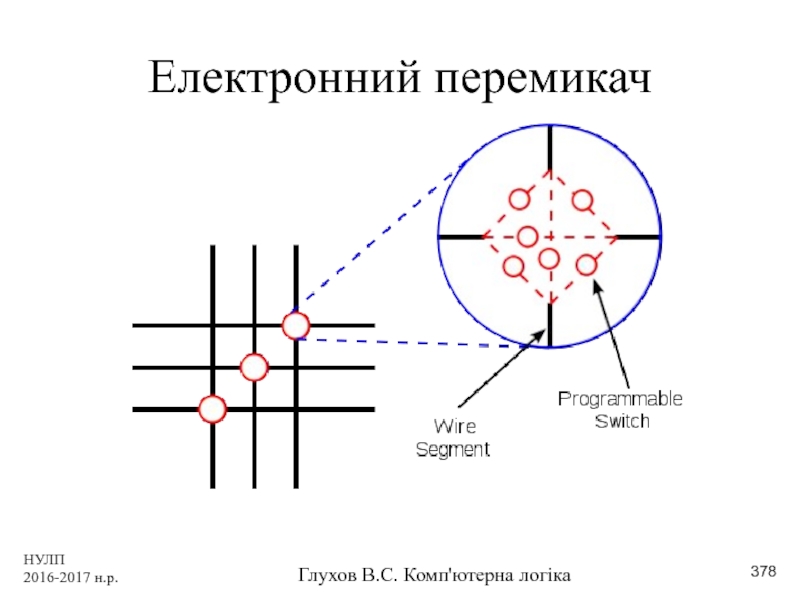
- 378. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Електронний перемикач
- 379. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Структура комп’ютера
- 380. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Загальна структурна схема цифрового автомата
- 381. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Структурна схема автомата Мура
- 382. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Структурна схема автомата Мілі
- 383. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка
- 384. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка
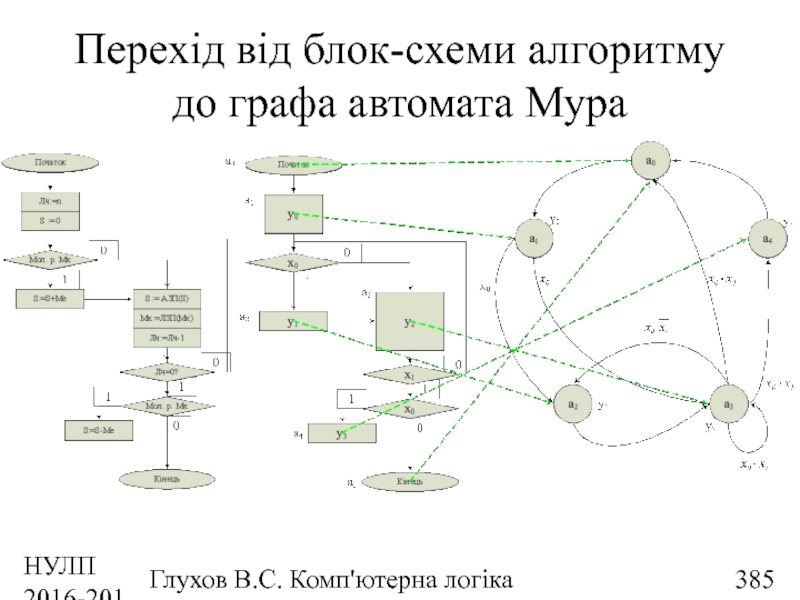
- 385. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Перехід від блок-схеми алгоритму до графа автомата Мура
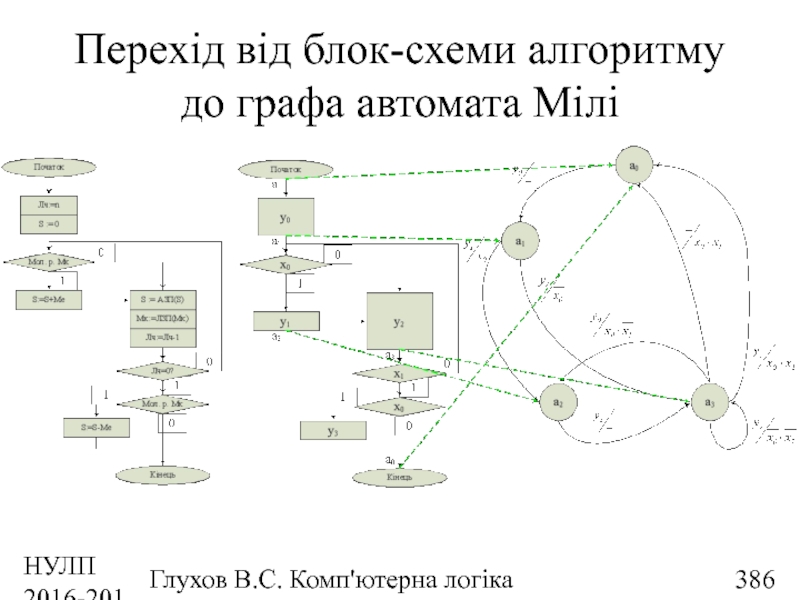
- 386. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Перехід від блок-схеми алгоритму до графа автомата Мілі
- 387. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Збудження тригерів
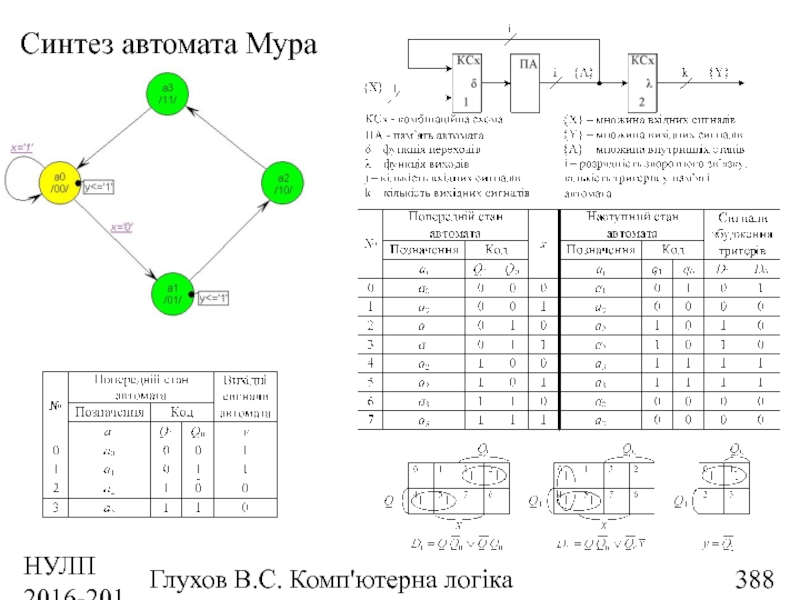
- 388. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Синтез автомата Мура
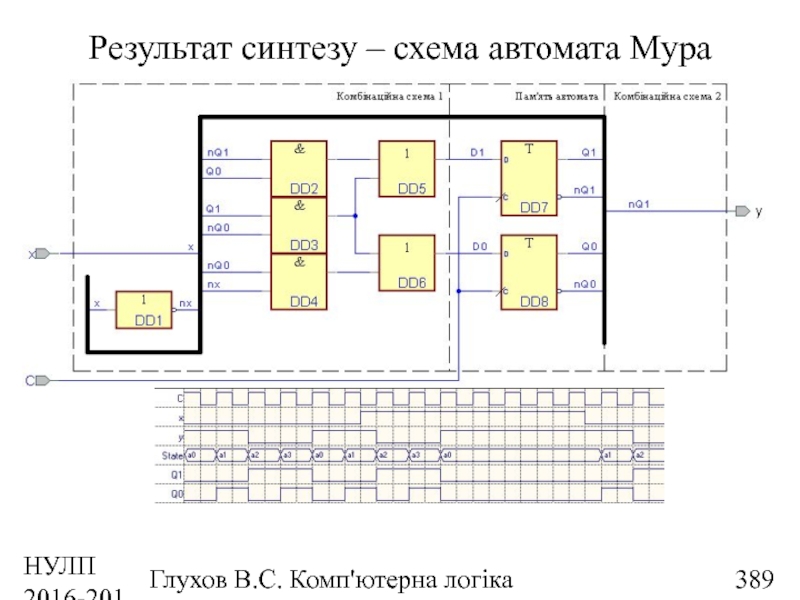
- 389. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Результат синтезу – схема автомата Мура
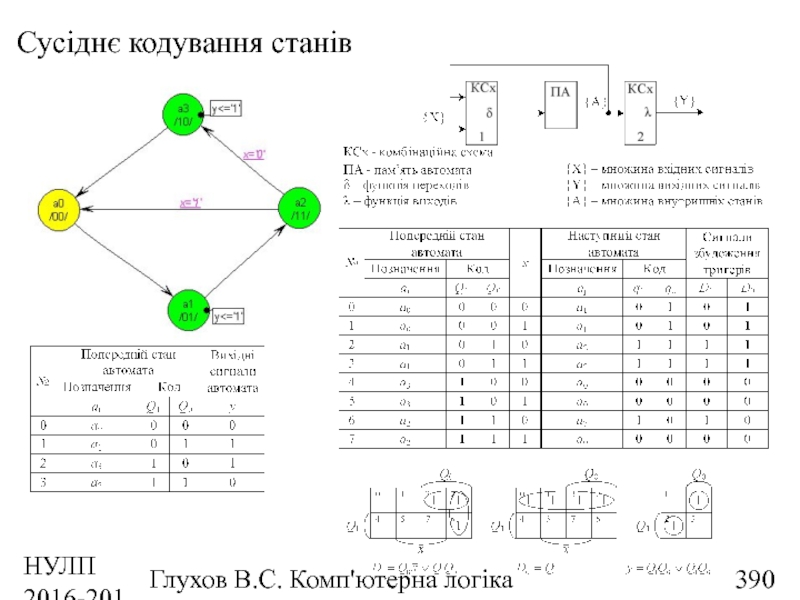
- 390. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Сусіднє кодування станів
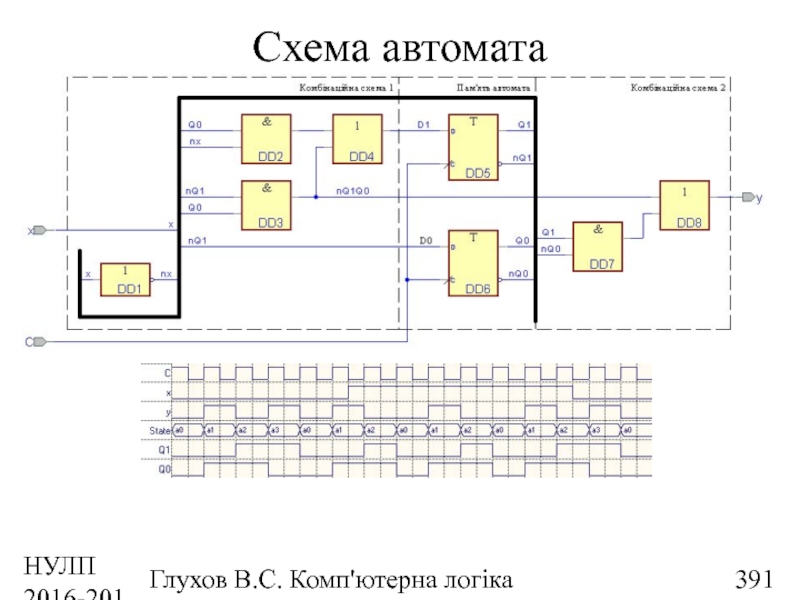
- 391. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Схема автомата
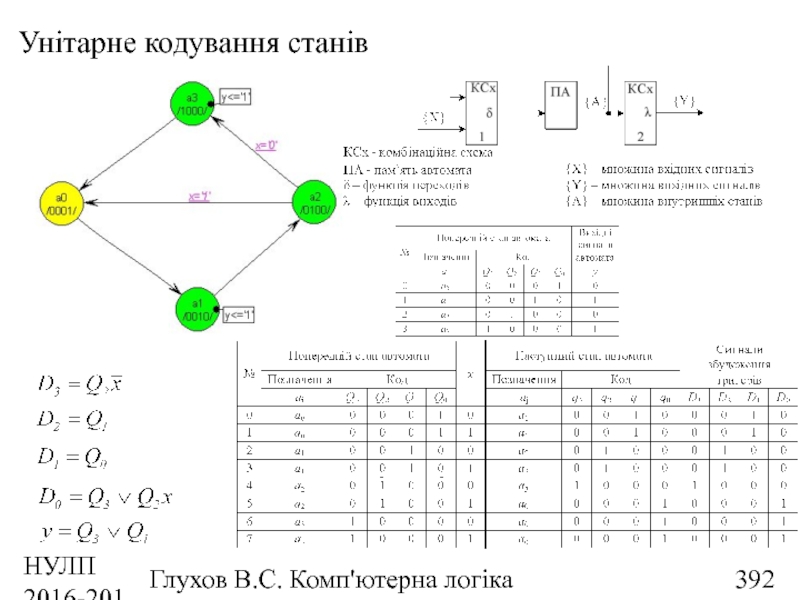
- 392. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Унітарне кодування станів
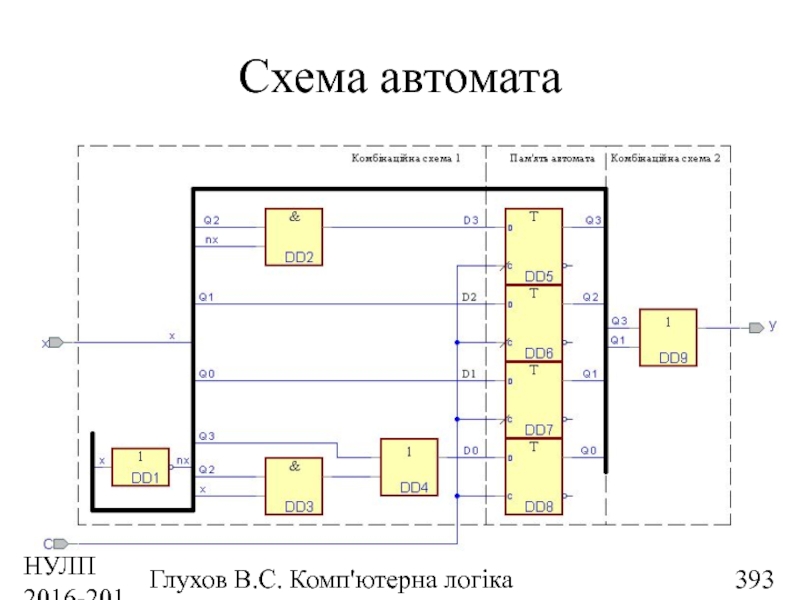
- 393. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Схема автомата
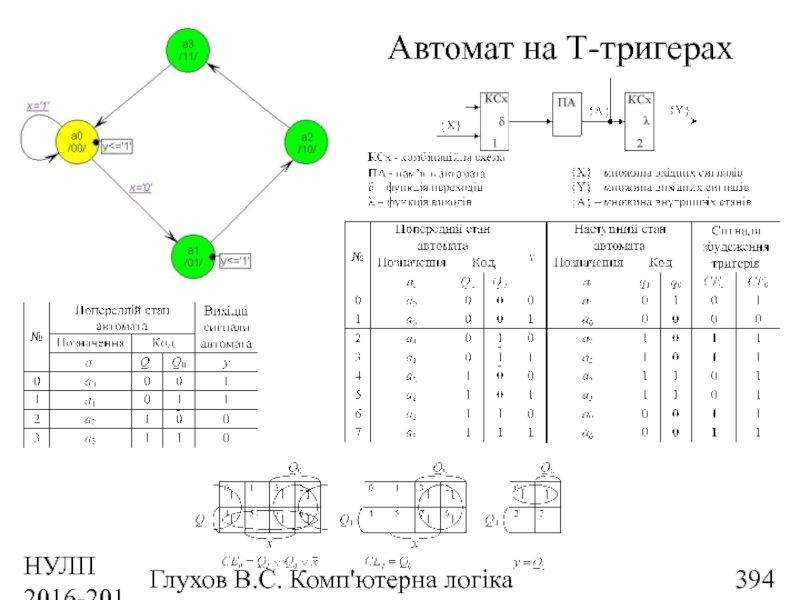
- 394. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Автомат на Т-тригерах
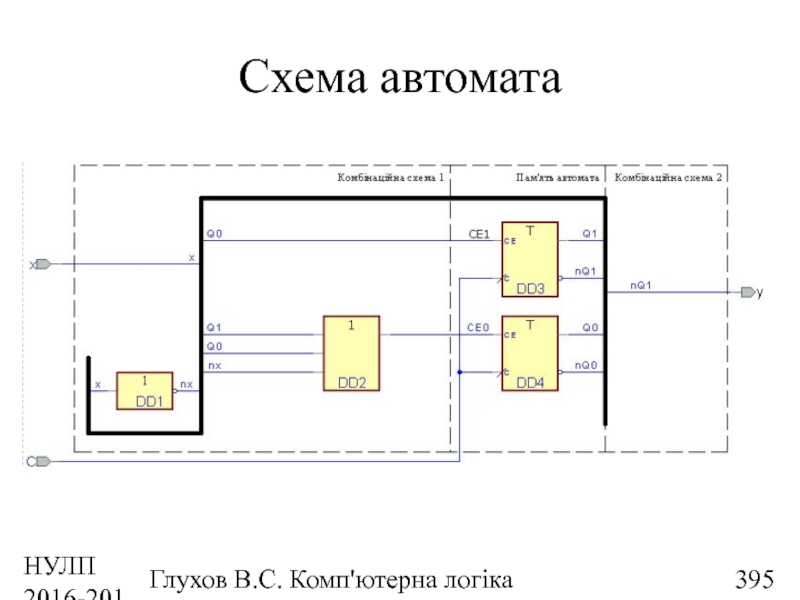
- 395. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Схема автомата
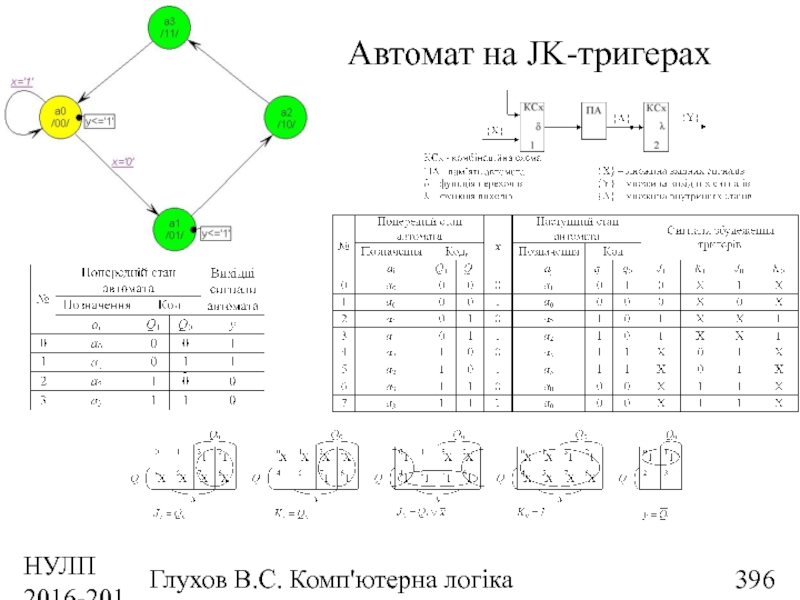
- 396. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Автомат на JK-тригерах
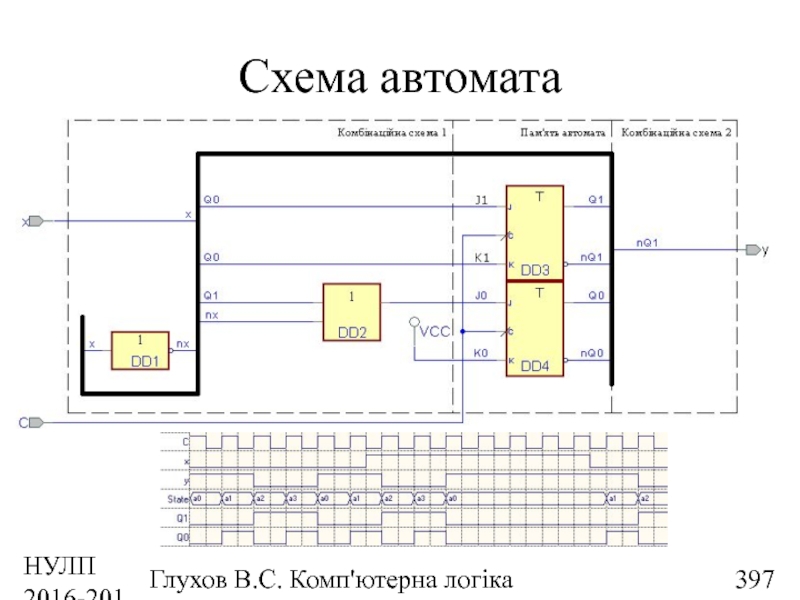
- 397. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Схема автомата
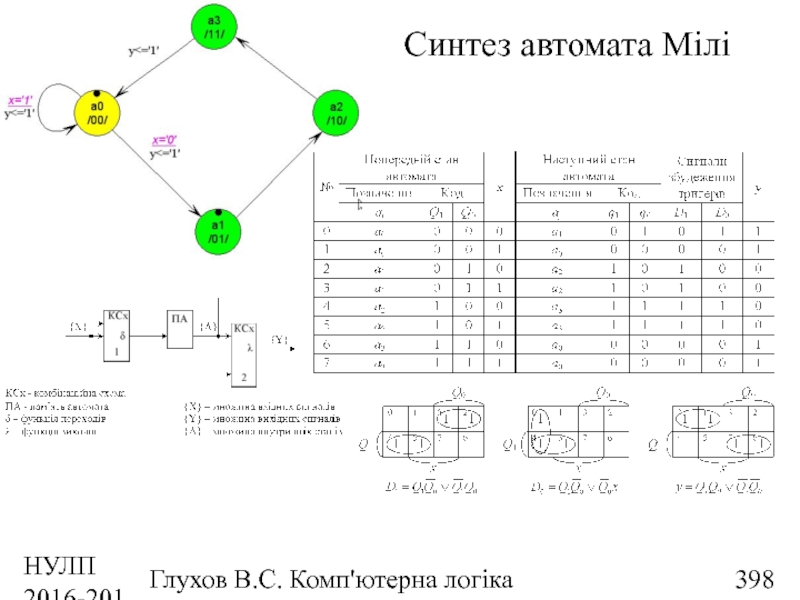
- 398. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Синтез автомата Мілі
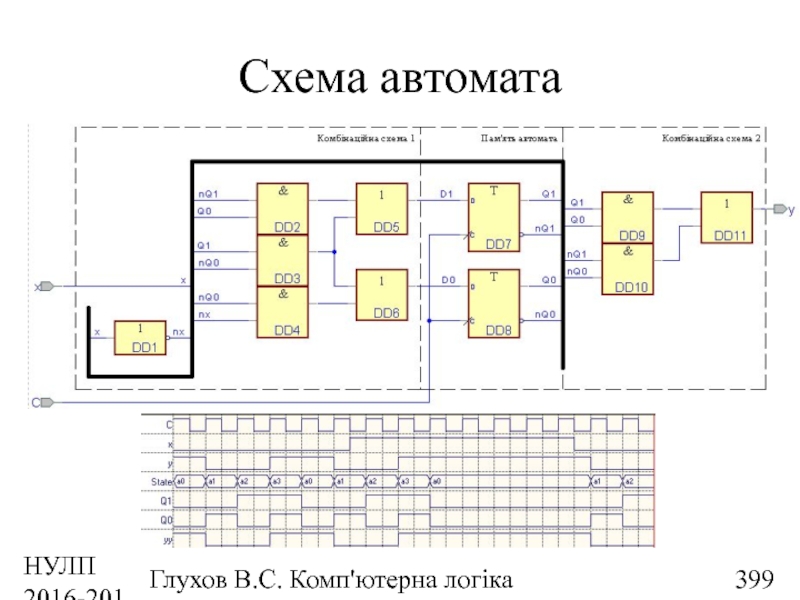
- 399. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Схема автомата
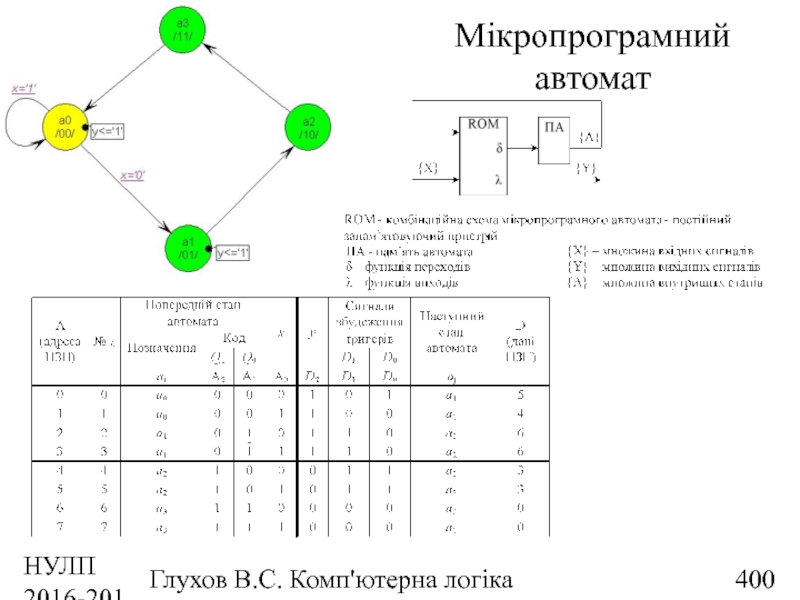
- 400. НУЛП 2016-2017 н.р. Глухов В.С. Комп'ютерна логіка Мікропрограмний автомат
Слайд 1НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
Національний університет «Львівська політехніка»
399 слайдів
Комп’ютерна логіка
Слайд 2НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
Лекція 1
Вступ - мета та задачі
Організаційні питання
Слайд 3НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
Розклад викладача, консультації – Пн, Чт
Слайд 4НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
Комп’ютерна логіка
ЛОГІКА - наука про закони і
КОМП’ЮТЕР – пристрій для передавання, зберігання та оброблення інформації
КОМП'ЮТЕРНА ЛОГІКА - умовна назва області досліджень, що ставиться до прикладної логіки, у якій логічні методи застосовуються для обробки даних і знань у комп'ютерних системах, при створенні системних програм, що забезпечують функціонування ЕОМ, при автоматизації програмування й при створенні ЕОМ нових поколінь. К. л. може виступати як сукупність засобів для імітації пізнавальних процесів у комп'ютерних системах з підвищеним рівнем інтелектуальних можливостей, забезпечуючи пошук необхідних знань для досягнення обраної мети й процес виводу результату, що відповідає цієї мети.
КОМП'ЮТЕРНА ЛОГІКА – наука про закони і різновиди мислення, якими користуються люди коли описують роботу комп’ютерів та працюють з ними (проектують, ремонтують, обслуговують, користуються)
Слайд 5НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
Національний університет “Львівська політехніка”
ІАРХ Архітектури
ІБІД Будівництва та інженерії
ІГДГ Геодезії
ІГСН Гуманітарних та соціальних наук
ІДН Дистанційного навчання
ІЕПТ Екології, природоохоронної діяльності та туризму ім. В’ячеслава Чорновола
ІНЕМ Економіки і менеджменту
ІЕСК Енергетики та систем керування
ІІМТ Інженерної механіки та транспорту
ІКНІ Комп'ютерних наук та інформаційних технологій
ІКТА Комп'ютерних технологій, автоматики та метрології
МІОК Міжнародний інститут освіти, культури та зв’язків з діаспорою
ІППТ Підприємництва та перспективних технологій
ІПДО Післядипломної освіти
ІНПП Права та психології
ІМФН Прикладної математики та фундаментальних наук
ІТРЕ Телекомунікацій, радіоелектроніки та електронної техніки
ІХХТ Хімії та хімічних технологій
Слайд 6НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
Комп'ютерних технологій, автоматики та метрології
БІТ Кафедра безпеки
ЕОМ Кафедра електронних обчислювальних машин
ЗІ Кафедра захисту інформації
ІВТ Кафедра інформаційно-вимірювальних технологій
КСА Кафедра комп'ютеризованих систем автоматики
МСС Кафедра метрології, стандартизації та сертифікації
ПТМ Кафедра приладів точної механіки
СКС Кафедра спеціалізованих комп'ютерних систем
Слайд 7НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
Кафедри ЕОМ та СКС
Бакалаврат (каф. ЕОМ
Магістри (спеціалізації каф. ЕОМ)
Комп’ютерні системи та мережі
Кіберфізичні системи
Системне програмування
Магістри (спеціалізація каф. СКС)
Спеціалізовані комп’ютерні системи
Слайд 8НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
Структура семестру
16 навчальних тижнів (16 лекцій,
Заліковий тиждень
Сесія (2 тижні)
Слайд 9НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
Державна оцінка (залік)
1. За результатами семестрової
2а. Оцінка на комісії
або
2б. Оцінка за результатами повторного вивчення курсу
Слайд 10НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
Стандартні вимоги до відповідей на заліках
Повинна бути дана відповідь на усі питання білету
Під час підготовки до відповіді нічим не можна користуватися
Під час підготовки до відповіді ні с ким не можна перемовлятися та обмінюватися інформацією
Для допуску до сесії потрібно виконати навчальний план
Слайд 11НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
Виконання навчального плану
Студент погоджується самостійно опрацювати
Здана розрахункова робота (є оцінка)
Виконано програму практичних занять
Написано усі 16 лекційних контрольних робіт
Дано відповідь на усі 10 питань семестрової контрольної роботи
Є конспект лекцій (приблизно 5 сторінок на лекцію)
Правильно дано відповіді на усі питання тестів до 1-ої частини Комп’ютерної логіки (1-ий курс) у ВНС
Слайд 12НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
Полегшені умови отримання семестрової оцінки
Білет семестрової
Виконано розрахункову роботу
За практичні заняття отримано більше 18 балів (з 25)
Написано усі лекційні контрольні роботи на дану дату
Правильно дано відповіді на усі питання тестів до 1-ої частини Комп’ютерної логіки (1-ий курс) у ВНС
Є конспект лекцій (приблизно 5 сторінок на лекцію)
Під час підготовки до відповіді дозволяється користуватися чим завгодно
Повинна бути дана відповідь на усі питання білету
Слайд 13НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
Оцінювання відповідей при стандартному підході
Оцінювання відповідей
Слайд 14НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
Покращення оцінок
Було 51 бал – 51%
(поточний контроль – 1 з 30, іспит - 50 з 70,
3% з 30 за поточку і 71% з 70 за іспит)
Хоче “добре” (71 бал – 71% від 100 балів)
Тоді треба набрати спочатку за поточний контроль 71% від 30 = 21 бал,
а після того -71% від 70 =50 балів за іспит.
Слайд 15НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
Методичні вказівки до курсової роботи “Арифметичні
ВСТУП
ЗАВДАННЯ НА РОБОТУ, ВКАЗІВКИ ЩОДО ВИБОРУ ВАРІАНТА РОБОТИ
1 МЕТОДИЧНІ ВКАЗІВКИ ЩОДО КОДУВАННЯ ІНФОРМАЦІЇ ТА ПЕРЕТВОРЕННЯ КОДІВ
1.1 W1
1.1.1. Переведення чисел до десяткової системи числення з іншої однорідної позиційної системи числення з основою k, коли дії виконуються в десятковій системі
1.1.2. Переведення чисел із десяткової системи числення до іншої однорідної позиційної системи числення з основою k, коли дії виконуються в десятковій системі
1.1.3. Переведення цілої частини числа
1.1.4. Переведення дробової частини числа
1.1.5. Переведення чисел з шістнадцяткової й вісімкової систем до двійкової і зворотне переведення чисел
1.2 W2 Ефективне кодування. Система залишкових класів
1.2.1. Алгоритм ефективного кодування Шеннона – Фано
1.2.2. Ентропія.
1.2.3. Система залишкових класів
1.3 Код Геммінга
1.4 Визначення помилкових станів при зміні двійкових кодів
Слайд 16НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
Методичні вказівки до курсової роботи “Арифметичні
2 МЕТОДИЧНІ ВКАЗІВКИ ЩОДО ВИКОРИСТАННЯ ФУНКЦІЙ АЛГЕБРИ ЛОГІКИ ТА МІНІМІЗАЦІЇ ЦИХ ФУНКЦІЙ У БАЗИСІ БУЛЯ
2.1 Функціональна повнота системи функцій алгебри логіки і наборів логічних елементів
2.2 Мінімізація функцій методом Квайна-МакКласкі-Петрика
2.3 Мінімізація функцій за допомогою карт Карно
2.4 Визначення сполучного терма
Слайд 18НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
Відробка пропущених лекційних контрольних робіт
Копія конспекту
Слайд 22НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
Конспект
Поле – для важливих приміток (дата,
Основна частина – для скороченого запису помилок, які робить викладач
Графічна частина
Текстові пояснення
Знизу - № сторінки, Прізвище І.П.
Слайд 23НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
Навички (компетенції) випускників
конвертувати академічні знання і
вирішувати складні задачі в галузі комп'ютерної техніки та ефективно адаптуватися у швидко мінливому середовищі;
використовувати систематичний і методичний стиль роботи;
застосовувати правильну термінологію і позначення як у письмовій формі так і в усній;
обговорювати основні теорії та методи аналізу і обробки аналогових і цифрових сигналів з використанням правильної термінології;
застосувати знання математики та фізики (у тому числі теорії ймовірності, статистики та дискретної математики, діференціального та інтегрального числення), інші досягнення науки і техніки;
Слайд 24НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
Навички (компетенції) випускників
визначити, формулювати та проводити
планувати і проводити експерименти та тести, а також аналізувати та інтерпретувати отримані експериментальні дані та робити обгрунтовані висновки;
критично мислити, аналізувати і приймати рішення, які належним чином враховують глобальні проблеми в
бізнесі,
етиці,
моралі,
суспільстві і
навколишньому середовищі;
Слайд 25НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
Навички (компетенції) випускників
проектувати комп’ютерні системи, компоненти
економічних,
екологічних,
соціальних,
політичних,
етичних,
здоров'я та безпеки,
технологічності і
стійкості;
Слайд 26НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
Навички (компетенції) випускників
розробляти та реалізовувати апаратні
продуктивності,
економічної ефективності,
безпеки,
маса-габаритних характеристик,
часу,
споживання,
ефективності і
ергономічності та ефективності користувальницьких інтерфейсів;
Слайд 27НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
Навички (компетенції) випускників
розуміти вплив технічних рішень
бути в змозі оцінити можливості та обмеження теорій та методів, застосовуваних на практиці;
працювати в команді;
ефективно працювати в рамках міждисциплінарних команд, у тому числі вміння працювати з колегами для того, щоб розробити і побудувати комплексну комп’ютерну систему;
Слайд 28НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
Навички (компетенції) випускників
розуміти фундаментальні засади ефективного
визначити, формулювати і вирішувати технічні задачі;
обговорювати концепції створення комп’ютерних системи та мереж, особливостей використання Інтернет-технологій;
визначати необхідність, проектувати, впроваджувати та оцінювати життєздатність рішень для вбудованих комп’ютерних систем, що працюють у реальному часі;
виявляти, формулювати, аналізувати і створювати інженерні рішення з використанням відповідних сучасних технологій, методів та інструментів, в тому числі і з міжперсональним спілкуванням;
доводи доцільність та правильність обраних теорій, методів, дизайну та реалізацій;
пояснювати та відстоювати методичний та системний підхід до проектування;
аргументувати вибрані рішення та пояснювати їхні обмеження;
оцінювати сильні і слабкі сторони різних рішень і тестів;
Слайд 29НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
Навички (компетенції) випускників
підтримувати проектування для забезпеченням
комбінувати варіанти об'єднання апаратного і програмного забезпечення для отримання бажаної функціональності комп’ютерної системи;
комбінувати загальнотехнічні та специфічні рішення при роботі з комп’ютерними системами;
представляти результати досліджень у вигляді презентацій, публікації та / або доповідях на конференціях та семінарах;
Слайд 30НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
Навички (компетенції) випускників
демонструвати розуміння та дотримуватися
мати уявлення, розуміти необхідність та дотримуватися особистої чесності, професійної етики та культурної свідомості;
розуміти і нести професійну, етичну і моральну відповідальність;
ефективно спілкуватися та обмінюватися технічною інформацією в різних форматах і різними способами (усно, письмово, електронними засобами) як із спеціалістами так і з неспеціалістами в галузі Комп’ютерної інженерії;
Слайд 31НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
Навички (компетенції) випускників
визначити власні потреби в
самостійно набувати ширшої освіти, необхідної для розуміння впливу інженерних рішень в
глобальному,
економічному,
екологічному та
соціальному значеннях;
визнавати необхідність і здатність займатися самоосвітою протягом усього життя;
розвиватися і підтримувати на належному сучасному рівні необхідні знання, а також відповідний рівень компетентності в сучасних наукових технологіях так, щоб бути в змозі формулювати і вирішувати нові технічні задачі і далі розвивати і підтримувати свої професійні навички впродовж усієї кар'єри;
розуміти необхідність, прагнути до безперервного навчання, бути винахідливим і здатним прийняти глобальні виклики та використати всі можливості, щоб зробити позитивний вплив на суспільство;
Слайд 32НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
Навички (компетенції) випускників
демонструвати знання сучасних проблем;
розуміти
громадського здоров'я та безпеки,
культурних,
соціальних,
моральних,
екологічних обмежень.
Слайд 33НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
Спеціальні навички (компетенції) випускників
вбудовані комп'ютерні системи
вбудовані комп'ютерні системи медичних пристроїв;
системи керування для автомобілів, літаків і поїздів;
широке коло додатків в областях:
телекомунікацій,
фінансових операцій,
інформаційних систем
Слайд 34НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
Спеціальні навички (компетенції) випускників
апаратно-програмні інтерфейси;
проектування
проектування цифрових, аналогових та змішаних схем;
автоматизація проектування;
тестування та діагностика;
комп’ютерні мережі;
вбудовані комп’ютерні системи;
розробка програмного забезпечення для широкого кола задач;
кібер-фізичні системи;
мови програмування: JAVA, C++, C, Assembly, VHDL, Matlab, Python;
операційні системи Android, iOS, UNIX, Linux, Windows.
Слайд 35НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
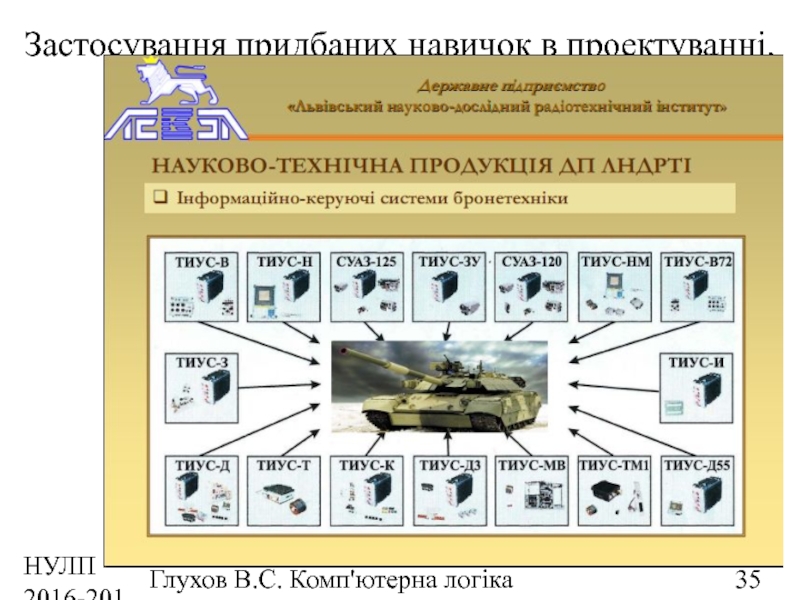
Застосування придбаних навичок в проектуванні.
Слайд 39НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
(Львівський центр Інституту космічних досліджень НАН
Слайд 40НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
Блоки і комірки для Січ-2 (Львівський
Слайд 41НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
Вбудована в атомну елекростанцію комп’ютерна система
Слайд 46НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
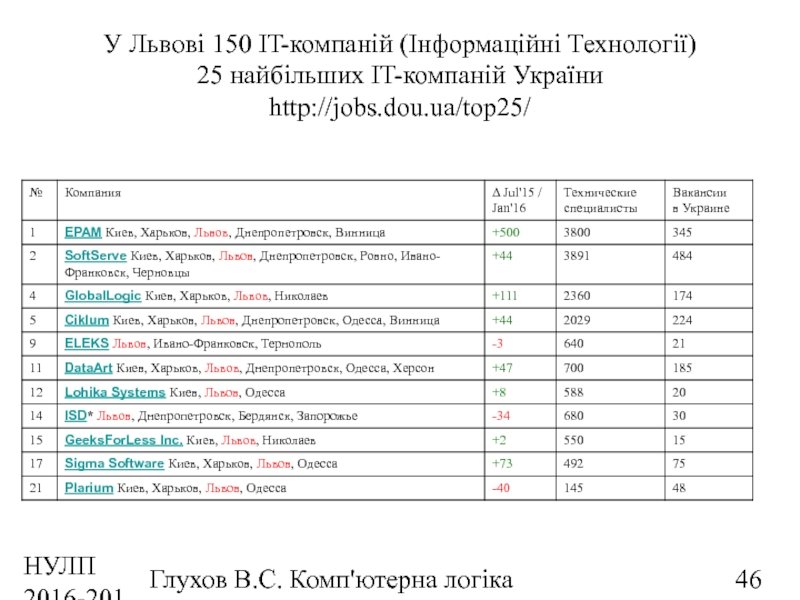
У Львові 150 IT-компаній (Інформаційні Технології)
25
Слайд 47НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
Комп’ютерна логіка і „Комп’ютерна інженерія”
Слайд 48НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
Лінгвістичні основи – грецька абетка
Α α
Γ γ — гамма Δ δ — дельта
Ε ε — епсилон Ζ ζ — дзета
Η η — ета Θ θ — тета
Ι ι — йота Κ κ — каппа
Λ λ — лямбда Μ μ — мю
Ν ν — ню Ξ ξ — ксі
Ο ο — омікрон Π π — пі
Ρ ρ — ро Σ σ ς — сигма
Τ τ — тау Υ υ — іпсилон
Φ φ — фі Χ χ — хі
Ψ ψ — псі Ω ω — омега
Слайд 49НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
Лінгвістичні основи – латинська абетка
Літера Назва
A
B b бе
C c це
D d де
E e е
F f еф
G g ґе, же
H h га, аш
I i і
J j йот, жі
K k ка
L l ель
M m ем
Літера Назва
N n ен
O o о
P p пе
Q q ку
R r ер
S s ес
T t те
U u у
V v ве
W w дубль ве
X x ікс
Y y іпсилон, ігрек
Z z зет (зета)
Слайд 50НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
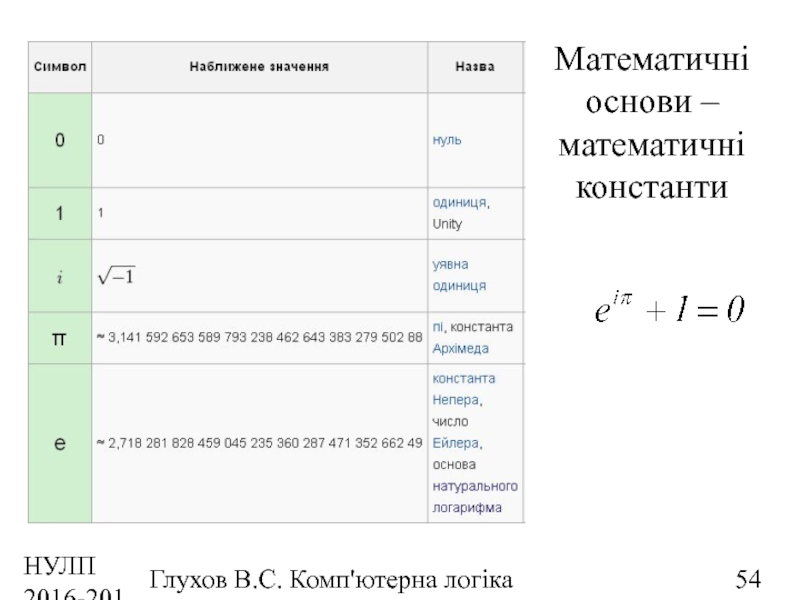
Математичні основи
Просте число — це
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101, 103, 107, 109, 113 , 127, 131, 137, 139, 149, 151, 157, 163, 167, 173, 179, 181, 191, 193, 197, 199, 211, 223, 227, 229, 233, 239, 241, 251, 257, 263, 269, 271, 277, 281, 283, 293, 307, 311, 313, 317, 331, 337, 347, 349, 353, 359, 367, 373, 379, 383, 389, 397, 401, 409, 419, 421, 431, 433, 439, 443, 449, 457, 461, 463, 467, 479, 487, 491, 499, 503, 509, 521, 523, 541, 547, 557, 563, 569, 571, 577, 587, 593, 599, 601, 607, 613, 617, 619, 631, 641, 643, 647, 653, 659, 661, 673, 677, 683, 691, 701, 709, 719, 727, 733, 739, 743, 751, 757, 761, 769, 773, 787, 797, 809, 811, 821, 823, 827, 829, 839, 853, 857, 859, 863, 877, 881, 883, 887, 907, 911, 919, 929, 937, 941, 947, 953, 967, 971, 977, 983, 991, 997…
Слайд 52НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
Математичні основи
(m + n)·k = m·k
(a+b)+c=a+(b+c) – асоціативний закон
ab=ba – комутативний закон
Слайд 53НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
Математичні основи
n! = 1 ⋅ 2
0! = 1
Слайд 55НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
Математичні основи – модульна арифметика
Два цілих
Еквівалентні визначення:
Різниця a-b ділиться на n націло. Тобто a - b = kn, де k — якесь ціле число.
Число a може бути записано у вигляді a = b + kn, де k — якесь ціле число.
Слайд 59НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
Фізичні основи
Напруга U (В), струм I
Закон Ома I = U/R
Потужність P = UI
Слайд 60НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
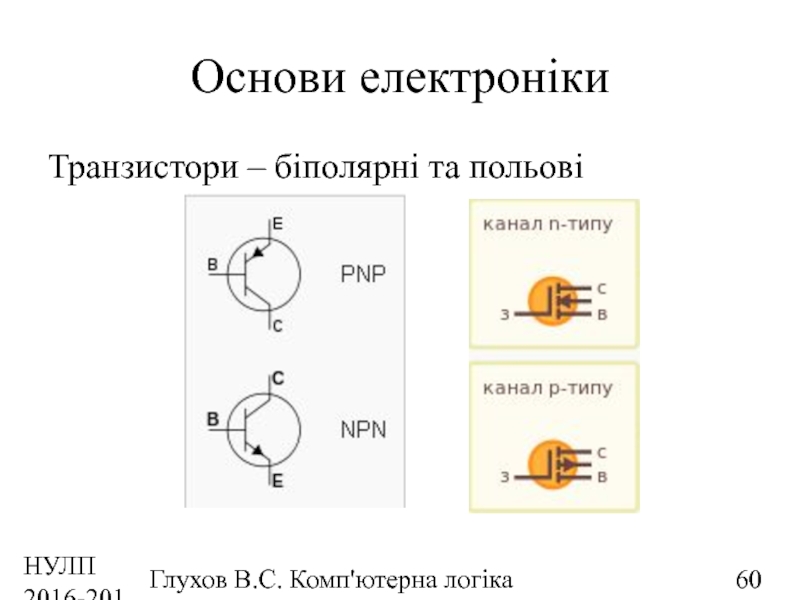
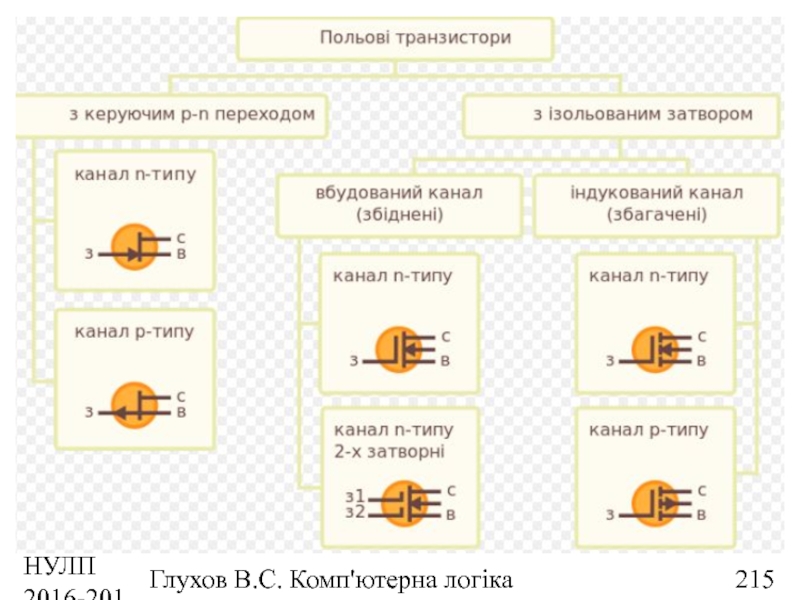
Основи електроніки
Транзистори – біполярні та польові
Слайд 61НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
Швидкість, продуктивність
v=F/t (F – шлях, об’єм
v=(Fк-Fп)/(tк-tп)=ΔF/ Δt
Δt →0 => dt
v=dF/ dt – перша похідна
Слайд 62НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
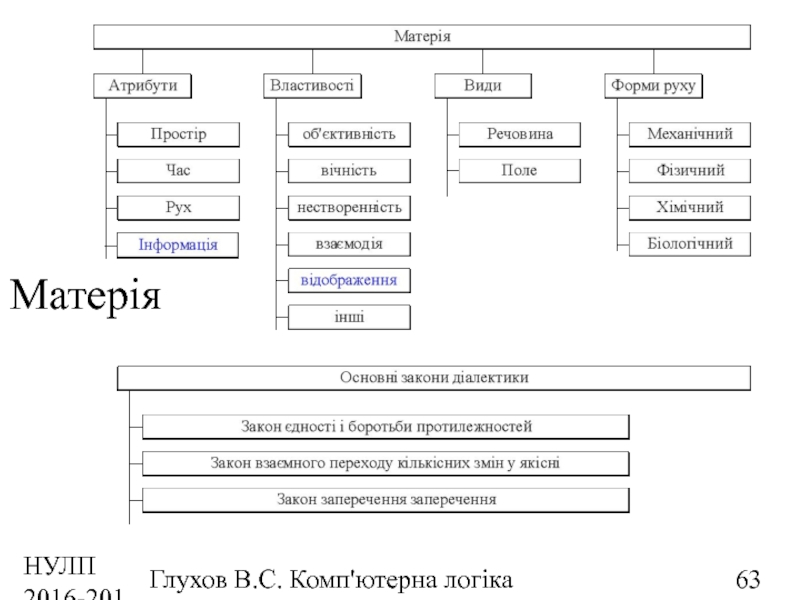
Філософські основи
Матерія - філософська категорія для
Катего́рія — загальне філософське поняття, яке відображає універсальні властивості і відношення об'єктивної дійсності, загальні закономірності розвитку всіх матеріальних, природних і духовних явищ.
Діале́ктика (грец. διαλεκτική — «мистецтво сперечатись», «міркувати») — метод філософії, що досліджує категорії розвитку.
Атрибут – невід’ємна характеристика
Слайд 64НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
Відображення
Відобра́ження — загальна властивість, що виявляється
Приватними і специфічними формами відображення є інформація, відчуття і свідомість.
Загальне поняття інформації подано у філософії, де під нею розуміють відображення реального світу.
Слайд 65НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
Інформація
Інформація - Відомості про факти, концепції,
Інформація – це поняття, що пов'язано з об'єктивною властивістю матеріальних об'єктів і явищ (процесів) породжувати різноманіття станів, які за допомогою взаємодії (фундаментальні взаємодії) передаються до інших об'єктів та відображаються в їх структурі. (В.М. Глушков, М.М. Амосов «Енциклопедія кібернетики», Київ. 1975 р.)
Конце́пція (лат. conceptio — розуміння) — система поглядів, те або інше розуміння явищ і процесів; єдиний, визначальний задум.
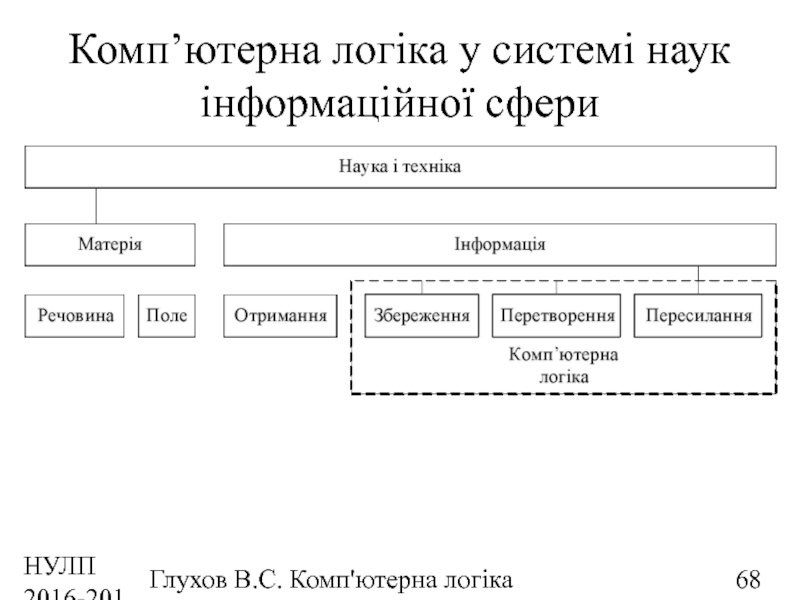
Слайд 68НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
Комп’ютерна логіка у системі наук інформаційної
Слайд 69НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
Структурна схема процесу передачі або оброблення
Слайд 70НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
Кодек, Модем
Кодек = кодер + декодер
Модем
Слайд 72НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
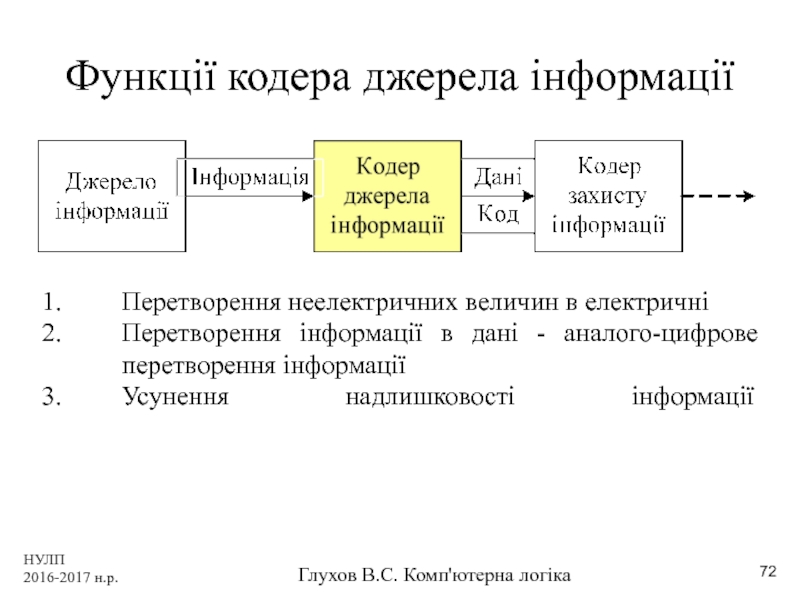
Функції кодера джерела інформації
Перетворення неелектричних величин
Перетворення інформації в дані - аналого-цифрове перетворення інформації
Усунення надлишковості інформації
Слайд 73НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
Дані
Дані - Інформація, представлена у вигляді,
Дискретний - Визначення, що відноситься до даних, представлених окремими елементами, наприклад, знаками або фізичними величинами, які приймають кінцеве число цілком певних значень
Числовий - Визначення, що відноситься до даних, які складаються з чисел
Цифровий - Визначення, що відноситься до даних, які складаються з цифр
Аналоговий - Визначення, що відноситься до даних, які представлені безперервними значеннями будь-якої фізичної змінної
Слайд 74НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
Кодування
Кодування даних Кодування
Процес побудови даних з
кодовий набір Скінчена множина елементів, з яких будують дані при кодуванні
алфавіт Кодовий набір, в якому встановлено відношення порядку
кодон Елемент кодового набору
Код даних Код Система, утворена кодовим набором і правилами, за якими з елементів цього кодового набору будують дані при кодуванні
Слайд 75НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
Сигнал та повідомлення
Сигнал - матеріальний носій
Сигнал може генеруватися, але його прийом не обов'язковий, на відміну від повідомлення, яке розраховане на прийняття приймаючою стороною, інакше воно не є повідомленням.
Сигналом може бути будь-який фізичний процес, параметри якого змінюються відповідно до переданого повідомлення.
Слайд 76НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
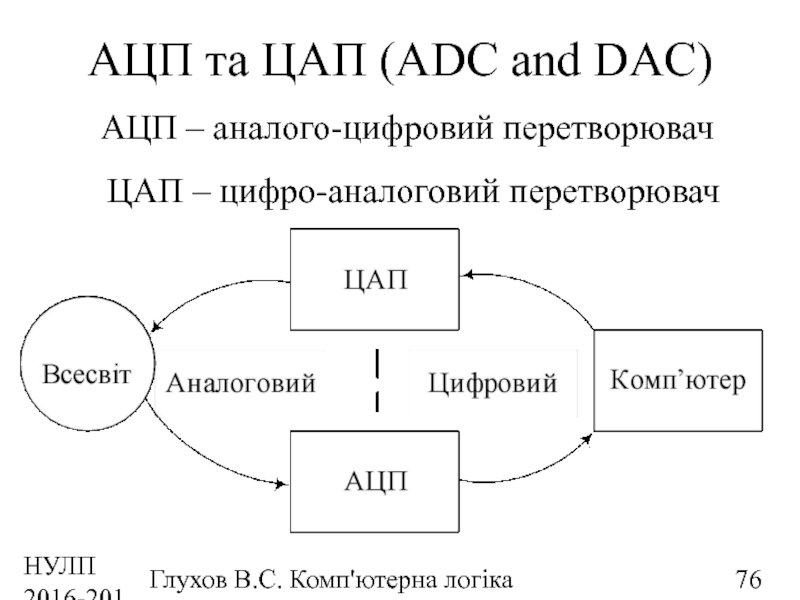
АЦП та ЦАП (ADC and DAC)
АЦП
ЦАП – цифро-аналоговий перетворювач
Слайд 77НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
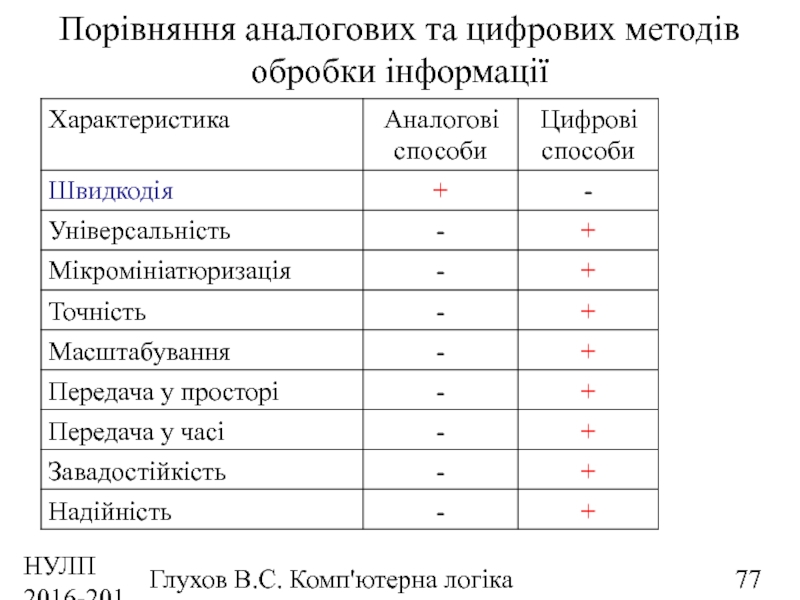
Порівняння аналогових та цифрових методів обробки
Слайд 78НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
Найпоширеніший аналоговий обчислювач (комп’ютер, помножувач)
Кут повороту
Слайд 79НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
Дискретизація та квантування
Під квантуванням (англ. quantization)
Не слід плутати квантування з дискретизацією (і, відповідно, рівень квантування з частотою дискретизації). При дискретизації величина, що змінюється в часі (сигнал) заміряється із заданою частотою (частотою дискретизації), таким чином, дискретизація розбиває сигнал за часовою складовою (на графіку — по вертикалі).
Сигнал, до якого застосована дискретизація й квантування, називається цифровим.
Слайд 80НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
Дискретиза́ція
Дискретиза́ція — перетворення функцій неперервних змінних
Слайд 81НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
Квантування
Під квантуванням розуміють перетворення неперервної за
Квант (крок квантування) - відстань між сусідніми рівнями квантування
Імпульс (електричний) – короткочасне збільшення або зменшення напруги або струму
Слайд 82НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
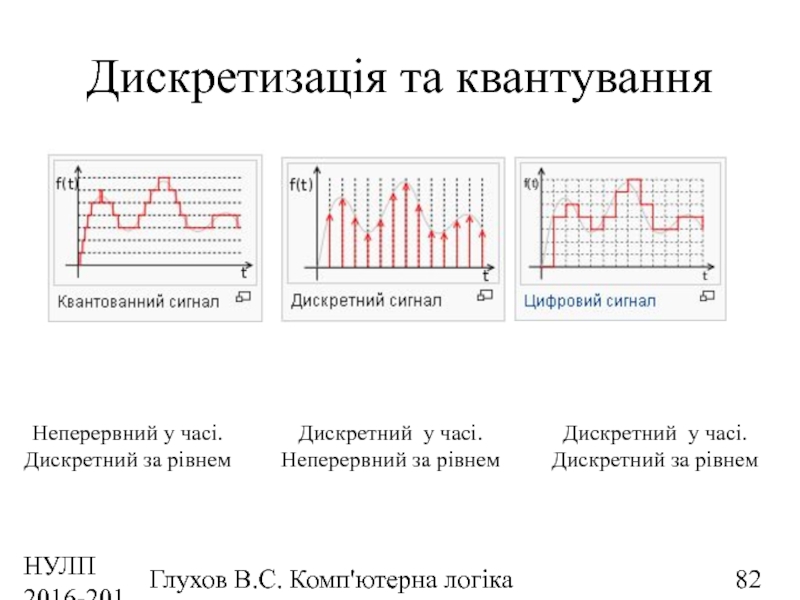
Дискретизація та квантування
Неперервний у часі.
Дискретний за
Дискретний у часі.
Неперервний за рівнем
Дискретний у часі.
Дискретний за рівнем
Слайд 83НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
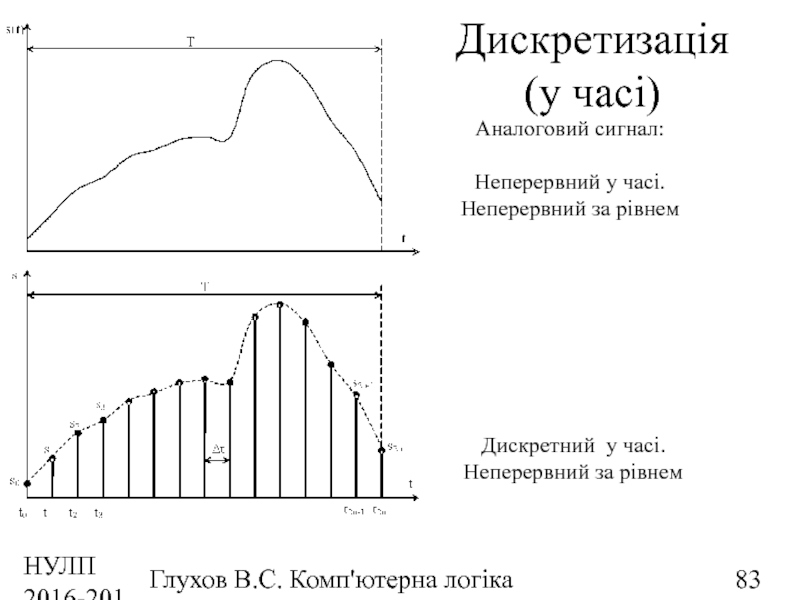
Дискретизація (у часі)
Аналоговий сигнал:
Неперервний у
Дискретний у часі.
Неперервний за рівнем
Слайд 84НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
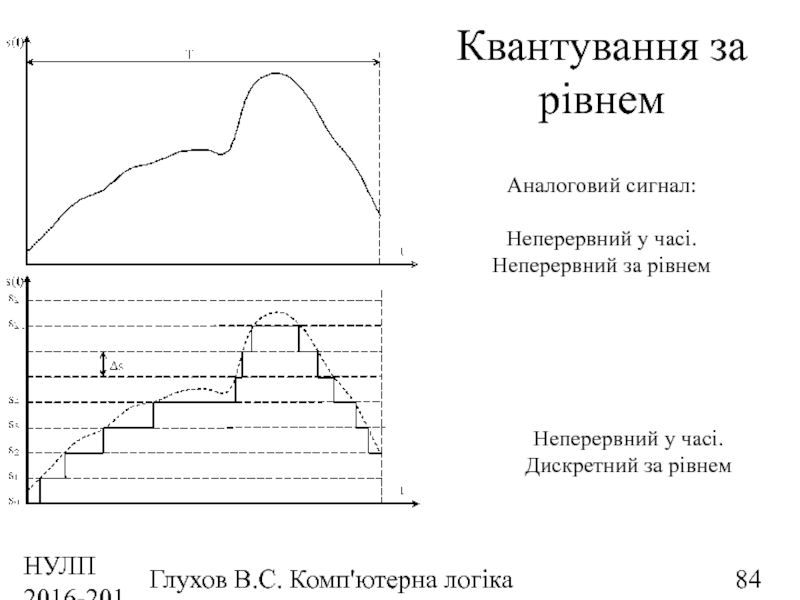
Квантування за рівнем
Неперервний у часі.
Дискретний
Аналоговий сигнал:
Неперервний у часі.
Неперервний за рівнем
Слайд 85НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
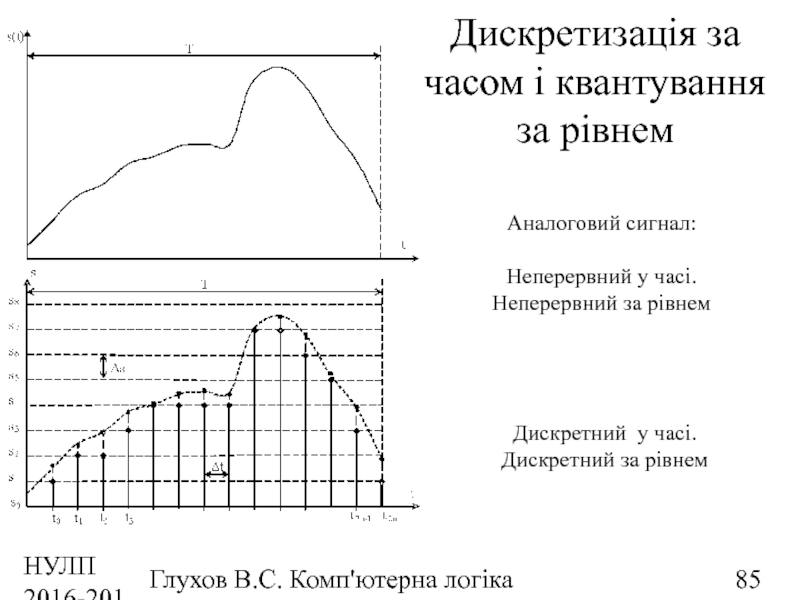
Дискретизація за часом і квантування за
Аналоговий сигнал:
Неперервний у часі.
Неперервний за рівнем
Дискретний у часі.
Дискретний за рівнем
Слайд 86НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
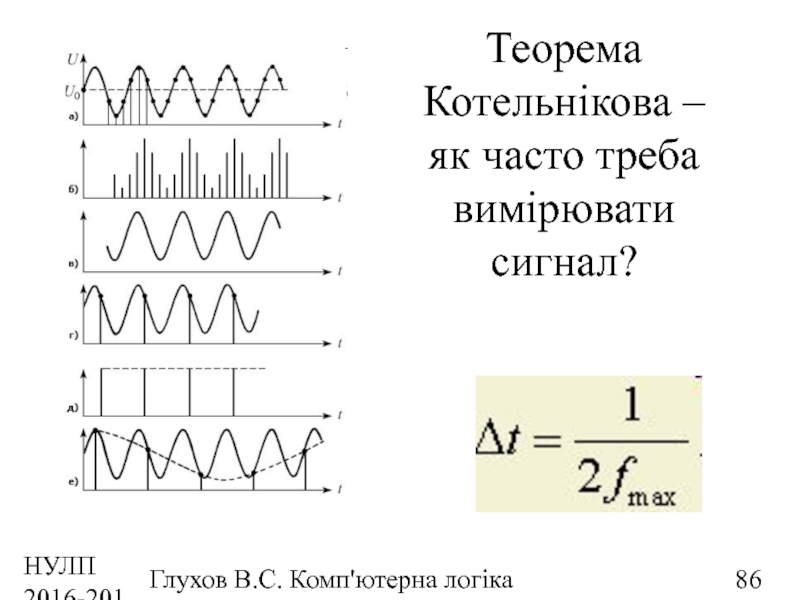
Теорема Котельнікова –
як часто треба
Слайд 87НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
Переваги кодування двома символами
Просто
Надійно
Слайд 88НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
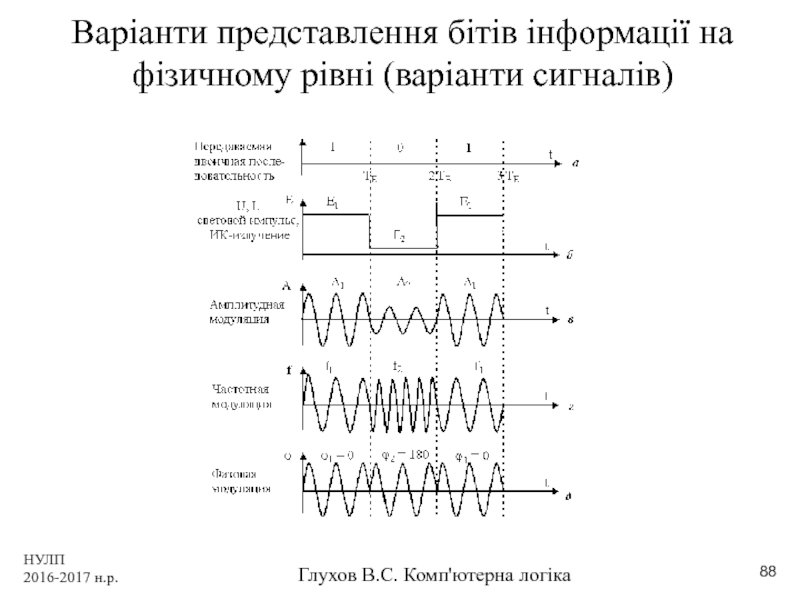
Варіанти представлення бітів інформації на фізичному
Слайд 90НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
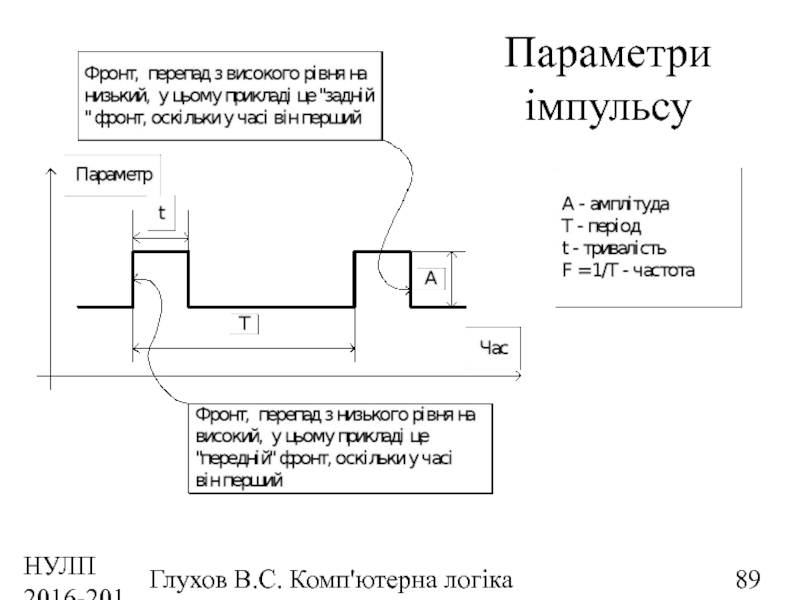
Характеристики імпульса
Амплітуда - найбільше значення, яке
Перíод колива́нь — проміжок часу між двома послідовними максимальними відхиленнями фізичної системи від положення рівноваги. Період коливань позначається зазвичай великою літерою T (c, 1 мс=10-3с, 1 мкс=10-6с, 1 нс=10-9с, 1 пс=10-12с)
Частота коливань обернено пропорційна періоду F = 1/T (Гц, 1 кГц =103 Гц, 1 МГц =103 Гц, 1 ГГц =103 Гц)
Фаза — кількісна характеристика коливання, що визначає відмінність між двома подібними коливаннями, які починаються в різні моменти часу.
Спектр - розподіл значень фізичної величини
Слайд 91НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
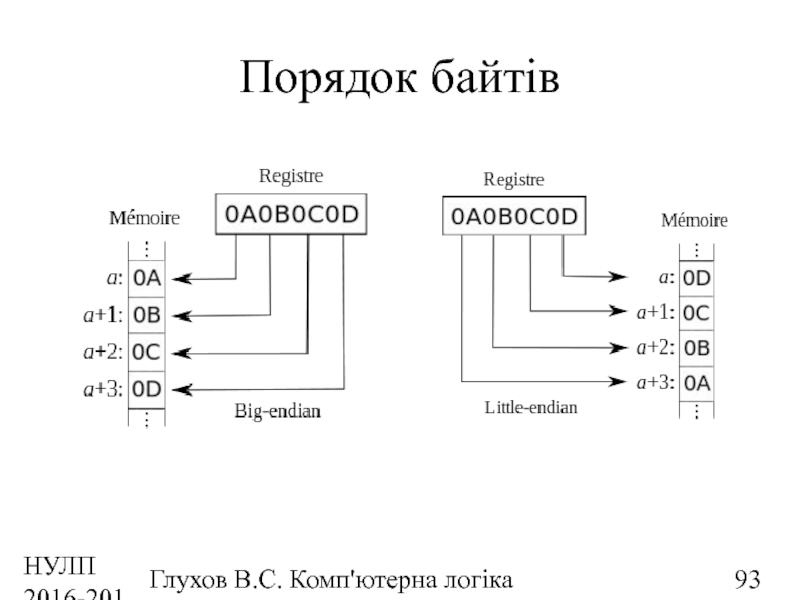
Дані
Числа
ФК
Без знаку
Із знаком (ПК, ОК, ДК,
РК
IEEE 754 (S, D, E, Q)
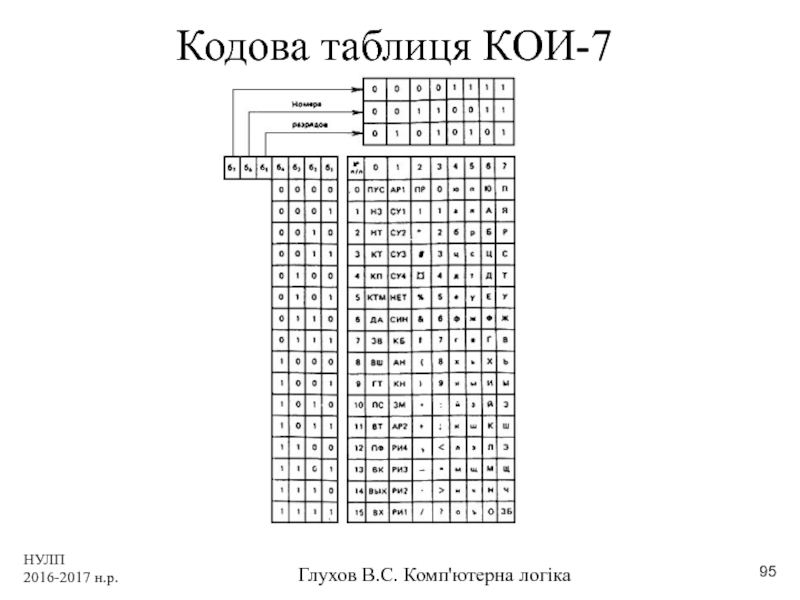
Текст
Укр (КОІ-8У), Рос (КОІ-7, КОІ-8Р), англ (ASCII)
Windows 1251, UTF
Відео
Аудіо
Інші
Слайд 98НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
Структура кодів UTF-8
(Unicode Transformation Formats )
Слайд 99НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
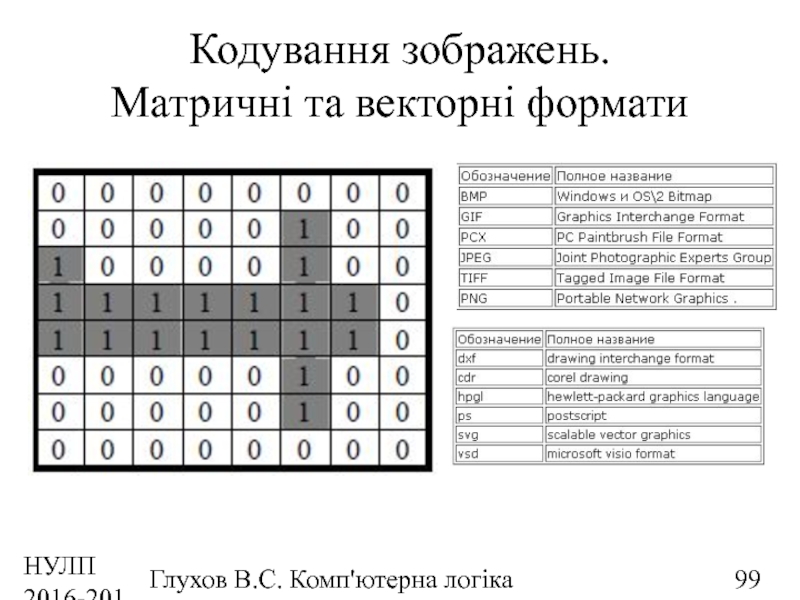
Кодування зображень.
Матричні та векторні формати
Слайд 103НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
Міри інформації
Структурні
Семантичні
Статистичні
Інші
Слайд 104НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
Структурні міри інформації
1.1 Фізичні – вага,
1.2 Геометричні – розміри, габарити
Слайд 105НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
1.3 Структурні комбінаторні міри
1.3.1 Сполучення по
Нехай є множина М, яка складається з l різних елементів. Будь-яка підмножина множини М, яка містить h елементів (h=0, 1, 2, ..., l), називається сполученням (combination) або комбінацією з даних l елементів по h елементів, якщо ці підмножини відрізняються хоча б одним елементом. Число різних сполучень із l елементів по l позначається (combination від combinare лат. сполучати).
Слайд 106НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
Структурні комбінаторні міри
1.3.1a Сполучення з повторенням
Слайд 107НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
Структурні комбінаторні міри
1.3.2 Перестановлення h елементів
Слайд 108НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
Структурні комбінаторні міри
1.3.3 Розміщення по l
Слайд 109НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
Структурні комбінаторні міри
1.3.3a Розміщення по l
Слайд 110НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
1.4 Міра Хартлі, США, 1928 р.
(Ральф
h – кількість різних елементів, система числення
l - довжина, розрядність
Q – можлива кількість повідомлень
1.4a Адитивна двійкова логарифмічна міра Хартлі
Слайд 111НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
Одиниця кількості інформації
Один двійковий розряд –
Байт (B, Б) – найчастіше це 8 біт.
Слайд 112НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
Похідні одиниці кількості інформації
1 К
1 М = 1024 К;
1 Г = 1024 М;
1 Т = 1024 Г;
1 П = 1024 Т.
Слайд 113НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
2. Семантична міра (за значенням)
властивості інформації:
повнота,
достовірність,
цінність,
адекватність,
актуальність,
чіткість,
доступність,
невичерпність,
кумулятивність,
зрозумілість,
суб'єктивність.
Слайд 114НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
Семантична міра
Повнота інформації характеризує якість інформації
Достовірність інформації - її властивість відображати реальні об'єкти з необхідною точністю.
Цінність інформації не може бути абстрактною. Інформація має бути корисною і цінною для певної категорії користувачів. Цінність інформації залежить від того, які задачі можна вирішувати за її допомогою.
Слайд 115НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
Семантична міра
Адекватність інформації характеризує ступінь відповідності
Актуальність інформації - ступінь зберігання цінності інформації для керування в момент її використання, що залежить від динаміки зміни її характеристик і від інтервалу часу, що пройшов із моменту виникнення певної інформації.
Слайд 116НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
Семантична міра
Своєчасність інформації - її надходження
Чіткість інформації - інформація має бути зрозуміла для того, кому вона призначена.
Слайд 117НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
Семантична міра
Доступність інформації - це можливість
Точність інформації - ступінь подібності отриманої інформації до реального стану об'єкта, процесу, явища тощо.
Суб'єктивність інформації. Інформація має суб'єктивний характер, оскільки її цінність визначається ступенем сприйняття суб'єкта (одержувача інформації).
Слайд 118НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
Семантична міра
Корисна інформація - властивість, що
Репрезентативність інформації - правильність її відбору і формування для адекватного відображення властивостей об'єкта.
Слайд 119НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
Семантична міра
Змістовність інформації - це відношення
Слайд 120НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
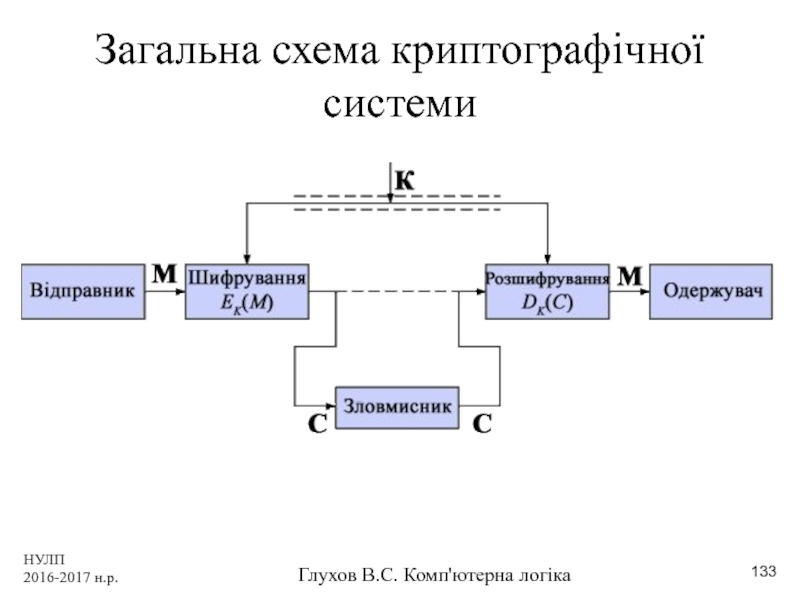
3. Статистична міра, Клод Шеннон, 1948,
Слайд 121НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
Ентропія джерела повідомлення – характеризує здатність
N –дослідів, k – різних,
i-тий результат повторюється ni разів та дає Ii інформації
Слайд 122НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
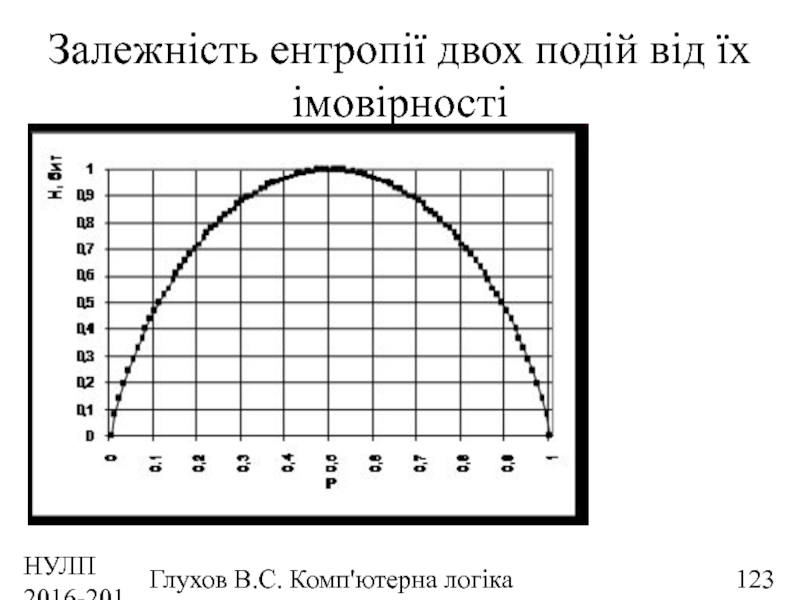
Властивості ентропії
Невід’ємна
= 0, коли ймовірність однієї
Максимальна, коли ймовірності всіх подій однакові
Слайд 123НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
Залежність ентропії двох подій від їх
Слайд 124НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
Кількість отриманої інформації
I = Hпочаткове –
Слайд 125НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
Усунення надлишковості інформації. Алгоритм ефективного кодування
повідомлення, які складаються з літер певного алфавіту, можна закодувати так, що середнє число двійкових символів на літеру буде як завгодно близьке до ентропії джерела цих повідомлень, але не менше цієї величини
Слайд 127НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
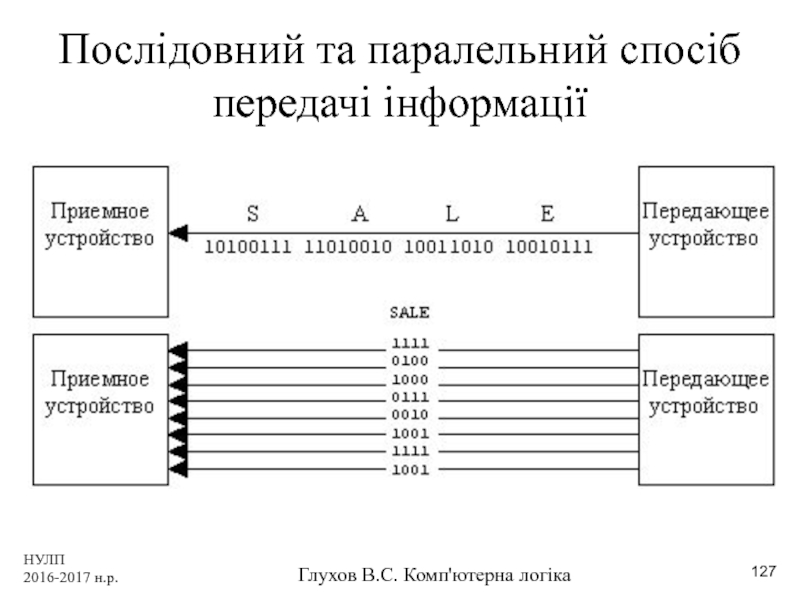
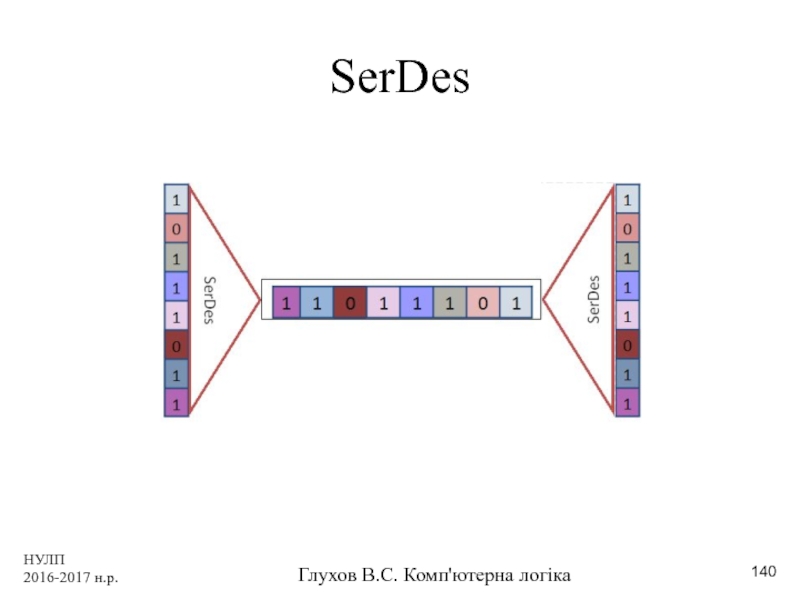
Послідовний та паралельний спосіб передачі інформації
Слайд 129НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
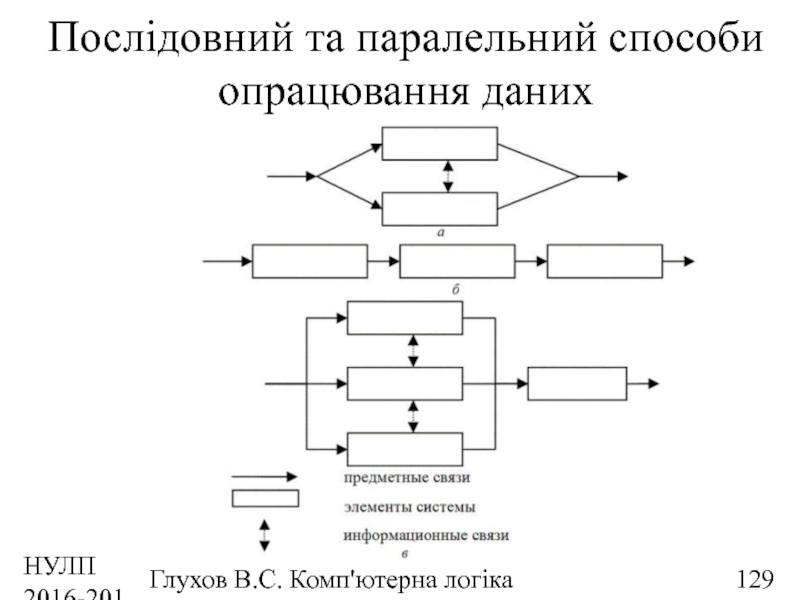
Послідовний та паралельний способи опрацювання даних
Слайд 130НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
Опрацювання даних з використанням зворотних зв’язків
Слайд 131НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
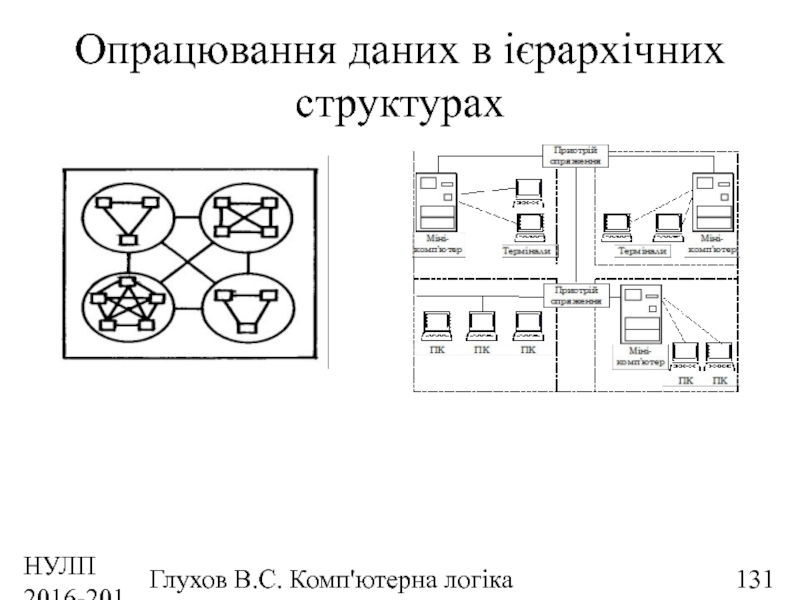
Опрацювання даних в ієрархічних структурах
Слайд 132НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
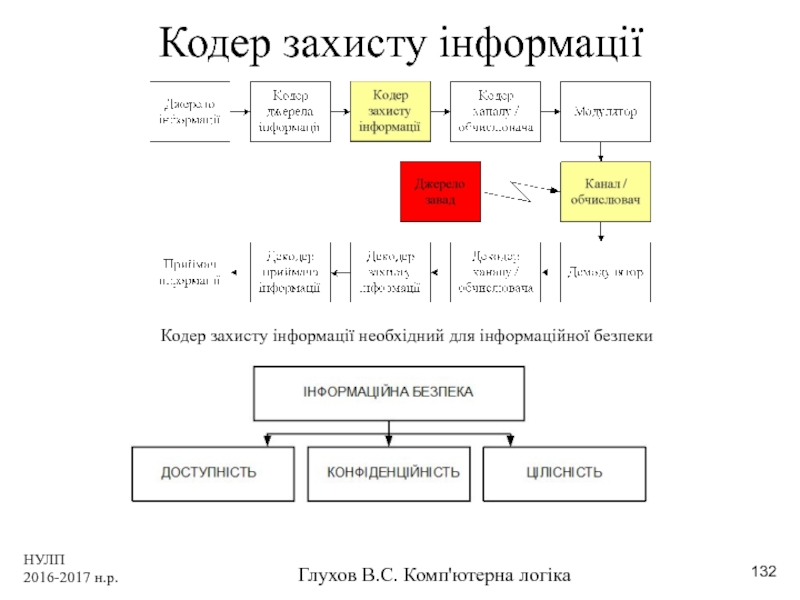
Кодер захисту інформації
Кодер захисту інформації необхідний
Слайд 137НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
Код Хеммінга
K1 = i3 ⊕
K2 = i3 ⊕ i6 ⊕ i7 ⊕ i10 ⊕ i11 ⊕ i14 ⊕ i15
K4 = i5 ⊕ i6 ⊕ i7 ⊕ i12 ⊕ i13 ⊕ i14 ⊕ i15
K8 = i9 ⊕ i10 ⊕ i11 ⊕ i12 ⊕ i13 ⊕ i14 ⊕ i15
K ⊕ k = (K8 ⊕ k8)(K4 ⊕ k4)(K2 ⊕ k2)(K1 ⊕ k1)
Слайд 138НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
Код Хеммінга
k1 = i3 ⊕ i5
k2 = i3 ⊕ i6 ⊕ i7 ⊕ i10 ⊕ i11 ⊕ i14 ⊕ i15;
k4 = i5 ⊕ i6 ⊕ i7 ⊕ i12 ⊕ i13 ⊕ i14 ⊕ i15;
k8 = i9 ⊕ i10 ⊕ i11 ⊕ i12 ⊕ i13 ⊕ i14 ⊕ i15;
Слайд 139НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
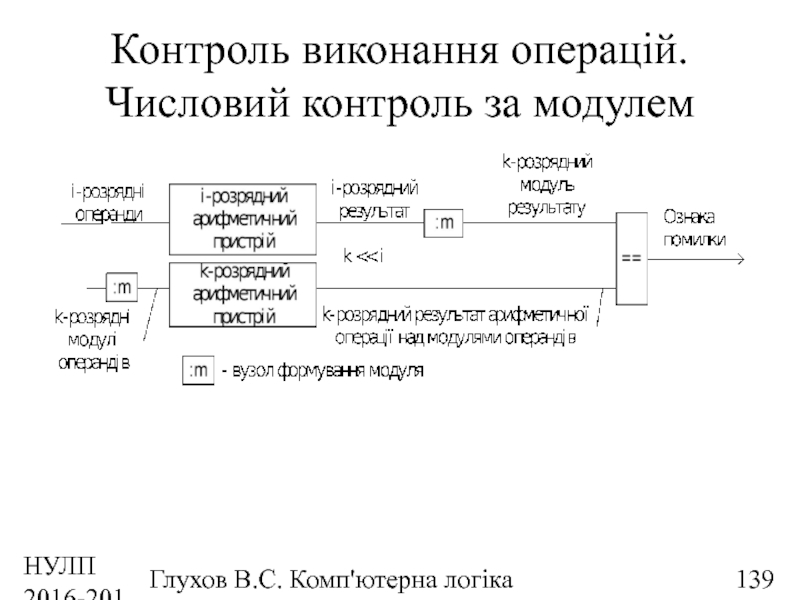
Контроль виконання операцій.
Числовий контроль за модулем
Слайд 142НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
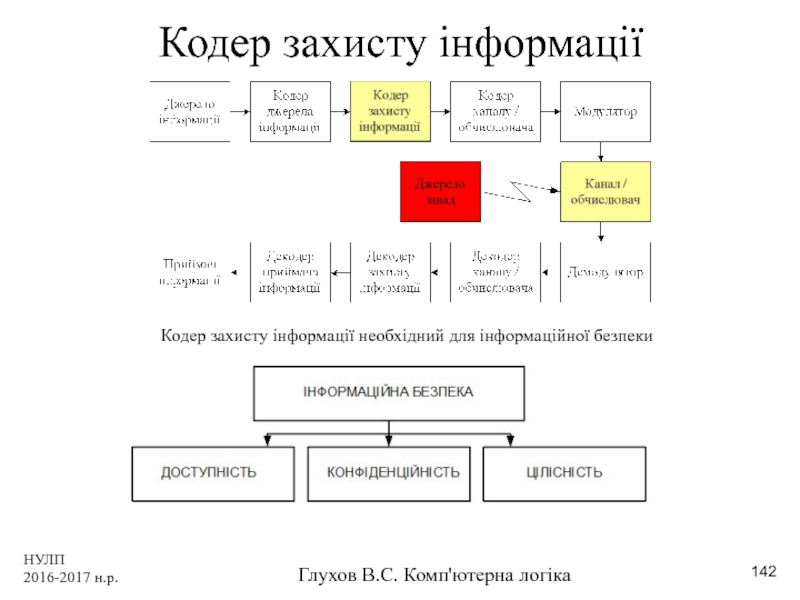
Кодер захисту інформації
Кодер захисту інформації необхідний
Слайд 146НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
Трійкова симетрична (врівноважена) система числення
Слайд 147НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
Системи числення з іраціональними основами
Класичний CORDIC-метод
обчислення
Слайд 154НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
Структурна схема процесу передачі або оброблення
Слайд 157НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
Алгоритм
Система формальних правил або приписів, які
Слайд 158НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
Характеристики алгоритму
3 множини:
Множина вхідних даних
Множина можливих
Множина проміжних результатів
4 правила:
Правило початку роботи
Правило безпосереднього перетворення даних
Правило закінчення роботи
Правило вилучення результату
Слайд 159НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
Властивості алгоритму
Скінченність, результативність
алгоритм має завжди завершуватись
Дискретність
процес, що визначається алгоритмом, можна розчленувати (розділити) на окремі елементарні етапи (кроки), кожен з яких називається кроком алгоритмічного процесу чи алгоритму.[31]
Визначеність, однозначність
кожен крок алгоритму має бути точно визначений. Дії, які необхідно здійснити, повинні бути чітко та недвозначно визначені для кожного можливого випадку.
Масовість, універсальність, повторюваність
властивість алгоритму, яка полягає в тому, що алгоритм повинен забезпечувати розв'язання будь-якої задачі з класу однотипних задач за будь-якими вхідними даними, що належать до області застосування алгоритму.
Ефективність
Алгоритм вважають ефективним, якщо всі його оператори досить прості для того, аби їх можна було точно виконати за скінченний проміжок часу з допомогою олівця та аркушу паперу.
Вхідні дані
алгоритм має деяку кількість (можливо, нульову) вхідних даних, тобто, величин, заданих до початку його роботи або значення яких визначають під час роботи алгоритму.
Вихідні дані
алгоритм має одне або декілька вихідних даних, тобто, величин, що мають досить визначений зв'язок із вхідними даними.
Слайд 160НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
Представлення алгоритмів
http://uk.wikipedia.org/wiki/Алгоритм
У процесі розробки алгоритму можуть
словесна або вербальна (неформальні мови, формульно-словесна);
псевдокод (формальні алгоритмічні мови);
Таблична;
Часові діаграми;
схемна:
Функціональні схеми;
блок-схема, виконується за вимогами стандарту
граф автомата
інші
Слайд 162НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
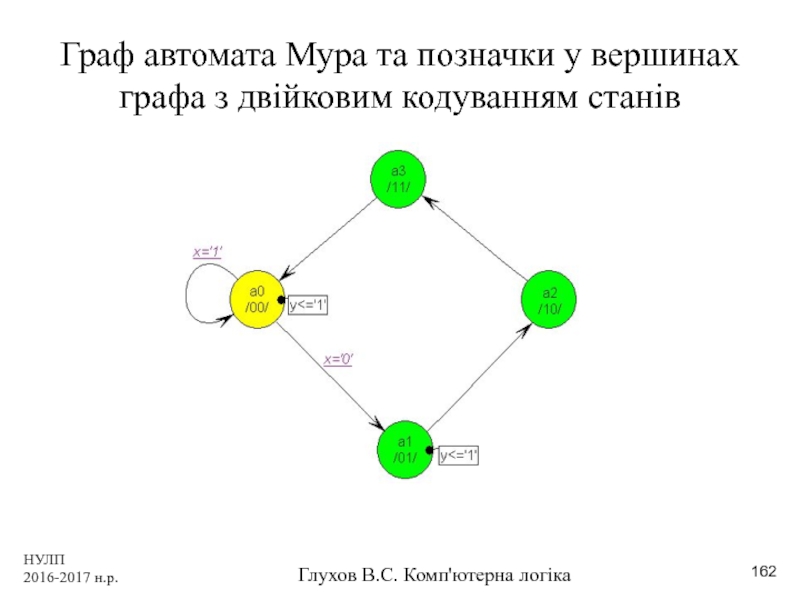
Граф автомата Мура та позначки у
Слайд 165НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
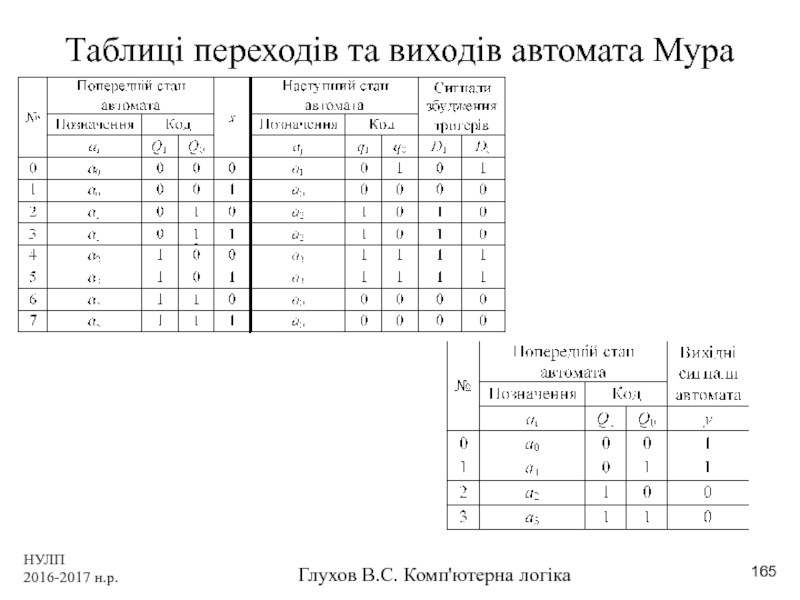
Таблиці переходів та виходів автомата Мура
Слайд 168НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
Опис автомата формальною (з правилами без
State_machine: process (c)
begin
if rising_edge(c) then
case State is
when a0 =>
if x='1' then
State <= a0;
elsif x='0' then
State <= a1;
end if;
when a1 =>
State <= a2;
when a2 =>
State <= a3;
when a3 =>
State <= a0;
when others =>
null;
end case;
end if;
end process;
y_assignment:
y <= '1' when (State = a0) else
'1' when (State = a1) else
'0';
end fsm1_arch;
Слайд 169НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
Теза Черча
Теза Черча — для кожного алгоритму
Слайд 170НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
Універсальні ФАС – можуть реалізувати будь-який
Рекурсивні функції
Машина Тюринга
Машина Поста
Схеми Колмогорова-Успенського
Нормальні алгорифми Маркова
Скінченні цифрові автомати (комп’ютери та їх програми)
зараз ФАС –
програма для універсального комп’ютера або
новий (спеціалізований) комп’ютер і програма для нього
http://uk.wikipedia.org/wiki/Алгоритм
Слайд 171НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
Повна побудова алгоритму
формулювання задачі;
побудови моделі
АБСТРАКТНИЙ - той, що є наслідком мисленого виділення з усіх ознак, властивостей і зв'язків конкретного предмета його основних, найзагальніших;
розроблення абстрактного алгоритму;
перевіряння правильності абстрактного алгоритму;
реалізації структурного алгоритму;
аналізу алгоритму і його складності;
перевіряння реалізації структурного алгоритму;
оформлення документації.
Слайд 172НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
Загальна структурна схема цифрового автомата
Слайд 175НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
Алгебра логіки (Булева логіка, двійкова логіка,
Використовується для опису комбінаційних схем
Розділ математичної логіки, що вивчає систему логічних операцій над висловлюваннями. Найчастіше передбачається, що висловлювання можуть бути тільки істинними або помилковими, тобто використовується так звана бінарна або двійкова логіка, на відміну від, наприклад, тризначної логіки.
Вивчає функції, які можуть приймати тільки два значення: 0 (істина) та 1 (хибність), так само, як і їх аргументи
Слайд 176НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
Змінні, набори і функції алгебри логіки
Слайд 178НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
Повторювач, інвертор
Інверсія, інвертор, НЕ
Слайд 180НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
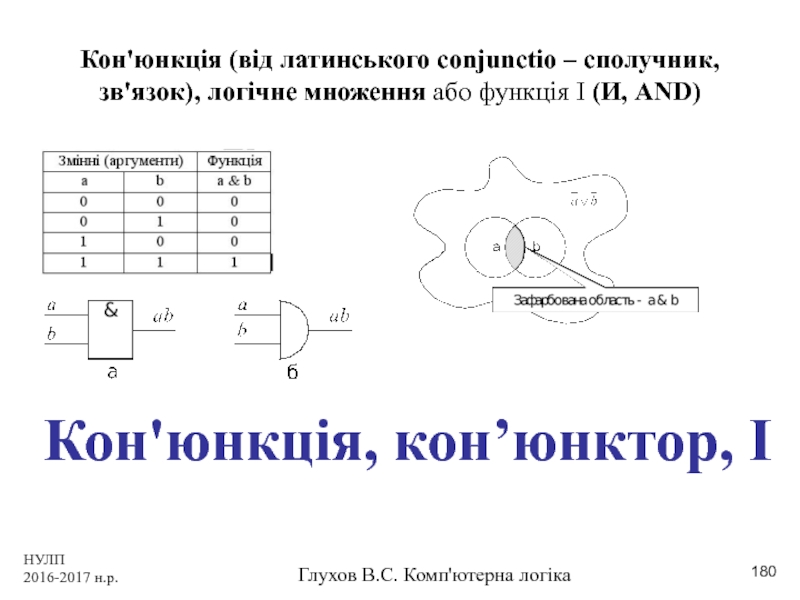
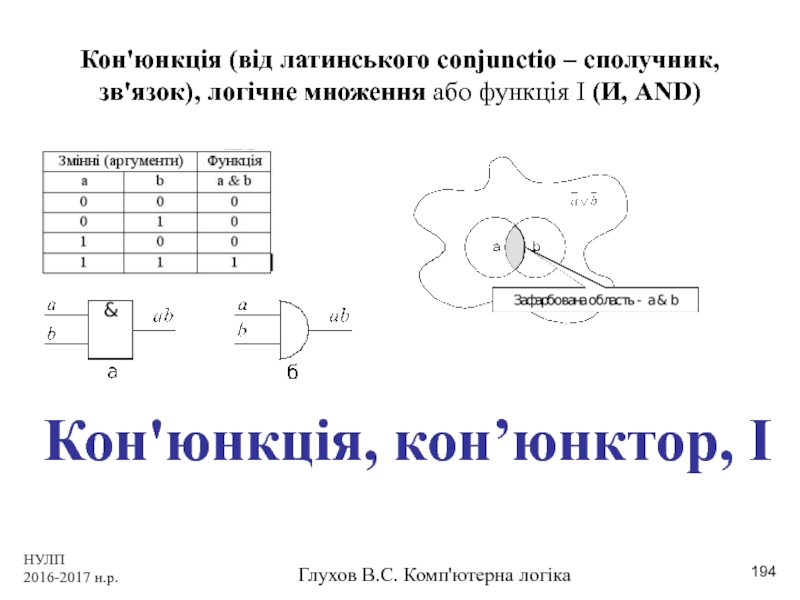
Кон'юнкція (від латинського conjunctio – сполучник,
Кон'юнкція, кон’юнктор, І
Слайд 181НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
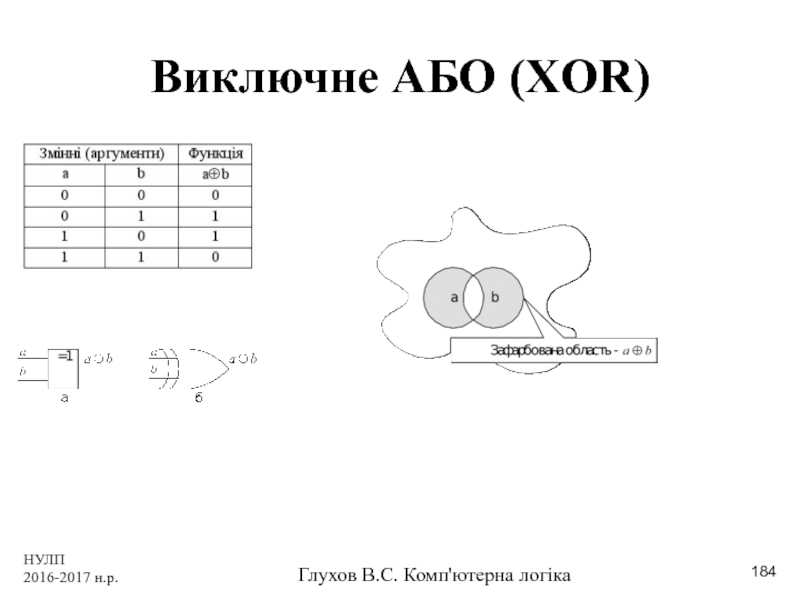
Диз'юнкція (від латинського disjunctio - роз'єднання),
Диз'юнкція, диз’юнктор, АБО
Слайд 182НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
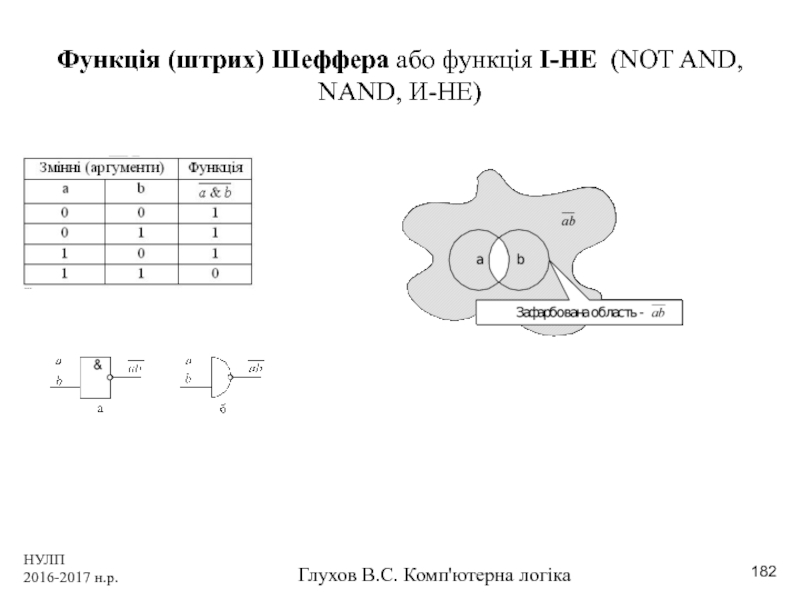
Функція (штрих) Шеффера або функція І-НЕ
Слайд 183НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
Функція (стрілка) Пірса (Вебба) або функція
Слайд 188НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
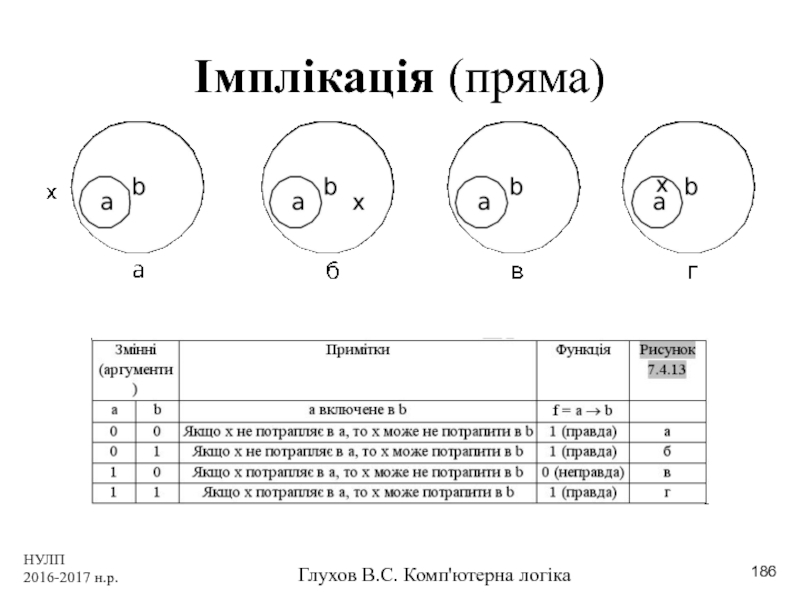
Заперечення імплікації (прямої)
Заперечення зворотної імплікації
Слайд 189НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
Теорема Поста-Яблонського про функціонально повні системи
З ФАЛ, які мають якусь властивість, можна утворити тільки ФАЛ, які мають цю ж властивість
З ФАЛ, які мають якусь властивість не можна утворити ФАЛ, які не мають цієї властивості
До ФПС повинна входити хоча би одна ФАЛ, яка:
1) не зберігає 0;
2) не зберігає 1;
3) несамодвоїсна;
4) немонотонна;
5) нелінійна
Слайд 190НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
Властивості ФАЛ, монобазиси, базиси
Базис Буля
Базис Жегалкіна
Базис
Базис АБО, НЕ
Слайд 194НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
Кон'юнкція (від латинського conjunctio – сполучник,
Кон'юнкція, кон’юнктор, І
Слайд 195НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
Диз'юнкція (від латинського disjunctio - роз'єднання),
Диз'юнкція, диз’юнктор, АБО
Слайд 196НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
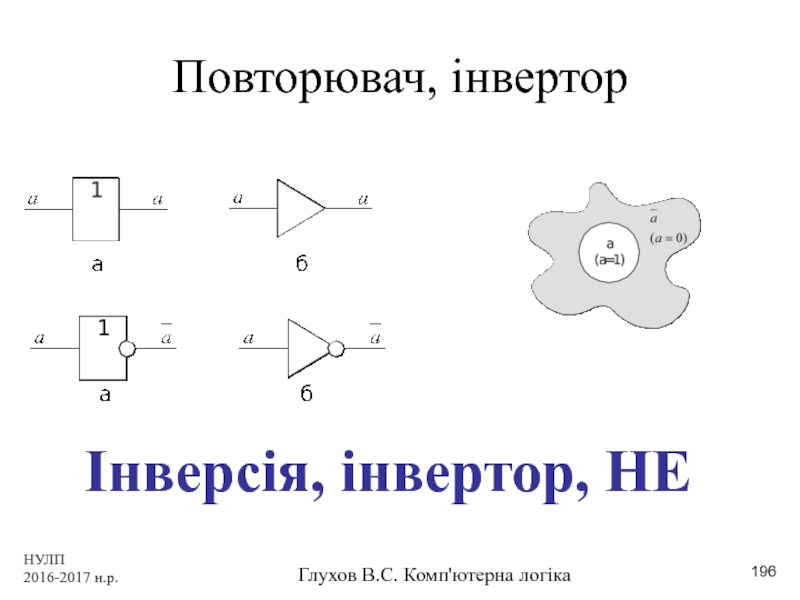
Повторювач, інвертор
Інверсія, інвертор, НЕ
Слайд 197НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
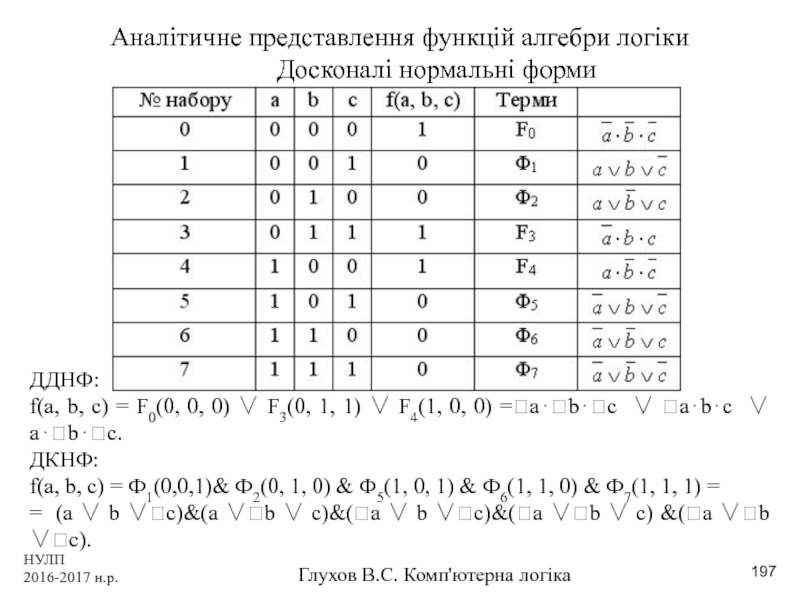
Аналітичне представлення функцій алгебри логіки
Досконалі нормальні
ДДНФ:
f(a, b, c) = F0(0, 0, 0) ∨ F3(0, 1, 1) ∨ F4(1, 0, 0) =a⋅b⋅c ∨ a⋅b⋅c ∨ a⋅b⋅c.
ДКНФ:
f(a, b, c) = Ф1(0,0,1)& Ф2(0, 1, 0) & Ф5(1, 0, 1) & Ф6(1, 1, 0) & Ф7(1, 1, 1) =
= (a ∨ b ∨c)&(a ∨b ∨ c)&(a ∨ b ∨c)&(a ∨b ∨ c) &(a ∨b ∨c).
Слайд 198НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
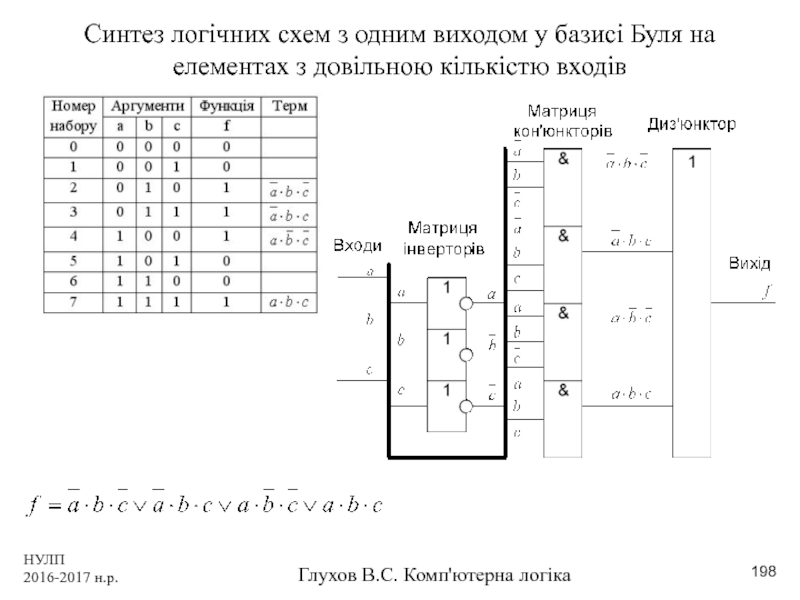
Синтез логічних схем з одним виходом
Слайд 201НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
Основні правила виконання операцій у базисі
Слайд 202НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
Мінімізація ФАЛ
Канонічна задача мінімізації
У базисі Буля
Над
Мета – зменшення кількості літер
Загальна задача мінімізації
Усі інші методи
Слайд 203НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
Методи розв’язання канонічної задачі мінімізації
Аналітичні
Квайна-МакКласскі-Петрика
Інші
Табличні
Геометричні
Графо-аналітичні
Карти Карно
Діаграми
Алгебро-топологічні
інші
Слайд 205НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
Основні правила виконання операцій у монобазисах
Слайд 207НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
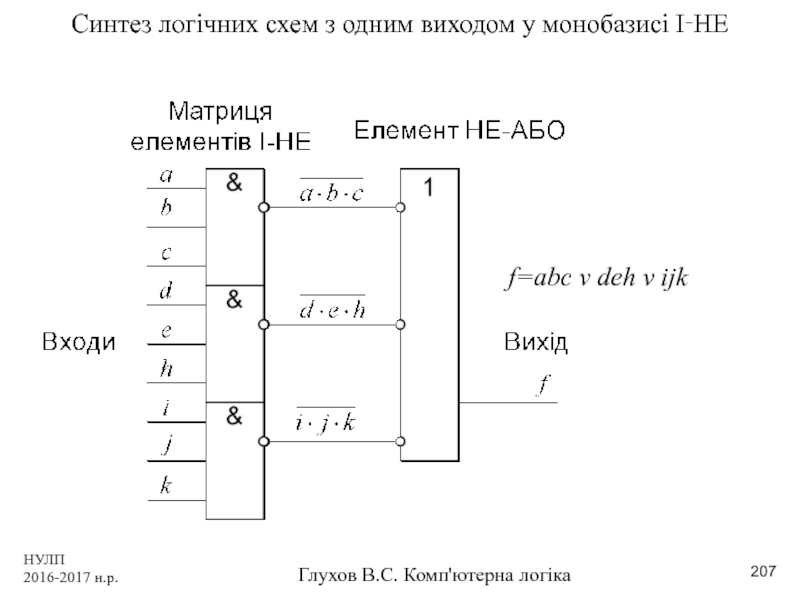
Синтез логічних схем з одним виходом
f=abc v deh v іjk
Слайд 209НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
Синтез логічних схем з одним виходом
f=abc v deh v іjk
Слайд 211НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
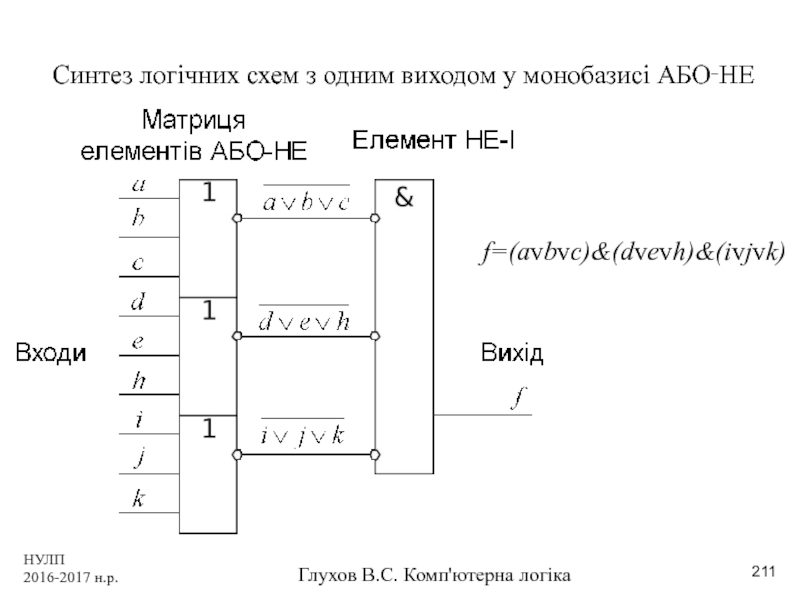
Синтез логічних схем з одним виходом
f=(avbvc)&(dvevh)&(іvjvk)
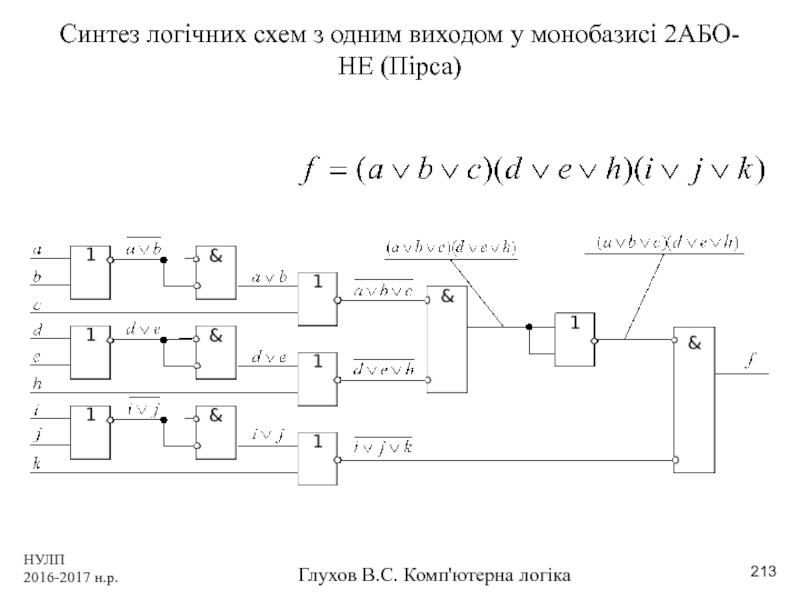
Слайд 213НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
Синтез логічних схем з одним виходом
Слайд 214НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
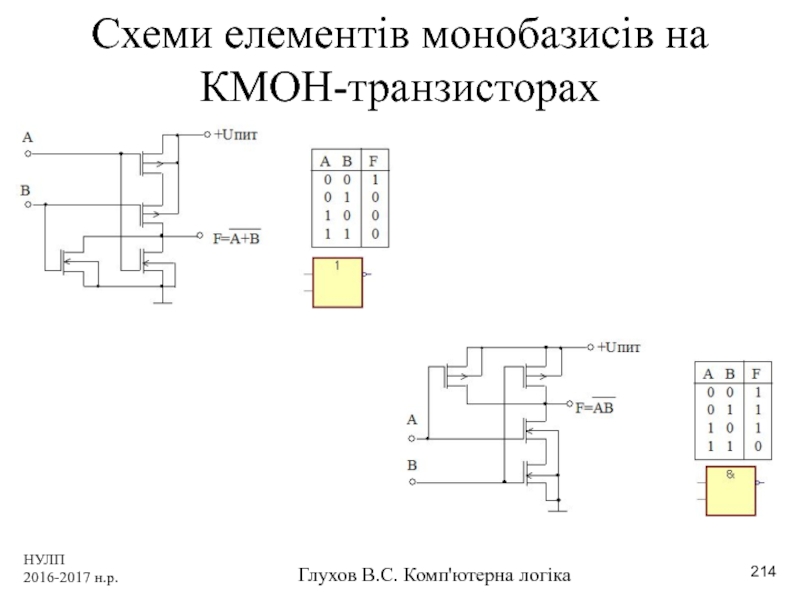
Схеми елементів монобазисів на КМОН-транзисторах
Слайд 216НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
Основні правила виконання операцій у базисі
Для цієї функції справедливі наступні аксіоми:
a ⊕ a = 0; a ⊕ a ⊕ a = a;
На підставі розглянутих аксіом і властивостей елементарних логічних функцій можна, наприклад, вивести правила представлення функцій І, АБО, НЕ через функцію додавання за модулем 2 і навпаки:
a v b = a ⊕ b ⊕ ab;
ab = (a ⊕ b) ⊕ (a v b).
Слайд 219НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
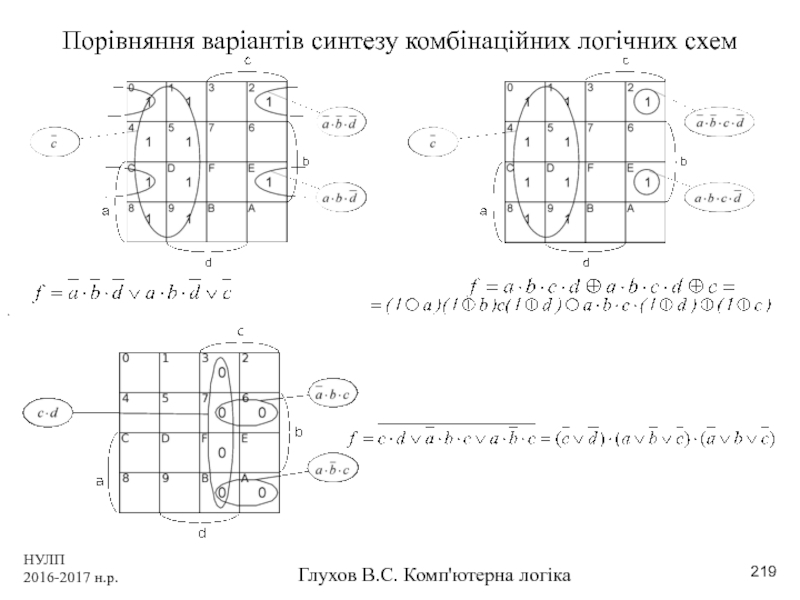
Порівняння варіантів синтезу комбінаційних логічних схем
.
Слайд 223НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
Небулеві базиси
Базис Жегалкіна (1, І, XOR)
Мажоритарний
Пороговий базис, wi, T - const
Штучний інтелект, wi, T - var
Слайд 225НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
Форми представлення ФАЛ
Табличні
Таблиці істинності
Сингулярні таблиці
Геометричні
Числові
Часові діаграми
Схеми
Аналітичні
інші
Слайд 227НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
Аналітичні форми представлення ФАЛ
Нормальні
Досконалі
ДДНФ
ДКНФ
інші
Скорочені (ДНФ, КНФ)
Глухого
Мінімальні – форма глухого кута з найменшою кількістю літер
Абсолютно мінімальні – мінімальна у базисі Буля
Анормальні
Дужкові
Із запереченням більше ніж над однією змінною
Слайд 228НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
Терм
Терм - це група літерал і
Диз'юнктивний терм (макстерм, елементарна диз’юнкція) - це логічна функція, що зв'язує всі літерали знаком диз'юнкції.
Наприклад:
f1 = a ∨b ∨ c ∨ d; f2 = a ∨ b.
Макстерм називають також конституентою нуля, тому що ця логічна функція дорівнює 0 тільки тоді, коли всі її літерали рівні 0 одночасно.
Кон'юнктивний терм (мінтерм, елементарна кон’юнкція) - це логічна функція, що зв'язує літерали знаком кон'юнкції.
Наприклад:
f1 =a & b &c & d; f2 = a ∧ b ∧ c.
Мінтерм називають також конституентою одиниці, тому що ця функція дорівнює 1 тільки тоді, коли всі її літерали одночасно дорівнюють одиниці.
Слайд 229НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
Нормальні форми з мінтермами
Будь-яка таблично задана
диз'юнкції скінченого числа мінтермів, на кожнім з яких функція дорівнює одиниці (диз’юнктивна нормальна форма, ДНФ):
f(a, b,..., z) = F1 ∨ F2 ∨ ... ∨F n,
суми за модулем 2 скінченого числа мінтермів, на кожнім з яких функція дорівнює одиниці (поліном Жегалкіна):
де i - номери наборів, на яких функція дорівнює 1.
Слайд 230НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
Нормальні форми з макстермами
Будь-яка таблично задана
кон'юнкції скінченого числа макстермів, на кожнім з яких функція дорівнює нулю (кон’юнктивна нормальна форма, КНФ):
f(a, b,..., z) = Ф1 & Ф2 & ... & Фm,
результату порівняння скінченого числа макстермів, на кожнім з яких функція дорівнює нулю (поліном рівнозначності):
де i - номери наборів, на яких функція дорівнює 1.
Слайд 231НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
Досконалі нормальні форми
Кількість термів дорівнює кількості
У кожному термі присутні усі змінні
Немає однакових термів
Слайд 232НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
Анормальні форми
Дужкова
Із запереченням більше ніж над
Слайд 233НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
Критерії синтезу схем ФАЛ
Правильна робота
Швидкодія (продуктивність)
Апаратні
Споживана потужність
Надійність
Складність
Однорідність структури
Ціна
інші
Слайд 234НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
Методи визначення ціни реалізації ФАЛ
Грошові одиниці
Негрошові
Кількість операцій
І, АБО, НЕ
І, АБО
І (АБО)
Кількість термів
В ДНФ
В КНФ
Кількість літер
В нормальних формах
В анормальних формах
Кількість входів
І, АБО, НЕ
І, АБО
І (АБО)
інші
Слайд 235НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
Мінімізація ФАЛ
Канонічна задача мінімізації
У базисі Буля
Над
Мета – зменшення кількості літер
Загальна задача мінімізації
Усі інші методи
Слайд 236НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
Методи розв’язання канонічної задачі мінімізації
Аналітичні
Квайна-МакКласскі-Петрика
Інші
Табличні
Геометричні
Графо-аналітичні
Карти Карно
Діаграми
Алгебро-топологічні
інші
Слайд 237НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
Методи розв’язання загальної задачі мінімізації (аналітичні)
Еврістичний
Винесення за дужки
Внесення надлишковості і глобального винесення за дужки
Перехід до небулевого базису
Метод функціональної декомпозиції
інші
Слайд 239НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
Винесення за дужки
Внесення надлишковості і глобального
Слайд 240НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
Метод функціональної декомпозиції
проста розділова і
загальний випадок
Слайд 242НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
4-розрядні суматори (у прямому, оберненому і
Слайд 244НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
Функціональна схема повного однорозрядного двійкового суматора
Слайд 245НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
Повний однорозрядний двійковий суматор (матрична схема)
Слайд 246НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
Двійкові однорозрядні напівсуматор (а)
та повний
c0 = ab;
.
Слайд 247НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
Багатозначні логіки. Нечітка логіка
Тризначна логіка Лукасевича
(ні, може бути, так)
N-значна логіка Лукасевича {0/n-1,1/n-1, …,n-1/n-1}
Тризначна логіка Поста {0,1,2}
N-значна логіка Поста {0,1,2, …,n-1}
Слайд 248НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
Національний університет «Львівська політехніка»
Lviv Polytechnic National
Комп’ютерна логіка (частина 2)
Слайд 249НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
Виконання навчального плану
Здана курсова робота
Виконано
Написано усі 16 лекційних контрольних робіт
Дано правильні відповіді на усі тести
Є конспект лекцій (приблизно 5 сторінок на лекцію)
Слайд 250НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
Державна оцінка (іспит)
1. Оцінка на іспиті
2.
3. Оцінка на комісії
або
3б. Оцінка за результатами повторного вивчення курсу – можливо більше не буде
Державна оцінка
(залік за курсову роботу)
Слайд 251НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
Стандартні вимоги до відповідей на іспиті
Повинна
Під час підготовки відповіді нічим не можна користуватися
Під час підготовки відповіді ні з ким не можна перемовлятися та обмінюватися інформацією
Для допуску до іспиту потрібно виконати навчальний план
Слайд 252НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
Полегшені умови до іспитів, комісії та
Студент погоджується самостійно опрацювати деякі питання учбового плану
Білет на іспит видається достроково за умови
До 15-го навчального тижня здано усі задачі курсової роботи і отримано за них більше 60 балів
У сумі за практичні заняття отримано більше 20 балів (з 30)
Написано усі лекційні контрольні роботи на дану дату
Правильно дано відповіді на усі питання тестів до 2-ої частини Комп’ютерної логіки (2-ий курс) у ВНС
Є конспект лекцій (приблизно 5 сторінок на лекцію)
Здано академрізницю (в кого вона є)
Складено іспит за повторне вивчення 1-ої частини Комп’ютерної логіки (кому це потрібно)
Під час підготовки до відповіді дозволяється користуватися чим завгодно
Повинна бути дана відповідь на усі питання білету
Слайд 253НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
Оцінювання відповідей при стандартному підході
Для іспиту:
Слайд 254НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
Оцінювання відповідей на іспиті при полегшеному
Слайд 255НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
Покращення оцінок
Було 51 бал – 51%
(поточний контроль – 1 з 30, іспит - 50 з 70,
3% з 30 за поточку і 71% з 70 за іспит)
Хоче “добре” (71 бал – 71% від 100 балів)
Тоді треба набрати спочатку за поточний контроль 71% від 30 = 21 бал,
а після того -71% від 70 =50 балів за іспит.
Слайд 256НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
Відпрацювання пропущених лекційних контрольних робіт
Копія власноручно
Ескізи слайдів, що демонструвалися на лекції, на якій писали пропущену контрольну роботу
Слайд 260НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
Комп’ютерна логіка. Курсова робота. Група КІ-21.
Слайд 263НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
Консультації – після закінчення останнього лекційного
Слайд 269НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
БАЗОВІ КОМБІНАЦІЙНІ ВУЗЛИ
дешифратори і демультиплексори;
мультиплексори;
шифратори;
перетворювачі кодів;
постійні
програмовані логічні матриці;
програмовані матриці логіки;
суматори і напівсуматори;
вузли порівняння;
арифметично-логічні пристрої;
вузли зсуву;
помножувачі;
вузли прискорення переносу;
інші.
Слайд 273НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
VHDL-опис дешифратора “3 у 8”
library IEEE;
use
use IEEE.STD_LOGIC_UNSIGNED.all;
entity DC is
port ( O : out STD_LOGIC_VECTOR (7 downto 0);
I : in STD_LOGIC_VECTOR (2 downto 0);
CS : in STD_LOGIC);
end entity;
architecture DC_arch of DC is
begin
O(0) <= CS when (I = 0) else '0';
O(1) <= CS when (I = 1) else '0';
O(2) <= CS when (I = 2) else '0';
O(3) <= CS when (I = 3) else '0';
O(4) <= CS when (I = 4) else '0';
O(5) <= CS when (I = 5) else '0';
O(6) <= CS when (I = 6) else '0';
O(7) <= CS when (I = 7) else '0';
end architecture;
Слайд 275НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
Нарощування розрядності дешифраторів
DC “4 у 16”
Слайд 276НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
Нарощування розрядності дешифраторів
DC “3 у 8”
Слайд 277НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
Демультиплексор DX = Дешифратор DC
Дані
Дані
Керування
Керування
Слайд 280НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
VHDL-опис
library IEEE;
use IEEE.std_logic_1164.all;
use IEEE.std_logic_unsigned.all;
entity mux is
port
S : in std_logic_vector (2 downto 0);
O : out std_logic);
end entity;
architecture mux_arch of mux is
begin
O <= I(CONV_INTEGER(S));
end architecture;
Слайд 289НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
Матрична схема перетворювача коду 8421 у
Слайд 290НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
Перетворювач кодів для семигементного індикатора
Слайд 291НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
Перетворювач кодів – дешифратор для 7-сегментного
Слайд 296НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
Опис ПЗП на мові VHDL
library IEEE;
use
use IEEE.std_logic_unsigned.all;
entity rom is
port ( CS : in STD_LOGIC;
A : in STD_LOGIC_VECTOR(2 downto 0);
D : out STD_LOGIC_VECTOR(3 downto 0));
end entity;
architecture rom_arch of rom is
begin
process(A, CS)
begin
if (CS = '1') then
case (A) is
when "000" => D <= "0100";
when "001" => D <= "0010";
when "010" => D <= "0111";
when "011" => D <= "0100";
when "100" => D <= "0001";
when "101" => D <= "0011";
when "110" => D <= "0101";
when "111" => D <= "0101";
when others => D <= "0000";
end case;
else
D <= "0000";
end if;
end process;
Слайд 305НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
Конфігуровані логічні блоки (CLB) та електронні
Слайд 307НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
Операційний пристрій на основі ПЗП
S =
Слайд 310НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
Вузол порівняння на основі DC
Вузол порівняння
Слайд 316НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
Дешифратор діапазону кодів
04B8F ...1Е3А4 (04B8F…0FFFF)
┌──┬────────────────────────────────┬───────┬─────────┐
│N │
│ │15 13 11 09 07 05 03 01 │0 1 2 3│ кодів │
│ │ 14 12 10 08 06 04 02 00│ │ │
│ ├────────────────────────────────┼───────┼────┬────┤
│ │A15 A13 A11 A9 A7 A5 A3 A1 │M │ від│ до │
│ │ A14 A12 A10 A8 A6 A4 A2 A0│ │ │ │
├──┼────────────────────────────────┼───────┼────┼────┤
│I0│ L H L L H L H H H L L L H H H H│A - - -│4B8F│4B8F│
│I1│ L H L L H L H H H L L H - - - -│A - - -│4B90│4B9F│
│I2│ L H L L H L H H H L H - - - - -│A - - -│4BA0│4BBF│
│I3│ L H L L H L H H H H - - - - - -│A - - -│4BC0│4BFF│
│I4│ L H L L H H - - - - - - - - - -│A - - -│4C00│4FFF│
│I5│ L H L H - - - - - - - - - - - -│A - - -│5000│5FFF│
│I6│ L H H - - - - - - - - - - - - -│A - - -│6000│7FFF│
│I7│ H - - - - - - - - - - - - - - -│A - - -│8000│FFFF│
└──┴────────────────────────────────┴───────┴────┴────┘
Слайд 317НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
Дешифратор діапазону кодів
04B8F ...1Е3А4 (10000…1E3A4)
┌──┬────────────────────────────────┬───────┬─────────┐
│N │
│ │15 13 11 09 07 05 03 01 │0 1 2 3│ кодів │
│ │ 14 12 10 08 06 04 02 00│ │ │
│ ├────────────────────────────────┼───────┼────┬────┤
│ │A15 A13 A11 A9 A7 A5 A3 A1 │S │ від│ до │
│ │ A14 A12 A10 A8 A6 A4 A2 A0│ │ │ │
├──┼────────────────────────────────┼───────┼────┼────┤
│I0│ H H H L L L H H H L H L L H L L│A - - -│E3A4│E3A4│
│I1│ H H H L L L H H H L H L L L - -│A - - -│E3A0│E3A3│
│I2│ H H H L L L H H H L L - - - - -│A - - -│E380│E39F│
│I3│ H H H L L L H H L - - - - - - -│A - - -│E300│E37F│
│I4│ H H H L L L H L - - - - - - - -│A - - -│E200│E2FF│
│I5│ H H H L L L L - - - - - - - - -│A - - -│E000│E1FF│
│I6│ H H L - - - - - - - - - - - - -│A - - -│C000│DFFF│
│I7│ H L - - - - - - - - - - - - - -│A - - -│8000│BFFF│
│I8│ L - - - - - - - - - - - - - - -│A - - -│0000│7FFF│
└──┴────────────────────────────────┴───────┴────┴────┘
Слайд 320НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
Зсуви
Логічний зсув ліворуч
Логічний зсув праворуч
Арифметичний зсув
Арифметичний зсув праворуч
Циклічний зсув ліворуч
Циклічний зсув праворуч
Слайд 321НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
Двійковий суматор з наскрізним (послідовним) переносом
Слайд 325НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
4-бітний суматор із схемою прискореного переносу
Слайд 326НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
16-бітний суматор із схемою прискореного переносу
Слайд 327НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
64-бітний суматор із схемою прискореного переносу
Слайд 328НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
Двійкові суматори
Суматор з паралельним переносом (1
Суматор з послідовним (наскрізним) переносом (немає вузлів прискорення переносу)
Суматор з груповим переносом (декілька вузлів прискорення переносу)
Слайд 329НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
Паралельний матричний помножувач на комірках Гілда
Слайд 330НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
Паралельний матричний помножувач на комірках Гілда
Слайд 331НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
Матричний (паралельний, комбінаційний) помножувач
Комірка Гілда
Слайд 337НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
Загальна структурна схема цифрового автомата
Слайд 340НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
Часові функції алгебри логіки
Для опису роботи
ЧФАЛ 1-го роду
ЧФАЛ 2-го роду
ЧФАЛ 3-го роду
Функціонально-повна система часових функцій алгебри логіки = ФПЧ ФАЛ + функція, що змінює час
Слайд 343НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
Часова функція 3-го роду
Зворотній зв’язок (техн)
Слайд 344НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
Загальна схема тригера
(trigger, flip-flop, latch)
Слайд 345НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
Тригер та генератор
Тригер – логічний елемент,
Генератор - логічний елемент, що може знаходитися у двох станах та переходити з одного стану в інший без дії зовнішніх сигналів
Слайд 353НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
Функціональна схема D-тригера, що спрацьовує по
Слайд 358НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
Тригери з асинхронними входами (R, S)
Слайд 362НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
Класифікація регістрів
За функціональним призначенням
регістри зсуву
Регістри для
За типом тригерів
За організацією зсуву
Ліворуч, праворуч, універсальні
За способом прийому і видачі даних при зсуві (вхід/вихід)
Послідовний/послідовний
Послідовний/паралельний
Паралельний/послідовний
Паралельний/паралельний
Слайд 366НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
Оперативний запам’ятовуючий пристрій (ОЗП)
Слайд 367НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
Ієрархія пам’яті
Основні кількісні характеристики ОЗП:
кількість
об’єм пам’яті V = N * m = 2n * m біт.
Слайд 376НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
Конфігуровані логічні блоки (CLB) та електронні
Слайд 380НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
Загальна структурна схема цифрового автомата
Слайд 383НУЛП 2016-2017 н.р.
Глухов В.С. Комп'ютерна логіка
Рекомендована послідовність синтезу цифрових автоматів
Синтез абстрактного
Синтез алгоритма роботи автомата.
Вибір структури автомата (Мура або Мілі).
Фіксація алгоритма у вигляді графа.
Синтез структурного автомата
Вибір елементної бази комбінаційної частини.
Вибір елементної бази пам’яті автомата.
Вибір способу кодування вхідних та вихідних сигналів.
Вибір способу кодування внутришніх станів автомата.
Створення таблиці переходів автомата.
Створення таблиці виходів автомата.
Мінімізація формул для сигналів збудження тригерів автомата. Фіксація результатів у вигляді диз’юнктивної нормальної форми (ДНФ).
Для деяких структурних автоматів (у яких комбінаційна частина реалізується на дешифраторах, мультиплексорах, а також для мікропрограмних автоматів, у яких комбінаційна частина реалізується на ПЗП) даний етап мінімізації непотрібний.
Мінімізація формул для виходів автомата. Фіксація результатів у вигляді диз’юнктивної нормальної форми (ДНФ).
Для деяких структурних автоматів (у яких комбінаційна частина реалізується на дешифраторах, мультиплексорах, а також для мікропрограмних автоматів, у яких комбінаційна частина реалізується на ПЗП) даний етап мінімізації непотрібний.
Синтез пам’яті автомата.
Синтез комбінаційної частини автомата.