октября 2010 года
Санкт-Петербург
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Командная олимпиада школьников Санкт- Петербурга по информатике и программированию. Разбор задач презентация
Содержание
- 1. Командная олимпиада школьников Санкт- Петербурга по информатике и программированию. Разбор задач
- 2. Задача A Бактерии
- 3. Автор задачи – Михаил Дворкин Условие –
- 4. Постановка задачи Дано целое число n За
- 5. Идея решения Определить, возможно ли получить m
- 6. Нахождение решения Рассмотреть задачу с конца ―
- 7. Решение Разложить оба числа на простые множители
- 8. Почему это работает? Единственный способ уменьшить показатель
- 9. Задача B Шахматная головоломка
- 10. Автор задачи – Виталий Аксенов Условие –
- 11. Условие задачи Дано расположение коня на доске
- 12. Как решать? Если слон или ладья бьют
- 13. Интересные клетки Ладья бьет все поля в
- 14. Задача C Шоколад
- 15. Автор задачи – Виталий Аксенов Условие –
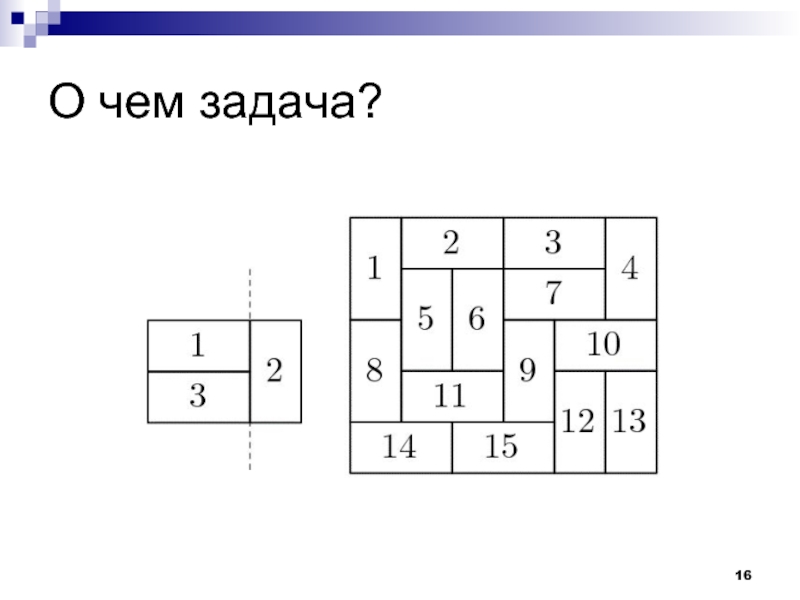
- 16. О чем задача?
- 17. Как решать? Перебрать всевозможные вертикальные и горизонтальные
- 18. Задача D Луна
- 19. Автор задачи – Юрий Петров Условие –
- 20. О чем задача? Необходимо найти луну на фотографии
- 21. Как решать? Ограничения небольшие – можно и
- 22. Как проверить луну? Проверить, что все точки
- 23. Задача E Ожерелье
- 24. Автор задачи – Михаил Дворкин Условие –
- 25. Как решать? Ожерелий из двух, трех, четырех
- 26. Альтернативное решение Генерируем случайное ожерелье Проверяем, есть ли ось симметрии
- 27. Задача F Гонки
- 28. Автор задачи – жюри олимпиады Условие –
- 29. За какое время проедет машина? Проедет x
- 30. Как решать? Время для одной машины x
- 31. Задача G Робот
- 32. Автор задачи – Михаил Дворкин Условие –
- 33. О чем задача Робот переместился из начала
- 34. Как решать? Длина каждого отрезка пути не
- 35. Пусть робот попадет в точку B, если
- 36. Если все направления, коэффициенты при которых не
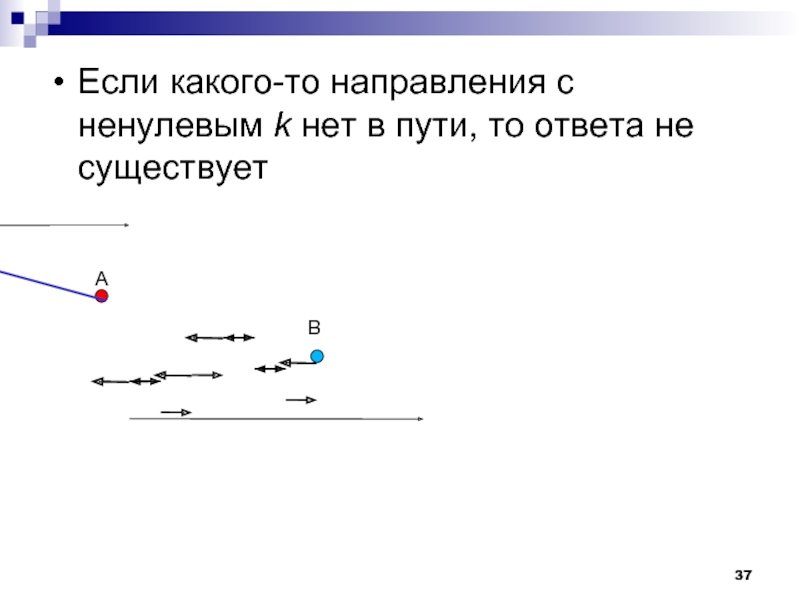
- 37. Если какого-то направления с ненулевым k нет
- 38. Задача H Санта
- 39. Автор задачи – Виталий Аксенов Условие –
- 40. О чем задача Даны два списка из
- 41. Как решать? Так как каждое число встречается
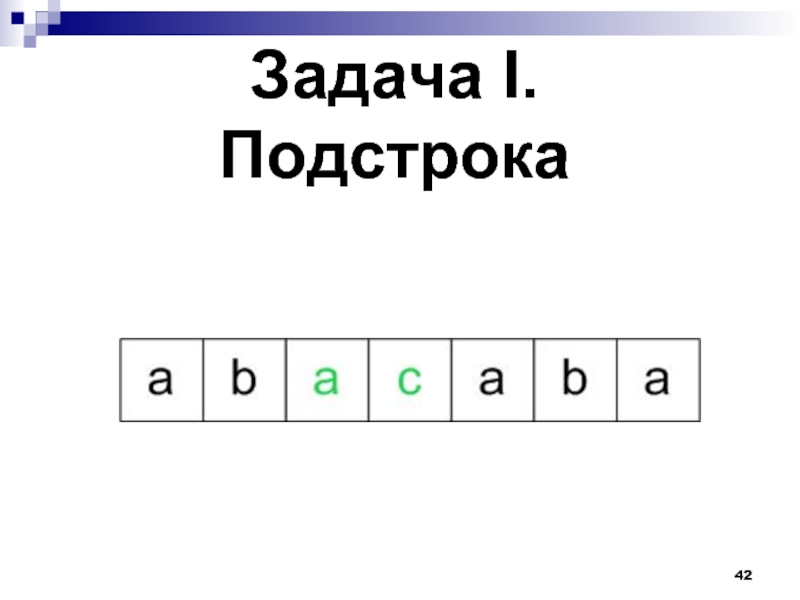
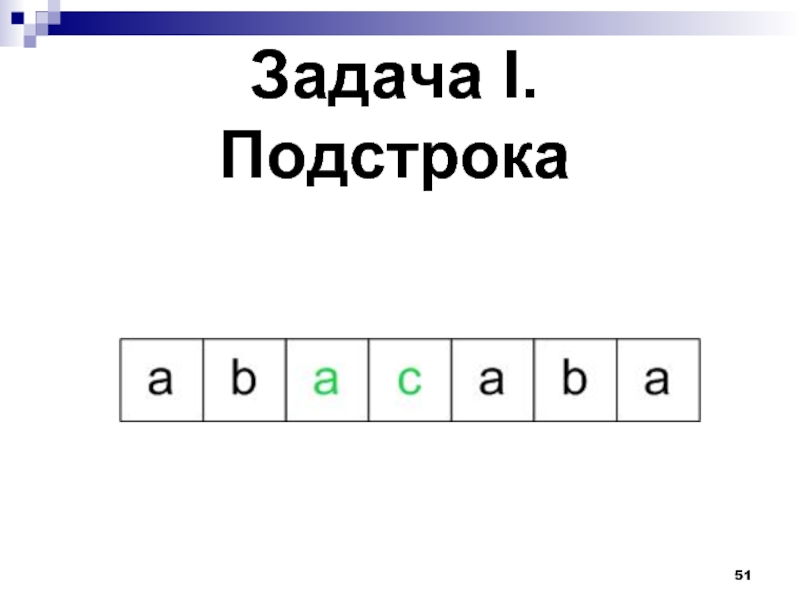
- 42. Задача I. Подстрока
- 43. Автор задачи – Антон Банных Условие –
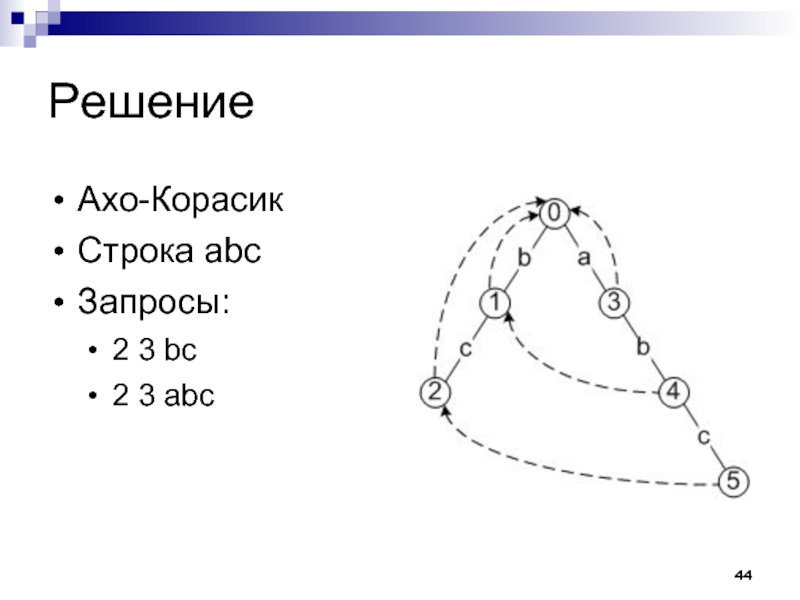
- 44. Решение Ахо-Корасик Строка abc Запросы: 2 3 bc 2 3 abc
- 45. Решение Для каждого префикса строки запишем, в
- 46. Решение Рассмотрим дерево, образованное суффиксными ссылками
- 47. Решение Для каждого запроса нужно определить, встречалась ли вершина из соответствующего поддерева в отрезке
- 48. Решение Перенумеруем вершины в порядке выхода из обхода в глубину
- 49. Вершины одного поддерева имеют последовательные номера Пусть
- 50. Решение Двумерное дерево отрезков — O(n log
- 51. Задача I. Подстрока
- 52. Автор задачи – Антон Банных Условие –
- 53. Как решать? Ахо-Корасик Суффиксный массив Суффиксное дерево Суффиксный автомат
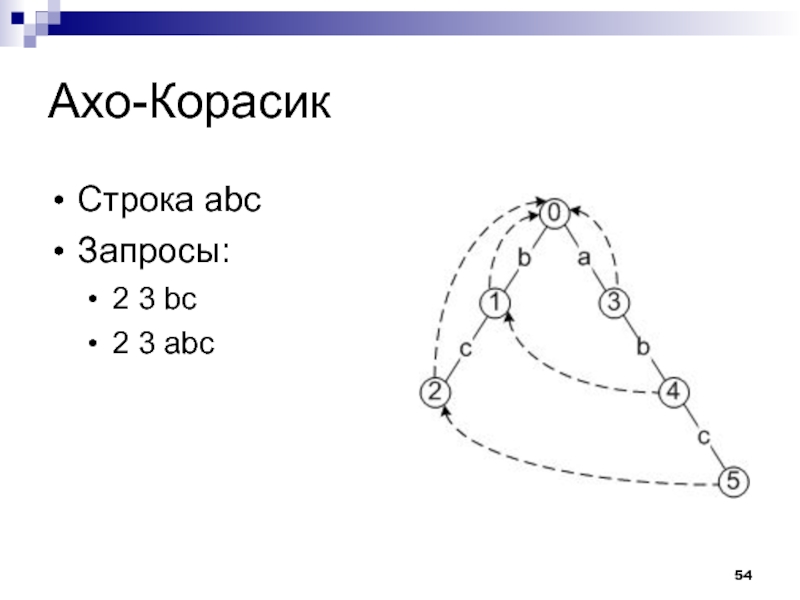
- 54. Ахо-Корасик Строка abc Запросы: 2 3 bc 2 3 abc
- 55. Решение Для каждого префикса строки запишем, в
- 56. Идея решения Рассмотрим дерево, образованное суффиксными ссылками
- 57. Задача Запрос: l, r, длина строки len
- 58. Решение Перенумеруем вершины в порядке выхода из обхода в глубину
- 59. Решение Вершины одного поддерева имеют последовательные номера
- 60. Решение
- 61. Решение Двумерное дерево отрезков: O(n log2 n)
- 62. Асимптотика Ахо-Корасик: O(n) Перенумерация вершин: O(n) Обработка запросов: O(n log n)
- 63. Задача J Вода
- 64. Автор задачи – Виталий Аксенов Условие –
- 65. Как решать? Поддерживаем текущий уровень воды Поддерживаем суммарную скорость вытекания воды Обрабатываем события
- 66. События Уровень воды достиг очередного отверстия Запрос
- 67. Решение Определяем ближайшее событие Вычисляем уровень воды к моменту наступления события Обрабатываем событие
- 68. Реализация Выделим «интересные высоты» ─ те, которые
- 69. Реализация Появление и починка течи ─ изменение
- 70. Асимптотика Выделение «интересных высот» сортировка: O(n log
- 71. Спасибо за внимание! Вопросы? http://neerc.ifmo.ru/school
Слайд 1XVIII Командная олимпиада школьников Санкт-Петербурга по информатике и программированию
Разбор задач
31
Слайд 3Автор задачи – Михаил Дворкин
Условие – Михаил Дворкин
Подготовка тестов – Сергей
Мельников
Разбор – Антон Ахи
Разбор – Антон Ахи
Слайд 4Постановка задачи
Дано целое число n
За один шаг можно:
Разделить n на любой
его простой делитель
Возвести число n в квадрат
Требуется за минимальное число шагов получить число m
Возвести число n в квадрат
Требуется за минимальное число шагов получить число m
Слайд 5Идея решения
Определить, возможно ли получить m
Разложить m на простые делители
Если хотя
бы один из них не является делителем n, то ответ «Impossible»
Слайд 6Нахождение решения
Рассмотреть задачу с конца ― получить из m число n,
если разрешены операции:
Извлечь корень
Домножить на произвольное простое число
Извлечь корень
Домножить на произвольное простое число
Слайд 7Решение
Разложить оба числа на простые множители
Пока существует простой делитель, который входит
в m в большей степени, чем в n, доводим каждый простой делитель m до четной степени и извлекаем корень
Домножаем на оставшиеся простые
Домножаем на оставшиеся простые
Слайд 8Почему это работает?
Единственный способ уменьшить показатель простого делителя ― извлечение корня,
которое возможно лишь при условии четности всех степеней
Перед любым извлечением корня невыгодно увеличивать показатель более чем на один
Перед любым извлечением корня невыгодно увеличивать показатель более чем на один
Слайд 10Автор задачи – Виталий Аксенов
Условие – Сергей Поромов
Подготовка тестов – Владимир
Ульянцев
Разбор – Антон Ахи
Разбор – Антон Ахи
Слайд 11Условие задачи
Дано расположение коня на доске
Требуется поставить ладью и слона на
доску, чтобы они били коня, но не били друг друга
Слайд 12Как решать?
Если слон или ладья бьют коня, то конь их не
бьет
Позиций на доске мало
Переберем все возможные позиции ладьи и слона, из которых они бьют коня
Проверим, что поставленные фигуры не бьют друг друга
Позиций на доске мало
Переберем все возможные позиции ладьи и слона, из которых они бьют коня
Проверим, что поставленные фигуры не бьют друг друга
Слайд 13Интересные клетки
Ладья бьет все поля в том же столбце или строке
Слон
бьет все поля с такой же разницей номеров строки и столбца
Слайд 15Автор задачи – Виталий Аксенов
Условие – Антон Ахи
Подготовка тестов – Нияз
Нигматуллин
Разбор – Сергей Поромов
Разбор – Сергей Поромов
Слайд 17Как решать?
Перебрать всевозможные вертикальные и горизонтальные разрезы
Проверить, можно ли хоть один
из них провести: с разных сторон от разреза должны быть различные дольки, то есть различные числа
Слайд 19Автор задачи – Юрий Петров
Условие – Юрий Петров
Подготовка тестов – Владимир
Ульянцев
Разбор – Сергей Поромов
Разбор – Сергей Поромов
Слайд 21Как решать?
Ограничения небольшие – можно и достаточно проверить всевозможные положения и
размеры луны, выбрать наибольший размер
Не забыть, что луна должна быть целиком на фотографии
Не забыть, что луна должна быть целиком на фотографии
Слайд 22Как проверить луну?
Проверить, что все точки фотографии на расстоянии не более
радиуса от центра луны белые
Расстояние можно считать в целых числах:
Проверка работает за O(w·h).
Расстояние можно считать в целых числах:
Проверка работает за O(w·h).
Слайд 24Автор задачи – Михаил Дворкин
Условие – Сергей Поромов
Подготовка тестов – Нияз
Нигматуллин
Разбор – Сергей Мельников
Разбор – Сергей Мельников
Слайд 25Как решать?
Ожерелий из двух, трех, четырех и пяти жемчужин нет
Для остальных
возьмем ожерелье
1 1 0 1 0 … 0
Оно подходит, так как ось может проходить лишь через 1, но все такие оси не являются осями симметрии
1 1 0 1 0 … 0
Оно подходит, так как ось может проходить лишь через 1, но все такие оси не являются осями симметрии
- 1
Слайд 28Автор задачи – жюри олимпиады
Условие – Антон Банных
Подготовка тестов – Виталик
Аксенов
Разбор – Сергей Мельников
Разбор – Сергей Мельников
Слайд 29За какое время проедет машина?
Проедет x div (tv) целых сегментов длинной
tv, сделает между ними
x div (tv) – 1 зарядок батарей
Если x mod (tv) не 0, то надо проехать ещё, а для этого зарядить батарею
Таким образом, число зарядок: ceil(x / (tv)) – 1
Остальное время едет со скоростью v
x div (tv) – 1 зарядок батарей
Если x mod (tv) не 0, то надо проехать ещё, а для этого зарядить батарею
Таким образом, число зарядок: ceil(x / (tv)) – 1
Остальное время едет со скоростью v
Слайд 30Как решать?
Время для одной машины
x / v + (ceil(x / (tv))
– 1) * t
Сравнить время, за которое машины достигнут финиша
Сравнить время, за которое машины достигнут финиша
Слайд 32Автор задачи – Михаил Дворкин
Условие – Михаил Дворкин
Подготовка тестов – Алексей
Цыпленков
Разбор – Алексей Цыпленков
Разбор – Алексей Цыпленков
Слайд 33О чем задача
Робот переместился из начала координат в точку A(x, y),
при этом робот поворачивал только на 90 градусов направо или налево
Дана последовательность поворотов
Определить длины отрезков пути робота или некорректность пути
Дана последовательность поворотов
Определить длины отрезков пути робота или некорректность пути
Слайд 34Как решать?
Длина каждого отрезка пути не меньше 1 и не больше
106
Для каждого направления (вверх, вниз, вправо, влево) найдем, есть ли отрезок пути робота, на котором он движется по этому направлению
Для каждого направления (вверх, вниз, вправо, влево) найдем, есть ли отрезок пути робота, на котором он движется по этому направлению
Слайд 35Пусть робот попадет в точку B, если всегда будет смещаться на
1
Чтобы попасть из В в А, нужно дополнительно сместиться на вектор А – В
Разложим вектор А – В по направлениям:
(все числа k1, k2, k3, k4 неотрицательны и не менее двух были равны нулю)
Чтобы попасть из В в А, нужно дополнительно сместиться на вектор А – В
Разложим вектор А – В по направлениям:
(все числа k1, k2, k3, k4 неотрицательны и не менее двух были равны нулю)
Слайд 36Если все направления, коэффициенты при которых не равны 0, были найдены
в пути робота, то ответ существует и строится следующим образом:
Длины всех отрезков принять за 1
Для каждого направления с ненулеывм k взять один произвольный отрезок движения по этому направлению и увеличить его длину на k
Длины всех отрезков принять за 1
Для каждого направления с ненулеывм k взять один произвольный отрезок движения по этому направлению и увеличить его длину на k
Слайд 39Автор задачи – Виталий Аксенов
Условие – Сергей Мельников
Подготовка тестов – Алексей
Цыпленков
Разбор – Алексей Цыпленков
Разбор – Алексей Цыпленков
Слайд 40О чем задача
Даны два списка из K и М натуральных чисел,
каждое не больше N. Найти все числа от 1 до N, которых нет в этом списке.
Каждое числе встречается в списках не более одного раза.
Каждое числе встречается в списках не более одного раза.
Слайд 41Как решать?
Так как каждое число встречается в списках не более одного
раза, то количество чисел, которых нет в списке, равно N – K
Так как N невелико, то за один линейный проход по спискам можно отметить все числа, которые в них есть
За линейный проход по массиву пометок вывести все числа, которых нет
Так как N невелико, то за один линейный проход по спискам можно отметить все числа, которые в них есть
За линейный проход по массиву пометок вывести все числа, которых нет
Слайд 43Автор задачи – Антон Банных
Условие – Антон Банных
Подготовка тестов – Антон
Банных
Разбор – Антон Банных
Разбор – Антон Банных
Слайд 45Решение
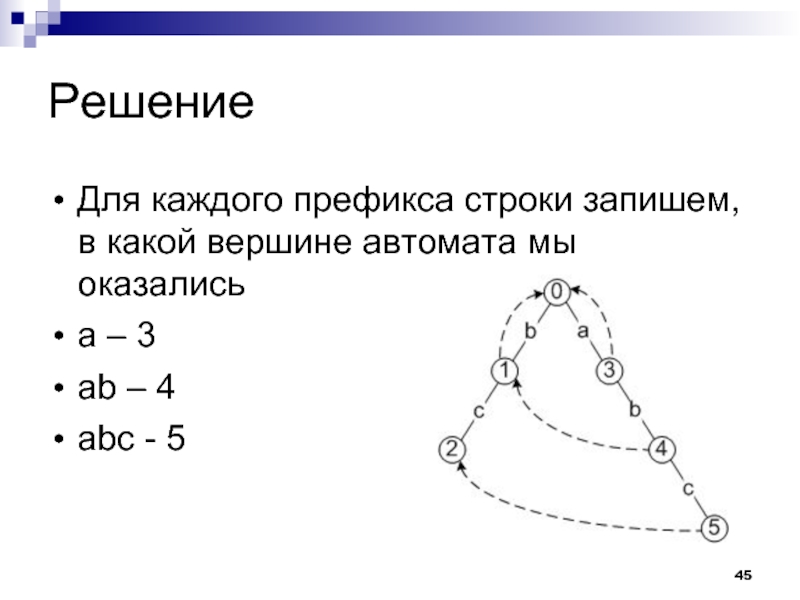
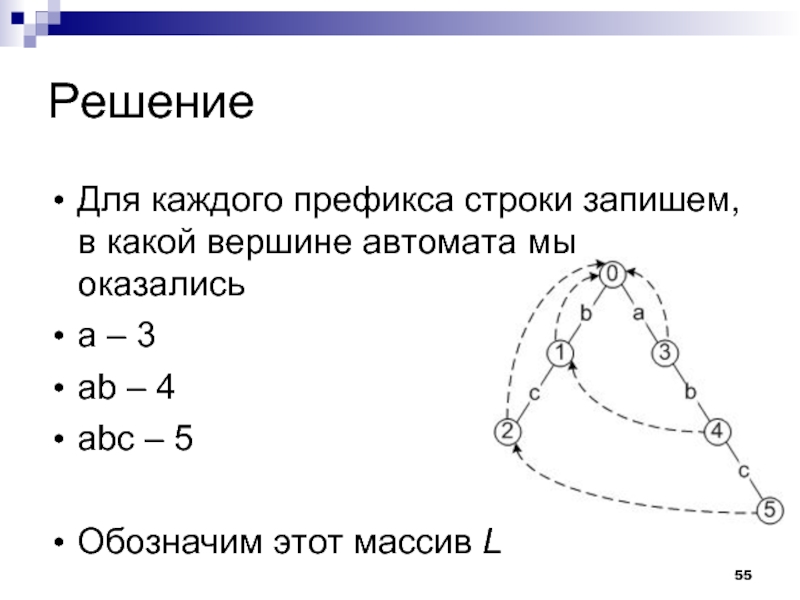
Для каждого префикса строки запишем, в какой вершине автомата мы оказались
а
– 3
ab – 4
abc - 5
ab – 4
abc - 5
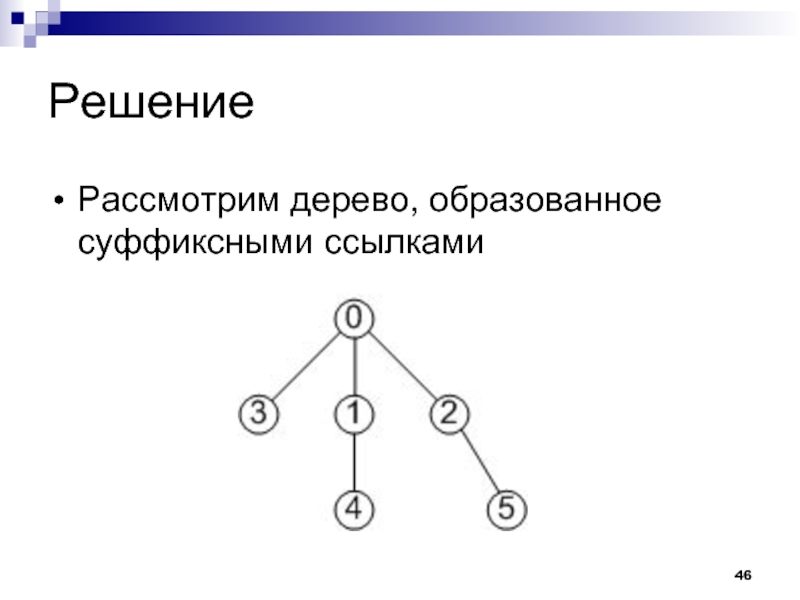
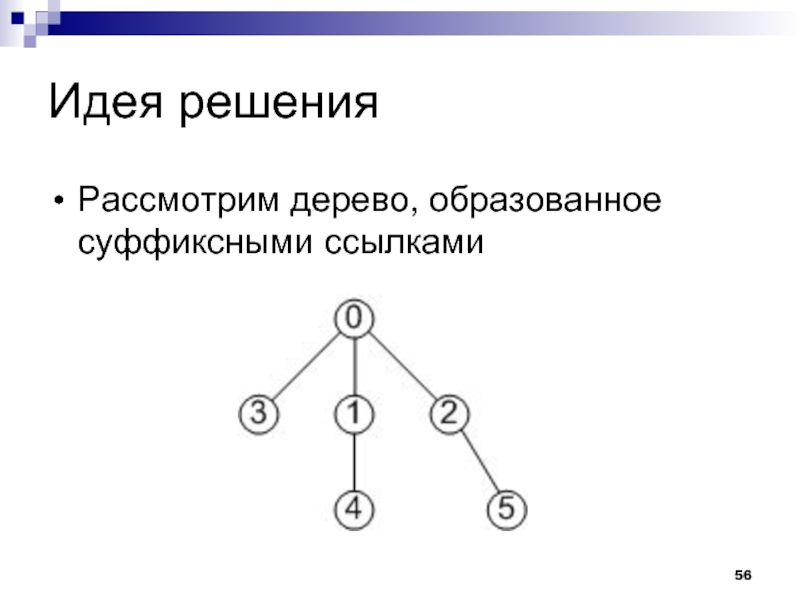
Слайд 47Решение
Для каждого запроса нужно определить, встречалась ли вершина из соответствующего поддерева
в отрезке
Слайд 49Вершины одного поддерева имеют последовательные номера
Пусть пара (префикс, номер вершины) —
точка
Запрос — есть ли точка в прямоугольнике
Запрос — есть ли точка в прямоугольнике
Решение
Слайд 50Решение
Двумерное дерево отрезков — O(n log n)
Одномерное дерево отрезков на сумму
События:
Начало
прямоугольника
Конец прямоугольника
Точка
Конец прямоугольника
Точка
Слайд 52Автор задачи – Антон Банных
Условие – Антон Банных
Подготовка тестов – Антон
Банных
Разбор – Антон Банных
Разбор – Антон Банных
Слайд 55Решение
Для каждого префикса строки запишем, в какой вершине автомата мы оказались
а
– 3
ab – 4
abc – 5
Обозначим этот массив L
ab – 4
abc – 5
Обозначим этот массив L
Слайд 57Задача
Запрос: l, r, длина строки len
Строке соответствует вершина x
Определить, встречалась ли
вершина из поддерева x в L[l + len – 1, r]
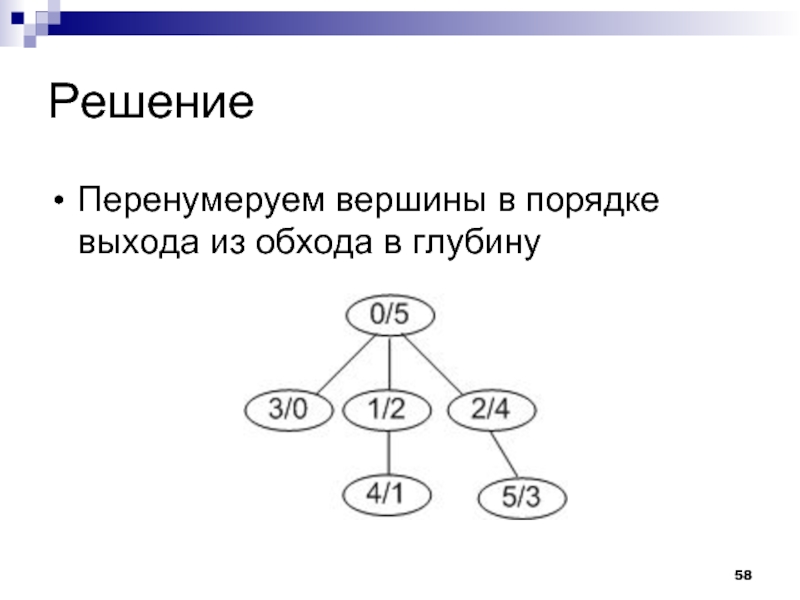
Слайд 59Решение
Вершины одного поддерева имеют последовательные номера
Пусть пара (префикс, номер вершины) –
точка
Запрос – есть ли точка в прямоугольнике
Запрос – есть ли точка в прямоугольнике
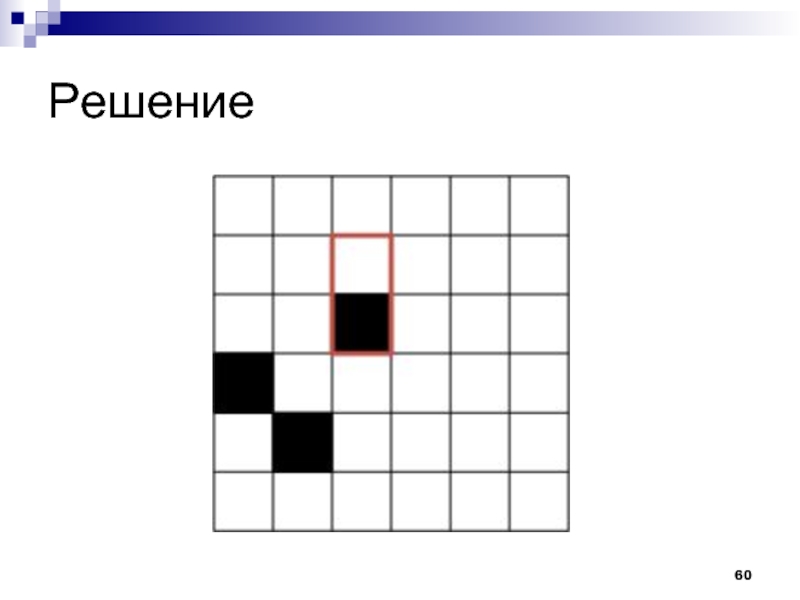
Слайд 61Решение
Двумерное дерево отрезков: O(n log2 n)
Одномерное дерево отрезков на сумму
События:
Начало прямоугольника
Конец
прямоугольника
Точка
Точка
Слайд 64Автор задачи – Виталий Аксенов
Условие – Антон Ахи
Подготовка тестов – Антон
Ахи
Разбор – Антон Банных
Разбор – Антон Банных
Слайд 65Как решать?
Поддерживаем текущий уровень воды
Поддерживаем суммарную скорость вытекания воды
Обрабатываем события
Слайд 66События
Уровень воды достиг очередного отверстия
Запрос на уровень воды
Появление новой течи
Устранение течи
Слайд 67Решение
Определяем ближайшее событие
Вычисляем уровень воды к моменту наступления события
Обрабатываем событие
Слайд 68Реализация
Выделим «интересные высоты» ─ те, которые встречаются в запросах
Храним скорость вытекания
воды через отверстия на высоте h
Событие ─ достижение «интересной высоты»
Событие ─ достижение «интересной высоты»
Слайд 69Реализация
Появление и починка течи ─ изменение соответствующего элемента массива и суммарной
скорости вытекания
Запрос на определение уровня воды ─ вывод текущего уровня
Достижение «интересной высоты» ─ изменение суммарной скорости вытекания
Запрос на определение уровня воды ─ вывод текущего уровня
Достижение «интересной высоты» ─ изменение суммарной скорости вытекания
Слайд 70Асимптотика
Выделение «интересных высот»
сортировка: O(n log n)
хеш-таблица: O(n)
Обработка событий: O(n)
Итого: O(n) или
O(n log n)