- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Формальные описания реальных объектов и процессов презентация
Содержание
- 1. Формальные описания реальных объектов и процессов
- 2. Ответами к заданиям являются слово, словосочетание,
- 3. Задание 1. Между населёнными пунктами А, В,
- 4. Понятия (что это?) Таблица Граф Дерево
- 5. Это виды представления информации
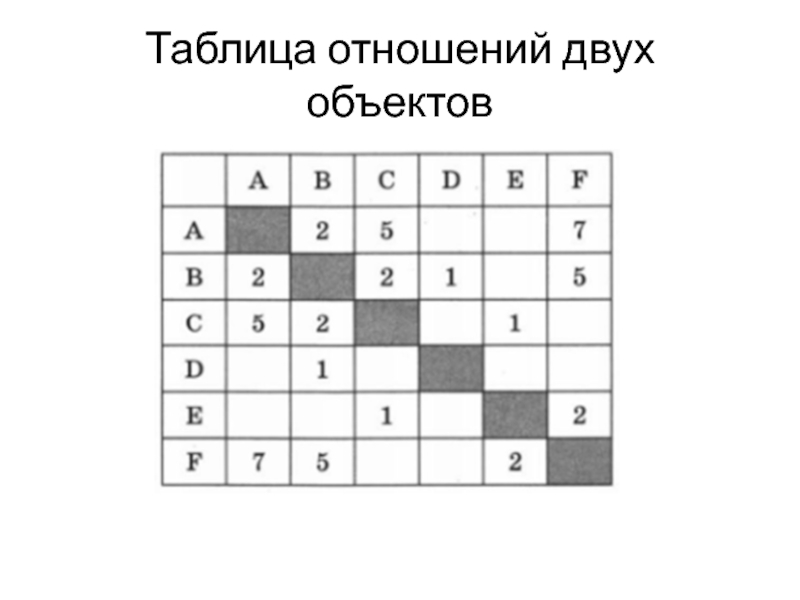
- 6. Таблица отношений двух объектов
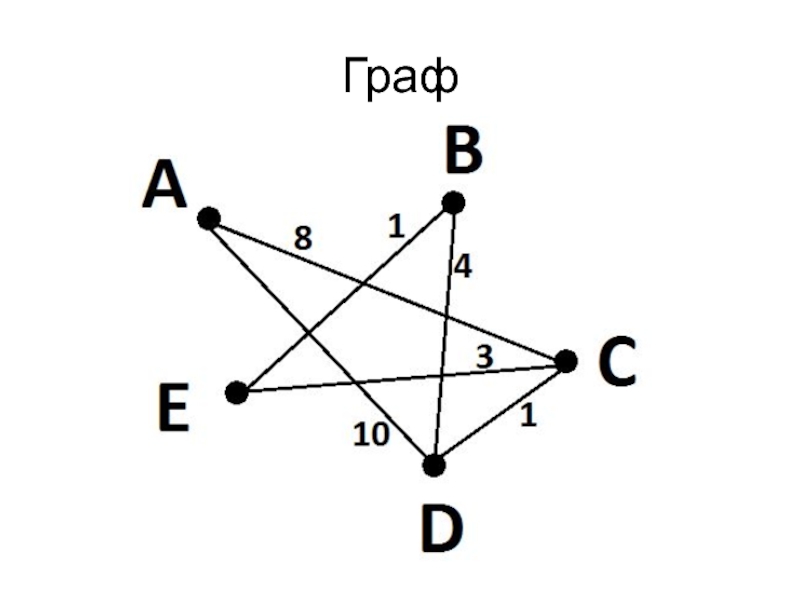
- 7. Граф
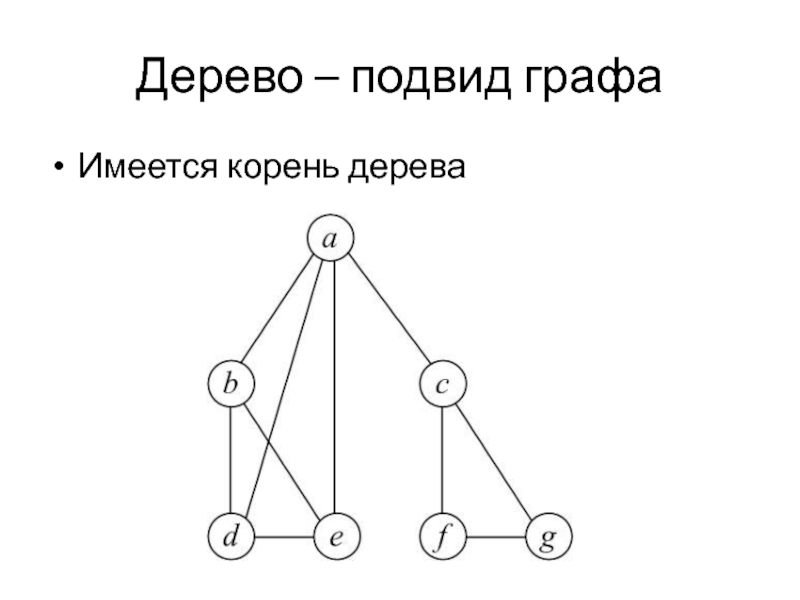
- 8. Дерево – подвид графа Имеется корень дерева
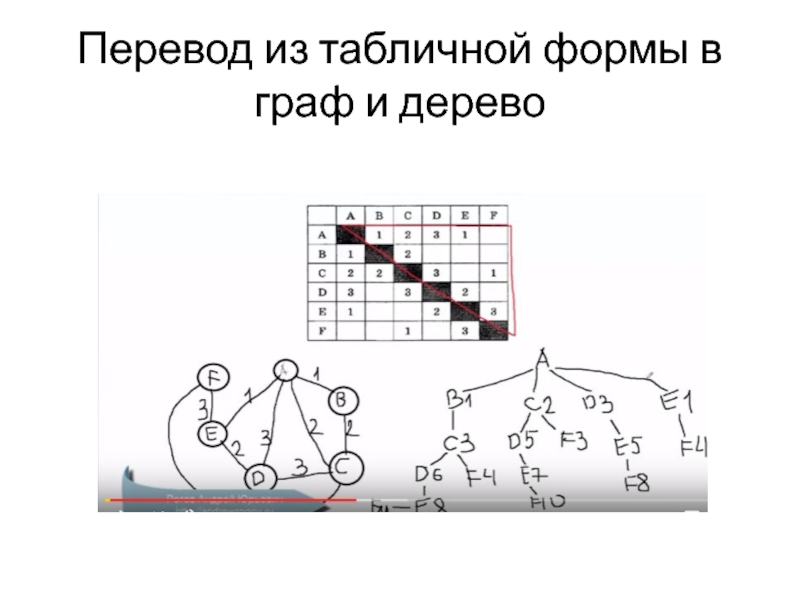
- 9. Для решения Необходимо из табличной формы представления информации сделать граф или наоборот.
- 10. Перевод из табличной формы в граф и дерево
- 11. Самостоятельно в тетради Между населёнными пунктами A,
- 12. Практика в Power Point Слайд № 1.
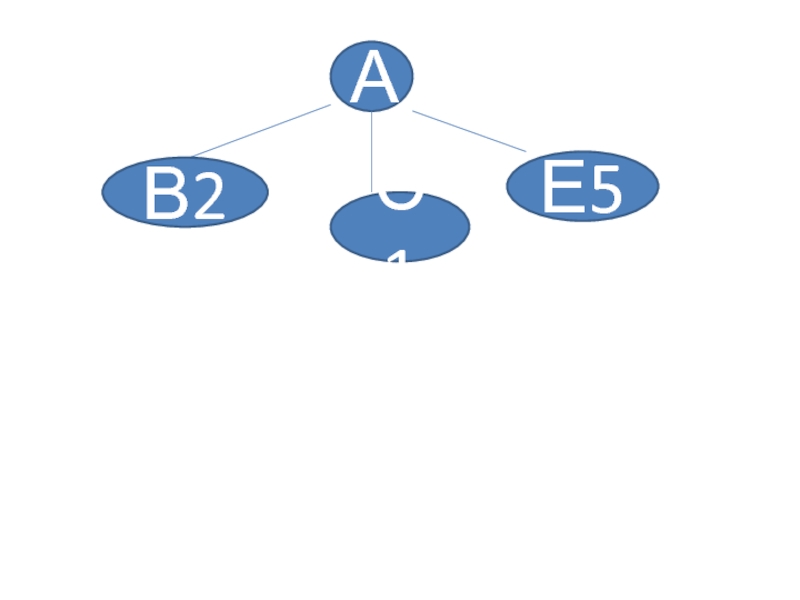
- 13. Слайд 3. Построить дерево по таблице, для каждого нового элемента создать анимацию появление
- 14. А В2 С1 Е5
- 15. Перемена
- 16. Задача 1. Между девятью планетами солнечной
- 17. Теперь сразу видно, что долететь с Земли до Марса нельзя.
- 18. Задача 3. В городе Маленьком 8
- 19. нет
- 20. Задача 6. Можно ли нарисовать изображенный
- 21. 7 Имеется группа островов, соединенных мостами
- 22. Задача8: Алия решила маме на день
- 23. Решение. Отметим точками цветы (РТГВК) (вершины
- 24. Задача9. Ранним утром Миша Маша, Асем
- 25. Задача10. Шесть футбольных команд должны сыграть
- 26. Задача5. В квартирах №1,2,3 жили три
- 27. Ответ: Айдар Тима Саша №1
- 28. Задача11. Арман, Мадии, Тимур, Сергей заняли
- 29. Ответ: С-1 Т-2 А -3 М-4.
- 30. Задача7. Григорий играли в шахматы. Каждый
- 31. Решение: Решим задачу с помощью полного
- 32. Задача8.Из города А в
- 33. Ответ: 6 партий .
- 34. Задача9. Андрей, Борис, Виктор и Григорий
- 35. Решение. I способ. С помощью стрелок
- 36. В эксель
- 37. Выехало три автомобиля из разных городов
Ответами к заданиям являются слово, словосочетание, число или последовательность слов, чисел. Запишите ответ без пробелов, запятых и других дополнительных символов.
Слайд 2
Ответами к заданиям являются слово, словосочетание, число или последовательность слов, чисел.
Запишите ответ без пробелов, запятых и других дополнительных символов.
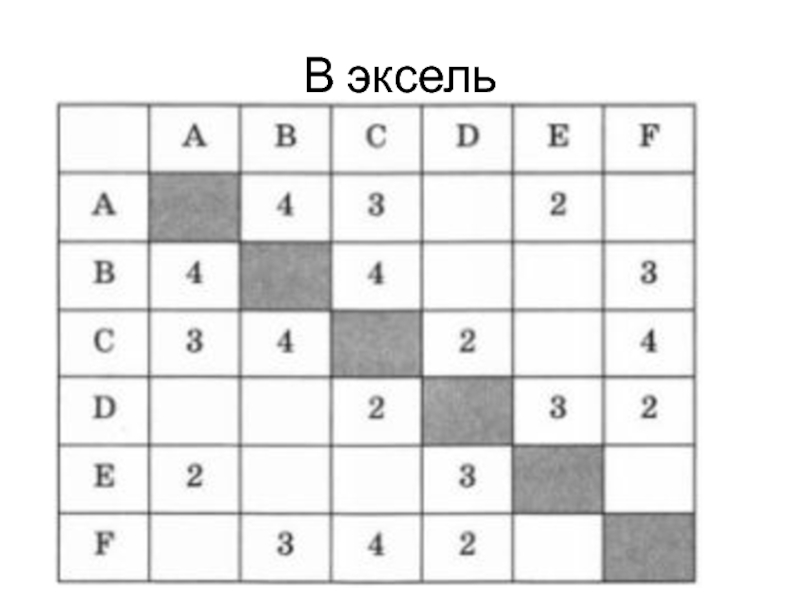
Слайд 3Задание 1.
Между населёнными пунктами А, В, С, D, Е, F построены
дороги, протяжённость которых приведена в таблице. (Отсутствие числа в таблице означает, что прямой дороги между пунктами нет.)
Определите длину кратчайшего пути между пунктами А и F (при условии, что передвигаться можно только по построенным дорогам).
1) 6
2) 7
3) 8
4) 9
Слайд 9Для решения
Необходимо из табличной формы представления информации сделать граф или
наоборот.
Слайд 11Самостоятельно в тетради
Между населёнными пунктами A, B, C, D, E построены
дороги, протяжённость которых (в километрах) приведена в таблице.
Определите длину кратчайшего пути между пунктами B и E (при условии, что передвигаться можно только по построенным дорогам).
1) 5 2) 6 3) 7 4) 8
Определите длину кратчайшего пути между пунктами B и E (при условии, что передвигаться можно только по построенным дорогам).
1) 5 2) 6 3) 7 4) 8
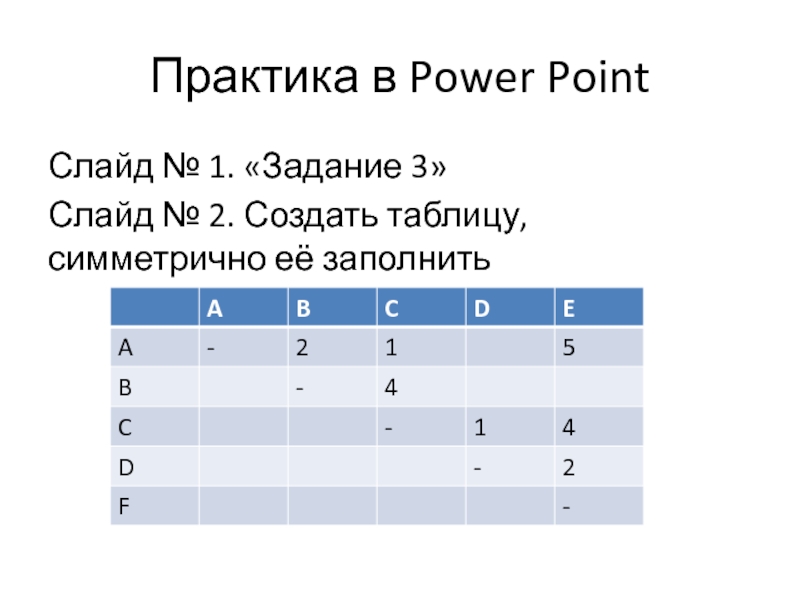
Слайд 12Практика в Power Point
Слайд № 1. «Задание 3»
Слайд № 2. Создать
таблицу, симметрично её заполнить
Слайд 16
Задача 1. Между девятью планетами солнечной системы установлено космическое сообщение. Рейсовые
ракеты летают по следующим маршрутам: Земля – Меркурий; Плутон – Венера; Земля – Плутон; Плутон – Меркурий; Меркурий – Вене; Уран – Нептун; Нептун – Сатурн; Сатурн – Юпитер; Юпитер – Марс и Марс – Уран. Можно ли долететь на рейсовых ракетах с Земли до Марса ?
Решение: Нарисуем схему условия: планеты изобразим точками, а маршруты ракет – линиями.
Решение: Нарисуем схему условия: планеты изобразим точками, а маршруты ракет – линиями.
Слайд 18
Задача 3. В городе Маленьком 8 телефонов. Можно ли их соединить
проводами так, чтобы каждый телефон был соединен ровно с пятью другими ?
Слайд 20
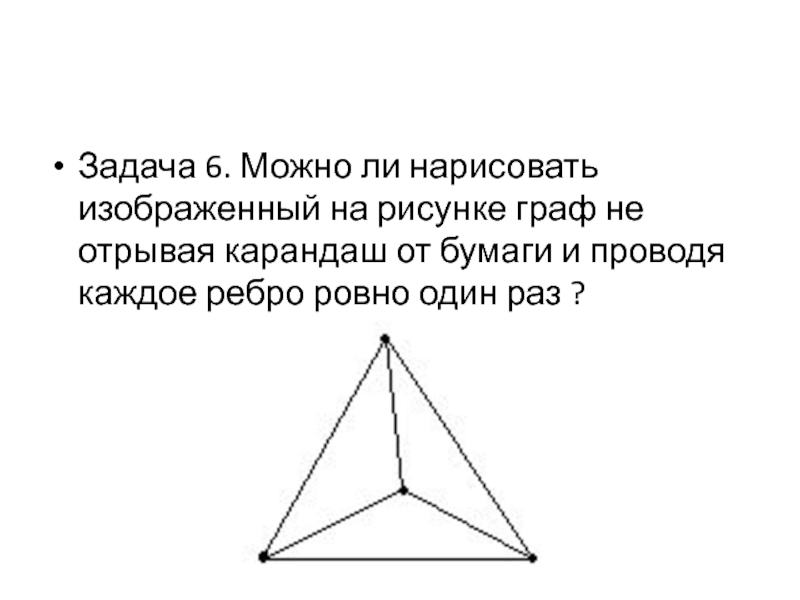
Задача 6. Можно ли нарисовать изображенный на рисунке граф не отрывая
карандаш от бумаги и проводя каждое ребро ровно один раз ?
Слайд 21
7 Имеется группа островов, соединенных мостами так, что от каждого острова
можно добраться до любого другого. Турист обошел все острова, пройдя по каждому мосту розно 1 раз. На острове Троекратном он побывал трижды. Сколько мостов ведет с Троекратного, если турист
а) не с него начал и не на нем закончил?
б) с него начал, но не на нем закончил?
в) с него начал и на нем закончил?
а) не с него начал и не на нем закончил?
б) с него начал, но не на нем закончил?
в) с него начал и на нем закончил?
Слайд 22
Задача8: Алия решила маме на день рождения подарить букет цветов (розы,
тюльпаны или гвоздики) и поставить из или в вазу или в кувшин.
Сколькими способами это можно сделать.
Сколькими способами это можно сделать.
Слайд 23
Решение. Отметим точками цветы (РТГВК) (вершины графа)
А связи между ними -линиями
между точками (рёбра графа)
По рисунку видно, что таких сопопбов - 6
* розы * тюльпан *гвоздики
* ваза *кувшин
По рисунку видно, что таких сопопбов - 6
* розы * тюльпан *гвоздики
* ваза *кувшин
Слайд 24
Задача9. Ранним утром Миша Маша, Асем обменялись приветствиями каждый с каждым.
Сколько всего было приветствий. Решите задачу с помощью графа.
Слайд 25
Задача10. Шесть футбольных команд должны сыграть матчи, каждая с каждой. Уже
сыграли матчи.
А с В, Г,Е Г с А,Д,Е
Б с В,Д,Е Д с Б,Г,Е
В с А,Б Е с А,Б,Г,Д
Сколько матчей сыграно и сколько осталось сыграть.
А с В, Г,Е Г с А,Д,Е
Б с В,Д,Е Д с Б,Г,Е
В с А,Б Е с А,Б,Г,Д
Сколько матчей сыграно и сколько осталось сыграть.
Слайд 26
Задача5. В квартирах №1,2,3 жили три друга: Айдар, Тима и Саша.
Известно, что в квартирах №1 и 2 жил не Айдар. Тима жил не в квартире №1. В какой квартире жил каждый из друзей.
Слайд 28
Задача11. Арман, Мадии, Тимур, Сергей заняли на математической олимпиаде четыре первых
места. Когда их спросили о распределений мест, они дали три ответа: Сергей – первый, Мади– второй, Сергей -второй, Арман – третий, Тимур – второй, Арман – четвертый. Известно, что в каждом ответе только одно утверждение верно. Как распределились места?
Слайд 30
Задача7. Григорий играли в шахматы. Каждый сыграл с каждым по одной
партии. Сколько партий было сыграно?
Слайд 31
Решение: Решим задачу с помощью полного графа с четырьмя вершинами А,
Б, В, Г, обозначенными по первым буквам имен каждого из мальчиков. В полном графе проводятся всевозможные ребра.
В данном случае отрезки-ребра обозначают сыгранные шахматные партии. Из рисунка видно, что граф имеет 6 ребер, значит, и партий было сыграно 6.
В данном случае отрезки-ребра обозначают сыгранные шахматные партии. Из рисунка видно, что граф имеет 6 ребер, значит, и партий было сыграно 6.
Слайд 32
Задача8.Из города А в город Б ведут две дороги, из города
Б в городок В -тоже две дороги и из города А в город В – тоже две дороги. Нарисуй схему и сосчитай все возможные пути из города А в город В.
Слайд 34
Задача9. Андрей, Борис, Виктор и Григорий после возвращения из спортивного лагеря
подарили на память друг другу свои фотографии. Причем каждый мальчик подарил каждому из своих друзей
по одной фотографии. Сколько всего фотографий было подарено?
по одной фотографии. Сколько всего фотографий было подарено?
Слайд 35
Решение. I способ. С помощью стрелок на ребрах полного графа с
вершинами А, Б, В и Г показан процесс обмена фотографиями. Очевидно, стрелок в 2 раза больше, чем ребер, т.е. 6*2 = 12. Столько же было подарено и фотографий.
II способ. Каждый из четверых мальчиков подарил друзьям 3 фотографии, следовательно, всего было роздано 3 • 4 = 12 фотографий.
О т в е т: 12 фотографий.
II способ. Каждый из четверых мальчиков подарил друзьям 3 фотографии, следовательно, всего было роздано 3 • 4 = 12 фотографий.
О т в е т: 12 фотографий.
Слайд 37
Выехало три автомобиля из разных городов и проехало по разным маршрутам.
Вычислить длину каждого маршрута.
