- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Элементарные сортировки. Сортировка выбором. Сортировка вставками. Сортировка Шелла. Перетасовка презентация
Содержание
- 1. Элементарные сортировки. Сортировка выбором. Сортировка вставками. Сортировка Шелла. Перетасовка
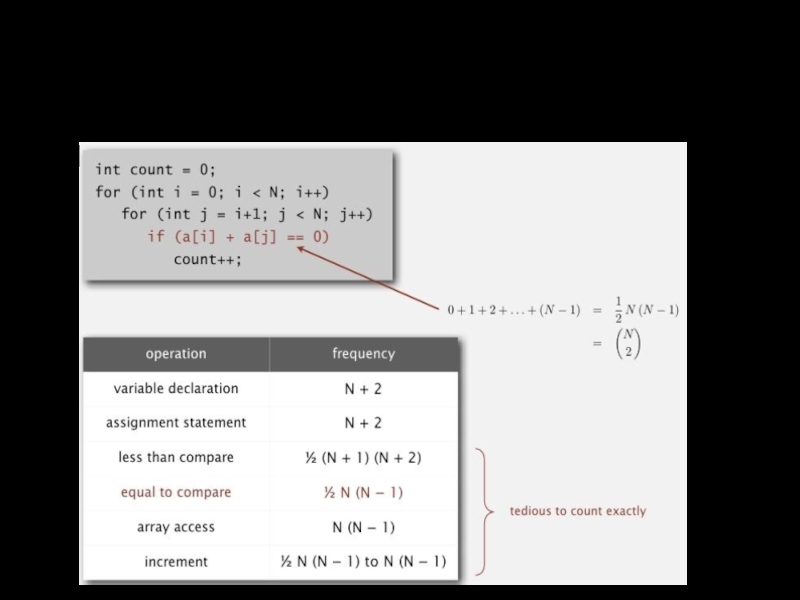
- 2. Пример: 2-Sum Подсчет количества инструкций, как функции от N.
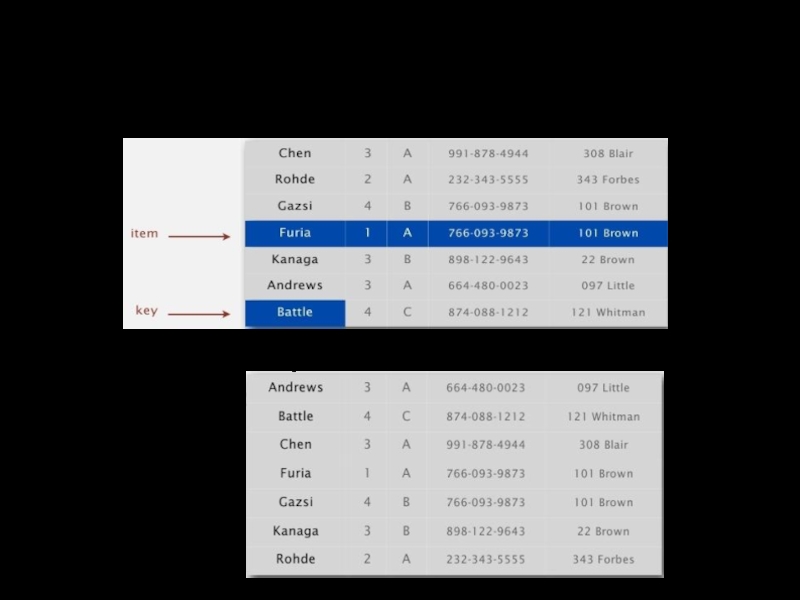
- 3. Проблема сортировки Пример. Список студентов Сортировка. Переставить N записей в массиве в определенном порядке
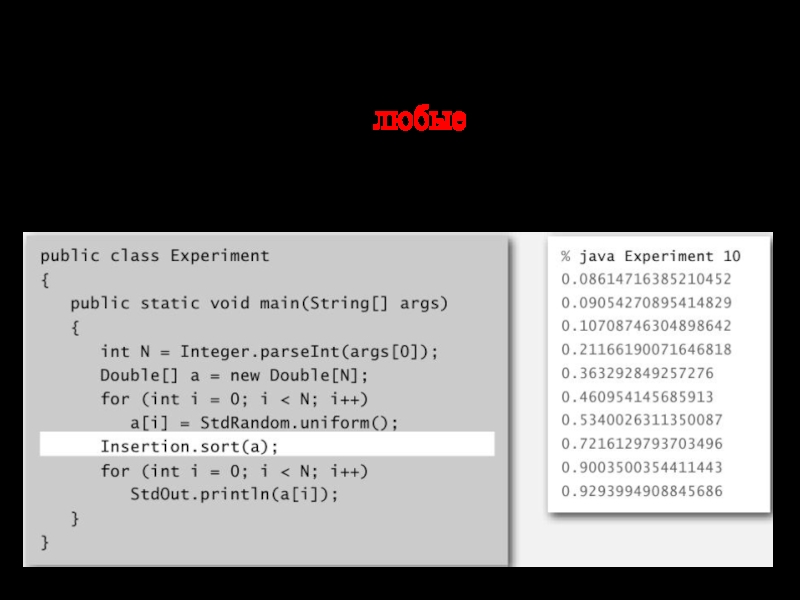
- 4. Пример сортировки Цель. Отсортировать любые типы данных Пример. Отсортировать случайные вещественные числа в порядке возрастания
- 5. Пример сортировки Цель. Отсортировать любые типы данных Пример. Отсортировать строки из файла в алфавитном порядке
- 6. Пример сортировки Цель. Отсортировать любые типы данных Пример. Сортировка файлов в директории по имени
- 7. Сортировка выбором
- 8. Сортировка выбором На итерации i найти минимальный
- 9. Сортировка выбором Алгоритм. Сканирование идет слева направо
- 10. Сортировка выбором: внутренний цикл
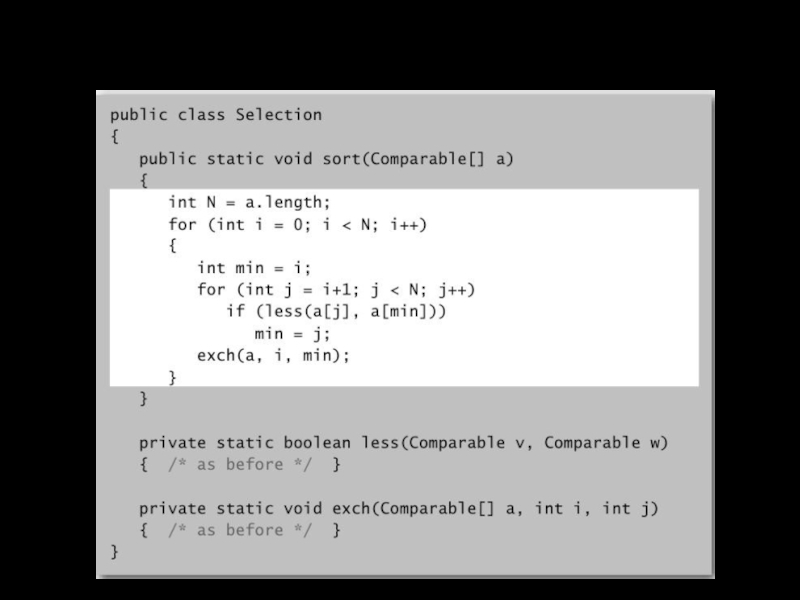
- 11. Сортировка выбором: реализация на Java
- 12. Сортировка выбором: математический анализ Утверждение. Сортировка выбором
- 13. Видео 2
- 14. Сортировка вставками
- 15. Сортировка вставками На итерации i поменять a[i]
- 16. Сортировка вставками Алгоритм. Сканирование идет слева направо
- 17. Сортировка вставками: внутренний цикл
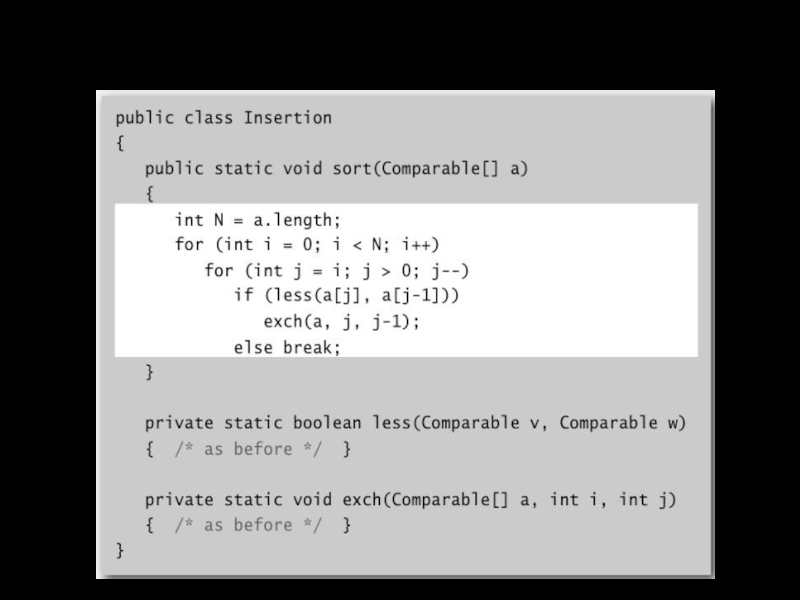
- 18. Сортировка вставками: реализация на Java
- 19. Сортировка вставками: математический анализ Утверждение. Сортировка вставками
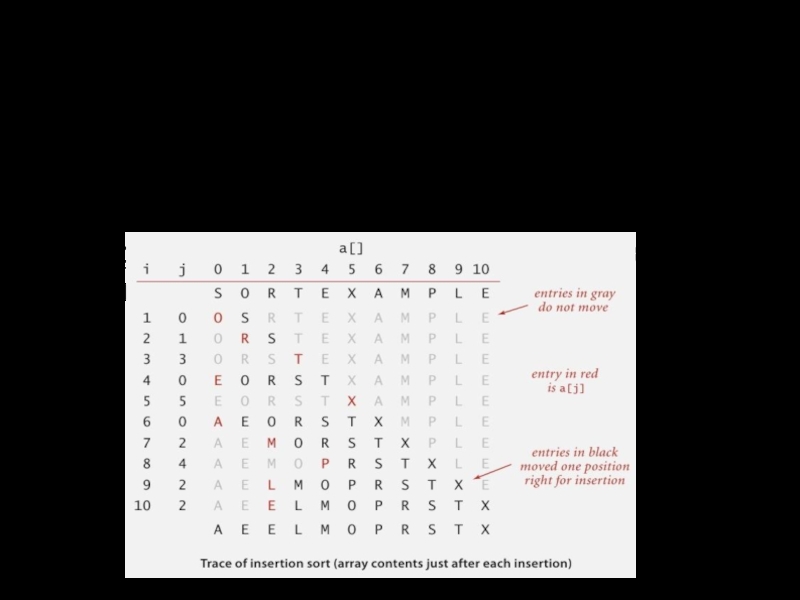
- 20. Сортировка вставками: пример
- 21. Видео 4
- 22. Сортировка вставками: лучший и худший случай Лучший
- 23. Видео 5
- 24. Сортировка вставками: частично упорядоченный массив Инверсия —
- 25. Видео 6
- 26. Сортировка Шелла
- 27. Сортировка Шелла: обзор Идея. Переупорядочить массив так,
- 28. h-sorting Сортировка вставками через шаг h Большой
- 30. Сортировка Шелла Утверждение. g-отсортированный массив остается g-отсортированным даже после h-сортировки
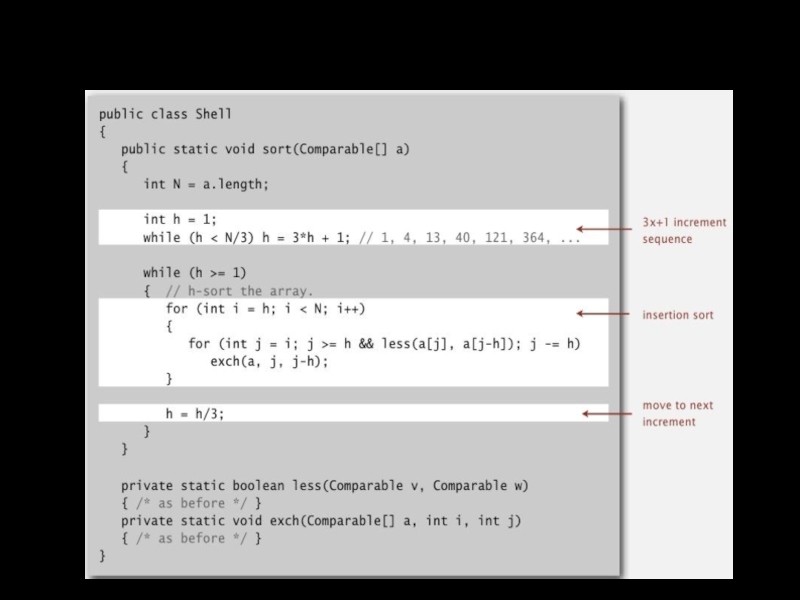
- 32. Сортировка Шелла: реализация на Java
- 34. Видео 7
- 35. Сортировка Шелла: анализ Утверждение. В худшем случае
- 36. Чем интересна Сортировка Шелла? Простая идея дает
- 37. Перетасовка
- 38. Как перетасовать элементы в массиве? Цель. Переставить
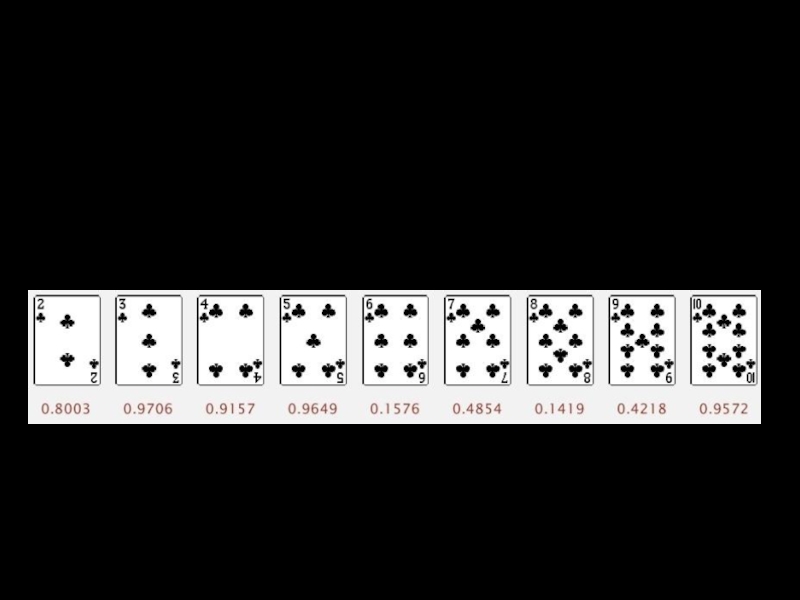
- 39. Сортировка Шелла Сгенерировать вещественные числа для каждого элемента Отсортировать массив
- 40. Перетасовка Кнута На итерации i выбрать r
- 41. Перетасовка Кнута На итерации i выбрать r
Слайд 3Проблема сортировки
Пример. Список студентов
Сортировка. Переставить N записей в массиве в определенном
порядке
Слайд 4Пример сортировки
Цель. Отсортировать любые типы данных
Пример. Отсортировать случайные вещественные числа в
порядке возрастания
Слайд 5Пример сортировки
Цель. Отсортировать любые типы данных
Пример. Отсортировать строки из файла в
алфавитном порядке
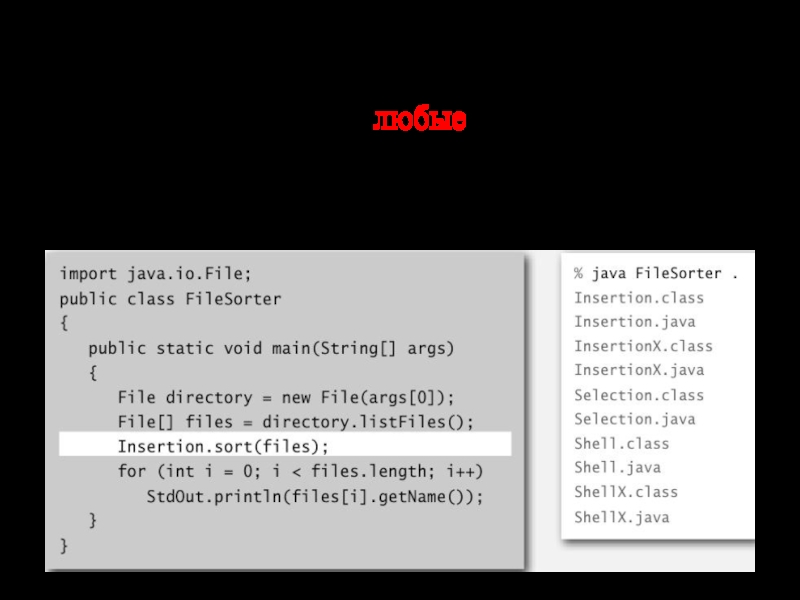
Слайд 6Пример сортировки
Цель. Отсортировать любые типы данных
Пример. Сортировка файлов в директории по
имени
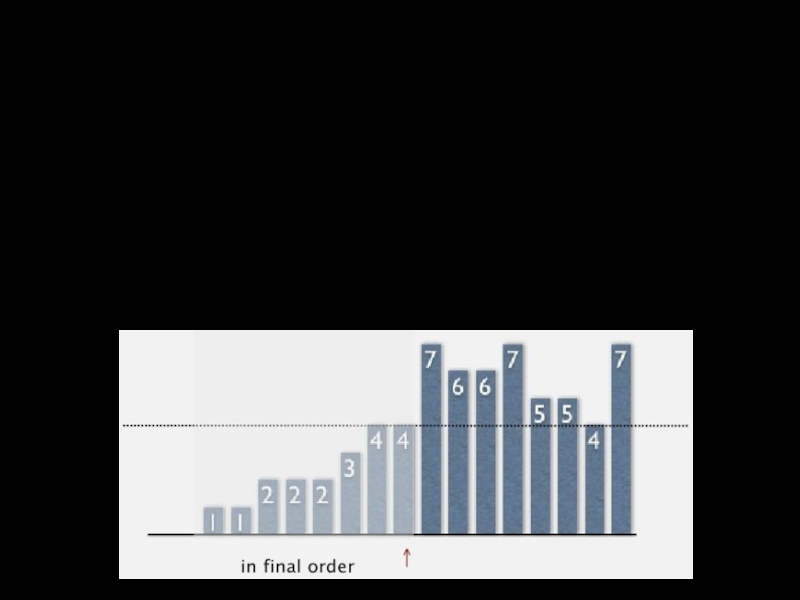
Слайд 8Сортировка выбором
На итерации i найти минимальный оставшийся элемент с индексом min
Поменять
местами a[i] и a[min]
Видео 1
Видео 1
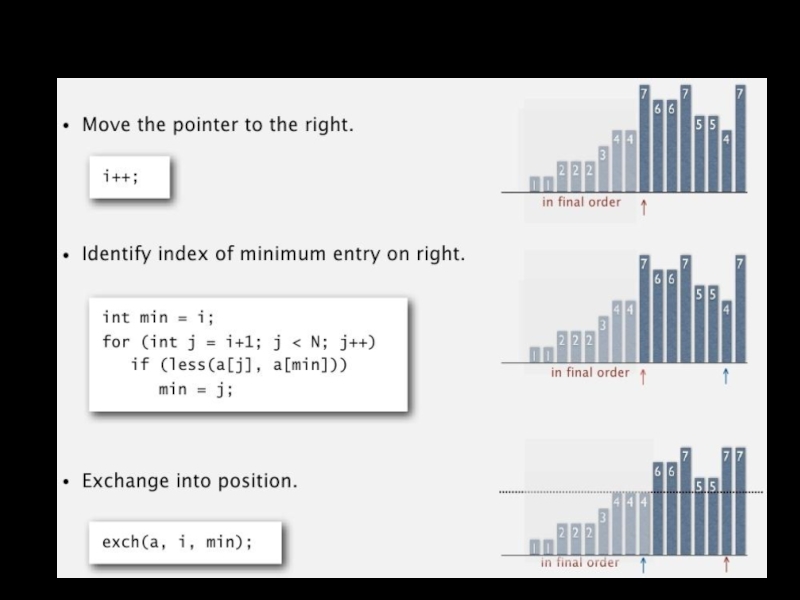
Слайд 9Сортировка выбором
Алгоритм. Сканирование идет слева направо
Элементы слева от стрелки отсортированы и
не меняются
Нет элемента справа от стрелки, который был бы меньше элемента слева от стрелки
Нет элемента справа от стрелки, который был бы меньше элемента слева от стрелки
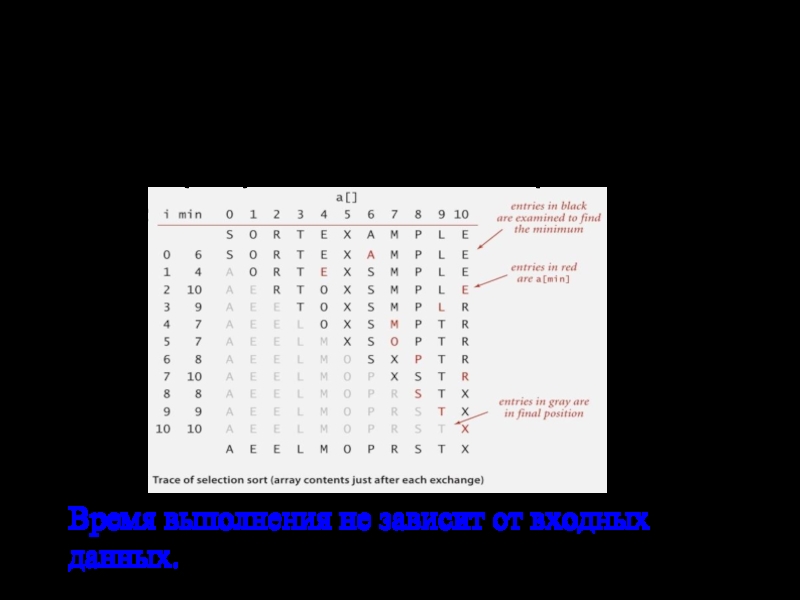
Слайд 12Сортировка выбором: математический анализ
Утверждение. Сортировка выбором использует (N-1) + (N-2) +
… + 1 + 0 ~ N2/2 сравнений и N перестановок
Время выполнения не зависит от входных данных. Квадратичное время, даже если массив отсортирован
Перемещение данных минимальное. Перестановки за линейное время
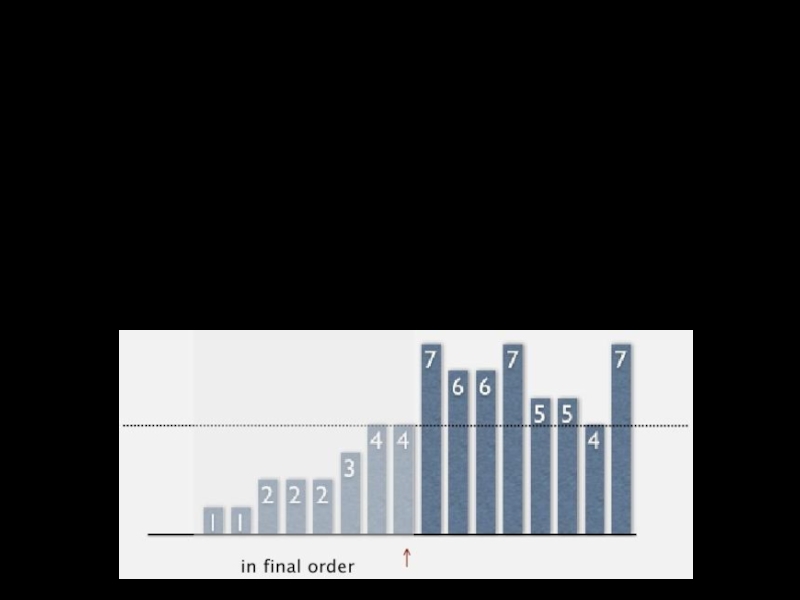
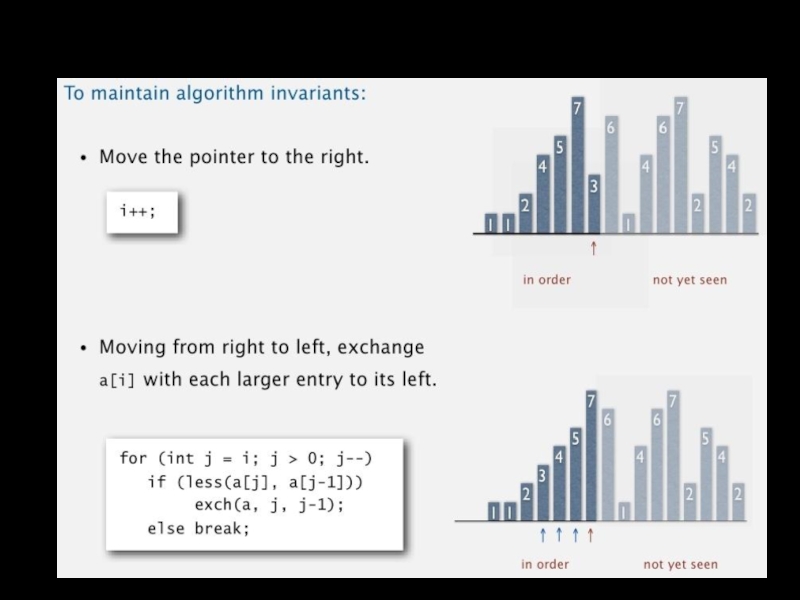
Слайд 16Сортировка вставками
Алгоритм. Сканирование идет слева направо
Элементы слева от стрелки отсортированы по
возрастанию
Элементы справа от стрелки еще не проверены
Элементы справа от стрелки еще не проверены
Слайд 19Сортировка вставками: математический анализ
Утверждение. Сортировка вставками использует ~ N2/4 сравнений и
~ N2/4 перестановок при случайном наборе данных
В среднем каждый ключ проходит половину пути
В среднем каждый ключ проходит половину пути
Слайд 22Сортировка вставками: лучший и худший случай
Лучший случай. Массив отсортирован; необходимо N-1
сравнений и 0 перестановок
A E E L M O P R S T X
Худший случай. Массив отсортирован в обратно порядке и нет дубликатов; ~ N2/2 сравнений и ~ N2/2 вставок
X T S R P O M L E E A
A E E L M O P R S T X
Худший случай. Массив отсортирован в обратно порядке и нет дубликатов; ~ N2/2 сравнений и ~ N2/2 вставок
X T S R P O M L E E A
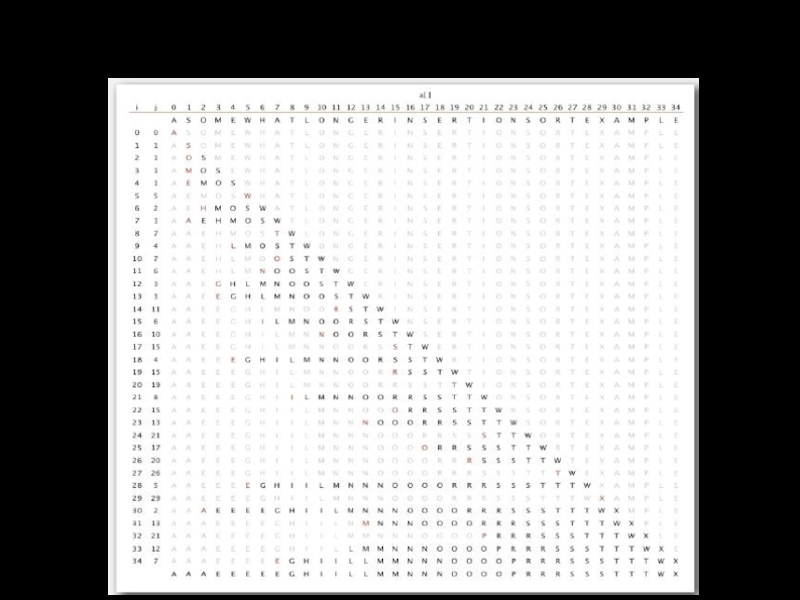
Слайд 24Сортировка вставками: частично упорядоченный массив
Инверсия — пара элементов, которая нарушает упорядоченность
в массиве
Частично упорядоченный массив — массив, в котором количество инверсий <= cN
Массив, каждый элемент которого находится неподалеку от своей окончательной позиции
Небольшой массив, добавленный к большому отсортированному массиву
Массив, в котором лишь несколько элементов находятся не на своем месте
Для частично упорядоченного массива сортировка вставками выполняется за линейное время
Количество перестановок равно количеству инверсий
Слайд 27Сортировка Шелла: обзор
Идея. Переупорядочить массив так, чтобы каждые h-е элементы (начиная
с любого места в массиве) составляли упорядоченную последовательность
Сортировка Шелла. [Shell 1959] Независимо отсортированные чередующиеся последовательности
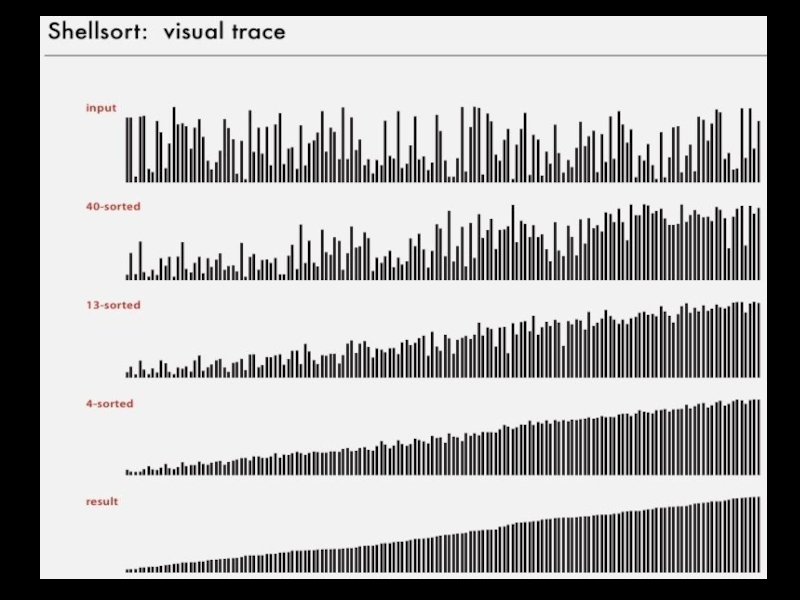
Слайд 28h-sorting
Сортировка вставками через шаг h
Большой шаг => маленькие подмассивы
Маленький шаг =>
массив почти упорядочен
Слайд 30Сортировка Шелла
Утверждение. g-отсортированный массив остается g-отсортированным даже после h-сортировки
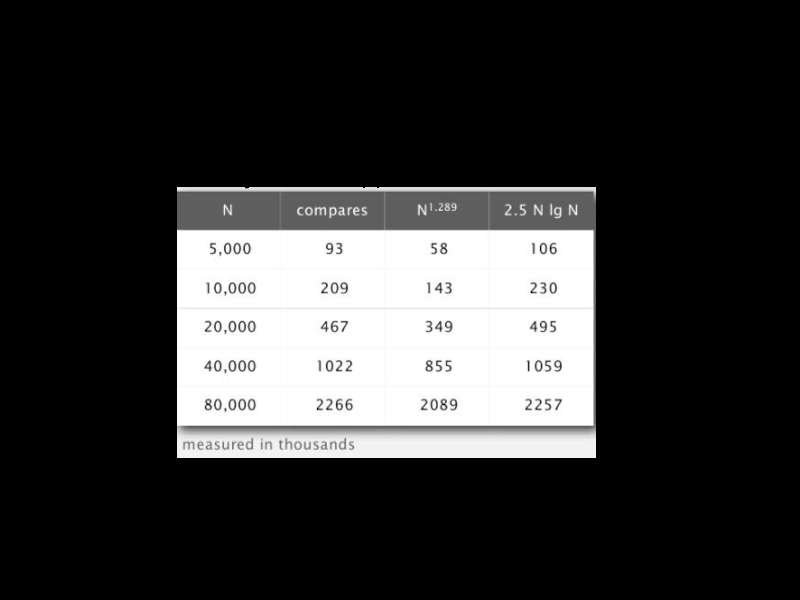
Слайд 35Сортировка Шелла: анализ
Утверждение. В худшем случае количество сравнений при последовательности 3x
+ 1 равно O(N3/2)
Точная модель для сортировки Шелла не разработана.
Слайд 36Чем интересна Сортировка Шелла?
Простая идея дает хорошую производительность
На практике
Работает быстро на
небольших массивах (bzip2/linux kernel)
Проста в реализации и используется во встраиваемых системах
Есть аппаратные реализации
Простой алгоритм, нетривиальная производительность
Асимптотический порядок роста?
Лучшая последовательность?
Производительность в среднем случае?
Некоторые замечательные алгоритмы ждут исследования
Проста в реализации и используется во встраиваемых системах
Есть аппаратные реализации
Простой алгоритм, нетривиальная производительность
Асимптотический порядок роста?
Лучшая последовательность?
Производительность в среднем случае?
Некоторые замечательные алгоритмы ждут исследования
Слайд 38Как перетасовать элементы в массиве?
Цель. Переставить элементы в массиве так, чтобы
они имели равномерное распределение
Слайд 40Перетасовка Кнута
На итерации i выбрать r между 0 и i при
нормальном распределении
Поменять a[i] и a[r]
Видео 8
Поменять a[i] и a[r]
Видео 8
Слайд 41Перетасовка Кнута
На итерации i выбрать r между 0 и i при
нормальном распределении
Поменять a[i] и a[r]
Поменять a[i] и a[r]
