- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
EER to Realtional Mapping. (Lecture 12) презентация
Содержание
- 1. EER to Realtional Mapping. (Lecture 12)
- 2. Mapping Specialization (Step 8) k
- 3. Mapping Specialization Option 8A: Multiple relations—superclass and
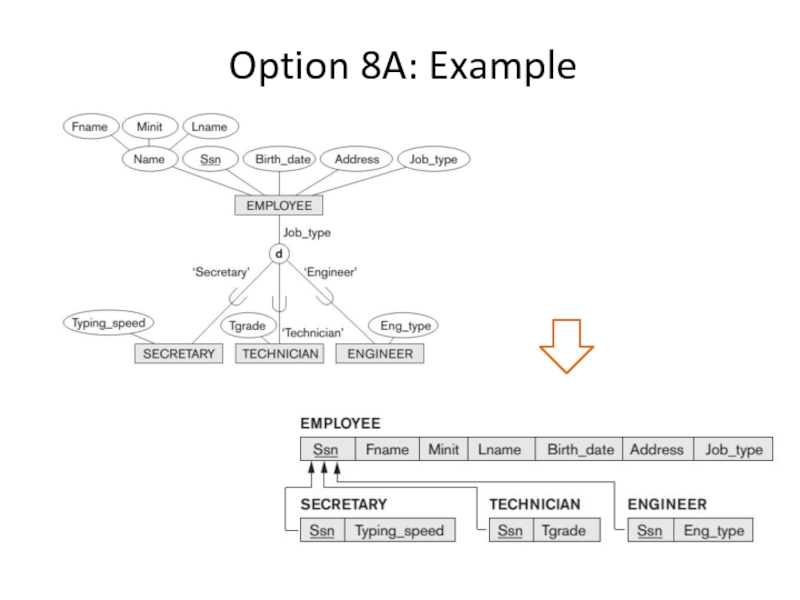
- 4. Option 8A: Example
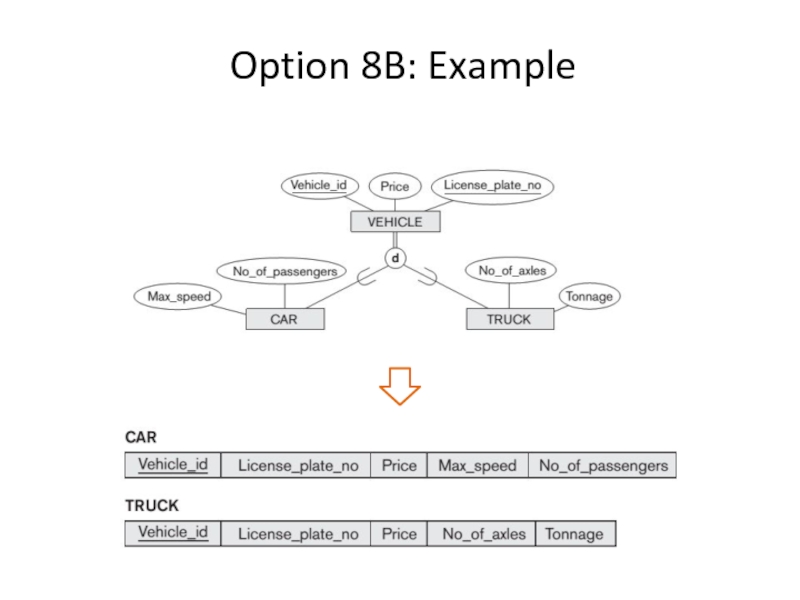
- 5. Mapping Specialization Option 8B: Multiple relations—subclass relations
- 6. Option 8B: Example
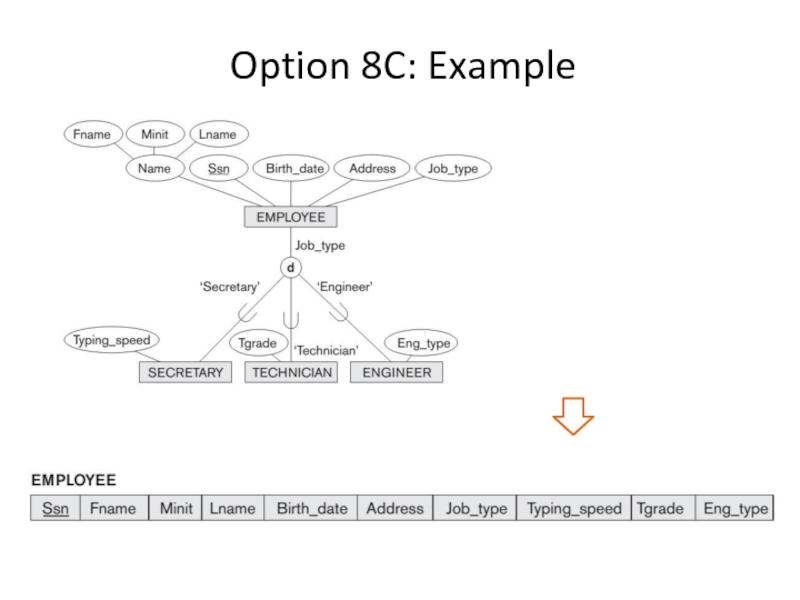
- 7. Mapping Specialization Option 8C: Single relation with
- 8. Option 8C: Example
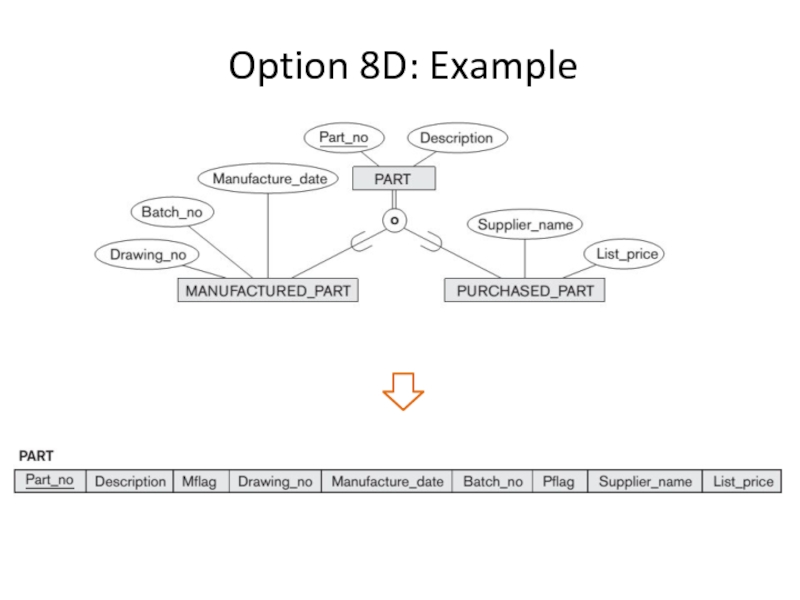
- 9. Mapping Specialization Option 8D: Single relation with
- 10. Option 8D: Example
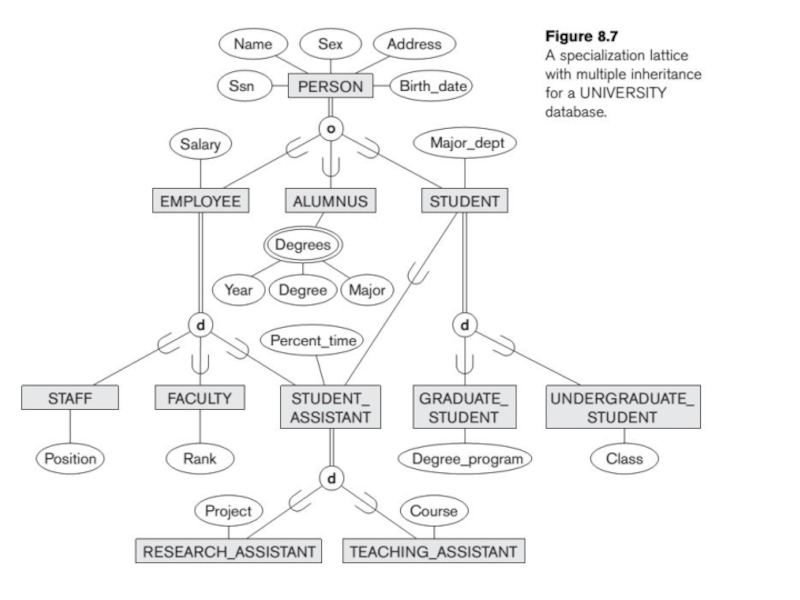
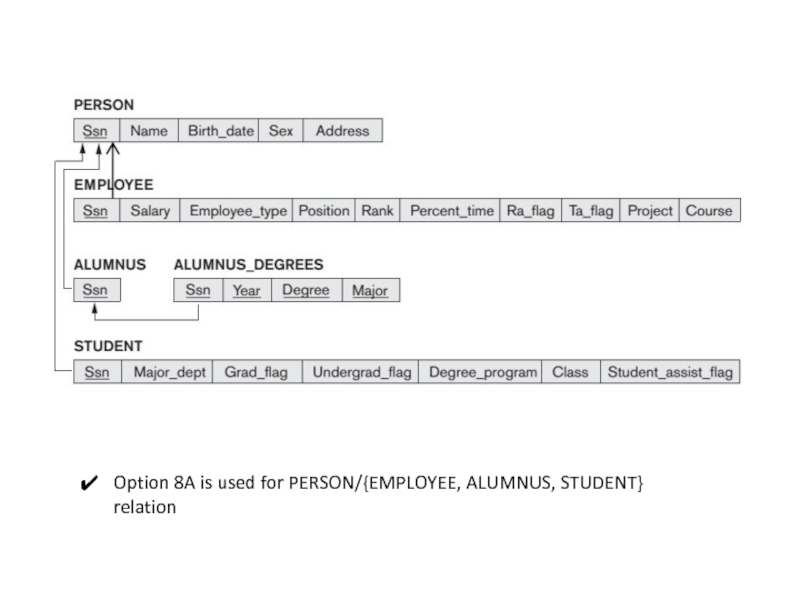
- 12. Option 8A is used for PERSON/{EMPLOYEE, ALUMNUS, STUDENT} relation
- 13. Option 8C is used for the
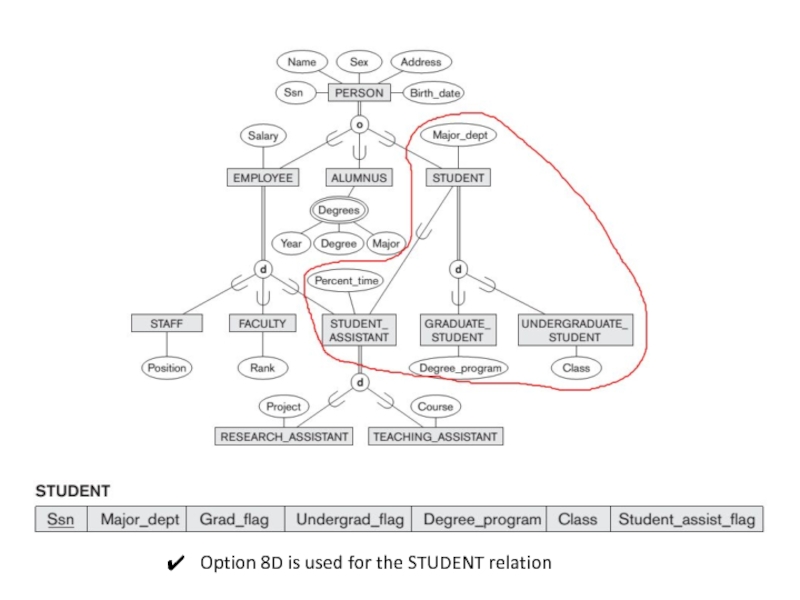
- 15. Option 8D is used for the STUDENT relation
- 16. Mapping of Union Subclasses (Step 9)
- 17. Mapping of Union Subclasses (Step 9) When
Слайд 2
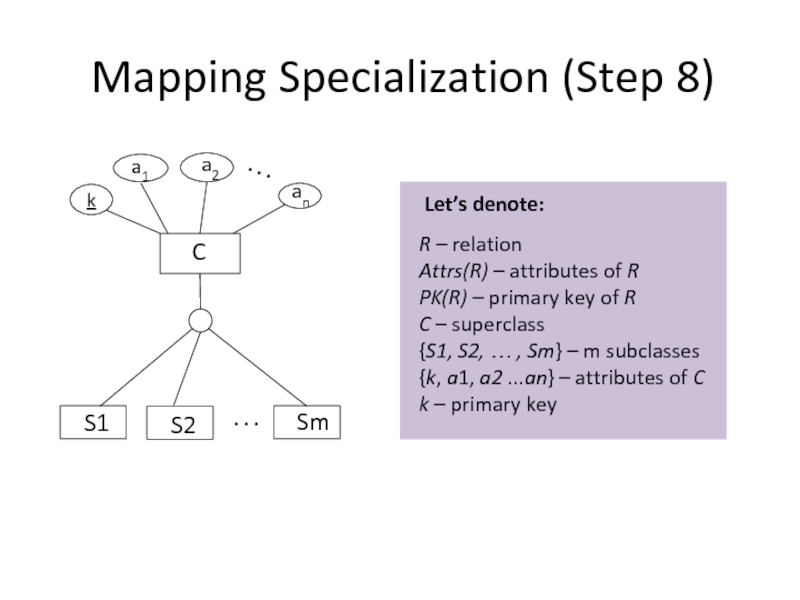
Mapping Specialization (Step 8)
k
a1
a2
an
S1
S2
Sm
. . .
. . .
C
R – relation
Attrs(R) –
PK(R) – primary key of R
C – superclass
{S1, S2, … , Sm} – m subclasses
{k, a1, a2 ...an} – attributes of C
k – primary key
Let’s denote:
Слайд 3Mapping Specialization
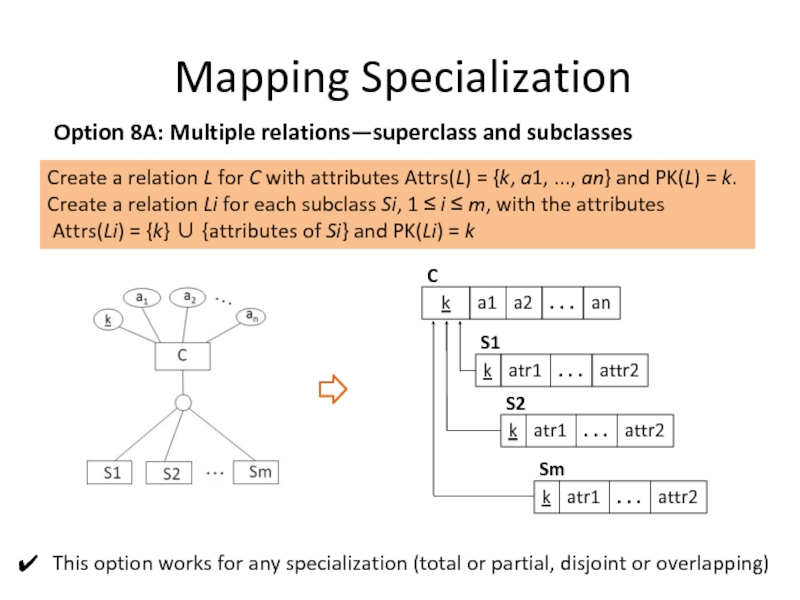
Option 8A: Multiple relations—superclass and subclasses
This option works for any
Create a relation L for C with attributes Attrs(L) = {k, a1, ..., an} and PK(L) = k.
Create a relation Li for each subclass Si, 1 ≤ i ≤ m, with the attributes
Attrs(Li) = {k} ∪ {attributes of Si} and PK(Li) = k
k
a1
a2
. . .
an
C
k
atr1
attr2
. . .
S1
k
atr1
attr2
. . .
S2
k
atr1
attr2
. . .
Sm
Слайд 5Mapping Specialization
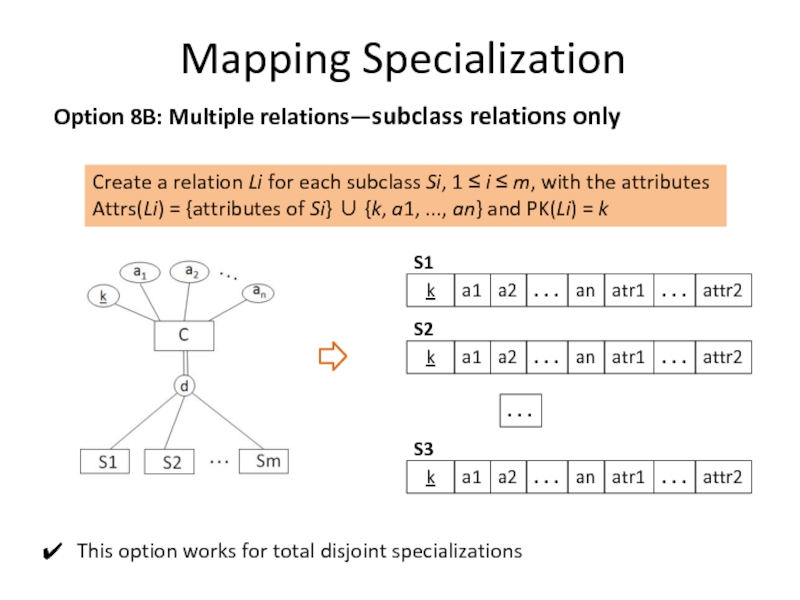
Option 8B: Multiple relations—subclass relations only
This option works for total
Create a relation Li for each subclass Si, 1 ≤ i ≤ m, with the attributes
Attrs(Li) = {attributes of Si} ∪ {k, a1, ..., an} and PK(Li) = k
atr1
attr2
. . .
S1
k
a1
a2
. . .
an
atr1
attr2
. . .
S2
k
a1
a2
. . .
an
atr1
attr2
. . .
S3
k
a1
a2
. . .
an
. . .
Слайд 7Mapping Specialization
Option 8C: Single relation with one type attribute
Create a single
Attrs(L) = {k, a1, ..., an} ∪ {attributes of S1} ∪ ... ∪ {attributes of Sm} ∪ {t} and PK(L) = k. The attribute t is called a type attribute whose value indicates the subclass to which each tuple belongs, if any.
This option works only for disjoint specializations, and has the potential for generating many NULL values
These options is not recommended if many specific attributes are defined for the subclasses
Слайд 9Mapping Specialization
Option 8D: Single relation with multiple type attributes
Create a single
Attrs(L) = {k, a1, ..., an} ∪ {attributes of S1} ∪ ... ∪ {attributes of S m} ∪
∪ {t1, t2, ..., tm} and PK(L) = k.
Each ti, 1 ≤ i ≤ m, is a Boolean type attribute indicating whether a tuple belongs to subclass Si
This option works for overlapping specializations, and has the potential for generating many NULL values (but will also work for a disjoint specialization).
These options is not recommended if many specific attributes are defined for the subclasses
Слайд 13
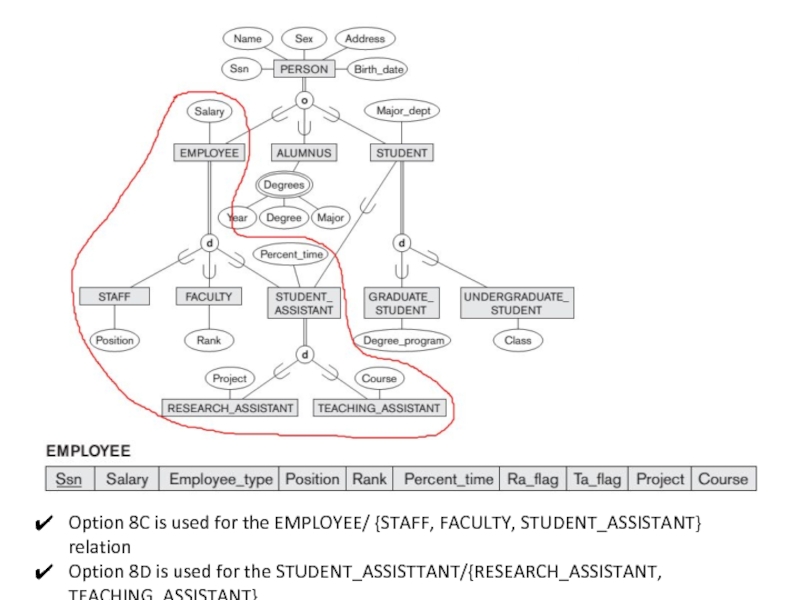
Option 8C is used for the EMPLOYEE/ {STAFF, FACULTY, STUDENT_ASSISTANT} relation
Option
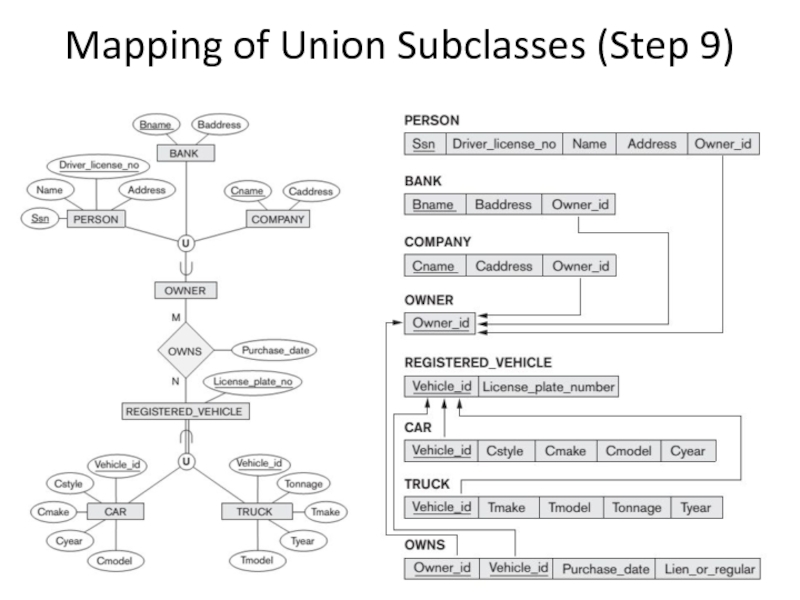
Слайд 17Mapping of Union Subclasses (Step 9)
When a union subclass is defined
surrogate key is used. For union subclass a separate relation is created with a surrogate key in a role of a primary key. Also a surrogate key is included as a foreign key in each relation corresponding to superclass. It is also recommended to add a type attribute to the relation corresponding to union subclass to indicate the particular entity type to which each tuple belongs.