- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Динамические структуры данных презентация
Содержание
- 1. Динамические структуры данных
- 2. ЛОСС Линейный однонаправленный связанный список – динамическая
- 3. ЛОСС Такой способ представления данных имеет преимущество
- 4. ЛОСС Линейный однонаправленный список имеет структуру
- 5. Каждый элемент списка содержит два поля:
- 6. ЛОСС Определим функциональную спецификацию структуры данных ЛОССТ:
- 7. ЛОСС на паскале После введения функциональной спецификации
- 8. Логическое описание ЛОСС Создание списка – это
- 9. Логическое описание ЛОСС Функция «Первый» - показать
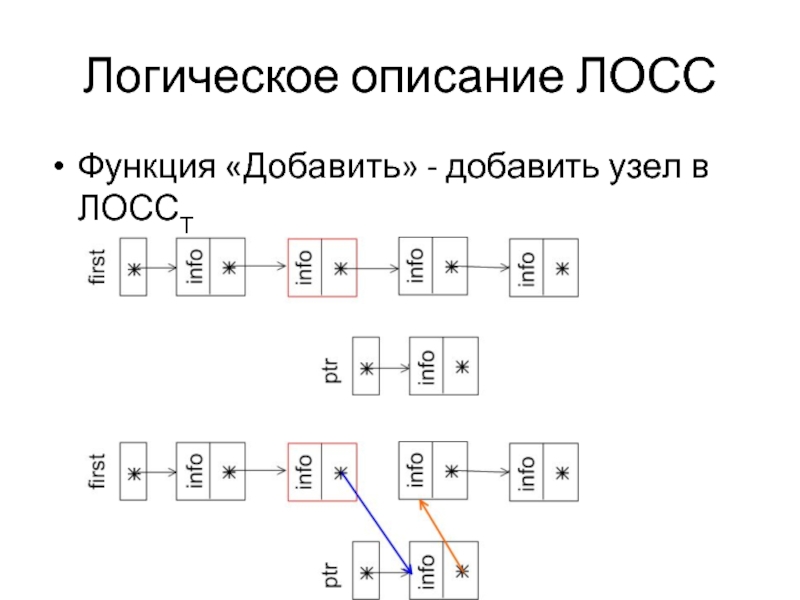
- 10. Логическое описание ЛОСС Функция «Добавить» - добавить узел в ЛОССТ
- 11. Procedure Add_node(var q:link; data:T);
- 12. Формирование списка Read(data); {читаются данные типа Т}
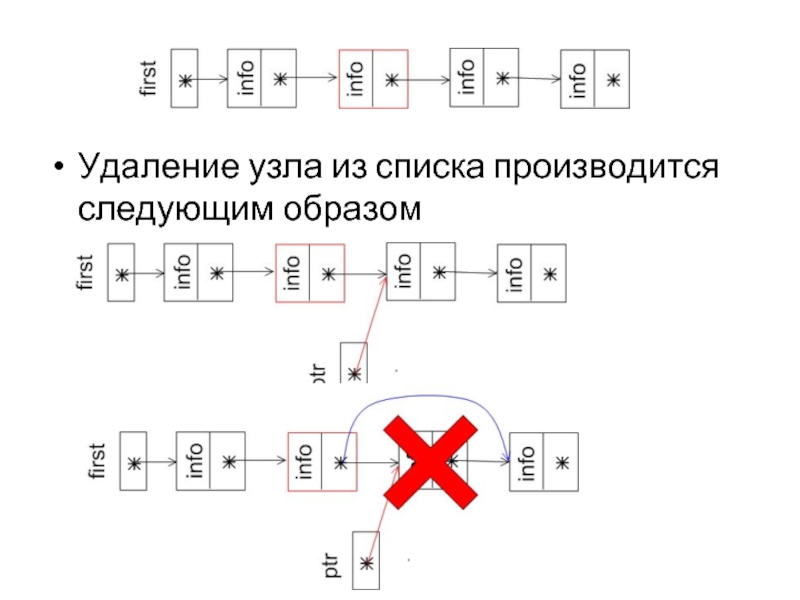
- 13. Удаление узла из списка производится следующим образом
- 14. Procedure Delete_node(q:link); var ptr:link;
- 15. Стек Стек – упорядоченный набор элементов, в
- 16. Стек Стек применяется при синтаксическом анализе текста,
- 17. Функциональная спецификация Для структуры данных СТЕКТ можно
- 18. Логическое описание Логическое описание стека осуществляется теми же средствами, что и ЛОСС.
- 19. Очередь Очередью называется упорядоченный набор элементов, которые
- 20. Очередь Динамическая
- 21. Дек Дек – это очередь с двойным
- 22. Деревья Деревья наилучшим образом приспособлены для решения
- 23. Деревья Деревом типа Т называется структура данных,
- 24. Деревья (терминология) Лист – это корень поддерева,
- 25. Двоичное дерево Двоичным деревом типа Т называют
- 26. Двоичное дерево Функциональная спецификация ДДТ: Создание_дерева :
- 27. Двоичное дерево (логическое описание) При представлении
- 28. Построение двоичного дерева Рассмотрим принцип построения дерева
ЛОСС Линейный однонаправленный связанный список – динамическая структура, в которой данные представляются в виде цепочки. Основная идея такого способа представления данных – элементы структуры данных распределяются в памяти ЭВМ в произвольном
Слайд 2ЛОСС
Линейный однонаправленный связанный список – динамическая структура, в которой данные представляются
в виде цепочки.
Основная идея такого способа представления данных – элементы структуры данных распределяются в памяти ЭВМ в произвольном месте, но с указанием того места, где находится следующий за ним элемент.
Основная идея такого способа представления данных – элементы структуры данных распределяются в памяти ЭВМ в произвольном месте, но с указанием того места, где находится следующий за ним элемент.
Слайд 3ЛОСС
Такой способ представления данных имеет преимущество перед использованием статического массива данных
или записи, поскольку обеспечивает быстрое выполнение операций вставки и удаления элемента данных.
Кроме того, память, отводимая для хранения вектора может использоваться весьма неэффективно
Кроме того, память, отводимая для хранения вектора может использоваться весьма неэффективно
Слайд 4ЛОСС
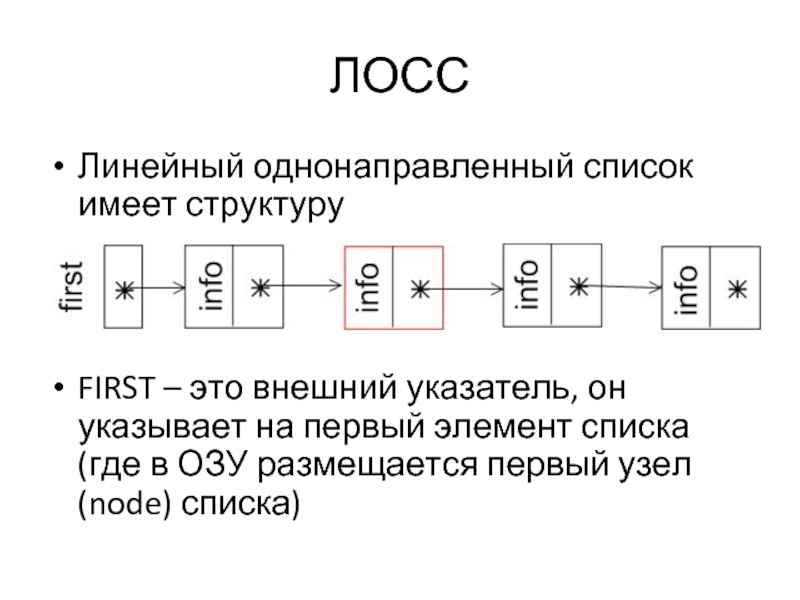
Линейный однонаправленный список имеет структуру
FIRST – это внешний указатель, он
указывает на первый элемент списка (где в ОЗУ размещается первый узел (node) списка)
Слайд 5
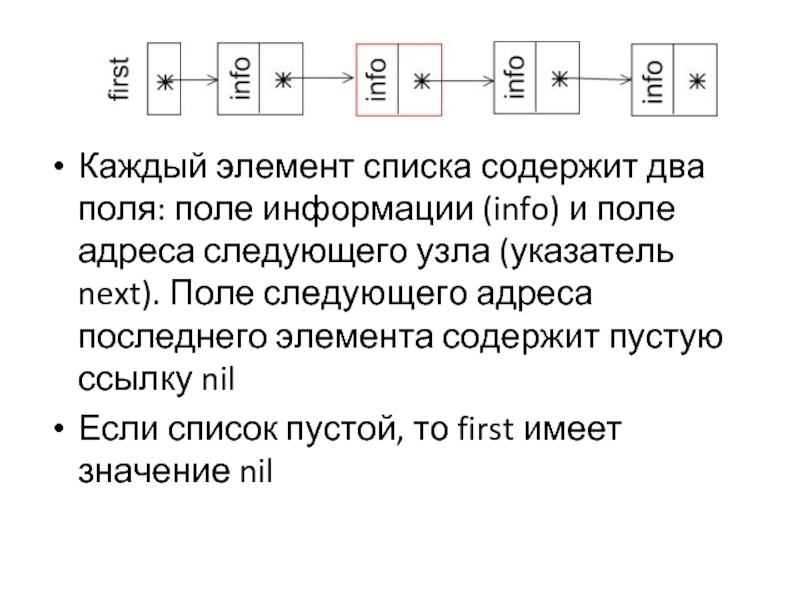
Каждый элемент списка содержит два поля: поле информации (info) и поле
адреса следующего узла (указатель next). Поле следующего адреса последнего элемента содержит пустую ссылку nil
Если список пустой, то first имеет значение nil
Если список пустой, то first имеет значение nil
Слайд 6ЛОСС
Определим функциональную спецификацию структуры данных ЛОССТ: (в информационной части узла info
находятся данные типа T):
Создать_список: → ЛОССТ
Список_пуст: ЛОССТ → лог
Добавить: ЛОССТ х Т → ЛОССТ
Удалить: ЛОССТ → ЛОССТ х Т
Первый: ЛОССТ → Т
Создать_список: → ЛОССТ
Список_пуст: ЛОССТ → лог
Добавить: ЛОССТ х Т → ЛОССТ
Удалить: ЛОССТ → ЛОССТ х Т
Первый: ЛОССТ → Т
Слайд 7ЛОСС на паскале
После введения функциональной спецификации структуры данных переходим к ее
логическому описание на основе одного из ЯП, например на паскале
Вводим тип указателя и тип узла
Type link = ^node;
node = record
info : T;
next : link;
end;
Var first, ptr : link; {описание внешнего и рабочего указателей}
Вводим тип указателя и тип узла
Type link = ^node;
node = record
info : T;
next : link;
end;
Var first, ptr : link; {описание внешнего и рабочего указателей}
Слайд 8Логическое описание ЛОСС
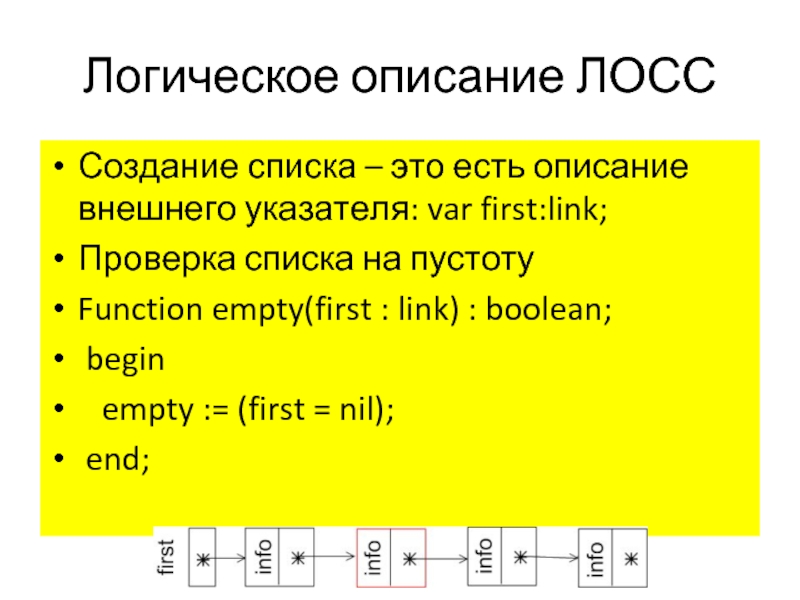
Создание списка – это есть описание внешнего указателя: var
first:link;
Проверка списка на пустоту
Function empty(first : link) : boolean;
begin
empty := (first = nil);
end;
Проверка списка на пустоту
Function empty(first : link) : boolean;
begin
empty := (first = nil);
end;
Слайд 9Логическое описание ЛОСС
Функция «Первый» - показать информационную часть первого узла
Function show_first(first
: link) : T;
begin
if not empty(first) then
show_first := first^.info
else
writeln(‘Нет первого узла’)
end;
begin
if not empty(first) then
show_first := first^.info
else
writeln(‘Нет первого узла’)
end;
Слайд 11
Procedure Add_node(var q:link; data:T);
var ptr:link;
begin
new(ptr); ptr^.info := data;
ptr^.next := q^.next;
q^.next := ptr;
end;
ptr^.next := q^.next;
q^.next := ptr;
end;
Слайд 12Формирование списка
Read(data); {читаются данные типа Т}
New(first); first^.info := data;
first^.next :=
nil;
ptr := first;
While <условие> do
begin
read(data); new (ptr^.next);
ptr := ptr^.next;
ptr^.info := data; ptr^.next := nil;
end;
ptr := first;
While <условие> do
begin
read(data); new (ptr^.next);
ptr := ptr^.next;
ptr^.info := data; ptr^.next := nil;
end;
Слайд 14
Procedure Delete_node(q:link);
var ptr:link;
begin
ptr
:= q^.next;
q^.next := ptr^.next;
dispose(ptr);
end;
q^.next := ptr^.next;
dispose(ptr);
end;
Слайд 15Стек
Стек – упорядоченный набор элементов, в котором размещение новых и удаление
существующих элементов производится только с одного его конца, называемого вершиной стека
В стеке последний размещенный элемент удаляется первым – First In - Last Out
В стеке последний размещенный элемент удаляется первым – First In - Last Out
Слайд 16Стек
Стек применяется при синтаксическом анализе текста, выполняемом в трансляторах ЯП ,
при вызове рекурсивной функции или процедуры
Слайд 17Функциональная спецификация
Для структуры данных СТЕКТ можно ввести следующую спецификацию
Создание_стека: → СТЕКТ
Стек_пуст:
СТЕКТ → лог
Засылка: Т х СТЕКТ → СТЕКТ
Выборка: СТЕКТ → Т х СТЕКТ
Последний: СТЕКТ → Т
Засылка: Т х СТЕКТ → СТЕКТ
Выборка: СТЕКТ → Т х СТЕКТ
Последний: СТЕКТ → Т
Слайд 19Очередь
Очередью называется упорядоченный набор элементов, которые могут удаляться с одного ее
конца (наз. Началом очереди), и помещаться в другой конец этого набора (наз. Концом очереди).
Пришедший первым уходит первым – First In – First Out
Логическое описание типа ОчередьТ строится аналогично ЛОССТ и стеку
Пришедший первым уходит первым – First In – First Out
Логическое описание типа ОчередьТ строится аналогично ЛОССТ и стеку
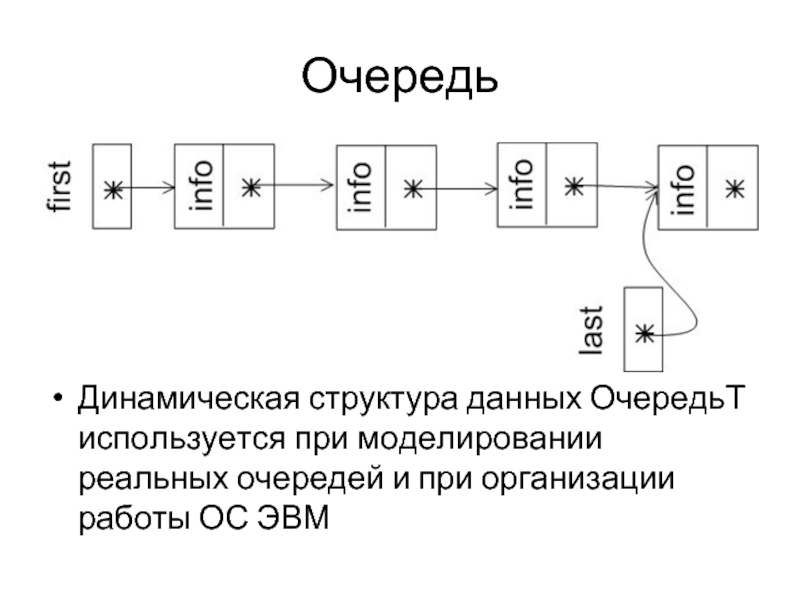
Слайд 20Очередь
Динамическая структура данных ОчередьТ используется при моделировании реальных очередей и при
организации работы ОС ЭВМ
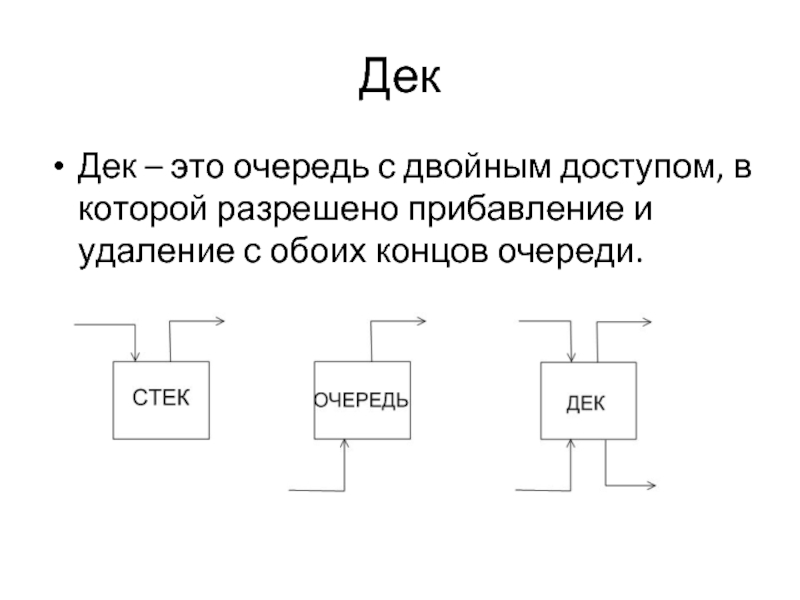
Слайд 21Дек
Дек – это очередь с двойным доступом, в которой разрешено прибавление
и удаление с обоих концов очереди.
Слайд 22Деревья
Деревья наилучшим образом приспособлены для решения задач искусственного интеллекта и синтаксического
анализа текста.
Примеры применения: программа игры в шашки или шахматы, докозательство теоремы, анализ зрительных или звуковых образов
Примеры применения: программа игры в шашки или шахматы, докозательство теоремы, анализ зрительных или звуковых образов
Слайд 23Деревья
Деревом типа Т называется структура данных, которая образована данным типа Т,
называемым корнем дерева, и конечным, возможно пустым множеством с переменным числом элементов – деревьев типа Т, называемых поддеревьями этого дерева (рекурсивное определение)
Слайд 24Деревья (терминология)
Лист – это корень поддерева, не имеющего, в свою очередь,
поддеревьев
Вершина – это корень подерева. Кореь и листья дерева являются особыми вершинами
Вершина связана с каждым из своих поддеревьев ветвью
Вершина – это корень подерева. Кореь и листья дерева являются особыми вершинами
Вершина связана с каждым из своих поддеревьев ветвью
Слайд 25Двоичное дерево
Двоичным деревом типа Т называют структуру, которая либо пуста либо
образована:
- данным типа Т, называемым корнем двоичного дерева
- двоичным деревом типа Т, называемым левым поддеревом двоичного дерева
- двоичным деревом типа Т, называемым правым поддеревом двоичного дерева
- данным типа Т, называемым корнем двоичного дерева
- двоичным деревом типа Т, называемым левым поддеревом двоичного дерева
- двоичным деревом типа Т, называемым правым поддеревом двоичного дерева
Слайд 26Двоичное дерево
Функциональная спецификация ДДТ:
Создание_дерева : → ДДТ
Дерево_пусто : ДДТ → лог
Чтение_корня
: ДДТ → Т
Слева : ДДТ → ДДТ
Справа : ДДТ → ДДТ
Построение Т х ДДТ Х ДДТ → ДДТ
Слева : ДДТ → ДДТ
Справа : ДДТ → ДДТ
Построение Т х ДДТ Х ДДТ → ДДТ
Слайд 27Двоичное дерево
(логическое описание)
При представлении данных в виде двоичного дерева будем
считать, что каждое звено (вершина дерева) будет записью, содержащей четыре поля: ключ записи, ссылка на левое поддерево, ссылка на правое поддерево и информационная часть.
Слайд 28Построение двоичного дерева
Рассмотрим принцип построения дерева при занесении записей в таблицу.
Пусть в первоначально пустую таблицу заносится последовательно поступающие записи с ключами 70, 60, 85, 87, 90, 45, 30, 88, 35, 20, 86.
Если ключ следующей записи окажется меньше k, то этой записи поставим в соответствие левую вершину, в противном случае – правую.
Если ключ следующей записи окажется меньше k, то этой записи поставим в соответствие левую вершину, в противном случае – правую.
