- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Детерминированные нелинейные модели с непрерывными переменными презентация
Содержание
- 1. Детерминированные нелинейные модели с непрерывными переменными
- 2. содержание Текущий контроль знаний Технологии исследования нелинейных
- 3. Текущий контроль знаний Решить графически задачу:
- 4. Исследование моделей Два класса технологий
- 5. Метод множителей Лагранжа Используется для решения однокритериальных
- 6. Создание и исследование функции Лагранжа
- 7. Пример: задача о консервной банке Содержательная постановка:
- 8. Функция Лагранжа и ее исследование на экстремум
- 9. Исследование экстремума Пусть новое значение радиуса банки
- 10. САМОСТОЯТЕЛЬНО 1 1. Пользуясь описанной выше
- 11. Достоинства и недостатки метода множителей Лагранжа 1.
Слайд 1Теория принятия решений
Лекция 2.2:
Детерминированные нелинейные модели с непрерывными переменными
Слайд 2содержание
Текущий контроль знаний
Технологии исследования нелинейных математических моделей:
аналитическое исследование методом множителей Лагранжа;
численное
исследование.
Слайд 3Текущий контроль знаний
Решить графически задачу:
Перейти к двойственной задаче и решить ее
графически:
Слайд 4Исследование моделей
Два класса технологий исследования нелинейных моделей с непрерывными
переменными:
Аналитическое исследование моделей.
Численное исследование:
рандомизированное;
детерминированное.
Аналитическое исследование моделей.
Численное исследование:
рандомизированное;
детерминированное.
Слайд 5Метод множителей Лагранжа
Используется для решения однокритериальных задач на условный экстремум вида:
Слайд 6Создание и исследование функции Лагранжа
Идея заключается в замене решения
системы (1) поиском экстремума функции Лагранжа L вида:
Экстремум L отвечает решению системы:
Экстремум L отвечает решению системы:
Слайд 7Пример: задача о консервной банке
Содержательная постановка: требуется выбрать такое соотношение между
высотой и диаметром консервной банки, чтобы ее поверхность была минимальной при заданном объеме.
Формальная постановка:
Формальная постановка:
Слайд 8Функция Лагранжа и ее исследование на экстремум
1. Функция Лагранжа:
(5)
2. Условия экстремума:
(6)
2. Условия экстремума:
(6)
Результат решения системы (6):
Слайд 9Исследование экстремума
Пусть новое значение радиуса банки равно r+Ɛ, где Ɛ>0, тогда
из системы (4) следует, что площадь банки равна S*:
Так как производная то определяемые (7) значения r и h отвечают минимуму S.
Так как производная то определяемые (7) значения r и h отвечают минимуму S.
Слайд 10САМОСТОЯТЕЛЬНО 1
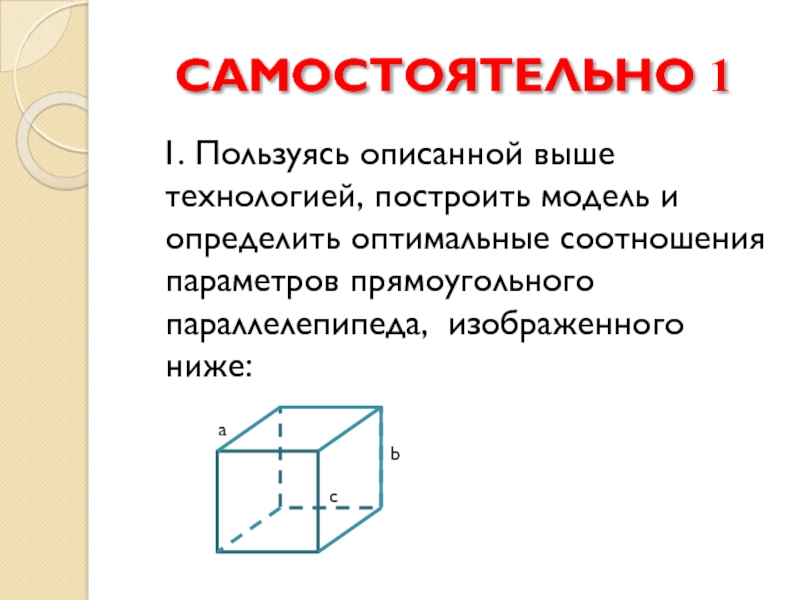
1. Пользуясь описанной выше технологией, построить модель и определить
оптимальные соотношения параметров прямоугольного параллелепипеда, изображенного ниже:
a
b
c
Слайд 11Достоинства и недостатки метода множителей Лагранжа
1. Достоинства:
Глобально оптимальное решение.
Ответ получается аналитически,
т.е. не требует для определения численных значений больших ресурсов компьютера.
Недостатки:
Возможность исследовать модель таким образом зависит от свойств полученной системы уравнений.
Недостатки:
Возможность исследовать модель таким образом зависит от свойств полученной системы уравнений.