- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Contact Manifolds презентация
Содержание
- 1. Contact Manifolds
- 2. Executive Summary Constraint solvers need contact points
- 3. Contact Contact occurs when two shapes touch.
- 4. Contact Manifolds For convex polyhedra, a contact
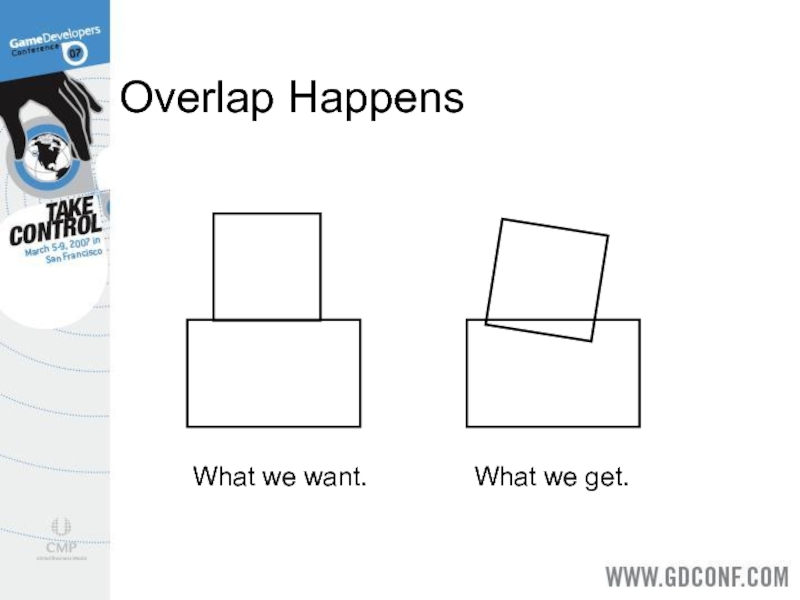
- 5. Overlap Happens What we want. What we get.
- 6. Approximate Manifolds We use a collection of
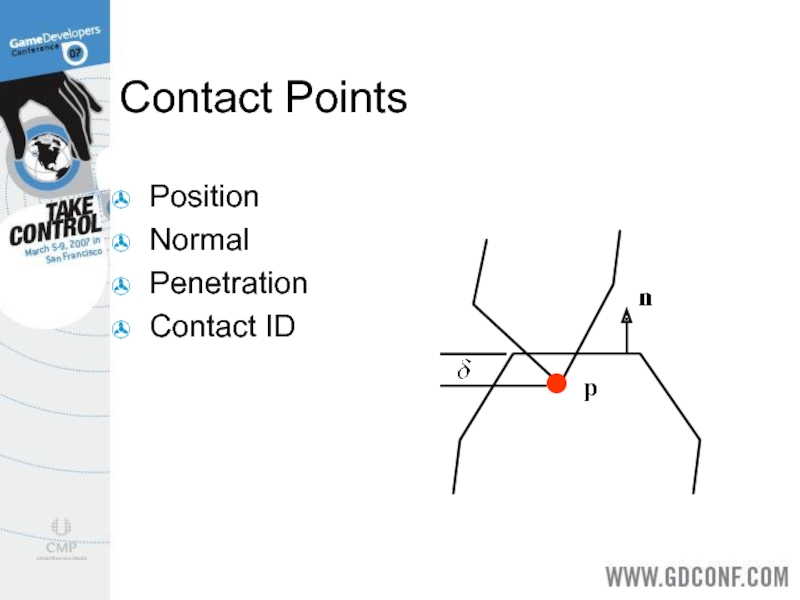
- 7. Contact Points Position Normal Penetration Contact ID
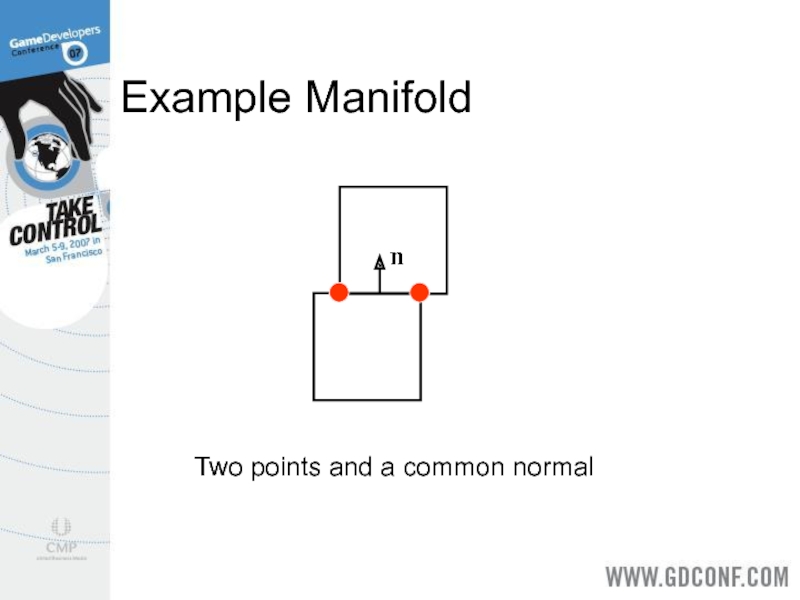
- 8. Example Manifold Two points and a common normal
- 9. Contact Manifold Quality When objects penetrate significantly
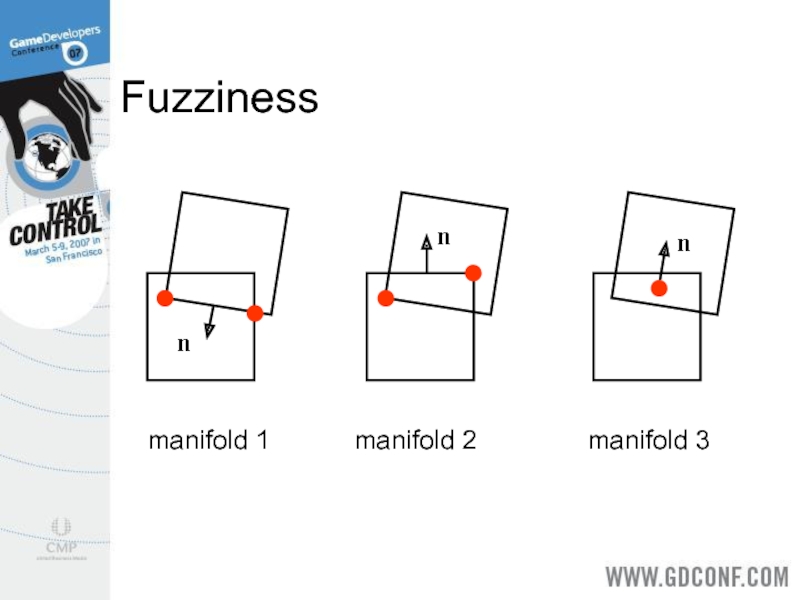
- 10. Fuzziness
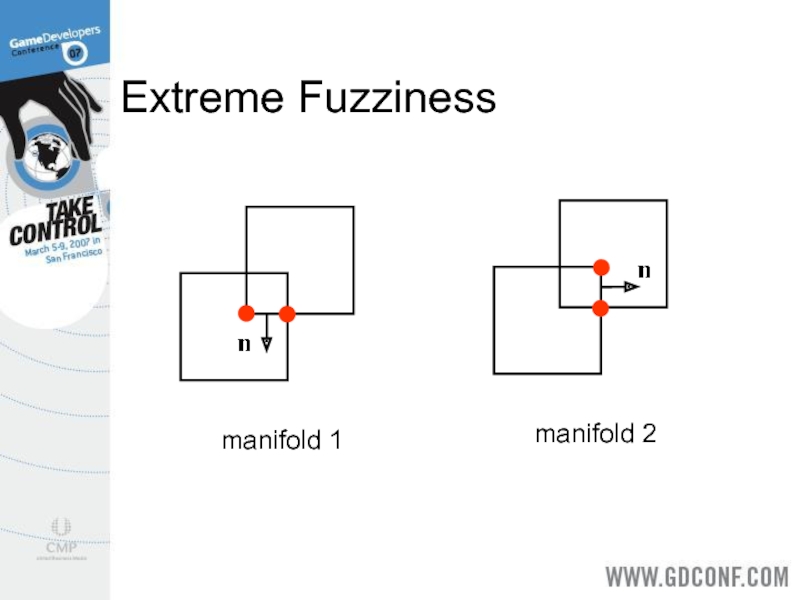
- 11. Extreme Fuzziness manifold 1 manifold 2
- 12. Using the SAT Mainly useful for convex
- 13. Example: 2D Box-Box SAT First
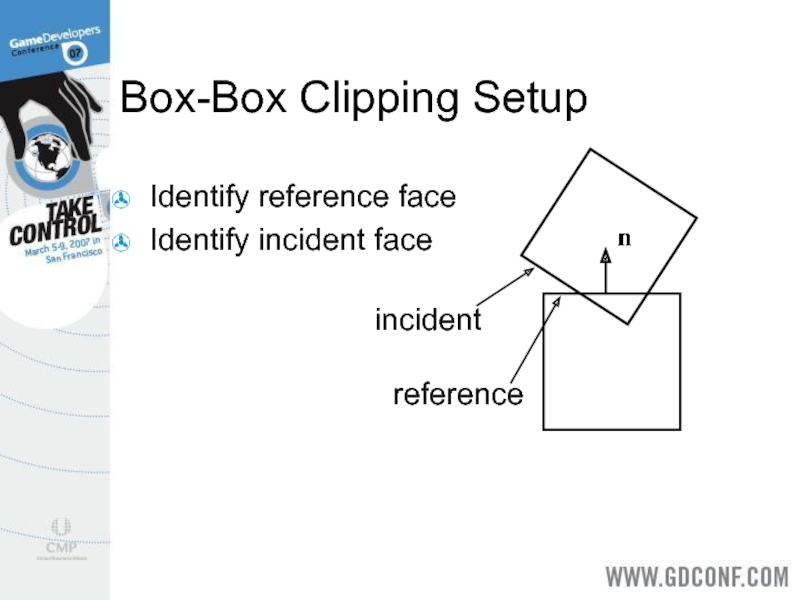
- 14. Box-Box Clipping Setup Identify reference face Identify incident face incident reference
- 15. Box-Box Clipping Clip incident face against reference
- 16. Feature Flip-Flop Which normal is the min
- 17. Coherence Apply old force/impulse solution at the
- 18. Feature-Based Contact Points Each contact point is
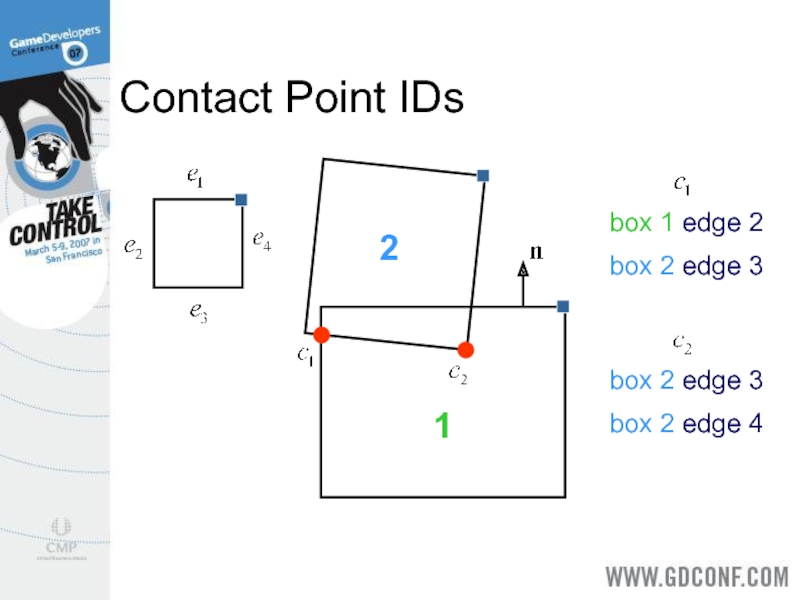
- 19. Contact Point IDs 1 2
- 20. GJK Contact Points Three cases: - No contact - Shallow contact - Deep contact
- 21. GJK Shallow Contact The support points are
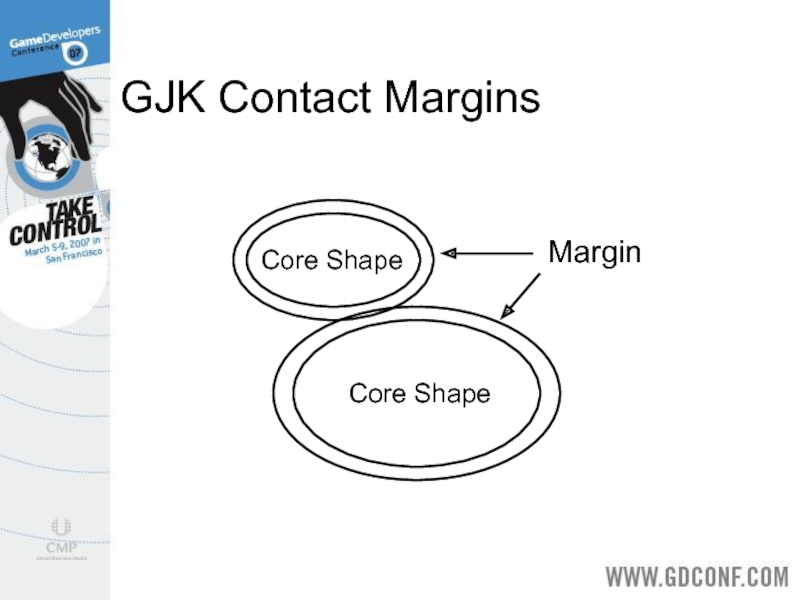
- 22. GJK Contact Margins Core Shape Margin Core Shape
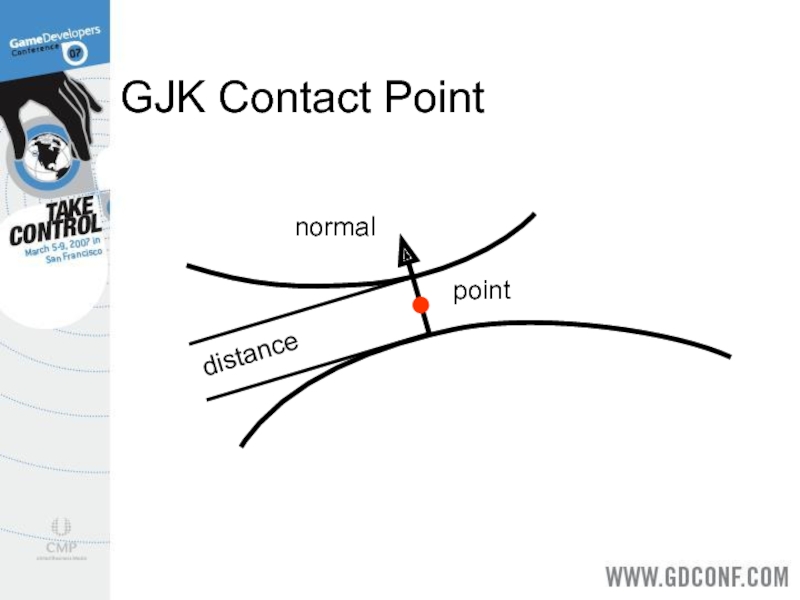
- 23. GJK Contact Point point normal distance
- 24. GJK Deep Contact An awkward encounter …
- 25. Deep Contact Use some other algorithm. It
- 26. GJK Manifolds GJK only gives one contact
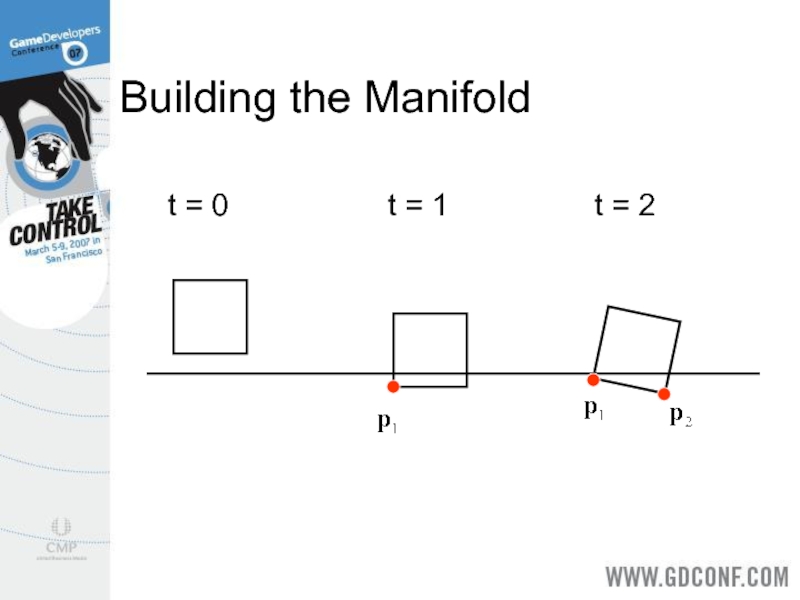
- 27. Building the Manifold t = 0
- 28. Manifold Persistence Track the points in each
- 29. Adding New Points Keep a minimal set
- 30. Manifold Reduction This applies to one-shot and
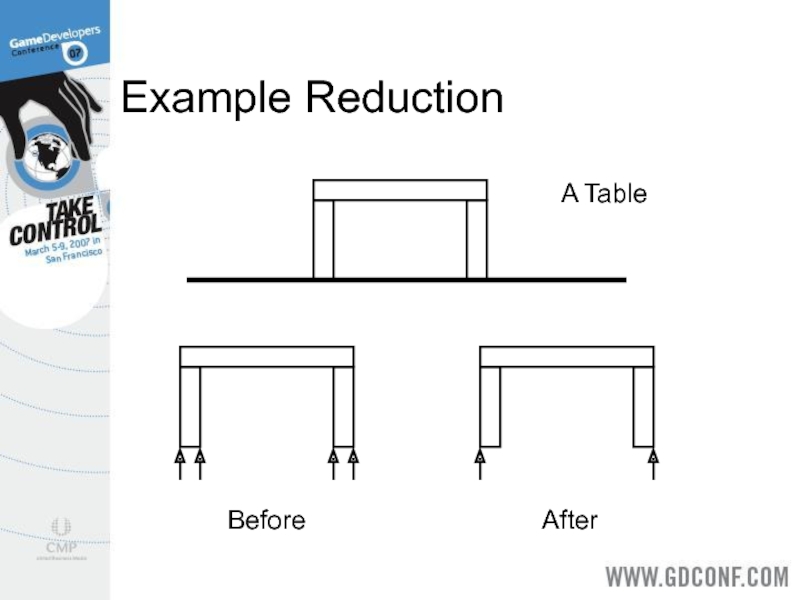
- 31. Example Reduction A Table Before After
- 32. Further Reading http://www.gphysics.com/downloads/ http://www.continuousphysics.com Collision Detection in
Executive Summary Constraint solvers need contact points to prevent penetration. We can use SAT to compute a contact manifold in one shot. We can use GJK to build up a contact
Слайд 2Executive Summary
Constraint solvers need contact points to prevent penetration.
We can use
SAT to compute a contact manifold in one shot.
We can use GJK to build up a contact manifold point-by-point.
We can use GJK to build up a contact manifold point-by-point.
Слайд 3Contact
Contact occurs when two shapes touch.
We model contact to prevent penetration
and to simulate friction.
Modeling contact requires some geometry and a lot of finesse.
Modeling contact requires some geometry and a lot of finesse.
Слайд 4Contact Manifolds
For convex polyhedra, a contact manifold is ideally a single
point, a line segment, or a convex polygon.
For general convex 3D shapes, the contact manifold is a convex 2D shape.
Did I mention overlap?
For general convex 3D shapes, the contact manifold is a convex 2D shape.
Did I mention overlap?
Слайд 6Approximate Manifolds
We use a collection of contact points to approximate the
contact manifold.
Our goal is fast, stable, and plausible simulation.
In this sense, computing good manifolds is an art.
Our goal is fast, stable, and plausible simulation.
In this sense, computing good manifolds is an art.
Слайд 9Contact Manifold Quality
When objects penetrate significantly the contact manifold is fuzzy.
Contact
solvers like coherence.
Be consistent from step-to-step.
Be consistent from step-to-step.
Слайд 12Using the SAT
Mainly useful for convex polyhedra (boxes, triangles, etc).
Find the
axis of minimum penetration.
For edge-edge contact, find the midpoint.
For face contact, use Sutherland-Hodgeman clipping.
For edge-edge contact, find the midpoint.
For face contact, use Sutherland-Hodgeman clipping.
Слайд 13Example: 2D Box-Box SAT
First find the separating axis with the minimum
penetration.
In 2D the separating axis is a face normal.
In 2D the separating axis is a face normal.
Слайд 15Box-Box Clipping
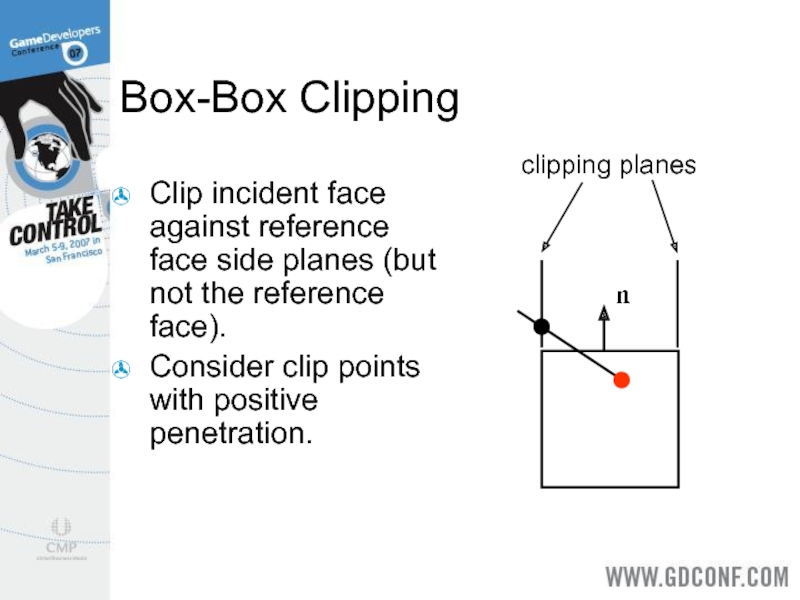
Clip incident face against reference face side planes (but not
the reference face).
Consider clip points with positive penetration.
Consider clip points with positive penetration.
clipping planes
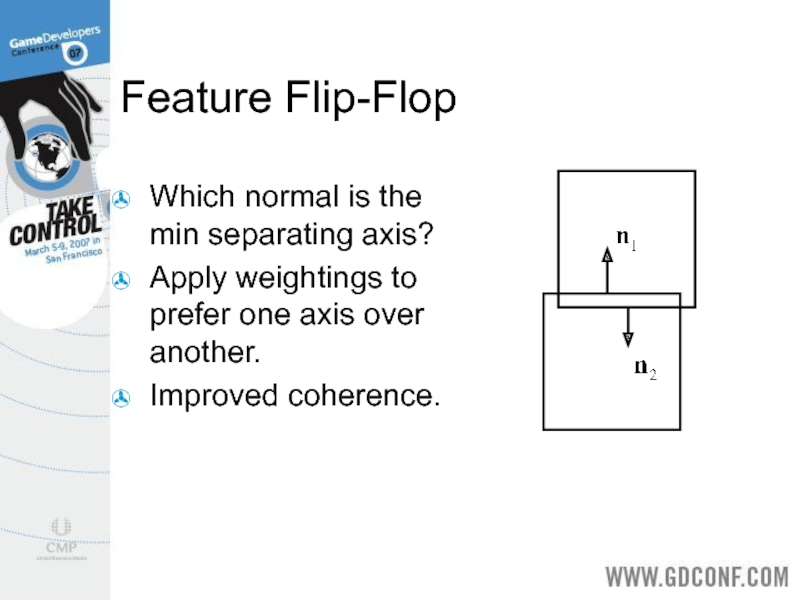
Слайд 16Feature Flip-Flop
Which normal is the min separating axis?
Apply weightings to prefer
one axis over another.
Improved coherence.
Improved coherence.
Слайд 17Coherence
Apply old force/impulse solution at the beginning of the step.
Fewer iterations
and greater stability.
We need a way to match old and new contacts.
We need a way to match old and new contacts.
Слайд 18Feature-Based Contact Points
Each contact point is the result of clipping.
It is
the junction of two different edges.
An edge may come from either box.
Store the two edge numbers with each contact point – this is the Contact ID.
An edge may come from either box.
Store the two edge numbers with each contact point – this is the Contact ID.
Слайд 21GJK Shallow Contact
The support points are scaled up by a small
margin to detect contact.
Compute the closest points (no margin).
This gives the position and normal.
The penetration is the margin minus the true distance.
Compute the closest points (no margin).
This gives the position and normal.
The penetration is the margin minus the true distance.
Слайд 25Deep Contact
Use some other algorithm.
It will be slower than GJK, but
it won’t last long.
SAT, EPA, brute force.
Read Gino’s book to learn EPA.
SAT, EPA, brute force.
Read Gino’s book to learn EPA.
Слайд 26GJK Manifolds
GJK only gives one contact point at a time.
We hold
on to and treasure each contact point.
Build a manifold over several time steps.
This automatically provides coherence.
Build a manifold over several time steps.
This automatically provides coherence.
Слайд 28Manifold Persistence
Track the points in each body.
If the points move too
far apart, dismiss them.
This is bad for sliding.
Use Contact IDs?
This is bad for sliding.
Use Contact IDs?
Слайд 29Adding New Points
Keep a minimal set of points per manifold (e.g.
4 points).
Reject new points that are too close to old points.
Reject new points that are too close to old points.
Слайд 30Manifold Reduction
This applies to one-shot and incremental manifolds.
We want to keep
the minimum number of contact points for a stable simulation.
This improves performance drastically.
This improves performance drastically.
Слайд 32Further Reading
http://www.gphysics.com/downloads/
http://www.continuousphysics.com
Collision Detection in Interactive 3D Environments by Gino van den
Bergen
Fast Contact Reduction for Dynamics Simulation by Adam Moravanszky and Pierre Terdiman in Game Programming Gems 4.
Fast Contact Reduction for Dynamics Simulation by Adam Moravanszky and Pierre Terdiman in Game Programming Gems 4.
