- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Численные методы решения задач презентация
Содержание
- 1. Численные методы решения задач
- 2. Интерполяция – приближенное или точное нахождение какой-либо
- 3. Постановка задачи. Предположим, что функция f(x) известна
- 4. Интерполяционная функция φ(x) имеет вид многочлена
- 5. Схема Горнера Фрагмент программы на
- 6. Интерполяционный полином Лагранжа имеет вид:
- 7. Интерполяционный полином Ньютона имеет вид:
- 8. Аналитическая формула, по которой находятся коэффициенты
- 9. Пример. Найти значения коэффициентов полинома Ньютона
- 10. Пример. Найти значения коэффициентов полинома Ньютона
- 11. Пример. Найти значения коэффициентов полинома Ньютона
- 12. Пример. Найти значения коэффициентов полинома Ньютона
- 13. Пример. Найти значения коэффициентов полинома Ньютона
- 14. Пример. Найти значения коэффициентов полинома Ньютона
- 15. Пример. Найти значения коэффициентов полинома Ньютона
- 16. Пример. Найти значения коэффициентов полинома Ньютона
- 17. Пример. Найти значения коэффициентов полинома Ньютона
- 18. Пример. Найти значения коэффициентов полинома Ньютона
- 19. Пример. Найти значения коэффициентов полинома Ньютона
- 20. Пример. Найти значения коэффициентов полинома Ньютона
- 21. Пример. Найти значения коэффициентов полинома Ньютона
- 22. Пример. Найти значения коэффициентов полинома Ньютона
- 23. Пример. Найти значения коэффициентов полинома Ньютона
- 24. Пример. Найти значения коэффициентов полинома Ньютона
- 25. Проверка.
- 26. Сплайном называется функция, определенная на отрезке [a;
- 27. Коэффициенты ai, bi, ci находятся при решении
- 28. Пример. Найти коэффициенты параболического сплайна для
- 29. Пример. Найти коэффициенты параболического сплайна для
- 30. Пример. Найти коэффициенты параболического сплайна для
- 31. Пример. Найти коэффициенты параболического сплайна для
- 32. Пример. Найти коэффициенты параболического сплайна для
- 33. В общем случае итерационная процедура нахождения
- 35. Кубическим сплайном называют совокупность многочленов третьей степени
- 36. Коэффициенты ai, bi, ci, di находятся при
- 37. Пример. Найти коэффициенты кубического сплайна для
- 38. Пример. Найти коэффициенты кубического сплайна для
- 39. Пример. Найти коэффициенты кубического сплайна для
- 40. Пример. Найти коэффициенты кубического сплайна для
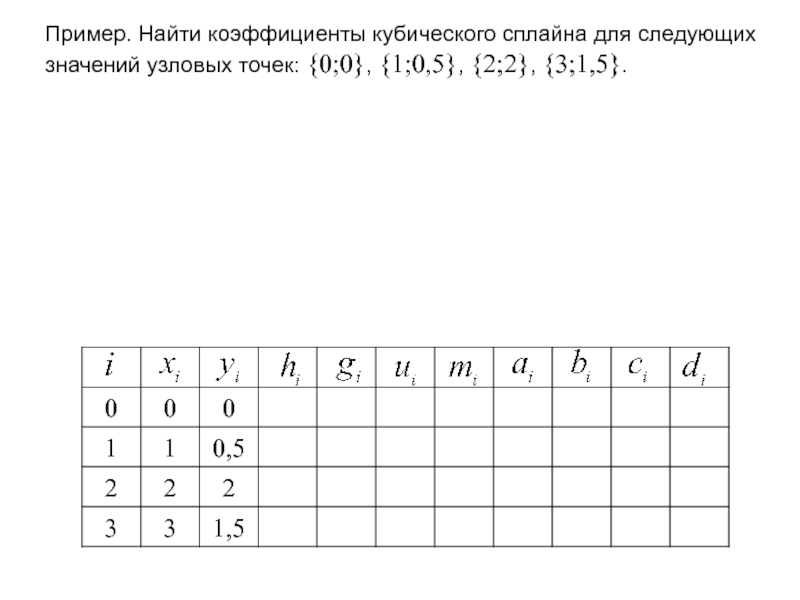
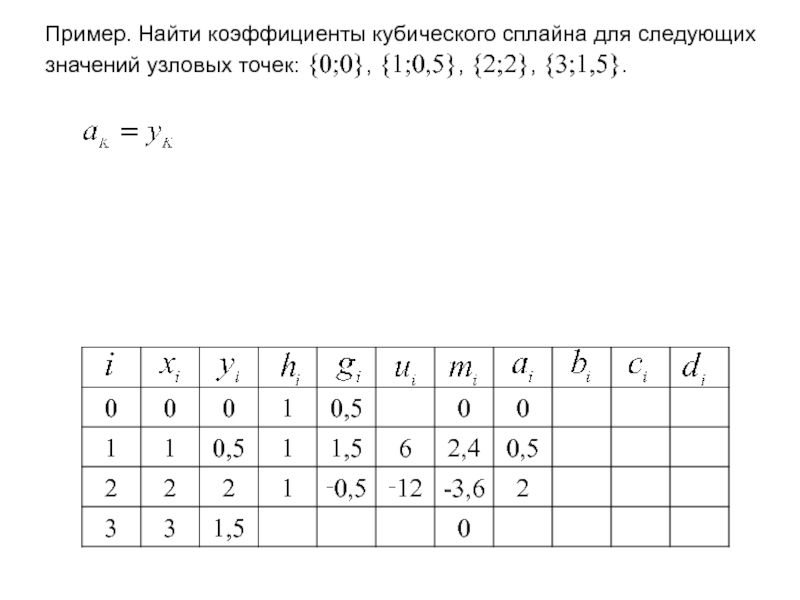
- 45. Пример. Найти коэффициенты кубического сплайна для
- 47. В общем случае итерационная процедура нахождения
- 48. В общем случае итерационная процедура нахождения
- 49. Пример. Найти коэффициенты кубического сплайна для
- 50. Пример. Найти коэффициенты кубического сплайна для
- 51. Пример. Найти коэффициенты кубического сплайна для
- 52. Пример. Найти коэффициенты кубического сплайна для
- 54. Пример. Найти коэффициенты кубического сплайна для
- 55. Пример. Найти коэффициенты кубического сплайна для
- 56. Пример. Найти коэффициенты кубического сплайна для
- 57. Пример. Найти коэффициенты кубического сплайна для
- 58. 6.5.6. Метод наименьших квадратов Постановка задачи.
- 59. 6.5.6. Метод наименьших квадратов – базисные
- 60. 6.5.6. Метод наименьших квадратов
- 61. 6.5.6. Метод наименьших квадратов
- 65. Пример. Даны результаты измерений: {0;0}, {1;0,5},
- 66. Пример. Даны результаты измерений: {0;0}, {1;0,5},
- 67. Пример. Даны результаты измерений: {0;0}, {1;0,5},
- 68. Пример. Даны результаты измерений: {0;0}, {1;0,5},
- 69. Пример. Даны результаты измерений: {0;0}, {1;0,5},
- 70. Пример. Даны результаты измерений: {0;0}, {1;0,5},
- 71. Пример. Даны результаты измерений: {0;0}, {1;0,5},
- 72. Пример. Даны результаты измерений: {0;0}, {1;0,5},
- 73. Пример. Даны результаты измерений: {0;0}, {1;0,5},
- 74. Пример. Даны результаты измерений: {0;0}, {1;0,5},
- 80. 6.5.7. Интерполяция тригонометрическим полиномом Если требуется
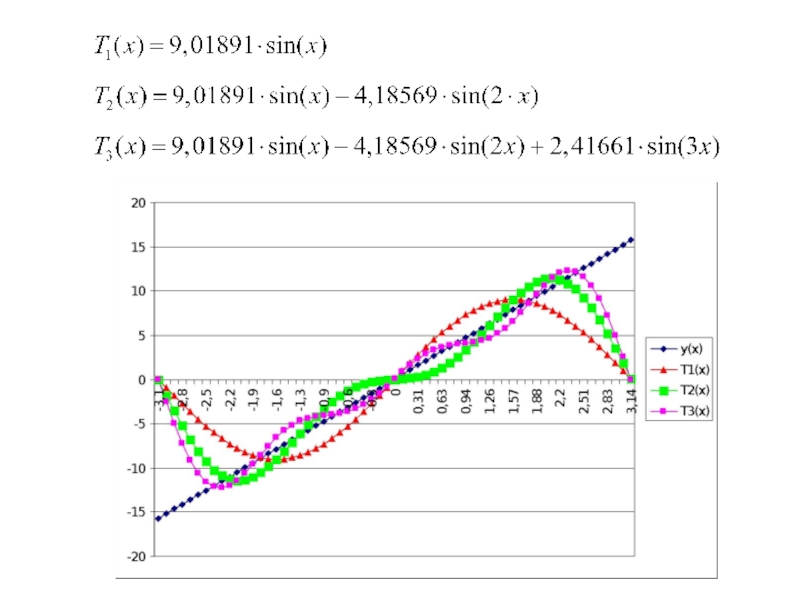
- 81. Пример. Аппроксимировать функцию y=5·x на интервале
- 82. Пример. Аппроксимировать функцию y=5·x на интервале
- 84. 6.5.8. Интерполяция кривой Безье Пьер Безье
- 85. 6.5.8. Интерполяция кривой Безье Кривая Безье
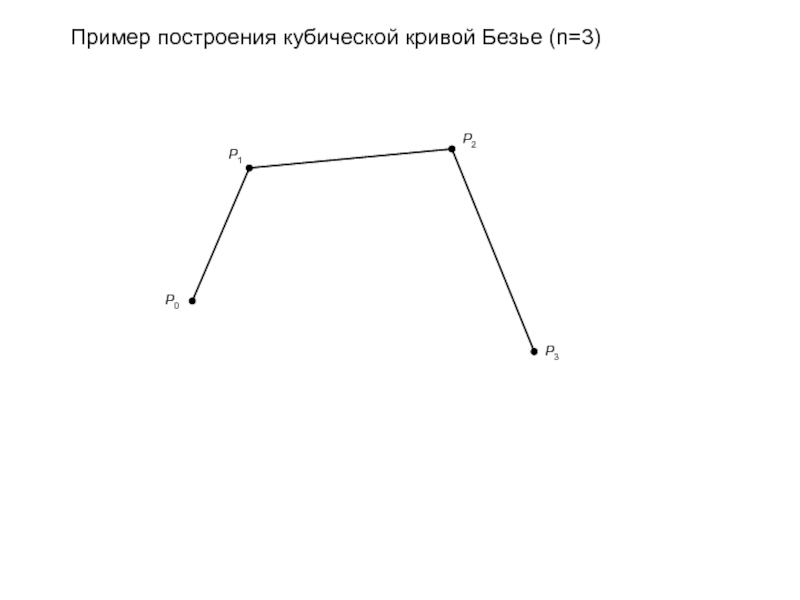
- 86. Кубические кривые Безье (n=3) широко используются в
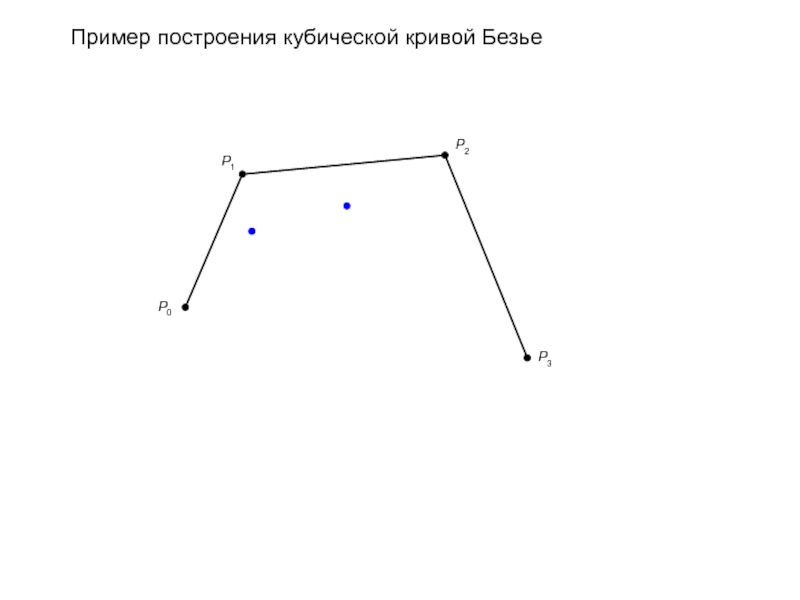
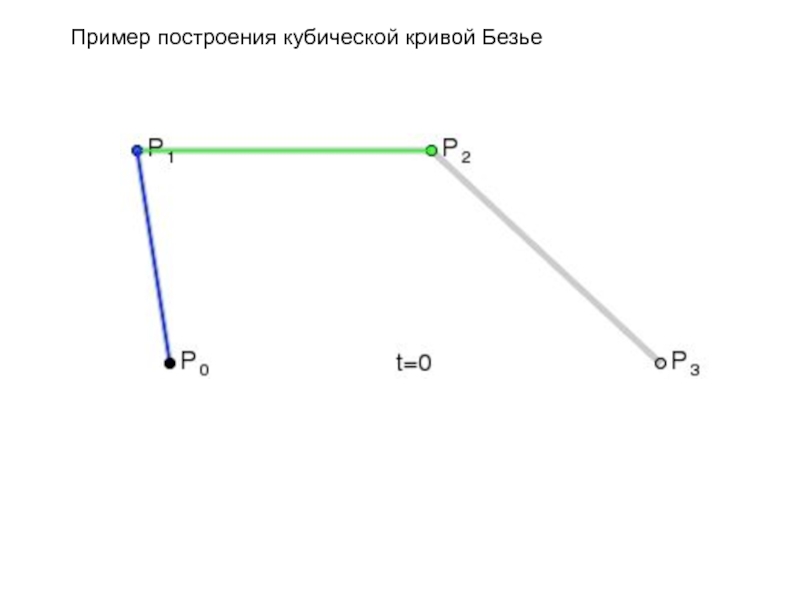
- 87. Пример построения кубической кривой Безье (n=3)
- 88. Пример построения кубической кривой Безье (n=3)
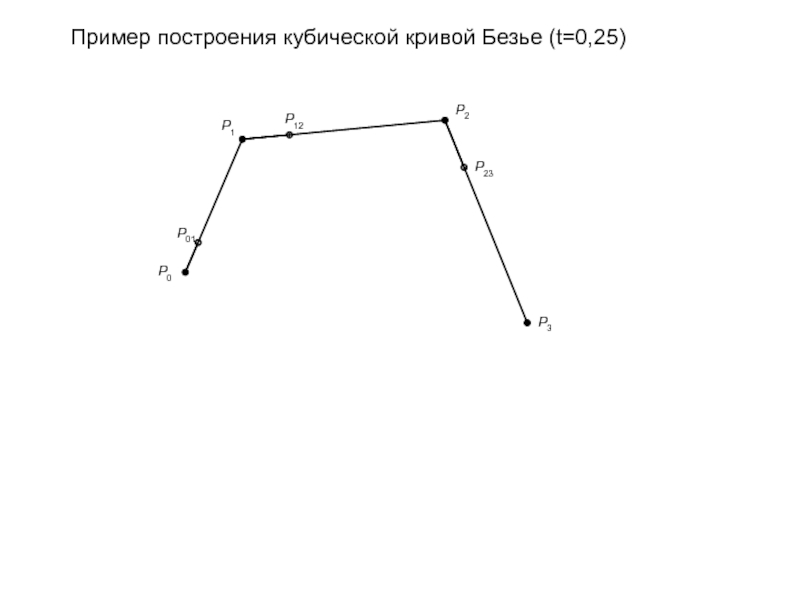
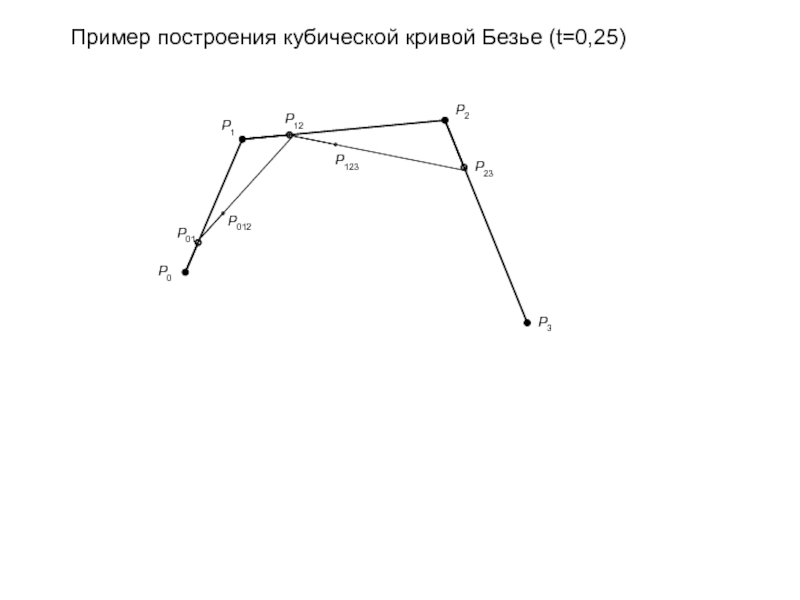
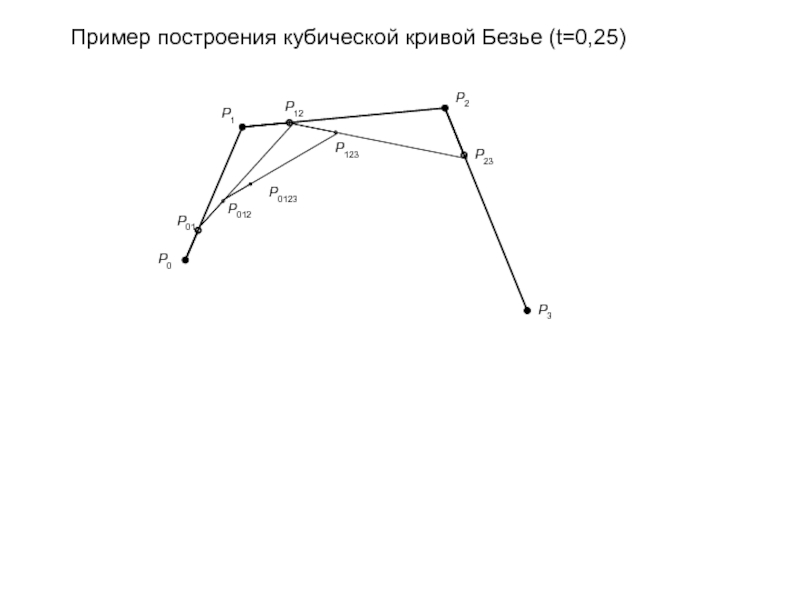
- 89. Пример построения кубической кривой Безье (t=0,25)
- 90. Пример построения кубической кривой Безье (t=0,25)
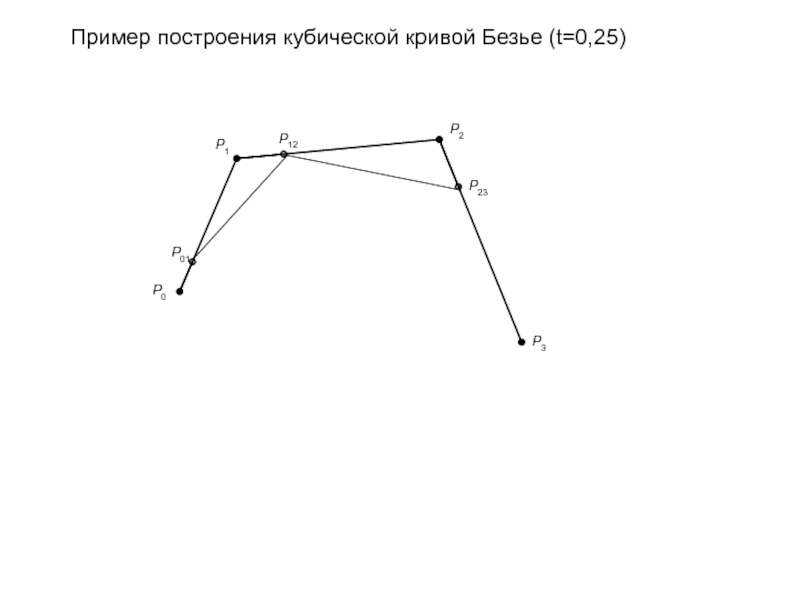
- 91. Пример построения кубической кривой Безье (t=0,25)
- 92. Пример построения кубической кривой Безье (t=0,25)
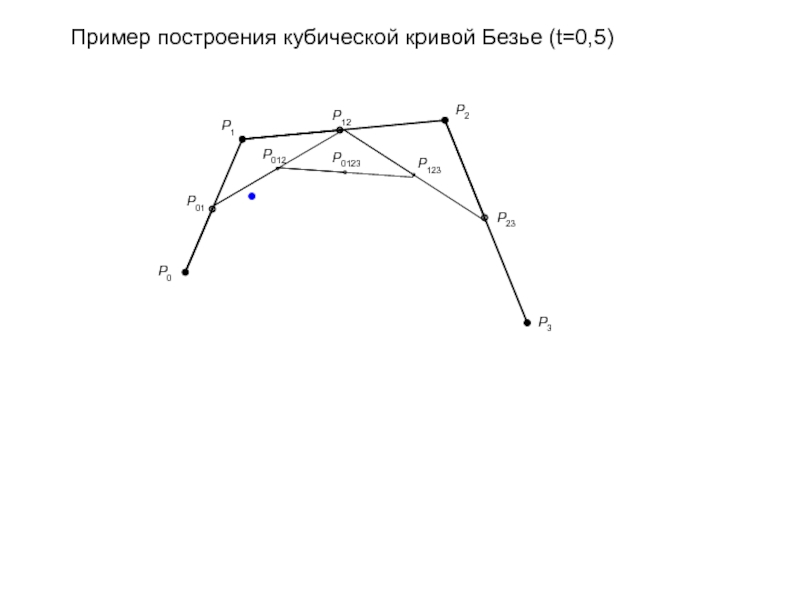
- 93. Пример построения кубической кривой Безье (t=0,5)
- 94. Пример построения кубической кривой Безье
- 95. Пример построения кубической кривой Безье
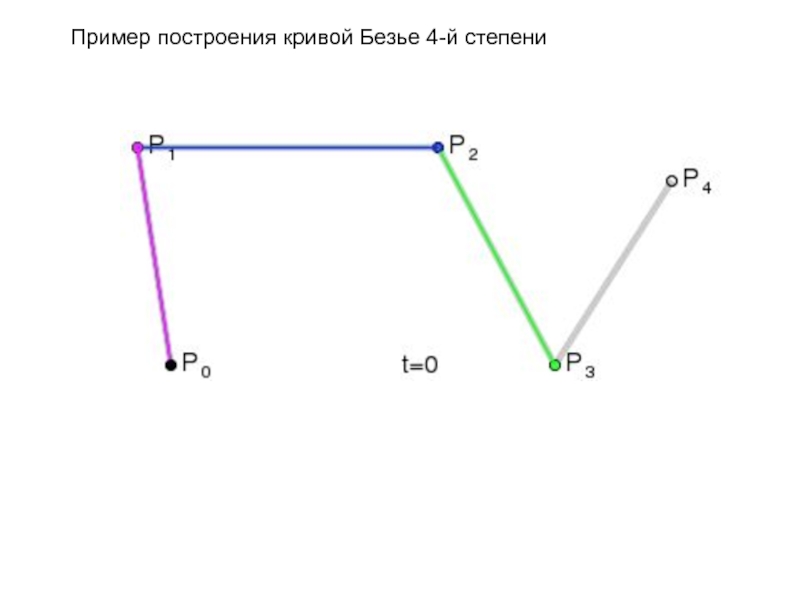
- 96. Пример построения кривой Безье 4-й степени
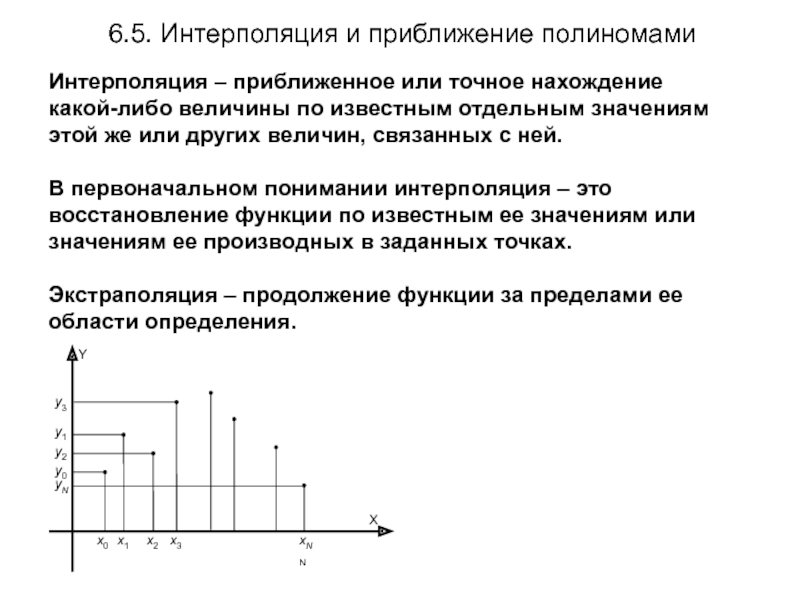
Слайд 2Интерполяция – приближенное или точное нахождение какой-либо величины по известным отдельным
В первоначальном понимании интерполяция – это восстановление функции по известным ее значениям или значениям ее производных в заданных точках.
Экстраполяция – продолжение функции за пределами ее области определения.
6.5. Интерполяция и приближение полиномами
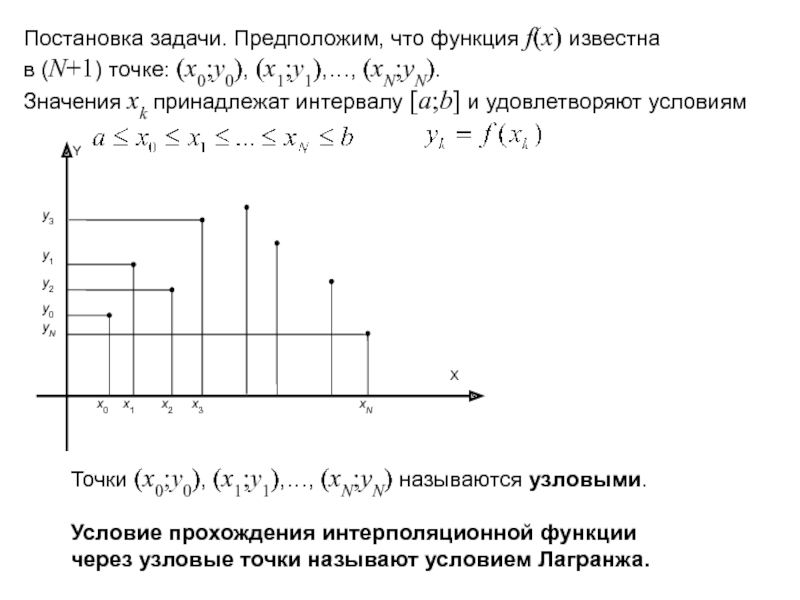
Слайд 3Постановка задачи. Предположим, что функция f(x) известна в (N+1) точке: (x0;y0),
Значения xk принадлежат интервалу [a;b] и удовлетворяют условиям
Точки (x0;y0), (x1;y1),…, (xN;yN) называются узловыми.
Условие прохождения интерполяционной функции через узловые точки называют условием Лагранжа.
Слайд 4Интерполяционная функция φ(x) имеет вид многочлена
6.5.1. Интерполяция алгебраическим полиномом
Слайд 5
Схема Горнера
Фрагмент программы на языке Си
p=c[n];
for(i=n-1; i>=0; i--)
p=c[i]+p*x;
Количество
Сложение
Умножение
Слайд 6
Интерполяционный полином Лагранжа имеет вид:
6.5.2. Интерполяционный полином Лагранжа
Достоинством полинома Лагранжа является
Слайд 7
Интерполяционный полином Ньютона имеет вид:
6.5.3. Интерполяционный полином Ньютона
– коэффициенты полинома
Коэффициенты полинома Ньютона находятся исходя из выполнения условия Лагранжа.
Слайд 8
Аналитическая формула, по которой находятся коэффициенты полинома, имеет сложный вид
Итерационная
Слайд 25
Проверка.
К достоинствам данного метода можно отнести
меньшая погрешность интерполяции при близкорасположенных
возможность использования вложенных умножений при вычислении значений полинома;
коэффициенты полинома получаются более простым способом, чем при интерполяции алгебраическим полиномом.
Недостатком является проведение предварительных расчетов коэффициентов.
Слайд 26Сплайном называется функция, определенная на отрезке [a; b], совпадающая на частичных
Параболическим сплайном называют совокупность многочленов второй степени вида
6.5.4. Интерполяция параболическим сплайном
– коэффициенты параболических полиномов
– число узловых точек
Слайд 27Коэффициенты ai, bi, ci находятся при решении системы линейных уравнений, которые
равенство значений сплайна и аппроксимируемой функции в узлах (условие Лагранжа)
непрерывность первой производной в узловых точках:
равенство некоторому значению D первой производной в начале или на конце интервала: или
– первая производная параболического многочлена
Слайд 28
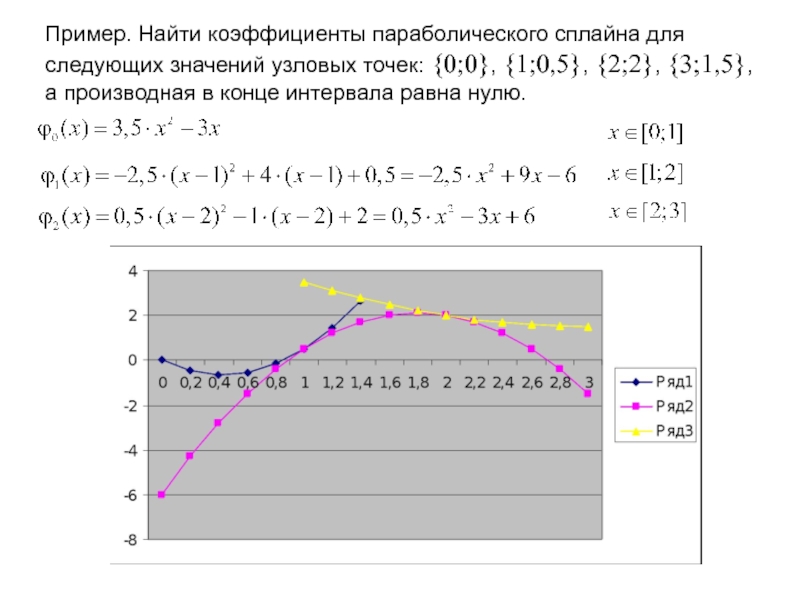
Пример. Найти коэффициенты параболического сплайна для следующих значений узловых точек: {0;0},
Слайд 29
Пример. Найти коэффициенты параболического сплайна для следующих значений узловых точек: {0;0},
Слайд 30
Пример. Найти коэффициенты параболического сплайна для следующих значений узловых точек: {0;0},
Слайд 31
Пример. Найти коэффициенты параболического сплайна для следующих значений узловых точек: {0;0},
Слайд 32
Пример. Найти коэффициенты параболического сплайна для следующих значений узловых точек: {0;0},
Слайд 33
В общем случае итерационная процедура нахождения коэффициентов параболического сплайна следующая:
1. Находятся
2. Находятся значения zK при K=0, 1, 2,…, (N–1) по формуле
3. Находятся значения aK, bK, cK при K=0, 1, 2,…, (N–1) по формулам
если задано значение первой производной D в начале интервала интерполяции
если задано значение первой производной D в конце интервала интерполяции
Слайд 34
Пример. Найти коэффициенты параболического сплайна для следующих значений узловых точек: {0;0},
Слайд 35Кубическим сплайном называют совокупность многочленов третьей степени вида
6.5.5. Интерполяция кубическим сплайном
–
– число узловых точек
Слайд 36Коэффициенты ai, bi, ci, di находятся при решении системы линейных уравнений,
равенство значений сплайна и аппроксимируемой функции в узлах (условие Лагранжа)
непрерывность первой и второй производной в узловых точках:
равенства нулю вторых производных на концах интервала:
– первая производная кубического многочлена
– вторая производная кубического многочлена
Слайд 37
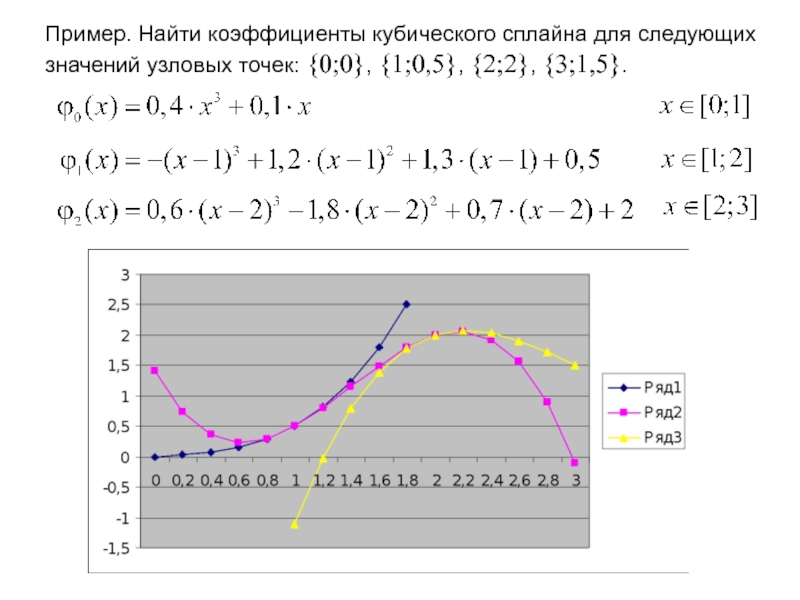
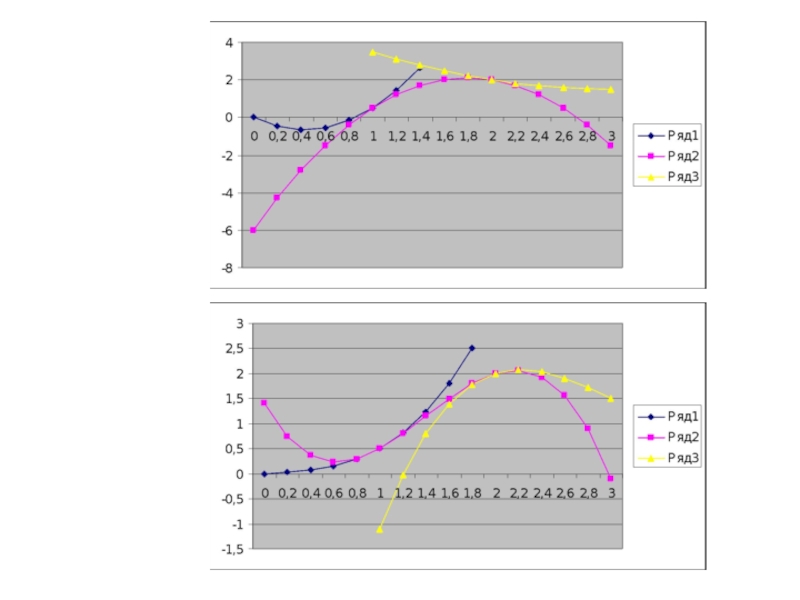
Пример. Найти коэффициенты кубического сплайна для следующих значений узловых точек: {0;0},
Слайд 38
Пример. Найти коэффициенты кубического сплайна для следующих значений узловых точек: {0;0},
Слайд 39
Пример. Найти коэффициенты кубического сплайна для следующих значений узловых точек: {0;0},
Слайд 40
Пример. Найти коэффициенты кубического сплайна для следующих значений узловых точек: {0;0},
Слайд 45
Пример. Найти коэффициенты кубического сплайна для следующих значений узловых точек: {0;0},
Слайд 47
В общем случае итерационная процедура нахождения коэффициентов кубического сплайна следующая:
1. Находятся
2. Находятся значения gK при K=0, 1, 2,…, (N–1) по формуле
3. Находятся значения uK при K=0, 1, 2,…, (N–1) по формуле
4. Находятся значения mK при решении системы линейных уравнений
Слайд 48
В общем случае итерационная процедура нахождения коэффициентов кубического сплайна следующая:
5. Принимается
6. Находятся значения коэффициентов aK, bK, cK, dK кубических полиномов при K=0, 1, 2,…, (N–1) по формулам
Слайд 49
Пример. Найти коэффициенты кубического сплайна для следующих значений узловых точек: {0;0},
Слайд 50
Пример. Найти коэффициенты кубического сплайна для следующих значений узловых точек: {0;0},
Слайд 51
Пример. Найти коэффициенты кубического сплайна для следующих значений узловых точек: {0;0},
Слайд 52
Пример. Найти коэффициенты кубического сплайна для следующих значений узловых точек: {0;0},
Слайд 54
Пример. Найти коэффициенты кубического сплайна для следующих значений узловых точек: {0;0},
Слайд 55
Пример. Найти коэффициенты кубического сплайна для следующих значений узловых точек: {0;0},
Слайд 56
Пример. Найти коэффициенты кубического сплайна для следующих значений узловых точек: {0;0},
Слайд 57
Пример. Найти коэффициенты кубического сплайна для следующих значений узловых точек: {0;0},
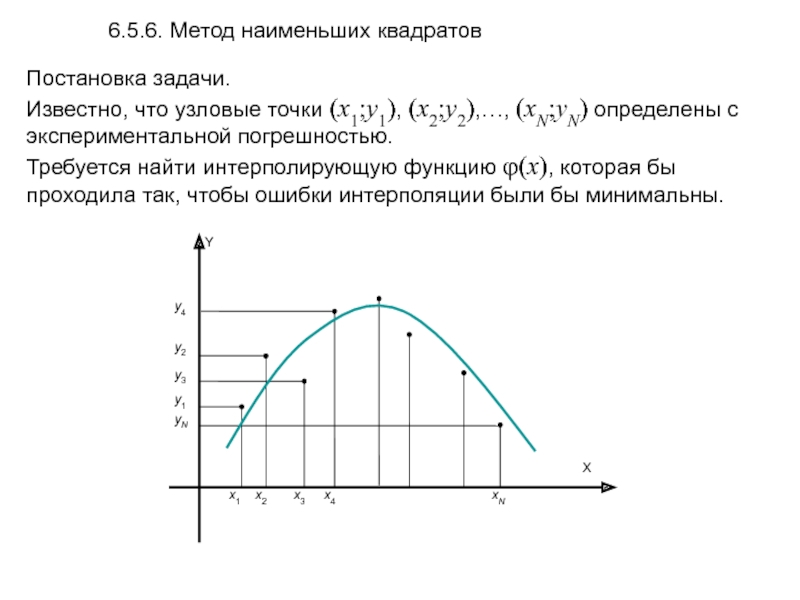
Слайд 586.5.6. Метод наименьших квадратов
Постановка задачи.
Известно, что узловые точки (x1;y1), (x2;y2),…,
Требуется найти интерполирующую функцию φ(x), которая бы проходила так, чтобы ошибки интерполяции были бы минимальны.
Слайд 596.5.6. Метод наименьших квадратов
– базисные функции.
– среднеквадратичная ошибка интерполяции.
Задача интерполяции по
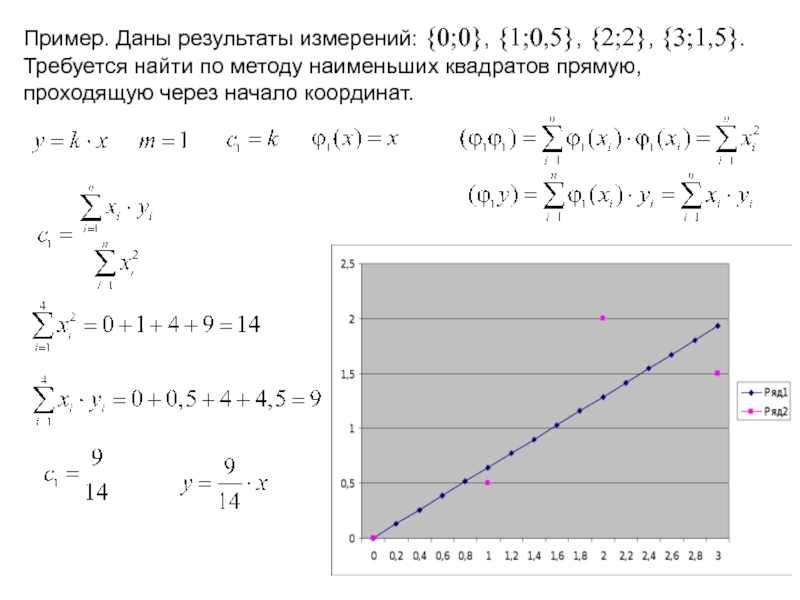
Слайд 65
Пример. Даны результаты измерений: {0;0}, {1;0,5}, {2;2}, {3;1,5}. Требуется найти по
Слайд 66
Пример. Даны результаты измерений: {0;0}, {1;0,5}, {2;2}, {3;1,5}. Требуется найти по
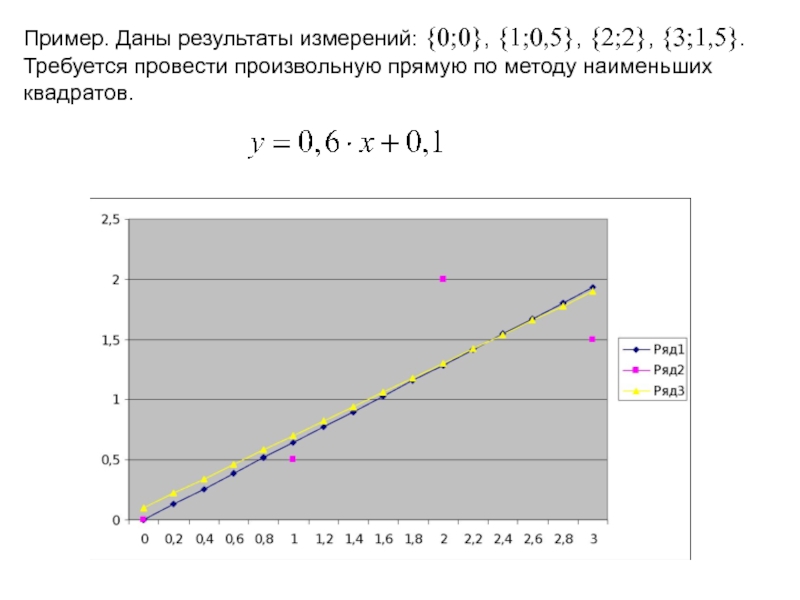
Слайд 67
Пример. Даны результаты измерений: {0;0}, {1;0,5}, {2;2}, {3;1,5}. Требуется провести произвольную
Слайд 68
Пример. Даны результаты измерений: {0;0}, {1;0,5}, {2;2}, {3;1,5}. Требуется провести произвольную
Слайд 69
Пример. Даны результаты измерений: {0;0}, {1;0,5}, {2;2}, {3;1,5}. Требуется провести произвольную
Слайд 70
Пример. Даны результаты измерений: {0;0}, {1;0,5}, {2;2}, {3;1,5}. Требуется провести произвольную
Слайд 71
Пример. Даны результаты измерений: {0;0}, {1;0,5}, {2;2}, {3;1,5}. Требуется провести параболу
Слайд 72
Пример. Даны результаты измерений: {0;0}, {1;0,5}, {2;2}, {3;1,5}. Требуется провести параболу
Слайд 73
Пример. Даны результаты измерений: {0;0}, {1;0,5}, {2;2}, {3;1,5}. Требуется провести параболу
Слайд 74
Пример. Даны результаты измерений: {0;0}, {1;0,5}, {2;2}, {3;1,5}. Требуется провести параболу
Слайд 78
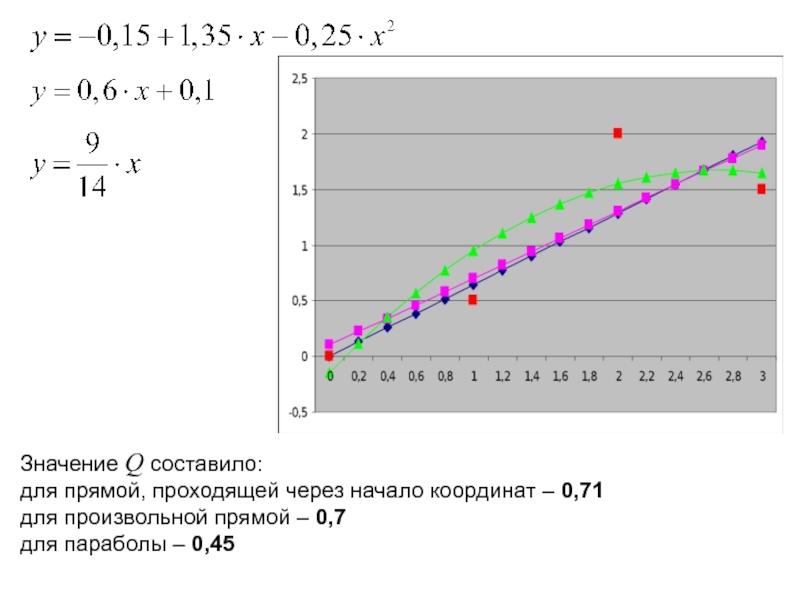
Значение Q составило:
для прямой, проходящей через начало координат – 0,71
для
для параболы – 0,45
Слайд 79
Увеличение степени полинома приводит, с одной стороны, к уменьшению суммарной ошибки
Для оценки приемлемого значения числа степени многочлена используют величину
За оптимальное значение степени многочлена следует принять то значение m, начиная с которого величина σm стабилизируется или начинает возрастать.
Слайд 806.5.7. Интерполяция тригонометрическим полиномом
Если требуется провести интерполяцию данных, имеющий периодический характер,
Тригонометрический полином порядка M имеет вид
Коэффициенты тригонометрического полинома находятся по методу наименьших квадратов.
Слайд 81
Пример. Аппроксимировать функцию y=5·x на интервале [–π; π] тригонометрическими полиномами порядка
Слайд 82
Пример. Аппроксимировать функцию y=5·x на интервале [–π; π] тригонометрическими полиномами порядка
Слайд 846.5.8. Интерполяция кривой Безье
Пьер Безье – французский инженер компании Рено, разработчик
Поль де Фаже де Кастельжо – французский математик и физик, автор рекурсивного способа построения кривых Безье
Слайд 856.5.8. Интерполяция кривой Безье
Кривая Безье – это параметрическая кривая, задаваемая выражением
–
– базисные функции кривой Безье.


![Схема Горнера Фрагмент программы на языке Сиp=c[n];for(i=n-1; i>=0; i--) p=c[i]+p*x; Количество](/img/tmb/5/434461/fcbd6c8672c66566c36ed4c182d22a75-800x.jpg)




















![Сплайном называется функция, определенная на отрезке [a; b], совпадающая на частичных отрезках [xi; xi+1] с](/img/tmb/5/434461/d2a6186820933fcf5c7120db9daf6a30-800x.jpg)













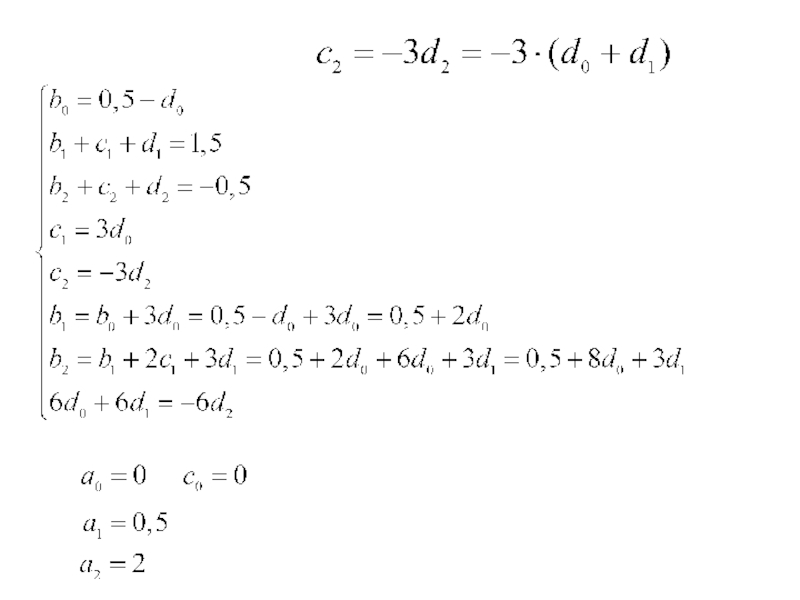
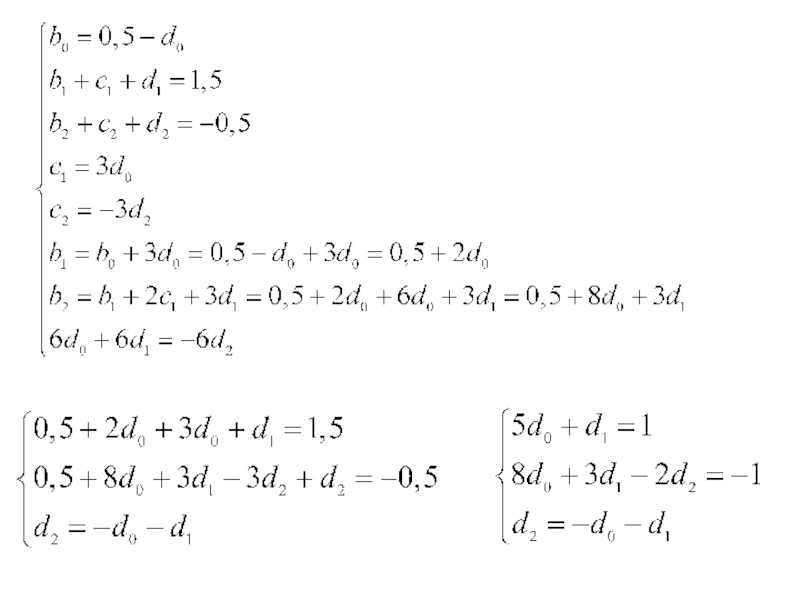
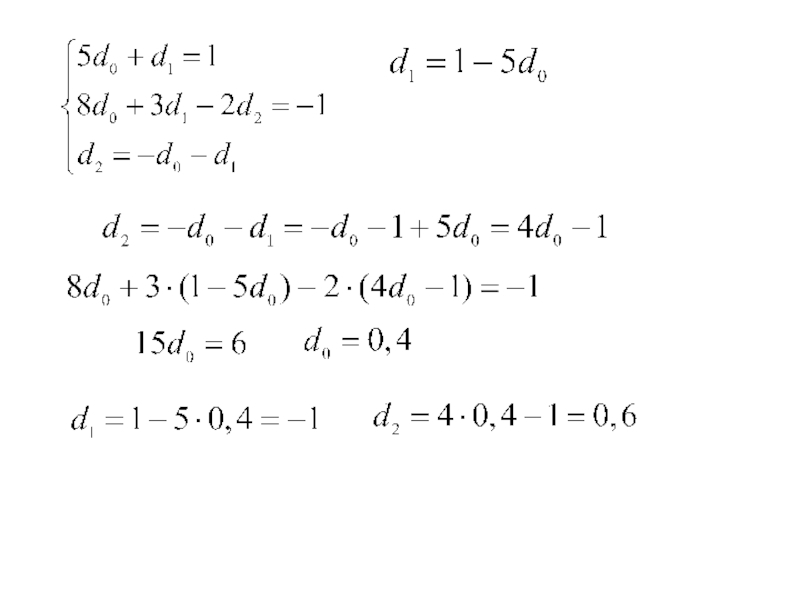
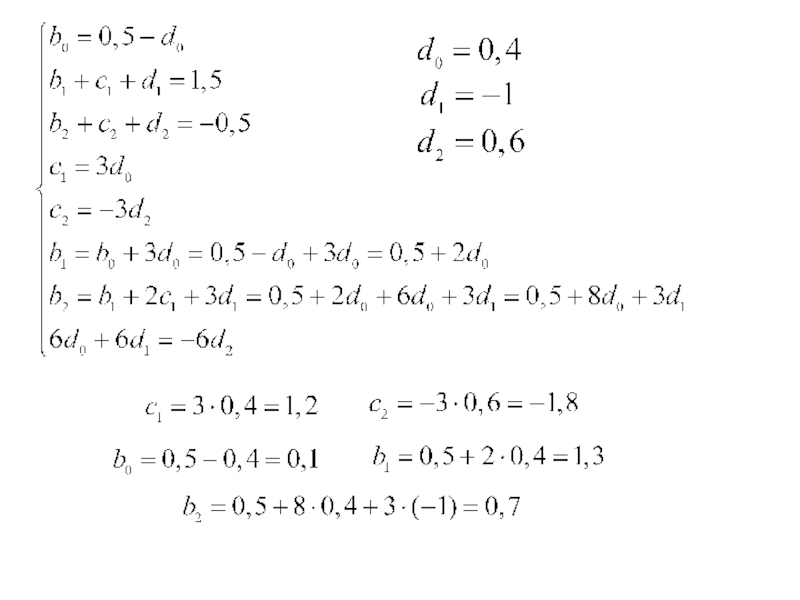












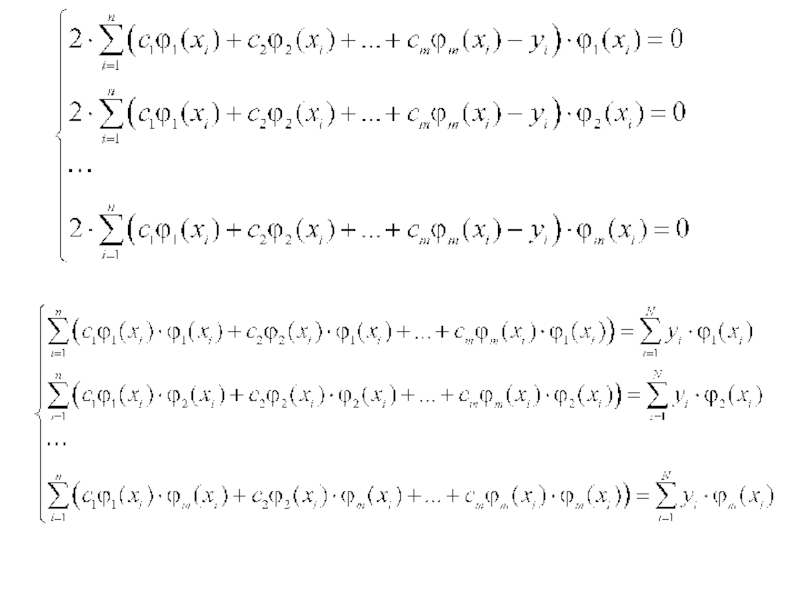
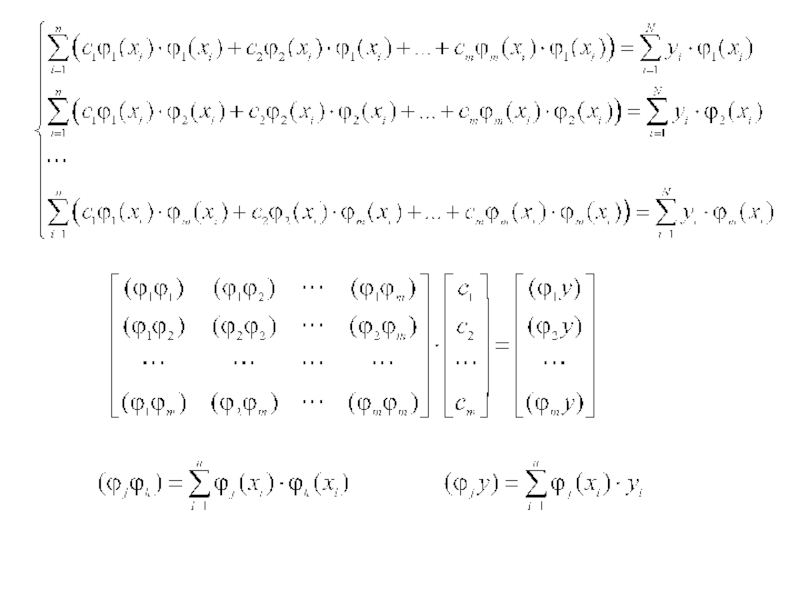









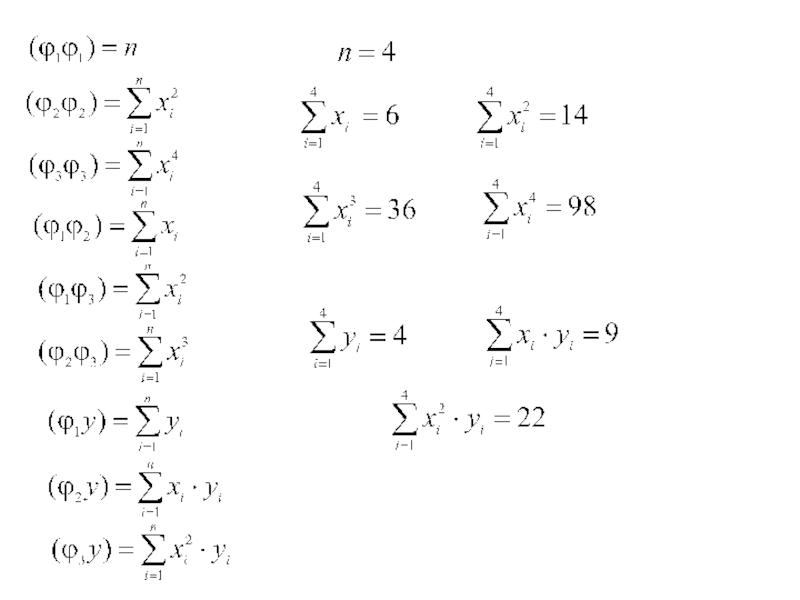




![Пример. Аппроксимировать функцию y=5·x на интервале [–π; π] тригонометрическими полиномами порядка 1, 2 и 3.](/img/tmb/5/434461/e0bb62405153fa3236e143b4affdde9e-800x.jpg)
![Пример. Аппроксимировать функцию y=5·x на интервале [–π; π] тригонометрическими полиномами порядка 1, 2 и 3.](/img/tmb/5/434461/685267ebe7dd374e07262dbec1d9a0e6-800x.jpg)