- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Calculus++. Find the radius of convergence for 3n презентация
Содержание
- 1. Calculus++. Find the radius of convergence for 3n
- 2. Question 3. Find the radius of convergence
- 3. Answers to Questions from Light #8:
- 4. Calculus++ Infinite Series
- 5. Picture of the Week Snowflake Curve We
- 6. The number of sides: n0 = 3
- 7. The number of sides: n1 = 4n0.
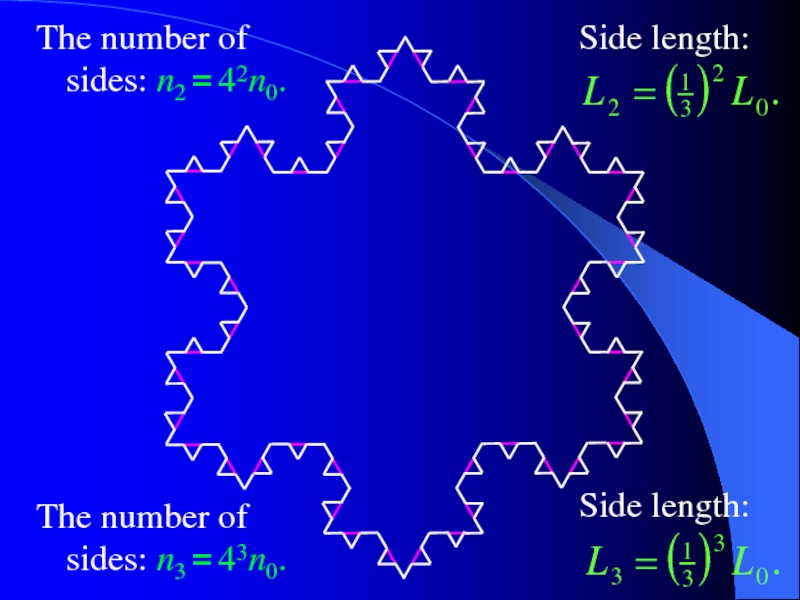
- 8. The number of sides: n2 = 42n0.
- 9. Total Perimeter after n steps Total Area after n steps as
- 10. Question 1 (December 2011 Exam, Q9). Determine
- 11. Let’s try x = 2 now. For we obtain Diverges. Limit comparison test: Converges
- 12. The limit comparison test. are series with
- 13. Question 2. Which of the following series
- 14. a. I only b. II only c. III only
- 15. a. I only b. II only c. III only
- 16. For any series with positive and negative
- 17. If the series of absolute value converges,
- 18. Example. The series of absolute values
- 19. A test for convergence of alternating series
- 20. Question 3. Which of the following series
- 21. a. I only b. II only c. III only
- 22. For series II: Let’s compare |an| with
- 23. To show that series II converges we
- 24. 3) The sequence The function correct
Слайд 3 Answers to Questions from Light #8:
Infinite Series II
Question 1:
Question 4:
S1
b) III only
S2 and S3 are divergent
Question 2:
Слайд 5Picture of the Week
Snowflake Curve
We construct a snowflake curve step by
At each step we count:
a) the number of straight-line segments in the curve,
b) the total length of all segments (perimeter of the curve),
c) the total area bounded by the curve.
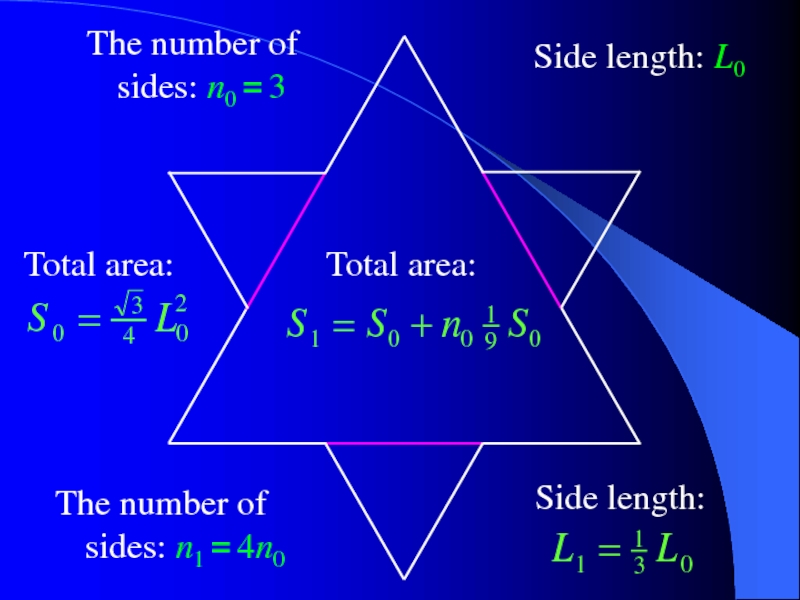
Слайд 6The number of sides: n0 = 3
Side length: L0
The number of
Side length:
Total area:
Total area:
Слайд 7The number of sides: n1 = 4n0.
Side length:
The number of sides:
Side length:
Total area:
Слайд 10Question 1 (December 2011 Exam, Q9).
Determine the convergence set for the
Solution: Let’s try your favourite values
and
For
we have
Converges.
Слайд 12The limit comparison test.
are series with positive terms.
number, then
Suppose that
and
where c is a finite positive
If
converges and c = 0, then
If
converges as well.
diverges and
If
then
diverges as well.
Слайд 13Question 2. Which of the following series are convergent?
a. I
d. I and II only e. II and III only
Solution: For series III
Consider
Then
Since
diverges, series III diverges as well.
Слайд 14a. I only b. II only c. III only
d. I and II only e.
Since the series
converges as well.
For series II
Consider
Then
the series
converges,
Слайд 15a. I only b. II only c. III only
d. I and II only e.
Since the geometric series
converges as well.
For series I
Consider
Then
the series
converges
Слайд 16For any series with positive and
negative terms we can obtain a
For example, for the series and
the series of absolute values are
series by taking absolute values:
given by and
Слайд 17If the series of absolute value converges, then
Using the Cauchy criterion
we say that the series converges absolutely.
series converges, then the series
converges as well.
Слайд 18Example.
The series of absolute values
converges absolutely.
converges.
Therefore the series
If
converges,
then we say that the series
converges conditionally.
diverges,
Слайд 19A test for convergence of alternating series
2) the sequence
then the series
converges.
is
If
where
Слайд 20Question 3. Which of the following series is conditionally convergent?
a.
d. II and III only e. I and III only
Solution: For series I:
and the sequence an does not converge to 0.
Thus, the necessary condition of convergence is not satisfied. Hence, series I diverges.
Слайд 21a. I only b. II only c. III only
d. II and III only e.
For series III:
Let’s compare |an| with
Hence, series III converges absolutely.
and
The series
converges.
Слайд 22For series II:
Let’s compare |an| with
Hence, the series
and
The series
diverges.
diverges as
Слайд 23To show that series II converges we have to show that:
3)
Consider the function
correct
is non-increasing, for n = 1,2,3…
Solutions:
for
Слайд 243) The sequence
The function
correct
is non-increasing, for n = 1,2,3…
decreases on
Hence, the sequence
decreases for n = 1,2,3…
Thus, the series
converges conditionally.