- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Асимметричные криптосистемы. Криптосистема шифрования данных RSA презентация
Содержание
- 1. Асимметричные криптосистемы. Криптосистема шифрования данных RSA
- 2. Ассиметричные криптосистемы Эффективными системами криптографической
- 3. Ассиметричные криптосистемы Первый
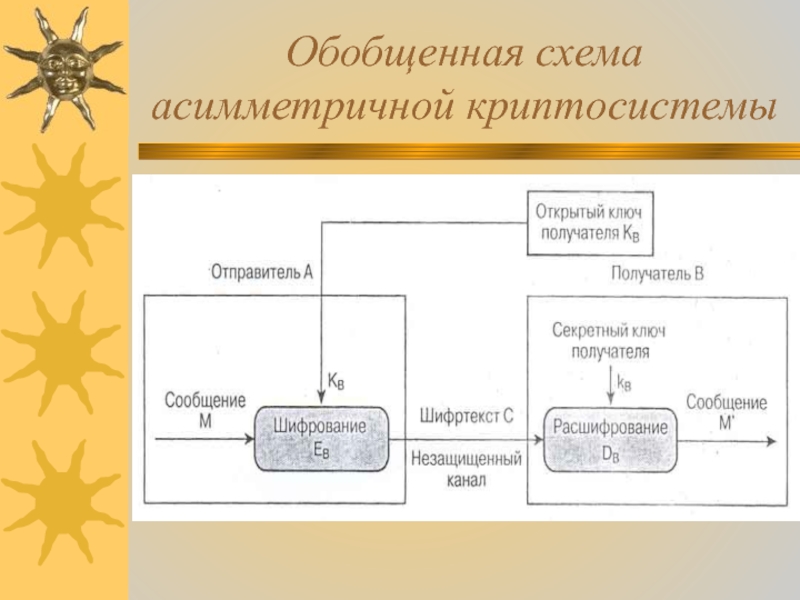
- 4. Обобщенная схема асимметричной криптосистемы
- 5. В этой
- 6. Алгоритм RSA Под простым
- 7. Алгоритм RSA Чтобы использовать алгоритм RSA
- 8. Алгоритм RSA Далее, чтобы зашифровать
- 9. Алгоритм RSA Чтобы расшифровать
- 10. Пример использования метода RSA Приведем простой
- 11. Пример использования метода RSA 5.Представим шифруемое
- 12. Пример использования метода RSA Попытаемся расшифровать
- 13. СПАСИБО ЗА ВНИМАНИЕ!
Слайд 2Ассиметричные криптосистемы
Эффективными системами криптографической защиты данных являются асимметричные криптосистемы,
называемые также криптосистемами с открытым ключом. В таких системах для зашифрования данных используется один ключ, а для расшифрования - другой ключ (отсюда и название асимметричные).
Слайд 3Ассиметричные
криптосистемы
Первый ключ является открытым и может быть
опубликован для использования всеми пользователями системы, которые зашифровывают данные. Расшифрование данных с помощью открытого ключа невозможно. Для расшифрования данных получатель зашифрованной информации
использует второй ключ, который является секретным. Разумеется, ключ расшифрования не может быть определен из ключа зашифрования.
использует второй ключ, который является секретным. Разумеется, ключ расшифрования не может быть определен из ключа зашифрования.
Слайд 5
В этой асимметричной криптосистеме применяют два
различных ключа:
- Кв - открытый
ключ отправителя А;
- кв - секретный ключ получателя В.
Генератор ключей целесообразно располагать на стороне получателя В (чтобы не пересылать секретный ключ кв по незащищенному каналу). Значения ключей Кв и кв зависят от начального состояния генератора ключей. Раскрытие секретного ключа кв по известному открытому ключу Кв должно быть вычислительно неразрешимой задачей.
- кв - секретный ключ получателя В.
Генератор ключей целесообразно располагать на стороне получателя В (чтобы не пересылать секретный ключ кв по незащищенному каналу). Значения ключей Кв и кв зависят от начального состояния генератора ключей. Раскрытие секретного ключа кв по известному открытому ключу Кв должно быть вычислительно неразрешимой задачей.
Слайд 6Алгоритм RSA
Под простым числом понимают такое число, которое
делится только на 1 и на само себя. Взаимно простыми числами называют такие числа, которые не имеют ни одного общего делителя, кроме 1. Под результатом операции I mod понимают остаток от целочисленного деления i на j.
Слайд 7Алгоритм RSA
Чтобы использовать алгоритм RSA ,надо сначала сгенерировать открытый и секретный
ключи, выполнив следующие шаги.
1.Выбрать два очень больших простых числа p и q.
2.Определить n как результат умножения p на q(n=pq).
3.Выбрать большое случайное число d. Оно должно быть взаимно простым с результатом умножения m=(p-1)(q-1).
4.Определить такое число e, для которого является истинным следующее соотношение:
e d (mod m)=1
5.Назвать открытым ключом числа e и n ,а секретным ключом –числа d и n
1.Выбрать два очень больших простых числа p и q.
2.Определить n как результат умножения p на q(n=pq).
3.Выбрать большое случайное число d. Оно должно быть взаимно простым с результатом умножения m=(p-1)(q-1).
4.Определить такое число e, для которого является истинным следующее соотношение:
e d (mod m)=1
5.Назвать открытым ключом числа e и n ,а секретным ключом –числа d и n
Слайд 8Алгоритм RSA
Далее, чтобы зашифровать данные по известному ключу {e,n},
необходимо разбить шифруемый текст на блоки, каждый из которых может быть представлен в виде числа M(i)=0,1,…,n-1;зашифровать текст, рассматриваемый как последовательность чисел M(i) по формуле
Слайд 9Алгоритм RSA
Чтобы расшифровать эти данные, используя секретный ключ{d,n},
необходимо выполнить следующие вычисления:
В результате будет получено множество чисел M(i), которое представляет собой исходный текст.
В результате будет получено множество чисел M(i), которое представляет собой исходный текст.
Слайд 10Пример использования метода RSA
Приведем простой пример использования метода RSA для
шифрования сообщения “ЕДА”. Для простоты будем использовать очень маленькие числа(на практике используются намного большие числа).
1.Выберем p = 3 и q=11.
2.Определим n =3*11=33.
3.Найдем (p-1)(q-1)=20. Следовательно , в качестве d выберем любое число , которое является взаимно простым с 20, например d = 3.
4.Выберем число e. В качестве такого числа может быть взято любое число , для которого удовлетворяется соотношение e*3mod(20)=1,например e = 7.
1.Выберем p = 3 и q=11.
2.Определим n =3*11=33.
3.Найдем (p-1)(q-1)=20. Следовательно , в качестве d выберем любое число , которое является взаимно простым с 20, например d = 3.
4.Выберем число e. В качестве такого числа может быть взято любое число , для которого удовлетворяется соотношение e*3mod(20)=1,например e = 7.
Слайд 11Пример использования метода RSA
5.Представим шифруемое сообщение как последовательность целых чисел
в диапазоне 0…32. Пусть буква Е изображается числом 6, буква Д – числом 5, а буква А – числом 1. Тогда сообщение можно представить в виде последовательности чисел 651. Зашифруем сообщение , используя ключ{7,33}:
Слайд 12Пример использования метода RSA
Попытаемся расшифровать сообщение{30,14,1} , полученное в результате
зашифрования по известному ключу, на основе секретного ключа {3,33}:
Таким образом , в результате расшифрования сообщения получено исходное сообщение “ЕДА”.
Таким образом , в результате расшифрования сообщения получено исходное сообщение “ЕДА”.