- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Аналіз вимірювання ПЗ. Регресійний аналіз. (Лекція 11) презентация
Содержание
- 1. Аналіз вимірювання ПЗ. Регресійний аналіз. (Лекція 11)
- 2. Лінійний та нелінійний регресійний аналіз. Побудова лінії регресії. Багатомірний регресійний аналіз.
- 3. Регресійний аналіз Найпростішою формою оцінки стохастичного зв'язку
- 4. Регресія Регресією називають таку криву, вздовж якої
- 5. Відтворення функції регресії ідентифікації вигляду регресійної залежності;
- 6. Початкові умови регресійного аналізу Сумісний розподіл випадкових
- 7. Ідентифікація регресії Метою процедури ідентифікації вигляду регресії
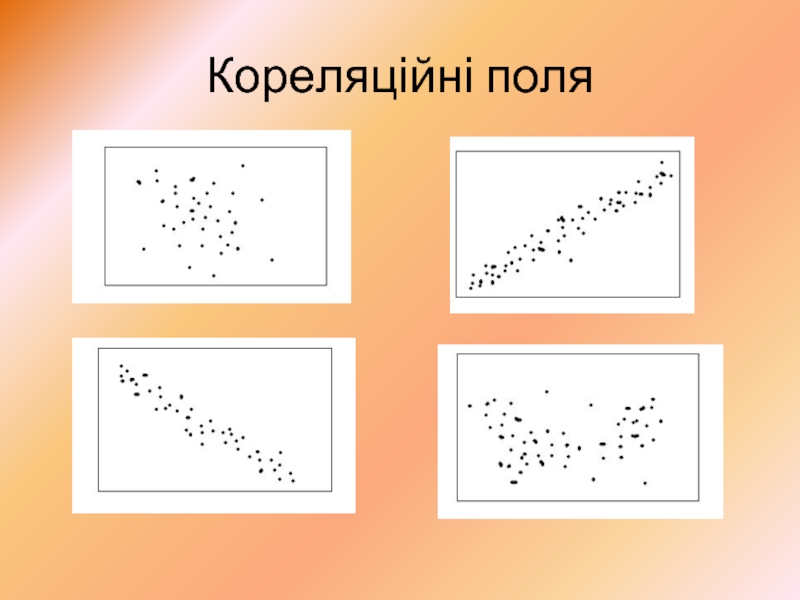
- 8. Кореляційні поля
- 9. Лінійний регресійний аналіз Лінійний зв’язок визначається
- 10. Довірче оцінювання емпіричної лінії регресії 1.
- 11. Нелінійний регресійний аналіз У процесі ідентифікації кореляційного
- 12. Метод найменших квадратів Використовується для відтворення параболічної
- 13. Метод найменших квадратів Після розв’язку системи отримуємо
- 14. Ортогональні поліноми Чебишева Найпростіша обчислювальна схема відтворення
- 15. Ортогональні поліноми Чебишева Підвищуючи ступінь полінома, для
- 16. Зведення нелінійний залежностей до лінійних Умовно всі
- 17. Зведення нелінійний залежностей до лінійних До третьої
- 18. Підбір оптимальної лінії регресії Задача в загальному
- 19. Множинний аналіз Множинна кореляція Множинний регресійний аналіз
- 20. Множинна кореляція Множинний коефіцієнт кореляції
- 21. Множинна кореляція У випадку, коли
- 22. Багатовимірний регресійний аналіз Багатовимірний статистичний аналіз визначає
- 23. Багатовимірний регресійний аналіз Задачею регресійного аналізу є
- 24. Висновки Задачею регресійного аналізу є виявлення виду закономірностей у залежностях між метриками програмного забезпечення
Слайд 2
Лінійний та нелінійний регресійний аналіз.
Побудова лінії регресії.
Багатомірний регресійний аналіз.
Слайд 3Регресійний аналіз
Найпростішою формою оцінки стохастичного зв'язку є одновимірний регресійний аналіз, за
яким формуються обчислювальні процедури відтворення лінії регресії.
Припускається, що дві нормально розподілені випадкові величини η та ξ пов'язані між собою лінійною регресійною залежністю
де ε - похибка, яка має нормальний розподіл
Припускається, що дві нормально розподілені випадкові величини η та ξ пов'язані між собою лінійною регресійною залежністю
де ε - похибка, яка має нормальний розподіл
Слайд 4Регресія
Регресією називають таку криву, вздовж якої розсіювання результатів спостереження мінімальне.
Лінійну регресію
визначають записом у формі
Слайд 5Відтворення функції регресії
ідентифікації вигляду регресійної залежності;
вибору типу функції регресії ;
оцінювання
нелінійних регресійних залежностей, якщо вони мають місце;
оцінювання точності оцінок параметрів ;
перевірки адекватності відтворення регресійної залежності.
оцінювання точності оцінок параметрів ;
перевірки адекватності відтворення регресійної залежності.
Слайд 6Початкові умови регресійного аналізу
Сумісний розподіл випадкових величин η, ξ має бути
нормальним.
Дисперсія залежної змінної у залишається постійною при зміні значення аргументу х, отже,
Підсумки спостережень xі, yі — стохастично незалежні, отже, результати, одержані на і -му кроці експерименту, не пов’язані з попереднім (і - 1) -м кроком і не містять інформації для (і + 1) - го кроку.
Якщо обсяг вибірок досить великий, припускається порушення першої умови.
Дисперсія залежної змінної у залишається постійною при зміні значення аргументу х, отже,
Підсумки спостережень xі, yі — стохастично незалежні, отже, результати, одержані на і -му кроці експерименту, не пов’язані з попереднім (і - 1) -м кроком і не містять інформації для (і + 1) - го кроку.
Якщо обсяг вибірок досить великий, припускається порушення першої умови.
Слайд 7Ідентифікація регресії
Метою процедури ідентифікації вигляду регресії є:
виявлення наявності зв'язку між X
та Y;
якщо зв'язок виявлено, проведення класифікації на лінійність або нелінійність як відносно змінних X та Y, так і відносно вектора параметрів .
Процедура ідентифікації зумовлює реалізацію як візуальної схеми, так і кількісної оцінки зв'язку. При візуалізації оцінюються початкові масиви, які відображаються на у вигляді кореляційного поля.
якщо зв'язок виявлено, проведення класифікації на лінійність або нелінійність як відносно змінних X та Y, так і відносно вектора параметрів .
Процедура ідентифікації зумовлює реалізацію як візуальної схеми, так і кількісної оцінки зв'язку. При візуалізації оцінюються початкові масиви, які відображаються на у вигляді кореляційного поля.
Слайд 10Довірче оцінювання емпіричної лінії регресії
1. Обчислення коефіцієнта детермінації R2.
2.
Побудова довірчого інтервалу для лінії регресії (x)=a+b(x- ) з урахуванням її оцінки .
3. Оцінка відхилень окремих значень = залежної змінної від емпіричної регресії .
4. Дослідження значущості і точності оцінок параметрів , .
3. Оцінка відхилень окремих значень = залежної змінної від емпіричної регресії .
4. Дослідження значущості і точності оцінок параметрів , .
Слайд 11Нелінійний регресійний аналіз
У процесі ідентифікації кореляційного поля виявляється, що у багатьох
випадках треба відтворювати нелінійну регресійну залежність. При цьому підбір кривої може бути здійснено на підставі:
поліноміальної регресії другого
або більш високого порядку
, k ≥ 3;
нелінійних залежностей як відносно параметрів, так і відноcно аргументів лінії регресії.
поліноміальної регресії другого
або більш високого порядку
, k ≥ 3;
нелінійних залежностей як відносно параметрів, так і відноcно аргументів лінії регресії.
Слайд 12Метод найменших квадратів
Використовується для відтворення параболічної регресії
Де
МНК:
, де і отримують з
Слайд 14Ортогональні поліноми Чебишева
Найпростіша обчислювальна схема відтворення поліноми регресії основана на ортогональних
поліномах Чебишева
З умови
знаходять оцінки параметрів:
З умови
знаходять оцінки параметрів:
Слайд 15Ортогональні поліноми Чебишева
Підвищуючи ступінь полінома, для кожної приєднаної функції φк(х) обчислюють
коефіцієнт регресії, зберігаючи одержані раніше параметри.
Оцінку якості відхилення емпіричної регресії (х) від теоретичної оцінюють на підставі статистичної характеристики
чим вище порядок регресійної кривої, тим більшим є розбіг довірчих меж при віддаленні від середнього
Оцінку якості відхилення емпіричної регресії (х) від теоретичної оцінюють на підставі статистичної характеристики
чим вище порядок регресійної кривої, тим більшим є розбіг довірчих меж при віддаленні від середнього
Слайд 16Зведення нелінійний залежностей до лінійних
Умовно всі квазілінійні регресійні залежності поділено на
чотири групи:
До першої групи віднесені залежності з двома невідомими параметрами, які приводяться до лінійного вигляду після відповідного перетворення координат без додаткових обчислень.
До другої групи віднесено залежності з трьома невідомими параметрами. Параметр у них визначається за формулою
До першої групи віднесені залежності з двома невідомими параметрами, які приводяться до лінійного вигляду після відповідного перетворення координат без додаткових обчислень.
До другої групи віднесено залежності з трьома невідомими параметрами. Параметр у них визначається за формулою
Слайд 17Зведення нелінійний залежностей до лінійних
До третьої групи віднесені теоретичні залежності, які
після першого перетворення координат приводяться до вигляду параболічної регресії. Тоді параметри визначаються за вищенаведеними процедурами.
До четвертої групи відносяться теоретичні залежності, які після перетворення приводяться до лінійного рівняння з трьома невідомими параметрами.
Подальший аналіз проводять для перетвореної в лінійну форму залежності, після чого, при необхідності, виконують зворотне перетворення.
До четвертої групи відносяться теоретичні залежності, які після перетворення приводяться до лінійного рівняння з трьома невідомими параметрами.
Подальший аналіз проводять для перетвореної в лінійну форму залежності, після чого, при необхідності, виконують зворотне перетворення.
Слайд 18Підбір оптимальної лінії регресії
Задача в загальному випадку зводиться до побудови декількох
ліній регресії та порівнянні оптимальних значень регресій з фактичними.
Вибирається лінія регресії, у якої відхилення фактичних значень найменше
Вибирається лінія регресії, у якої відхилення фактичних значень найменше
Слайд 20Множинна кореляція
Множинний коефіцієнт кореляції
є мірою лінійної залежності між змінною Xi та набором Х1, ..., Xi-1, Хі+1, ..., Хk, причому
0 < < 1
Якщо = 0,
то говорять про відсутність залежності Хі від інших змінних з множини X.
0 < < 1
Якщо = 0,
то говорять про відсутність залежності Хі від інших змінних з множини X.
Слайд 21Множинна кореляція
У випадку, коли
= 1
має місце лінійна залежність, при якій змінна Xt визначається лінійною комбінацією змінних Х1, ..., Xi-1, Хі+1, ..., Хk:
Xi = β0 + β1 X1 + βi-1 Xi-1 + βi+1 Xi+1 + ...+ βk Xk.
Квадрат коефіцієнта множинної кореляції оцінює частку дисперсії Xі, яка пояснюється лінійною регресією Х1, ..., Xi-1, Хі+1, ..., Хk.
має місце лінійна залежність, при якій змінна Xt визначається лінійною комбінацією змінних Х1, ..., Xi-1, Хі+1, ..., Хk:
Xi = β0 + β1 X1 + βi-1 Xi-1 + βi+1 Xi+1 + ...+ βk Xk.
Квадрат коефіцієнта множинної кореляції оцінює частку дисперсії Xі, яка пояснюється лінійною регресією Х1, ..., Xi-1, Хі+1, ..., Хk.
Слайд 22Багатовимірний регресійний аналіз
Багатовимірний статистичний аналіз визначає причинно-наслідкові зв’язки об’єкта дослідження і
його показників (вхідних та вихідних характеристик)
Слайд 23Багатовимірний регресійний аналіз
Задачею регресійного аналізу є дослідження зв’язку між залежними та
незалежними величинами
Для вирішення поставленої задачі початковий масив даних переформуються у матриці спостережень
Для вирішення поставленої задачі початковий масив даних переформуються у матриці спостережень
Слайд 24Висновки
Задачею регресійного аналізу є виявлення виду закономірностей у залежностях між метриками
програмного забезпечення