- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Алгоритм Евклида презентация
Содержание
- 1. Алгоритм Евклида
- 2. Алгоритм Евклида ЕВКЛИД - древнегреческий математик.
- 3. Постановка задачи: Требуется составить программу
- 5. Алгоритм нахождения НОД Разложить числа на простые множители. Найти общие множители. Найти их произведение.
- 6. Алгоритм Евклида Идея
- 7. Алгоритм Евклида Если числа равны, то взять
- 8. Блок-схема алгоритма Евклида Н А Ч
- 9. Структура алгоритма Евклида Н А Ч
- 10. Структура алгоритма Евклида Н А Ч
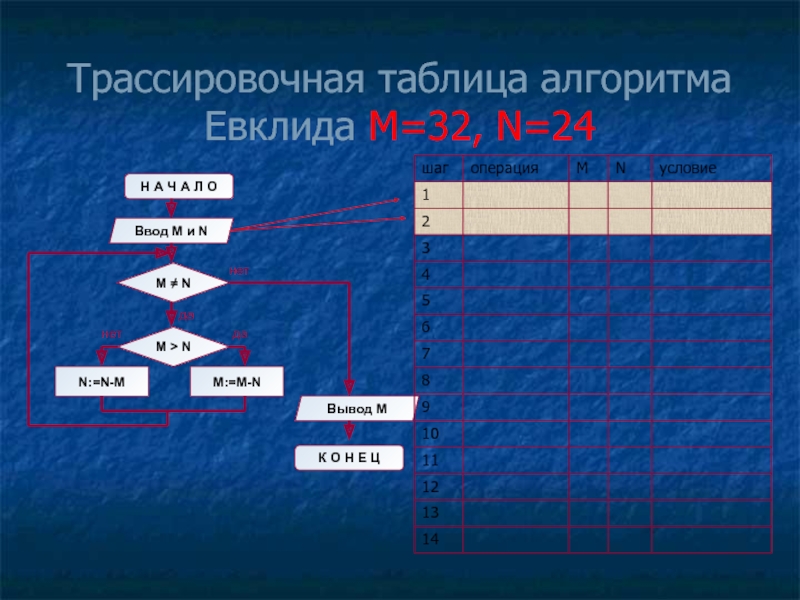
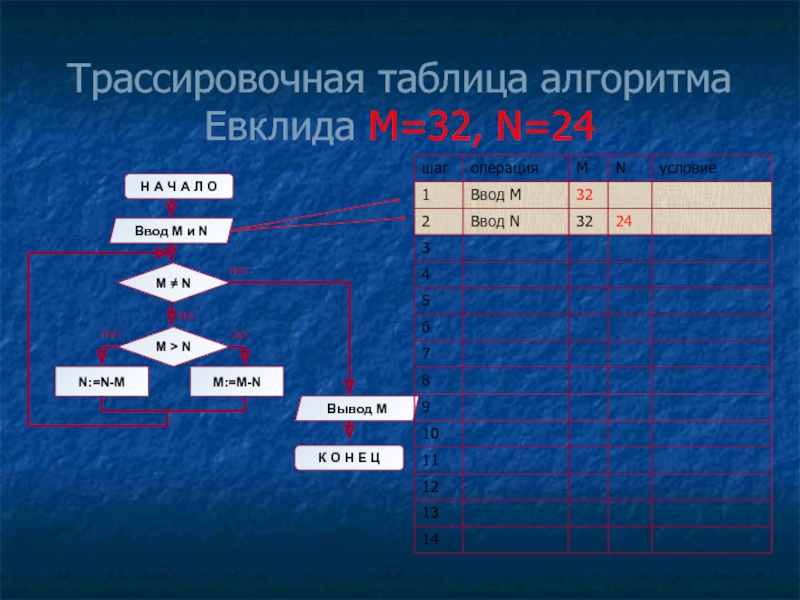
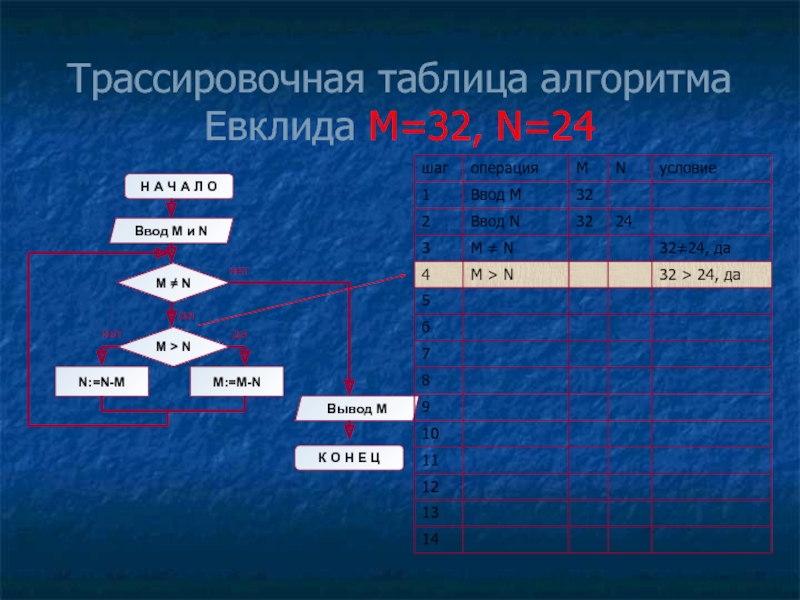
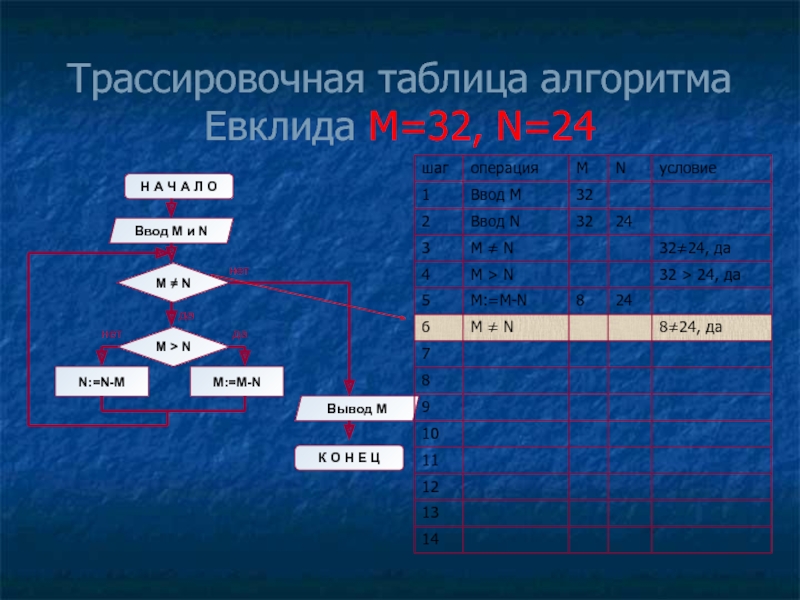
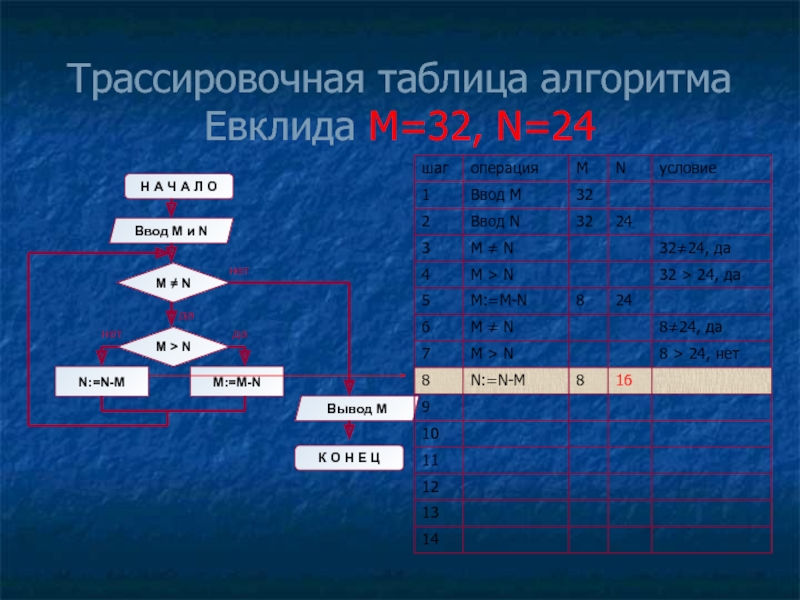
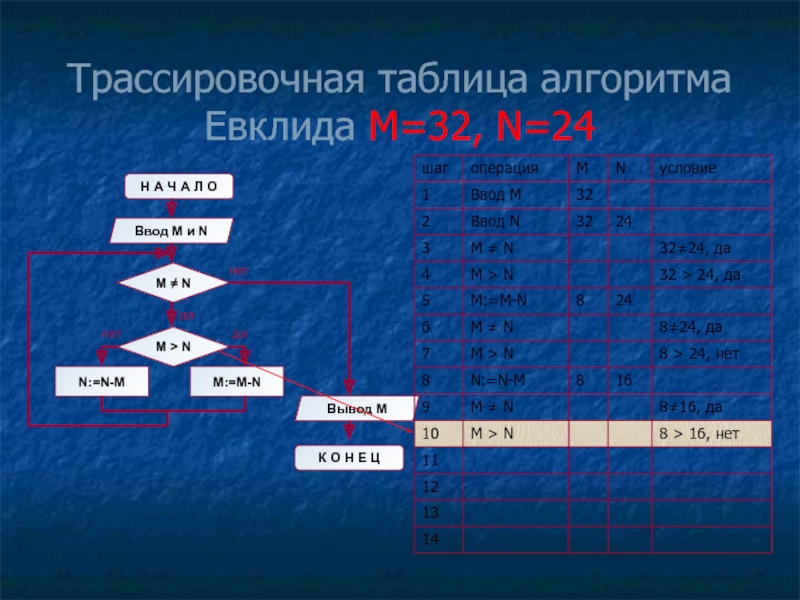
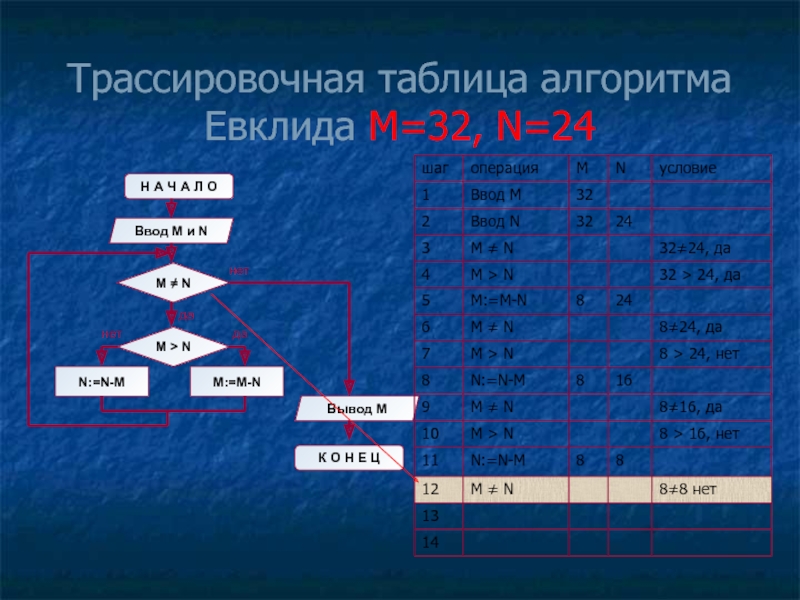
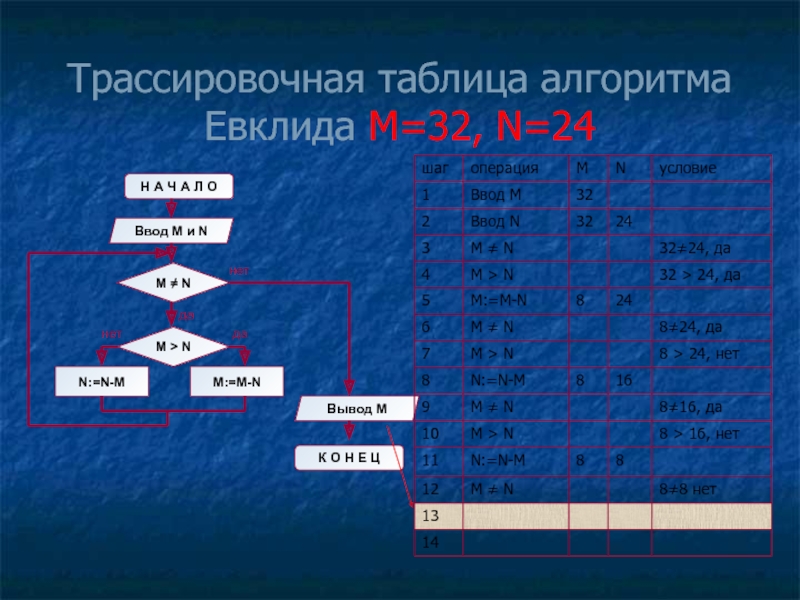
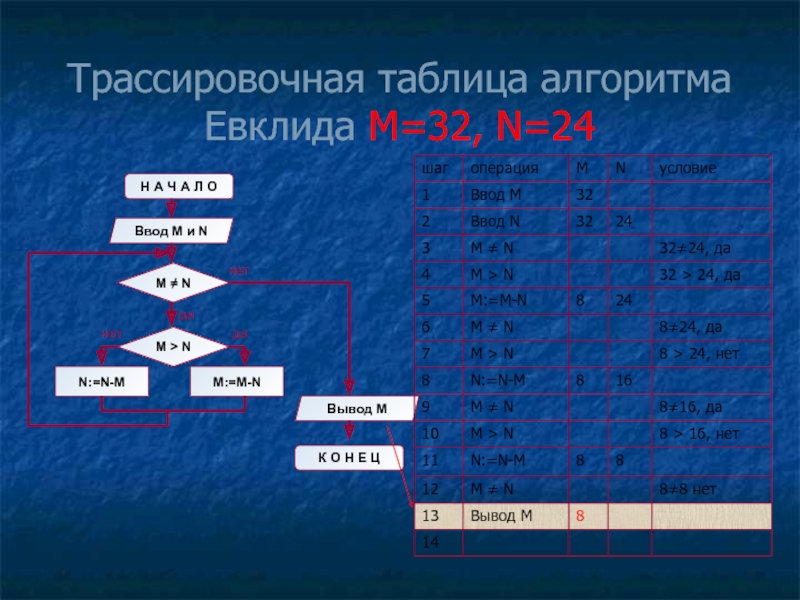
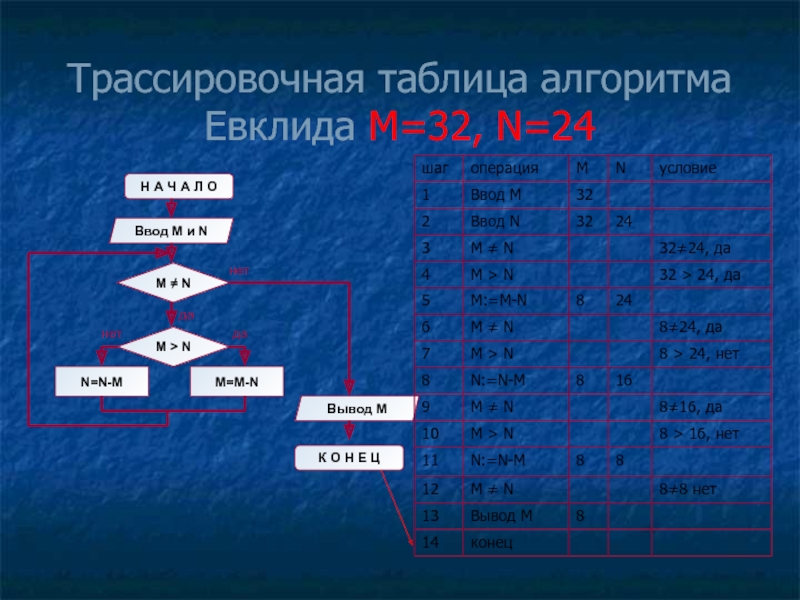
- 11. Трассировочная таблица алгоритма Евклида М=32, N=24
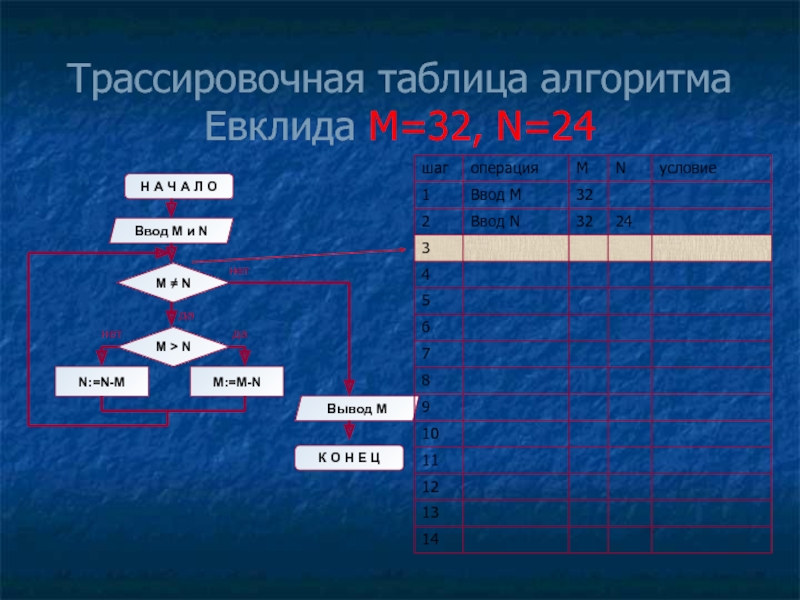
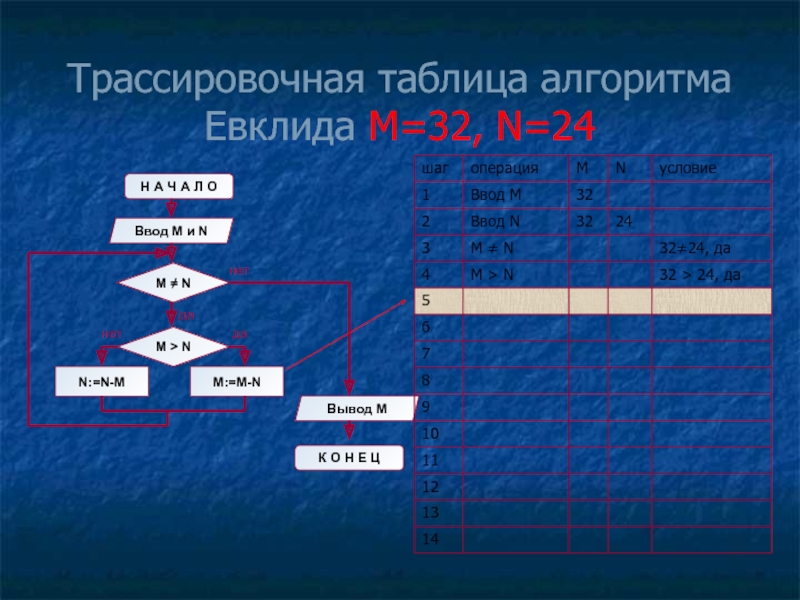
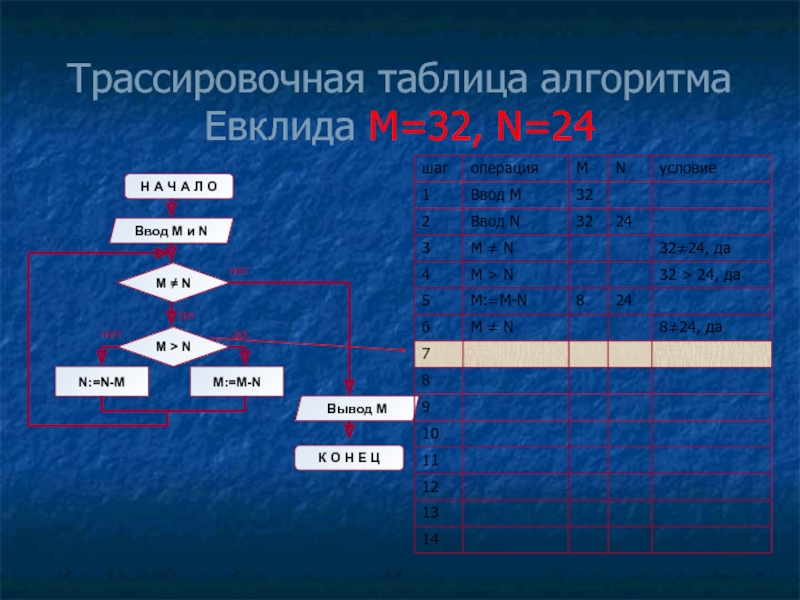
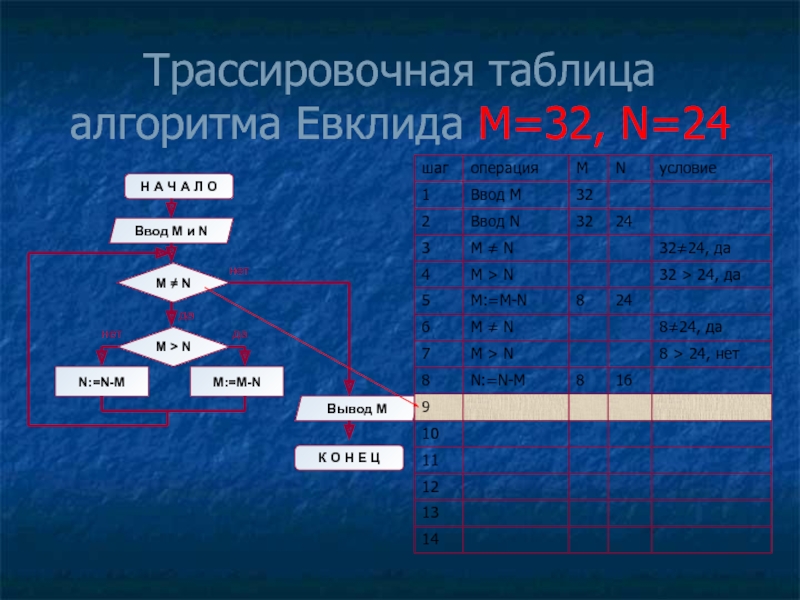
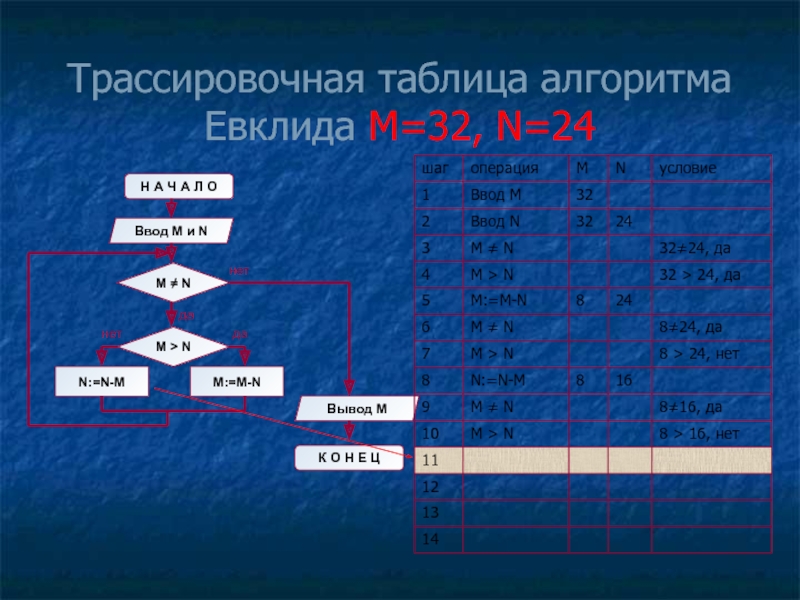
- 12. Трассировочная таблица алгоритма Евклида М=32, N=24
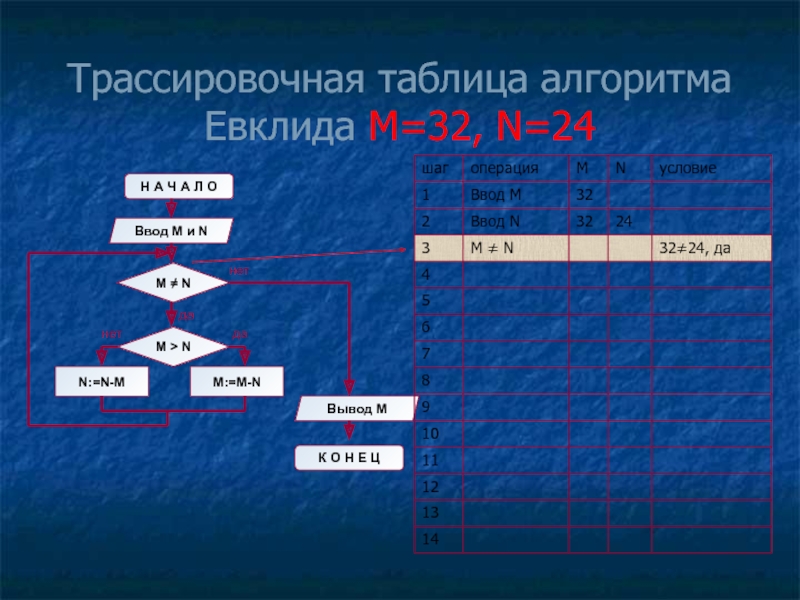
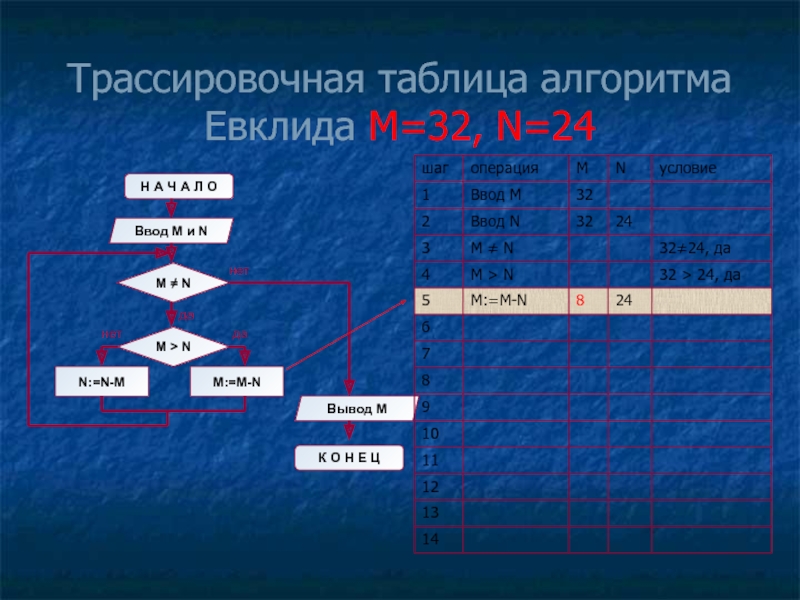
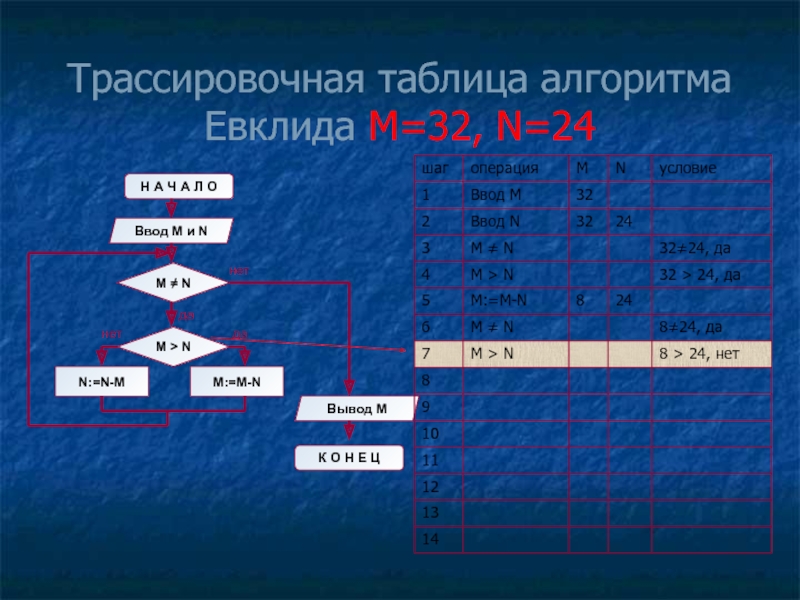
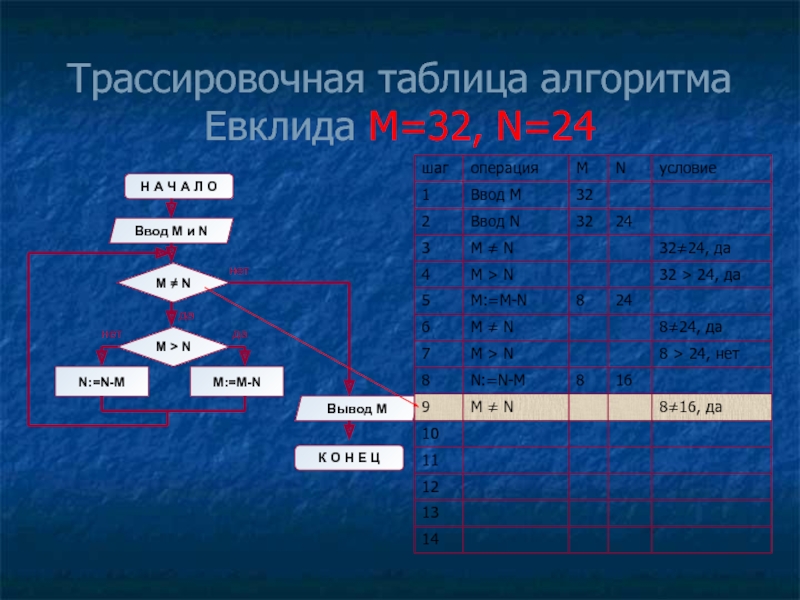
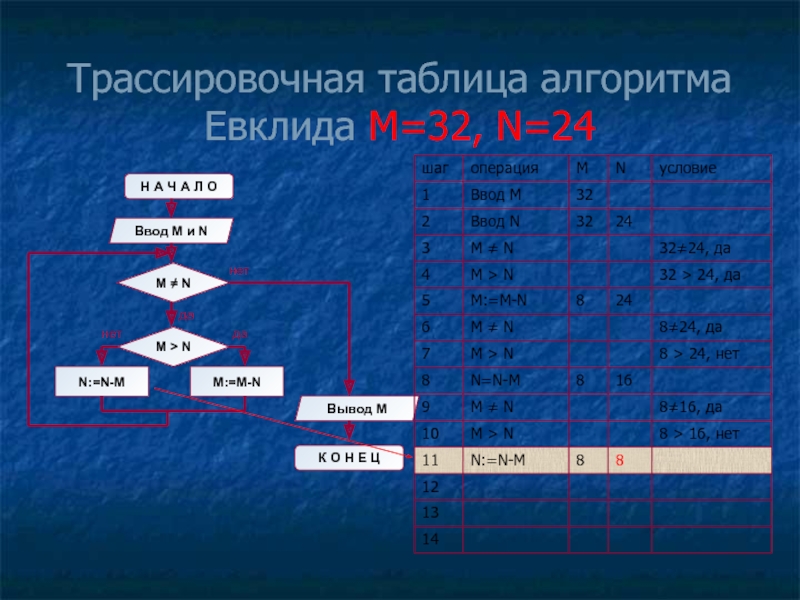
- 13. Трассировочная таблица алгоритма Евклида М=32, N=24
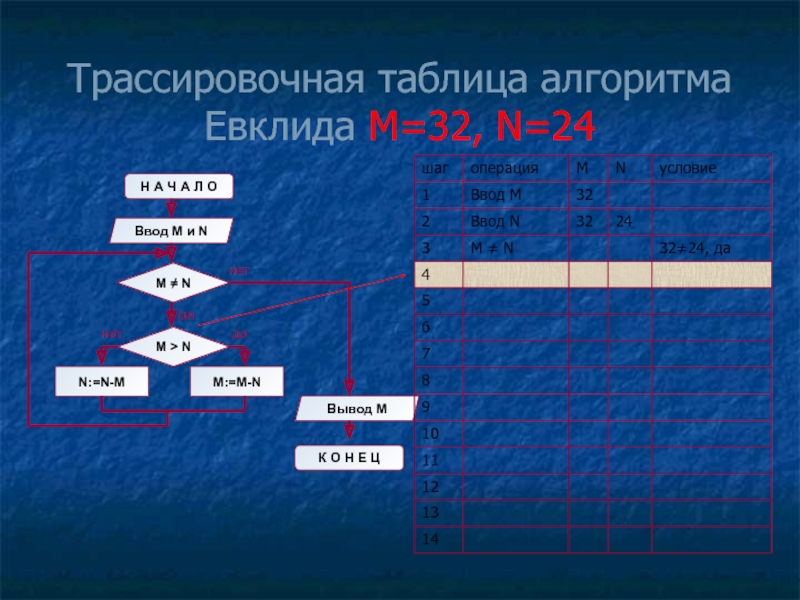
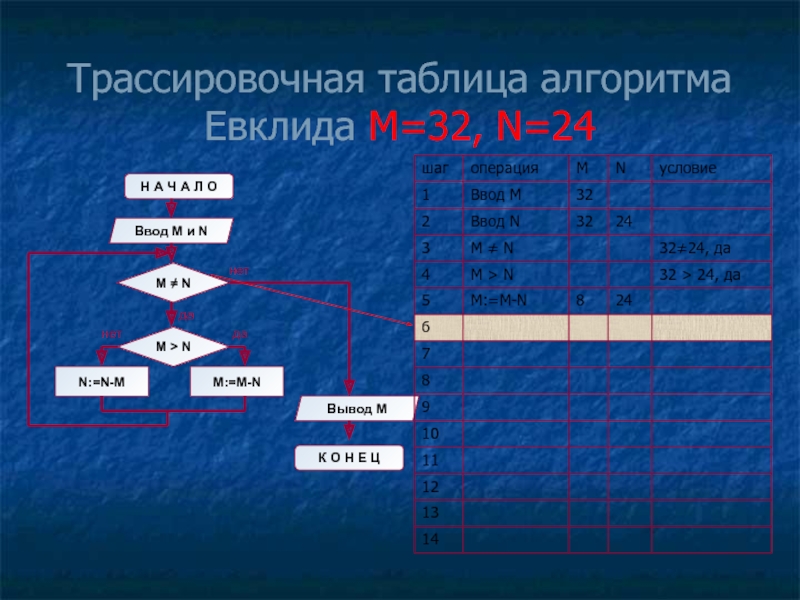
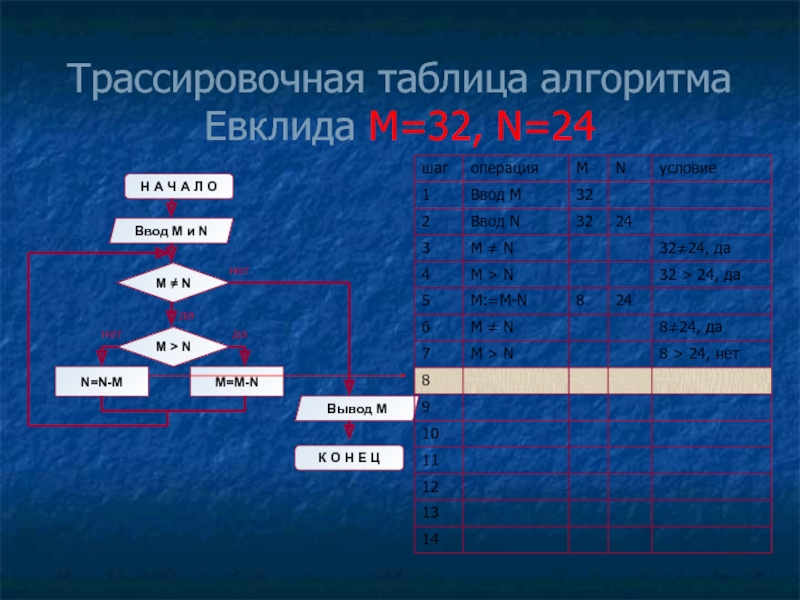
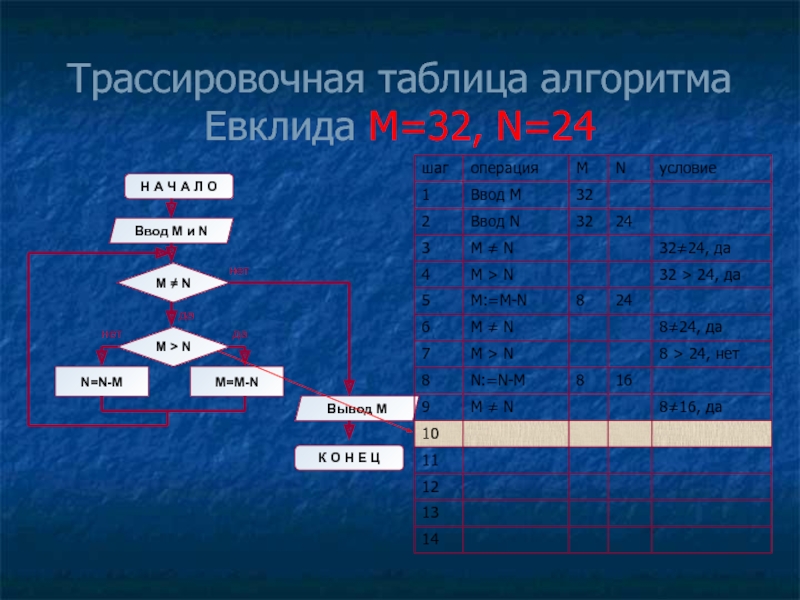
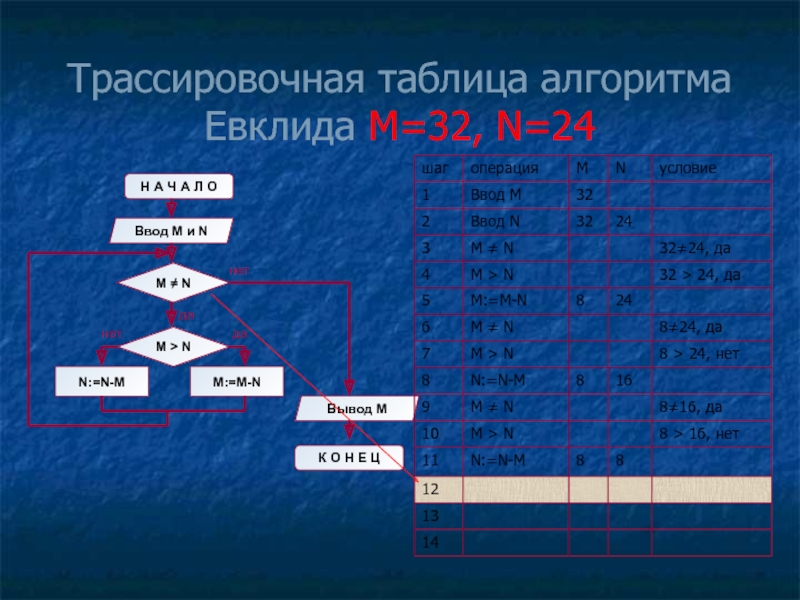
- 14. Трассировочная таблица алгоритма Евклида М=32, N=24
- 15. Трассировочная таблица алгоритма Евклида М=32, N=24
- 16. Трассировочная таблица алгоритма Евклида М=32, N=24
- 17. Трассировочная таблица алгоритма Евклида М=32, N=24
- 18. Трассировочная таблица алгоритма Евклида М=32, N=24
- 19. Трассировочная таблица алгоритма Евклида М=32, N=24
- 20. Трассировочная таблица алгоритма Евклида М=32, N=24
- 21. Трассировочная таблица алгоритма Евклида М=32, N=24
- 22. Трассировочная таблица алгоритма Евклида М=32, N=24
- 23. Трассировочная таблица алгоритма Евклида М=32, N=24
- 24. Трассировочная таблица алгоритма Евклида М=32, N=24
- 25. Трассировочная таблица алгоритма Евклида М=32, N=24
- 26. Трассировочная таблица алгоритма Евклида М=32, N=24
- 27. Трассировочная таблица алгоритма Евклида М=32, N=24
- 28. Трассировочная таблица алгоритма Евклида М=32, N=24
- 29. Трассировочная таблица алгоритма Евклида М=32, N=24
- 30. Трассировочная таблица алгоритма Евклида М=32, N=24
- 31. Трассировочная таблица алгоритма Евклида М=32, N=24
- 32. Трассировочная таблица алгоритма Евклида М=32, N=24
- 33. Трассировочная таблица алгоритма Евклида М=32, N=24
- 34. Трассировочная таблица алгоритма Евклида М=32, N=24
- 35. Трассировочная таблица алгоритма Евклида М=32, N=24
- 36. Блок-схема алгоритма Евклида Н А Ч
- 37. Программа на Паскале Program
- 38. Отладка и тестирование Выполнить
- 39. Постановка задачи: Составить программу нахождения
- 40. Н А Ч А Л О
- 41. Домашнее задание Составить программу нахождения
Алгоритм Евклида ЕВКЛИД - древнегреческий математик. Работал в Александрии в 3 в. до н. э. Евклид оказал огромное влияние на развитие математики. Главный труд - «Начала» (состоит из 15 книг)
Слайд 2Алгоритм Евклида
ЕВКЛИД - древнегреческий математик. Работал в Александрии в 3
в. до н. э. Евклид оказал огромное влияние на развитие математики. Главный труд - «Начала» (состоит из 15 книг) -содержит основы античной математики, элементарной геометрии, теории чисел, общей теории отношений и методы определения площадей и объемов. Евклиду принадлежат также работы по астрономии, оптике, теории музыки.
Слайд 3Постановка задачи:
Требуется составить программу определения наибольшего общего делителя (НОД)
двух натуральных чисел
НОД двух натуральных чисел - это самое большое натуральное число, на которое они делятся нацело
Например: НОД (12, 18) = 6
Слайд 5Алгоритм нахождения НОД
Разложить числа на простые множители.
Найти общие множители.
Найти их произведение.
Слайд 6Алгоритм Евклида
Идея алгоритма основана на двух свойствах:
1. Если M>N, то
НОД (M, N) = НОД (M-N, N)
2. НОД (M, M) = M
НОД (12, 18) = НОД (12, 18-12) = НОД (12, 6) =
= НОД (12-6, 6) = НОД (6, 6) = 6
НОД (M, N) = НОД (M-N, N)
2. НОД (M, M) = M
НОД (12, 18) = НОД (12, 18-12) = НОД (12, 6) =
= НОД (12-6, 6) = НОД (6, 6) = 6
Слайд 7Алгоритм Евклида
Если числа равны, то взять любое из них в качестве
ответа, в противном случае продолжить выполнение алгоритма.
Заменить большее число разностью большего и меньшего из чисел.
Вернуться к выполнению п. 1.
Заменить большее число разностью большего и меньшего из чисел.
Вернуться к выполнению п. 1.
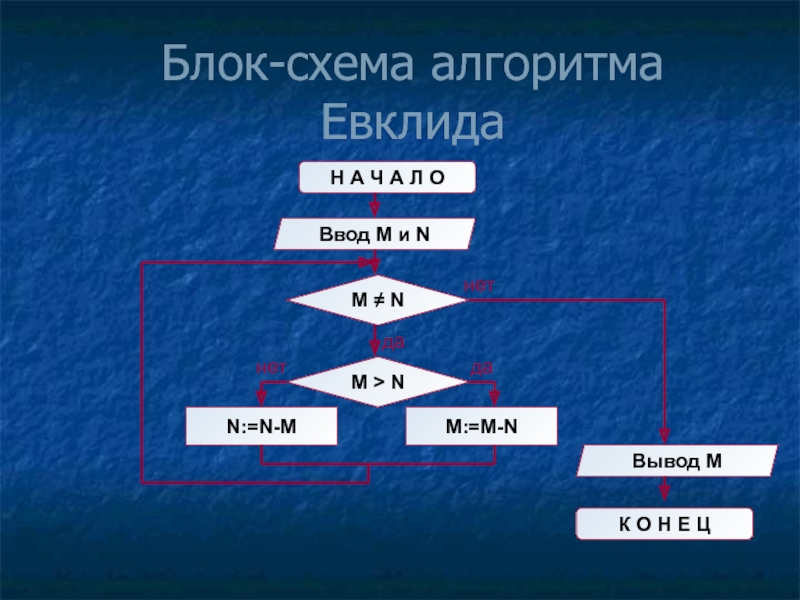
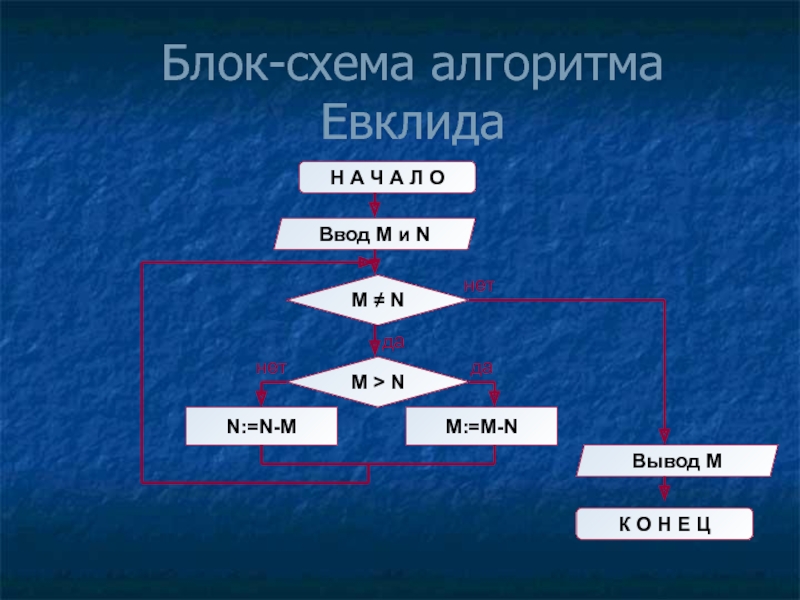
Слайд 8Блок-схема алгоритма Евклида
Н А Ч А Л О
Ввод M
и N
M ≠ N
N:=N-M
M:=M-N
M > N
нет
да
да
нет
Вывод M
К О Н Е Ц
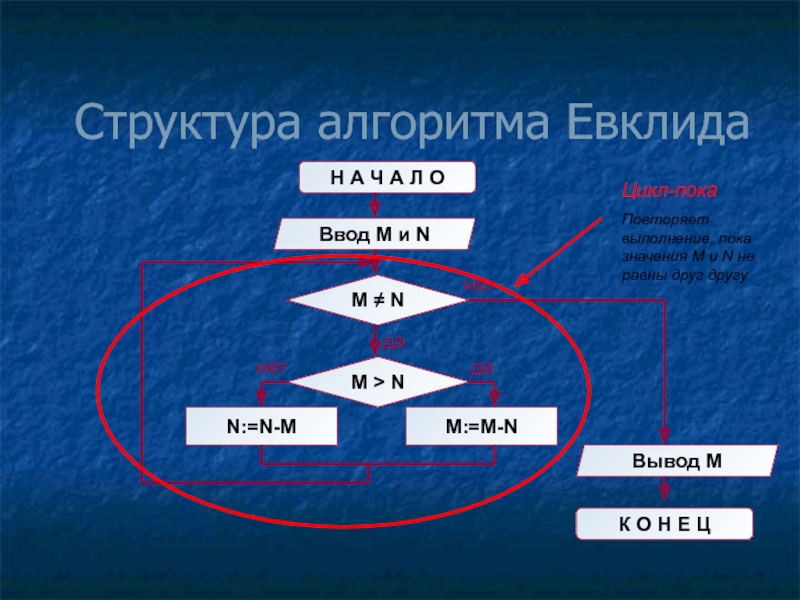
Слайд 9Структура алгоритма Евклида
Н А Ч А Л О
Ввод M
и N
M ≠ N
N:=N-M
M:=M-N
M > N
нет
да
да
нет
Вывод M
К О Н Е Ц
Цикл-пока
Повторяет выполнение, пока значения M и N не равны друг другу
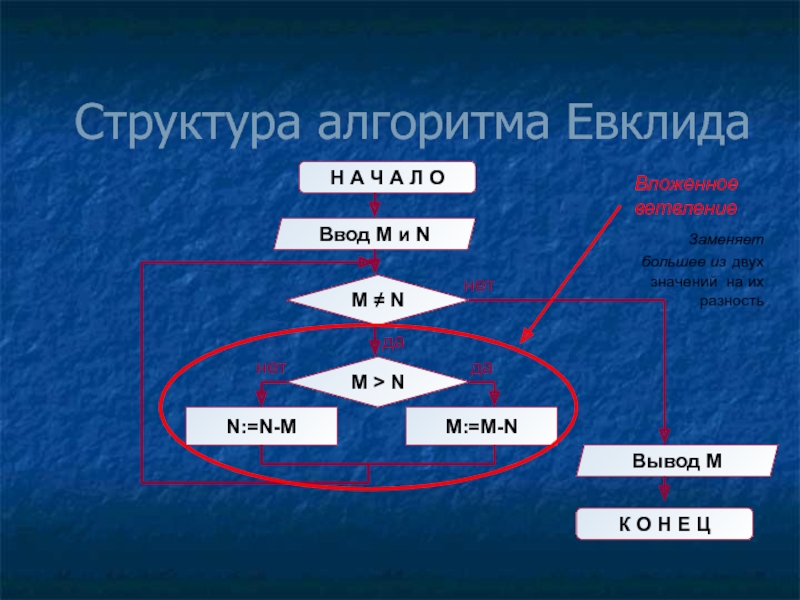
Слайд 10Структура алгоритма Евклида
Н А Ч А Л О
Ввод M
и N
M ≠ N
N:=N-M
M:=M-N
M > N
нет
да
да
нет
Вывод M
К О Н Е Ц
Вложенное ветвление
Заменяет большее из двух значений на их разность
Слайд 36Блок-схема алгоритма Евклида
Н А Ч А Л О
Ввод M
и N
M ≠ N
N:=N-M
M:=M-N
M > N
нет
да
да
нет
Вывод M
К О Н Е Ц
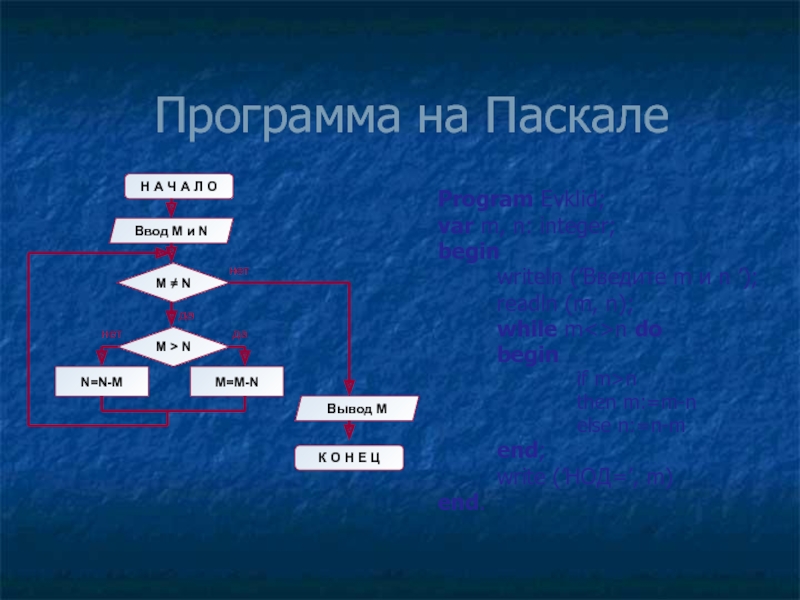
Слайд 37Программа на Паскале
Program Evklid;
var m, n:
integer;
begin
writeln (’Введите m и n ’);
readln (m, n);
while m<>n do
begin
if m>n
then m:=m-n
else n:=n-m
end;
write (’НОД=’, m)
end.
begin
writeln (’Введите m и n ’);
readln (m, n);
while m<>n do
begin
if m>n
then m:=m-n
else n:=n-m
end;
write (’НОД=’, m)
end.
Слайд 38Отладка и тестирование
Выполнить на компьютере программу.
Протестировать
ее на значениях:
1) M=32, N=24;
2) M=696, N=234
1) M=32, N=24;
2) M=696, N=234
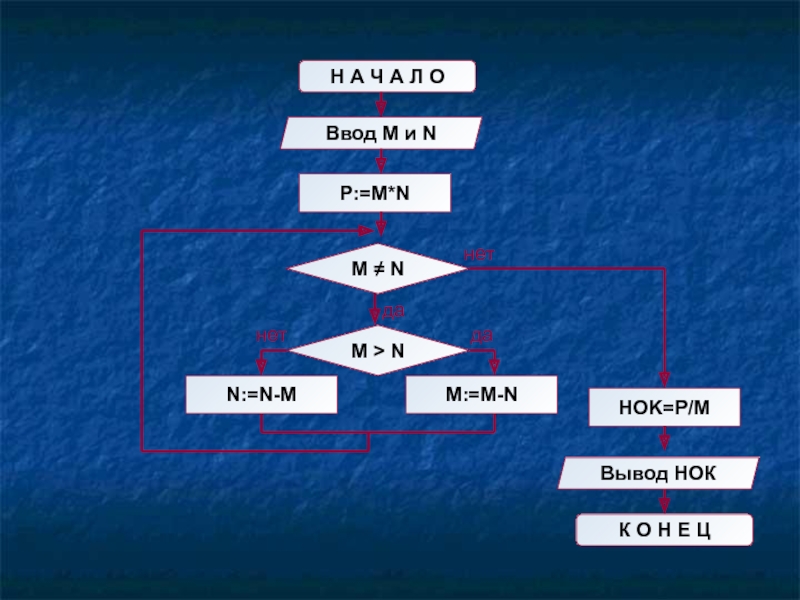
Слайд 39Постановка задачи:
Составить программу нахождения наименьшего общего кратного (НОК) двух
чисел, используя формулу:
M х N = НОД (M, N) х НОК (M, N)
M х N = НОД (M, N) х НОК (M, N)
Слайд 41Домашнее задание
Составить программу нахождения наибольшего общего делителя трех чисел,
используя формулу:
НОД (A, B, C) = НОД (НОД (A, B), C)
НОД (A, B, C) = НОД (НОД (A, B), C)
