- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Введение. Кристаллография презентация
Содержание
- 1. Введение. Кристаллография
- 2. Практическое занятие 1. Введение Кристаллография — наука
- 3. Практическое занятие 1. Введение
- 4. Практическое занятие 1. Введение Задачей кристаллографии является
- 5. Практическое занятие 1. Понятие кристалла и элементов
- 6. Практическое занятие 1. Понятие кристалла и элементов поверхности кристалла
- 7. Практическое занятие 1. Понятие кристалла и элементов
- 8. Практическое занятие 1. Понятие симметрии и элементов
- 9. Практическое занятие 1. Понятие симметрии и элементов
- 10. Практическое занятие 1. Понятие симметрии и элементов
- 11. Практическое занятие 1. Центр симметрии Центр симметрии
- 12. Практическое занятие 1. Центр симметрии Правило наличия
- 13. Практическое занятие 1. Центр симметрии В
- 14. Практическое занятие 1. Центр симметрии Определите,
- 15. Практическое занятие 1. Ось симметрии Осью симметрии
- 16. Практическое занятие 1. Ось симметрии Оси симметрии
- 17. Практическое занятие 1. Ось симметрии Угол, при
- 18. Практическое занятие 1. Ось симметрии Оси первого
- 19. Практическое занятие 1. Ось симметрии Инверсионной осью
- 20. Практическое занятие 1. Ось симметрии Для кристаллов
- 21. Практическое занятие 1. Ось симметрии Li1 =
- 22. Практическое занятие 1. Плоскость симметрии Плоскостью симметрии
- 23. Практическое занятие 1. Плоскость симметрии В равнобедренном
- 24. Практическое занятие 1. Плоскость симметрии Определите количество плоскостей симметрии в данном прямоугольнике
- 25. Практическое занятие 1. Закон симметрии кристаллов Закон
- 26. Практическое занятие 1. Закон симметрии кристаллов Это
- 27. Практическое занятие 1. Закон симметрии кристаллов
Слайд 1Практическое занятие №1
1. Введение
2. Понятие кристалла и элементов поверхности кристалла
3. Понятие симметрии и элементов симметрии кристалла
4. Плоскость симметрии, ось симметрии и центр симметрии
5. Закон симметрии кристаллов
Слайд 2Практическое занятие 1. Введение
Кристаллография — наука о кристаллах, их структуре, возникновении
Слайд 4Практическое занятие 1. Введение
Задачей кристаллографии является изучение строения, физических свойств кристаллов,
Подразделяют кристаллографию на:
физическую кристаллографию (изучает физические свойства кристаллов — механические, тепловые, оптические);
геометрическую кристаллографию (изучает формы кристаллов);
кристаллогенезис (изучает образование и рост кристаллов);
кристаллохимию (изучает связь между химическим составом вещества и его физическими и химическими свойствами).
Слайд 5Практическое занятие 1.
Понятие кристалла и элементов поверхности кристалла
Кристаллом называется твердое тело,
Элементы поверхности кристалла:
грани (плоскости, ограничивающие кристалл);
ребра (линии пересечения граней);
вершины (точка пересечения ребер).
Слайд 7Практическое занятие 1.
Понятие кристалла и элементов поверхности кристалла
Определите количество граней и
Слайд 8Практическое занятие 1.
Понятие симметрии и элементов симметрии кристалла
Симметрия в переводе с
Явление симметрии широко развито в живой природе. В неживой природе яркими представителями симметричных тел являются кристаллические многогранники. Симметрия кристаллов обязана их внутренней структуре, в которой материальные частицы закономерно ориентированы.
Слайд 9Практическое занятие 1.
Понятие симметрии и элементов симметрии кристалла
Под симметрией кристаллов понимается
Вспомогательные геометрические образы (прямая линия, плоскость, точка), с помощью которых обнаруживается симметрия кристалла, называются элементами симметрии.
Слайд 10Практическое занятие 1.
Понятие симметрии и элементов симметрии кристалла
К элементам симметрии кристалла
ось симметрии,
плоскость симметрии,
центр симметрии.
Приняты следующие символы для их обозначения: ось симметрии – L, плоскость симметрии – Р, центр симметрии – С.
Слайд 11Практическое занятие 1.
Центр симметрии
Центр симметрии (С) – точка внутри кристалла, в
Это особая точка внутри фигуры. Любая проведенная через центр симметрии прямая по обе стороны от нее и на равных расстояниях встречает соответственные точки фигуры.
Слайд 12Практическое занятие 1.
Центр симметрии
Правило наличия центра симметрии: если в кристалле центр
Слайд 13Практическое занятие 1.
Центр симметрии
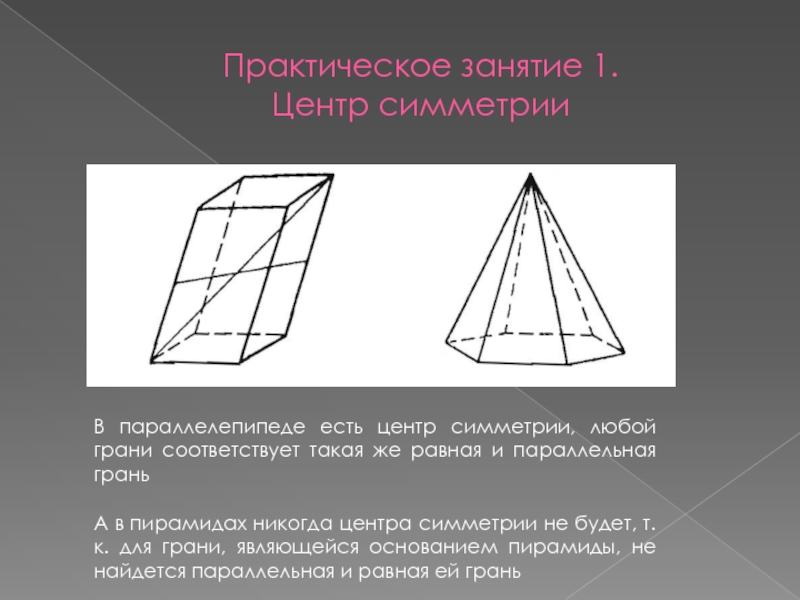
В параллелепипеде есть центр симметрии, любой грани соответствует
А в пирамидах никогда центра симметрии не будет, т.к. для грани, являющейся основанием пирамиды, не найдется параллельная и равная ей грань
Слайд 14Практическое занятие 1.
Центр симметрии
Определите, есть ли центр симметрии в многогранниках, представленных
Слайд 15Практическое занятие 1.
Ось симметрии
Осью симметрии (L) называется прямая линия, при повороте
Число совмещений кристалла со своим исходным положением при повороте на 360° называется порядком оси симметрии.
Слайд 16Практическое занятие 1.
Ось симметрии
Оси симметрии будем обозначать как Ln, где подстрочный
Слайд 17Практическое занятие 1.
Ось симметрии
Угол, при повороте на который происходит совмещение кристалла
Слайд 18Практическое занятие 1.
Ось симметрии
Оси первого порядка не отмечаются, так как они
Возможное количество осей симметрии одного и того же порядка следующее:
L2 – 0, 1, 2, 3, 4, 6;
L3 – 0, 1, 4;
L4 – 0, 1, 3;
L6 – 0, 1.
Оси симметрии могут выходить:
в центре граней,
в середине ребер,
в вершинах многогранных углов.
Слайд 19Практическое занятие 1.
Ось симметрии
Инверсионной осью называется такая прямая линия, при повороте
Подобный элемент симметрии представляет как бы совокупность простой оси симметрии и центра инверсии, действующих не порознь, а совместно. Участвуя лишь в качестве составной части инверсионной оси, центр инверсии может не проявляться в виде самостоятельного элемента симметрии. На всех моделях, где практически приходится определять инверсионные оси, отдельного центра инверсии нет.
Слайд 20Практическое занятие 1.
Ось симметрии
Для кристаллов доказана возможность существования инверсионных осей следующих
На практике приходится иметь дело лишь с Li4 и Li6. Все остальные отвечают уже известным нам элементам симметрии.
Слайд 21Практическое занятие 1.
Ось симметрии
Li1 = C,
Li2 = P,
Li3 = L3C,
Li4 =
Li6 = L3P (плоскость симметрии перпендикулярна оси симметрии третьего порядка)
Слайд 22Практическое занятие 1.
Плоскость симметрии
Плоскостью симметрии (Р) называется такая плоскость, которая делит
Плоскости симметрии проходят перпендикулярно к граням и ребрам (через их середины) и вдоль ребер.
Слайд 23Практическое занятие 1.
Плоскость симметрии
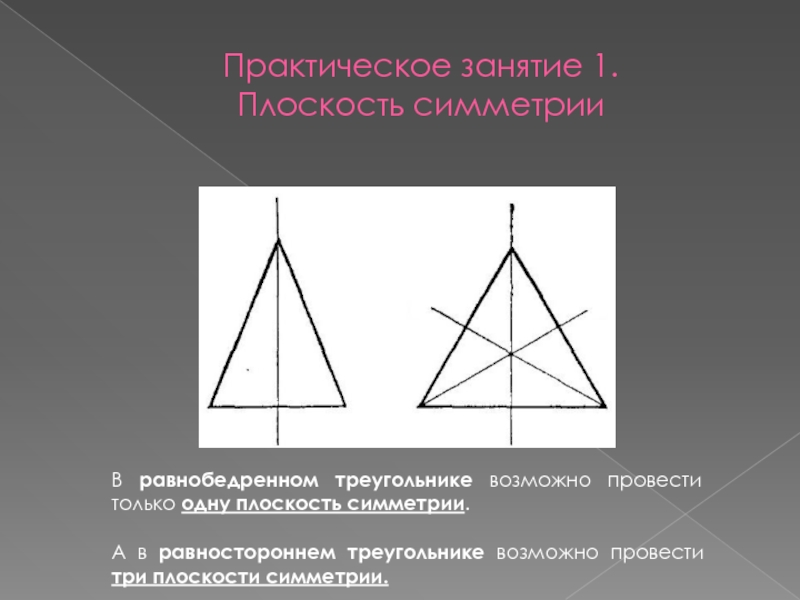
В равнобедренном треугольнике возможно провести только одну плоскость
А в равностороннем треугольнике возможно провести три плоскости симметрии.
Слайд 24Практическое занятие 1.
Плоскость симметрии
Определите количество плоскостей симметрии в данном прямоугольнике
Слайд 25Практическое занятие 1.
Закон симметрии кристаллов
Закон симметрии кристаллов: в кристаллах возможны оси
В кристаллах возможны 1, 2, 3, 4, 5, 6, 7 и 9 плоскостей. Нет кристаллов с 8 плоскостями и больше 9.