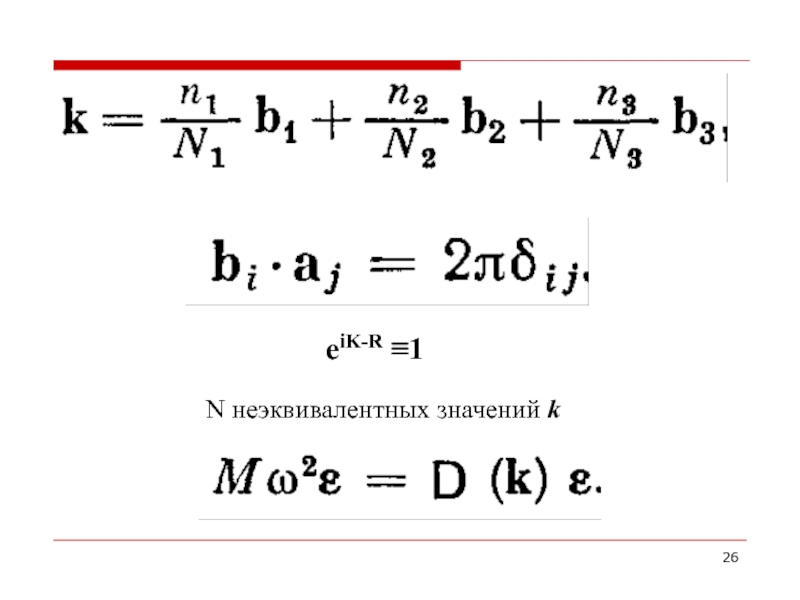- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Классическая теория гармонического кристалла. Гармоническое приближение. Адиабатическое приближение презентация
Содержание
- 1. Классическая теория гармонического кристалла. Гармоническое приближение. Адиабатическое приближение
- 2. Считаем, что среднее равновесное положение каждого иона
- 3. u (R) — отклонение от равновесия для иона, равновесное положение которого есть R
- 4. P(R) — импульс атома с равновесным положением R, М — масса атома.
- 5. ГАРМОНИЧЕСКОЕ ПРИБЛИЖЕНИЕ a
- 7. НОРМАЛЬНЫЕ МОДЫ ОДНОМЕРНОЙ МОНОАТОМНОЙ РЕШЕТКИ БРАВЭ
- 8. Уравнения движения -π/a - π/a
- 9. поэтому при заданном k решение существует, если ω = ω (k), где
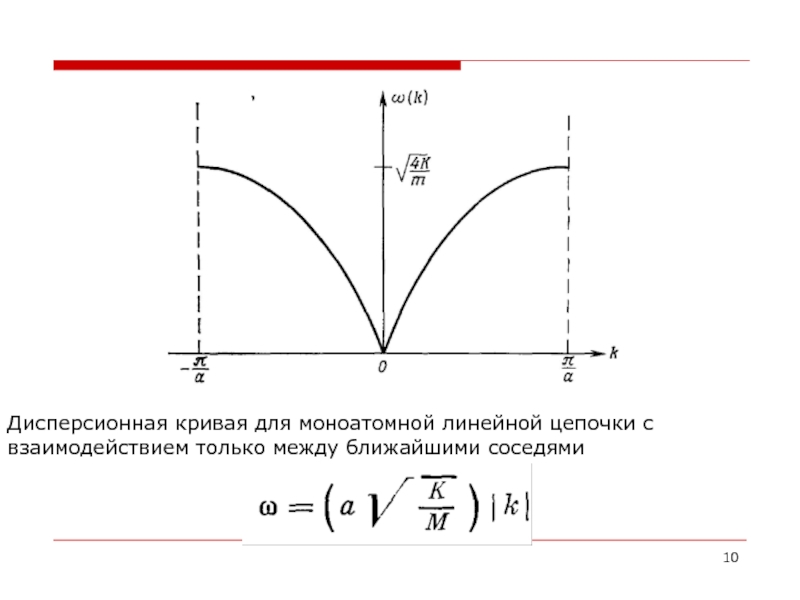
- 10. Дисперсионная кривая для моноатомной линейной цепочки с взаимодействием только между ближайшими соседями
- 11. НОРМАЛЬНЫЕ МОДЫ ОДНОМЕРНОЙ РЕШЕТКИ С БАЗИСОМ
- 13. Для каждого из N значений k имеется
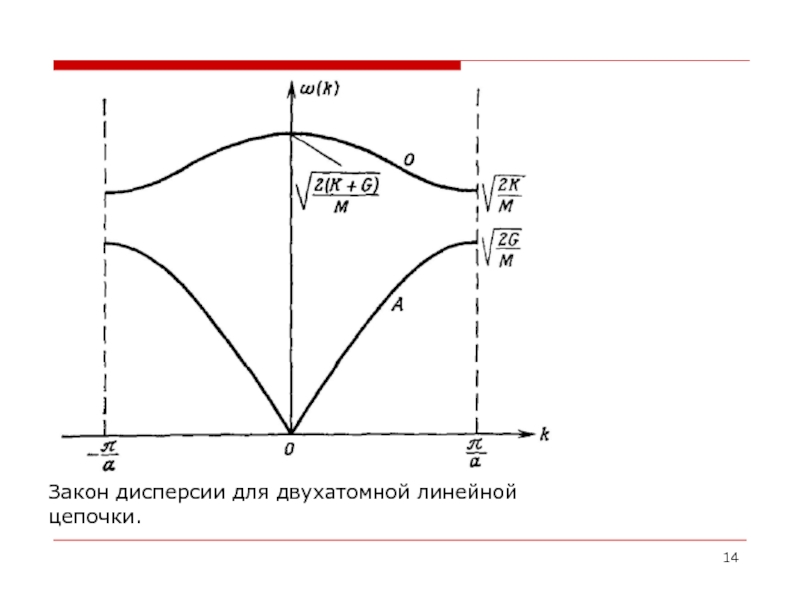
- 14. Закон дисперсии для двухатомной линейной цепочки.
- 15. Случай 1. ε2 = ± ε1
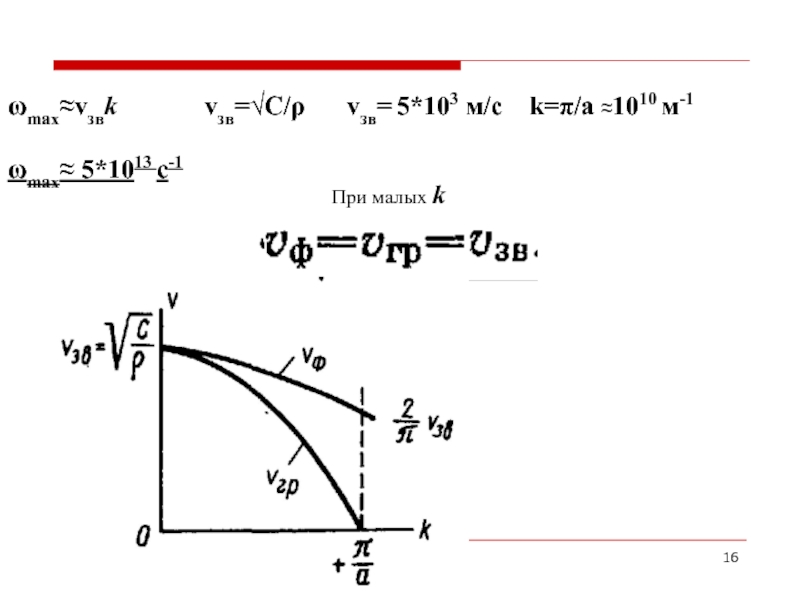
- 16. ωmax≈vзвk
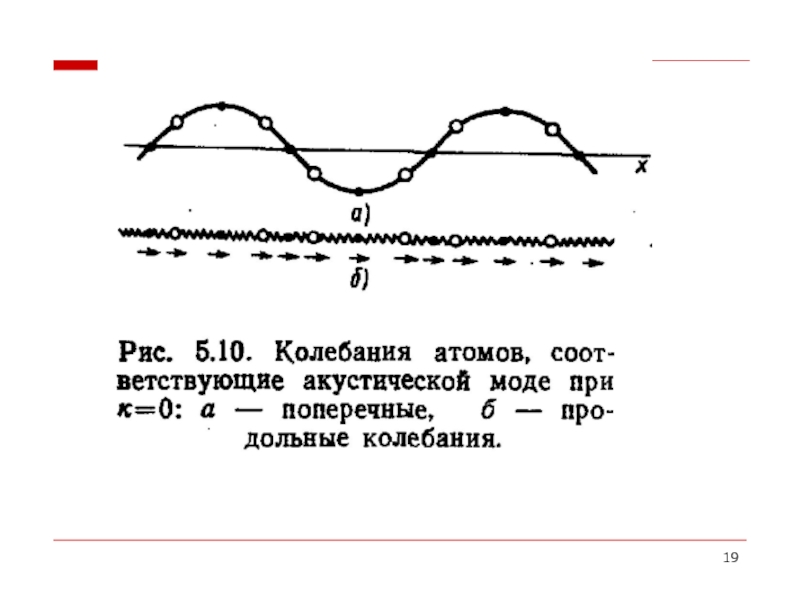
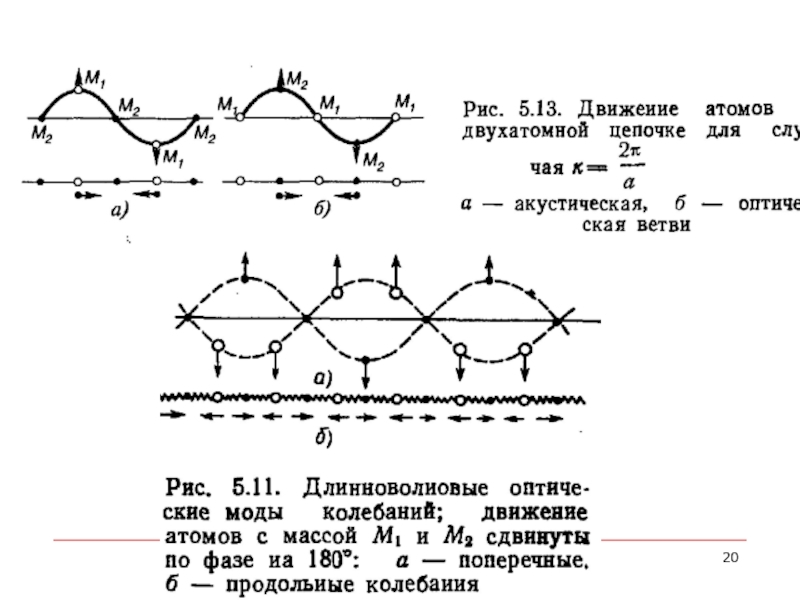
- 17. Случай 2 Акустическая (а) и оптическая
- 18. Случай 3. К >> G. В первом
- 21. НОРМАЛЬНЫЕ МОДЫ МОНОАТОМНОЙ ТРЕХМЕРНОЙ РЕШЕТКИ БРАВЭ
- 22. Первое свойство симметрии
- 23. Второе свойство симметрии Третье свойство симметрии или
- 25. вектор поляризации нормальной моды ε Борна-Кармана условие
- 26. eiK-R ≡1 N неэквивалентных значений k
- 27. динамическая матрица
- 28. D(k) есть четная функция от k и действительная матрица. матрица D(k) симметрична
- 29. в длинноволновом пределе (при малых k) √
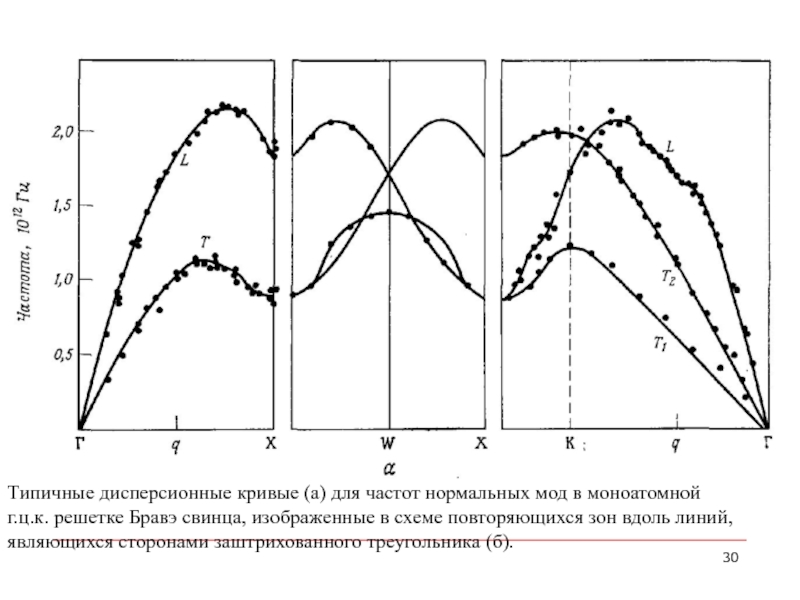
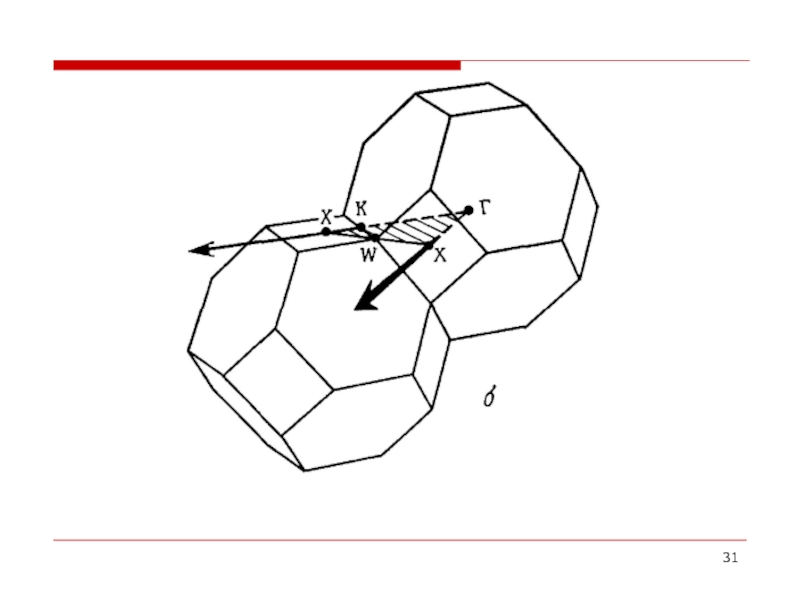
- 30. Типичные дисперсионные кривые (а) для частот нормальных
- 32. НОРМАЛЬНЫЕ МОДЫ ТРЕХМЕРНОЙ РЕШЕТКИ С БАЗИСОМ
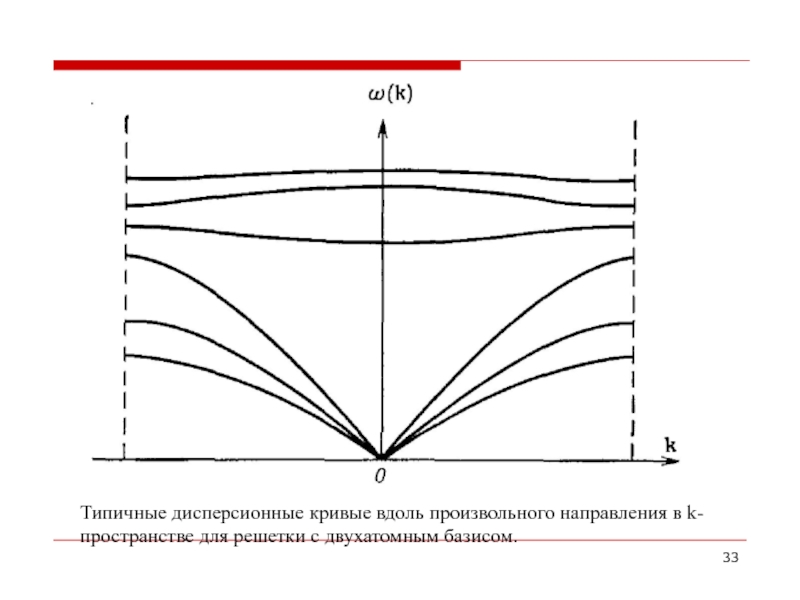
- 33. Типичные дисперсионные кривые вдоль произвольного направления в k-пространстве для решетки с двухатомным базисом.
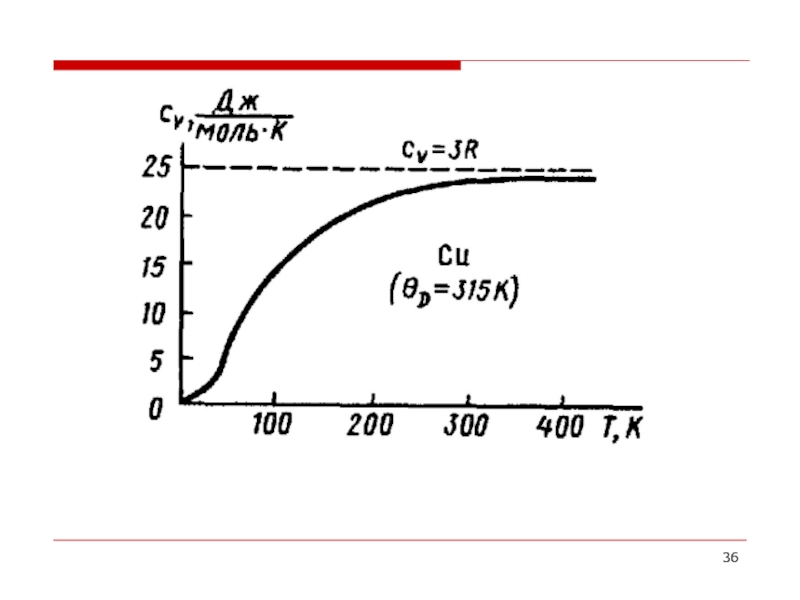
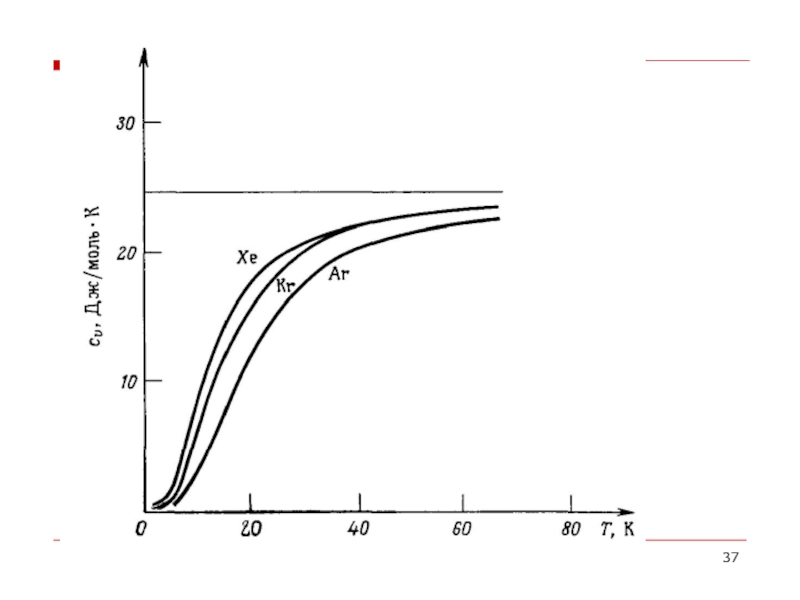
- 34. Удельная теплоемкость вещества отнесенная к 1 молю
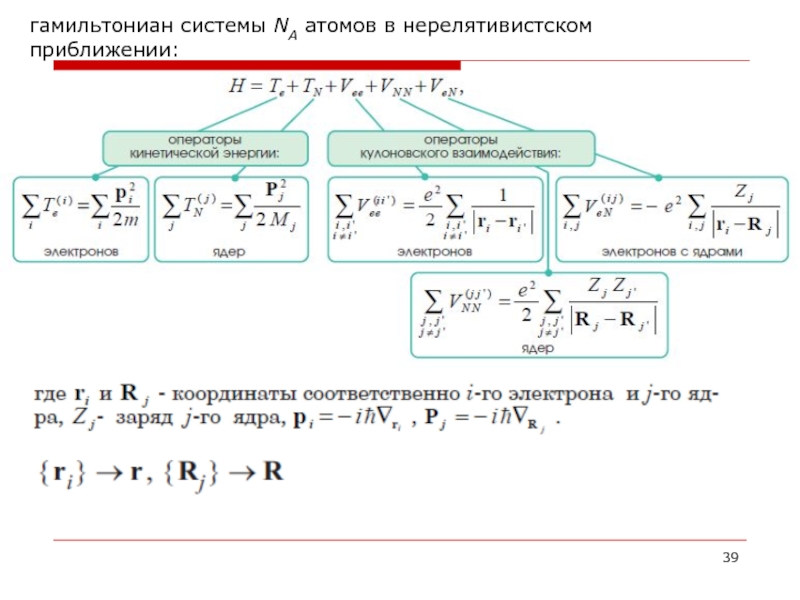
- 39. гамильтониан системы NA атомов в нерелятивистском приближении:
- 41. κ Собственные значения и собственные функции зависят от координат Х как от параметров
- 42. Движение ядер ограничено малой окрестностью Х0 Х-Х0 -малое u- ядерная координата
- 45. Решение 0-го порядка
- 48. × Гармоническое приближение
- 50. Оператор He не содержит производных по R
- 51. dr ×
- 53. - квантовомеханическое усреднение N - полное число атомов в системе
- 54. гармоническое приближение
- 55. Теорема вириала для гармонического осциллятора: характерные значения импульса и амплитуды колебаний амплитуда колебаний
- 56. Для энергии тепловых колебаний ядер в твердом
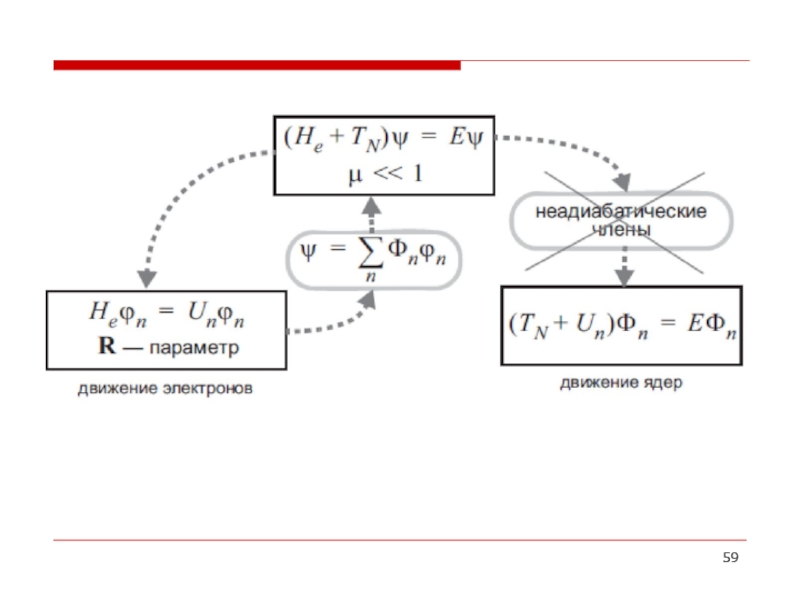
- 57. Неадиабатические слагаемые
- 58. в адиабатическом приближении
Считаем, что среднее равновесное положение каждого иона совпадает с узлом решетки Бравэ. с каждым ионом связан определенный узел R решетки Бравэ, относительно которого он совершает колебания,
Слайд 1
Тема 3 (Лекция 5-6)
КЛАССИЧЕСКАЯ ТЕОРИЯ
ГАРМОНИЧЕСКОГО КРИСТАЛЛА
ГАРМОНИЧЕСКОЕ ПРИБЛИЖЕНИЕ
АДИАБАТИЧЕСКОЕ ПРИБЛИЖЕНИЕ
ОДНОМЕРНАЯ МОНОАТОМНАЯ РЕШЕТКА БРАВЭ
ОДНОМЕРНАЯ РЕШЕТКА С БАЗИСОМ
ТРЕХМЕРНАЯ МОНОАТОМНАЯ РЕШЕТКА БРАВЭ
УДЕЛЬНАЯ ТЕМПЛОЕМКОСТЬ КЛАССИЧЕСКОГО КРИСТАЛЛА
Слайд 2Считаем, что среднее равновесное положение каждого иона совпадает с узлом решетки
Бравэ.
с каждым ионом связан определенный узел R решетки Бравэ, относительно которого он совершает колебания,
узел R есть лишь среднее положение иона, а не его фиксированное мгновенное положение.
2. Принимаем, что типичные отклонения каждого иона от его положения равновесия малы по сравнению с расстоянием между ионами.
с каждым ионом связан определенный узел R решетки Бравэ, относительно которого он совершает колебания,
узел R есть лишь среднее положение иона, а не его фиксированное мгновенное положение.
2. Принимаем, что типичные отклонения каждого иона от его положения равновесия малы по сравнению с расстоянием между ионами.
Слайд 7НОРМАЛЬНЫЕ МОДЫ
ОДНОМЕРНОЙ МОНОАТОМНОЙ РЕШЕТКИ БРАВЭ
Κ= φ ''(a)
φ (х) — энергия взаимодействия двух ионов, находящихся на расстоянии х вдоль прямой.
Слайд 10Дисперсионная кривая для моноатомной линейной цепочки с взаимодействием только между ближайшими
соседями
Слайд 11НОРМАЛЬНЫЕ МОДЫ ОДНОМЕРНОЙ РЕШЕТКИ С БАЗИСОМ
где через u1(na) -смещение иона,
совершающего колебания вблизи узла nа, а через u2(nа) — смещение иона, колеблющегося вблизи узла nа+d. К ≥ G
Слайд 13Для каждого из N значений k имеется два решения, что дает
2N нормальных мод, как должно быть при 2N степенях свободы (по два иона в каждой из N элементарных ячеек).
Слайд 15Случай 1.
ε2 = ± ε1
акустическая (а) и оптическая (б) моды
в двухатомной линейной цепочке
Короткие волны распространяются медленнее, чем длинные
Цепочка из одинаковых атомов при распространении акустических волн ведет как упругая струна только при λ>>2a
±
Слайд 17Случай 2
Акустическая (а) и оптическая (б) моды двухатомной линейной цепочки
при
k = ± π/a, т. е. на краях зоны Бриллюэна.
k = ± π/a, т. е. на краях зоны Бриллюэна.
Слайд 18Случай 3. К >> G. В первом порядке по отношению G/K
Случай
4. К = G.
Моноатомная решетка Бравэ, с постоянной решетки а/2
Моноатомная решетка Бравэ, с постоянной решетки а/2
Слайд 30Типичные дисперсионные кривые (а) для частот нормальных мод в моноатомной
г.ц.к.
решетке Бравэ свинца, изображенные в схеме повторяющихся зон вдоль линий, являющихся сторонами заштрихованного треугольника (б).
Слайд 32НОРМАЛЬНЫЕ МОДЫ
ТРЕХМЕРНОЙ РЕШЕТКИ С БАЗИСОМ
Для каждого значения k имеется
Зр нормальных мод, где р — число ионов в базисе.
Частоты ωs (k) (s = 1, . . ., Зр) являются функциями k и обладают периодичностью обратной решетки;
Частоты ωs (k) (s = 1, . . ., Зр) являются функциями k и обладают периодичностью обратной решетки;
3 из Зр ветвей — акустические;
3 (р — 1) ветвей — оптические;
Векторы поляризации нормальных мод уже не связаны простыми соот-
ношениями ортогональности типа
Слайд 33Типичные дисперсионные кривые вдоль произвольного направления в k-пространстве для решетки с
двухатомным базисом.
Слайд 34Удельная теплоемкость вещества отнесенная к 1 молю – энергия, которую необходимо
сообщить молю вещества, чтобы повысить температуру на 1 градус
Дюлонг-Пти – при высоких температурах есть величина постоянная, не зависящая от температуры – 25 Дж/моль*К
Объяснение в рамках классической физики – из закона равномерного распределения энергии по степеням свободы
Слайд 50Оператор He не содержит производных по R и зависит от R
как от параметра .
Пусть ϕn (r ,R) и Un(R) - собственные функции и собственные значения электронного гамильтониана He, соответственно
ψ(r ,R, t )
Слайд 55Теорема вириала для гармонического осциллятора:
характерные значения импульса и амплитуды колебаний
амплитуда
колебаний
Слайд 56Для энергии тепловых колебаний ядер в твердом теле
Энергия колебаний
где T
- температура, Tпл < 103 K - температура плавления, κ - по-
стоянная Больцмана (1.38⋅10− 16 эрг K)
стоянная Больцмана (1.38⋅10− 16 эрг K)
