- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Фазовые равновесия раствор-пар в двухкомпонентных системах из двух летучих жидкостей презентация
Содержание
- 1. Фазовые равновесия раствор-пар в двухкомпонентных системах из двух летучих жидкостей
- 2. 1. Идеальные растворы из неограниченно смешивающихся жидкостей
- 3. 1. Идеальные растворы из неограниченно смешивающихся жидкостей
- 4. 1. Идеальные растворы из неограниченно смешивающихся жидкостей
- 5. 1. Идеальные растворы из неограниченно смешивающихся жидкостей
- 6. 1. Идеальные растворы из неограниченно смешивающихся
- 7. 1. Идеальные растворы из неограниченно смешивающихся жидкостей
- 8. 1. Идеальные растворы из неограниченно смешивающихся жидкостей
- 9. 1. Идеальные растворы из неограниченно смешивающихся жидкостей
- 10. 1. Идеальные растворы из неограниченно смешивающихся жидкостей
- 11. 1. Идеальные растворы из неограниченно смешивающихся жидкостей
- 12. 2. Законы Коновалова Состав жидкого
- 14. 2. Законы Коновалова Проведем
- 15. 2. Законы Коновалова Линия
- 16. 2. Законы Коновалова Область ниже линии кипения,
- 17. 2. Законы Коновалова Область выше линии конденсации,
- 18. 2. Законы Коновалова Область между кривыми, соответствует
- 19. 2. Законы Коновалова Чтобы определить состав сосуществующих
- 20. 2. Законы Коновалова Соотношение между
- 21. 2. Законы Коновалова Формулировка второго
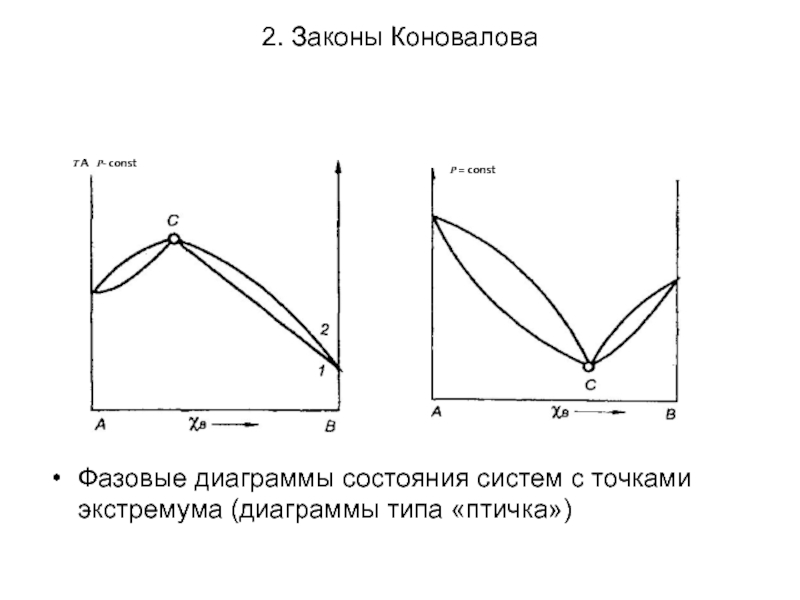
- 22. 2. Законы Коновалова Фазовые диаграммы состояния систем с точками экстремума (диаграммы типа «птичка»)
- 23. 2. Законы Коновалова Применение правила фаз
- 24. 3. Перегонка растворов Перегонка -
- 25. 3. Перегонка растворов Виды перегонок: Простая перегонка
- 26. 3. Перегонка растворов
- 27. 3. Перегонка растворов 2. Фракционная перегонка применяется
- 28. 3. Перегонка растворов
- 29. 3. Перегонка растворов 3. Ректификация - непрерывная
- 30. 3. Перегонка растворов Схема
- 31. 3. Перегонка растворов Поступающая в
- 32. 3. Перегонка растворов Методы разделения азеотропных смесей:
- 33. 3. Перегонка растворов Разделение азеотропной смеси путем
- 34. 3. Перегонка растворов Последовательная ректификация на двух
Слайд 1ОМСКИЙ ГОСУДАРСТВЕННЫЙ МЕДИЦИНСКИЙ УНИВЕРСИТЕТ
КАФЕДРА ХИМИИ
Лекция 8. Фазовые равновесия «раствор-пар» в двухкомпонентных
Идеальные растворы состоящие из неограниченно смешивающихся жидкостей.
Состав пара и состав равновесного с ним жидкого раствора. Первый и второй законы Коновалова.
3. Перегонка растворов.
Лектор: канд. пед. наук, доцент Григорьева Марина Викторовна
Слайд 21. Идеальные растворы из неограниченно смешивающихся жидкостей
Жидкие вещества при
Слайд 31. Идеальные растворы из неограниченно смешивающихся жидкостей
С практической точки зрения
Слайд 41. Идеальные растворы из неограниченно смешивающихся жидкостей
Неограниченно растворимые
Идеальные бинарные летучие растворы, подчиняющиеся закону Рауля;
С положительными или отрицательными отклонениями от закона Рауля, но без максимума или минимума на кривой зависимости давления насыщенного пара от состава раствора;
С максимумом или минимумом на кривой зависимости давления насыщенного пара от состава раствора.
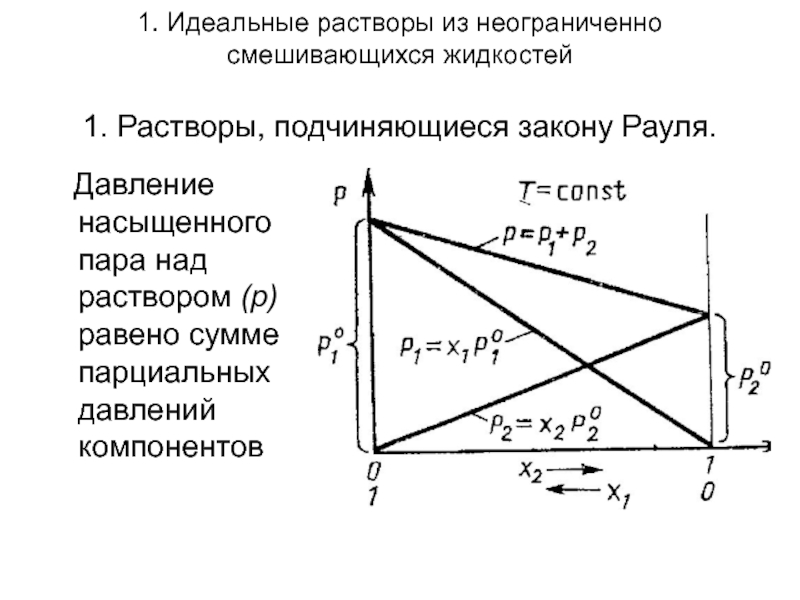
Слайд 51. Идеальные растворы из неограниченно смешивающихся жидкостей 1. Растворы, подчиняющиеся закону Рауля.
Давление насыщенного пара над раствором (р) равено сумме парциальных давлений компонентов
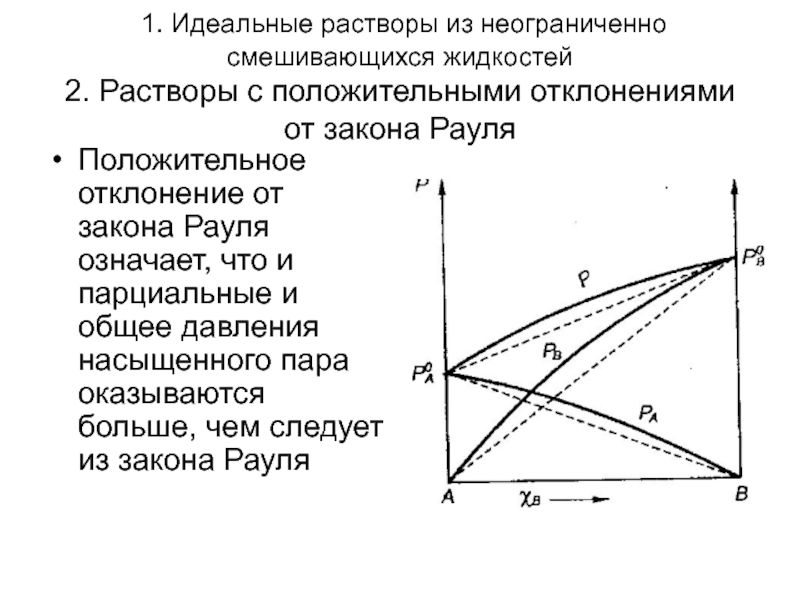
Слайд 6 1. Идеальные растворы из неограниченно смешивающихся жидкостей 2. Растворы с положительными
Положительное отклонение от закона Рауля означает, что и парциальные и общее давления насыщенного пара оказываются больше, чем следует из закона Рауля
Слайд 71. Идеальные растворы из неограниченно смешивающихся жидкостей
Положительные отклонения от
Слайд 81. Идеальные растворы из неограниченно смешивающихся жидкостей Растворы с отрицательными отклонениями от
Отрицательные отклонения от закона Рауля наблюдаются в том случае, когда молекулы в чистых жидкостях связаны друг с другом слабее, чем в растворе. Поэтому при данной температуре из раствора молекул испаряется меньше, чем из чистых жидкостей, следовательно, давление над таким раствором будет ниже.
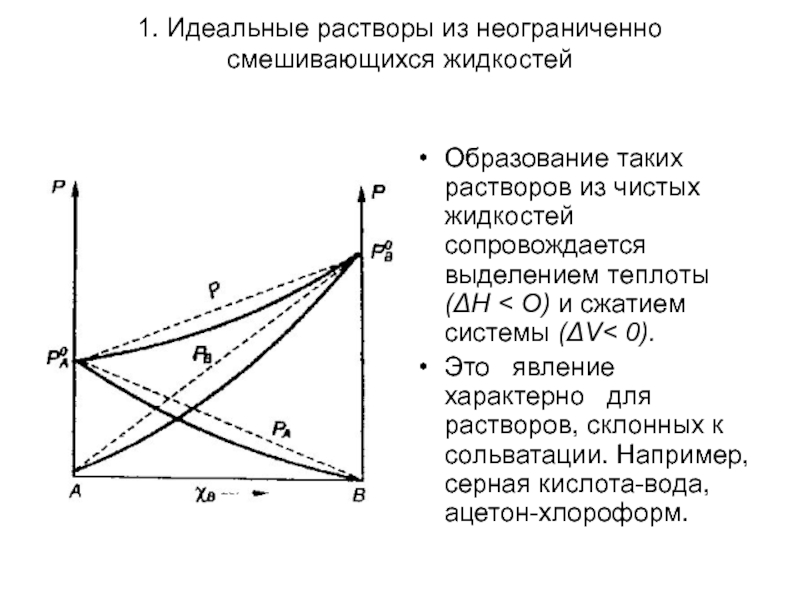
Слайд 91. Идеальные растворы из неограниченно смешивающихся жидкостей
Образование таких растворов из чистых
Это явление характерно для растворов, склонных к сольватации. Например, серная кислота-вода, ацетон-хлороформ.
Слайд 101. Идеальные растворы из неограниченно смешивающихся жидкостей
3. В некоторых системах, где
Слайд 111. Идеальные растворы из неограниченно смешивающихся жидкостей
Жидкие смеси, состав
Таким образом, азеотропы – это нераздельнокипящие однородные смеси из двух или нескольких жидкостей, которые невозможно разделить на чистые компоненты путем фракционной перегонки.
Слайд 122. Законы Коновалова
Состав жидкого раствора и пара в момент
Слайд 142. Законы Коновалова
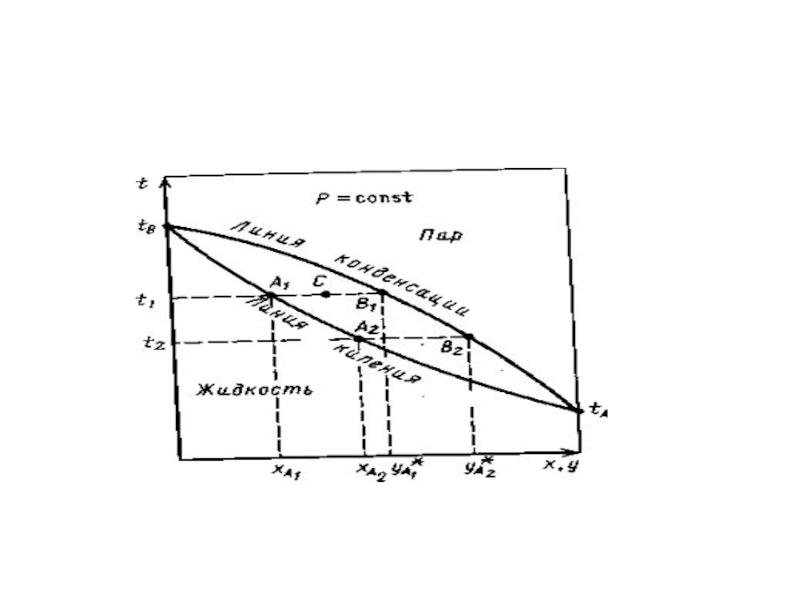
Проведем фазовый анализ диаграммы «температура -
Линия кипения - зависимость температуры кипения от состава жидкого раствора (она выпуклая, так как в системе наблюдается положительное отклонение от закона Рауля).
Линия кипения дает возможность определить при какой температуре начинает закипать жидкость данного состава.
Слайд 152. Законы Коновалова
Линия конденсации отделяет область ненасыщенного пара
Она дает возможность определить - при какой температуре начинается конденсация пара данного состава.
Слайд 162. Законы Коновалова
Область ниже линии кипения, соответствует некипящей жидкости (жидкости без
Слайд 172. Законы Коновалова
Область выше линии конденсации, соответствует ненасыщенному пару (пару без
Слайд 182. Законы Коновалова
Область между кривыми, соответствует сосуществованию пара и жидкости (кипящая
Следовательно, можно произвольно, в определенных пределах изменять только 1 параметр: давление или мольную долю не изменяя при этом числа и вида фаз в системе. Второй параметр будет изменяться строго определенным образом в зависимости от линий пара и жидкости.
Слайд 192. Законы Коновалова
Чтобы определить состав сосуществующих фаз в системе, надо через
Слайд 202. Законы Коновалова
Соотношение между составами равновесных жидкости и пара,
Д.П. Коновалова (1888 г.):
Повышение относительного содержания данного компонента в жидкой фазе всегда вызывает относительное увеличение содержания его в парах.
Слайд 212. Законы Коновалова
Формулировка второго закона Коновалова:
точки максимума или
Слайд 222. Законы Коновалова
Фазовые диаграммы состояния систем с точками экстремума (диаграммы типа
Слайд 232. Законы Коновалова
Применение правила фаз Гиббса показывает, что для любой точки,
Однако для точки С существует математическое уравнение, связывающее концентрации веществ, а именно: Хвж = Хвп . Наличие этого уравнения понижает на единицу число независимых компонентов: К = 2 - 1 = 1. Тогда С = 1-2 + 1=0. Это означает, что состав растворов не меняется при кипении и температура кипения при заданном внешнем давлении остается постоянной, как у чистых веществ.
Слайд 243. Перегонка растворов
Перегонка - процесс разделения жидких смесей, основанный
Разделение осуществляется тем легче, чем больше различаются по составу жидкий раствор и пар. Для количественной характеристики используют коэффициент относительной летучести (α):
α = Р0А/ Р0В
Слайд 253. Перегонка растворов
Виды перегонок:
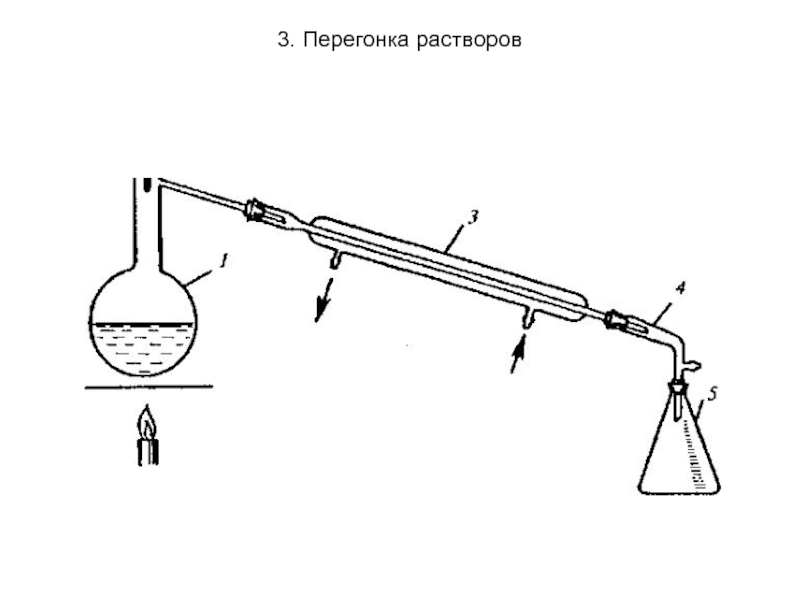
Простая перегонка заключается в непрерывном нагревании жидкого раствора
Слайд 273. Перегонка растворов
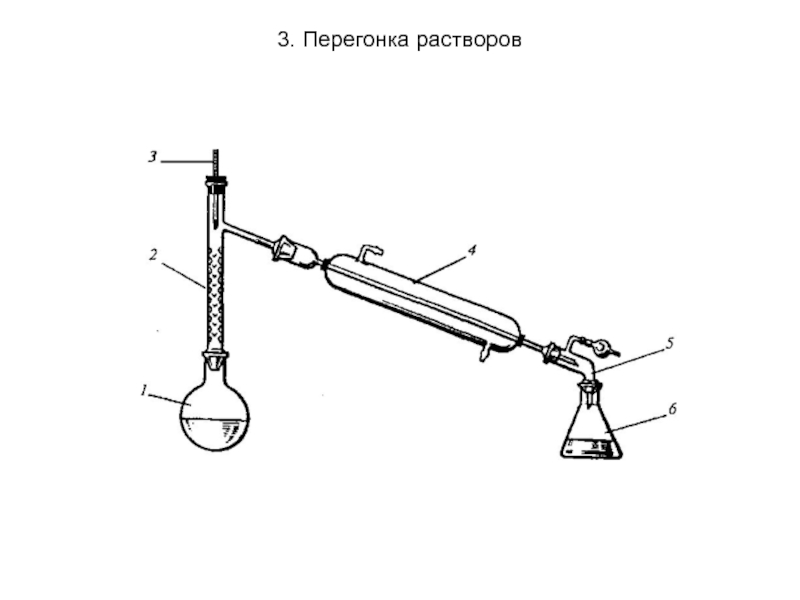
2. Фракционная перегонка применяется для разделения смесей жидкостей, которые
Слайд 293. Перегонка растворов
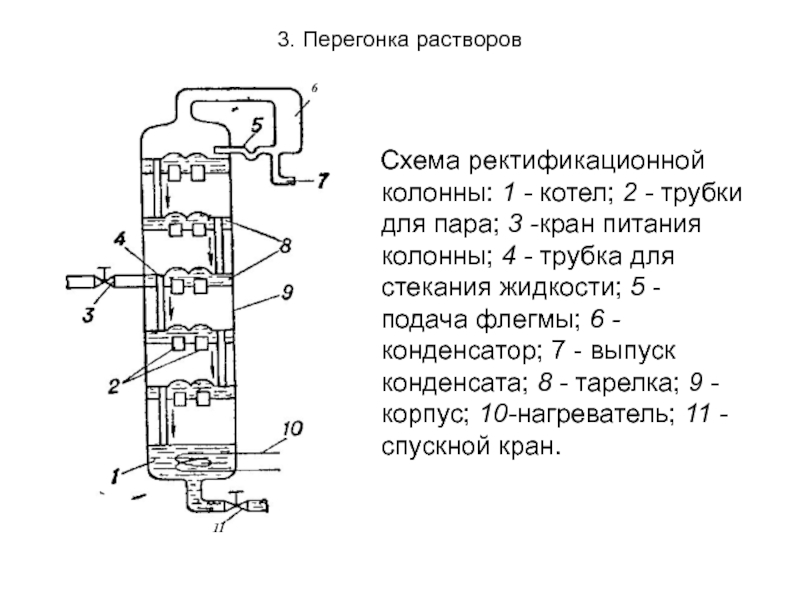
3. Ректификация - непрерывная фракционная перегонка, осуществляемая в специальных
Внизу колонки находится нагреватель. Колонка устроена так, что в ней постоянно происходит и движение жидкой фазы вниз, к нагревателю, и движение пара вверх.
Слайд 303. Перегонка растворов
Схема ректификационной колонны: 1 - котел; 2
Слайд 313. Перегонка растворов
Поступающая в колонку жидкость (А+В) быстро доводится
Таким образом, жидкая фаза постепенно перетекает вниз, все более обогащаясь менее летучим компонентом. В итоге, выходящий из колонки пар представлен почти только чистым веществом В, а вещество А остается в жидком состоянии.