1 семестр
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Виды проецирования. Признак принадлежности точки – прямой. Деление отрезка прямой в заданном отношении. Теорема Фалеса презентация
Содержание
- 1. Виды проецирования. Признак принадлежности точки – прямой. Деление отрезка прямой в заданном отношении. Теорема Фалеса
- 2. Целью дисциплины является формирование у студента системы
- 3. Трудоемкость дисциплины составляет 5 зачетных единиц, 180
- 4. Темы, рассматриваемые в 1 семестре
- 5. Лекция 1 Виды проецирования. Образование комплексного чертежа.
- 6. Символы и обозначения графических элементов _
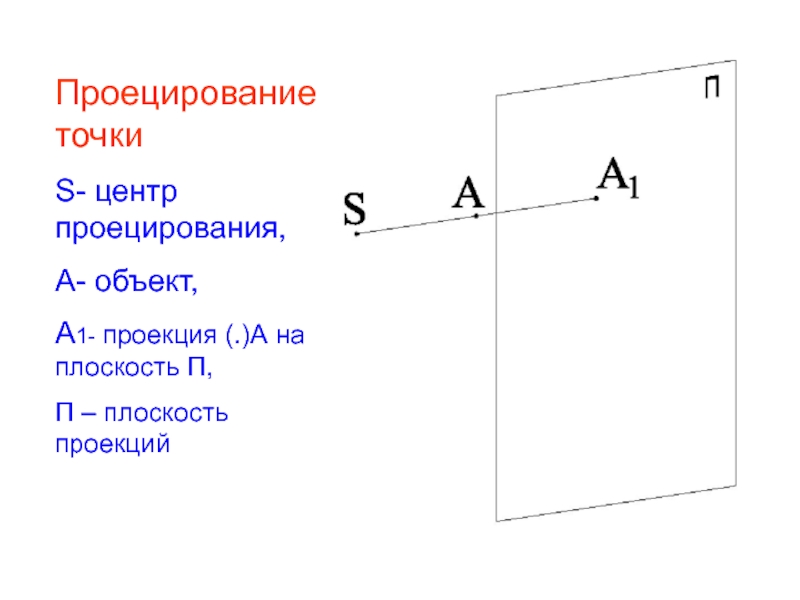
- 7. Проецирование точки S- центр проецирования,
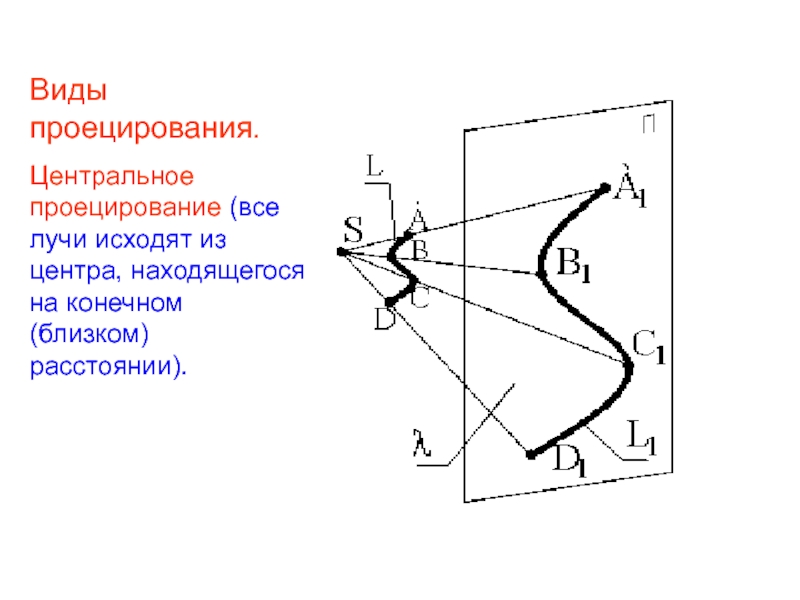
- 8. Виды проецирования. Центральное проецирование (все
- 9. Центральное проецирование Применяется при
- 10. Виды проецирования. Параллельное косоугольное проецирование-
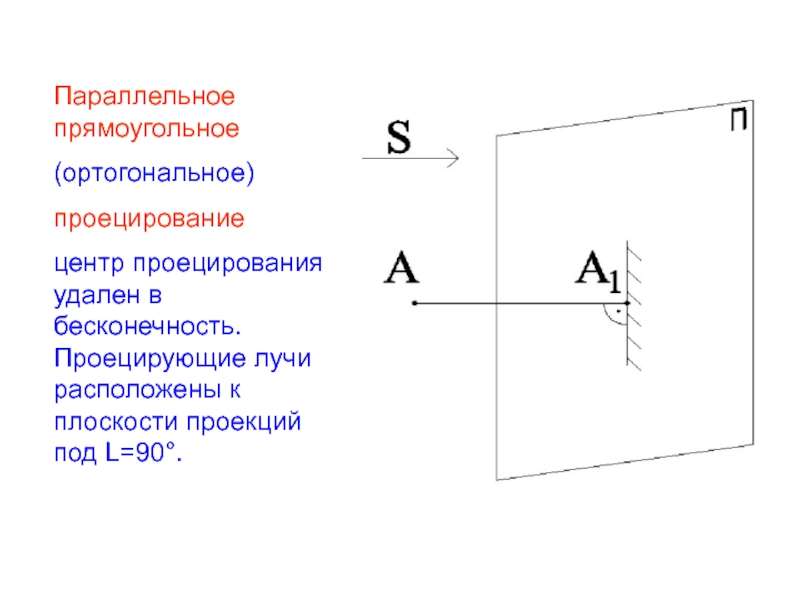
- 11. Параллельное прямоугольное (ортогональное) проецирование центр
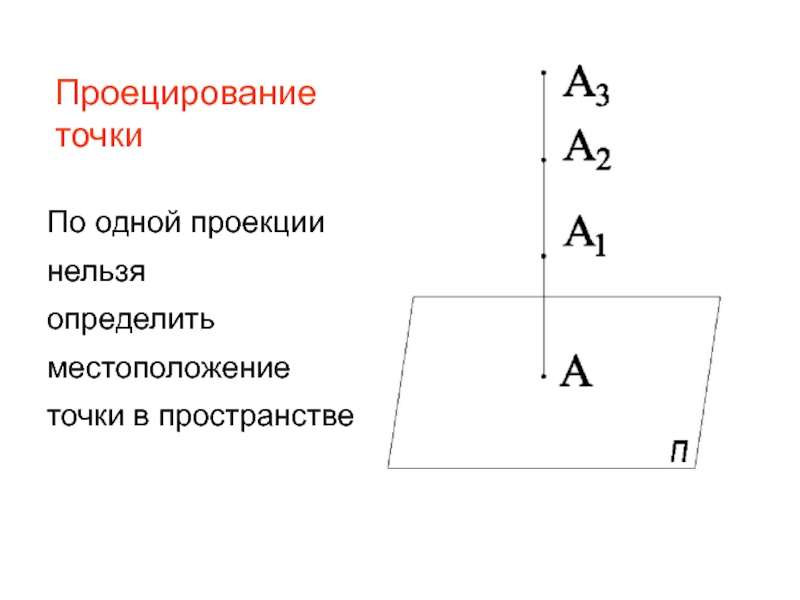
- 12. Проецирование точки По одной проекции нельзя определить местоположение точки в пространстве
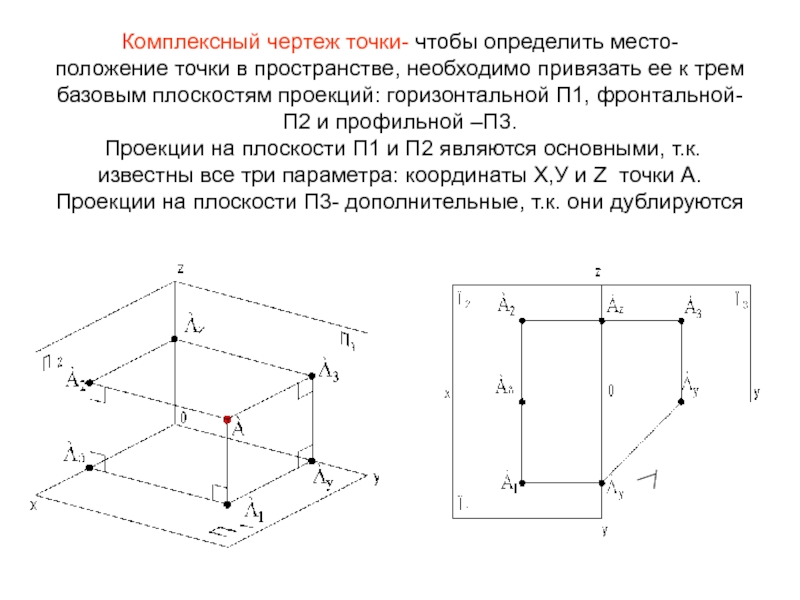
- 13. Комплексный чертеж точки- чтобы определить
- 14. . Т.о. третий
- 16. Конкурирующие точки- точки, лежащие на
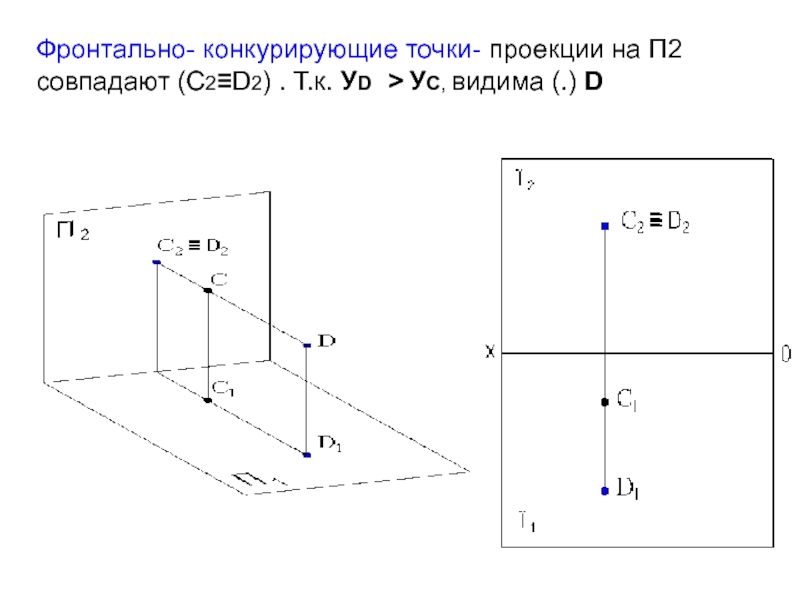
- 17. Фронтально- конкурирующие точки- проекции на
- 20. Фронталь f1 f3 f2
- 22. 2.Проецирующие прямые- перпендикулярные плоскости проекций
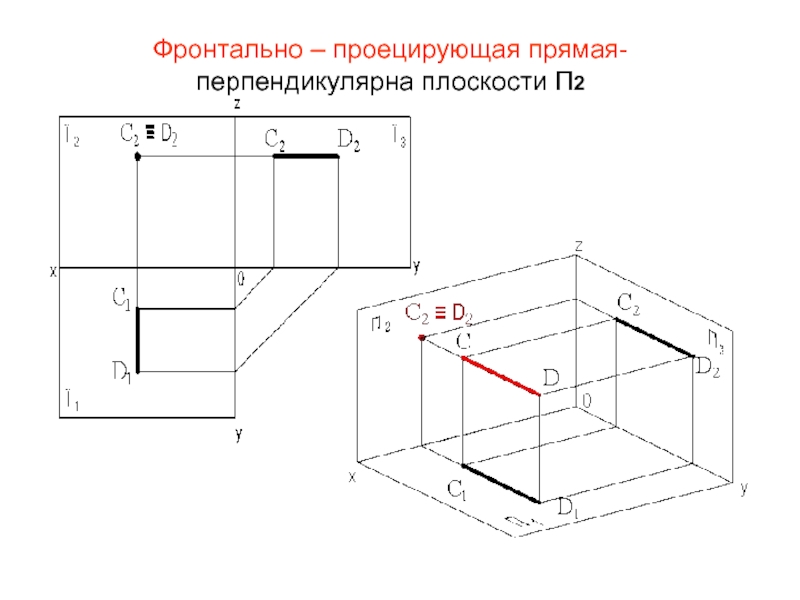
- 23. Фронтально – проецирующая прямая- перпендикулярна плоскости П2
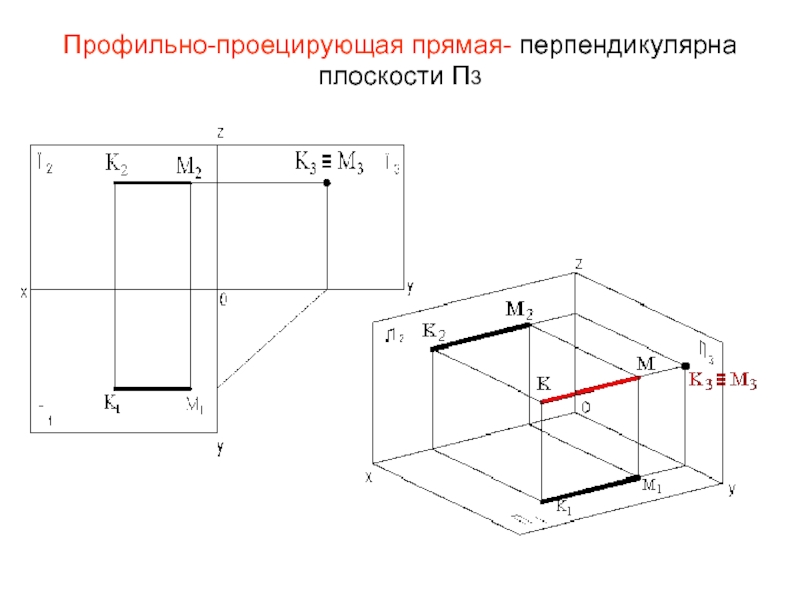
- 24. Профильно-проецирующая прямая- перпендикулярна плоскости П3
- 25. Принадлежность точки прямой линии Е Если точка
- 26. Деление отрезка в заданном отношении (теорема Фалеса)
- 27. Деление отрезка в заданном отношении (теорема Фалеса)
- 28. Деление отрезка в заданном отношении (теорема Фалеса)
- 29. Деление отрезка в заданном отношении (теорема Фалеса)
- 30. Деление отрезка в заданном отношении (теорема Фалеса)
- 31. Определение натуральной величины отрезка прямой линии
- 32. Определение натуральной величины отрезка прямой линии
- 33. Определение натуральной величины отрезка прямой линии Рассмотрим
- 34. Определение натуральной величины отрезка прямой линии Выберем
- 35. Определение натуральной величины отрезка прямой линии
- 36. Гипотенуза треугольника является натуральной величиной отрезка
- 37. Для нахождения угла наклона
- 38. Следы прямой линии
- 39. Следы прямой линии Чтобы найти горизонтальный след
Целью дисциплины является формирование у студента системы теоретических знаний об основных способах построения изображения пространственных форм на плоскости (инварианты центрального и ортогонального проецирования). Развитие пространственного воображения, творческого мышления и способности свободного
Слайд 1 Кафедра Графики информационных технологий архитектурного проектирования Начертательная геометрия Направление подготовки:
07.03.01 «Архитектура» (бакалавриат академический);
07.03.04 «Градостроительство» (бакалавриат академический);
Слайд 2Целью дисциплины является формирование у студента системы теоретических знаний об основных
способах построения изображения пространственных форм на плоскости (инварианты центрального и ортогонального проецирования). Развитие пространственного воображения, творческого мышления и способности свободного владения формой.
задачи:
освоение способов изображения различных форм, поверхностей, архитектурных деталей в ортогональных, аксонометрических и перспективных проекциях
развитие визуально-пластической культуры и способности к анализу и моделированию сложных композиционных решений с использованием различных типов поверхностей;
изучение теории теней и использование полученных знаний для выявления объема на плоскости. Овладение основами построения теней в ортогональных, аксонометрических и перспективных проекциях;
овладение различными способами построения перспективных проекций для максимально объективного изображения заданного или спроектированного объекта.
формирование профессиональных качеств, практических навыков и умений по созданию и чтению различных чертежей, знакомство с приемами и правилами их выполнения и оформления;
развитие графических навыков работы с различными чертежными инструментами
освоение способов изображения различных объектов при вертикальной планировке территории.
Слайд 3Трудоемкость дисциплины составляет 5 зачетных единиц, 180 час ( в том
числе: 64 часа лекционных , 32 практических и 66 час. самостоятельных занятий, экзамен 18 час )
Форма отчетности: 1 семестр - зачет, 2 семестр-экзамен
Форма отчетности: 1 семестр - зачет, 2 семестр-экзамен
Слайд 4Темы, рассматриваемые
в 1 семестре
Ортогональные проекции точки, прямой, плоскости.
Методы преобразования
проекций.
Кривые линии и поверхности.
Пересечение поверхности плоскостью и прямой линией.
Взаимное пересечение поверхностей.
Развертки поверхностей.
Теория теней: тени в аксонометрии и ортогональных проекциях
Кривые линии и поверхности.
Пересечение поверхности плоскостью и прямой линией.
Взаимное пересечение поверхностей.
Развертки поверхностей.
Теория теней: тени в аксонометрии и ортогональных проекциях
Слайд 5Лекция 1
Виды проецирования.
Образование комплексного чертежа.
Точка. Проекции точки. Конкурирующие точки.
Прямая. Образование прямой
линии. Прямые уровня. Проецирующие прямые.
Признак принадлежности точки – прямой.
Деление отрезка прямой в заданном отношении. Теорема Фалеса.
Определение натуральной величины отрезка прямой.
Следы прямой линии
Признак принадлежности точки – прямой.
Деление отрезка прямой в заданном отношении. Теорема Фалеса.
Определение натуральной величины отрезка прямой.
Следы прямой линии
Слайд 7
Проецирование точки
S- центр проецирования,
А- объект,
А1- проекция (.)А на плоскость П,
П –
плоскость проекций
Слайд 8
Виды проецирования.
Центральное проецирование (все лучи исходят из центра, находящегося на конечном
(близком) расстоянии).
Слайд 9
Центральное проецирование
Применяется при построении: а)перспективных изображений (центр S- глаза наблюдателя).
б) при построении факельных теней в интерьере (центр S- лампочка, проецирующие лучи- лучи света; проекция линии L на плоскость П- L1- падающая тень от предмета).
Слайд 10
Виды проецирования.
Параллельное косоугольное проецирование- центр проецирования удален в бесконечность. Проецирующие лучи
расположены к плоскости проекций под L≠90°.
Слайд 11
Параллельное прямоугольное
(ортогональное)
проецирование
центр проецирования удален в бесконечность. Проецирующие лучи расположены к плоскости
проекций под L=90°.
Слайд 13
Комплексный чертеж точки- чтобы определить место-
положение точки в пространстве, необходимо привязать
ее к трем базовым плоскостям проекций: горизонтальной П1, фронтальной-П2 и профильной –П3.
Проекции на плоскости П1 и П2 являются основными, т.к. известны все три параметра: координаты Х,У и Z точки А. Проекции на плоскости П3- дополнительные, т.к. они дублируются
Слайд 14
.
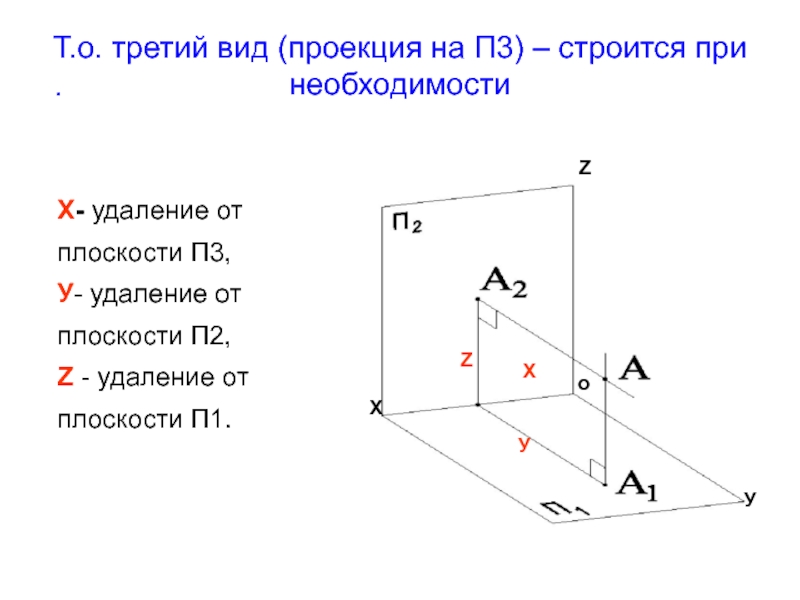
Т.о. третий вид (проекция на П3) – строится при необходимости
Х-
удаление от плоскости П3,
У- удаление от плоскости П2,
Z - удаление от плоскости П1.
У- удаление от плоскости П2,
Z - удаление от плоскости П1.
Х
У
Z
о
Х
У
Z
Слайд 15
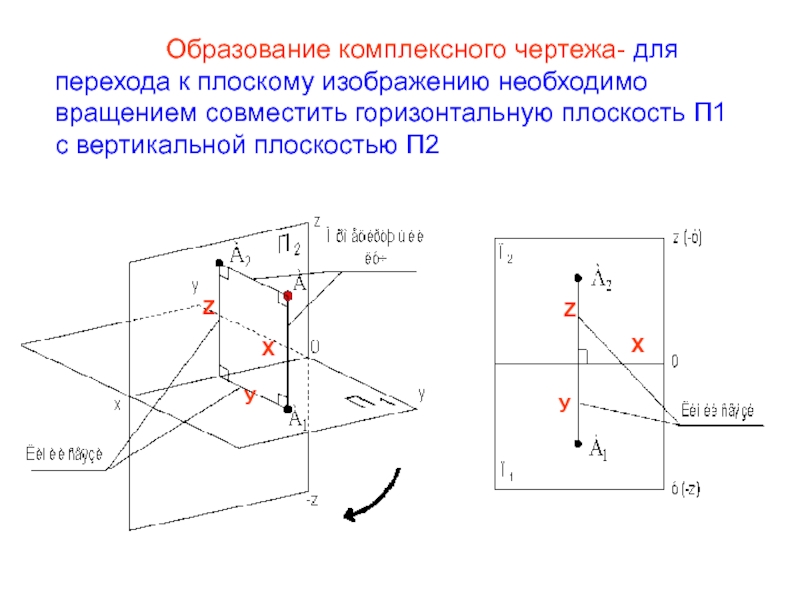
Образование комплексного чертежа-
для перехода к плоскому изображению необходимо вращением совместить горизонтальную плоскость П1 с вертикальной плоскостью П2
Х
Х
У
У
Z
Z
Слайд 16
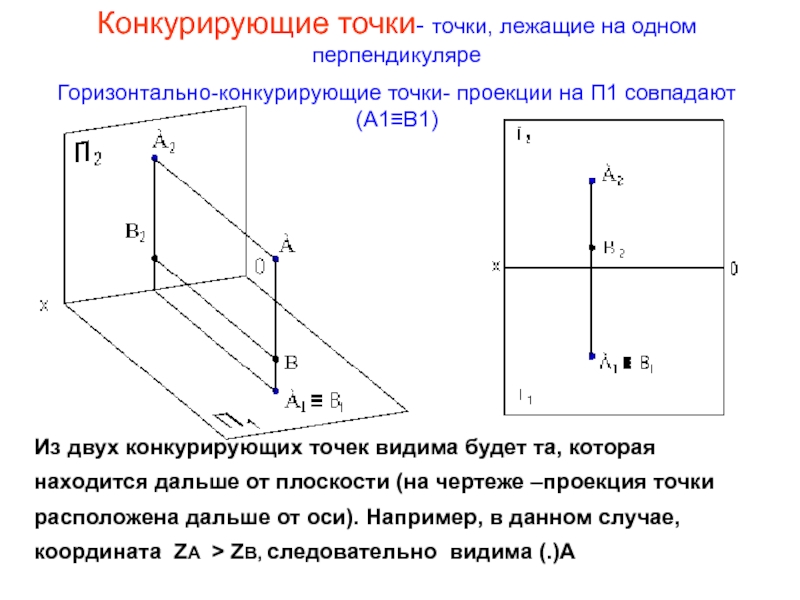
Конкурирующие точки- точки, лежащие на одном перпендикуляре
Горизонтально-конкурирующие точки- проекции на П1
совпадают (А1≡В1)
Из двух конкурирующих точек видима будет та, которая находится дальше от плоскости (на чертеже –проекция точки расположена дальше от оси). Например, в данном случае, координата ZА > ZВ, следовательно видима (.)А
Слайд 17
Фронтально- конкурирующие точки- проекции на П2 совпадают (С2≡D2) . Т.к. УD
> УС, видима (.) D
Слайд 18
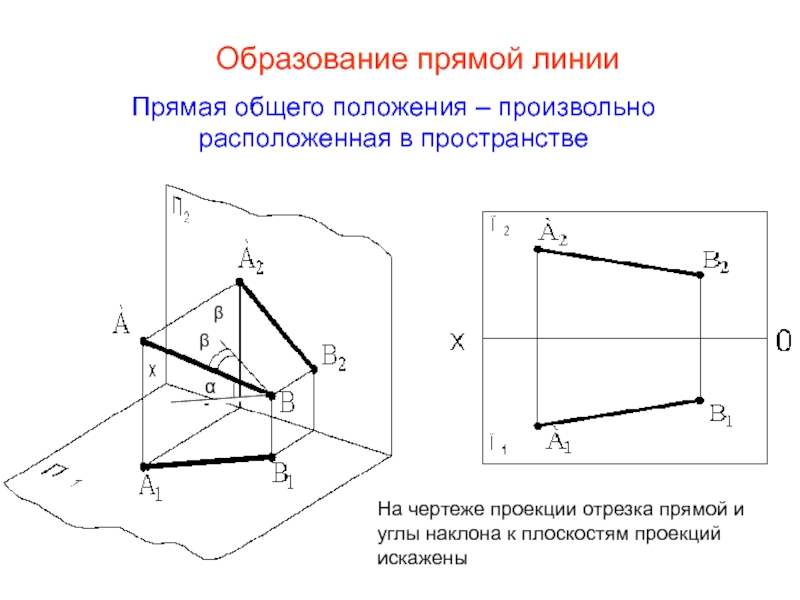
Образование
прямой линии
Прямая общего положения – произвольно расположенная в пространстве
Прямая общего положения – произвольно расположенная в пространстве
β
α
β
На чертеже проекции отрезка прямой и углы наклона к плоскостям проекций искажены
Слайд 19
Прямые
частного положения
1.Линии уровня- прямые, параллельные плоскостям проекций
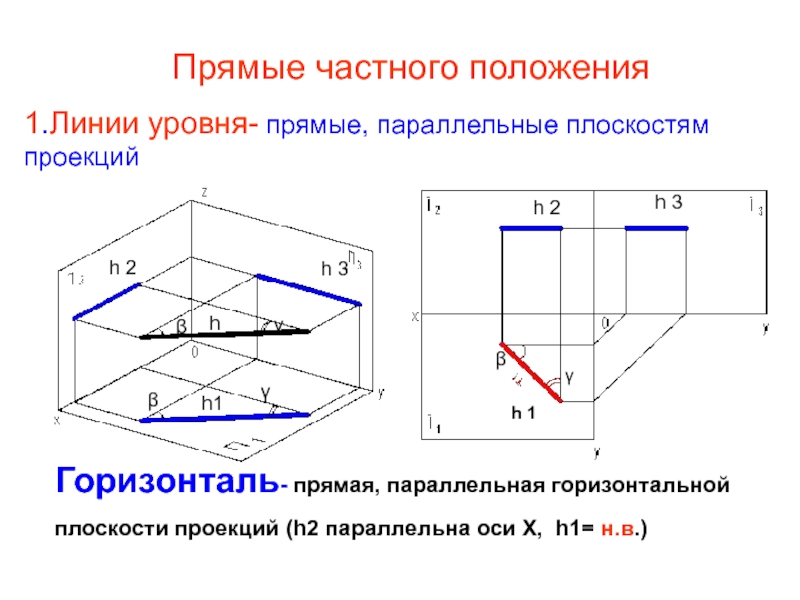
1.Линии уровня- прямые, параллельные плоскостям проекций
β
γ
h 1
γ
h
Горизонталь- прямая, параллельная горизонтальной плоскости проекций (h2 параллельна оси Х, h1= н.в.)
β
γ
β
h 3
h 2
h 3
h 2
h1
Слайд 20
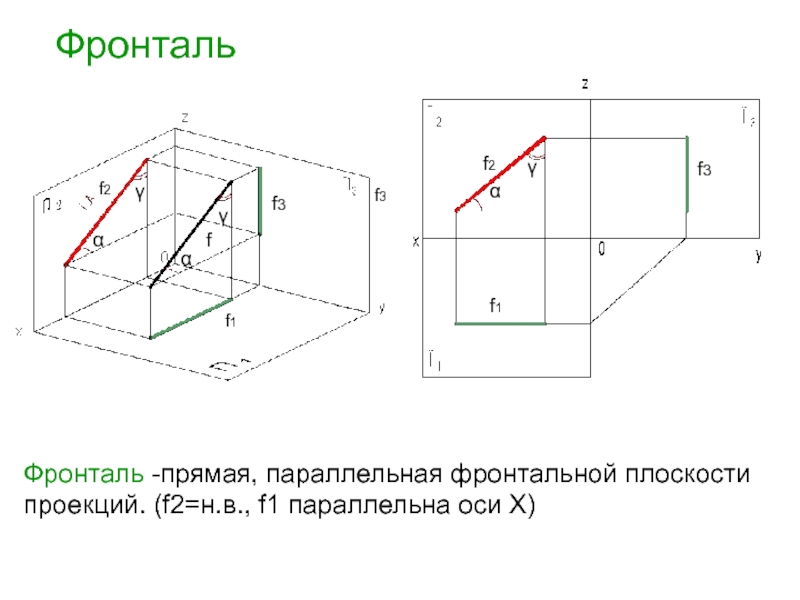
Фронталь
f1
f3
f2
α
f3
f1
f2
α
γ
α
γ
f
Фронталь -прямая, параллельная фронтальной плоскости проекций. (f2=н.в., f1 параллельна оси
Х)
γ
f3
Слайд 21
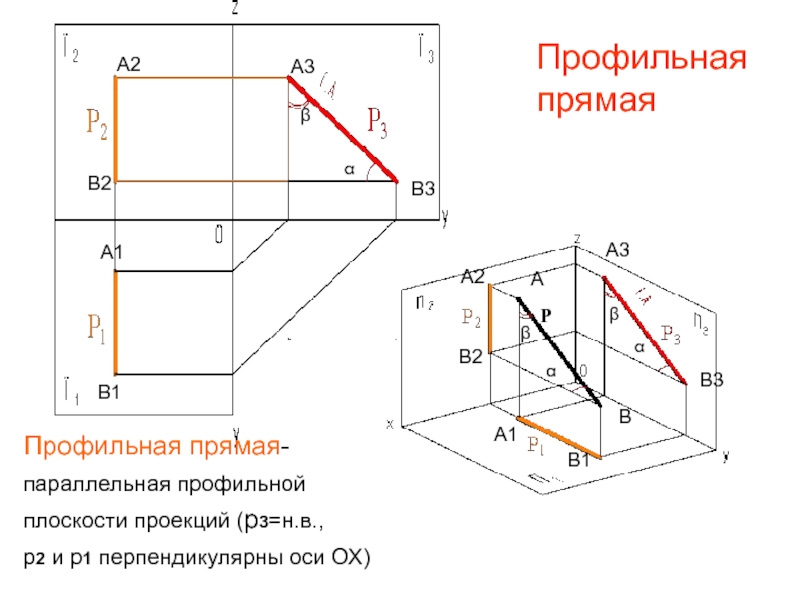
Профильная
прямая
β
α
α
α
β
β
P
Профильная прямая-
параллельная профильной
плоскости проекций (р3=н.в.,
р2 и р1 перпендикулярны оси ОХ)
А2
А1
А1
А2
А3
А3
В1
В1
В2
В2
В3
В3
В
А
Слайд 22
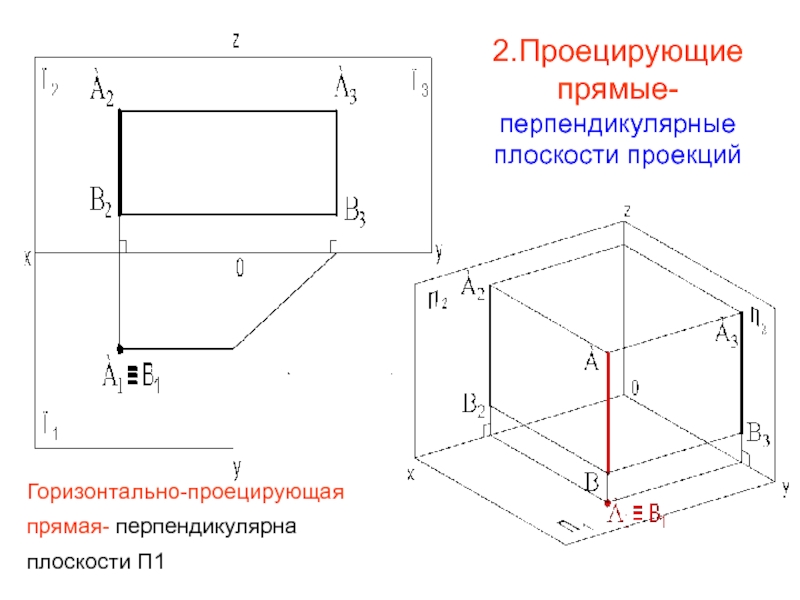
2.Проецирующие прямые- перпендикулярные плоскости проекций
Горизонтально-проецирующая прямая- перпендикулярна плоскости
П1
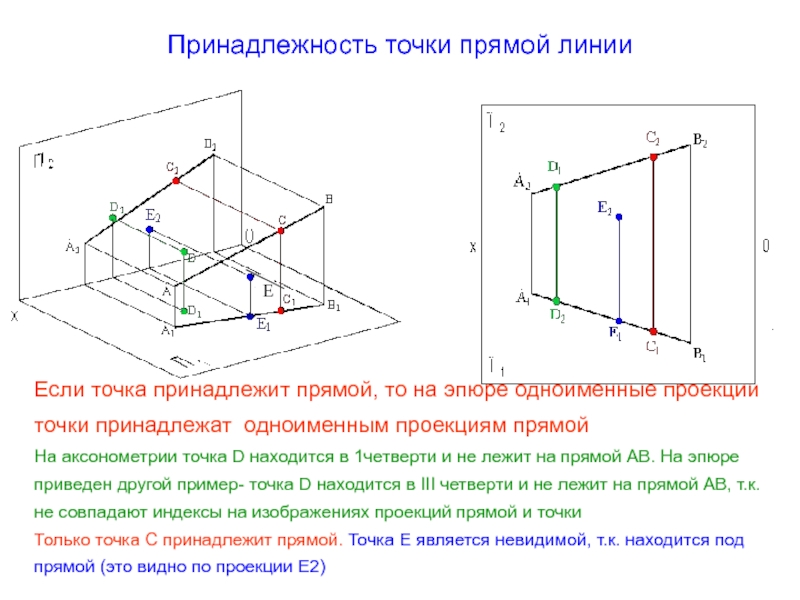
Слайд 25Принадлежность точки прямой линии
Е
Если точка принадлежит прямой, то на эпюре одноименные
проекции точки принадлежат одноименным проекциям прямой
На аксонометрии точка D находится в 1четверти и не лежит на прямой АВ. На эпюре приведен другой пример- точка D находится в III четверти и не лежит на прямой АВ, т.к. не совпадают индексы на изображениях проекций прямой и точки
Только точка С принадлежит прямой. Точка Е является невидимой, т.к. находится под прямой (это видно по проекции Е2)
На аксонометрии точка D находится в 1четверти и не лежит на прямой АВ. На эпюре приведен другой пример- точка D находится в III четверти и не лежит на прямой АВ, т.к. не совпадают индексы на изображениях проекций прямой и точки
Только точка С принадлежит прямой. Точка Е является невидимой, т.к. находится под прямой (это видно по проекции Е2)
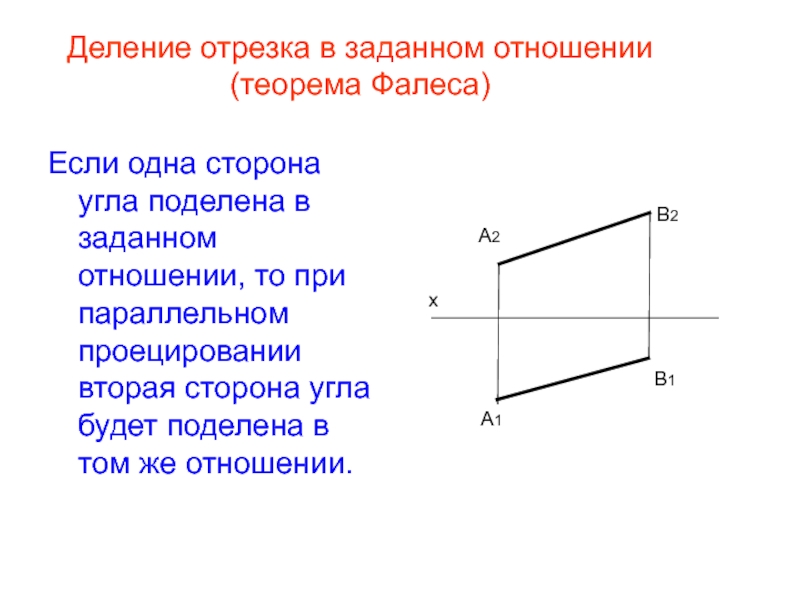
Слайд 26Деление отрезка в заданном отношении (теорема Фалеса)
Если одна сторона угла поделена
в заданном отношении, то при параллельном проецировании вторая сторона угла будет поделена в том же отношении.
А2
В2
А1
В1
х
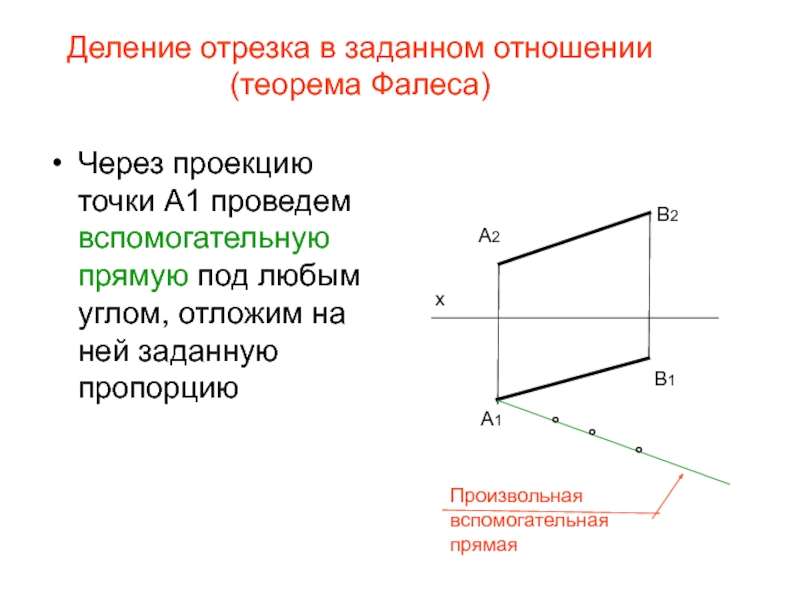
Слайд 27Деление отрезка в заданном отношении (теорема Фалеса)
Через проекцию точки А1 проведем
вспомогательную прямую под любым углом, отложим на ней заданную пропорцию
А2
В2
А1
В1
°
°
°
х
Произвольная вспомогательная прямая
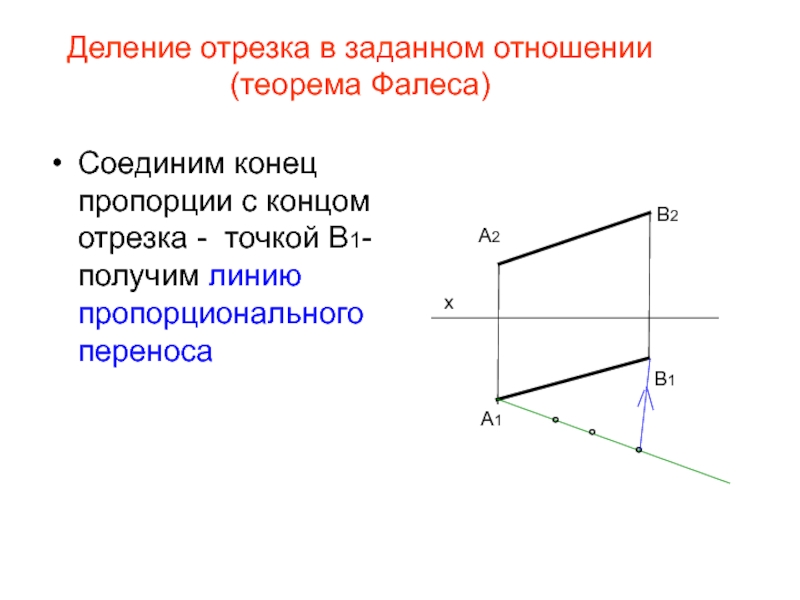
Слайд 28Деление отрезка в заданном отношении (теорема Фалеса)
Соединим конец пропорции с концом
отрезка - точкой В1-получим линию пропорционального переноса
А2
В2
А1
В1
°
°
°
х
Слайд 29Деление отрезка в заданном отношении (теорема Фалеса)
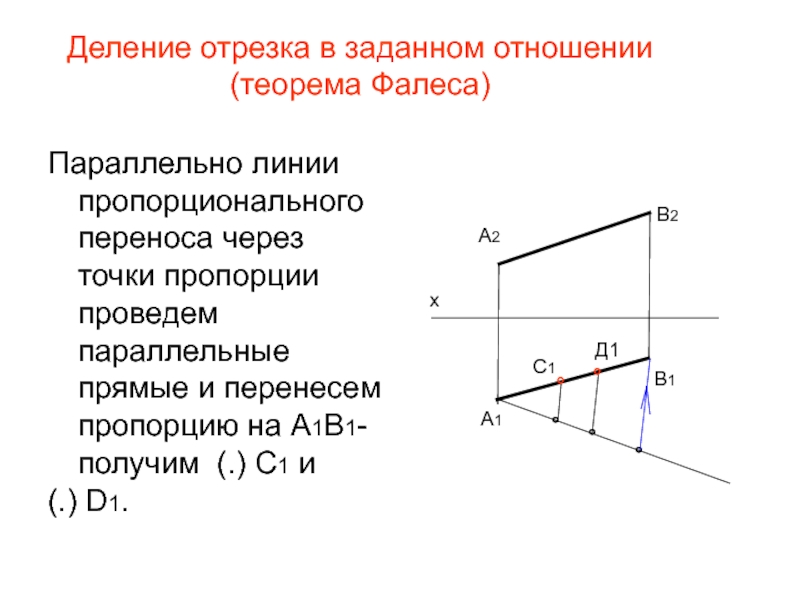
Параллельно линии пропорционального переноса через
точки пропорции проведем параллельные прямые и перенесем пропорцию на А1В1- получим (.) С1 и
(.) D1.
(.) D1.
А2
В2
А1
В1
°
°
°
С1
Д1
°
°
х
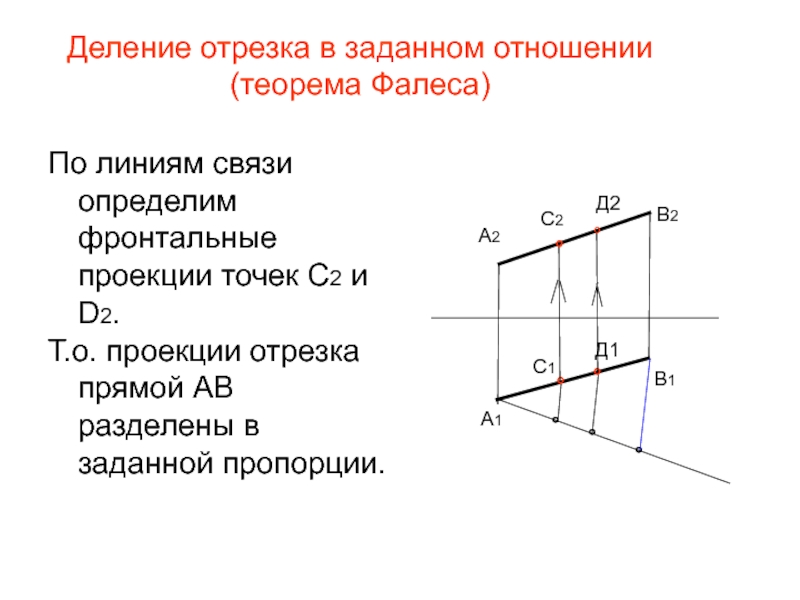
Слайд 30Деление отрезка в заданном отношении (теорема Фалеса)
По линиям связи определим фронтальные
проекции точек С2 и D2.
Т.о. проекции отрезка прямой АВ разделены в заданной пропорции.
Т.о. проекции отрезка прямой АВ разделены в заданной пропорции.
А2
В2
А1
В1
°
°
°
С1
Д1
°
°
С2
Д2
°
°
Слайд 31Определение натуральной величины отрезка прямой линии
в'
α
α
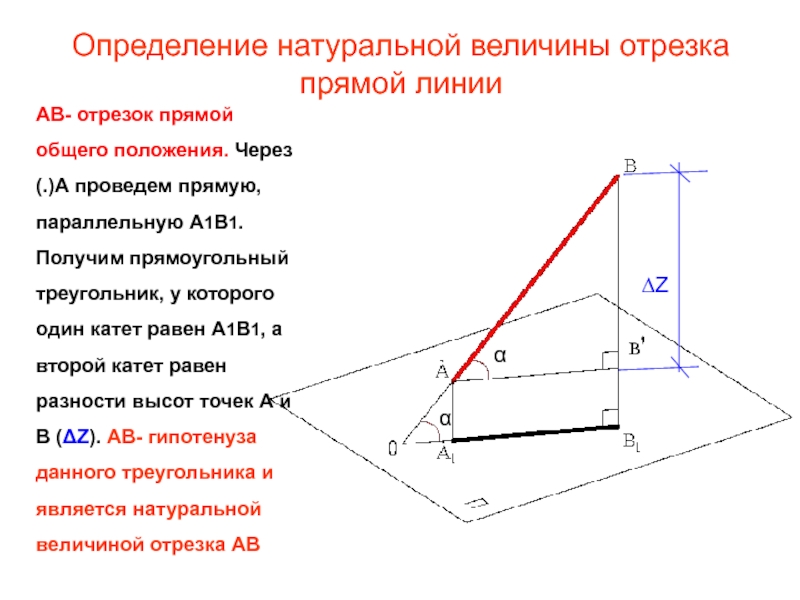
АВ- отрезок прямой общего положения. Через
(.)А проведем прямую, параллельную А1В1. Получим прямоугольный треугольник, у которого один катет равен А1В1, а второй катет равен разности высот точек А и В (ΔZ). АВ- гипотенуза данного треугольника и является натуральной величиной отрезка АВ
∆Z
Слайд 32Определение натуральной величины отрезка прямой линии
Теорема: Натуральная величина отрезка прямой
равна гипотенузе прямоугольного треугольника, у которого один катет есть проекция отрезка на плоскость, а другой катет равен разности расстояний от концов отрезка до данной плоскости.
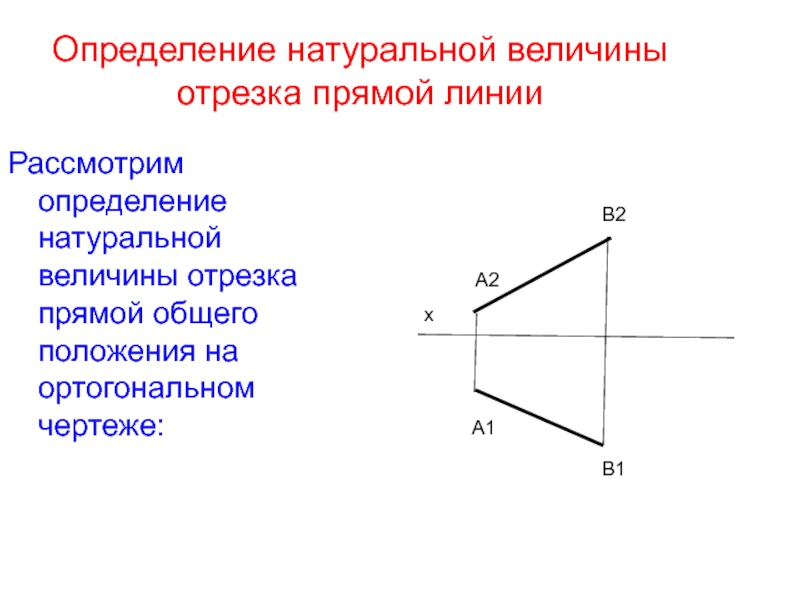
Слайд 33Определение натуральной величины отрезка прямой линии
Рассмотрим определение натуральной величины отрезка прямой
общего положения на ортогональном чертеже:
х
А2
В2
А1
В1
Слайд 34Определение натуральной величины отрезка прямой линии
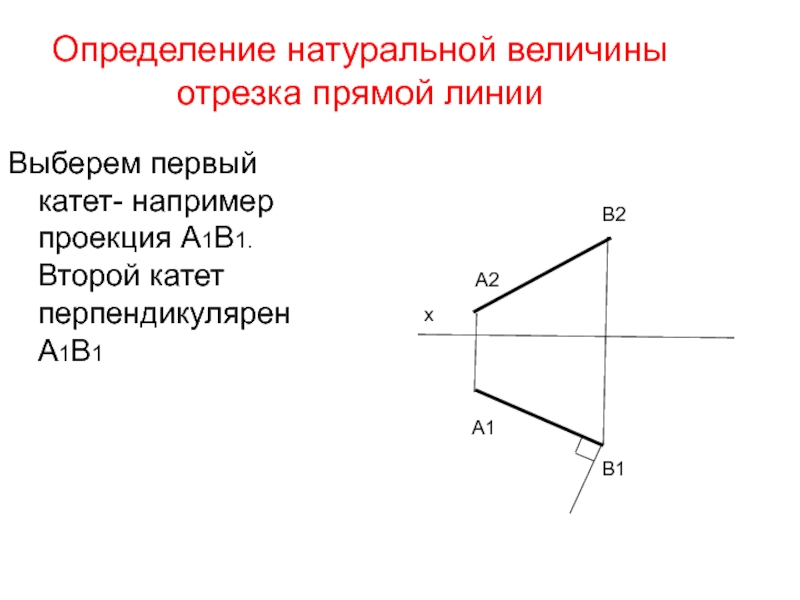
Выберем первый катет- например проекция А1В1.
Второй катет перпендикулярен А1В1
х
А2
В2
А1
В1
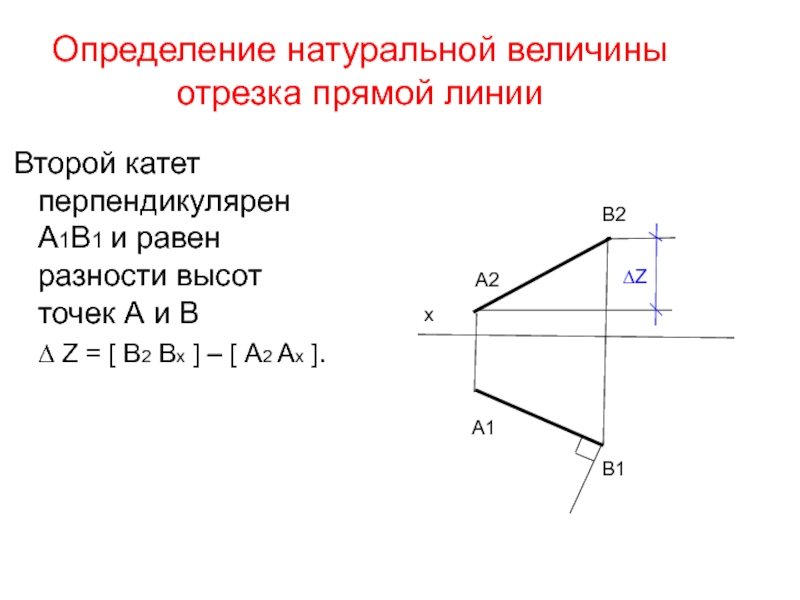
Слайд 35Определение натуральной величины отрезка прямой линии
Второй катет перпендикулярен А1В1 и
равен разности высот точек А и В
∆ Z = [ B2 Bx ] – [ А2 Ах ].
∆ Z = [ B2 Bx ] – [ А2 Ах ].
х
А2
В2
А1
В1
∆Z
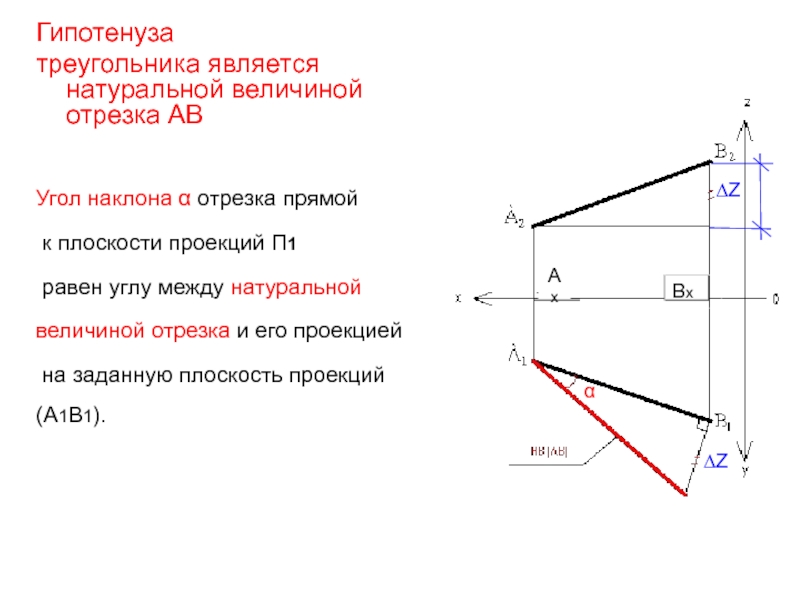
Слайд 36Гипотенуза
треугольника является натуральной величиной отрезка АВ
∆Z
∆Z
α
Ах
Вх
Угол наклона α отрезка прямой
к плоскости проекций П1
равен углу между натуральной
величиной отрезка и его проекцией
на заданную плоскость проекций (А1В1).
равен углу между натуральной
величиной отрезка и его проекцией
на заданную плоскость проекций (А1В1).
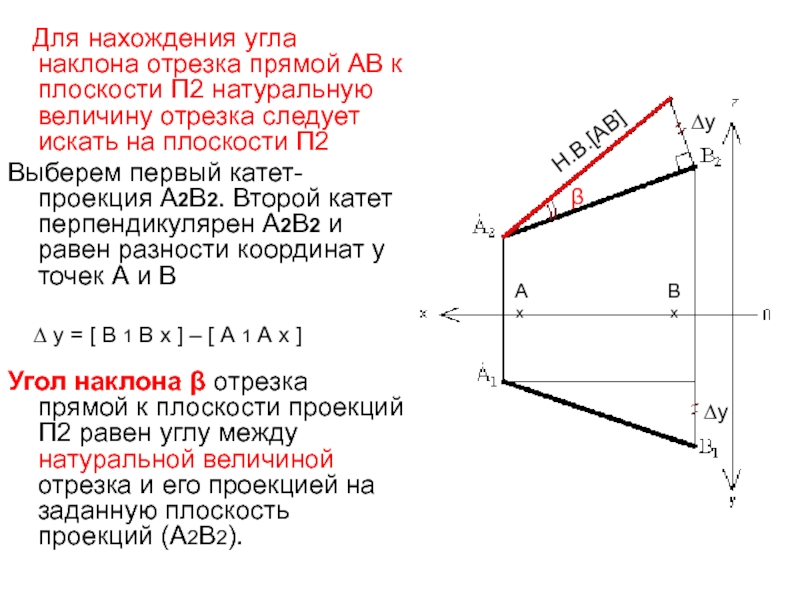
Слайд 37 Для нахождения угла наклона отрезка прямой АВ к
плоскости П2 натуральную величину отрезка следует искать на плоскости П2
Выберем первый катет- проекция А2В2. Второй катет перпендикулярен А2В2 и равен разности координат у точек А и В
∆ y = [ B 1 B x ] – [ А 1 А х ]
Угол наклона β отрезка прямой к плоскости проекций П2 равен углу между натуральной величиной отрезка и его проекцией на заданную плоскость проекций (А2В2).
Выберем первый катет- проекция А2В2. Второй катет перпендикулярен А2В2 и равен разности координат у точек А и В
∆ y = [ B 1 B x ] – [ А 1 А х ]
Угол наклона β отрезка прямой к плоскости проекций П2 равен углу между натуральной величиной отрезка и его проекцией на заданную плоскость проекций (А2В2).
β
∆у
∆у
Н.В.[АВ]
Ах
Вх
Слайд 38
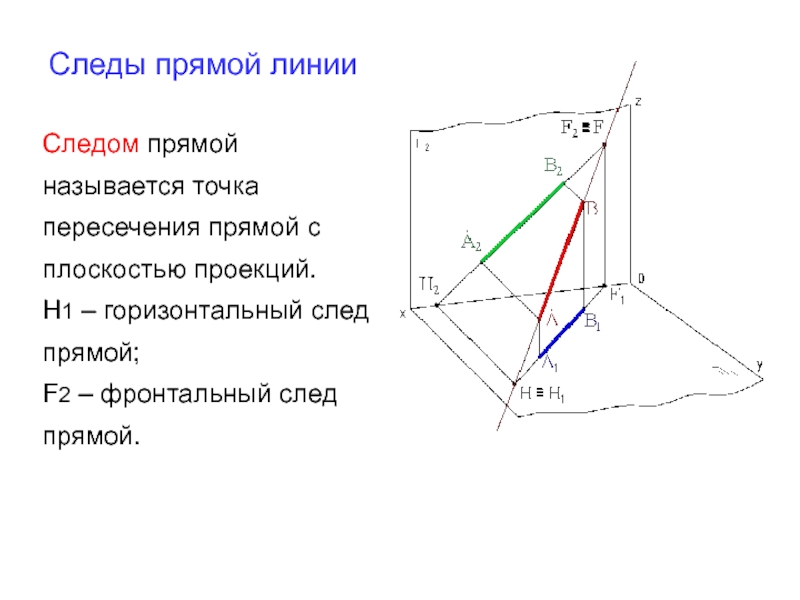
Следы прямой линии
Следом прямой
называется точка пересечения прямой с плоскостью проекций.
Н1
– горизонтальный след прямой;
F2 – фронтальный след прямой.
F2 – фронтальный след прямой.
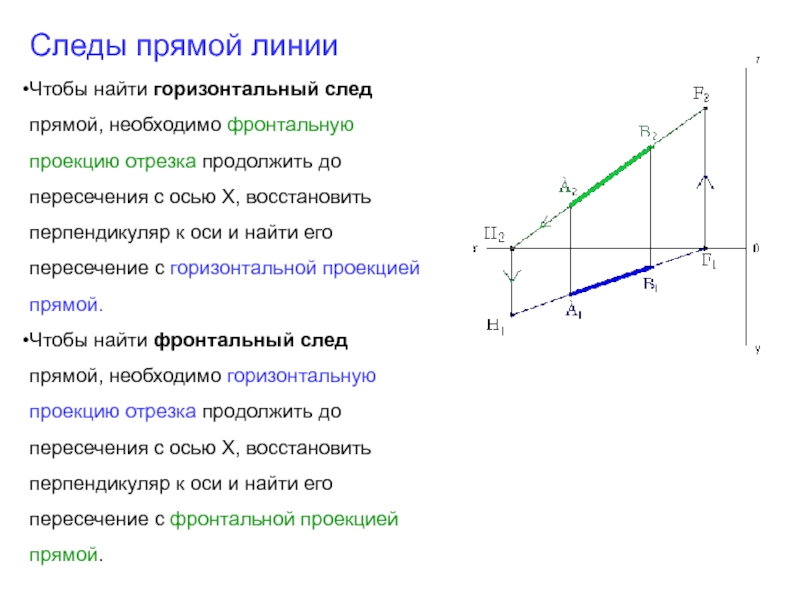
Слайд 39Следы прямой линии
Чтобы найти горизонтальный след прямой, необходимо фронтальную проекцию отрезка
продолжить до пересечения с осью Х, восстановить перпендикуляр к оси и найти его пересечение с горизонтальной проекцией прямой.
Чтобы найти фронтальный след прямой, необходимо горизонтальную проекцию отрезка продолжить до пересечения с осью Х, восстановить перпендикуляр к оси и найти его пересечение с фронтальной проекцией прямой.
Чтобы найти фронтальный след прямой, необходимо горизонтальную проекцию отрезка продолжить до пересечения с осью Х, восстановить перпендикуляр к оси и найти его пересечение с фронтальной проекцией прямой.
