Данилова У.Б., Елисеева О.И.
Московский государственный технический университет имени Н.Э.Баумана
2015г.
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Взаимное положение прямой и плоскости, двух плоскостей презентация
Содержание
- 1. Взаимное положение прямой и плоскости, двух плоскостей
- 2. Прямая параллельна плоскости, 1. Параллельность прямой
- 3. 1. Задаем горизонталь в плоскости, заданной прямыми
- 4. Две плоскости параллельны, если две пересекающиеся прямые
- 5. Задача 37а. Построить проекции плоскости, проходящей через
- 6. Задача 37б. Построить проекции плоскости, проходящей через
- 7. Перпендикулярность прямой и плоскости. Прямая перпендикулярна плоскости,
- 8. n b α, n v b
- 9. Задача 38б. Построить проекции прямой, проходящей через
- 10. Задача 39б. Построить проекции плоскости, перпендикулярной к
- 11. Задача 40. Построить горизонтальную проекцию прямой b,
Прямая параллельна плоскости, 1. Параллельность прямой и плоскости. если плоскости принадлежит прямая, параллельная данной. a II a: a II b (b v a) . a b a
Слайд 1Начертательная геометрия Семинар №5 Взаимное положение прямой и плоскости, двух плоскостей . Подготовили:
Слайд 2Прямая параллельна плоскости,
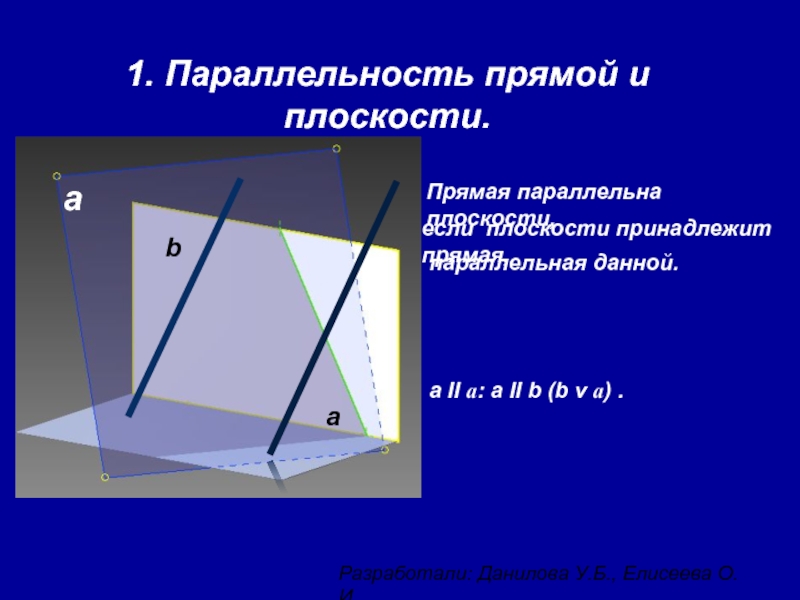
1. Параллельность прямой и плоскости.
если плоскости принадлежит прямая,
параллельная
данной.
a II a: a II b (b v a) .
a
b
a
Слайд 31. Задаем горизонталь в плоскости, заданной прямыми a и b.
2.
Через точку А проводим горизонталь, параллельную заданной.
Задача 35. Построить проекции горизонтальной прямой , проходящей через точку А параллельно плоскости, заданной прямыми а и b.
1’’
2’’
2’
1’
h’A
h’ab
h’’ab
h’’A
Слайд 4Две плоскости параллельны, если две пересекающиеся прямые одной плоскости параллельны двум
пересекающимся прямым второй плоскости.
1. Параллельность двух плоскостей.
a
b
a II b , т.к. a II c , b II d :
(a, b v a) , (c, d v b).
b
a
d
c
Слайд 5Задача 37а. Построить проекции плоскости, проходящей через точку А, параллельно плоскости,
заданной на чертеже. Плоскости задать горизонталью и фронталью.
Решение.
a-Плоскость общего положения, заданная треугольником BCD.
Задаем горизонталь в плоскости ВCD .
Задаем фронталь в плоскости ВCD.
Через точку А проводим горизонталь и фронталь, параллельно найденным:
hA” II h” , fA” II f”,
hA’ II h’, fA’ II f’.
1’’
h’’
1’
h’
f’
2’
2’’
f’’
hА’’
fА’’
hА’
fА’
Слайд 6Задача 37б. Построить проекции плоскости, проходящей через точку А, параллельно плоскости,
заданной на чертеже. Плоскости задать следами.
1’’
1’
f0b
Решение.
a-Плоскость общего положения, заданная следами.
Если α II β, то следы плоскости b должны быть параллельными следам плоскости a
Чтобы точка А (см. задачу 26 б) принадлежала плоскости β соответствующие проекции точки А должны принадлежать проекциям прямой, принадлежащей плоскости.
Задаем горизонталь, проходящую через точку А, h’ II hoα
Находим фронтальный след горизонтали точку 1.
Через точку 1’’ проводим фронтальный след плоскости β.
h0b
h’A
h”A
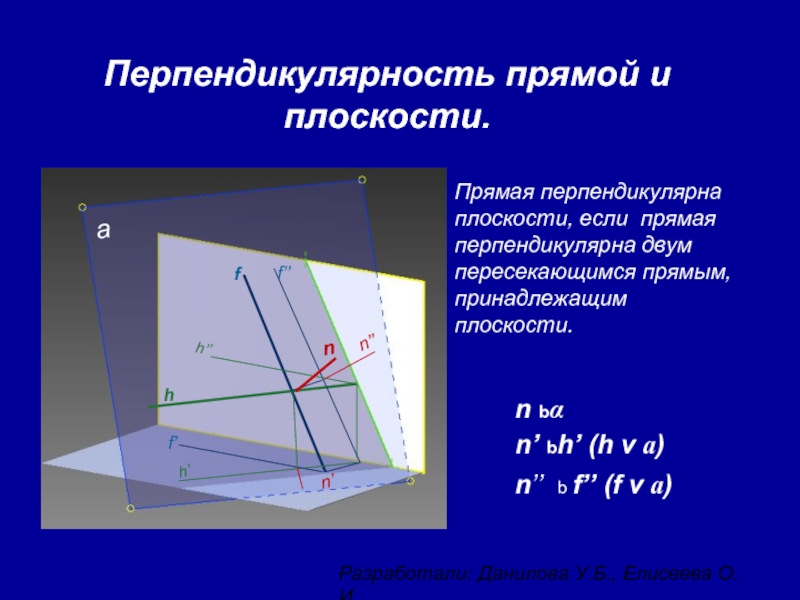
Слайд 7Перпендикулярность прямой и плоскости.
Прямая перпендикулярна плоскости, если прямая перпендикулярна двум пересекающимся
прямым, принадлежащим плоскости.
f
f’
f’’
h
h’
h’’
a
n
n’’
n’
n bα
n’ bh’ (h v a)
n’’ b f’’ (f v a)
Слайд 8n b α, n v b
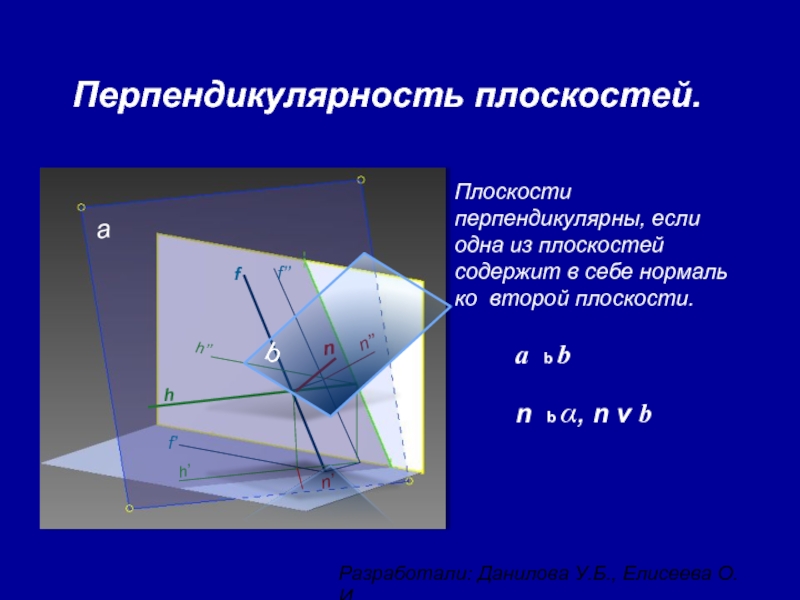
Перпендикулярность плоскостей.
Плоскости перпендикулярны, если одна из
плоскостей содержит в себе нормаль ко второй плоскости.
f
f’
f’’
h
h’
h’’
a
n
n’’
n’
b
a b b
Слайд 9Задача 38б. Построить проекции прямой, проходящей через точку А, перпендикулярно к
заданной плоскости.
Решение.
a-Плоскость общего положения, заданная треугольником ABC.
Задаем h v a
Задаем f v a
n” b f” , n’ b h’.
1’’
h’’
1’
h’
f’
2’
2’’
f’’
n’’
n’
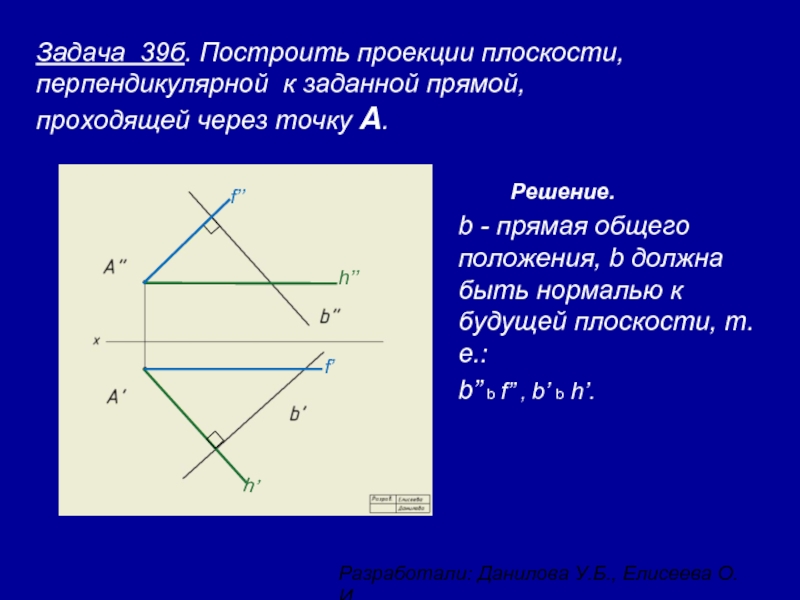
Слайд 10Задача 39б. Построить проекции плоскости, перпендикулярной к заданной прямой, проходящей через
точку А.
Решение.
b - прямая общего положения, b должна быть нормалью к будущей плоскости, т.е.:
b” b f” , b’ b h’.
h’’
h’
f’
f’’
Слайд 11Задача 40. Построить горизонтальную проекцию прямой b, пересекающей прямую a в
точке А, если прямые a и b взаимно перпендикулярны.
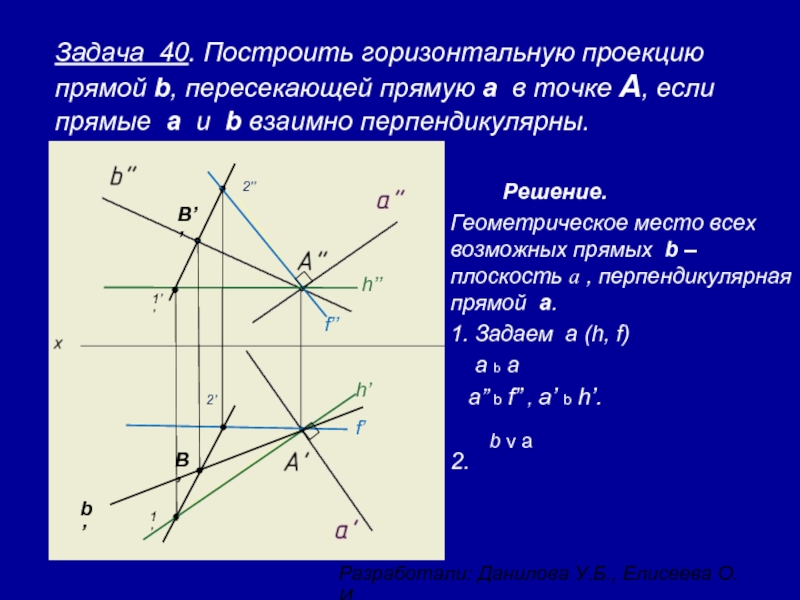
Решение.
Геометрическое место всех возможных прямых b –плоскость a , перпендикулярная прямой a.
1. Задаем a (h, f)
a b a
a” b f” , a’ b h’.
2.
1’’
h’’
1’
h’
f’
2’
2’’
f’’
В’
b v a
В’’
b’
