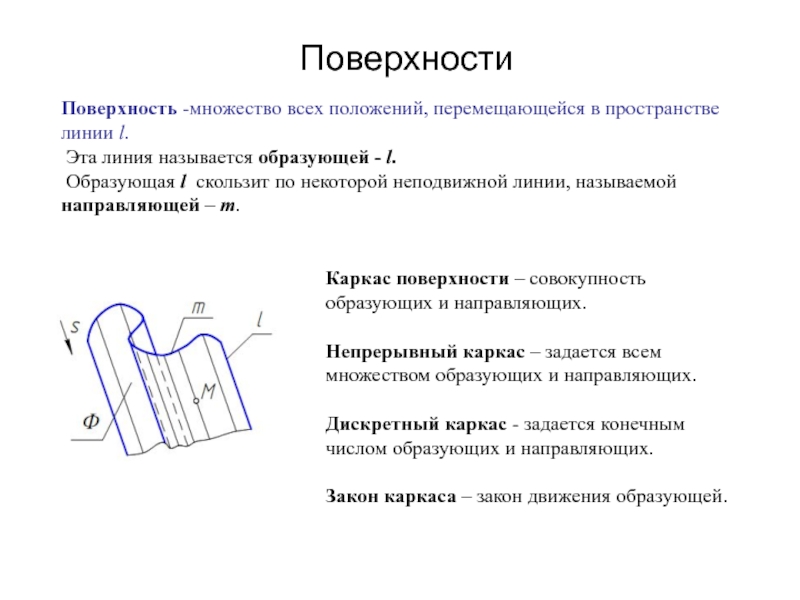
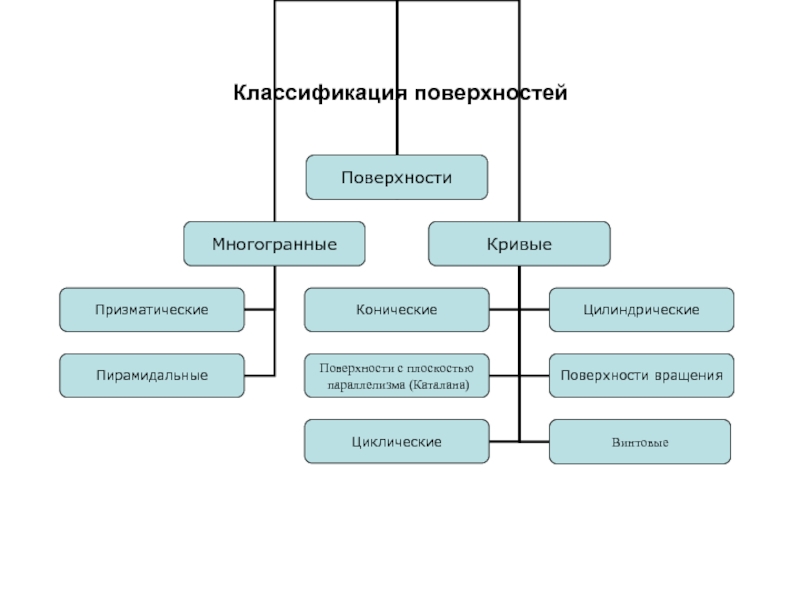
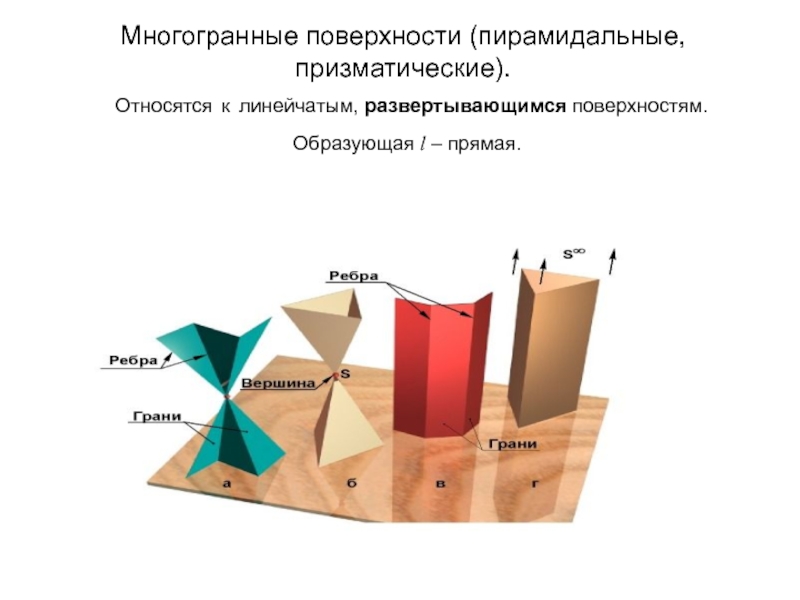
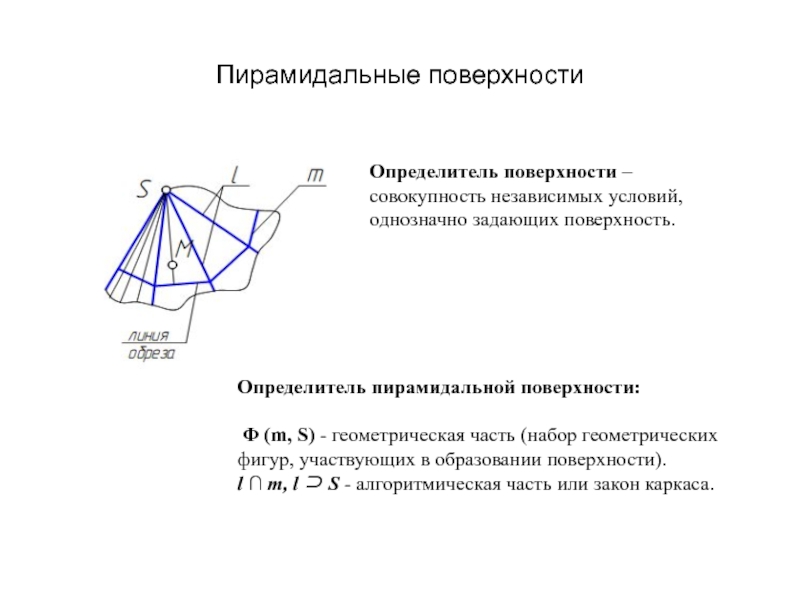
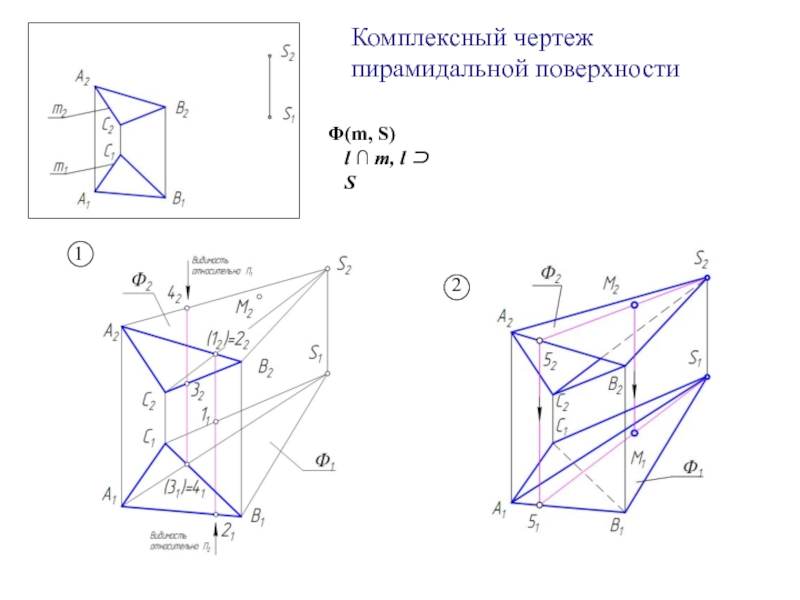
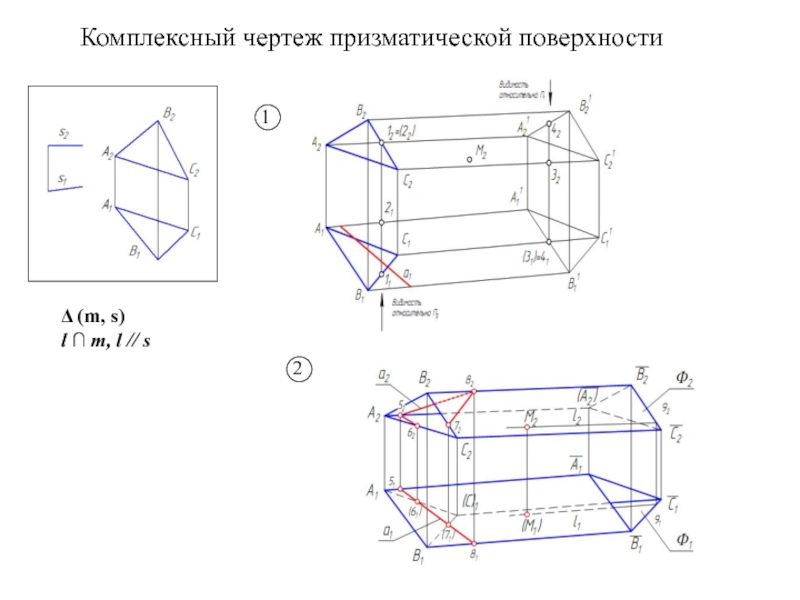
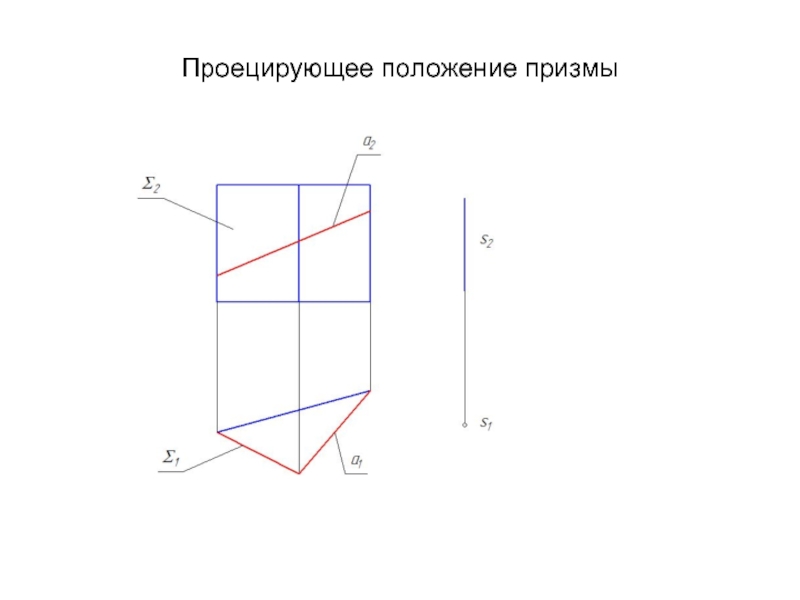
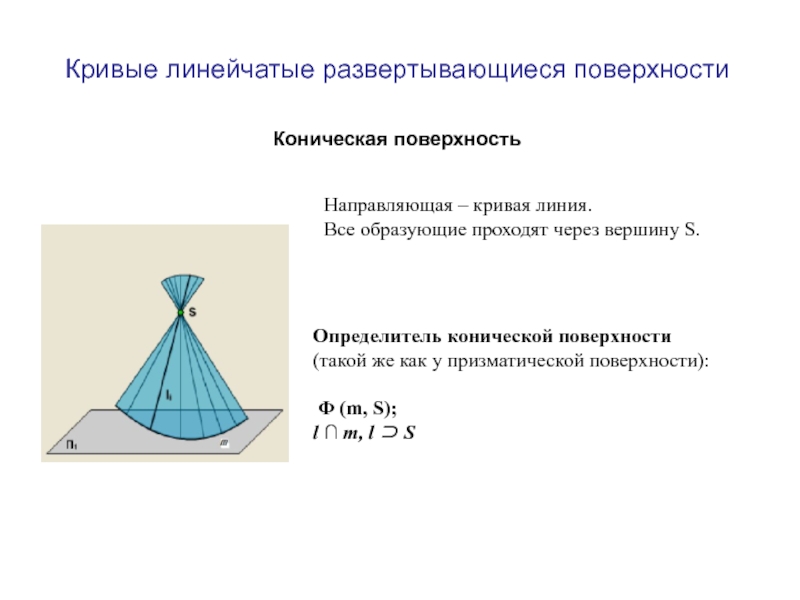
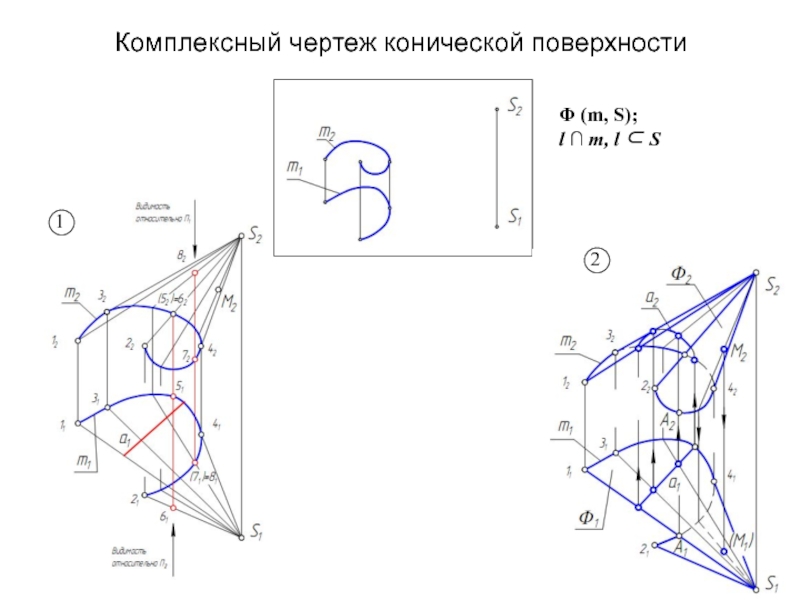
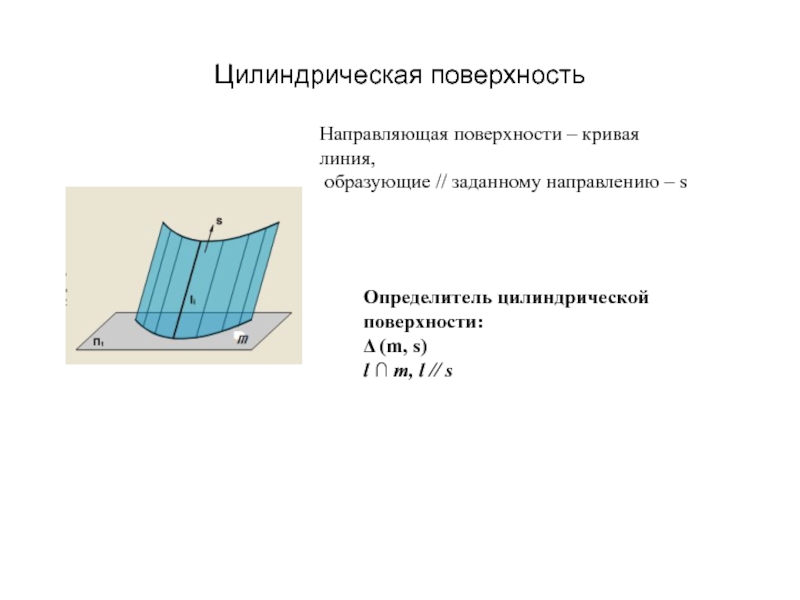
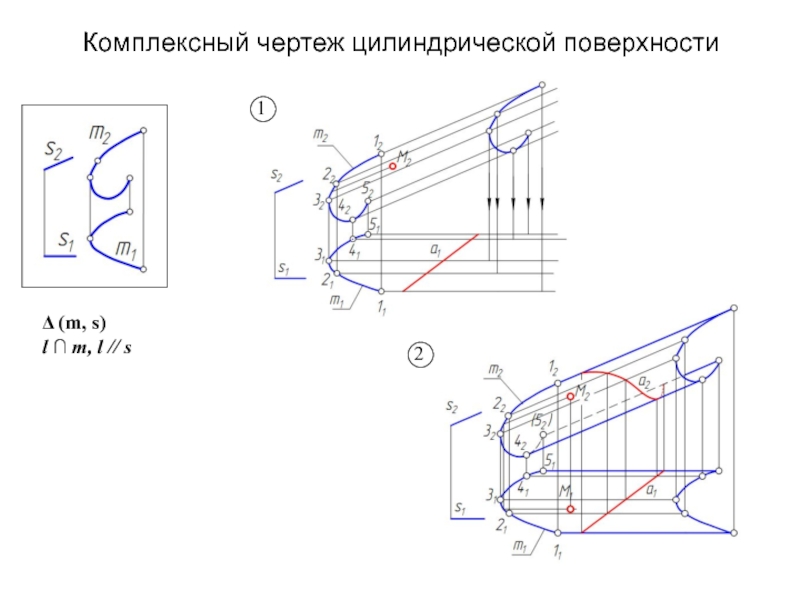
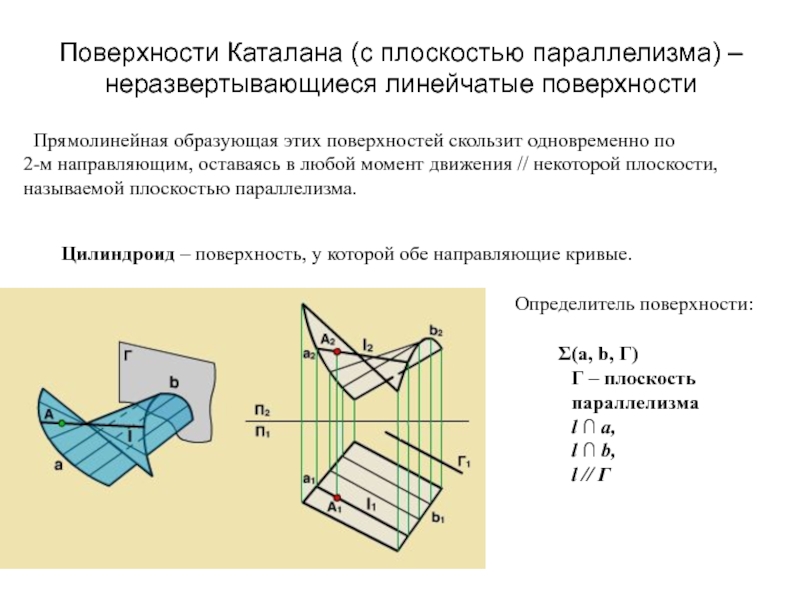
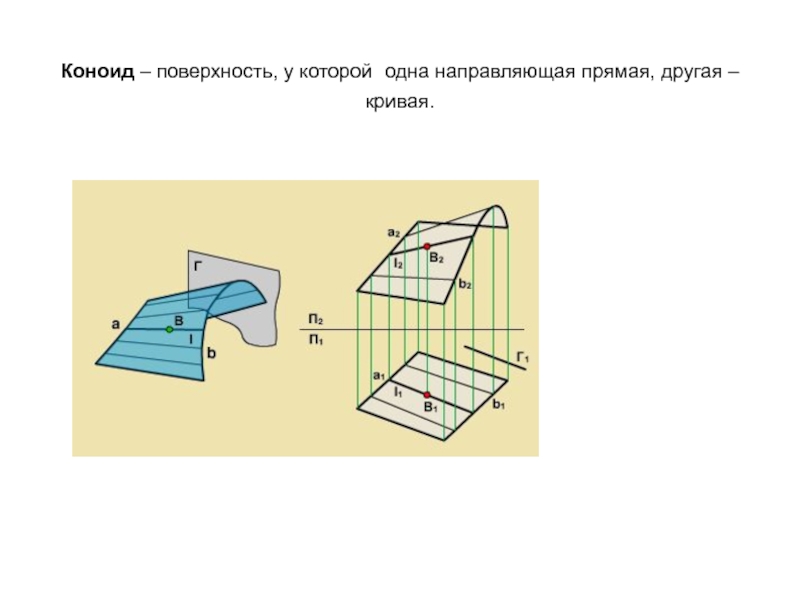
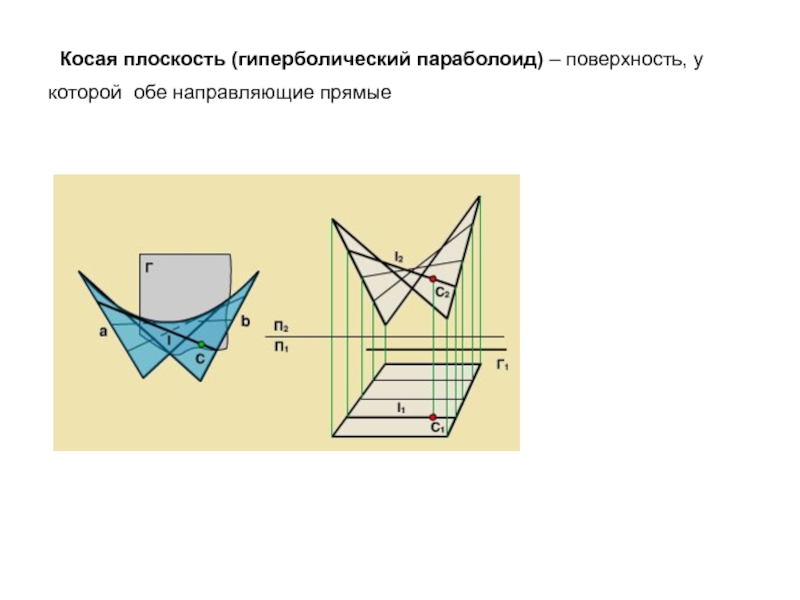
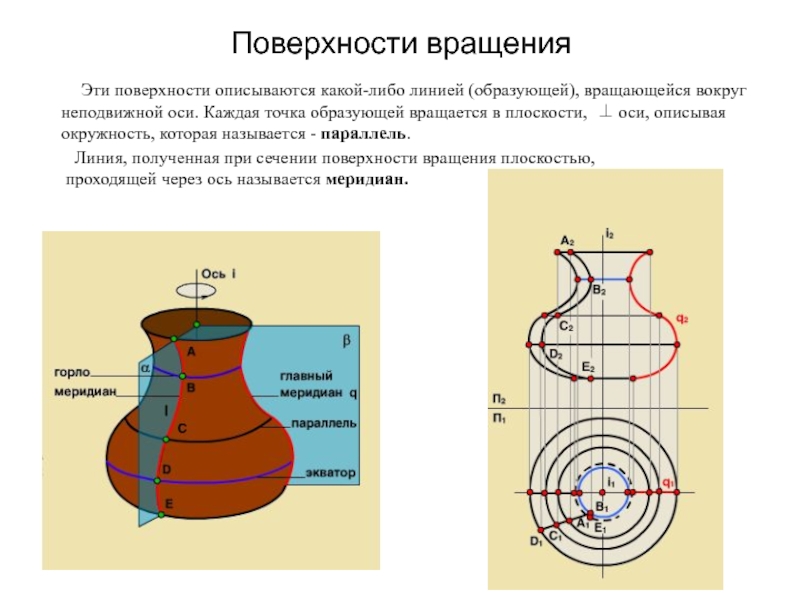
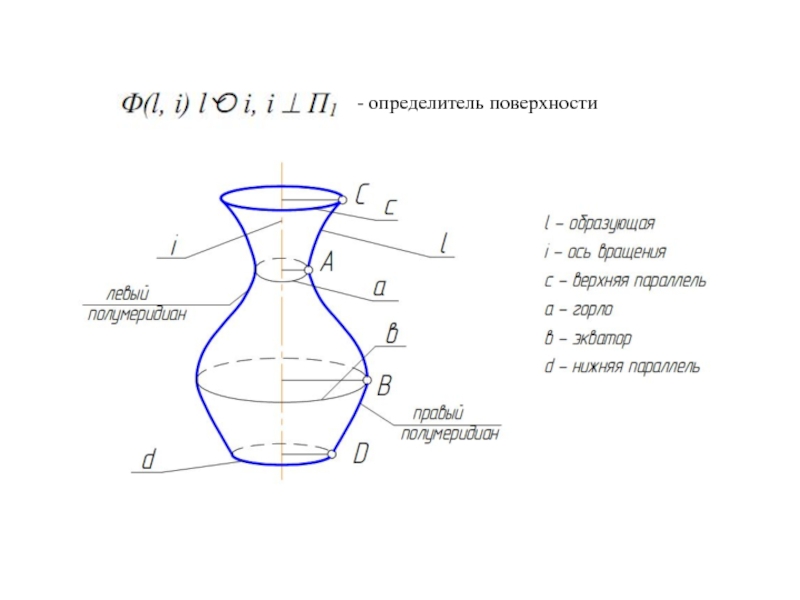
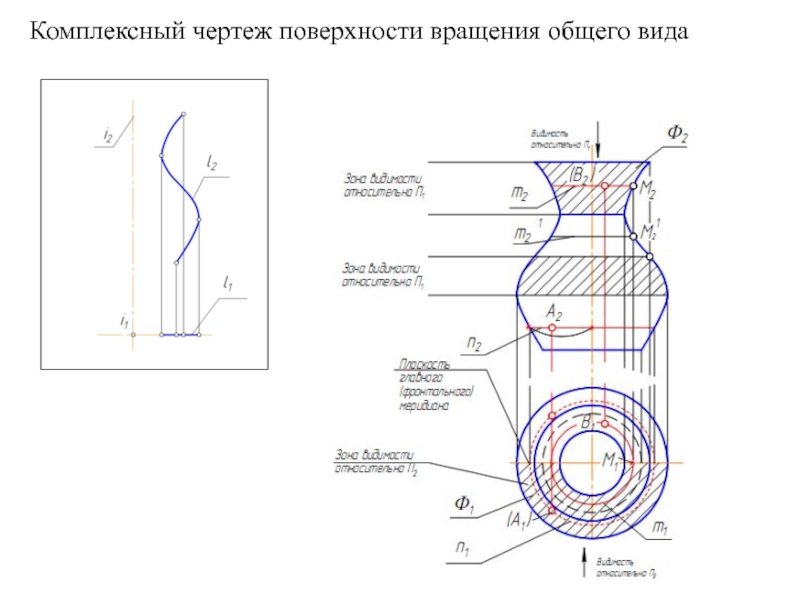
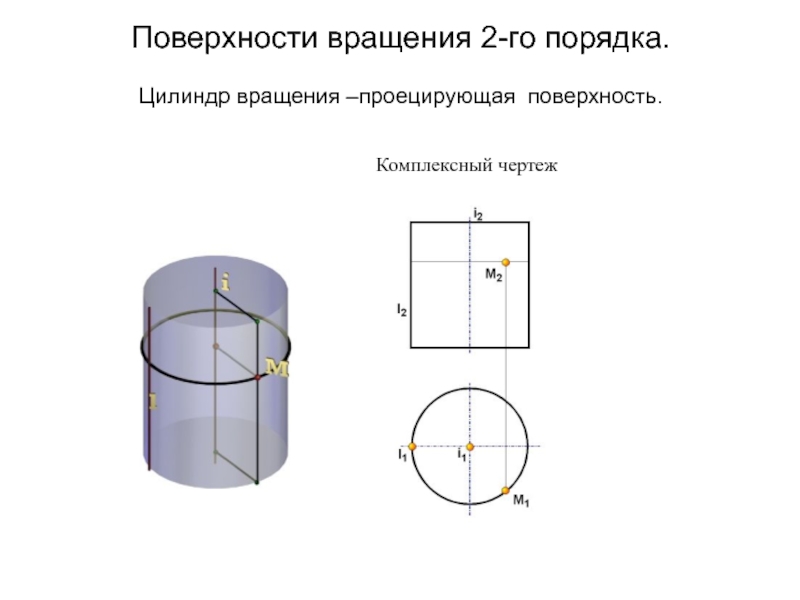
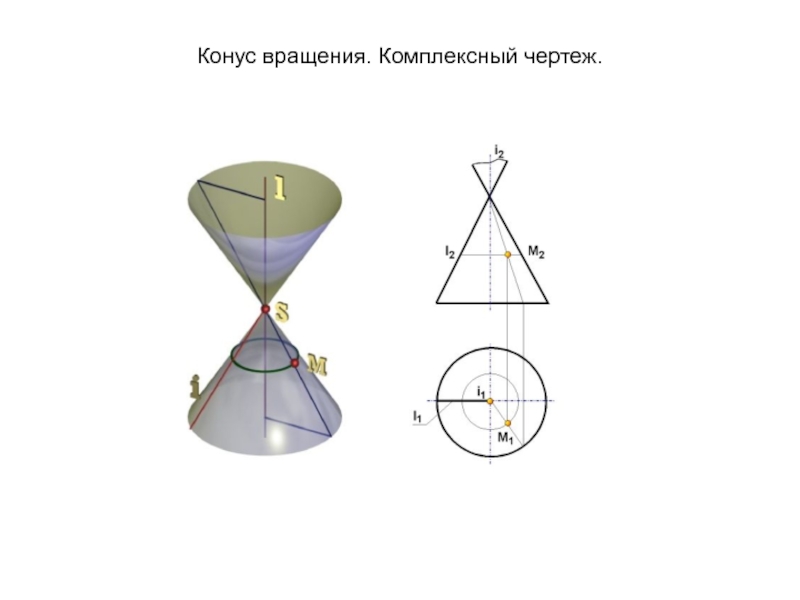
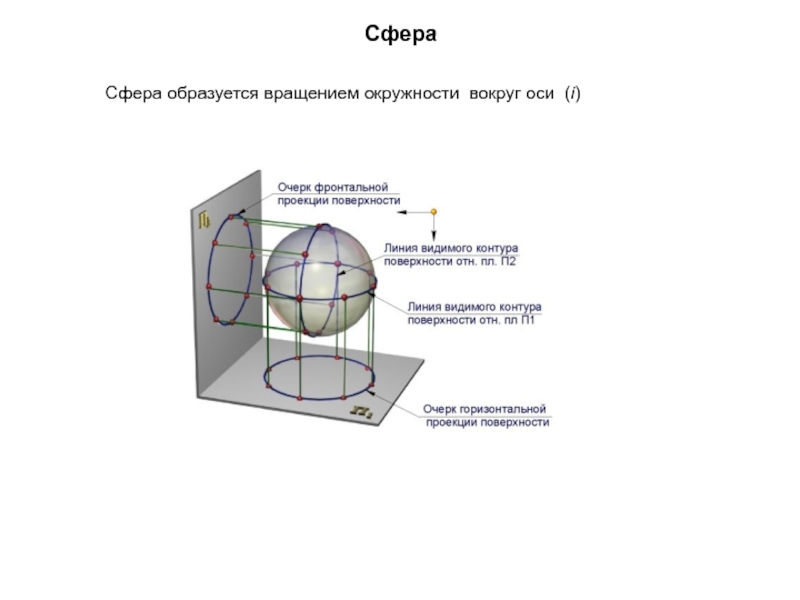
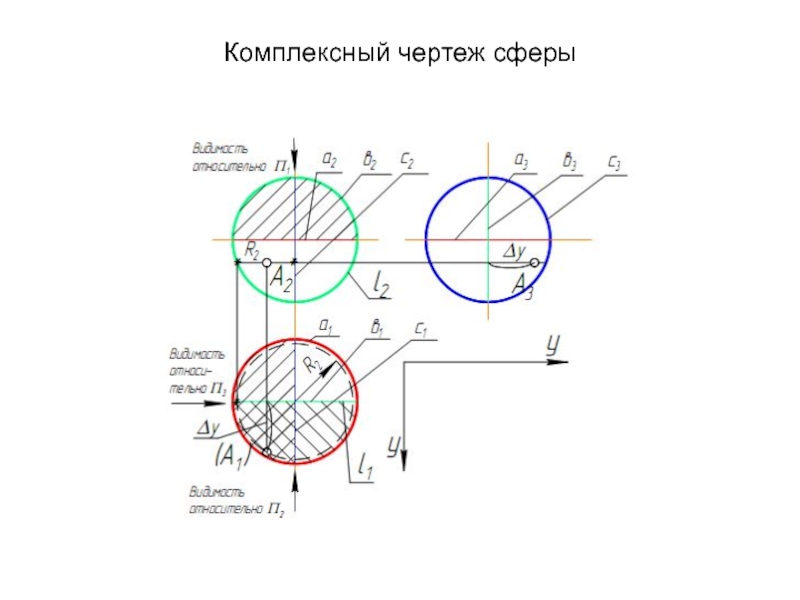
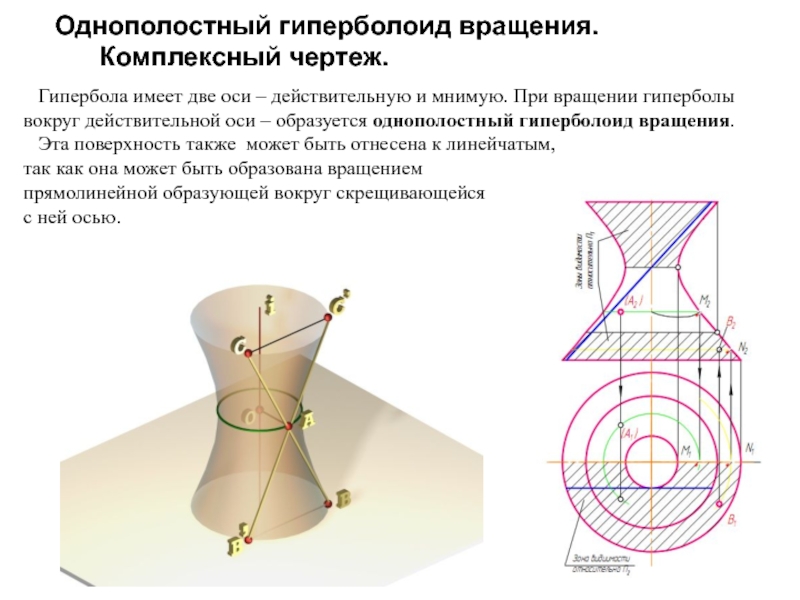
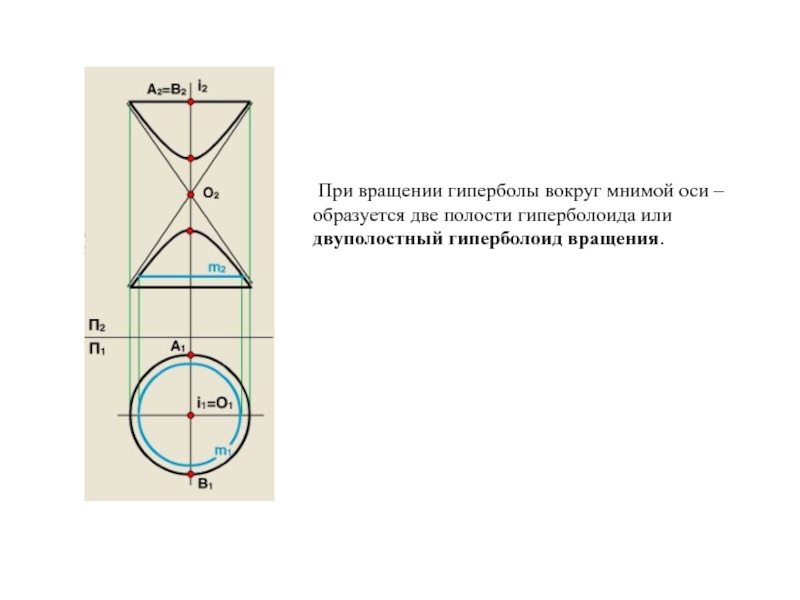
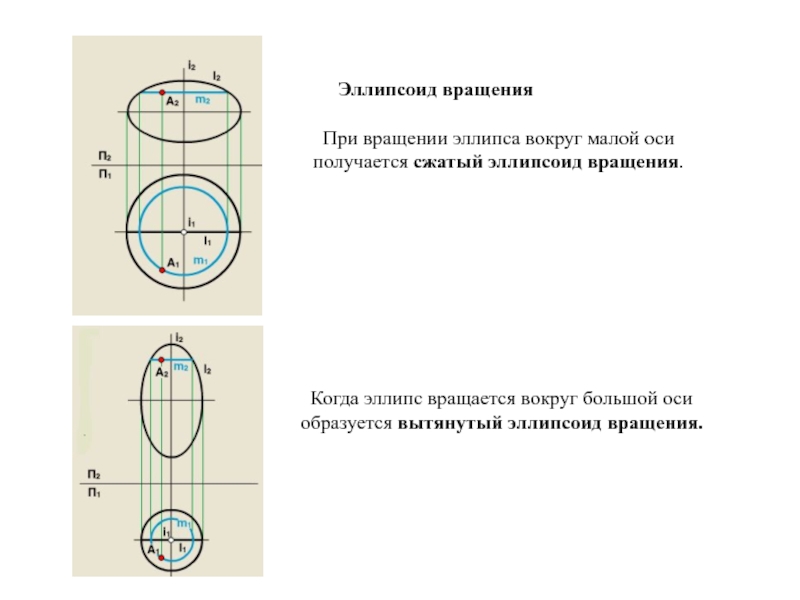
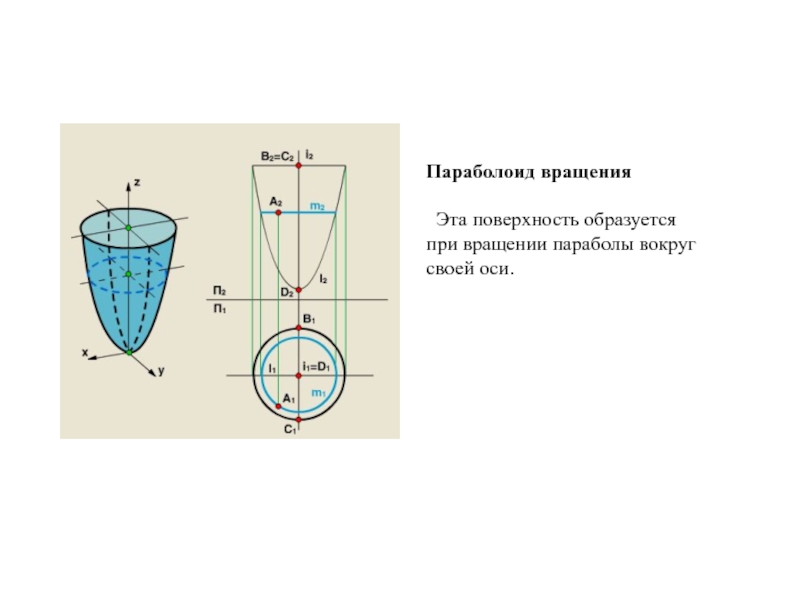
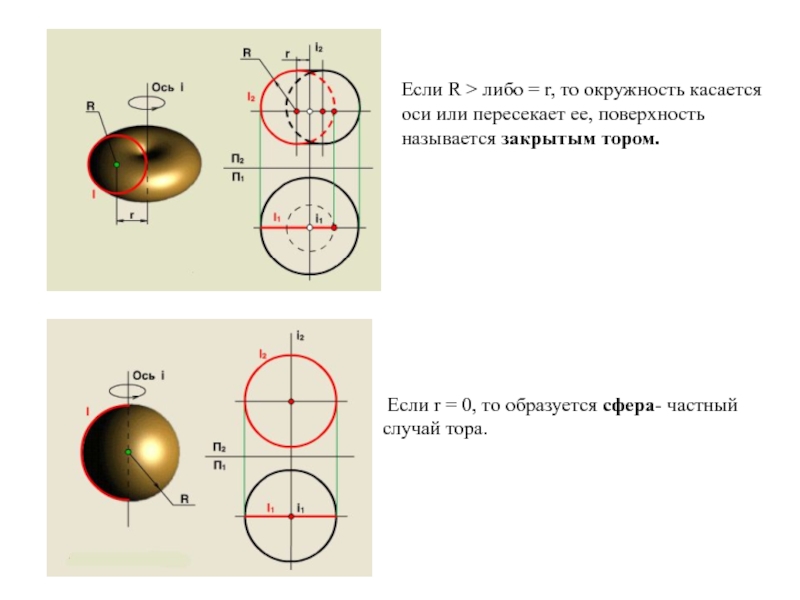
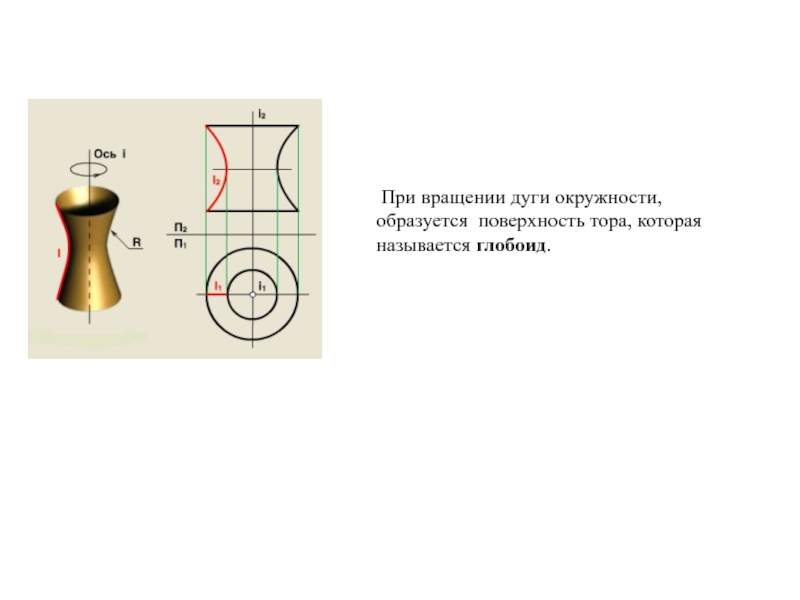
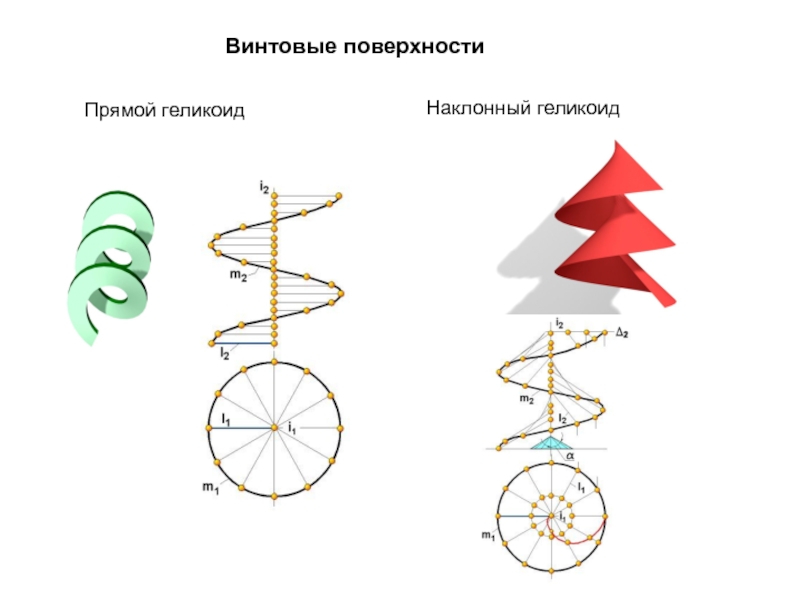
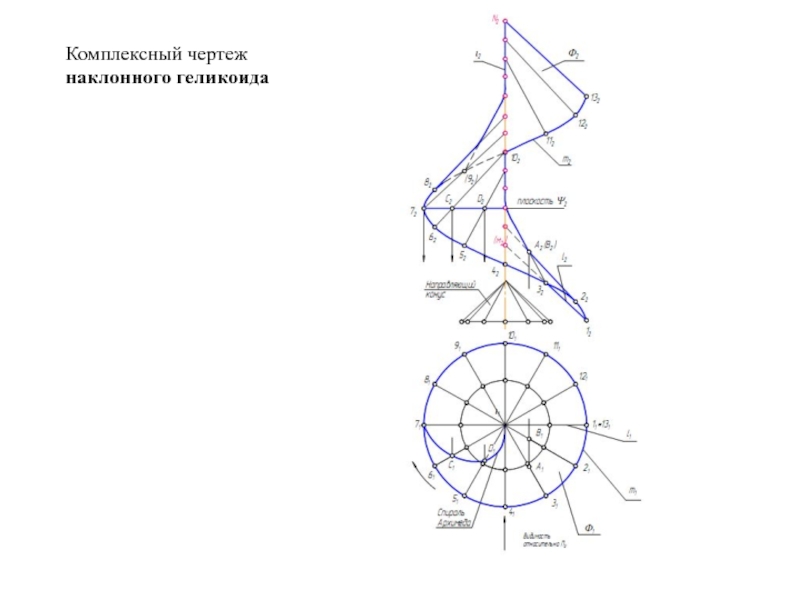
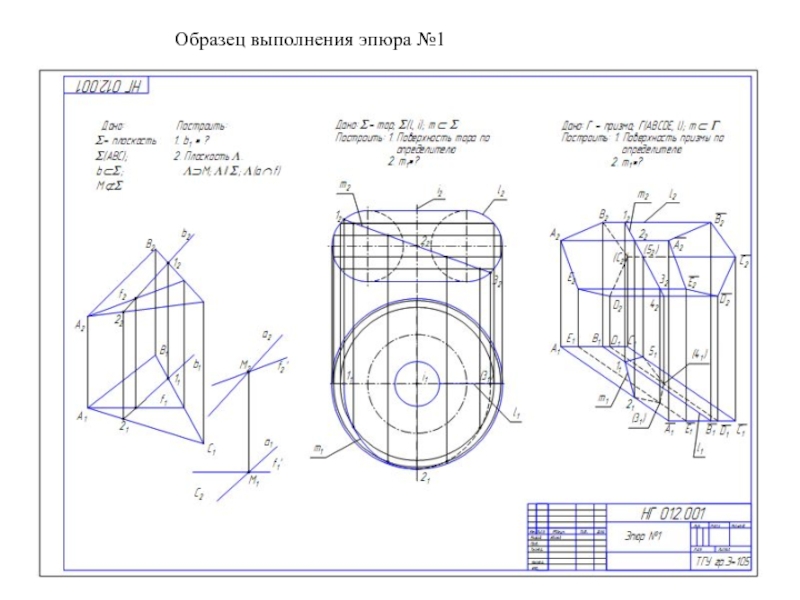
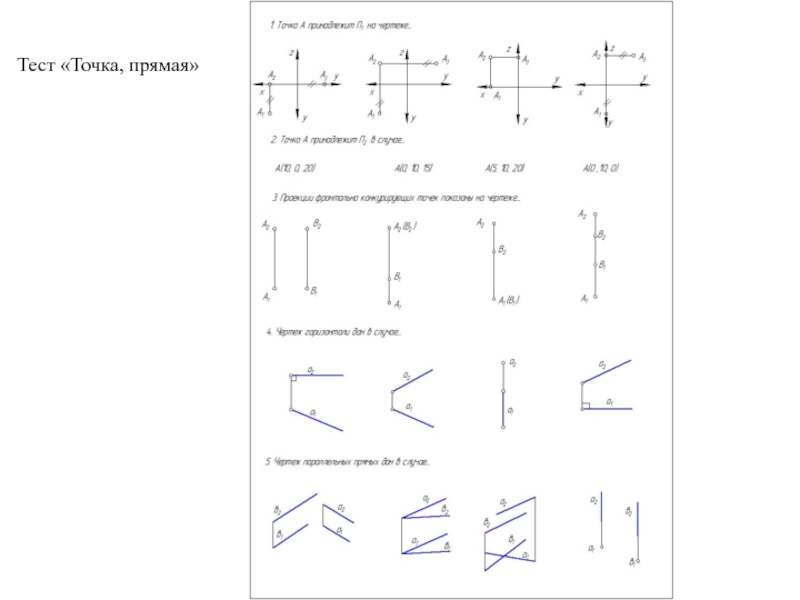
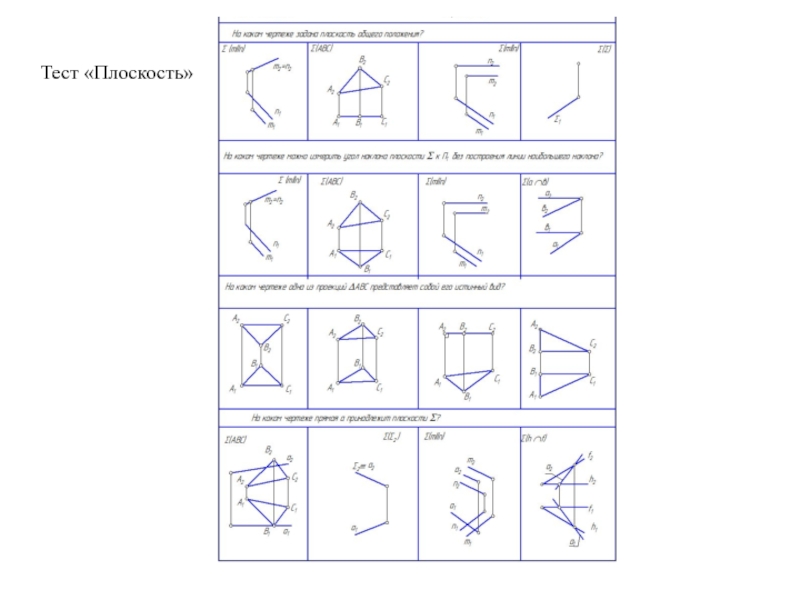
Образующая l скользит по некоторой неподвижной линии, называемой направляющей – m.
Каркас поверхности – совокупность образующих и направляющих.
Непрерывный каркас – задается всем множеством образующих и направляющих.
Дискретный каркас - задается конечным числом образующих и направляющих.
Закон каркаса – закон движения образующей.