- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Назначение геометрических преобразований презентация
Содержание
- 1. Назначение геометрических преобразований
- 2. Цель курса Изучение основных правил и требований
- 3. Геометрический язык По С.А. Фролову геометрический язык
- 4. Основные понятия и определения Плоскостью называется поверхность,
- 5. Обозначение геометрических фигур Геометрическая фигура обозначается —
- 6. 3. Линии, произвольно расположенные по отношению к
- 7. 4. Поверхности обозначаются строчными буквами греческого алфавита:
- 8. 5. Углы обозначаются: ABC —
- 9. 7. Расстояния между геометрическими фигурами обозначаются двумя
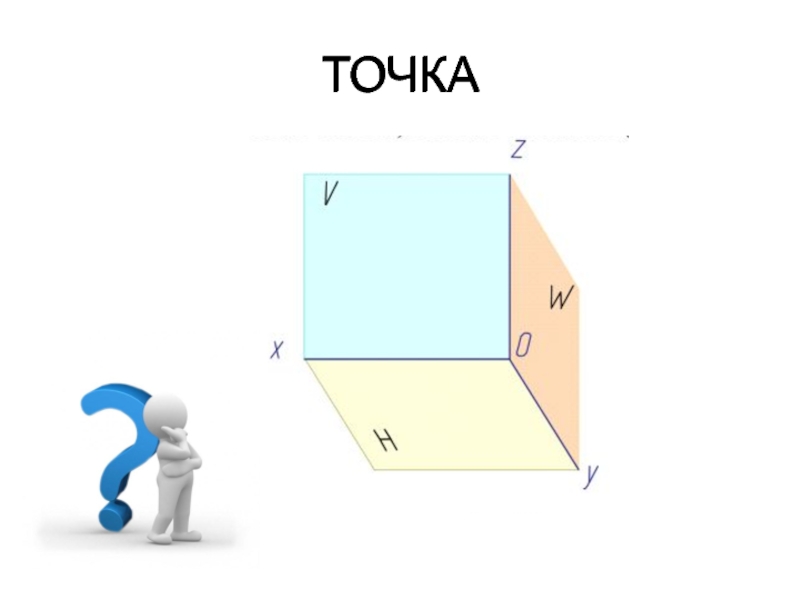
- 10. 8. Для плоскостей проекций приняты обозначения:π1, и
- 11. 10. Проекции точек, линий, поверхностей, любой геометрической
- 12. 12. Следы прямых (линий) обозначаются заглавными буквами,
- 13. 11. Следы плоскостей (поверхностей) обозначаются теми же
- 14. 13. Последовательность точек, линий (любой фигуры) отмечается
- 15. Аксонометрические проекции 14. Аксонометрические проекции точек, линий,
- 16. Вторичные проекции точек в аксонометрических проекциях обозначаются
- 17. СВОЙСТВА ЕВКЛИДОВА ПРОСТРАНСТВА С позиции теории
- 18. Вместо выражений «точка А лежит на
- 19. Отношения принадлежности между элементами евклидова пространства могут
- 20. 2. Две различные точки А и В
- 21. 4. Если две точки А и В,
- 22. 5. Две прямые, принадлежащие одной плоскости, могут
- 23. Предложение 5 утверждает, что в евклидовой плоскости
- 24. Этапы конструирования, изготовления и реализации изделия превратить
- 25. ПЕРЕРЫВ
- 26. Центральное проецирование При заданных плоскости проекции и
- 27. Центральное проецирование
- 28. Основные свойства центрального проецирования Точка проецируется в
- 29. Параллельное проецирование Если направление проецирования перпендикулярно плоскости
- 30. Основные свойства параллельного проецирования Точка проецируется в
- 31. Основные свойства параллельного проецирования Параллельные проекции взаимно
- 32. Параллельный перенос плоскости проекций или фигуры не меняет вида и размеров проекции фигуры
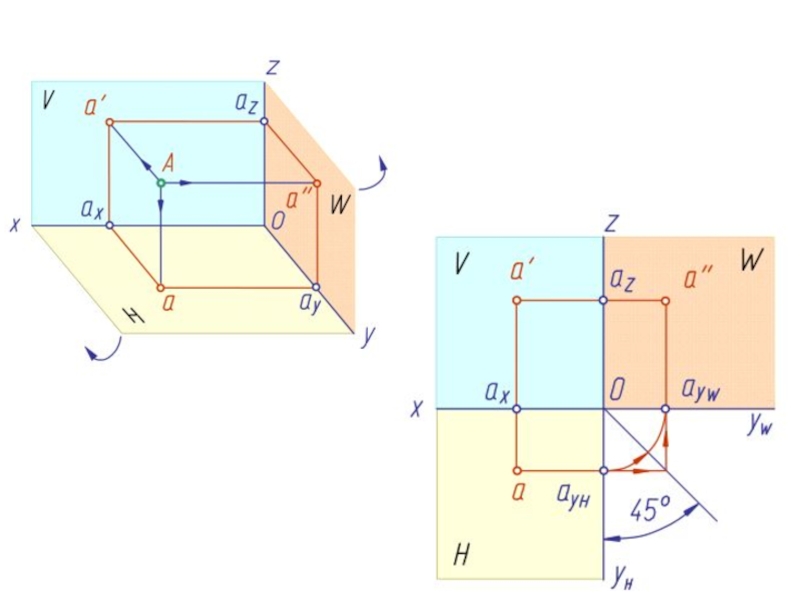
- 33. ТОЧКА ТОЧКА
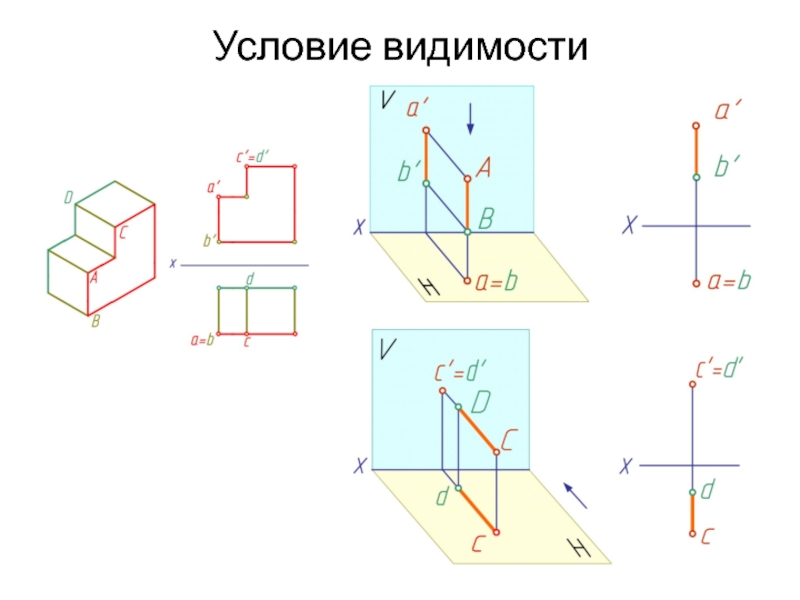
- 35. Условие видимости
Слайд 2Цель курса
Изучение основных правил и требований к порядку разработки, оформления и
обращения конструкторской документации
Слайд 3Геометрический язык
По С.А. Фролову геометрический язык состоит из обозначений и символов,
принятых в курсе математики :
- обозначения геометрических фигур и отношений между ними;
обозначения логических операций.
Особое внимание необходимо уделять символам, которые применяются для обозначения проекций геометрических фигур.
- обозначения геометрических фигур и отношений между ними;
обозначения логических операций.
Особое внимание необходимо уделять символам, которые применяются для обозначения проекций геометрических фигур.
Слайд 4Основные понятия и определения
Плоскостью называется поверхность, образуемая движением примой линии, которая
движется параллельно самой себе на неподвижной направляющей.
Поверхность – множество последовательных положений движущейся линии
Поверхность – множество последовательных положений движущейся линии
Слайд 5Обозначение геометрических фигур
Геометрическая фигура обозначается — Ф.
2. Точки обозначаются прописными буквами
латинского алфавита или
арабскими цифрами:
(курсив) А, В, С, D, ..., L, M, N, ..
(прямой шрифт) 1,2, 3,4,..., 12, 13, 14,...
(курсив) А, В, С, D, ..., L, M, N, ..
(прямой шрифт) 1,2, 3,4,..., 12, 13, 14,...
Слайд 63. Линии, произвольно расположенные по отношению к плоскостям проекций, обозначаются строчными
буквами латинского алфавита:
а, b, с, d, l, m, n, ...
Линии уровня обозначаются:
h — горизонталь;
f — фронталь.
Для прямых используются также следующие обозначения: (AB) — прямая, проходящая через точки А и В; [AB) - луч с началом в точке А;
[AB] — отрезок прямой, ограниченный точками А и В.
а, b, с, d, l, m, n, ...
Линии уровня обозначаются:
h — горизонталь;
f — фронталь.
Для прямых используются также следующие обозначения: (AB) — прямая, проходящая через точки А и В; [AB) - луч с началом в точке А;
[AB] — отрезок прямой, ограниченный точками А и В.
Слайд 74. Поверхности обозначаются строчными буквами греческого алфавита:
α — альфа, β —
бэта, — γ гамма, σ — cигма, …, ξ— кси, η — эта, ν – ню (ни), …
Чтобы подчеркнуть способ задания поверхности, следует указывать геометрические элементы, которыми она определяется, например:
α (а || b) — плоскость α определяется параллельными прямыми а и b;
Чтобы подчеркнуть способ задания поверхности, следует указывать геометрические элементы, которыми она определяется, например:
α (а || b) — плоскость α определяется параллельными прямыми а и b;
Слайд 85. Углы обозначаются:
ABC — угол с вершиной в точке
В, а также a°, β°,..., φ°, ...
6. Угловая величина (градусная мера) обозначается знаком , который ставится над углом:
ABC — величина угла ABC, φ° — величина угла φ.
Прямой угол отмечается квадратом с точкой внутри .
6. Угловая величина (градусная мера) обозначается знаком , который ставится над углом:
ABC — величина угла ABC, φ° — величина угла φ.
Прямой угол отмечается квадратом с точкой внутри .
Слайд 97. Расстояния между геометрическими фигурами обозначаются двумя вертикальными отрезками — | |
.
Например:
|АВ| — расстояние между точками А и В (длина отрезка AB);
|Аа| — расстояние от точки А до линии а;
|Аα|— расстояние от точки А до поверхности α;
|аb| — расстояние между линиями а и b;
|αβ| — расстояние между поверхностями α и β.
Например:
|АВ| — расстояние между точками А и В (длина отрезка AB);
|Аа| — расстояние от точки А до линии а;
|Аα|— расстояние от точки А до поверхности α;
|аb| — расстояние между линиями а и b;
|αβ| — расстояние между поверхностями α и β.
Слайд 108. Для плоскостей проекций приняты обозначения:π1, и π2,
где π1 — горизонтальная
плоскость проекций;
π2 — фронтальная плоскость проекций.
При замене плоскостей проекций или введении новых плоскостей последние обозначают π3, π4 и т.д.
π2 — фронтальная плоскость проекций.
При замене плоскостей проекций или введении новых плоскостей последние обозначают π3, π4 и т.д.
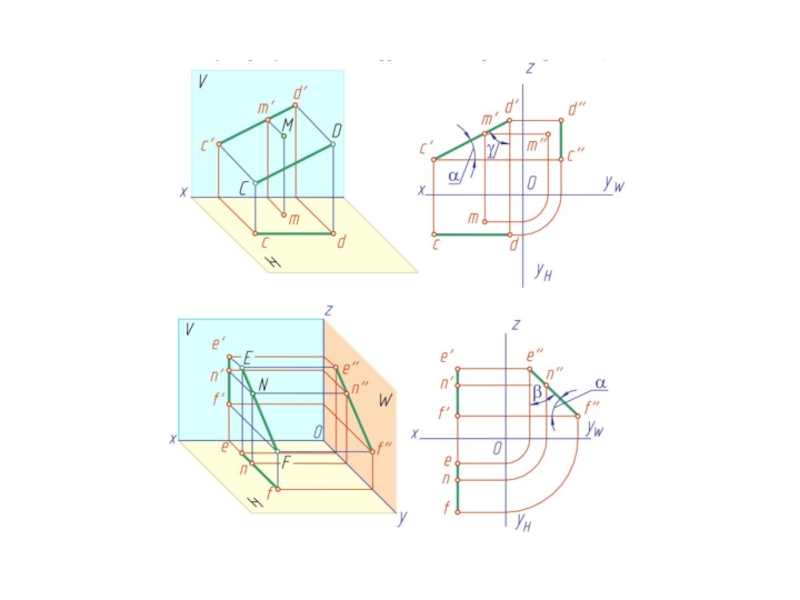
Слайд 1110. Проекции точек, линий, поверхностей, любой геометрической фигуры обозначаются теми же
буквами (или цифрами), что и оригинал, с добавлением верхнего индекса, соответствующего плоскости проекции,
на которой они получены:
A', B', C', D', ..., L', M', N', ... — горизонтальные проекции точек; А", В", С", D", ..., L", M", N", ... — фронтальные проекции точек; a', b', c', d', ...,l, m', n', ... — горизонтальные проекции линий; а", b", с", d",...,l, m", n", ... — фронтальные проекции линий; α', β', γ', δ', ..., ζ', η', ν', ... — горизонтальные проекции поверхностей; α", β", γ", δ", ..., ζ", η", ν",... — фронтальные проекции поверхностей.
A', B', C', D', ..., L', M', N', ... — горизонтальные проекции точек; А", В", С", D", ..., L", M", N", ... — фронтальные проекции точек; a', b', c', d', ...,l, m', n', ... — горизонтальные проекции линий; а", b", с", d",...,l, m", n", ... — фронтальные проекции линий; α', β', γ', δ', ..., ζ', η', ν', ... — горизонтальные проекции поверхностей; α", β", γ", δ", ..., ζ", η", ν",... — фронтальные проекции поверхностей.
Слайд 1212. Следы прямых (линий) обозначаются заглавными буквами, с которых начинаются слова,
определяющие название (в латинской транскрипции) плоскости проекции, которую пересекает линия, с подстрочным индексом, указывающим принадлежность к линии.
Например: На — горизонтальный след прямой (линии) а;
Fa — фронтальный след прямой (линии) а.
Например: На — горизонтальный след прямой (линии) а;
Fa — фронтальный след прямой (линии) а.
Слайд 1311. Следы плоскостей (поверхностей) обозначаются теми же буквами, что и горизонталь или
фронталь, с добавлением подстрочного индекса 0α,
подчеркивающего, что эти линии лежат в плоскости проекции и принадлежат плоскости (поверхности) α.
Так: h0а — горизонтальный след плоскости (поверхности) α;
f0а — фронтальный след плоскости (поверхности) α.
Так: h0а — горизонтальный след плоскости (поверхности) α;
f0а — фронтальный след плоскости (поверхности) α.
Слайд 1413. Последовательность точек, линий (любой фигуры) отмечается подстрочными индексами 1, 2,
3, … , n:
А1, А2,А3, …, Аn;
а1, а2,а3, … ,аn –последовательность линий
α1, α2, α3,..., αn;- последовательность поверхностей
Ф1, Ф2, Ф3,..., Фn – последовательность фигур
Вспомогательная проекция точки, полученная в результате преобразования для получения действительной величины геометрической фигуры, обозначается той же буквой с подстрочным индексом 0:
A0, B0, С0, D0, ...
А1, А2,А3, …, Аn;
а1, а2,а3, … ,аn –последовательность линий
α1, α2, α3,..., αn;- последовательность поверхностей
Ф1, Ф2, Ф3,..., Фn – последовательность фигур
Вспомогательная проекция точки, полученная в результате преобразования для получения действительной величины геометрической фигуры, обозначается той же буквой с подстрочным индексом 0:
A0, B0, С0, D0, ...
Слайд 15Аксонометрические проекции
14. Аксонометрические проекции точек, линий, поверхностей обозначаются теми же буквами,
что и натура с добавлением верхнего индекса 0 :
A0,B0, C0, D0, ...
1°, 2°, 3°, 4°,...
a0, b0,c0,d0 … ;
α0, β0, γ0,δ0,... ;
A0,B0, C0, D0, ...
1°, 2°, 3°, 4°,...
a0, b0,c0,d0 … ;
α0, β0, γ0,δ0,... ;
Слайд 16Вторичные проекции точек в аксонометрических проекциях обозначаются путем добавления верхнего индекса
1:
А10, В10, С10, D10,...
110, 210, 310, 410,...
a10, b10 , с10, d10,...
α10, β 10, γ 10, δ 10,...
А10, В10, С10, D10,...
110, 210, 310, 410,...
a10, b10 , с10, d10,...
α10, β 10, γ 10, δ 10,...
Слайд 17 СВОЙСТВА ЕВКЛИДОВА ПРОСТРАНСТВА
С позиции теории множеств геометрическая фигура есть не
пустое множество.
Точки, прямые и плоскости евклидова пространства находятся в определенном взаимоотношении, которое может быть обозначено словом принадлежность или инцидентность.
Термин «инцидентность» заменяет такие понятия, как «лежать на», «проходить через».
Точки, прямые и плоскости евклидова пространства находятся в определенном взаимоотношении, которое может быть обозначено словом принадлежность или инцидентность.
Термин «инцидентность» заменяет такие понятия, как «лежать на», «проходить через».
Слайд 18 Вместо выражений «точка А лежит на плоскости а», «прямая а
проходит через точку В» можно употреблять выражения «точка А инцидентна (принадлежит) плоскости а», «точка В инцидентна (принадлежит) прямой а».
В символической форме эти выражения можно записать А ∈ α; В ∈ а.
В символической форме эти выражения можно записать А ∈ α; В ∈ а.
Слайд 19Отношения принадлежности между элементами евклидова пространства могут быть выражены следующими предложениями.
1.
Если точка А принадлежит прямой а, а прямая а принадлежит плоскости α, то точка А принадлежит плоскости α:
А ∈ а ⊂ α ⇒ А ∈α .
А ∈ а ⊂ α ⇒ А ∈α .
Слайд 202. Две различные точки А и В всегда принадлежат одной и
той же и только одной прямой а или каждой прямой а принадлежат, по крайней
мере, две точки А и В:
∀(A, В) (А ≠ В) ⇒(∃1a) ∍ (А, В).
Три различные точки А, В и С, не принадлежащие одной прямой, принадлежат одной и той же и только одной плоскости:
(∀А, В,С)(A ≠ В ≠ С) ∧ (А, В, С∉ а) ⇒ (∃1α a)(α э А, В, С).
∀(A, В) (А ≠ В) ⇒(∃1a) ∍ (А, В).
Три различные точки А, В и С, не принадлежащие одной прямой, принадлежат одной и той же и только одной плоскости:
(∀А, В,С)(A ≠ В ≠ С) ∧ (А, В, С∉ а) ⇒ (∃1α a)(α э А, В, С).
Слайд 214. Если две точки А и В, принадлежащие прямой а, принадлежат
плоскости α, то прямая а принадлежит плоскости α:
(∀А, B)(A ≠ B)(A, В а) ∧ (А, В ∈α) ⇒ (а⊂ α).
Кроме приведенных выше, могут быть сформулированы и другие предложения принадлежности для элементов евклидова пространства. К таким предложениям, в частности, относятся:
(∀А, B)(A ≠ B)(A, В а) ∧ (А, В ∈α) ⇒ (а⊂ α).
Кроме приведенных выше, могут быть сформулированы и другие предложения принадлежности для элементов евклидова пространства. К таким предложениям, в частности, относятся:
Слайд 225. Две прямые, принадлежащие одной плоскости, могут принадлежать одной точке, но
этого может и не быть.
6. Две плоскости могут принадлежать одной и той же прямой, но этого может и не быть.
7. Плоскость и не принадлежащая ей прямая могут принадлежать одной точке, но этого может и не быть.
Последние три предложения по существу перефразируют аксиому о параллельности.
6. Две плоскости могут принадлежать одной и той же прямой, но этого может и не быть.
7. Плоскость и не принадлежащая ей прямая могут принадлежать одной точке, но этого может и не быть.
Последние три предложения по существу перефразируют аксиому о параллельности.
Слайд 23Предложение 5 утверждает, что в евклидовой плоскости две прямые либо пересекаются
(принадлежат одной точке), либо не имеют общей точки — в этом случае они называются параллельными. Аналогично предложение 6 говорит о том, что в евклидовом пространстве две плоскости либо пересекаются (принадлежат одной прямой) либо они параллельны, а предложение 7 - о том, что прямая, не принадлежащая плоскости, либо пересекает ее (прямая и плоскость принадлежат одной точке), либо они параллельны.
Слайд 24Этапы конструирования, изготовления и реализации изделия
превратить физическую или мысленную модель изделия
в графическую;
графическую модель описать аналитически;
выполнить численный анализ изделия на конструкторскую и экономическую обосно-ванность графической модели изделия.
разработать математическую модель управления процессом разработки изделия, модификации и реализации.
графическую модель описать аналитически;
выполнить численный анализ изделия на конструкторскую и экономическую обосно-ванность графической модели изделия.
разработать математическую модель управления процессом разработки изделия, модификации и реализации.
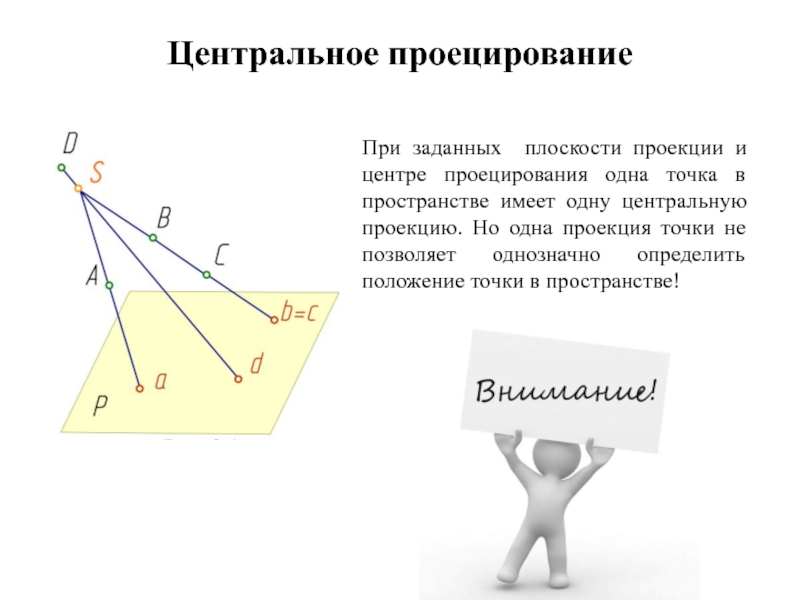
Слайд 26Центральное проецирование
При заданных плоскости проекции и центре проецирования одна точка в
пространстве имеет одну центральную проекцию. Но одна проекция точки не позволяет однозначно определить положение точки в пространстве!
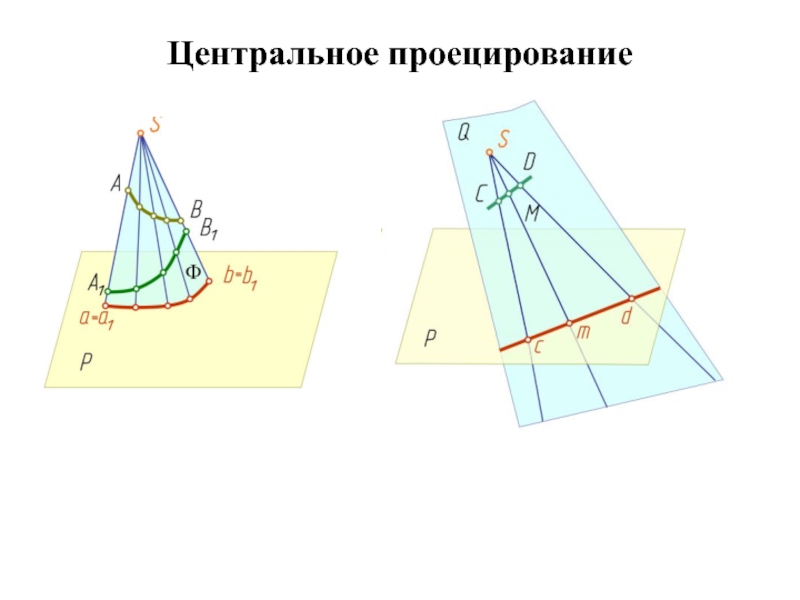
Слайд 28Основные свойства центрального проецирования
Точка проецируется в точку;
Прямая, не проходящая через
центр проецирования, проецируется в прямую (иначе в точку);
Плоская фигура не принадлежащая проецирующей плоскости, проецируется в двумерную фигуру (иначе в прямую линию).
Трехмерная фигура проецируется в двумерную.
Плоская фигура не принадлежащая проецирующей плоскости, проецируется в двумерную фигуру (иначе в прямую линию).
Трехмерная фигура проецируется в двумерную.
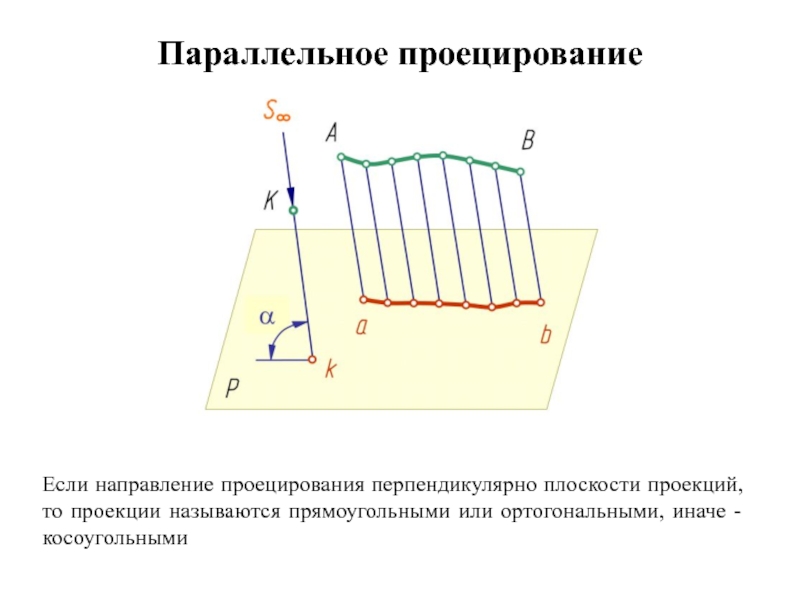
Слайд 29Параллельное проецирование
Если направление проецирования перпендикулярно плоскости проекций, то проекции называются прямоугольными
или ортогональными, иначе - косоугольными
Слайд 30Основные свойства параллельного проецирования
Точка проецируется в точку;
Прямая проецируется в прямую;
Если
точка принадлежит линии, то проекция этой точки принадлежит проекции линии (свойство принадлежности).
Если отрезок прямой делится точкой в некотором отношении, то проекция отрезка делится проекцией этой точки в том же отношении.
Если отрезок прямой делится точкой в некотором отношении, то проекция отрезка делится проекцией этой точки в том же отношении.
Слайд 31Основные свойства параллельного проецирования
Параллельные проекции взаимно параллельных прямых параллельны, о отношение
длин отрезков этих прямых равно отношению длин их проекций;
Плоская фигура, параллельная плоскости проекций, проецируется на эту же плоскость в такую же фигуру;
Параллельный перенос фигуры в пространстве или плоскости проекций не изменяет вида или размеров проекций.
Плоская фигура, параллельная плоскости проекций, проецируется на эту же плоскость в такую же фигуру;
Параллельный перенос фигуры в пространстве или плоскости проекций не изменяет вида или размеров проекций.
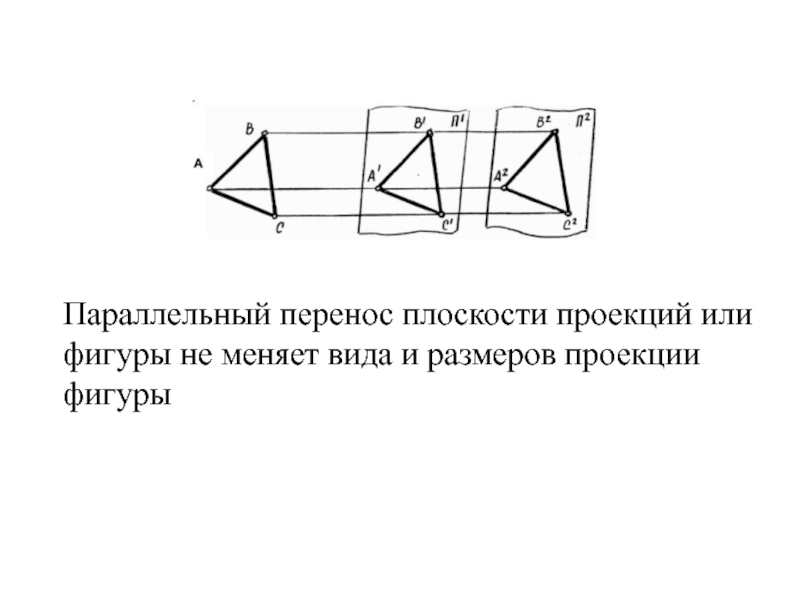
Слайд 32Параллельный перенос плоскости проекций или фигуры не меняет вида и размеров
проекции фигуры