- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Метрические задачи. Преобразования комплексного чертежа презентация
Содержание
- 1. Метрические задачи. Преобразования комплексного чертежа
- 2. Метрические задачи Преобразования комплексного чертежа
- 3. Метрические задачи Метрическими (от греческих слов metron
- 4. Все метрические задачи сводятся к
- 5. Основные принципы и последовательность решения метрических задач
- 6. Для решения задач предлагается следующая
- 7. Определение расстояний Решение задач на определение расстояний
- 8. Определение расстояния между двумя точками способом прямоугольного
- 9. Пример определения расстояния способом прямоугольного треугольника X2,1
- 10. Расстояние между двумя точками определяется длиной отрезка
- 11. Решение задачи с помощью преобразования комплексного чертежа
- 12. Пути преобразования комплексного чертежа 1. Изменение положения
- 13. Задачи на преобразование комплексного чертежа 1. Преобразование
- 14. Определение расстояния между двумя точками (Задача 1)
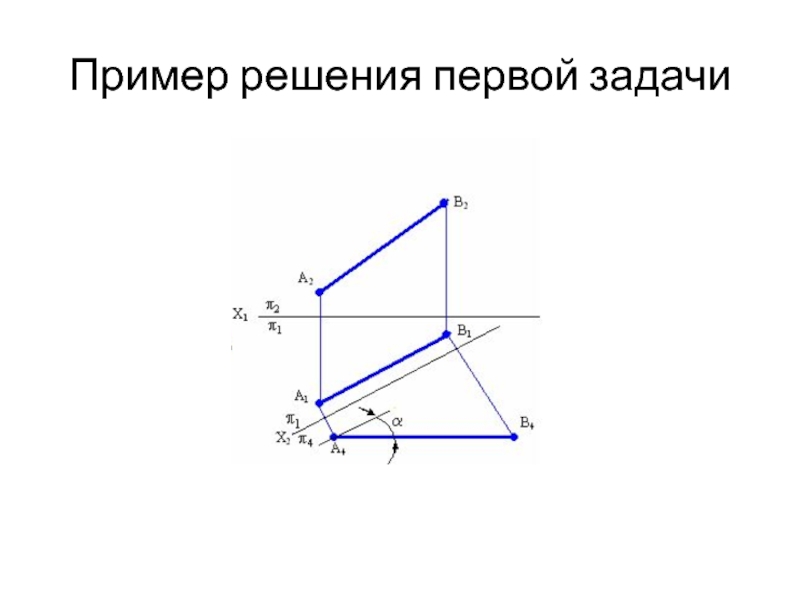
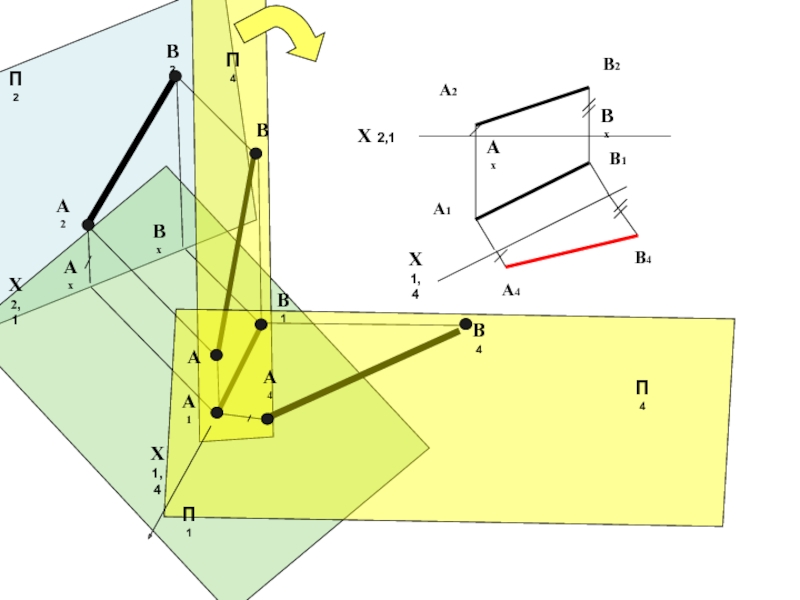
- 15. Пример решения первой задачи
- 16. Алгоритм решения первой задачи Для решения
- 17. П4 П4 X1,4
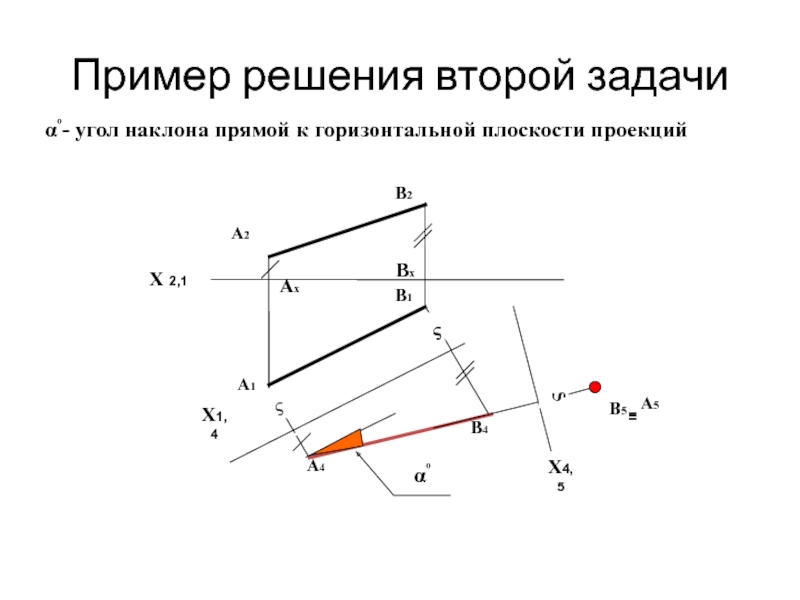
- 18. Пример решения второй задачи Bx Ax Х
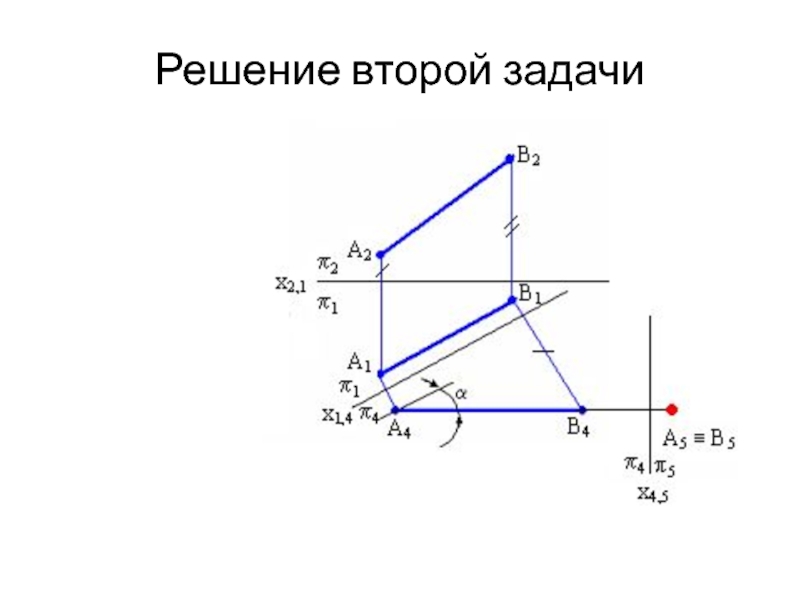
- 19. Решение второй задачи
- 20. Алгоритм решения второй задачи Построения на комплексном
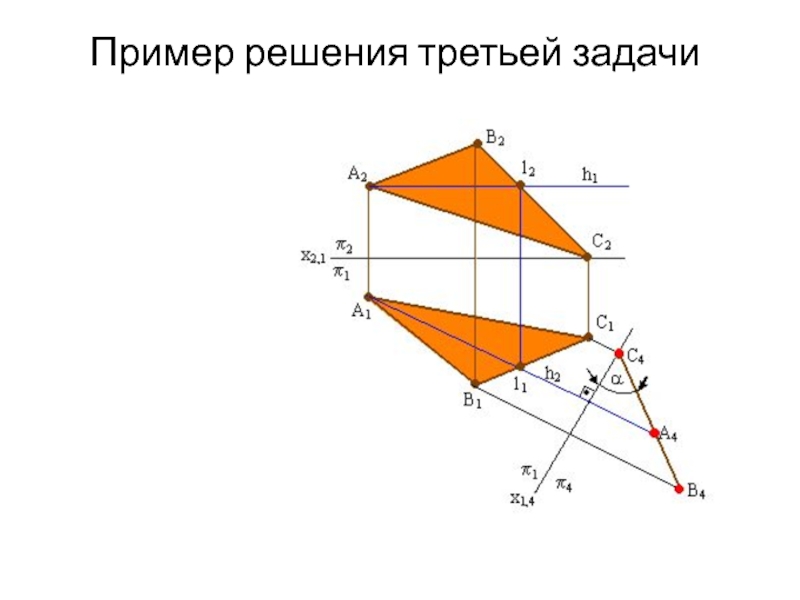
- 21. Пример решения третьей задачи
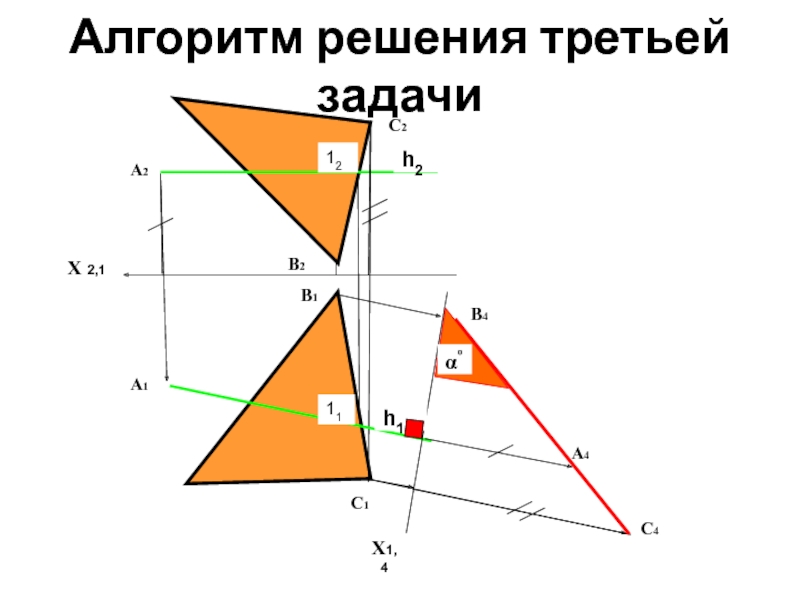
- 22. Алгоритм решения третьей задачи Для решения задачи
- 23. На чертеже плоскость (АВС) преобразована во фронтально
- 24. Алгоритм решения третьей задачи Х
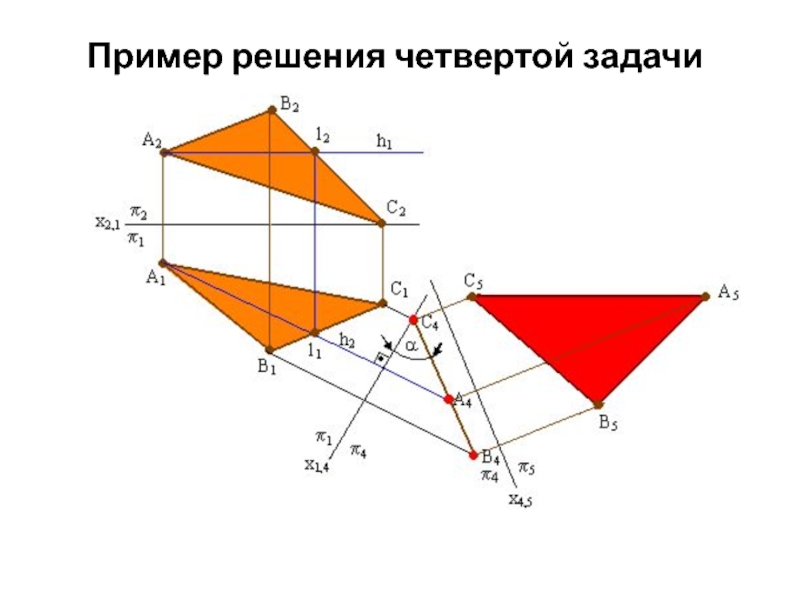
- 25. Пример решения четвертой задачи
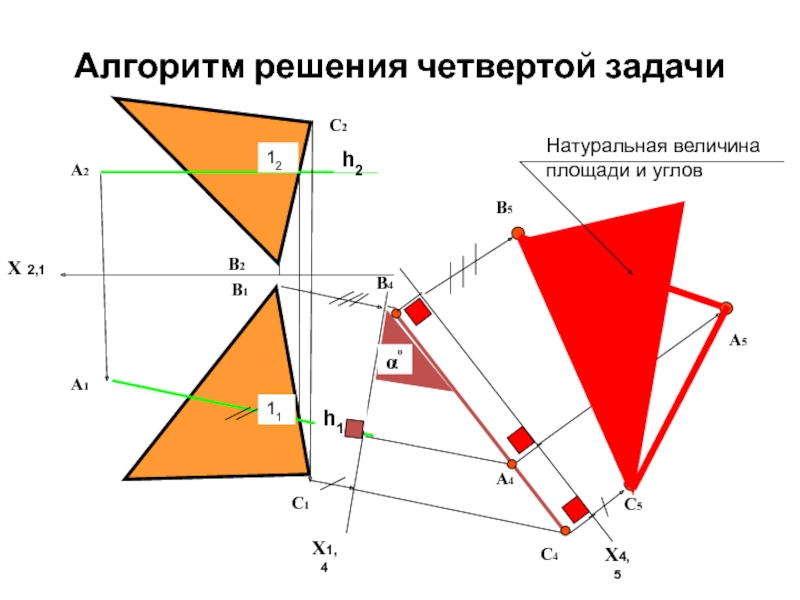
- 26. Алгоритм решения четвертой задачи Х
- 27. Алгоритм решения четвертой задачи Плоскость общего положения
- 28. Для того чтобы плоскость общего положения преобразовать
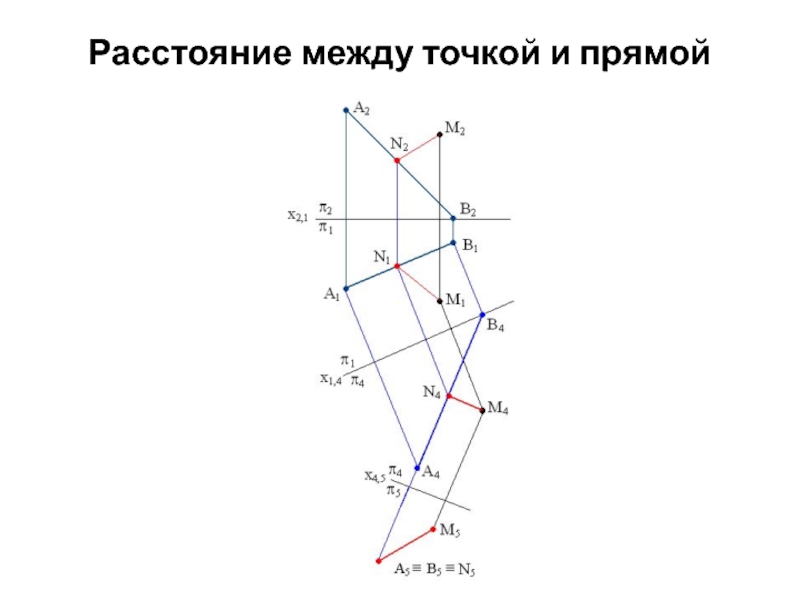
- 29. Расстояние между точкой и прямой
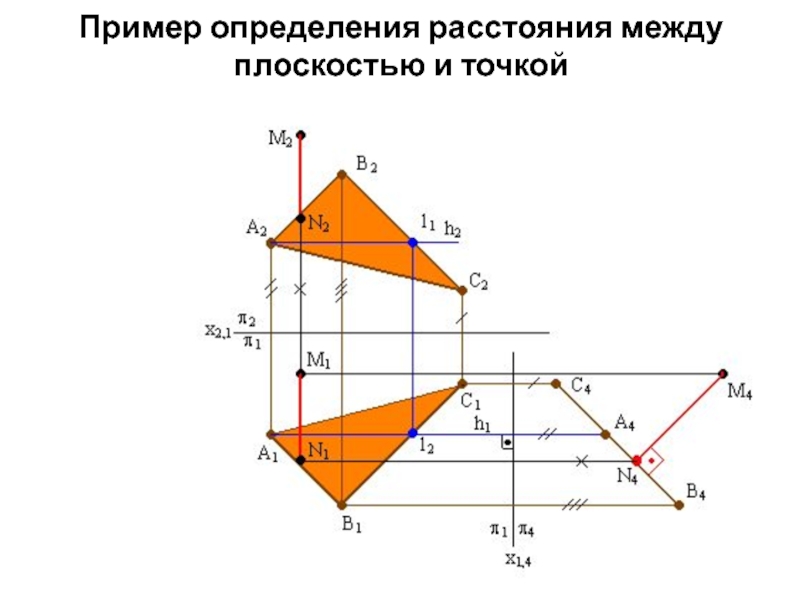
- 30. Пример определения расстояния между плоскостью и точкой
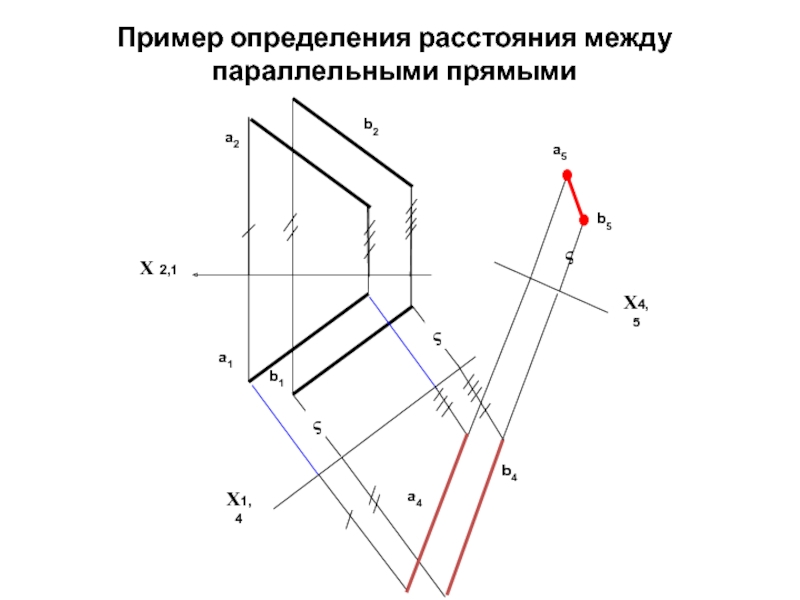
- 31. Пример определения расстояния между параллельными прямыми Х
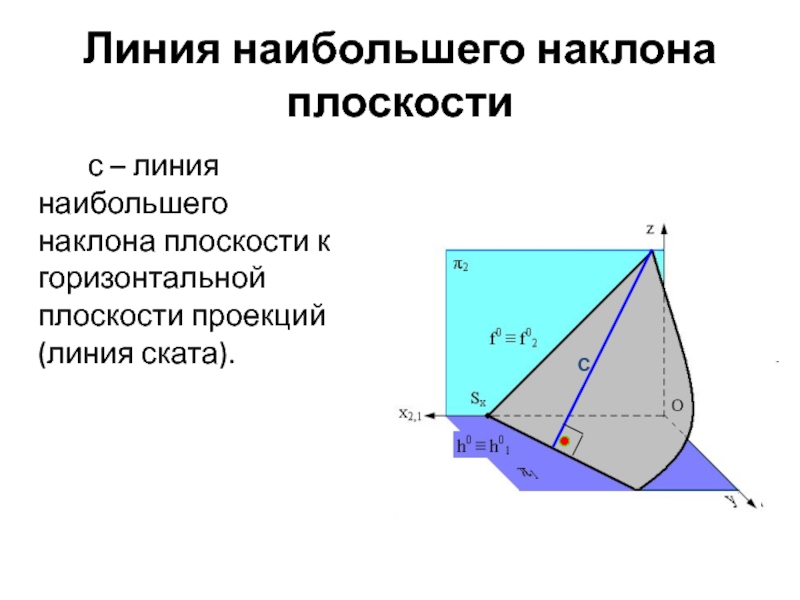
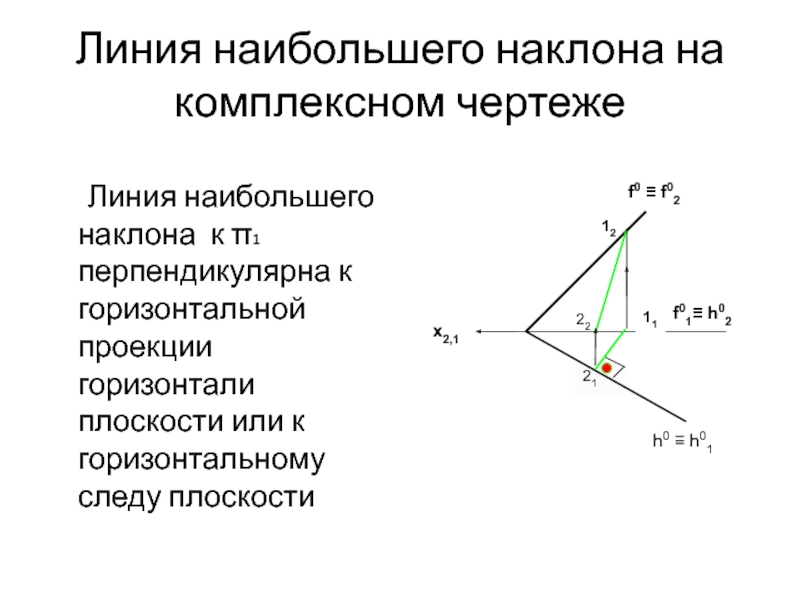
- 32. Линия наибольшего наклона плоскости с – линия
- 33. 12 21 22 Линия наибольшего наклона на
Слайд 2
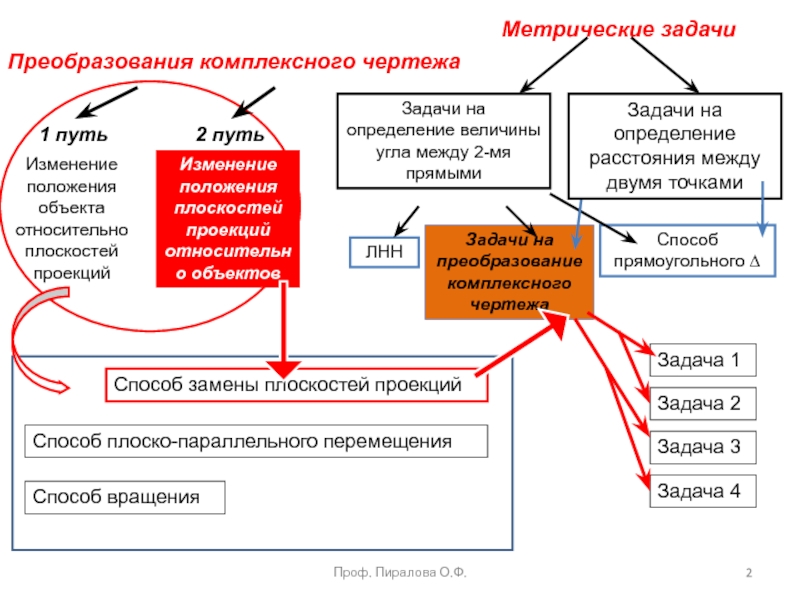
Метрические задачи
Преобразования комплексного чертежа
Задачи на определение величины угла между 2-мя
Задачи на определение расстояния между двумя точками
ЛНН
Способ прямоугольного ∆
Задачи на преобразование комплексного чертежа
1 путь
2 путь
Изменение положения объекта относительно плоскостей проекций
Изменение положения плоскостей проекций относительно объектов
Способ замены плоскостей проекций
Способ плоско-параллельного перемещения
Способ вращения
Задача 1
Задача 2
Задача 3
Задача 4
Проф. Пиралова О.Ф.
Слайд 3Метрические задачи
Метрическими (от греческих слов metron –мера, metreo - мерить)называются задачи,
Наиболее сложные задачи, при решении которых используют как метрические, так и позиционные свойства геометрических фигур, называют комплексными.
Слайд 4 Все метрические задачи сводятся к двум видам:
А) задачи на
Б) задачи на нахождение величины угла между двумя пересекающимися прямыми.
Решать такие задачи удобно с помощью различных способов преобразования комплексного чертежа.
Слайд 5Основные принципы и последовательность решения метрических задач
Алгоритмы решения всех метрических задач
1. Теорему (прямую и обратную) о проецировании прямого угла;
2. Свойство любой плоской фигуры проецироваться без искажения, в конгруэнтную фигуру, на ту плоскость проекций, которая параллельна этой фигуре.
Слайд 6
Для решения задач предлагается следующая последовательность:
Первый этап. Сосредоточиться и осмыслить
Второй этап. Поиск связи между исходными данными и искомыми. Третий этап. Реализация (графическая) плана; здесь необходим контроль правильности решения и точности графических операций.
Завершающий этап. Анализ решения задачи – при каких условиях и сколько решений возможно.
Слайд 7Определение расстояний
Решение задач на определение расстояний между точкой и прямой, двумя
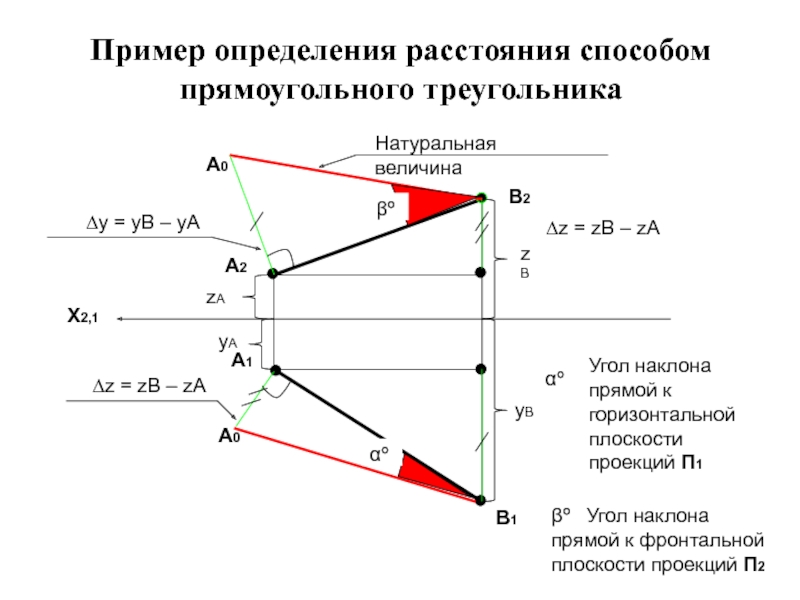
Слайд 8Определение расстояния между двумя точками способом прямоугольного треугольника
Натуральная величина отрезка равна
Слайд 9Пример определения расстояния способом прямоугольного треугольника
X2,1
A2
B2
B1
A1
A0
A0
αº
βº
Натуральная величина
yA
yB
∆y = yB – yA
zB
zA
∆z = zB – zA
αº
Угол наклона прямой к горизонтальной плоскости проекций П1
βº Угол наклона прямой к фронтальной плоскости проекций П2
∆z = zB – zA
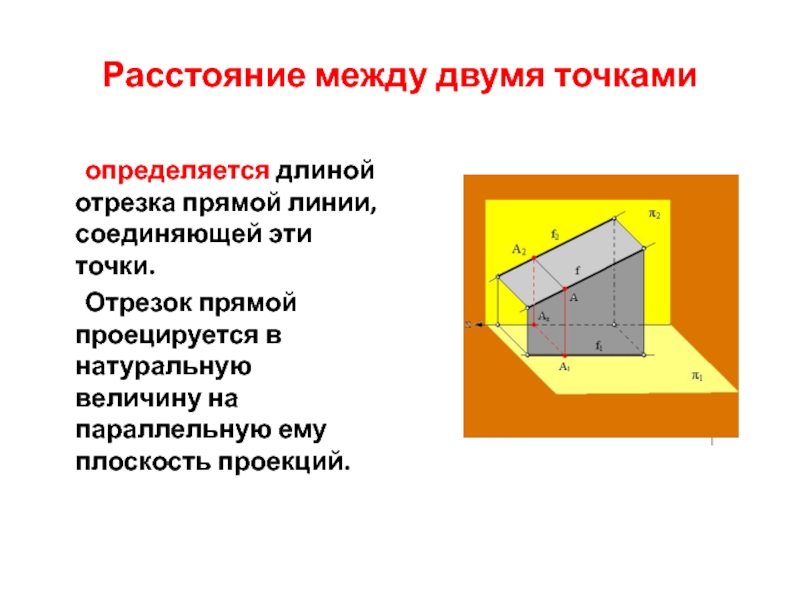
Слайд 10Расстояние между двумя точками
определяется длиной отрезка прямой линии, соединяющей эти точки.
Отрезок
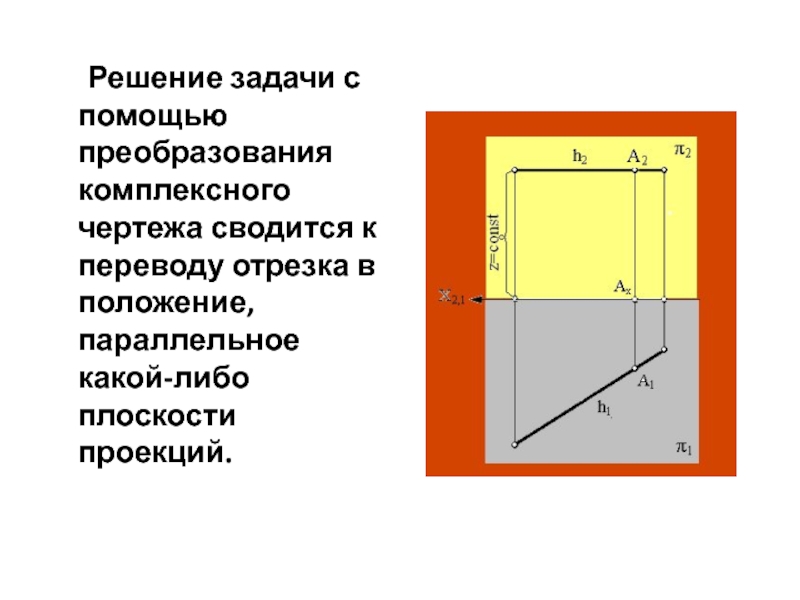
Слайд 11 Решение задачи с помощью преобразования комплексного чертежа сводится к переводу отрезка
Слайд 12Пути преобразования комплексного чертежа
1. Изменение положения объекта относительно плоскостей проекций.
2. Изменение
Слайд 13Задачи на преобразование комплексного чертежа
1. Преобразование прямой общего
положения
2. Преобразование прямой общего положения в прямую
проецирующую.
3. Преобразование плоскости общего
положения в плоскость
проецирующую.
4. Преобразование плоскости общего
положения в плоскость уровня.
Слайд 14Определение расстояния между двумя точками (Задача 1)
Для решения задачи необходимо заменить
Отрезок [АВ] прямой проецируется на плоскость П4 в истинную величину, т.е. | А4В4 | = | АB |, α- величина угла наклона прямой АВ к плоскости П1.
Слайд 16Алгоритм решения первой задачи
Для решения первой основной задачи на преобразование
Слайд 18Пример решения второй задачи
Bx
Ax
Х 2,1
А2
В2
X1,4
А1
В1
А4
В4
X4,5
ς
ς
ς
В5
А5
≡
αº
αº- угол наклона прямой к горизонтальной
Слайд 20Алгоритм решения второй задачи
Построения на комплексном чертеже: 1) проводим новую ось
Слайд 22Алгоритм решения третьей задачи
Для решения задачи необходимо заменить плоскость П1 или
Слайд 23 На чертеже плоскость (АВС) преобразована во фронтально проецирующую (см. рис.) путем
Слайд 26Алгоритм решения четвертой задачи
Х 2,1
А2
X1,4
А1
В1
А4
В4
С4
С1
С2
В2
h1
h2
11
12
αº
X4,5
С5
А5
В5
Натуральная величина площади и углов
Слайд 27Алгоритм решения четвертой задачи
Плоскость общего положения преобразовать в плоскость уровня заменой
Слайд 28 Для того чтобы плоскость общего положения преобразовать в плоскость уровня, необходимо
Вначале плоскость необходимо преобразовать в проецирующую, т. е. решить задачу 3, а затем проецирующую плоскость преобразовать в плоскость уровня.
На рис. показано преобразование плоскости ∆(АВС) в горизонтальную плоскость уровня.
Слайд 32Линия наибольшего наклона плоскости
с – линия наибольшего наклона плоскости к горизонтальной
С
Слайд 3312
21
22
Линия наибольшего наклона на комплексном чертеже
Линия наибольшего наклона к π1
11
x2,1
f0 ≡ f02
h0 ≡ h01
f01≡ h02