- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Линейчатые поверхности. Образование поверхностей презентация
Содержание
- 1. Линейчатые поверхности. Образование поверхностей
- 2. Линейчатой поверхностью называется поверхность, образованная перемещением прямолинейной образующей по одной или более направляющим
- 3. Цилиндрическая
- 6. Однополостный гиперболоид
- 7. Многогранные поверхности – это поверхности, образованные частями
- 8. S ℓ m
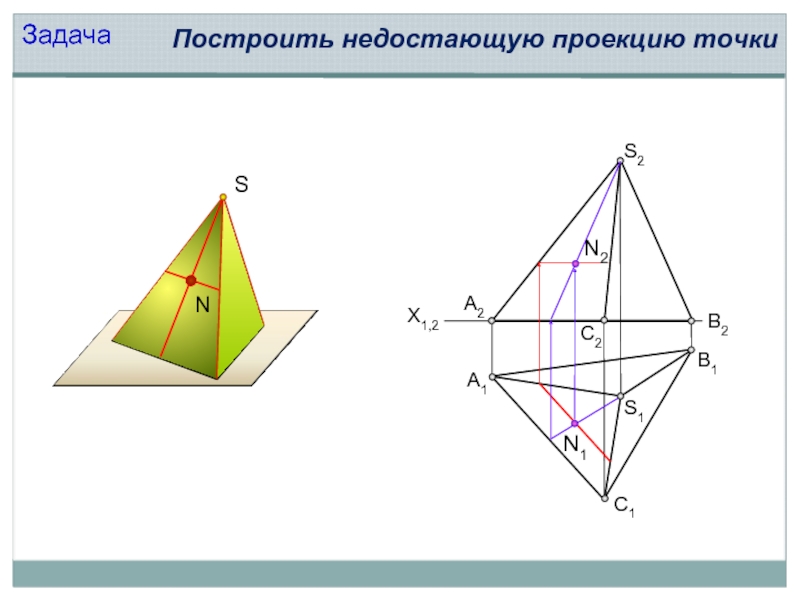
- 9. Принадлежность точки поверхности
- 13. Поверхности Каталана
- 15. Поверхность с плоскостью параллелизма и двумя
- 16. m2 n2 n1
- 17. Винтовой поверхностью называют поверхность, образованную винтовым
- 18. n2 n1
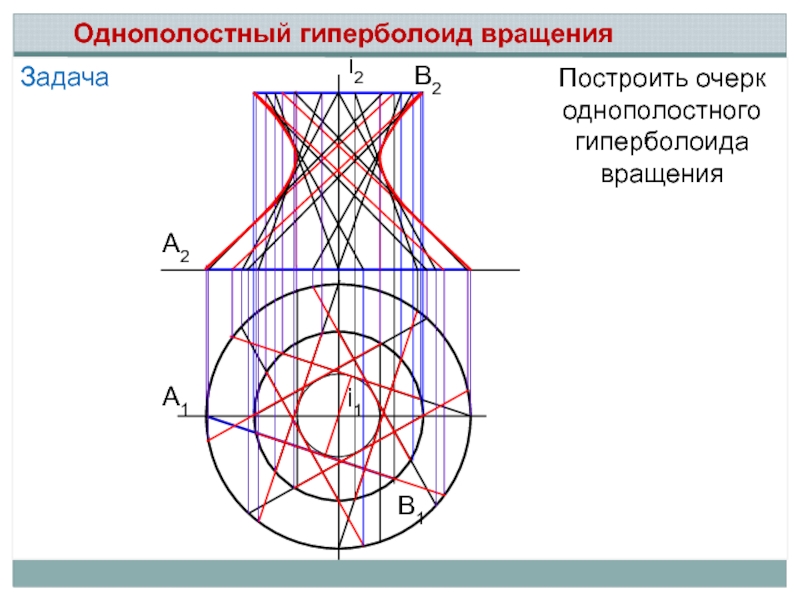
- 19. Задача А2 А1 В1
Линейчатой поверхностью называется поверхность, образованная перемещением прямолинейной образующей по одной или более направляющим
Слайд 2Линейчатой поверхностью называется поверхность, образованная перемещением прямолинейной образующей по одной или
более направляющим
Слайд 3
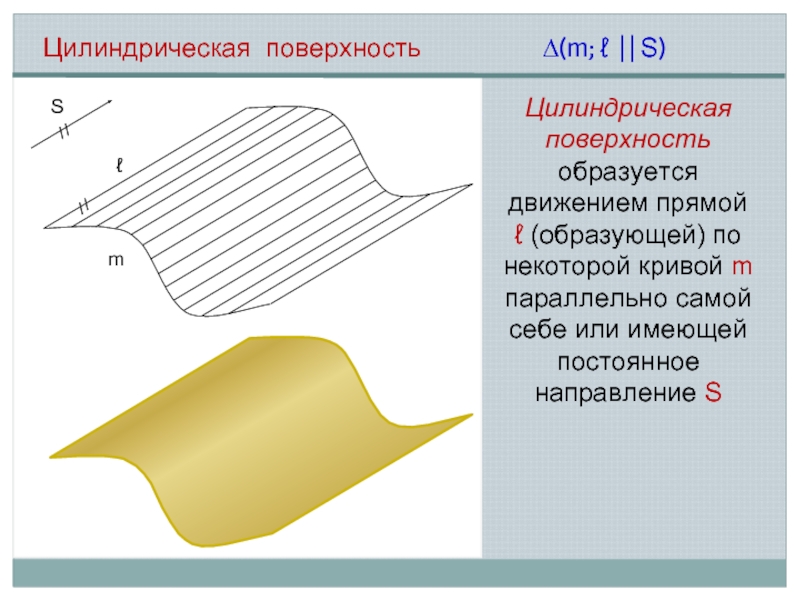
Цилиндрическая поверхность
ℓ
m
∆(m; ℓ ⎜⎜S)
S
//
//
Цилиндрическая поверхность образуется движением прямой ℓ (образующей) по
некоторой кривой m параллельно самой себе или имеющей постоянное направление S
Слайд 4
i
m
ℓ
∆(i, ℓ∩m; ℓ∩i )
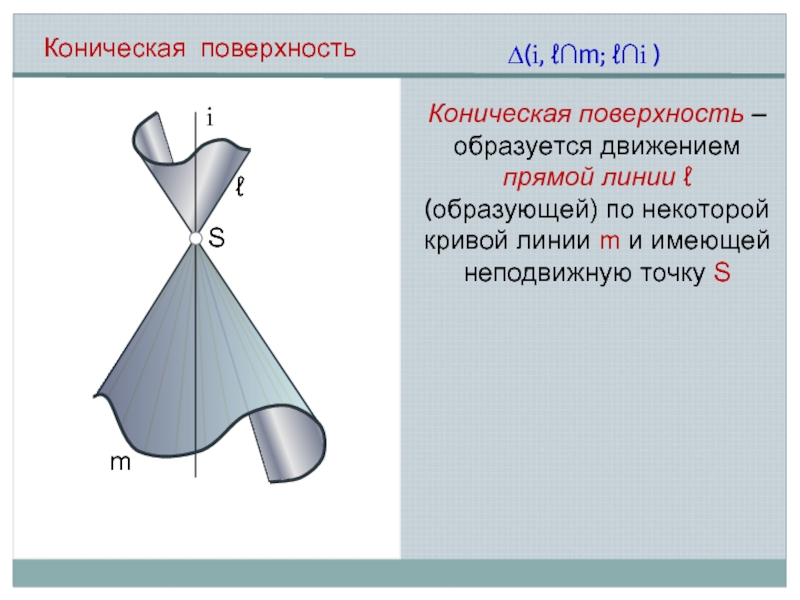
Коническая поверхность
Коническая поверхность – образуется движением прямой линии
ℓ (образующей) по некоторой кривой линии m и имеющей неподвижную точку S
S
Слайд 5
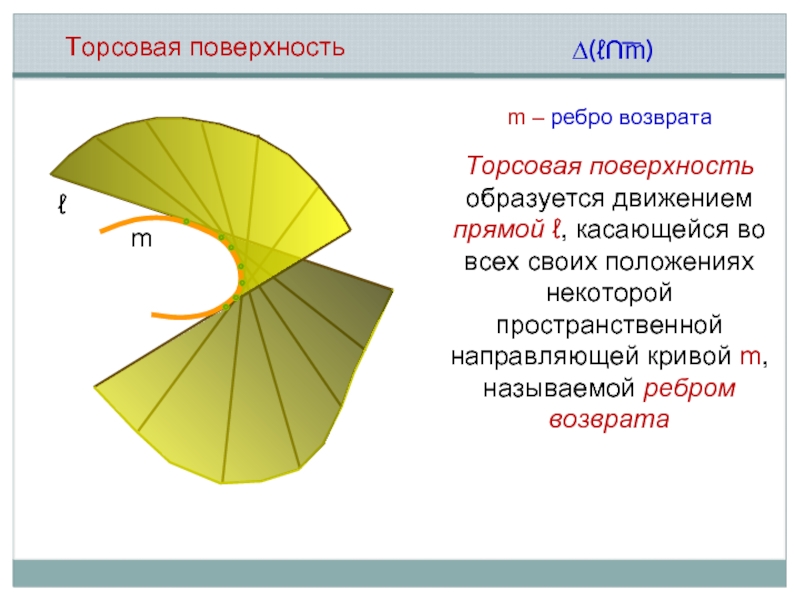
Торсовая поверхность
m
m – ребро возврата
ℓ
∆(ℓ∩m)
Торсовая поверхность образуется движением прямой ℓ, касающейся
во всех своих положениях некоторой пространственной направляющей кривой m, называемой ребром возврата
Слайд 7Многогранные поверхности – это поверхности, образованные частями (отсеками) пересекающихся плоскостей
Многогранником называется
тело, ограниченное многогранной поверхностью, состоящей из плоских многоугольников
Отсеки плоскостей называются гранями,
а линии их пересечения – ребрами
Отсеки плоскостей называются гранями,
а линии их пересечения – ребрами
Точки пересечения ребер называются вершинами
Слайд 8
S
ℓ
m
S
m
Пирамидальная поверхность
S
m
Пирамида
m – замкнутый контур
Если направляющая m ломаная, а все образующие
ℓ пересекаются в одной точке, такая поверхность называется пирамидальной
Поверхность с замкнутой ломаной направляющей (m), общей точкой пересечения образующих ребер и граней называется пирамидой
Слайд 11
m
S
ℓ
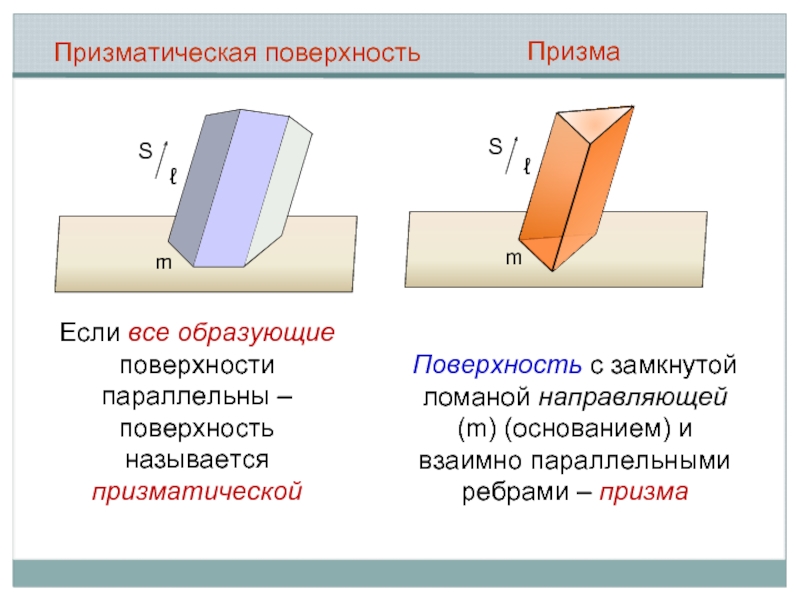
Призматическая поверхность
m
S
ℓ
Призма
Если все образующие поверхности параллельны – поверхность называется
призматической
Поверхность с замкнутой ломаной направляющей (m) (основанием) и взаимно параллельными ребрами – призма
Слайд 12
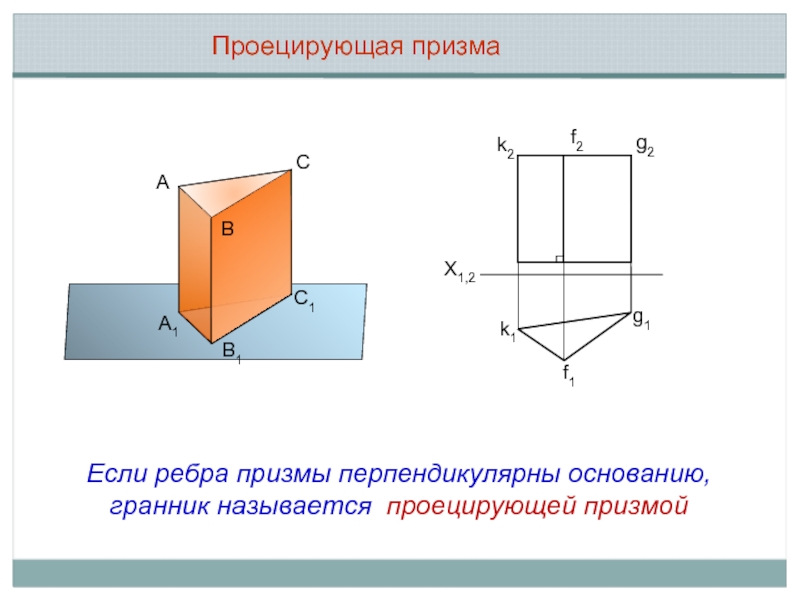
Проецирующая призма
А
В
С
С1
В1
А1
k2
k1
f1
g1
g2
f2
X1,2
Если ребра призмы перпендикулярны основанию, гранник называется проецирующей призмой
Слайд 14
0
m1
n1
ℓ
ℓ1
ℓ1
n
m
n1
∽
m1
∽
ℓ2
m2
∽
n2
∽
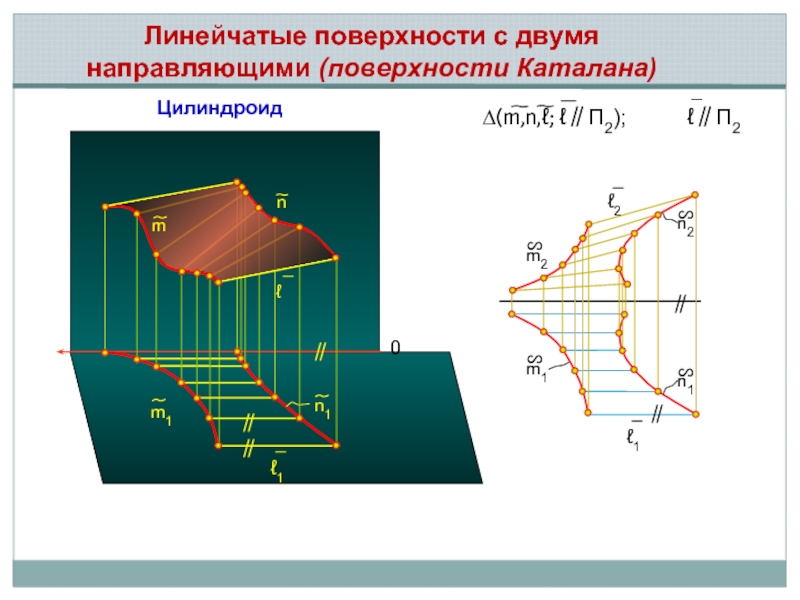
Линейчатые поверхности с двумя направляющими (поверхности Каталана)
ℓ∥П2
∥
∥
∥
∆(m,n,ℓ; ℓ∥П2);
∥
∥
Цилиндроид
Слайд 15
Поверхность с плоскостью параллелизма и двумя скрещивающимися направляющими называется гиперболическим параболоидом,
или косой плоскостью
Гипар
Слайд 16
m2
n2
n1
m1
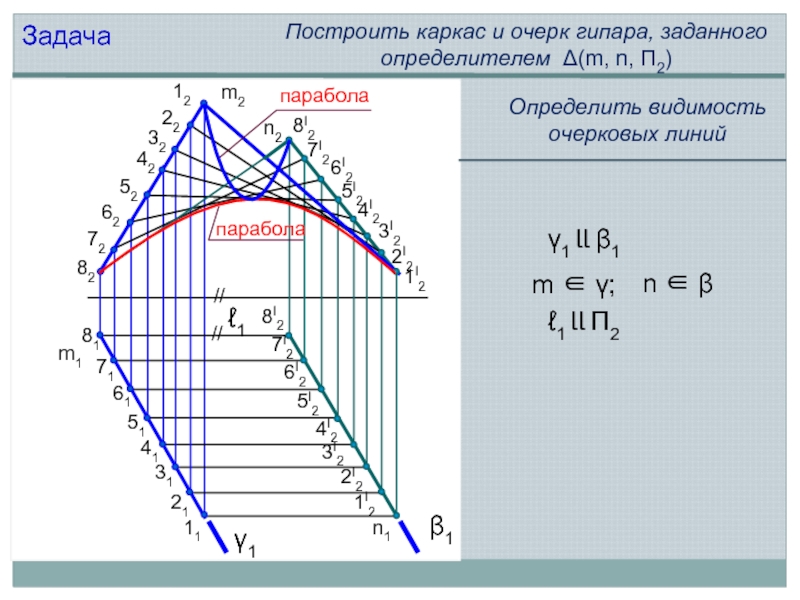
Задача
Построить каркас и очерк гипара, заданного определителем Δ(m, n, П2)
12
11
22
32
42
52
62
72
82
1I2
2I2
3I2
4I2
5I2
6I2
7I2
8I2
21
31
41
51
61
71
81
1I2
2I2
3I2
4I2
5I2
6I2
7I2
8I2
//
//
парабола
парабола
γ1
β1
γ1 ll
β1
n ∈ β
m ∈ γ;
ℓ1
ℓ1 ll П2
Определить видимость очерковых линий
Слайд 17
Винтовой поверхностью называют поверхность, образованную винтовым движением образующей
Винтовым движением называют движение,
при котором каждая точка А образующей вращается вокруг неподвижной оси i и одновременно перемещается поступательно вдоль этой оси
Винтовая поверхность
Слайд 18
n2
n1
гелиса
А1
В1
ί1
ί2
Задача
Построить каркас и очерк прямого геликоида
А2
В2
01
11
21
31
41
51
61
71
81
91
101
111
12
22
32
42
52
62
72
82
92
102
112
122
(Прямой винтовой коноид)
Δ(n, i)
Слайд 19
Задача
А2
А1
В1
В2
i2
i1
Построить очерк однополостного гиперболоида вращения
Однополостный гиперболоид вращения
