- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
НГ-1 презентация
Содержание
- 1. НГ-1
- 2. Начертательная геометрия (НГ) – это дисциплина, которая
- 3. Джоконда
- 4. Дама с горностаем
- 5. Тайная вечеря
- 6. Создатель этих вечных живописных полотен – Леонардо
- 7. ОСНОВОПОЛОЖНИКИ НГ Леонардо да Винчи
- 8. Леонардо да Винчи, родился 15 апреля 1452
- 9. Летательный аппарат ИЗОБРЕТЕНИЯ ДА ВИНЧИ
- 10. Осадный арбалет ИЗОБРЕТЕНИЯ ДА ВИНЧИ
- 11. ОСНОВОПОЛОЖНИКИ НГ Гаспа́р Монж, граф де Пелю́з.
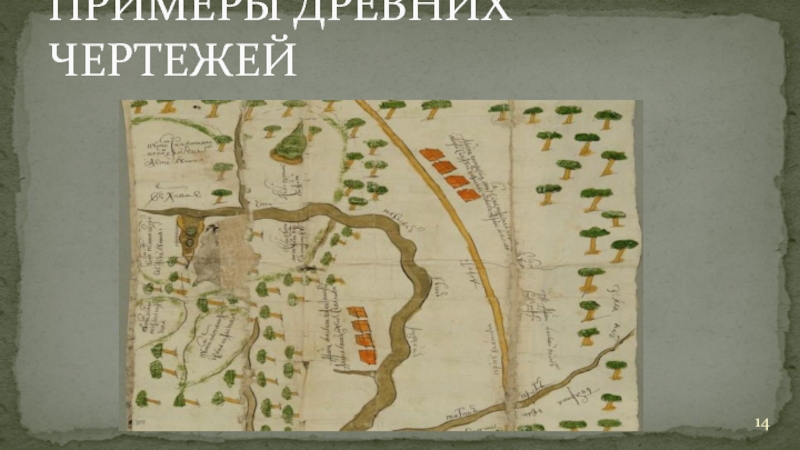
- 12. ПРИМЕРЫ ДРЕВНИХ ЧЕРТЕЖЕЙ
- 13. Современные методы технической (и в том числе
- 14. ПРИМЕРЫ ДРЕВНИХ ЧЕРТЕЖЕЙ
- 15. ПРИМЕРЫ ДРЕВНИХ ЧЕРТЕЖЕЙ
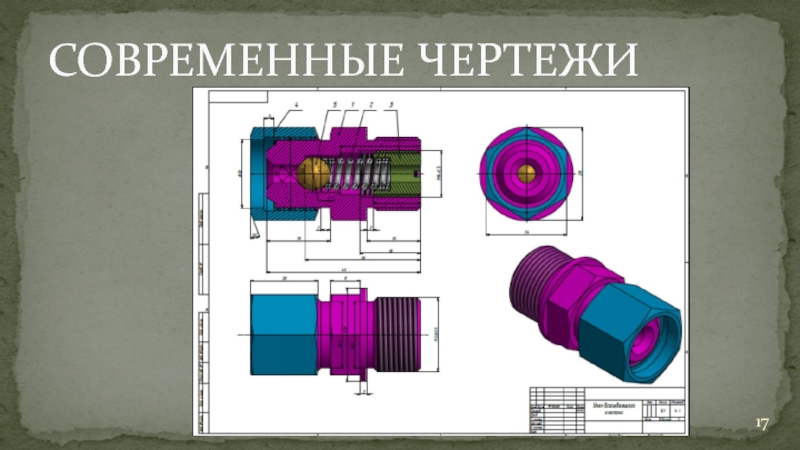
- 16. СОВРЕМЕННЫЕ ЧЕРТЕЖИ Построение в 3D
- 17. СОВРЕМЕННЫЕ ЧЕРТЕЖИ
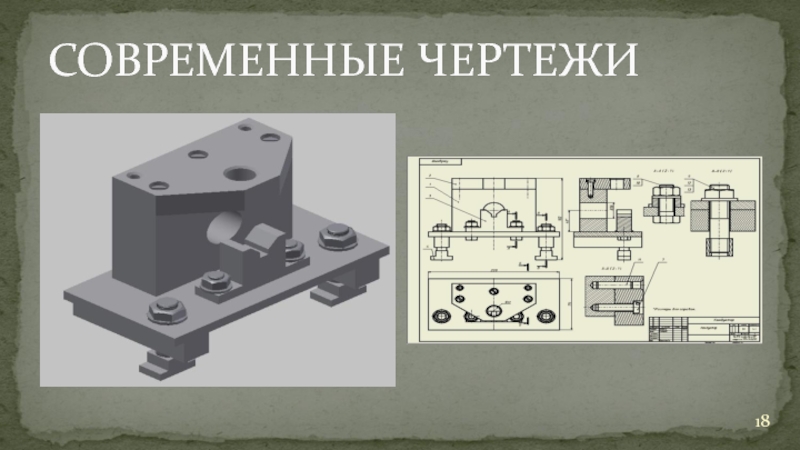
- 18. СОВРЕМЕННЫЕ ЧЕРТЕЖИ
- 19. КОМПЬЮТЕРНАЯ ГРАФИКА
- 20. Вы входите в мир начертательной геометрии
- 21. 7 лекций в течение первого полусеместра (8
- 22. На лекциях и практических занятиях для решения
- 24. СОДЕРЖАНИЕ ЦЕЛЬ КУРСА НАЧЕРТАТЕЛЬНОЙ ГЕОМЕТРИИ ЛИТЕРАТУРА ЗАДАЧИ
- 25. Развитие пространственного представления и воображения, необходимых в
- 26. ЛИТЕРАТУРА Фролов С.А. Начертательная геометрия. М.: Машиностроение,1983
- 27. ЗАДАЧИ НАЧЕРТАТЕЛЬНОЙ ГЕОМЕТРИИ Метрические – задачи на
- 28. ГЕОМЕТРИЧЕСКИЕ ОБЪЕКТЫ Точка Прямая Плоскость Поверхность
- 29. ПРИНЯТЫЕ ОБОЗНАЧЕНИЯ Точки в пространстве – прописными
- 30. ПРИНЯТЫЕ ОБОЗНАЧЕНИЯ Плоскости проекций – строчной буквой
- 31. ПРИНЯТЫЕ ОБОЗНАЧЕНИЯ Оси проекций – строчными буквами
- 32. ПРИНЯТЫЕ ОБОЗНАЧЕНИЯ Проекции линий –
- 33. = Равенство || Параллельны ~ Подобны ⊥
- 34. МЕТОДЫ ПРОЕЦИРОВАНИЯ Проецирование – замена реально существующего
- 35. ЦЕНТРАЛЬНОЕ ПРОЕЦИРОВАНИЕ Проецирование предмета из данного центра
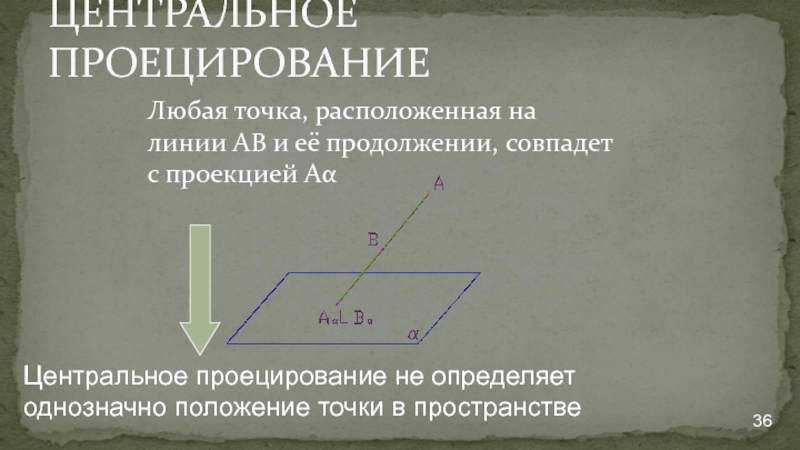
- 36. ЦЕНТРАЛЬНОЕ ПРОЕЦИРОВАНИЕ Любая точка, расположенная на линии
- 37. ПАРАЛЛЕЛЬНОЕ ПРОЕЦИРОВАНИЕ Проецирование предмета из бесконечно
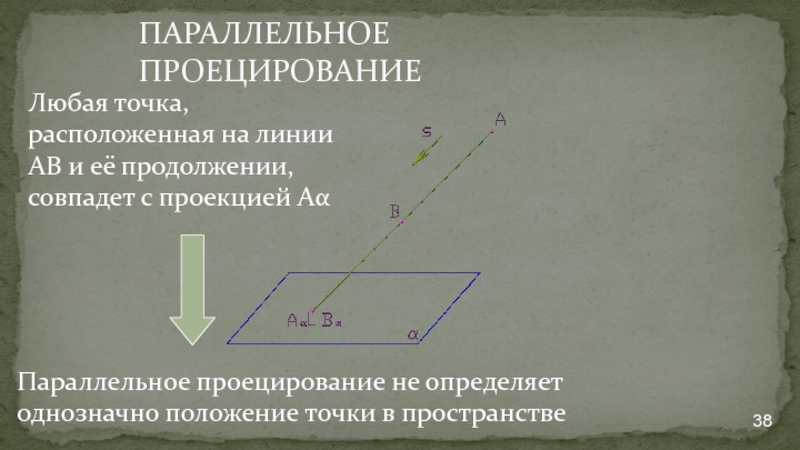
- 38. ПАРАЛЛЕЛЬНОЕ ПРОЕЦИРОВАНИЕ Любая точка, расположенная на линии
- 39. ЦЕНТРАЛЬНОЕ И ПАРАЛЛЕЛЬНОЕ ПРОЕЦИРОВАНИЕ. ВЫВОДЫ Одна
- 40. ОРТОГОНАЛЬНОЕ (ПРЯМОУГОЛЬНОЕ) ПРОЕЦИРОВАНИЕ Ортогональное проецирование –
- 41. ОРТОГОНАЛЬНОЕ ПРОЕЦИРОВАНИЕ При ортогональном проецировании
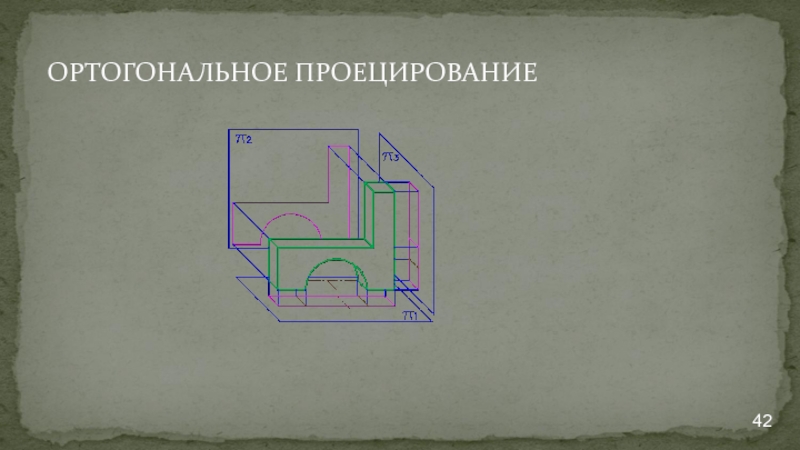
- 42. ОРТОГОНАЛЬНОЕ ПРОЕЦИРОВАНИЕ
- 43. ПОЛОЖЕНИЕ ТОЧКИ В ПРОСТРАНСТВЕ Определение положения точек
- 44. ДЕКАРТОВА СИСТЕМА КООРДИНАТНЫХ ОСЕЙ Все пространственные объекты
- 45. Почему центральное проецирование не может использоваться для построения чертежа? ВОПРОС 1
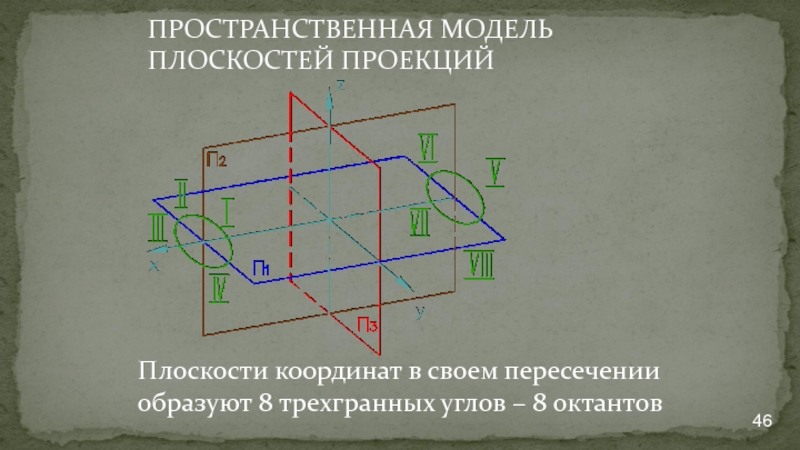
- 46. Плоскости координат в своем пересечении образуют 8
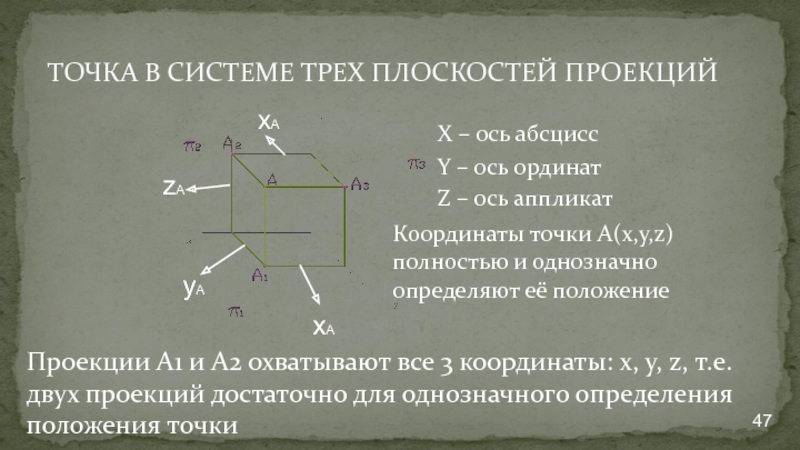
- 47. X – ось абсцисс Y – ось
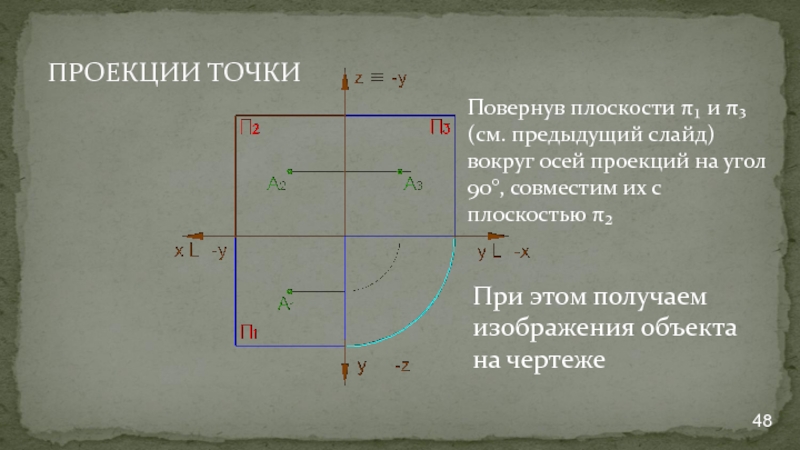
- 48. Повернув плоскости π₁ и π₃ (см. предыдущий
- 49. ПРОЕКЦИИ ТОЧКИ. ЭПЮР МОНЖА Чертеж в системе
- 50. ЧЕРТЕЖ В дальнейшем эпюр Монжа, а также
- 51. Вид проецирования, который используется при построении чертежа ВОПРОС 2
- 52. ИНВАРИАНТНЫЕ СВОЙСТВА ОРТОГОНАЛЬНОГО ПРОЕЦИРОВАНИЯ 1. Проекция точки
- 53. ИНВАРИАНТНЫЕ СВОЙСТВА ОРТОГОНАЛЬНОГО ПРОЕЦИРОВАНИЯ 3. Проекции точек,
- 54. ИНВАРИАНТНЫЕ СВОЙСТВА ОРТОГОНАЛЬНОГО ПРОЕЦИРОВАНИЯ 4. Точки, принадлежащие
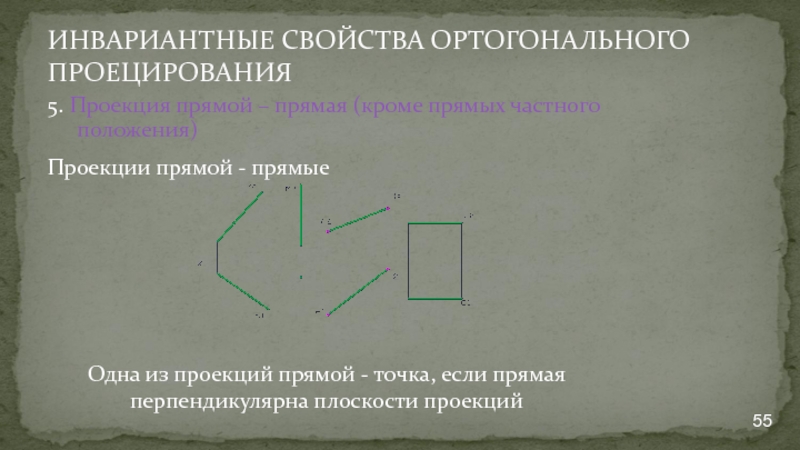
- 55. ИНВАРИАНТНЫЕ СВОЙСТВА ОРТОГОНАЛЬНОГО ПРОЕЦИРОВАНИЯ 5. Проекция прямой
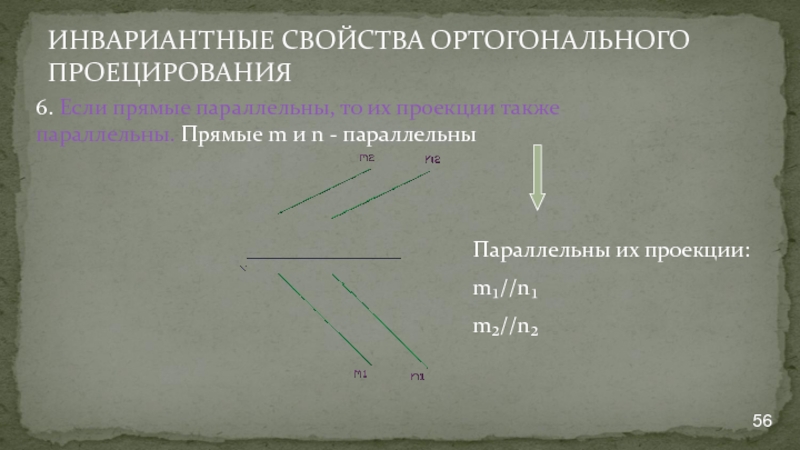
- 56. ИНВАРИАНТНЫЕ СВОЙСТВА ОРТОГОНАЛЬНОГО ПРОЕЦИРОВАНИЯ 6. Если прямые
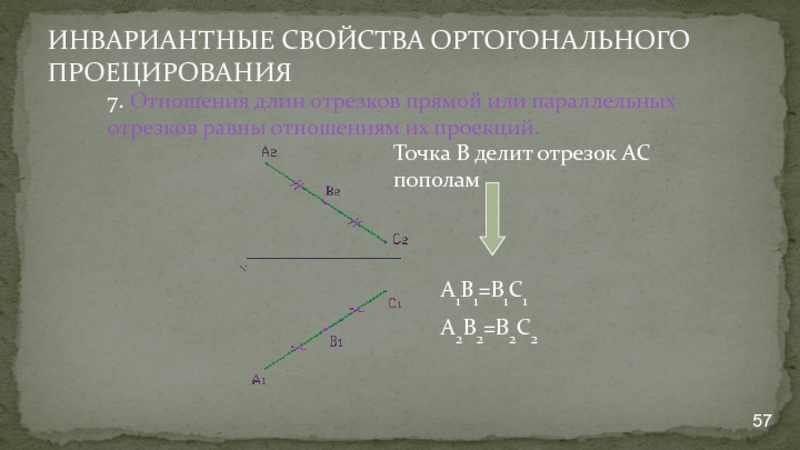
- 57. ИНВАРИАНТНЫЕ СВОЙСТВА ОРТОГОНАЛЬНОГО ПРОЕЦИРОВАНИЯ 7. Отношения длин
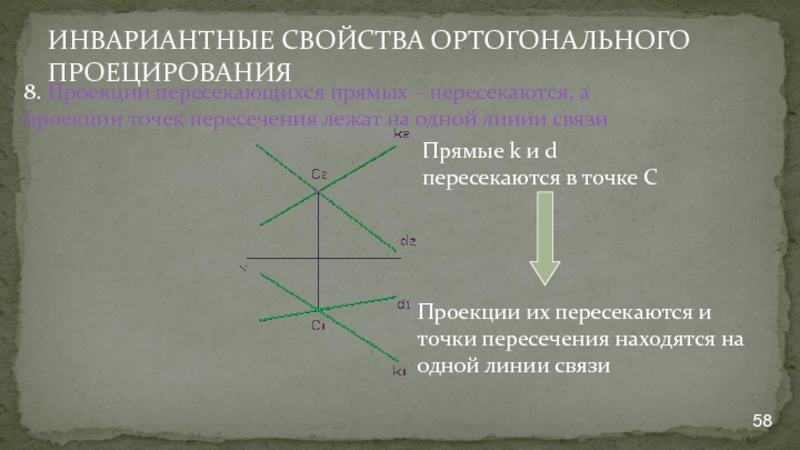
- 58. ИНВАРИАНТНЫЕ СВОЙСТВА ОРТОГОНАЛЬНОГО ПРОЕЦИРОВАНИЯ 8. Проекции пересекающихся
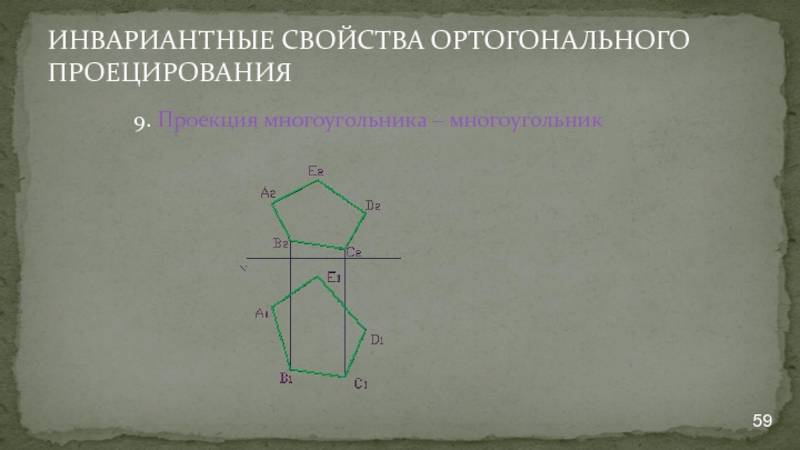
- 59. ИНВАРИАНТНЫЕ СВОЙСТВА ОРТОГОНАЛЬНОГО ПРОЕЦИРОВАНИЯ 9. Проекция многоугольника – многоугольник
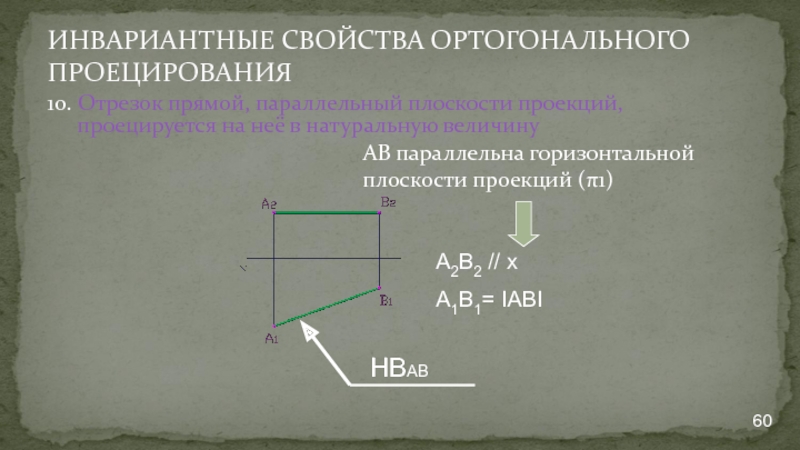
- 60. ИНВАРИАНТНЫЕ СВОЙСТВА ОРТОГОНАЛЬНОГО ПРОЕЦИРОВАНИЯ 10. Отрезок прямой,
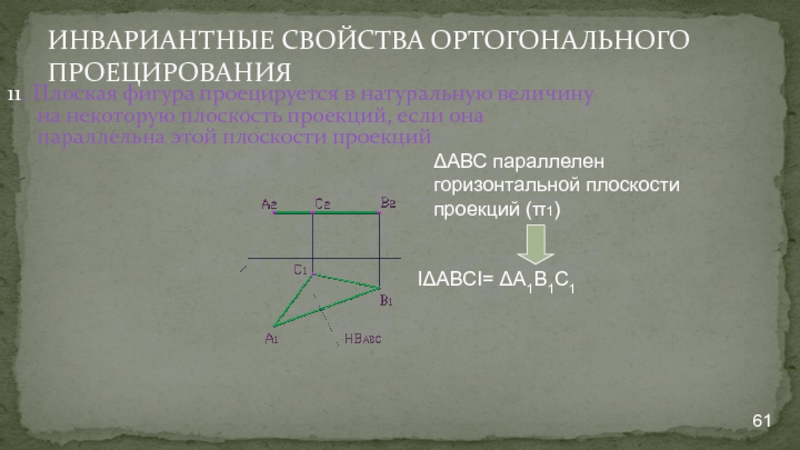
- 61. ИНВАРИАНТНЫЕ СВОЙСТВА ОРТОГОНАЛЬНОГО ПРОЕЦИРОВАНИЯ 11. Плоская фигура
- 62. ИНВАРИАНТНЫЕ СВОЙСТВА ОРТОГОНАЛЬНОГО ПРОЕЦИРОВАНИЯ 12. Прямой угол,
- 63. Дано: Угол АСВ равен 90° Катет АС параллелен π₁
- 64. 3.Привести пример конкурирующих точек 4.Привести пример чертежа
- 65. ВЫВОДЫ Ортогональное проецирование – прямоугольное, параллельное проецирование
- 66. ВЫВОДЫ Положение точки определяется её ортогональными проекциями
Слайд 1Автор презентации:
доцент кафедры «Инженерная графика»
Тамара Владимировна Нестерова
НАЧЕРТАТЕЛЬНАЯ ГЕОМЕТРИЯ
Слайд 2Начертательная геометрия (НГ) – это дисциплина, которая
поможет Вам увидеть окружающий
подготовит к изучению машиностроительного черчения, созданию чертежа
позволит сделать первый шаг в мир творчества, созидания, изобретений и открытий
ВВЕДЕНИЕ
Слайд 6Создатель этих вечных живописных полотен – Леонардо да Винчи
Секрет Мастера раскрывается
ОСНОВОПОЛОЖНИКИ НГ
Слайд 8Леонардо да Винчи, родился 15 апреля 1452 по юлианскому календарю в
ИСТОРИЧЕСКАЯ СПРАВКА
Слайд 11ОСНОВОПОЛОЖНИКИ НГ
Гаспа́р Монж, граф де Пелю́з. Родился во Франции в 1746
Слайд 13Современные методы технической (и в том числе компьютерной) графики имеют свою
ИСТОКИ РАЗВИТИЯ ЧЕРТЕЖА
Слайд 20Вы входите в мир начертательной геометрии
Это мир, который поможет Вам
Вы научитесь смотреть на чертеж и видеть предмет, а также по изделию создавать чертежи
Удачи Вам на этом пути!
ЗАКЛЮЧЕНИЕ
Слайд 217 лекций в течение первого полусеместра (8 недель). Цель лекции –
16 практических занятий (1 семестр). Цель практических занятий – контроль знаний по темам дисциплины и помощь в освоении алгоритмов решения графических задач
ГРАФИК ИЗУЧЕНИЯ НГ
Слайд 22На лекциях и практических занятиях для решения графических задач нужны чертежные
Треугольники (углы 45°, 30°)
Циркуль
Ластик
2 тетради в клетку:
для лекционных и практических занятий
для решения РГР
ИНСТРУМЕНТЫ
Слайд 24СОДЕРЖАНИЕ
ЦЕЛЬ КУРСА НАЧЕРТАТЕЛЬНОЙ ГЕОМЕТРИИ
ЛИТЕРАТУРА
ЗАДАЧИ НАЧЕРТАТЕЛЬНОЙ ГЕОМЕТРИИ
ГЕОМЕТРИЧЕСКИЕ ОБЪЕКТЫ
ПРИНЯТЫЕ ОБОЗНАЧЕНИЯ
СИМВОЛЫ, ОБОЗНАЧАЮЩИЕ ОТНОШЕНИЯ МЕЖДУ
МЕТОДЫ ПРОЕЦИРОВАНИЯ
ПРОЕКЦИИ ТОЧКИ
ИНВАРИАНТНЫЕ СВОЙСТВА ОРТОГОНАЛЬНОГО ПРОЕЦИРОВАНИЯ
ПРЯМАЯ
СЛЕДЫ ПРЯМОЙ
СПОСОБ ПРЯМОУГОЛЬНОГО ТРЕУГОЛЬНИКА
Слайд 25Развитие пространственного представления и воображения, необходимых в техническом творчестве
Для создания
Научиться не только строить изображения предметов, но и мысленно воспроизводить в пространстве сами предметы по их изображениям
ЦЕЛЬ КУРСА НАЧЕРТАТЕЛЬНОЙ ГЕОМЕТРИИ
Слайд 26ЛИТЕРАТУРА
Фролов С.А. Начертательная геометрия. М.: Машиностроение,1983
Гордон В.О. Курс начертательной геометрии. М.:
Крылов Н.Н. и др. Начертательная геометрия. М.: Высшая школа, 2000
Нартова Л.Г. Начертательная геометрия. М.: Дрофа, 2003
Чекмарев А.А. Начертательная геометрия и черчение. М.: Высшая школа, 2003
Фролов С.А. Сборник задач по начертательной геометрии. М.: Машиностроение,1986
Гордон В.О. Сборник задач по курсу начертательной геометрии. М.: Высшая школа, 2003
Слайд 27ЗАДАЧИ НАЧЕРТАТЕЛЬНОЙ ГЕОМЕТРИИ
Метрические – задачи на определение длин линий, размеров углов,
Позиционные – задачи на установление взаимного положения и взаимопринадлежности рассматриваемых геометрических объектов
Слайд 29ПРИНЯТЫЕ ОБОЗНАЧЕНИЯ
Точки в пространстве – прописными буквами латинского алфавита А, В,
Линии в пространстве – по точкам, определяющим линию, и строчными буквами латинского алфавита а, b, c …
Углы – строчными буквами греческого алфавита – φ (фи), ψ (пси), ω (омега), σ (сигма)
Плоскости – α (альфа), β (бета), γ (гамма), δ (дельта)
Слайд 30ПРИНЯТЫЕ ОБОЗНАЧЕНИЯ
Плоскости проекций – строчной буквой греческого алфавита π
Горизонтальная плоскость π1
Фронтальная
Профильная плоскость π3
Любая дополнительная плоскость π4, π5, … πn
Слайд 31ПРИНЯТЫЕ ОБОЗНАЧЕНИЯ
Оси проекций – строчными буквами x, y, z
При введении дополнительных
π₁/ π₄, π₂/ π₄, π₄/ π₅, …
Проекции точек:
На плоскость α – Аα
На горизонтальную плоскость π₁ – А₁
На фронтальную плоскость π₂ – А₂
На профильную плоскость π₃ – А₃
На дополнительную плоскость π₄ – А₄
Слайд 32ПРИНЯТЫЕ ОБОЗНАЧЕНИЯ
Проекции линий –
по проекциям точек, определяющих линию:
строчными буквами:
На горизонтальную плоскость π₁ – m₁, n₁…
На фронтальную плоскость π₂ – m₂, n₂, …
На профильную плоскость π₃ – m₃, n₃, …
Слайд 33= Равенство
|| Параллельны
~ Подобны
⊥ Перпендикулярны
≅ Конгруэнтны
→ Отображается
∩ Пересекаются
=> Если…..то
∊ Принадлежит
Скрещиваются
СИМВОЛЫ,
Слайд 34МЕТОДЫ ПРОЕЦИРОВАНИЯ
Проецирование – замена реально существующего объекта его изображением на плоскости,
Методы проецирования:
Центральное
Параллельное
Ортогональное
Слайд 35ЦЕНТРАЛЬНОЕ ПРОЕЦИРОВАНИЕ
Проецирование предмета из данного центра называют центральным или коническим проецированием.
Слайд 36ЦЕНТРАЛЬНОЕ ПРОЕЦИРОВАНИЕ
Любая точка, расположенная на линии АВ и её продолжении, совпадет
Центральное проецирование не определяет однозначно положение точки в пространстве
Слайд 37ПАРАЛЛЕЛЬНОЕ ПРОЕЦИРОВАНИЕ
Проецирование предмета из бесконечно удаленного центра называют параллельным или цилиндрическим
Чтобы спроецировать точку А на плоскость α, надо провести через эту точку параллельно направлению проецирования S прямую линию (проецирующий луч) до пересечения с плоскостью проекций α
Слайд 38ПАРАЛЛЕЛЬНОЕ ПРОЕЦИРОВАНИЕ
Любая точка, расположенная на линии АВ и её продолжении, совпадет
Параллельное проецирование не определяет однозначно положение точки в пространстве
Слайд 39ЦЕНТРАЛЬНОЕ И ПАРАЛЛЕЛЬНОЕ ПРОЕЦИРОВАНИЕ. ВЫВОДЫ
Одна центральная проекция как и одна параллельная
по такому изображению нельзя определить форму и размеры предмета и его положение в пространстве
Слайд 40ОРТОГОНАЛЬНОЕ (ПРЯМОУГОЛЬНОЕ) ПРОЕЦИРОВАНИЕ
Ортогональное проецирование – единственный способ построения машиностроительных чертежей
Ортогональное
Прямоугольные проекции:
Наиболее распространены в конструкторской практике
Позволяют получить изображения, простые с точки зрения графических построений
Обеспечивают точное соотношение размеров изображений предметов на плоскости
Слайд 41ОРТОГОНАЛЬНОЕ ПРОЕЦИРОВАНИЕ
При ортогональном проецировании предметы располагают относительно плоскостей проекций таким
При этом предмет находится между наблюдателем и плоскостью проекций
Слайд 43ПОЛОЖЕНИЕ ТОЧКИ В ПРОСТРАНСТВЕ
Определение положения точек в пространстве производится по их
Слово «прямоугольный» часто заменяют словом «ортогональный», образованным из слов древнегреческого языка, обозначающих «прямой» и «угол»
Слайд 44ДЕКАРТОВА СИСТЕМА КООРДИНАТНЫХ ОСЕЙ
Все пространственные объекты ориентируют относительно пространственной декартовой системы
Слайд 46Плоскости координат в своем пересечении образуют 8 трехгранных углов – 8
ПРОСТРАНСТВЕННАЯ МОДЕЛЬ ПЛОСКОСТЕЙ ПРОЕКЦИЙ
Слайд 47X – ось абсцисс
Y – ось ординат
Z – ось аппликат
Координаты точки
xA
yA
xA
zA
Проекции А1 и А2 охватывают все 3 координаты: x, y, z, т.е. двух проекций достаточно для однозначного определения положения точки
ТОЧКА В СИСТЕМЕ ТРЕХ ПЛОСКОСТЕЙ ПРОЕКЦИЙ
Слайд 48Повернув плоскости π₁ и π₃ (см. предыдущий слайд) вокруг осей проекций
При этом получаем изображения объекта на чертеже
ПРОЕКЦИИ ТОЧКИ
Слайд 49ПРОЕКЦИИ ТОЧКИ. ЭПЮР МОНЖА
Чертеж в системе π₁, π₂ известен под названием
Слайд 50ЧЕРТЕЖ
В дальнейшем эпюр Монжа, а также проекционные чертежи, в основе которых
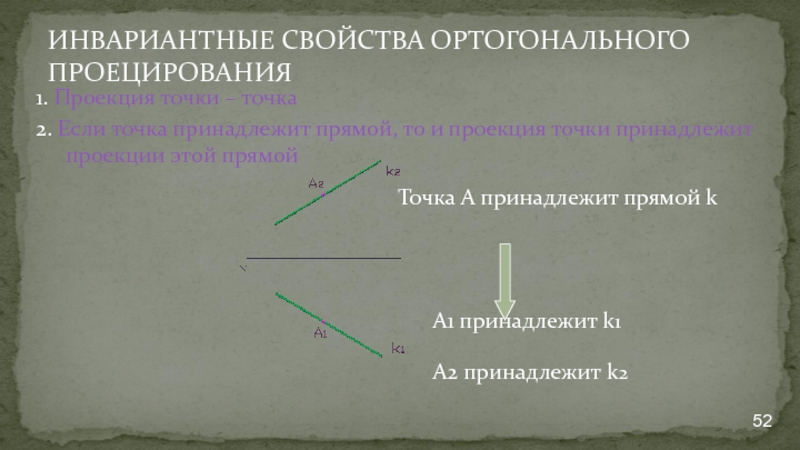
Слайд 52ИНВАРИАНТНЫЕ СВОЙСТВА ОРТОГОНАЛЬНОГО ПРОЕЦИРОВАНИЯ
1. Проекция точки – точка
2. Если точка принадлежит
А1 принадлежит k1
А2 принадлежит k2
Точка А принадлежит прямой k
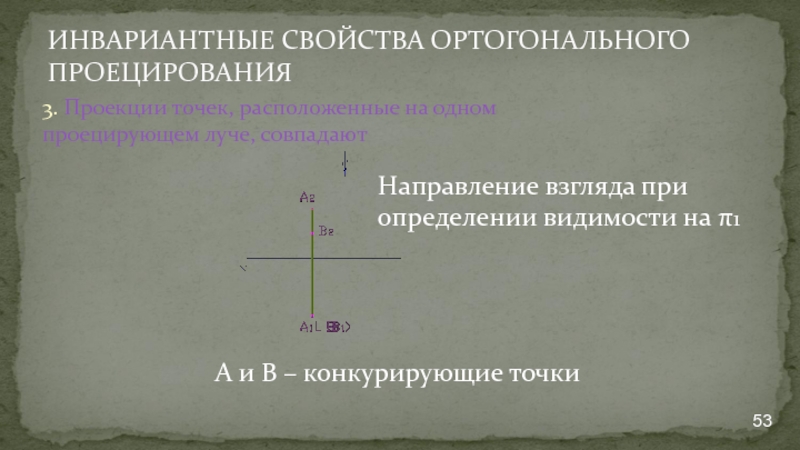
Слайд 53ИНВАРИАНТНЫЕ СВОЙСТВА ОРТОГОНАЛЬНОГО ПРОЕЦИРОВАНИЯ
3. Проекции точек, расположенные на одном проецирующем луче,
Направление взгляда при определении видимости на π1
А и В – конкурирующие точки
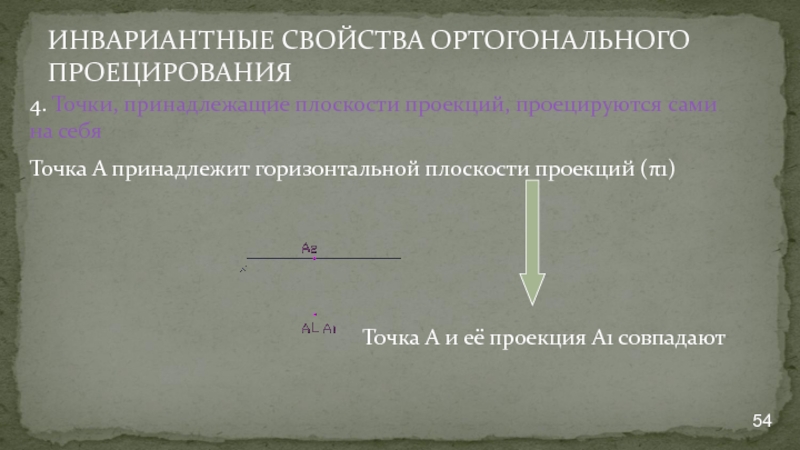
Слайд 54ИНВАРИАНТНЫЕ СВОЙСТВА ОРТОГОНАЛЬНОГО ПРОЕЦИРОВАНИЯ
4. Точки, принадлежащие плоскости проекций, проецируются сами на
Точка А принадлежит горизонтальной плоскости проекций (π1)
Точка А и её проекция А1 совпадают
Слайд 55ИНВАРИАНТНЫЕ СВОЙСТВА ОРТОГОНАЛЬНОГО ПРОЕЦИРОВАНИЯ
5. Проекция прямой – прямая (кроме прямых частного
Проекции прямой - прямые
Одна из проекций прямой - точка, если прямая перпендикулярна плоскости проекций
Слайд 56ИНВАРИАНТНЫЕ СВОЙСТВА ОРТОГОНАЛЬНОГО ПРОЕЦИРОВАНИЯ
6. Если прямые параллельны, то их проекции также
Параллельны их проекции:
m₁//n₁
m₂//n₂
Слайд 57ИНВАРИАНТНЫЕ СВОЙСТВА ОРТОГОНАЛЬНОГО ПРОЕЦИРОВАНИЯ
7. Отношения длин отрезков прямой или параллельных отрезков
А1В1=В1С1
А2В2=В2С2
Точка В делит отрезок АС пополам
Слайд 58ИНВАРИАНТНЫЕ СВОЙСТВА ОРТОГОНАЛЬНОГО ПРОЕЦИРОВАНИЯ
8. Проекции пересекающихся прямых – пересекаются, а проекции
Проекции их пересекаются и точки пересечения находятся на одной линии связи
Прямые k и d пересекаются в точке С
Слайд 59ИНВАРИАНТНЫЕ СВОЙСТВА ОРТОГОНАЛЬНОГО ПРОЕЦИРОВАНИЯ
9. Проекция многоугольника – многоугольник
Слайд 60ИНВАРИАНТНЫЕ СВОЙСТВА ОРТОГОНАЛЬНОГО ПРОЕЦИРОВАНИЯ
10. Отрезок прямой, параллельный плоскости проекций, проецируется на
A2B2 // x
A1B1= IАВI
НВАВ
АВ параллельна горизонтальной плоскости проекций (π1)
Слайд 61ИНВАРИАНТНЫЕ СВОЙСТВА ОРТОГОНАЛЬНОГО ПРОЕЦИРОВАНИЯ
11. Плоская фигура проецируется в натуральную величину на
IΔАВСI= ΔА1В1С1
ΔАВС параллелен горизонтальной плоскости проекций (π1)
Слайд 62ИНВАРИАНТНЫЕ СВОЙСТВА ОРТОГОНАЛЬНОГО ПРОЕЦИРОВАНИЯ
12. Прямой угол, у которого хотя бы один
Слайд 643.Привести пример конкурирующих точек
4.Привести пример чертежа точки, принадлежащей П2
5.Условие, при котором
ВОПРОСЫ 3_5