- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Кривые линии презентация
Содержание
- 1. Кривые линии
- 2. Если в образовании кривой линии
- 3. Если уравнение кривой линии представляет собой
- 4. Линии, все точки которых не
- 5. Линии, все точки которых принадлежат одной плоскости,
- 6. Пi t B
- 7. Предельное положение секущей t называется касательной
- 8. Особые точки кривой
- 9. Точки перегиба (Н) – точки, в которых
Слайд 2
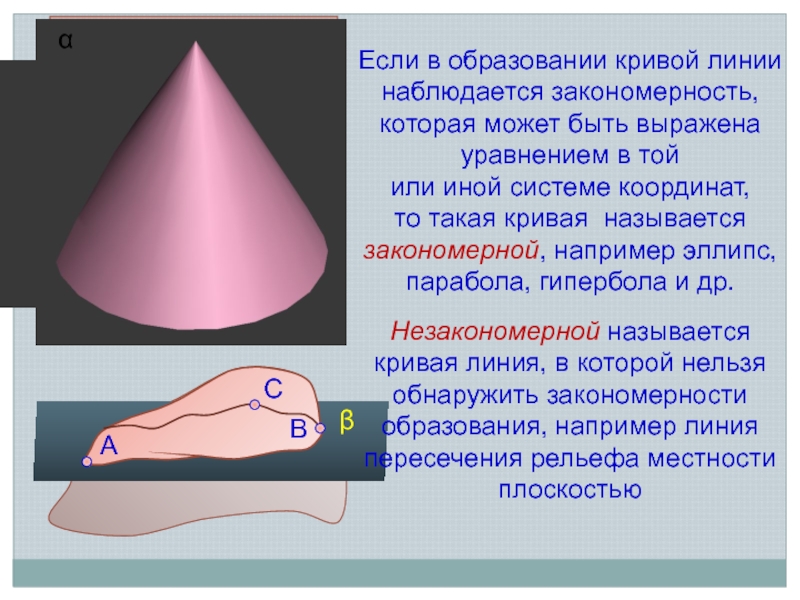
Если в образовании кривой линии
наблюдается закономерность, которая может быть выражена
или иной системе координат,
то такая кривая называется закономерной, например эллипс, парабола, гипербола и др.
Незакономерной называется кривая линия, в которой нельзя обнаружить закономерности образования, например линия пересечения рельефа местности плоскостью
гипербола
α
β
В
С
А
Слайд 3Если уравнение кривой линии представляет собой
алгебраический многочлен, то она называется
Если кривую нельзя задать
алгебраическим многочленом, то она называется
трансцендентной
Слайд 4
Линии, все точки которых не принадлежат одной плоскости, называются пространственными
Порядок алгебраической
Пi
ℓ
1
2
3
4
Слайд 5Линии, все точки которых принадлежат одной плоскости, называются плоскими
Порядок плоской алгебраической
1
2
m
ℓ
Слайд 6
Пi
t
B
A
m
mi
Bi
ti
Класс кривой соответствует
числу касательных к кривой,
проведенных через внешнюю
точку
F
Ai
Fi
g
gi
Прямая, касательная
к кривой,
проецируется в прямую
(в общем случае),
касательную к проекции кривой
Слайд 7
Предельное положение секущей t называется касательной к кривой
в точке А
Прямая
Пi
t
1
2
m
mi
1i
2i
ti
Секущей называется прямая,
имеющая, по меньшей мере,
две общие точки с кривой
n
ni
A
Ai
tI
tiI
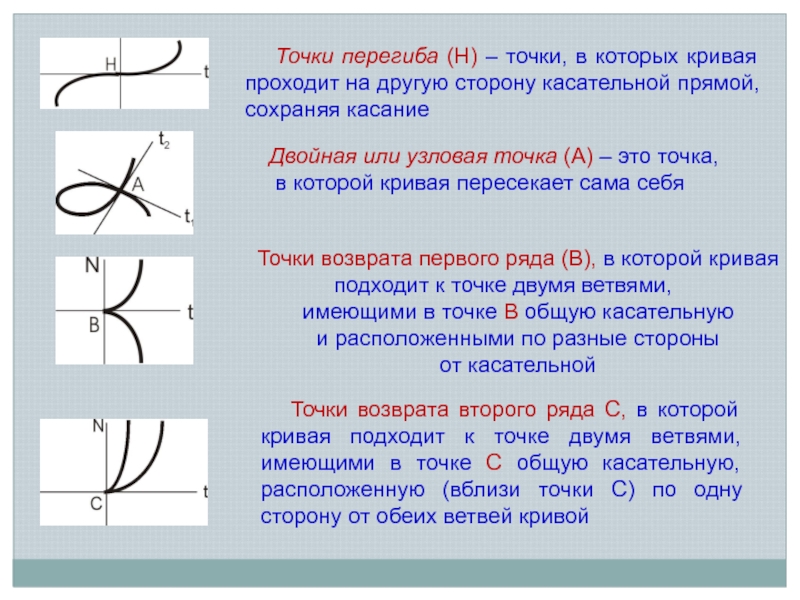
Слайд 9Точки перегиба (Н) – точки, в которых кривая проходит на другую
Двойная или узловая точка (А) – это точка,
в которой кривая пересекает сама себя
Точки возврата первого ряда (В), в которой кривая подходит к точке двумя ветвями,
имеющими в точке В общую касательную
и расположенными по разные стороны
от касательной
Точки возврата второго ряда С, в которой кривая подходит к точке двумя ветвями, имеющими в точке С общую касательную, расположенную (вблизи точки С) по одну сторону от обеих ветвей кривой