- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Аксонометрические проекции презентация
Содержание
- 1. Аксонометрические проекции
- 2. Аксонометрическая проекцияАксонометрическая проекция (от др.-греч.Аксонометрическая проекция (от
- 4. Прямоугольная изометрия Масштаб Кх=Ку=Кz=1 Прямоугольная диметрия масштаб
- 5. Изометри́ческая прое́кция — это разновидность аксонометрической проекцииИзометри́ческая прое́кция —
- 6. Прямоугольная изометрия
- 7. Диметрическая проекция Для построения угла, приблизительно
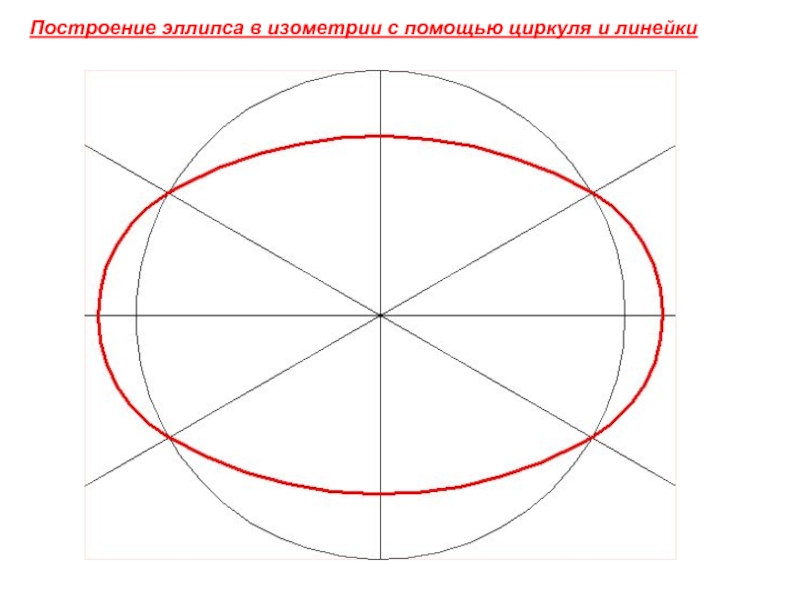
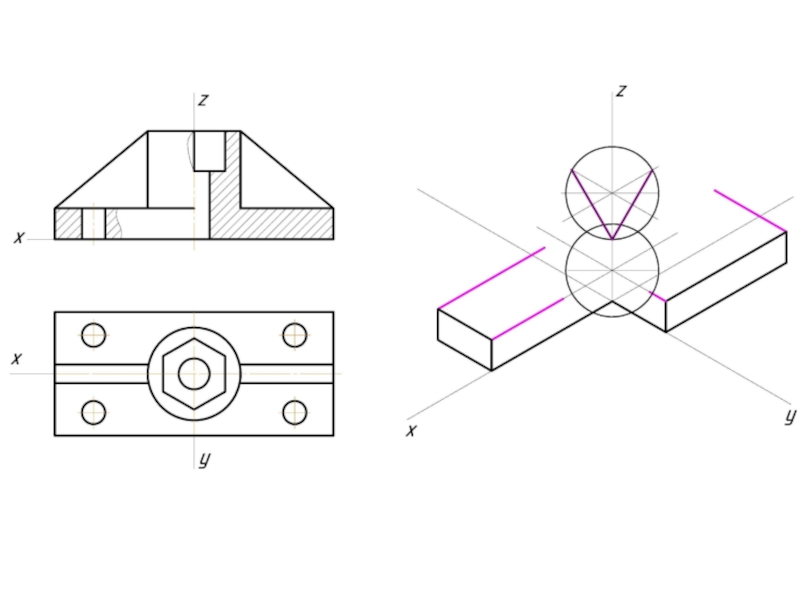
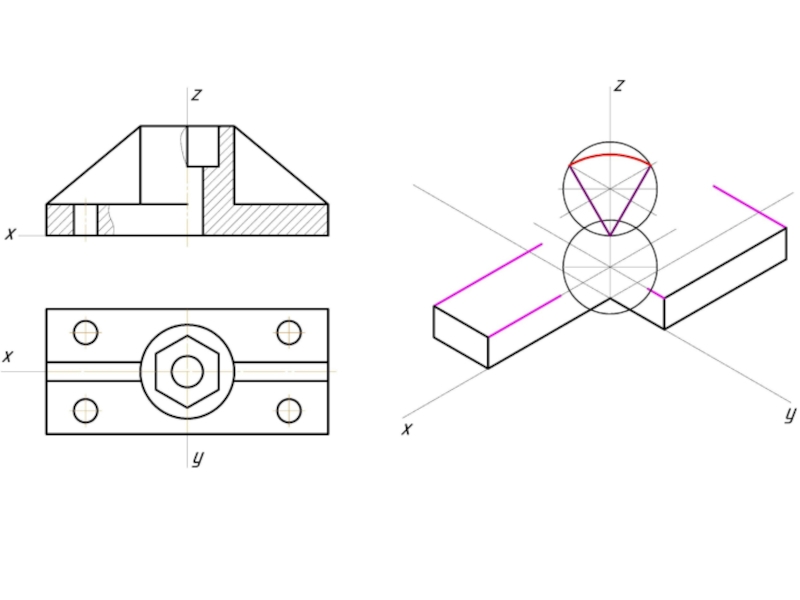
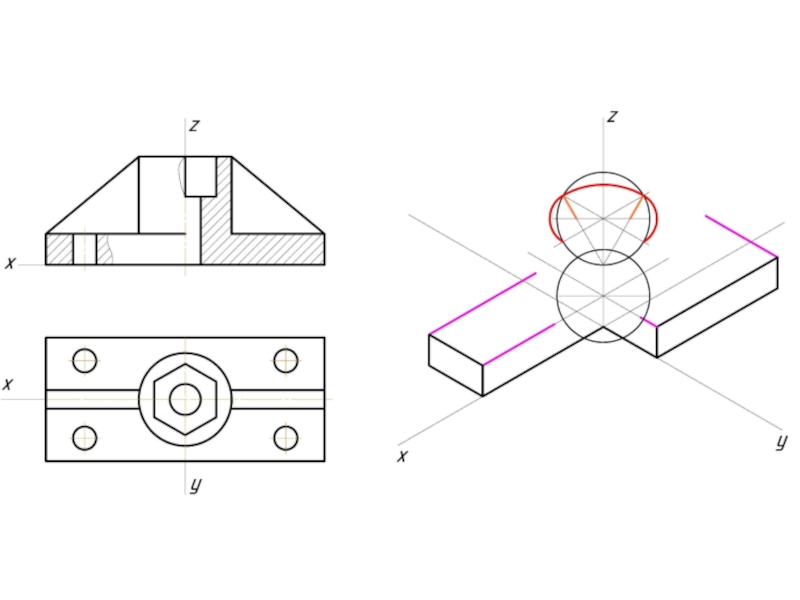
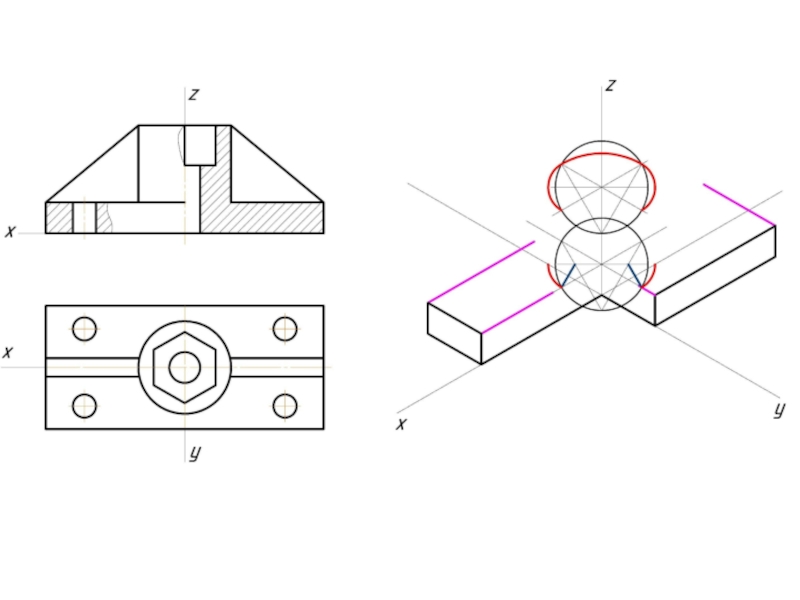
- 10. Построение эллипса в изометрии с помощью циркуля и линейки
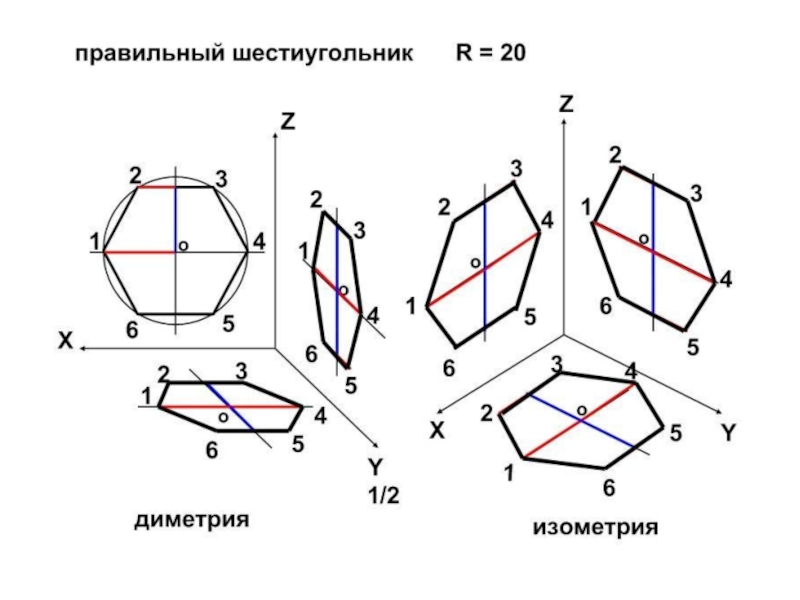
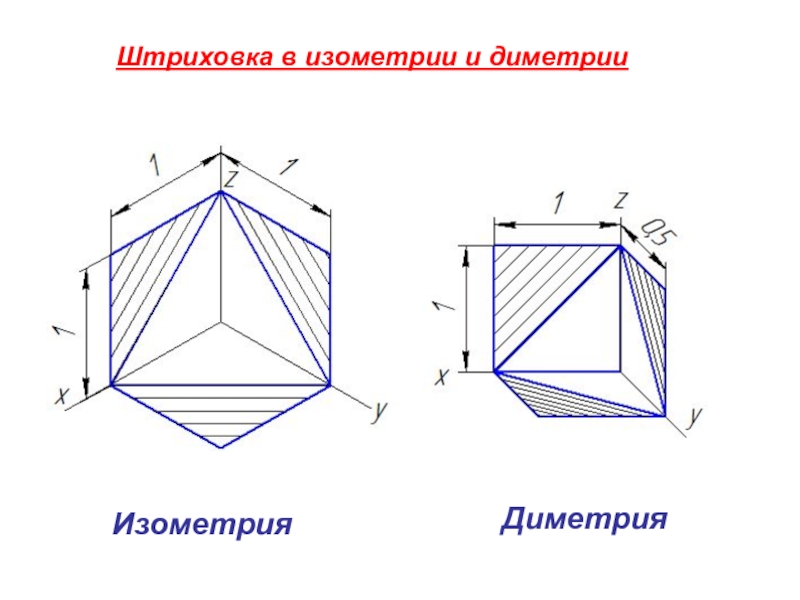
- 11. Штриховка в изометрии и диметрии Изометрия Диметрия
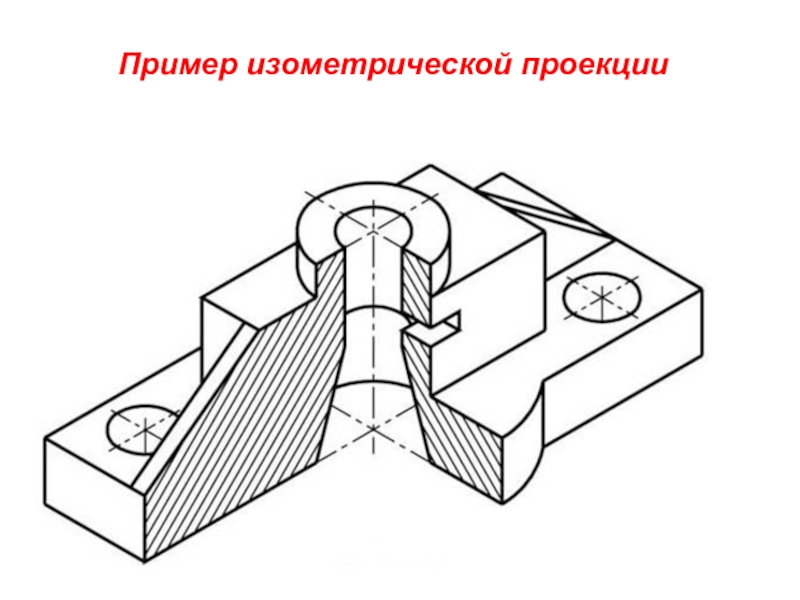
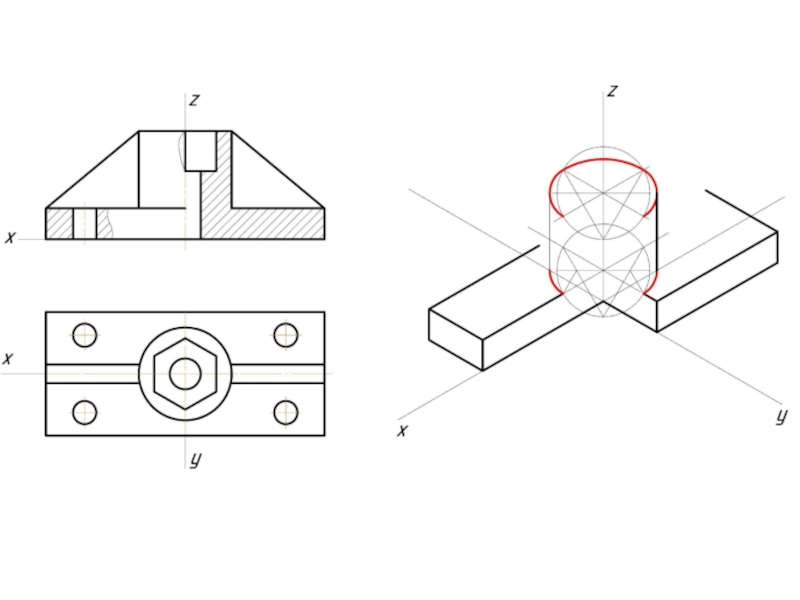
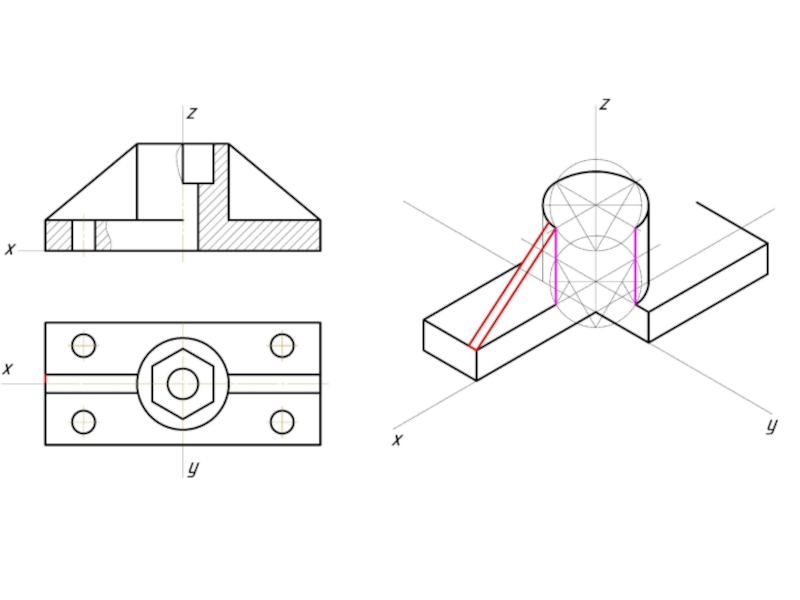
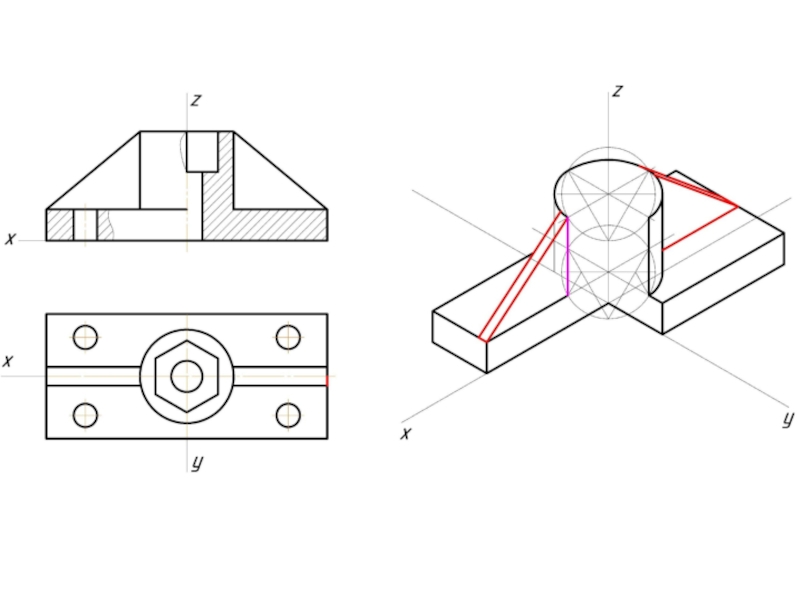
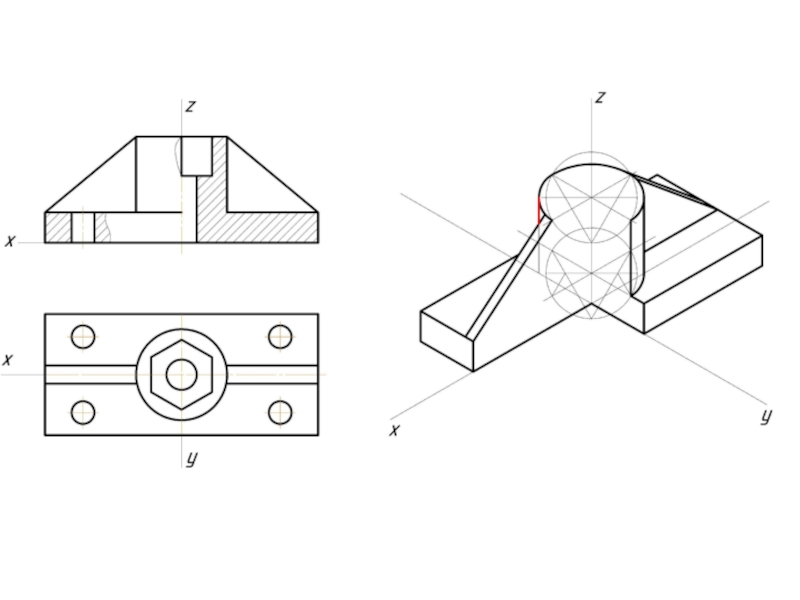
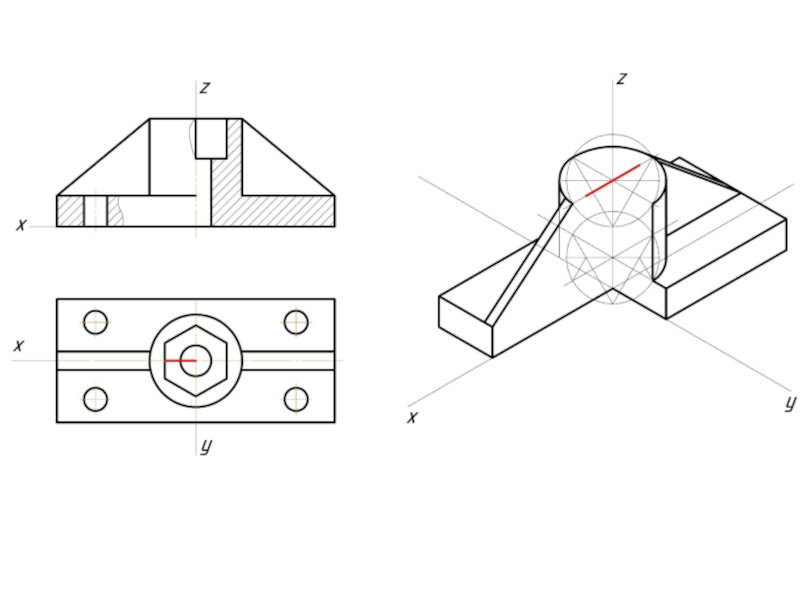
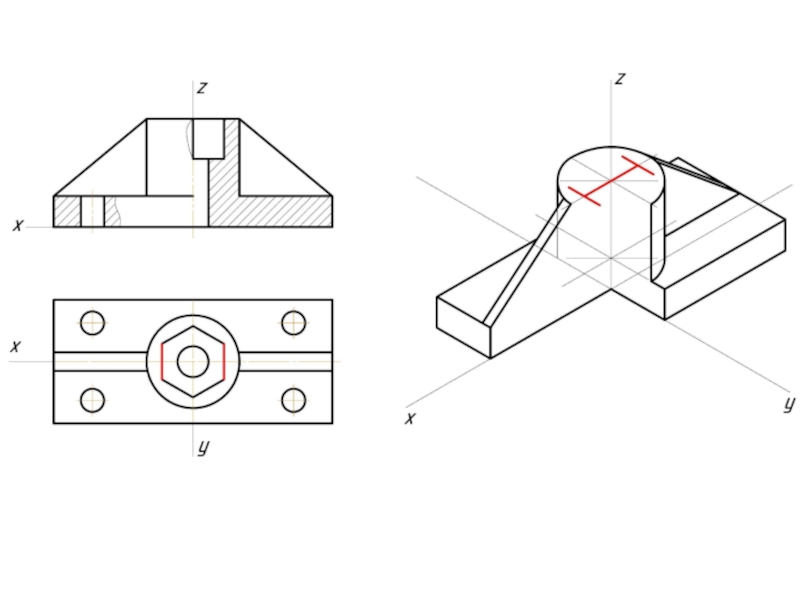
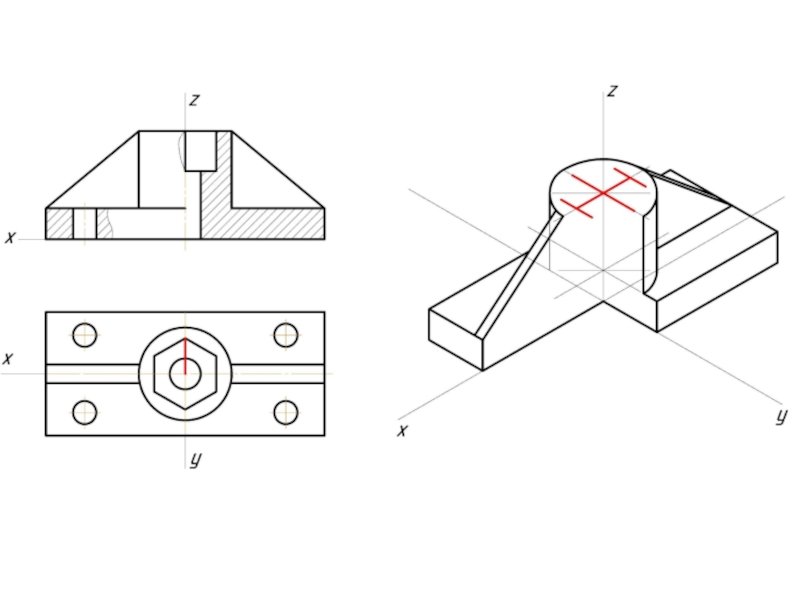
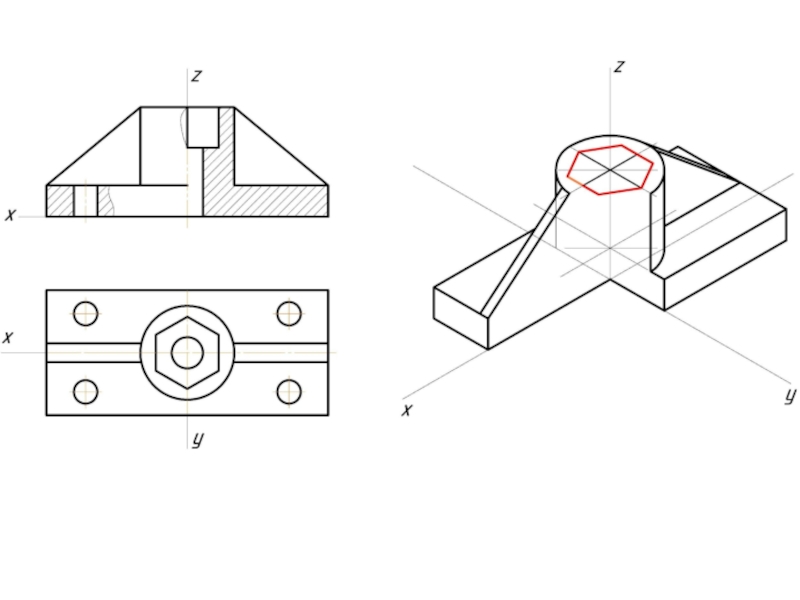
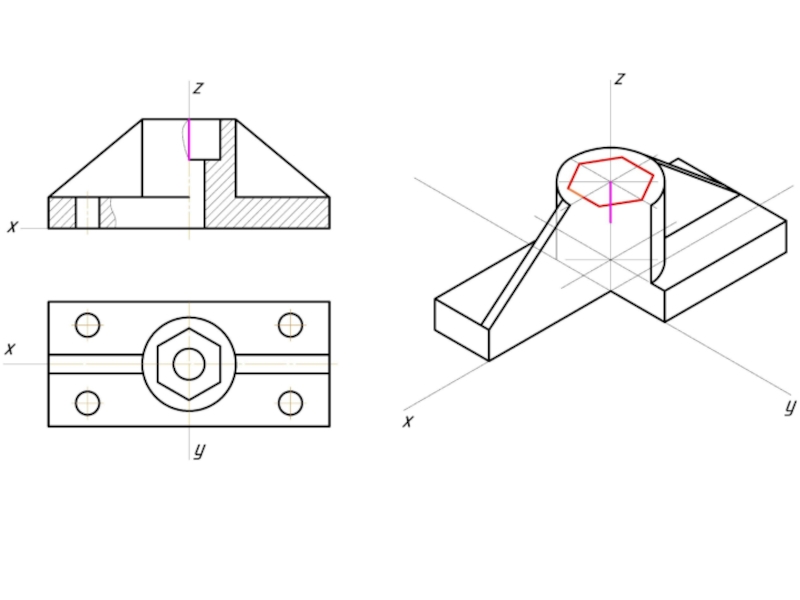
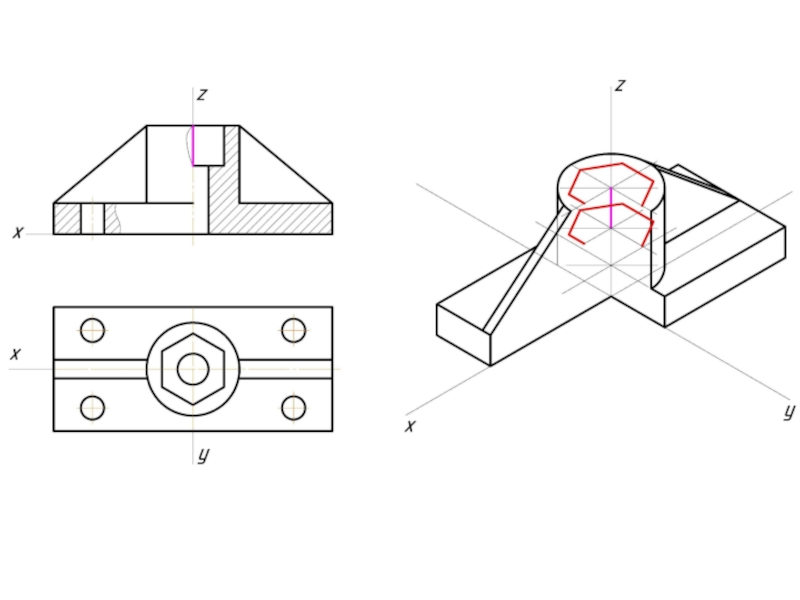
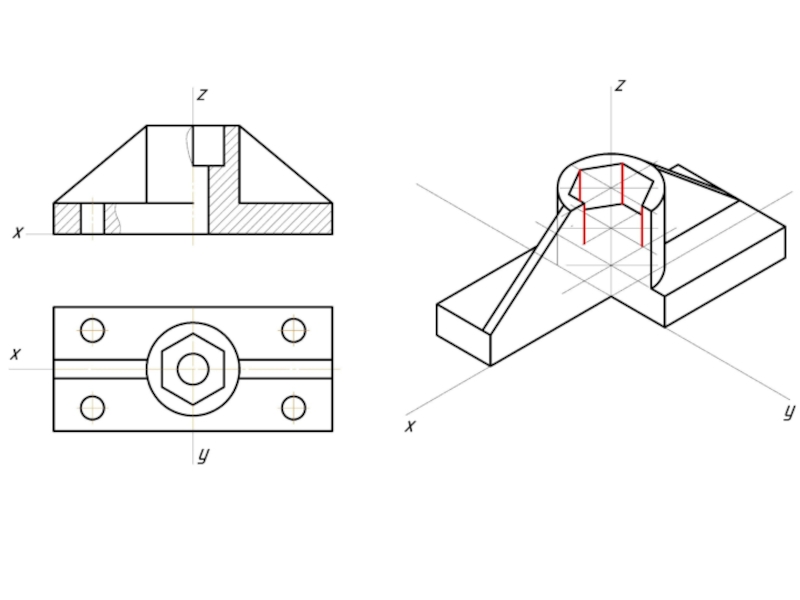
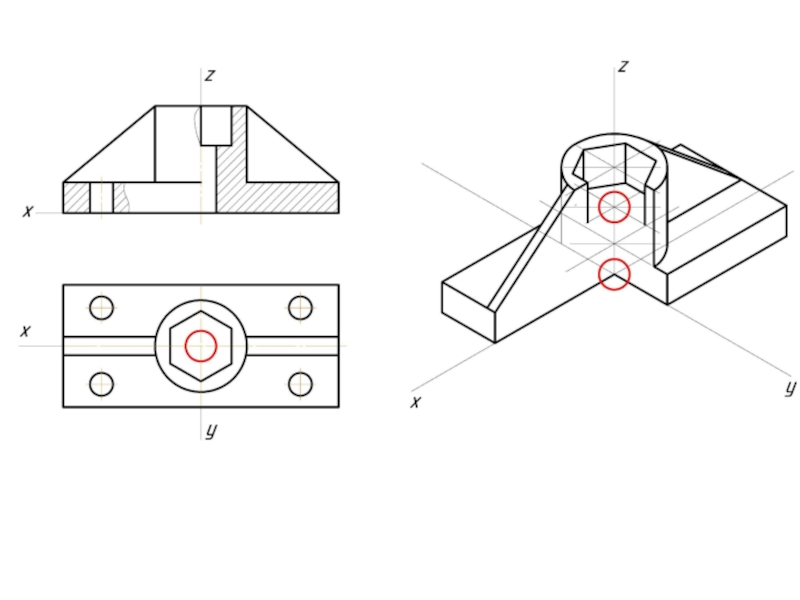
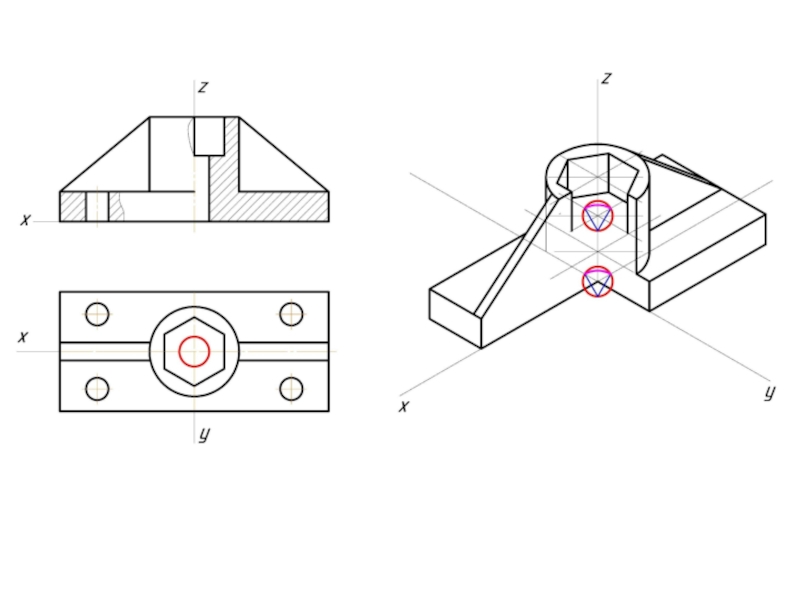
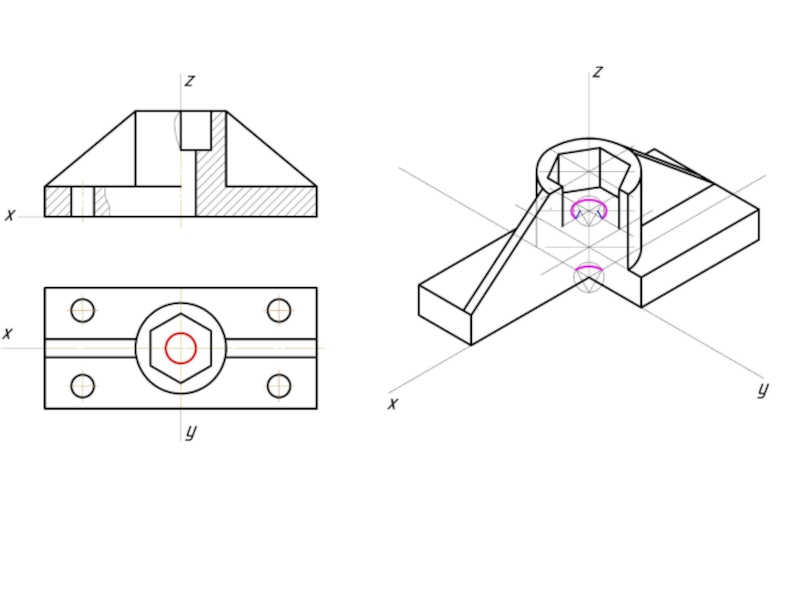
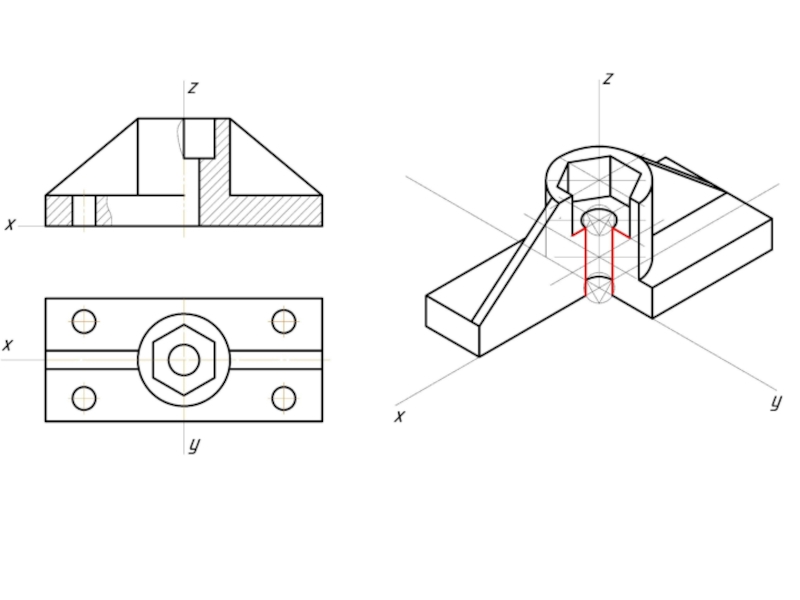
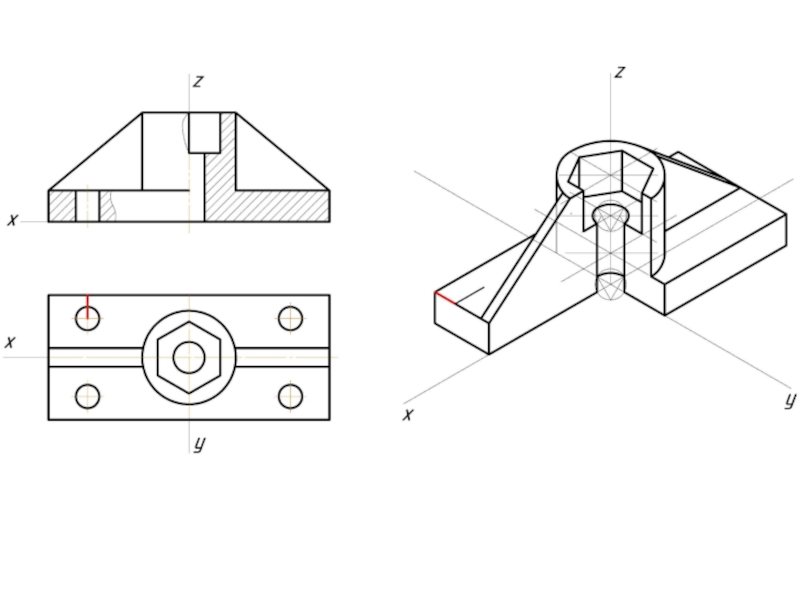
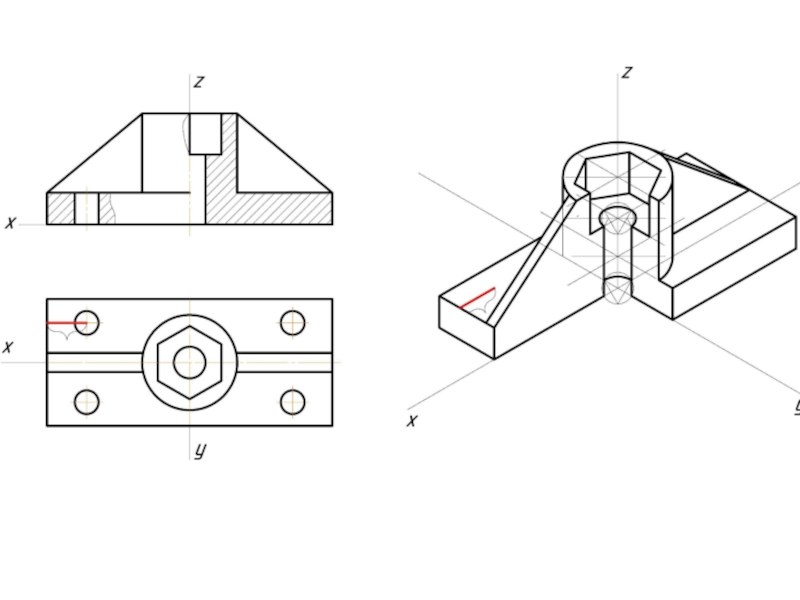
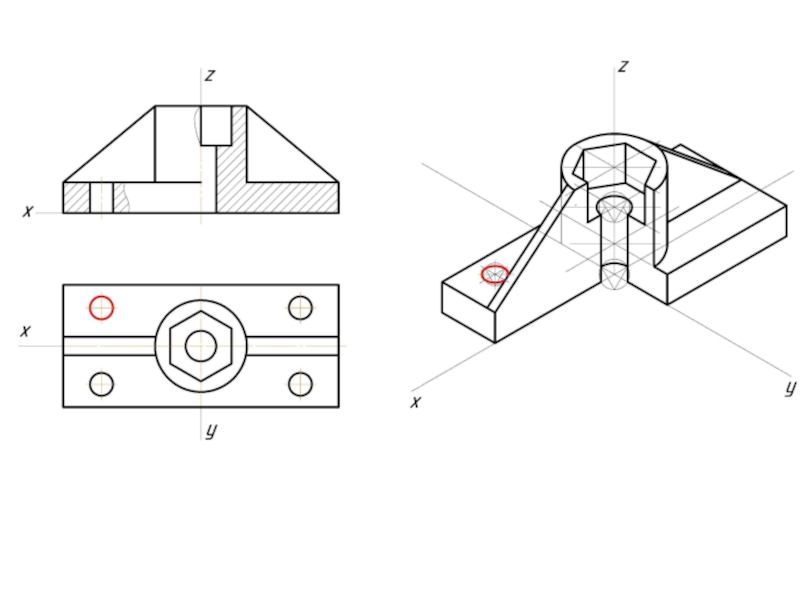
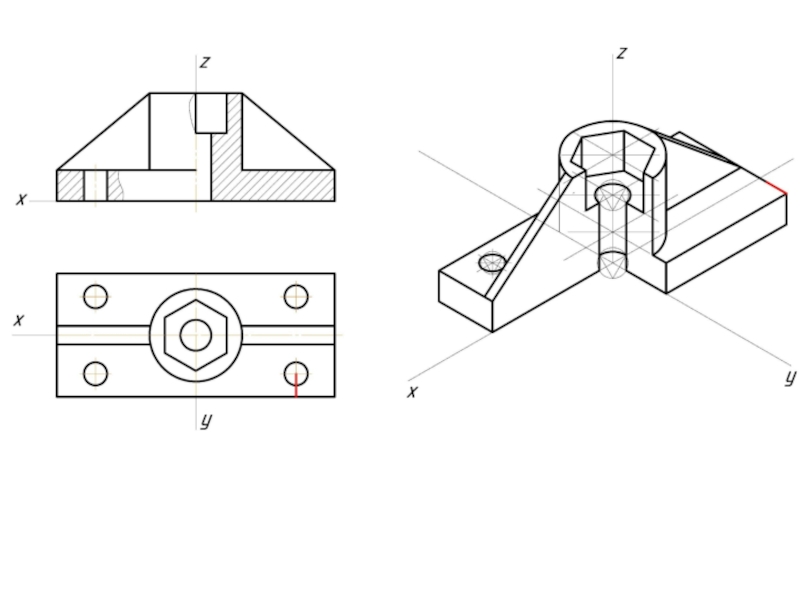
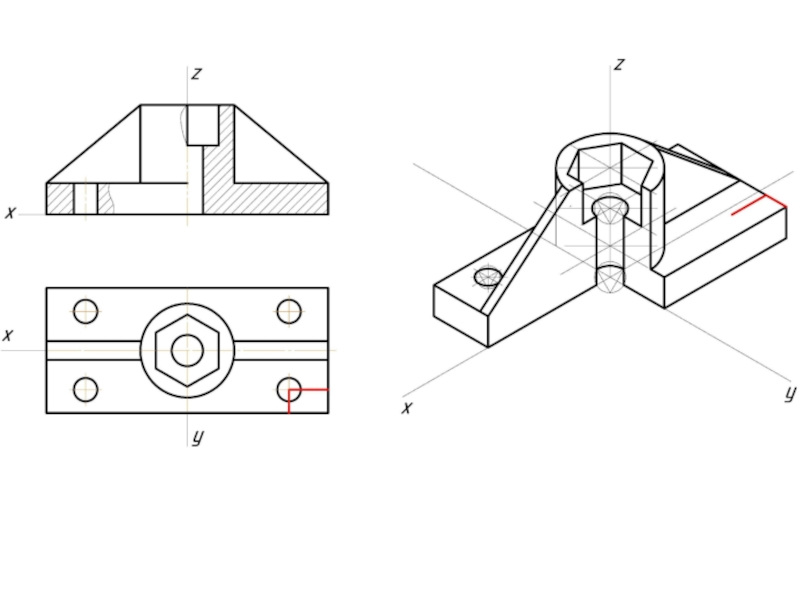
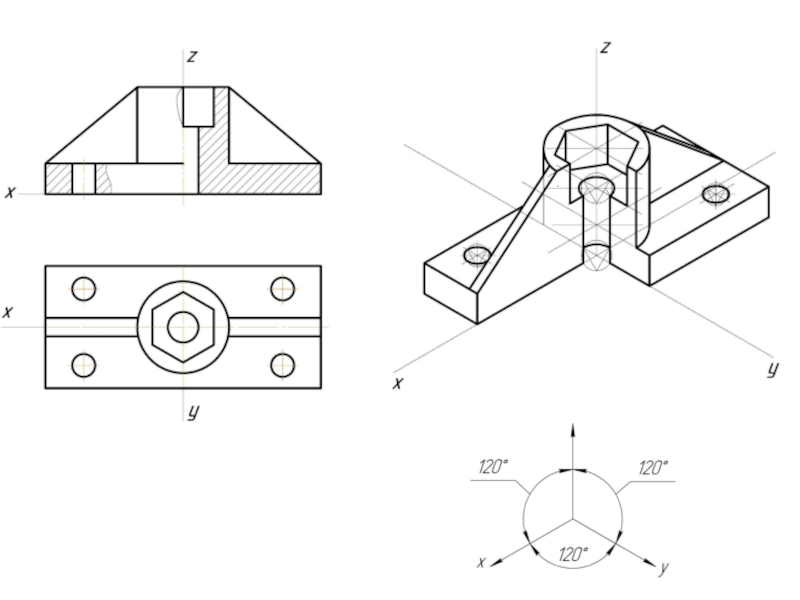
- 12. Пример изометрической проекции
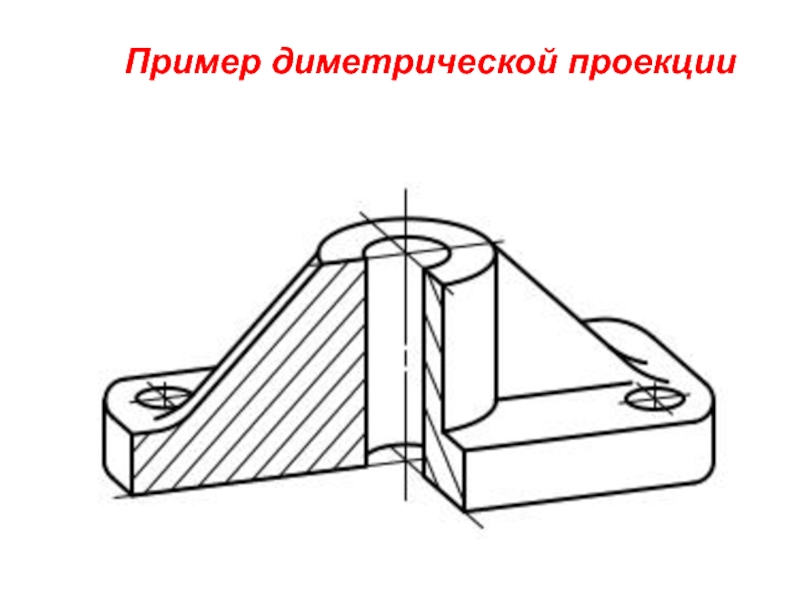
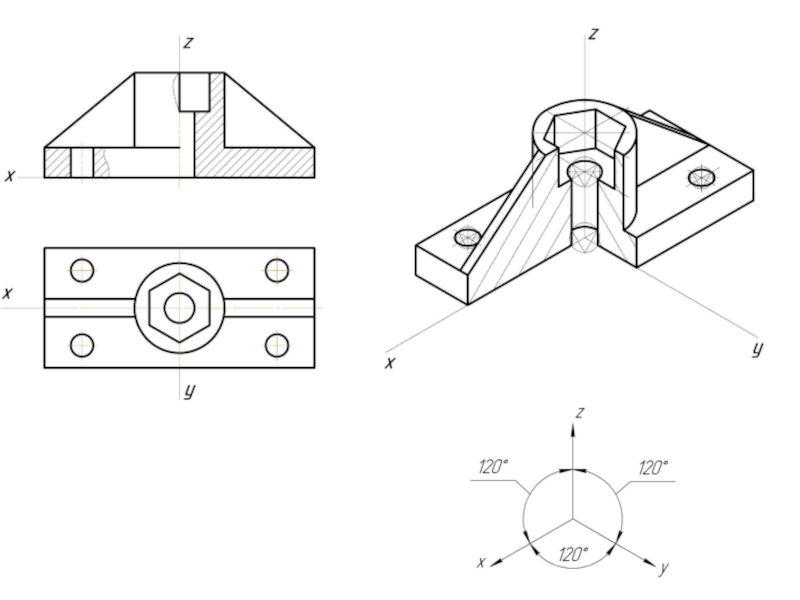
- 13. Пример диметрической проекции
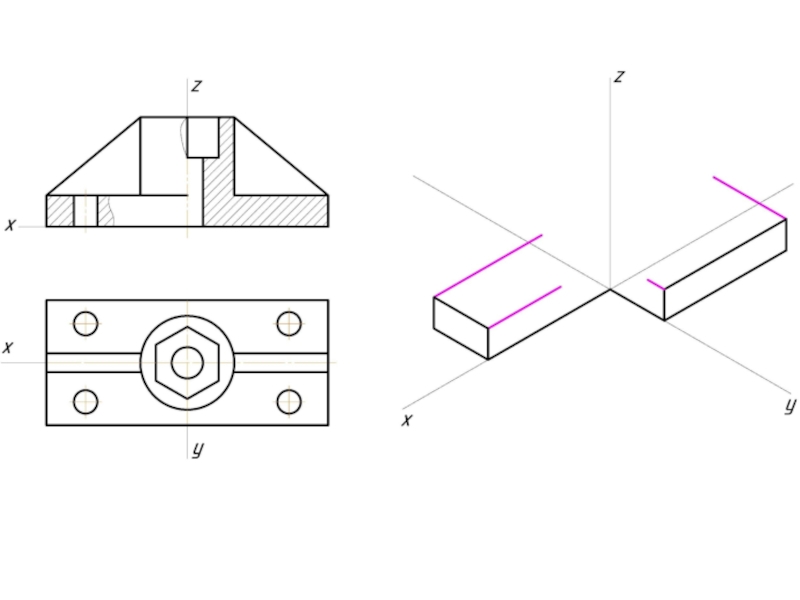
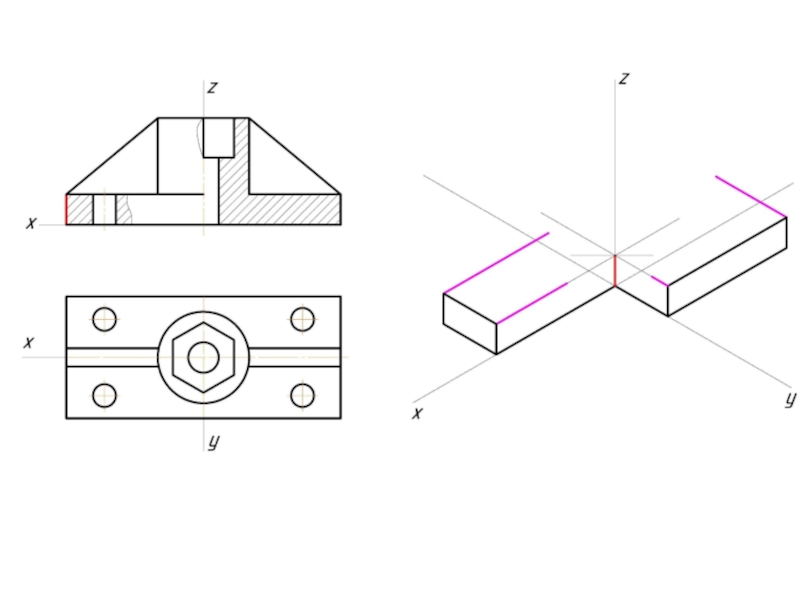
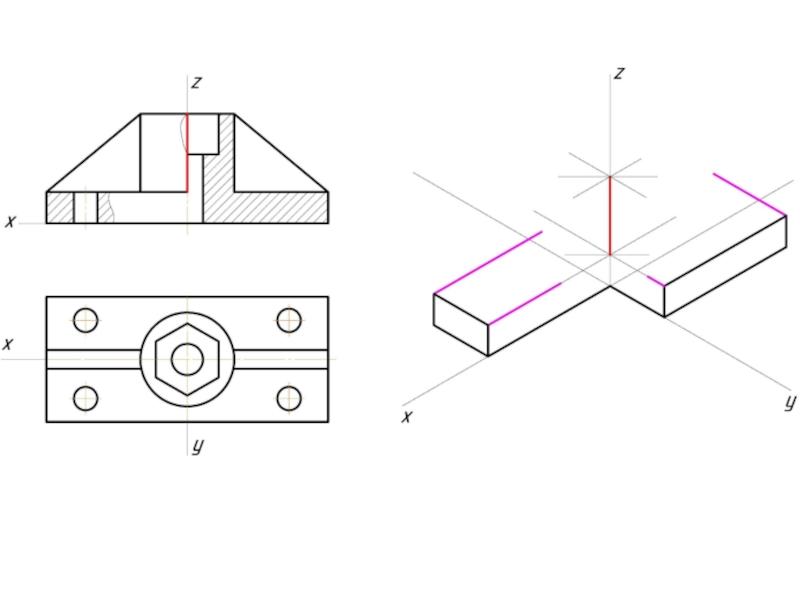
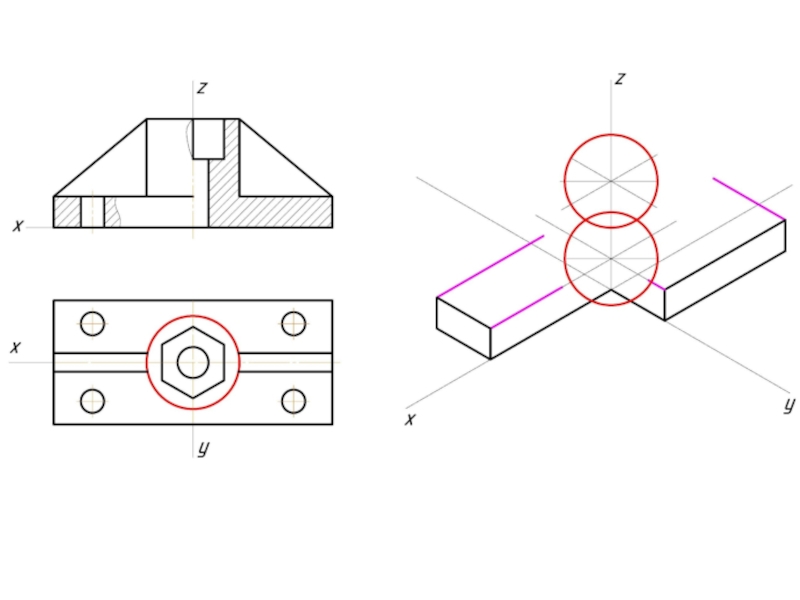
Слайд 2Аксонометрическая проекцияАксонометрическая проекция (от др.-греч.Аксонометрическая проекция (от др.-греч. ἄξων «ось» и др.-греч.Аксонометрическая
Предмет с системой координатПредмет с системой координат, к которой он отнесён, проецируют на произвольную плоскость (картинная плоскостьПредмет с системой координат, к которой он отнесён, проецируют на произвольную плоскость (картинная плоскость аксонометрической проекции) таким образом, чтобы эта плоскость не совпадала с его координатной плоскостью. В этом случае получаются две взаимосвязанные проекции одной фигуры на одну плоскость, что позволяет восстановить положение в пространстве, получив наглядное изображение предмета. Так как картинная плоскость не параллельна ни одной из координатных осей, то имеются искажения отрезков по длине параллельных координатным осям. Это искажение может быть равным по всем трём осям — изометрическая проекцияПредмет с системой координат, к которой он отнесён, проецируют на произвольную плоскость (картинная плоскость аксонометрической проекции) таким образом, чтобы эта плоскость не совпадала с его координатной плоскостью. В этом случае получаются две взаимосвязанные проекции одной фигуры на одну плоскость, что позволяет восстановить положение в пространстве, получив наглядное изображение предмета. Так как картинная плоскость не параллельна ни одной из координатных осей, то имеются искажения отрезков по длине параллельных координатным осям. Это искажение может быть равным по всем трём осям — изометрическая проекция, одинаковыми по двум осям — диметрическая проекцияПредмет с системой координат, к которой он отнесён, проецируют на произвольную плоскость (картинная плоскость аксонометрической проекции) таким образом, чтобы эта плоскость не совпадала с его координатной плоскостью. В этом случае получаются две взаимосвязанные проекции одной фигуры на одну плоскость, что позволяет восстановить положение в пространстве, получив наглядное изображение предмета. Так как картинная плоскость не параллельна ни одной из координатных осей, то имеются искажения отрезков по длине параллельных координатным осям. Это искажение может быть равным по всем трём осям — изометрическая проекция, одинаковыми по двум осям — диметрическая проекция и с искажениями разными по всем трём осям — триметрическая проекция.
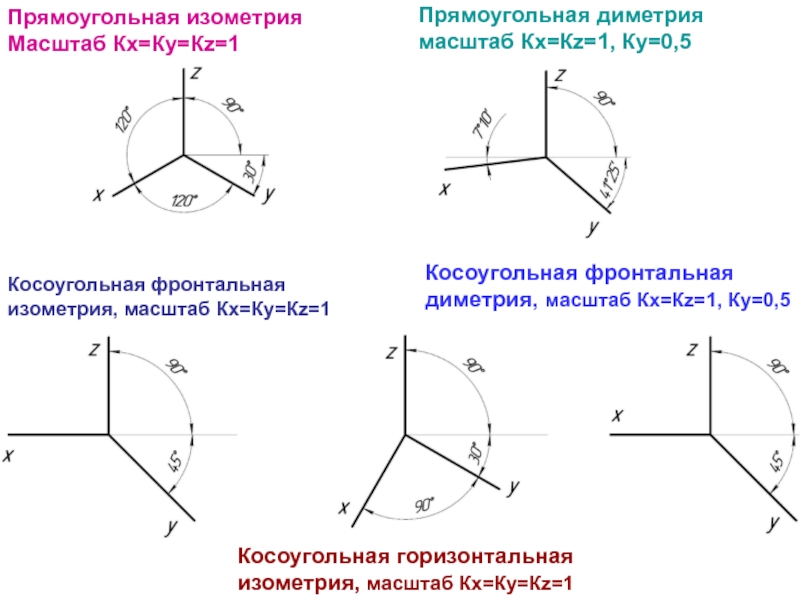
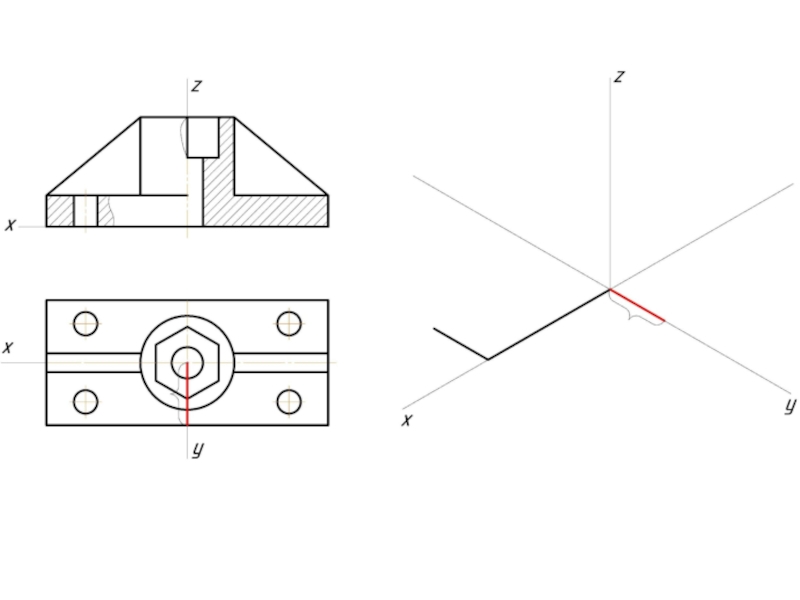
Слайд 4Прямоугольная изометрия
Масштаб Кх=Ку=Кz=1
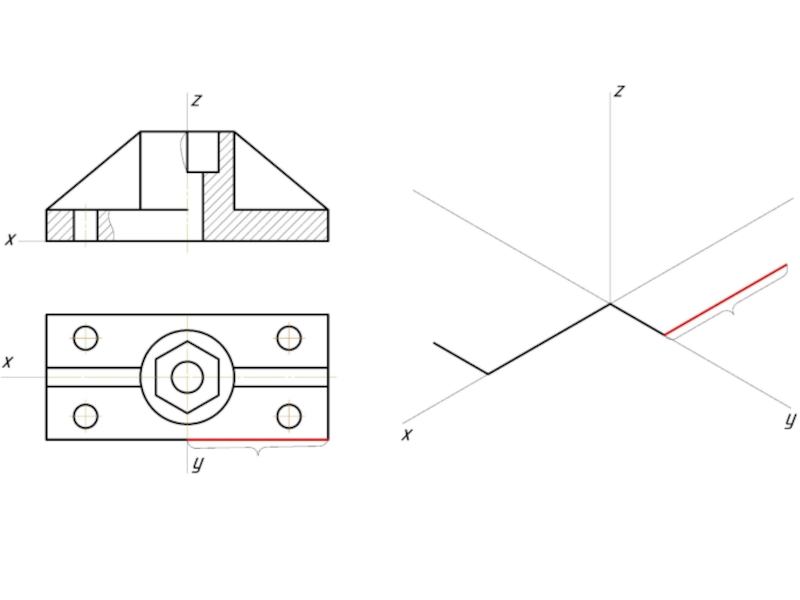
Прямоугольная диметрия
масштаб Кх=Кz=1, Ку=0,5
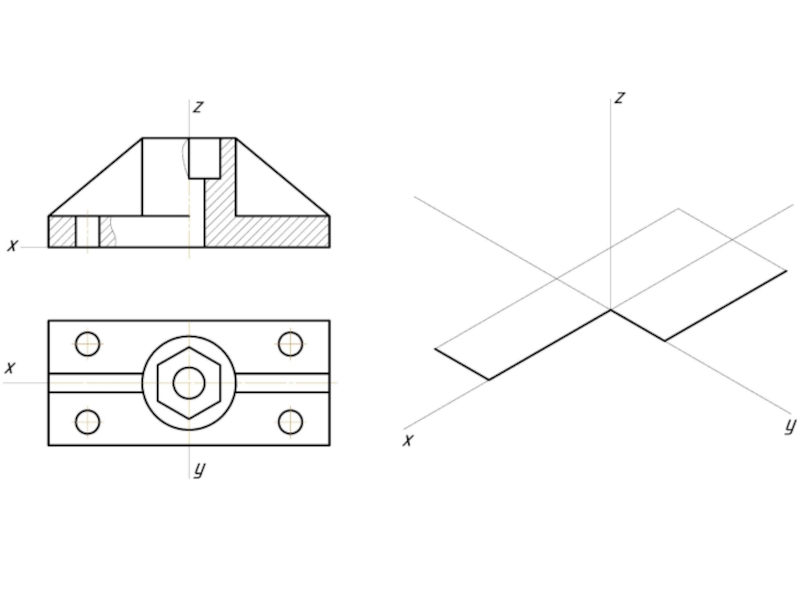
Косоугольная фронтальная
изометрия, масштаб Кх=Ку=Кz=1
Косоугольная горизонтальная
изометрия, масштаб
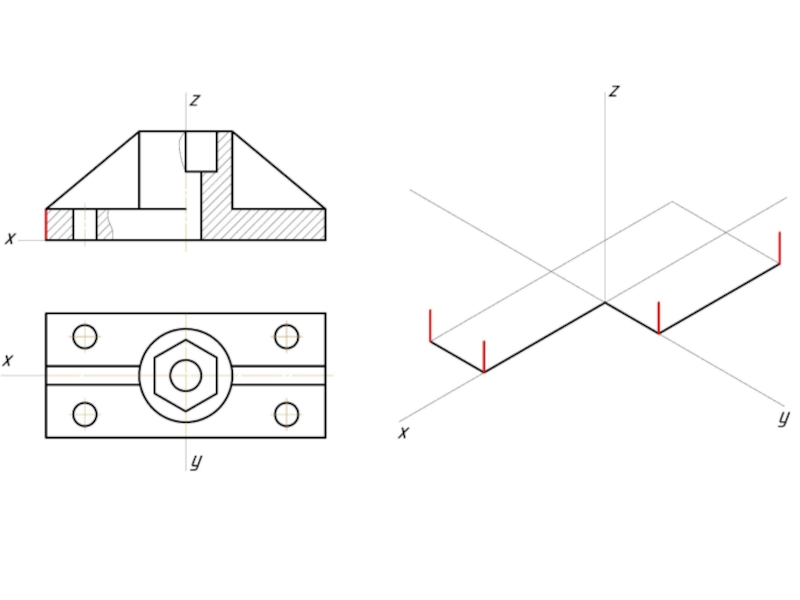
Косоугольная фронтальная
диметрия, масштаб Кх=Кz=1, Ку=0,5
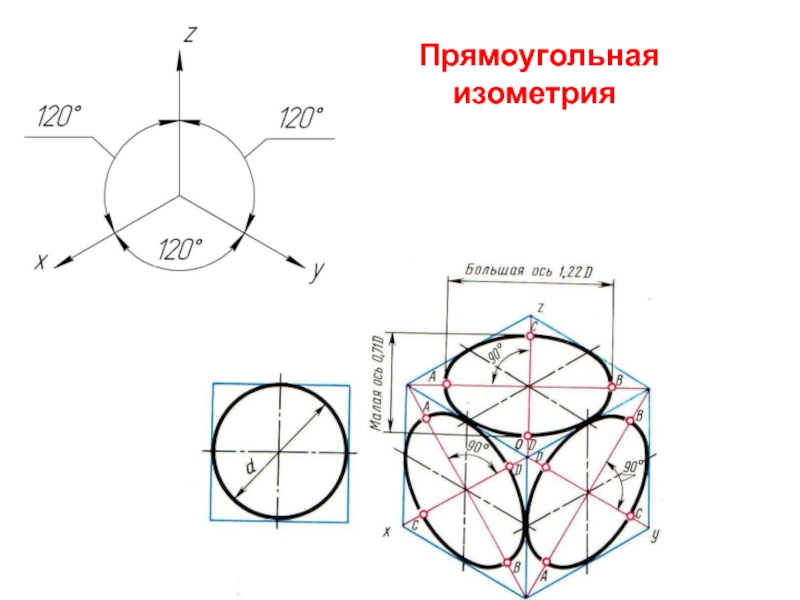
Слайд 5Изометри́ческая прое́кция — это разновидность аксонометрической проекцииИзометри́ческая прое́кция — это разновидность аксонометрической проекции,
Действительные коэффициенты искажения по осям OX, OY и OZ равны 0,82. Но с такими значениями коэффициентов искажения работать не удобно, поэтому, на практике, используются приведенные коэффициенты искажений. Эта проекция обычно выполняется без искажения, поэтому, приведенные коэффициенты искажений принимается k = m = n =1. Окружности, лежащие в плоскостях, параллельных плоскостям проекций, проецируются в эллипсы, большая ось которых равна 1,22, а малая – 0,71 диаметра образующей окружности D.
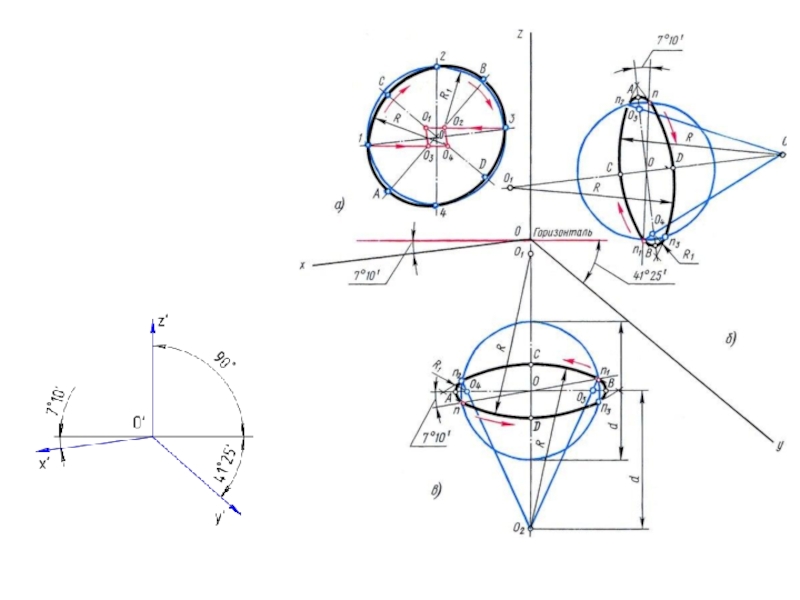
Слайд 7Диметрическая проекция
Для построения угла, приблизительно равного 7º10´, строится прямоугольный треугольник, катеты
Коэффициенты искажения по осям ОХ и OZ k=n=0,94 а по оси OY – m=0,47. При округлении этих параметров принимается k=n=1 и m=0,5. В этом случае размеры осей эллипсов будут: большая ось эллипса 1 равна 0,95D и эллипсов 2 и 3 – 0,35D (D – диаметр окружности). На Рисунке 4.5 большие оси эллипсов 1, 2 и 3 расположены под углом 90º к осям OY, OZ и OX, соответственно.