- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Оценка статистических параметров потока событий термоакустической эмиссии по данным датчика интегральной акустики презентация
Содержание
- 1. Оценка статистических параметров потока событий термоакустической эмиссии по данным датчика интегральной акустики
- 2. Исследование термических разрушений горных пород: отслеживание эволюции
- 3. Исследование термических разрушений горных пород: схема лабораторной
- 4. Факторы, влияющие на параметры потока импульсов ТАЭ
- 5. Факторы, влияющие на параметры потока импульсов ТАЭ
- 6. Факторы, влияющие на параметры потока импульсов ТАЭ
- 7. Факторы, влияющие на параметры потока импульсов ТАЭ
- 8. Факторы, влияющие на параметры потока импульсов ТАЭ
- 9. Факторы, влияющие на параметры потока импульсов ТАЭ
- 10. Факторы, влияющие на параметры потока импульсов ТАЭ
- 11. Факторы, влияющие на параметры потока импульсов ТАЭ
- 12. Факторы, влияющие на параметры потока импульсов
- 13. Факторы, влияющие на параметры потока импульсов ТАЭ
- 14. Факторы, влияющие на параметры потока импульсов ТАЭ
- 15. Факторы, влияющие на параметры потока импульсов ТАЭ
- 16. Оценка влияния факторов: расчетная модель
- 17. Оценка влияния факторов: расчетная модель образец
- 18. Оценка влияния факторов: расчетная модель для нахождения
- 19. Оценка влияния факторов: распределение регистрируемых импульсов по
- 20. Оценка влияния факторов: распределение регистрируемых импульсов по
- 21. Оценка влияния факторов: распределение регистрируемых импульсов по
- 22. Оценка влияния факторов: распределение регистрируемых импульсов по
- 23. Анализ экспериментальных данных: методика оценки характера закона
- 24. Анализ экспериментальных данных: методика оценки характера закона
- 25. Анализ экспериментальных данных – примеры: распределение импульсов
- 26. Анализ экспериментальных данных – примеры: этапы эксперимента
- 27. Анализ экспериментальных данных – примеры: этапы эксперимента
- 28. Анализ экспериментальных данных – примеры: этапы эксперимента
- 29. Анализ экспериментальных данных: инициация ТАЭ градиентом температуры
- 30. Анализ экспериментальных данных: инициация ТАЭ градиентом температуры
- 31. Анализ экспериментальных данных: инициация ТАЭ градиентом температуры
- 32. Анализ экспериментальных данных: инициация ТАЭ градиентом температуры
- 33. Анализ экспериментальных данных: инициация ТАЭ градиентом температуры
- 34. Выводы Затухание (энергии) импульсов ТАЭ в
- 35. Спасибо за внимание!
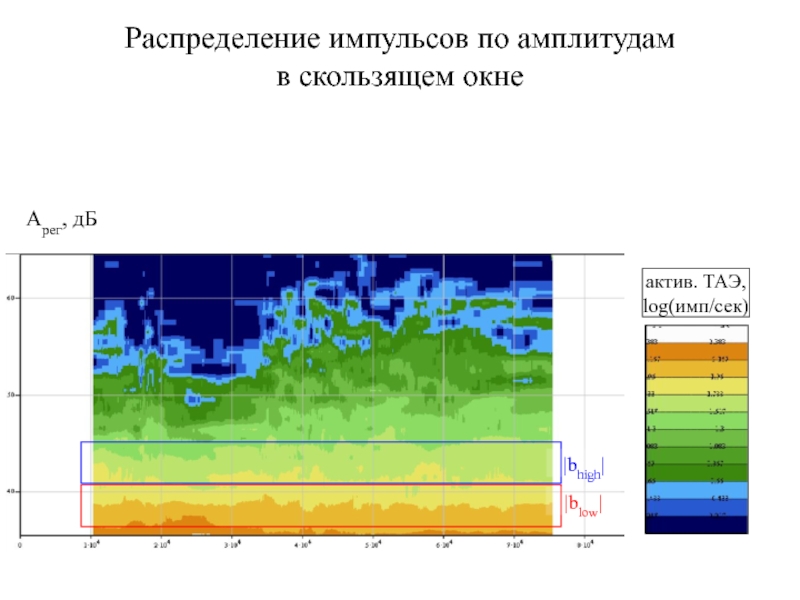
- 37. Распределение импульсов по амплитудам в скользящем окне
Слайд 1Актуальные вопросы метода акустической эмиссии
(АПМАЭ-2018)
ТГУ, 28 мая – 01 июня 2018
Оценка статистических параметров потока событий термоакустической эмиссии по данным датчика интегральной акустики
н.с. лаб. 301 ИФЗ РАН, к.т.н. Казначеев Павел Александрович,
Майбук З.-Ю.Я., Пономарев А.В., Смирнов В.Б., Бондаренко Н.Б.
Тольятти, ТГУ - 2018
Слайд 2Исследование термических разрушений горных пород:
отслеживание эволюции
Эволюция разрушения отслеживается по данным об
При воздействии высоких температур (более 200°С) затруднен доступ к образцу для установки массива датчиков АЭ.
На практике лабораторная установка позволяет установить один или два датчика, «снимающих» сигнал АЭ с одного или двух торцов цилиндрического образца.
Соответственно, невозможна полноценная локация и определение энергии события АЭ.
→ Возникает задача определения параметров событий ТАЭ по параметрам импульсов ТАЭ, регистрируемых одиночным датчиком АЭ. Прежде всего, это касается оценки статистических параметров потока событий по параметрам потока импульсов – распределения по энергиям, b-value и т.п.
Слайд 3Исследование термических разрушений горных пород:
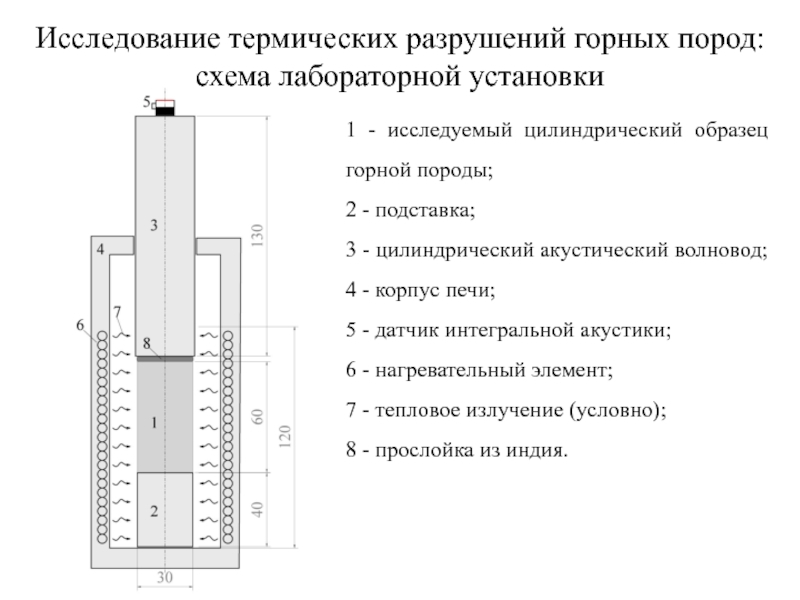
схема лабораторной установки
1 - исследуемый цилиндрический образец
2 - подставка;
3 - цилиндрический акустический волновод; 4 - корпус печи;
5 - датчик интегральной акустики;
6 - нагревательный элемент;
7 - тепловое излучение (условно);
8 - прослойка из индия.
Слайд 4Факторы, влияющие на параметры потока импульсов ТАЭ
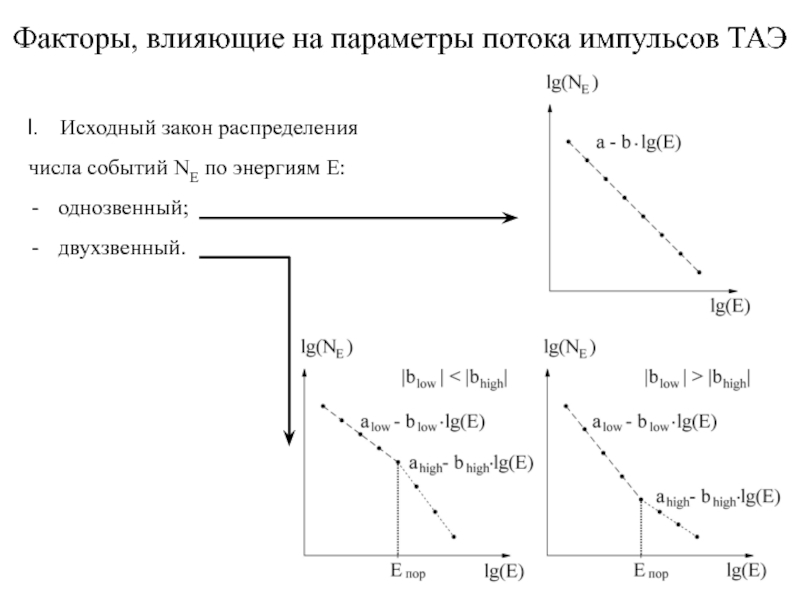
Исходный закон распределения
числа событий
однозвенный;
двухзвенный.
Слайд 5Факторы, влияющие на параметры потока импульсов ТАЭ
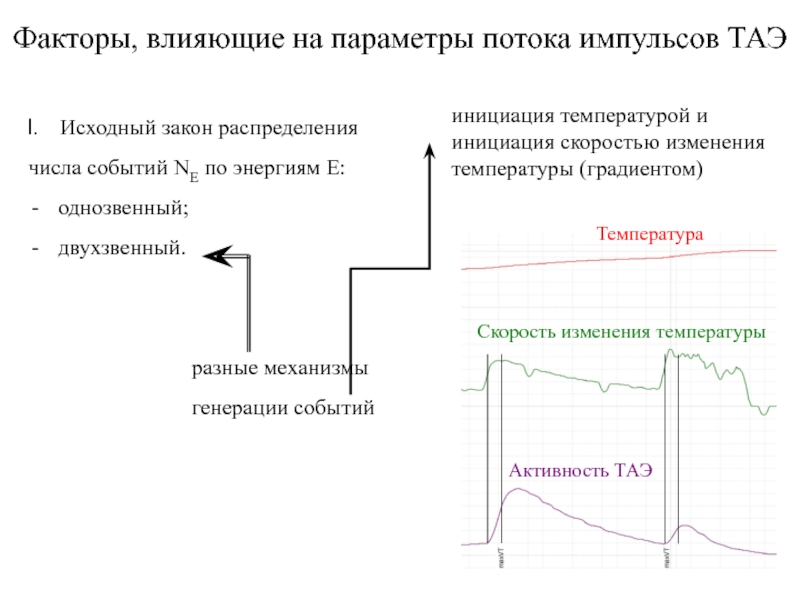
инициация температурой и инициация скоростью
Исходный закон распределения
числа событий NE по энергиям E:
однозвенный;
двухзвенный.
разные механизмы
генерации событий
Слайд 6Факторы, влияющие на параметры потока импульсов ТАЭ
Исходный закон распределения
числа событий
однозвенный;
двухзвенный.
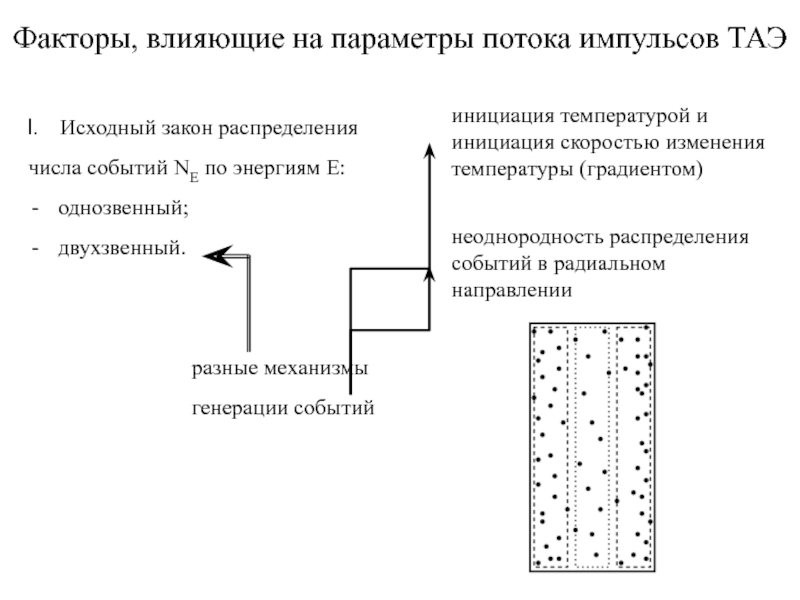
разные механизмы
генерации событий
инициация температурой и инициация скоростью изменения температуры (градиентом)
неоднородность распределения событий в радиальном направлении
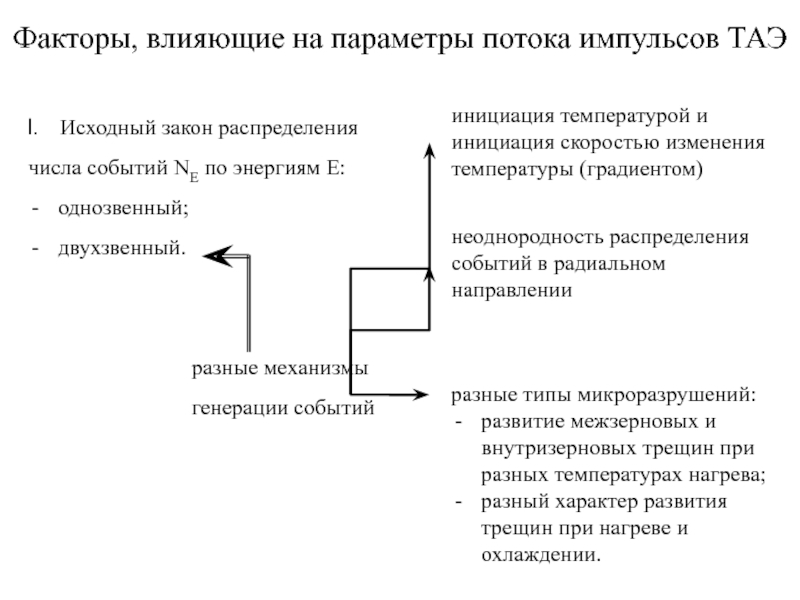
Слайд 7Факторы, влияющие на параметры потока импульсов ТАЭ
Исходный закон распределения
числа событий
однозвенный;
двухзвенный.
разные механизмы
генерации событий
инициация температурой и инициация скоростью изменения температуры (градиентом)
разные типы микроразрушений:
развитие межзерновых и внутризерновых трещин при разных температурах нагрева;
разный характер развития трещин при нагреве и охлаждении.
неоднородность распределения событий в радиальном направлении
Слайд 8Факторы, влияющие на параметры потока импульсов ТАЭ
Исходный закон распределения
числа событий
(однозвенный и двухзвенный).
II. Затухание акустического импульса:
расхождение;
поглощение.
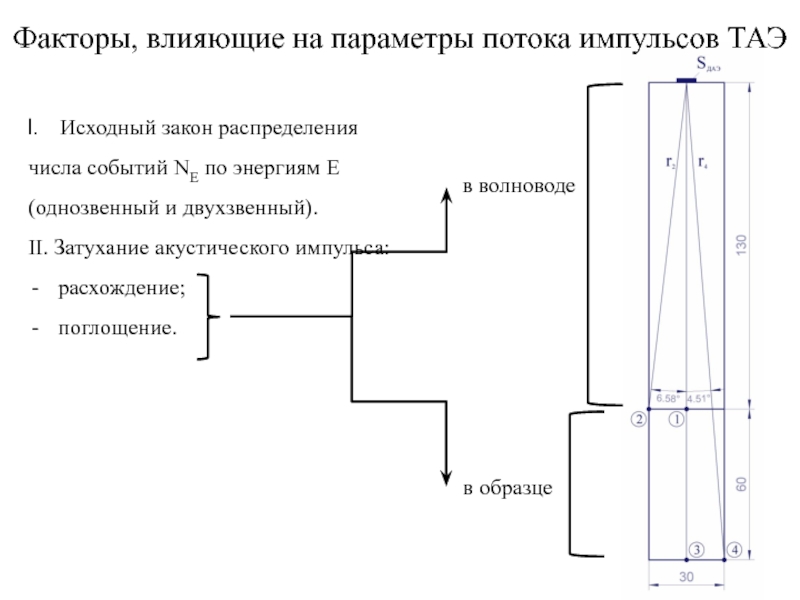
Слайд 9Факторы, влияющие на параметры потока импульсов ТАЭ
Исходный закон распределения
числа событий
(однозвенный и двухзвенный).
II. Затухание акустического импульса:
расхождение;
поглощение.
в волноводе
в образце
Слайд 10Факторы, влияющие на параметры потока импульсов ТАЭ
Исходный закон распределения
числа событий
(однозвенный и двухзвенный).
II. Затухание акустического импульса:
расхождение;
поглощение.
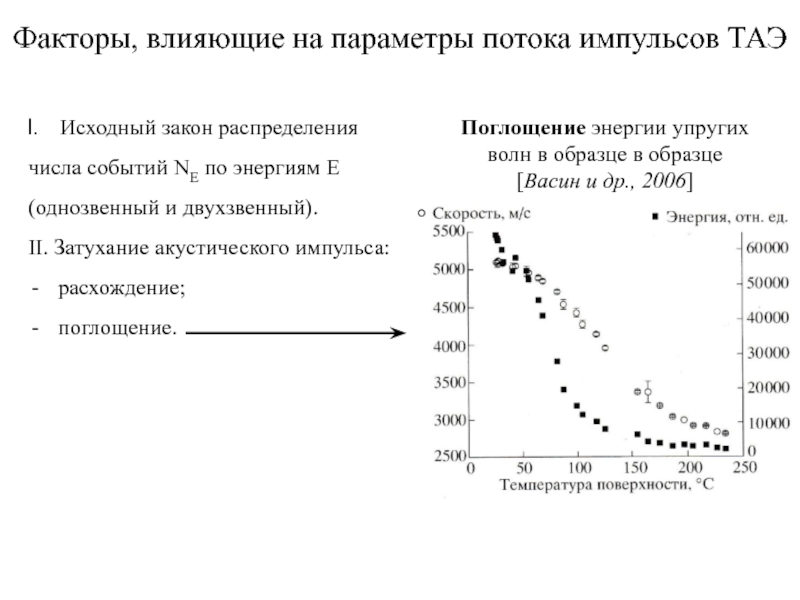
Поглощение энергии упругих волн в образце в образце
[Васин и др., 2006]
Слайд 11Факторы, влияющие на параметры потока импульсов ТАЭ
Исходный закон распределения
числа событий
(однозвенный и двухзвенный).
II. Затухание акустического импульса:
расхождение;
поглощение.
Поглощение энергии упругих волн в образце в образце
[Васин и др., 2006]
Увеличение коэффициента удельного поглощения на
~450 дБ/м (!)
Слайд 12
Факторы, влияющие на параметры потока импульсов ТАЭ
Исходный закон распределения
числа событий
(однозвенный и двухзвенный).
II. Затухание акустического импульса:
расхождение;
поглощение.
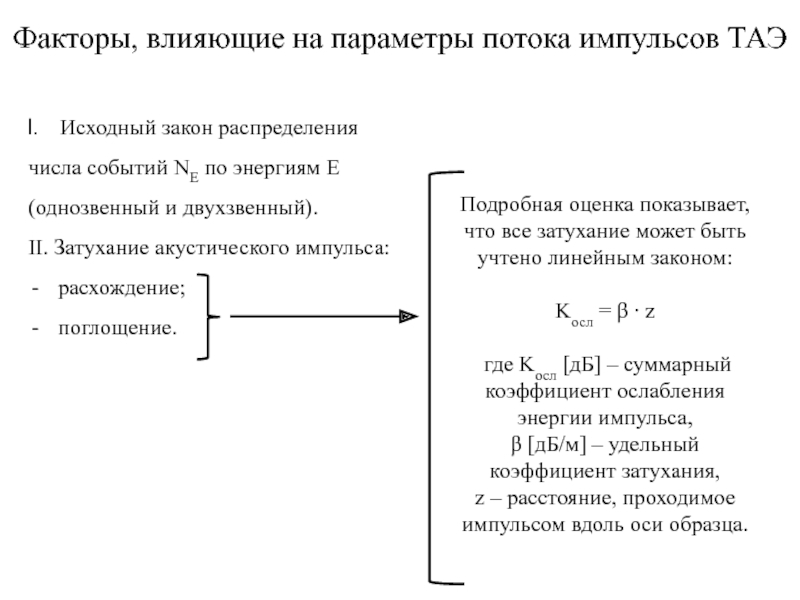
Подробная оценка показывает, что все затухание может быть учтено линейным законом:
Kосл = β ∙ z
где Kосл [дБ] – суммарный коэффициент ослабления энергии импульса,
β [дБ/м] – удельный коэффициент затухания,
z – расстояние, проходимое импульсом вдоль оси образца.
Слайд 13Факторы, влияющие на параметры потока импульсов ТАЭ
Исходный закон распределения
числа событий
(однозвенный и двухзвенный).
II. Затухание акустического импульса
(расхождение и поглощение).
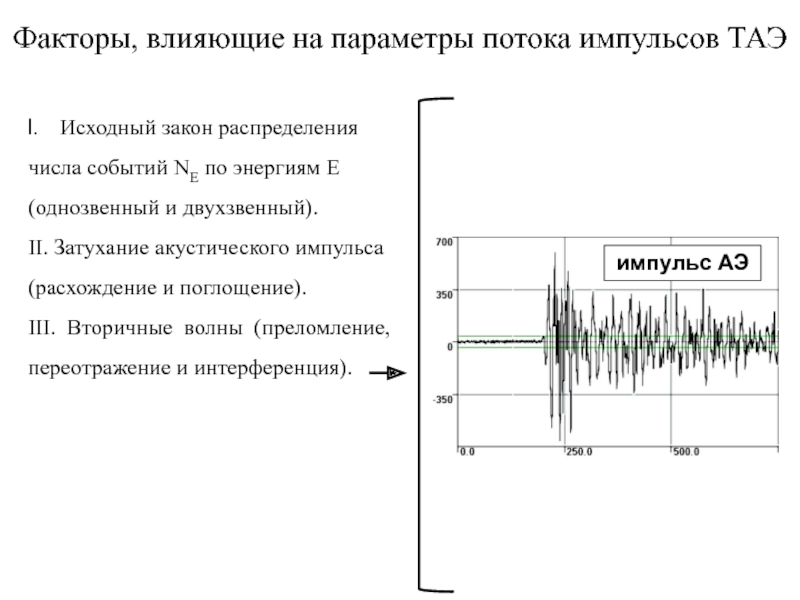
III. Вторичные волны (преломление, переотражение и интерференция).
импульс АЭ
Слайд 14Факторы, влияющие на параметры потока импульсов ТАЭ
Исходный закон распределения
числа событий
(однозвенный и двухзвенный).
II. Затухание акустического импульса
(расхождение и поглощение).
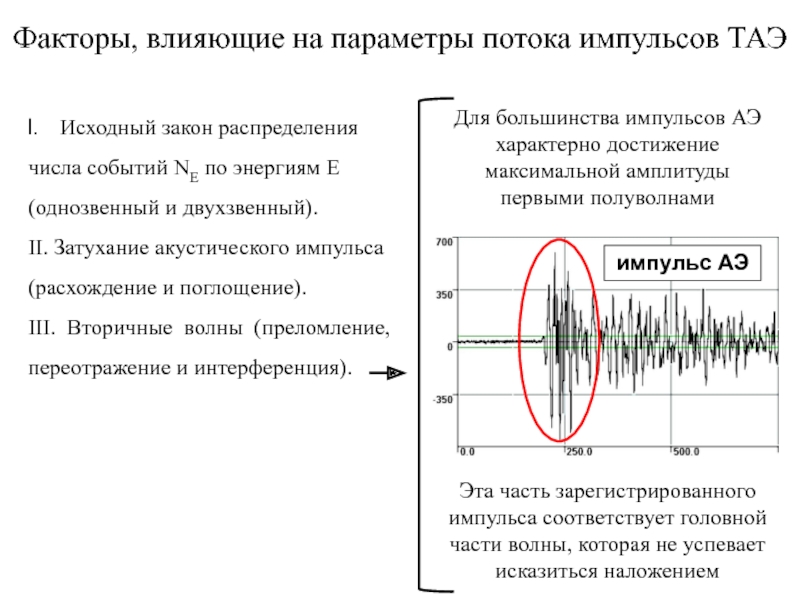
III. Вторичные волны (преломление, переотражение и интерференция).
Для большинства импульсов АЭ характерно достижение максимальной амплитуды первыми полуволнами
Эта часть зарегистрированного импульса соответствует головной части волны, которая не успевает исказиться наложением
импульс АЭ
Слайд 15Факторы, влияющие на параметры потока импульсов ТАЭ
Исходный закон распределения
числа событий
(однозвенный и двухзвенный).
II. Затухание акустического импульса
(расхождение и поглощение).
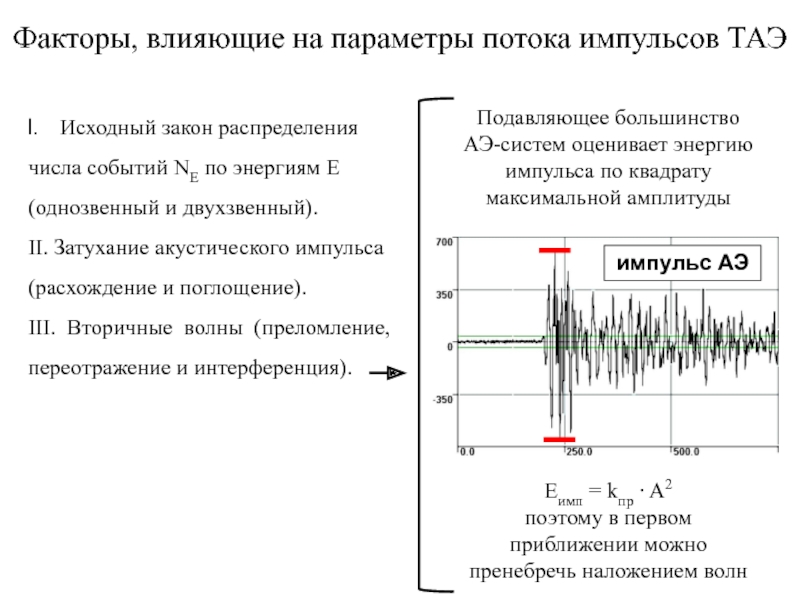
III. Вторичные волны (преломление, переотражение и интерференция).
Подавляющее большинство АЭ-систем оценивает энергию импульса по квадрату максимальной амплитуды
Eимп = kпр ∙ A2
поэтому в первом приближении можно пренебречь наложением волн
импульс АЭ
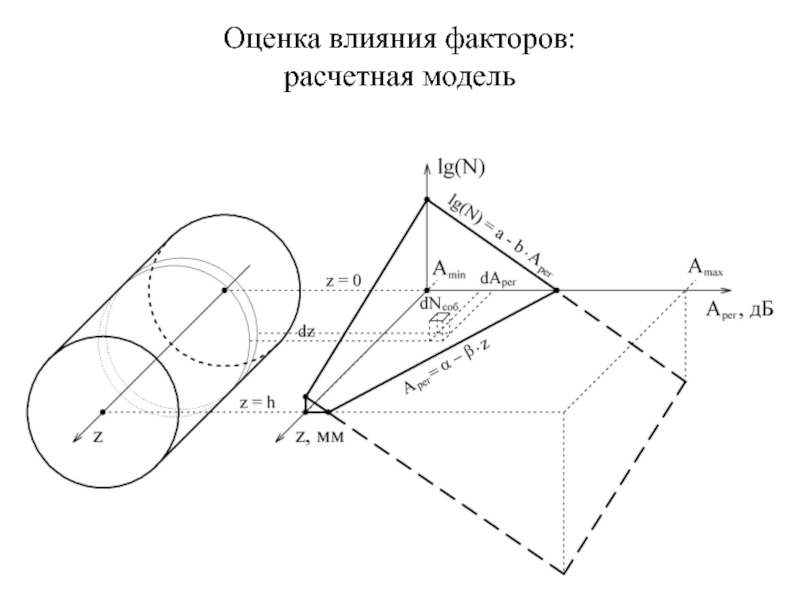
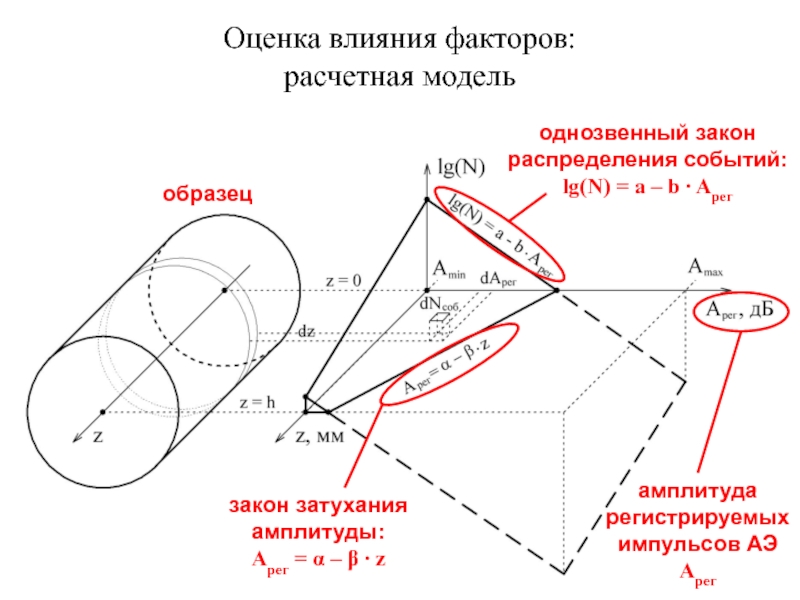
Слайд 17Оценка влияния факторов:
расчетная модель
образец
однозвенный закон
распределения событий:
lg(N) = a – b ∙
закон затухания
амплитуды:
Aрег = α – β ∙ z
амплитуда
регистрируемых
импульсов АЭ
Aрег
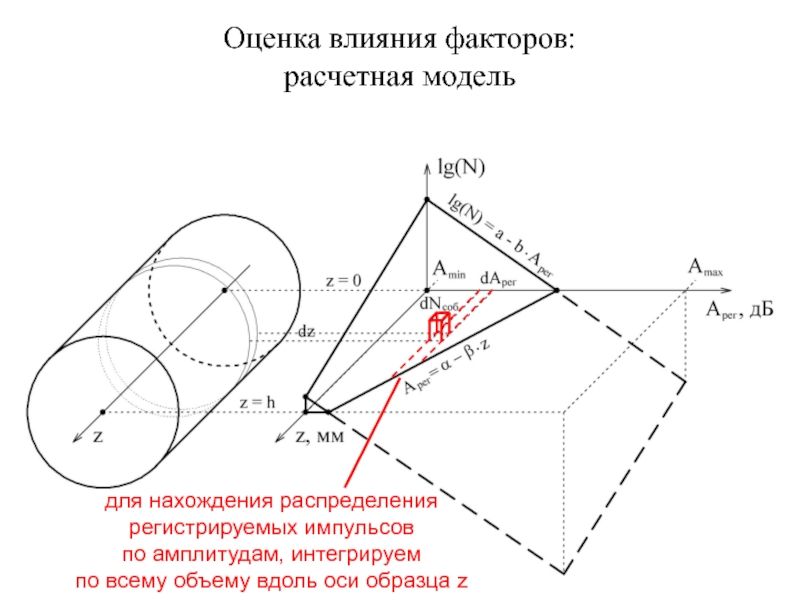
Слайд 18Оценка влияния факторов:
расчетная модель
для нахождения распределения
регистрируемых импульсов
по амплитудам, интегрируем
по всему объему
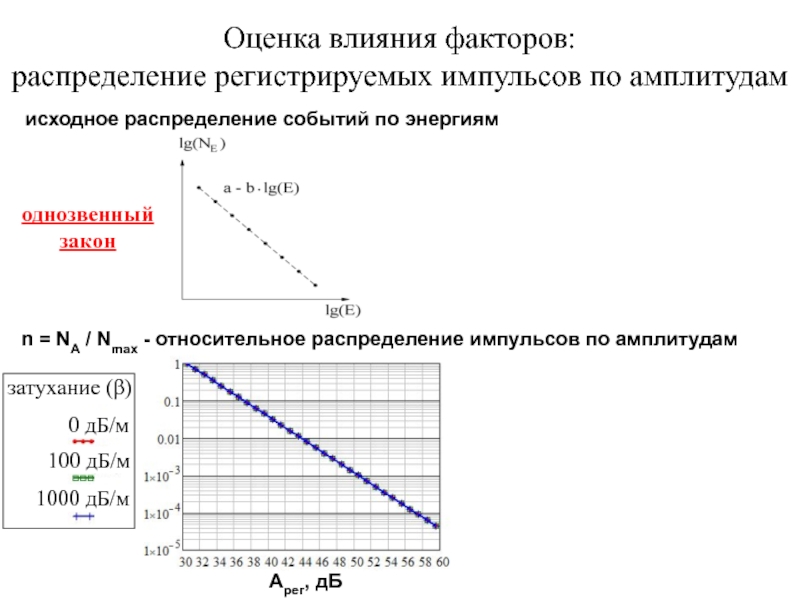
Слайд 19Оценка влияния факторов:
распределение регистрируемых импульсов по амплитудам
исходное распределение событий по энергиям
однозвенный
закон
Aрег, дБ
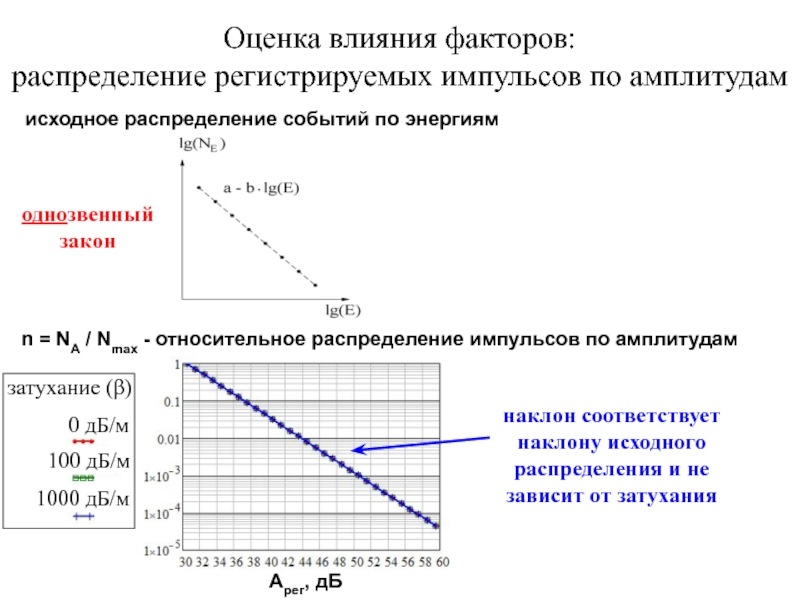
Слайд 20Оценка влияния факторов:
распределение регистрируемых импульсов по амплитудам
исходное распределение событий по энергиям
однозвенный
закон
Aрег, дБ
наклон соответствует наклону исходного распределения и не зависит от затухания
Слайд 21Оценка влияния факторов:
распределение регистрируемых импульсов по амплитудам
исходное распределение событий по энергиям
двухзвенный
закон
Aрег, дБ
Aрег, дБ
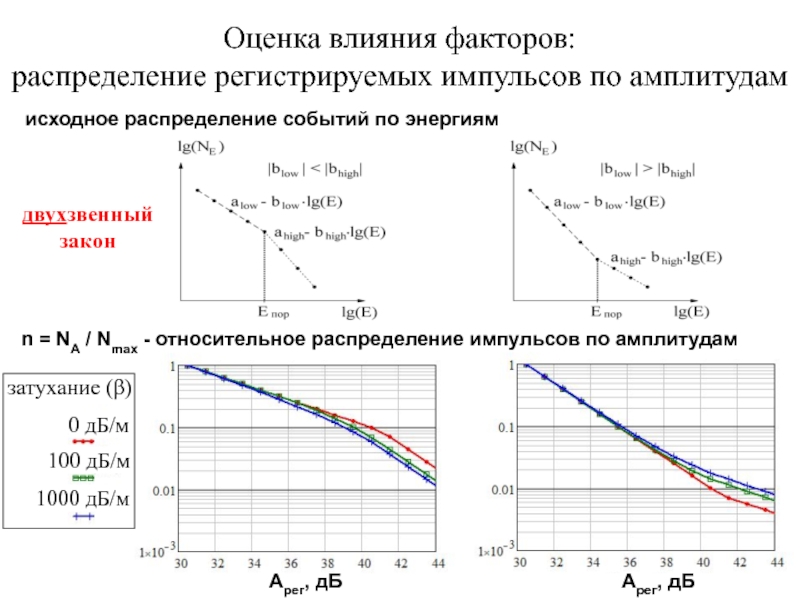
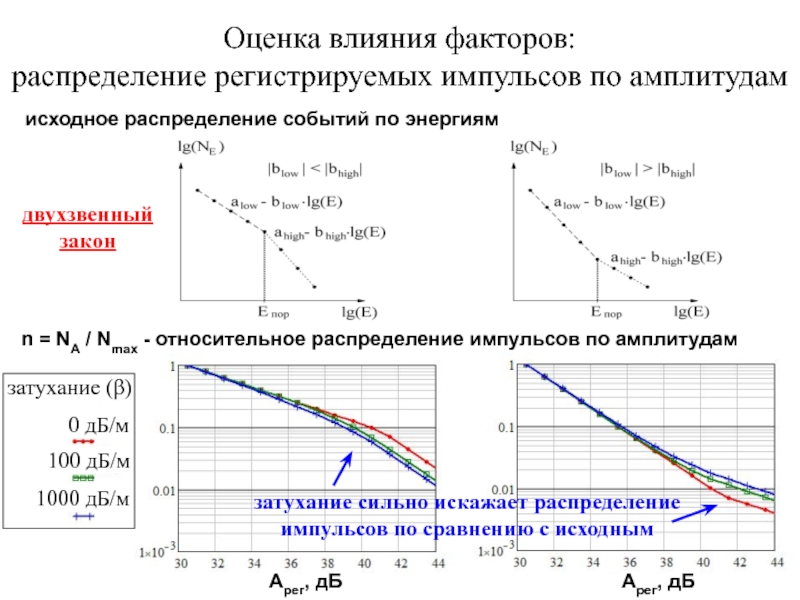
Слайд 22Оценка влияния факторов:
распределение регистрируемых импульсов по амплитудам
исходное распределение событий по энергиям
двухзвенный
закон
Aрег, дБ
Aрег, дБ
затухание сильно искажает распределение импульсов по сравнению с исходным
Слайд 23Анализ экспериментальных данных:
методика оценки характера закона распределения и b-value
Aрег, дБ
Aрег,
Выявление характера распределения – однозвенный или более сложный
Оценка b-value
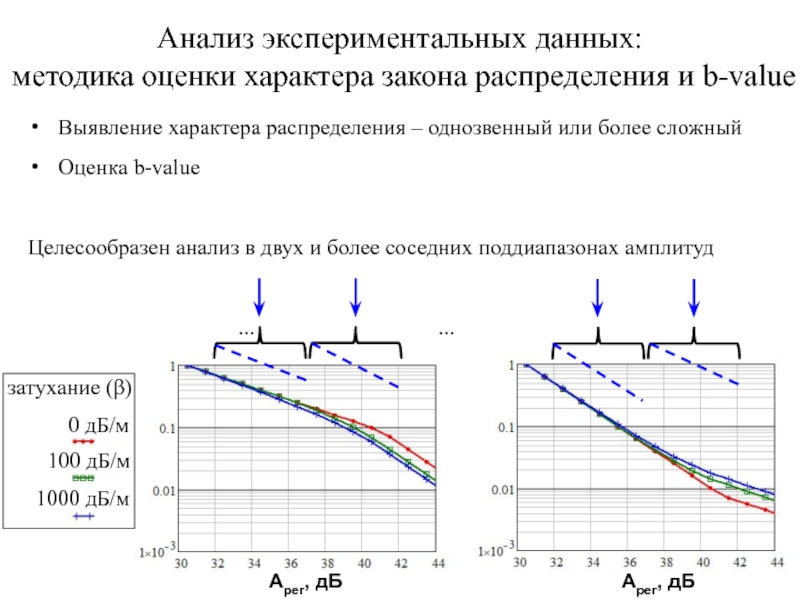
Слайд 24Анализ экспериментальных данных:
методика оценки характера закона распределения и b-value
Aрег, дБ
Aрег,
Выявление характера распределения – однозвенный или более сложный
Оценка b-value
Целесообразен анализ в двух и более соседних поддиапазонах амплитуд
... ...
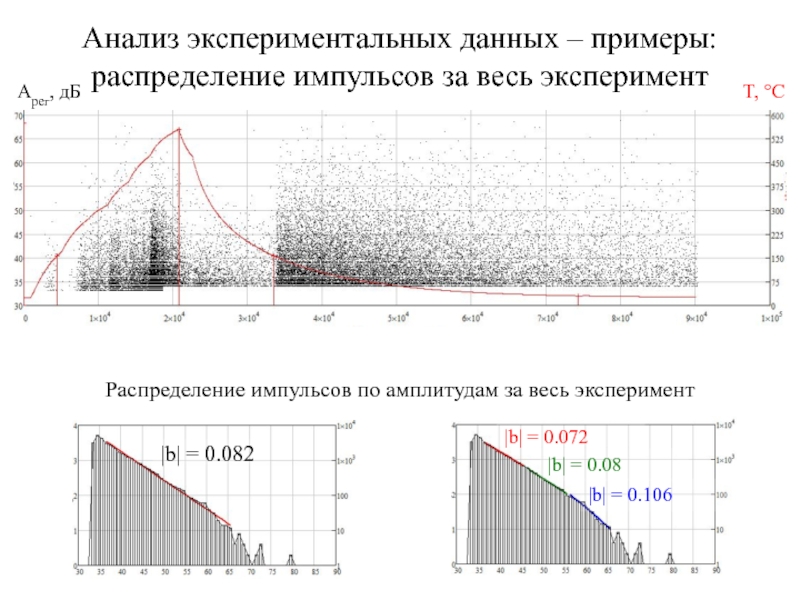
Слайд 25Анализ экспериментальных данных – примеры:
распределение импульсов за весь эксперимент
Aрег, дБ
T, °С
|b| = 0.082
|b| = 0.072
|b| = 0.08
|b| = 0.106
Распределение импульсов по амплитудам за весь эксперимент
Слайд 26Анализ экспериментальных данных – примеры:
этапы эксперимента
актив. ТАЭ, имп/сек
T, °С
b-value
Н
O-I и О-II – первый и второй этапы остывания;
In-кр – кристаллизация индия.
T, °С
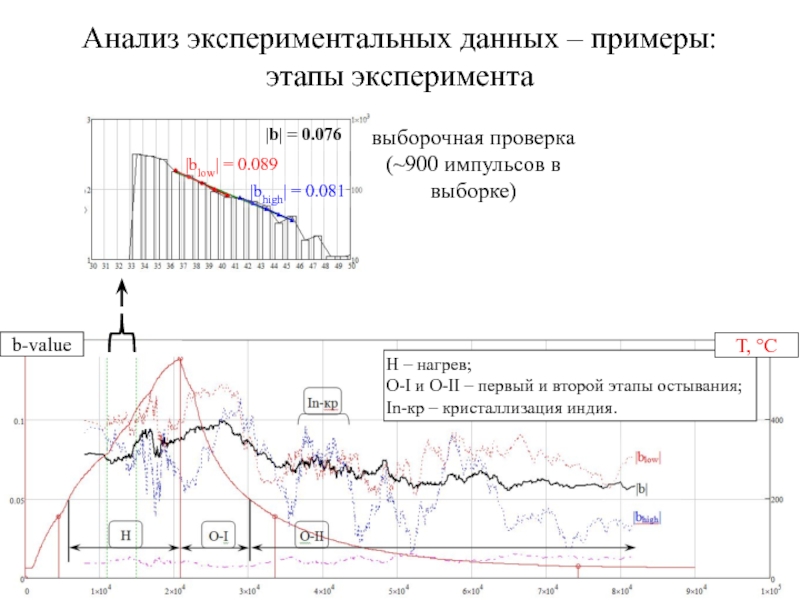
Слайд 27Анализ экспериментальных данных – примеры:
этапы эксперимента
b-value
Н – нагрев;
O-I и О-II
In-кр – кристаллизация индия.
T, °С
|blow| = 0.089
|bhigh| = 0.081
|b| = 0.076
выборочная проверка
(~900 импульсов в выборке)
Слайд 28Анализ экспериментальных данных – примеры:
этапы эксперимента
b-value
Н – нагрев;
O-I и О-II
In-кр – кристаллизация индия.
T, °С
|bhigh| = 0.071
|blow| = 0.093
|b| = 0.097
|b| = 0.082
|b| = 0.066
|bhigh| = 0.087
|blow| = 0.112
|bhigh| = 0.056
|blow| = 0.065
|b| ≈ 0.072
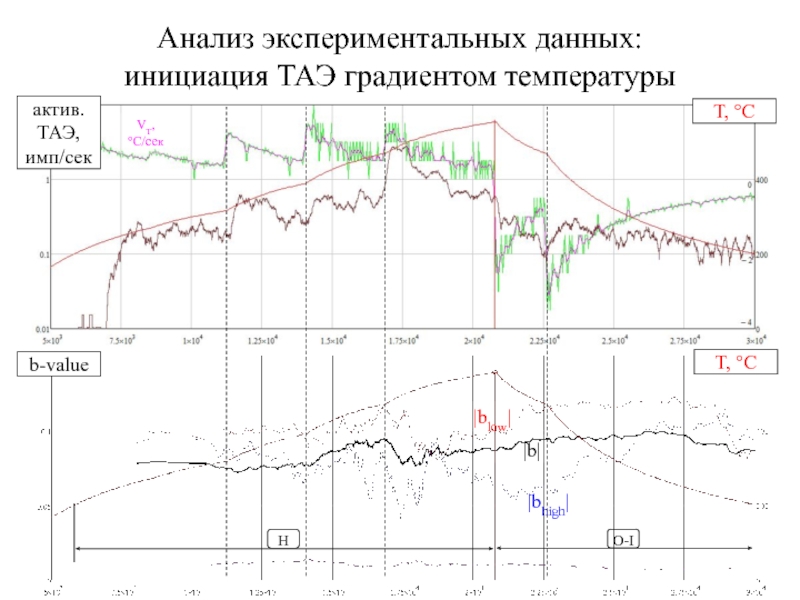
Слайд 29Анализ экспериментальных данных:
инициация ТАЭ градиентом температуры
|b|
|bhigh|
|blow|
Н
О-I
VT,
°С/сек
T, °С
b-value
актив. ТАЭ, имп/сек
T, °С
Слайд 30Анализ экспериментальных данных:
инициация ТАЭ градиентом температуры
T, °С
b-value
образец – гранит мелкозерн.
пористость до / после нагрева ~ 0.1 / 1.0 %
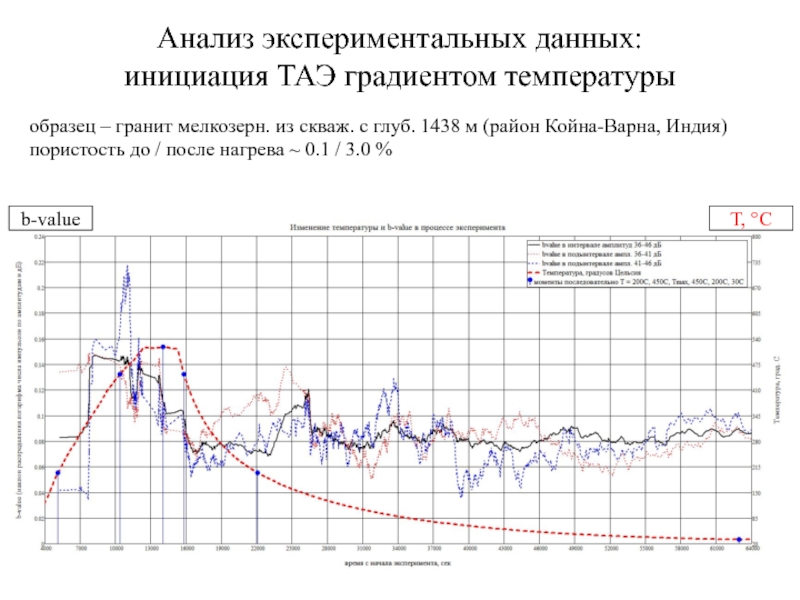
Слайд 31Анализ экспериментальных данных:
инициация ТАЭ градиентом температуры
T, °С
b-value
образец – гранит мелкозерн.
пористость до / после нагрева ~ 0.1 / 3.0 %
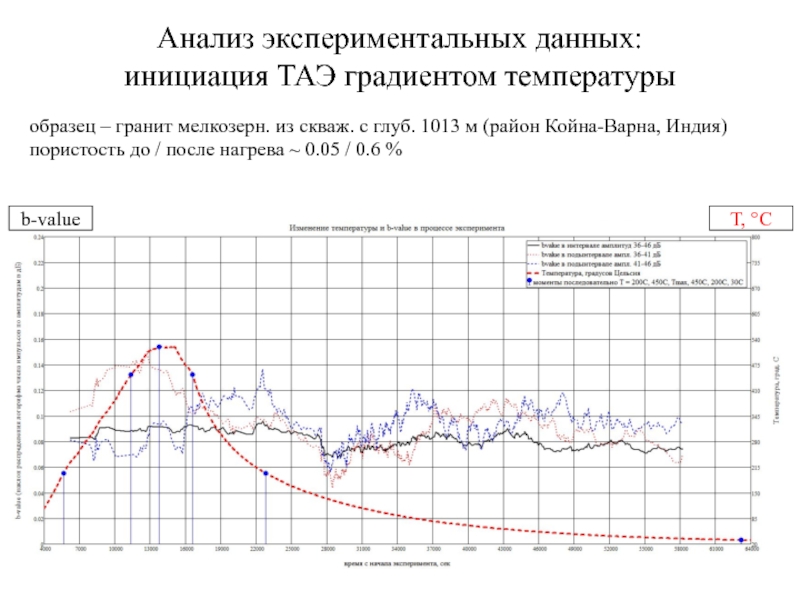
Слайд 32Анализ экспериментальных данных:
инициация ТАЭ градиентом температуры
T, °С
b-value
образец – гранит мелкозерн.
пористость до / после нагрева ~ 0.05 / 0.6 %
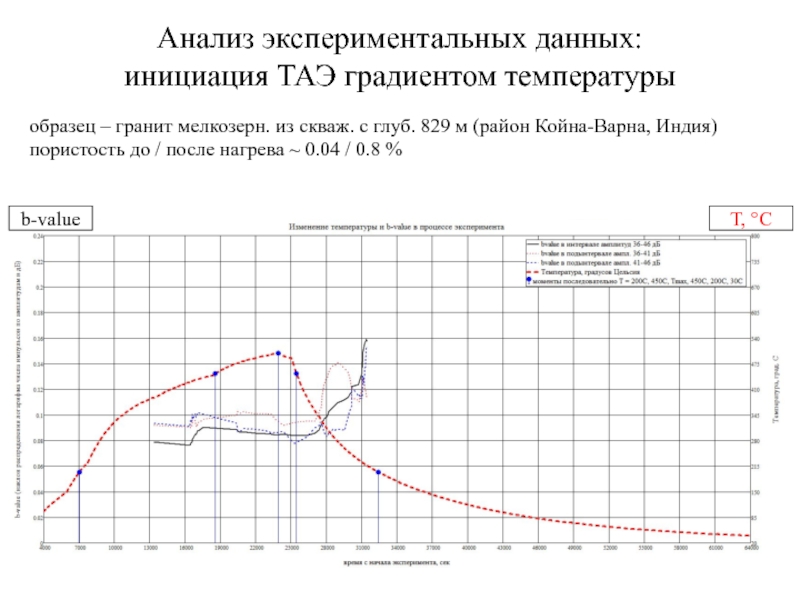
Слайд 33Анализ экспериментальных данных:
инициация ТАЭ градиентом температуры
T, °С
b-value
образец – гранит мелкозерн.
пористость до / после нагрева ~ 0.04 / 0.8 %
Слайд 34Выводы
Затухание (энергии) импульсов ТАЭ в настоящей экспериментальной установке (и подобной ей
Для однозвенного закона распределения событий ТАЭ по энергиям затухание не искажает форму распределения импульсов ТАЭ по амплитудам по сравнению с исходной.
Для двухзвенного закона распределения событий ТАЭ затухание существенно искажает вид распределения импульсов, теряется сам двухзвенный характер распределения.
Оценка b-value в соседних поддиапазонах амплитуд позволяет сделать вывод о характере закона распределения событий ТАЭ (одно-, двухзвенный или более сложный) и оценить b-value, близкое к исходному.
На экспериментальных данных такая методика показала возможность различения механизмов генерации ТАЭ, связанных с разными этапами эксперимента по термическим разрушениям горных пород.
Обнаружено, что исходное распределение событий ТАЭ может быть двухзвенным с уменьшением b-value с ростом амплитуды («вогнутым»), что представляет интерес для дальнейшего изучения.