- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Гидрологические расчеты. Расчет расходов воды ( Лекция 3) презентация
Содержание
- 1. Гидрологические расчеты. Расчет расходов воды ( Лекция 3)
- 2. Основные темы лекции: Расчет максимальных расходов воды
- 3. 1. Расчет максимальных расходов воды при неоднородности
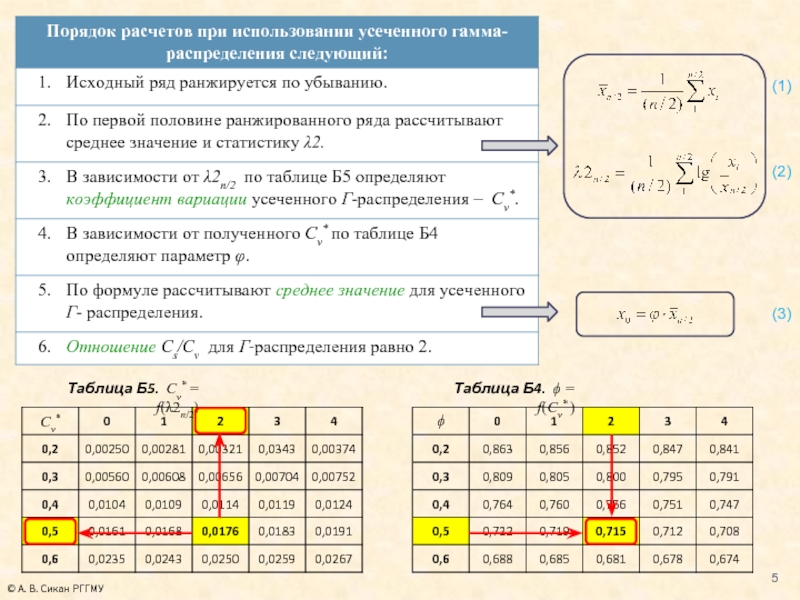
- 4. Усеченными называют кривые обеспеченностей, аппроксимирующие не всю
- 5. Таблица Б5. Cv*
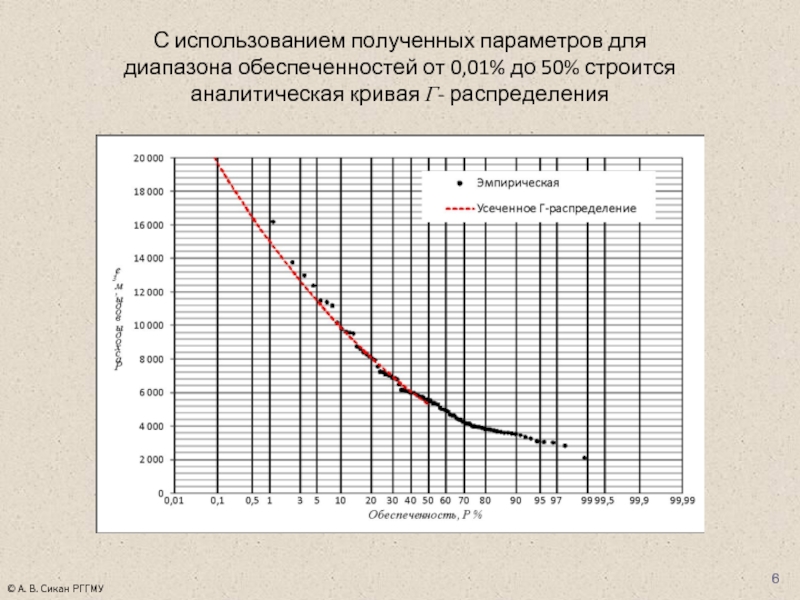
- 6. С использованием полученных параметров для диапазона обеспеченностей
- 7. Этот тип составной кривой обеспеченностей строится в
- 8. Построение составной кривой обеспеченностей при наличии в
- 9. 1.2.2. Построение составной кривой обеспеченностей при наличии
- 10. Построение составной кривой обеспеченностей при наличии в
- 11. 2. Определение расчетных гидрологических характеристик при недостаточности данных гидрометрических наблюдений © А. В. Сикан РГГМУ
- 12. 2.1. Расчет при недостаточности данных гидрометрических наблюдений
- 13. n
- 14. 2.2. Расчет погрешностей статистических
- 15. 2.3. Расчет при наличии кратковременных наблюдений (менее
- 16. Вопросы для самопроверки Когда допускается применять усеченные
- 17. © А. В. Сикан РГГМУ Владимиров А.М.
Слайд 1к.г.н., доц. Сикан Александр Владимирович
Российский государственный гидрометеорологический университет
Гидрологические расчеты
Часть II
лекция №
Слайд 2Основные темы лекции:
Расчет максимальных расходов воды при неоднородности ряда гидрометрических наблюдений.
Усеченные
Составные кривые обеспеченностей.
Определение расчетных гидрологических характеристик при недостаточности данных гидрометрических наблюдений
© А. В. Сикан РГГМУ
Слайд 31. Расчет максимальных расходов воды при неоднородности ряда гидрометрических наблюдений
Основные причины
изменение климата,
влияние антропогенных факторов
генетическая неоднородность.
В этой ситуации, действующие в России нормативные документы, допускают использовать при выполнении инженерных расчетов усеченные и составные кривые обеспеченностей.
В настоящее время многие гидрологические ряды являются неоднородными.
© А. В. Сикан РГГМУ
Слайд 4Усеченными называют кривые обеспеченностей, аппроксимирующие не всю эмпирическую кривую, а только
В СП 33-101-2003 представлена методика построения усеченной кривой обеспеченностей максимальных расходов воды на базе двухпараметрического гамма-распределения. Оценка параметров выполняется методом наибольшего правдоподобия.
При использовании этого метода исходный ряд ранжируется по убыванию и затем делится на две части по медиане. В дальнейшем рассматривают только верхнюю часть исходного ряда.
1. 1. Усеченные кривые обеспеченностей
© А. В. Сикан РГГМУ
Слайд 6С использованием полученных параметров для диапазона обеспеченностей от 0,01% до 50%
© А. В. Сикан РГГМУ
Слайд 7Этот тип составной кривой обеспеченностей строится в том случае, когда имеются
Например, требуется построить кривую обеспеченностей наибольших в году максимальных расходов воды. При этом годовой максимум может наблюдаться в одни годы – в период весеннего половодья, в другие – в период дождевых паводков.
В этом случае строится кривая обеспеченностей для максимальных расходов дождевых паводков и максимальных расходов весеннего половодья. Затем на основе этих кривых строится составная кривая.
1.2.1. ПОСТРОЕНИЕ СОСТАВНОЙ КРИВОЙ ОБЕСПЕЧЕННОСТЕЙ ПРИ НАЛИЧИИ В КАЖДОМ ГОДУ НАБЛЮДЕНИЙ ЗА ВСЕМИ ОДНОРОДНЫМИ ЭЛЕМЕНТАМИ ВОДНОГО РЕЖИМА
1.2. Составные кривые обеспеченностей
© А. В. Сикан РГГМУ
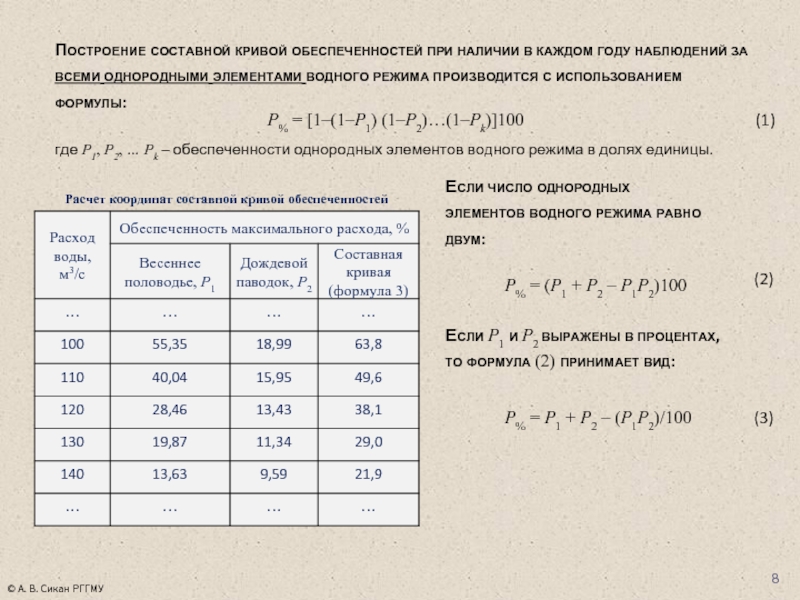
Слайд 8Построение составной кривой обеспеченностей при наличии в каждом году наблюдений за
P% = [1–(1–P1) (1–P2)…(1–Pk)]100
P% = (P1 + P2 – P1P2)100
Если число однородных элементов водного режима равно двум:
(1)
(2)
где P1, P2, … Pk – обеспеченности однородных элементов водного режима в долях единицы.
Если P1 и P2 выражены в процентах, то формула (2) принимает вид:
P% = P1 + P2 – (P1P2)/100
(3)
Расчет координат составной кривой обеспеченностей
© А. В. Сикан РГГМУ
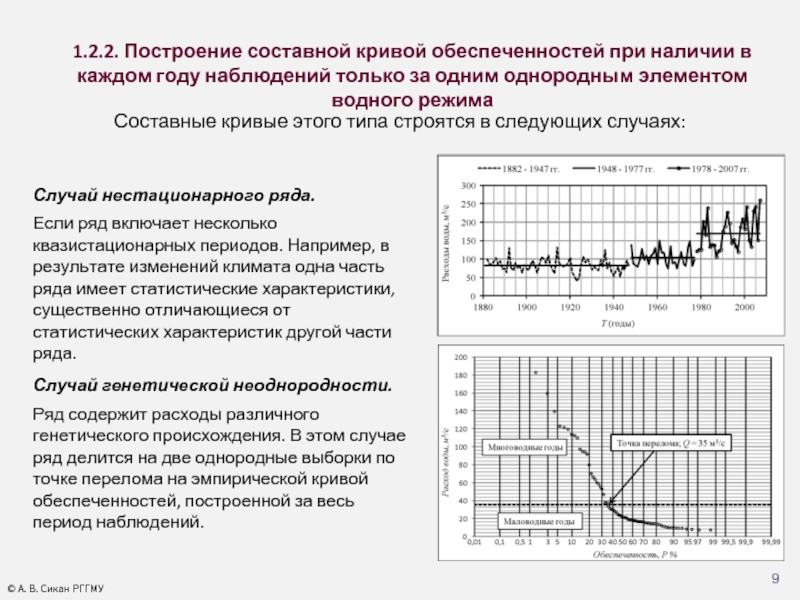
Слайд 91.2.2. Построение составной кривой обеспеченностей при наличии в каждом году наблюдений
Составные кривые этого типа строятся в следующих случаях:
Случай нестационарного ряда.
Если ряд включает несколько квазистационарных периодов. Например, в результате изменений климата одна часть ряда имеет статистические характеристики, существенно отличающиеся от статистических характеристик другой части ряда.
Случай генетической неоднородности.
Ряд содержит расходы различного генетического происхождения. В этом случае ряд делится на две однородные выборки по точке перелома на эмпирической кривой обеспеченностей, построенной за весь период наблюдений.
© А. В. Сикан РГГМУ
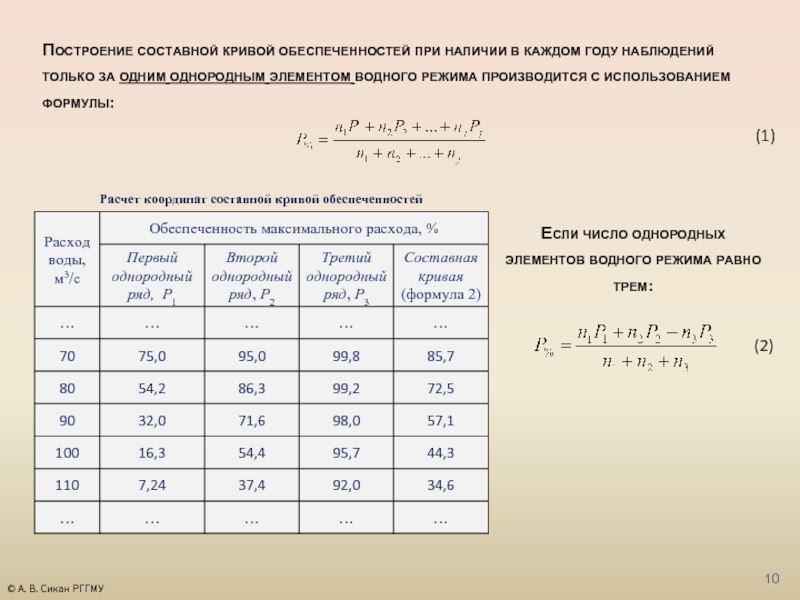
Слайд 10Построение составной кривой обеспеченностей при наличии в каждом году наблюдений только
Если число однородных элементов водного режима равно трем:
(1)
(2)
Расчет координат составной кривой обеспеченностей
© А. В. Сикан РГГМУ
Слайд 112. Определение расчетных гидрологических характеристик при недостаточности данных гидрометрических наблюдений
© А.
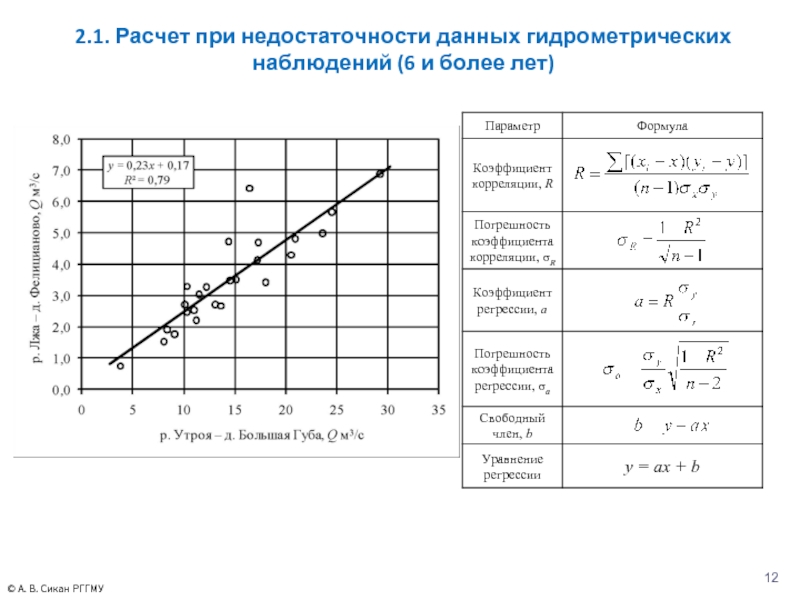
Слайд 122.1. Расчет при недостаточности данных гидрометрических наблюдений (6 и более лет)
©
Слайд 13
n ≥ 6; | R |
Уравнение регрессии можно рекомендовать для практических расчетов, если выполнены следующие условия:
Восстановление ряда расчетной реки:
Расчет параметров распределения:
(1)
(2)
(3)
(4)
(5)
© А. В. Сикан РГГМУ
Слайд 14
2.2. Расчет погрешностей статистических характеристик восстановленного ряда
Относительная среднеквадратическая погрешность среднего значения
Случайные среднеквадратические погрешности восстановленного ряда можно определить по «обычным» формулам с учетом объема информации, эквивалентной наблюденным данным.
(1)
(2)
(3)
© А. В. Сикан РГГМУ
Слайд 152.3. Расчет при наличии кратковременных наблюдений (менее 6 лет)
Метод отношений
Метод отношений
При наличии нескольких пунктов-аналогов расчеты осуществляют последовательно по всем аналогам (не более трех аналогов), затем – результаты осредняют.
Основа метода:
Расчетная формула:
Пример:
?
© А. В. Сикан РГГМУ
Слайд 16Вопросы для самопроверки
Когда допускается применять усеченные кривые обеспеченностей?
Алгоритм построения усеченного Г-распределения.
В
Как построить составную кривую обеспеченностей для наибольших в году максимальных расходов воды, если весенние и дождевые максимумы близки по величине?
Как построить составную кривую обеспеченностей при наличии в каждом году наблюдений только за одним однородным элементом водного режима?
Как производится расчет максимального стока при недостаточности данных гидрометрических наблюдений при длине ряда 6 и более лет.
Как производится расчет максимального стока при недостаточности данных гидрометрических наблюдений при длине ряда менее 6 лет?
© А. В. Сикан РГГМУ
Слайд 17© А. В. Сикан РГГМУ
Владимиров А.М. Гидрологические расчёты: п.9.3.
СП 33-101-2003.
Методические рекомендации по определению расчетных гидрологических характеристик при наличии данных гидрометрических наблюдений: п.3, п.9.
Методические рекомендации по определению расчетных гидрологических характеристик при недостаточности данных гидрометрических наблюдений.
Рекомендуемые материалы для изучения:
Конец лекции №3