- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Жарық дифракциясы. Френельдің аумақ әдісі. Жарықтың түзу сызықпен таралуы. Аумақ пластинасы презентация
Содержание
- 1. Жарық дифракциясы. Френельдің аумақ әдісі. Жарықтың түзу сызықпен таралуы. Аумақ пластинасы
- 2. Осындай жағдайларды дифракция деп атайды. Оптикада Френель
- 3. Френельдің аумақтық әдісі Френель дифракциялық суреттерді есептеудің
- 5. (1) (1)
- 6. а мен b-ға
- 7. Френель әдісі бойынша тұрғызу толқындық шепті теңдей
- 8. Екі көрші аумақтан нүктесіне келетін тербелістердің фазалары
- 9. Аумақ саны жұп болған жағдайда бұлардың әрекеттері
- 10. Қорытқы тербелістің Аm амплитудасы:
- 11. мұндағы “+”-
- 12. Ал, m-і адиусы аумақ
- 13. Егерде тесіктің мөлшерін шексіздікке дейін өсіретін болсақ,
- 14. Басында дифракцияны толқындардың қоршауларды орағыта өту құбылысы
- 15. Екінші және бірінші ретті толқындардың интерференциясы қозғалатын
- 16. Френель аумағы Екінші ретті толқындық фронттың өрісінің
- 17. Е векторы Жарық толқынында А амплитудасының ролін
- 18. Бірнеше зона Жаңа зоналар ашылған сайын
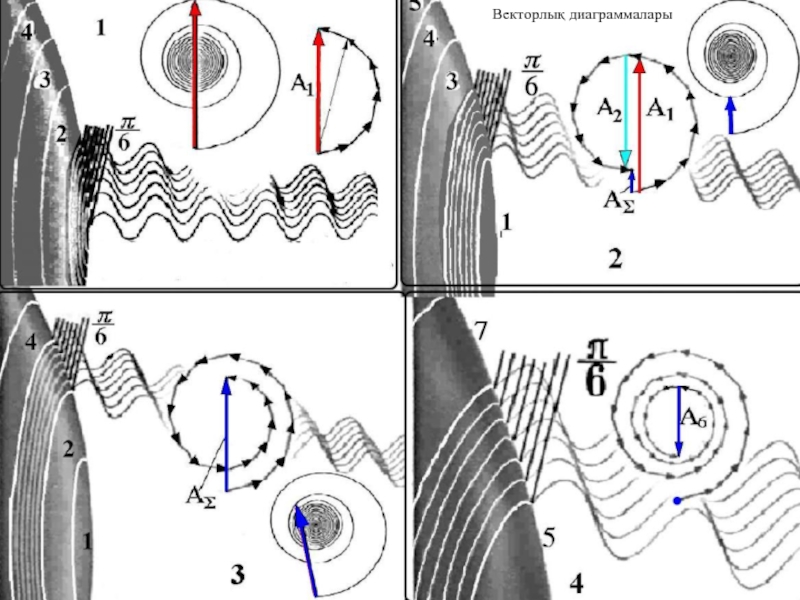
- 19. Векторлық диаграммалары
- 20. Толқындық фронттың кіші элементтері толқын амплитудасы a0
- 21. Дөңгелек қуыста дифракция кезінде интенсивтіліктің көлденең (Р’
- 22. Радиусы R қуысқа орналасқан Френель аумағының саны
- 23. Пуассон дағы D және L мәніне тәуелсіз
- 24. Егер барлық жұп (немес тақ) аумақтарды
- 25. Пластинка Вуда Егер мөлдір емес масканың орнына
- 26. λ/2 Разбиение на зоны (зоны Шустера) ведется
- 27. Векторная диаграмма на комплексной плоскости для данного
- 28. Дифракция Френеля на щели сводится
Слайд 1Лекция - 5. Жарық дифракциясы. Френельдің аумақ әдісі. Жарықтың түзу сызықпен
Слайд 2Осындай жағдайларды дифракция деп атайды. Оптикада Френель дифракциясы және Фраунгофер дифракциясы деп
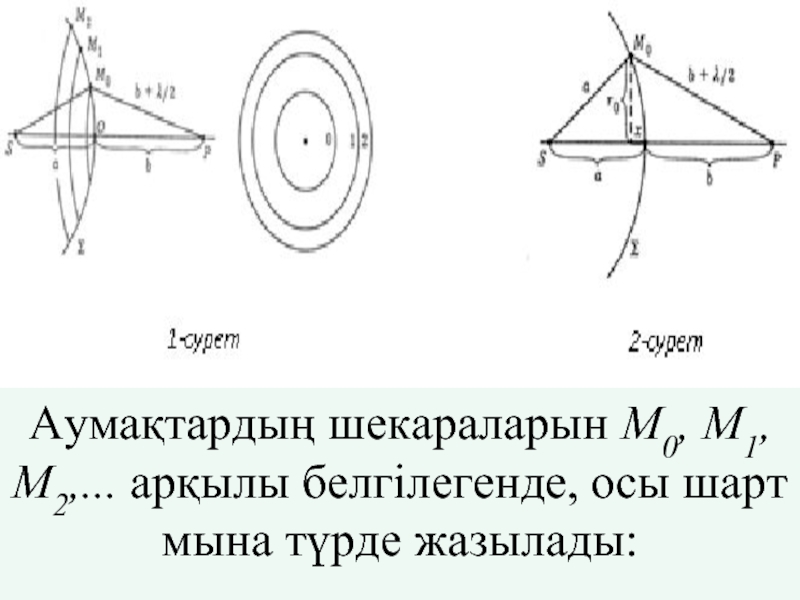
Слайд 3Френельдің аумақтық әдісі Френель дифракциялық суреттерді есептеудің жарты-толқындық аумақтар немесе Френель аумақтары
Слайд 5 (1) (1) мұндағы λ-жарықтың толқыны ұзындығы, Р- өріс бақыланатын нүкте, О-Френельдік
Слайд 6 а мен b-ға салыстырғанда λ кіші шама (а, b>>λ) болуы себепті
Слайд 7Френель әдісі бойынша тұрғызу толқындық шепті теңдей аумақтарға бөледі, бұлардың әрқайсысының
Слайд 8Екі көрші аумақтан нүктесіне келетін тербелістердің фазалары қарама-қарсы болатындықтан, m аумақ
Слайд 9Аумақ саны жұп болған жағдайда бұлардың әрекеттері қос-қостан бірін-бірі әлсіретеді де,
Слайд 11 мұндағы “+”- аумақ саны тақ, “-” – аумақ саны жұп болғанда
Слайд 12 Ал, m-і адиусы аумақ радиусы радиусы rm қалқадағы қарастырылып отырған тесік радиусы
Слайд 13Егерде тесіктің мөлшерін шексіздікке дейін өсіретін болсақ, яғни толқындық шептің бүкіл
Слайд 14Басында дифракцияны толқындардың қоршауларды орағыта өту құбылысы ғана деп түсінген. Алдыңғы
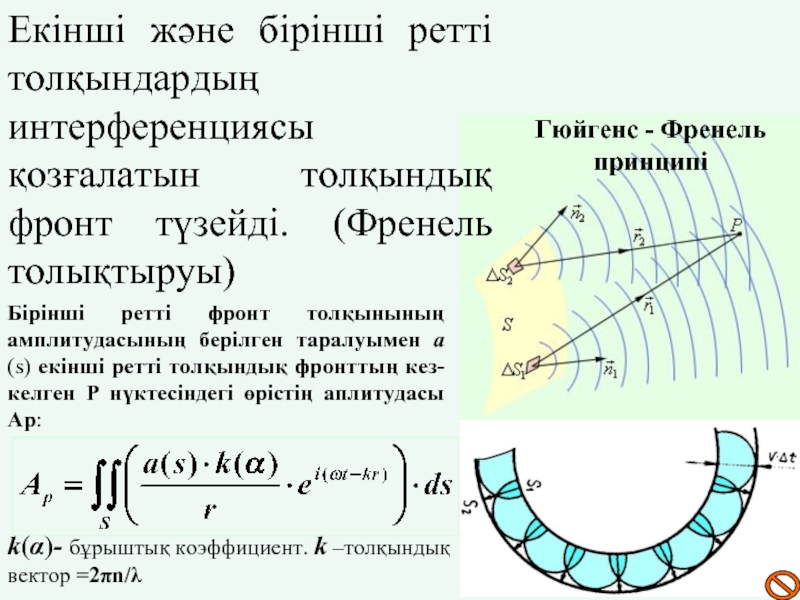
Слайд 15Екінші және бірінші ретті толқындардың интерференциясы қозғалатын толқындық фронт түзейді. (Френель
Бірінші ретті фронт толқынының амплитудасының берілген таралуымен а(s) екінші ретті толқындық фронттың кез-келген Р нүктесіндегі өрістің аплитудасы Ар:
Гюйгенс - Френель принципі
k(α)- бұрыштық коэффициент. k –толқындық вектор =2πn/λ
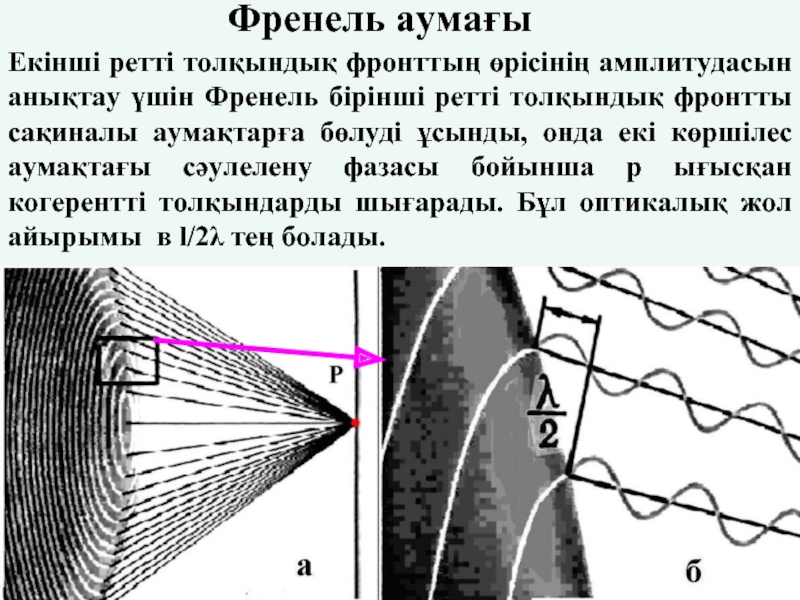
Слайд 16Френель аумағы
Екінші ретті толқындық фронттың өрісінің амплитудасын анықтау үшін Френель бірінші
Слайд 17Е векторы
Жарық толқынында А амплитудасының ролін электр өрісінің кернеулігі Е атқарады
Слайд 18
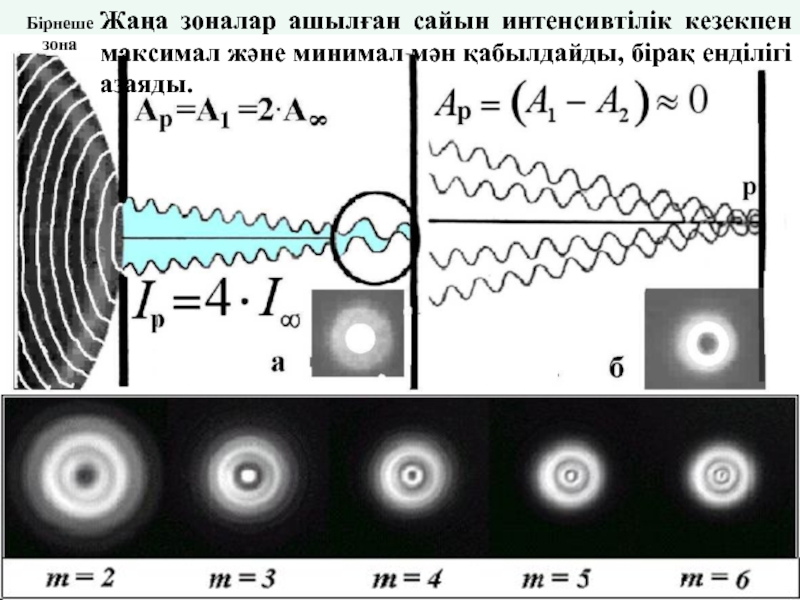
Бірнеше зона
Жаңа зоналар ашылған сайын интенсивтілік кезекпен максимал және минимал мән
Слайд 20Толқындық фронттың кіші элементтері толқын амплитудасы a0 exp (if ), комплекстік
Комплекстік жазықтық
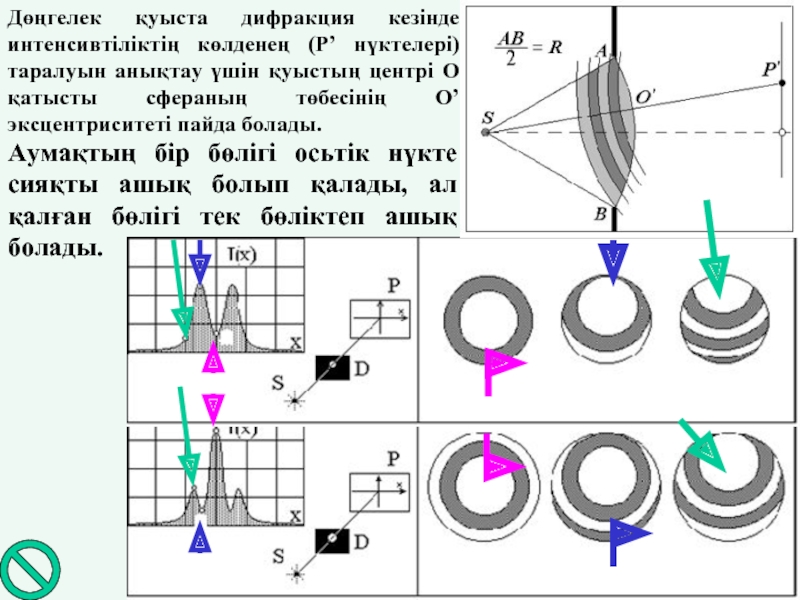
Слайд 21Дөңгелек қуыста дифракция кезінде интенсивтіліктің көлденең (Р’ нүктелері) таралуын анықтау үшін
Аумақтың бір бөлігі осьтік нүкте сияқты ашық болып қалады, ал қалған бөлігі тек бөліктеп ашық болады.
Поперечное распределение
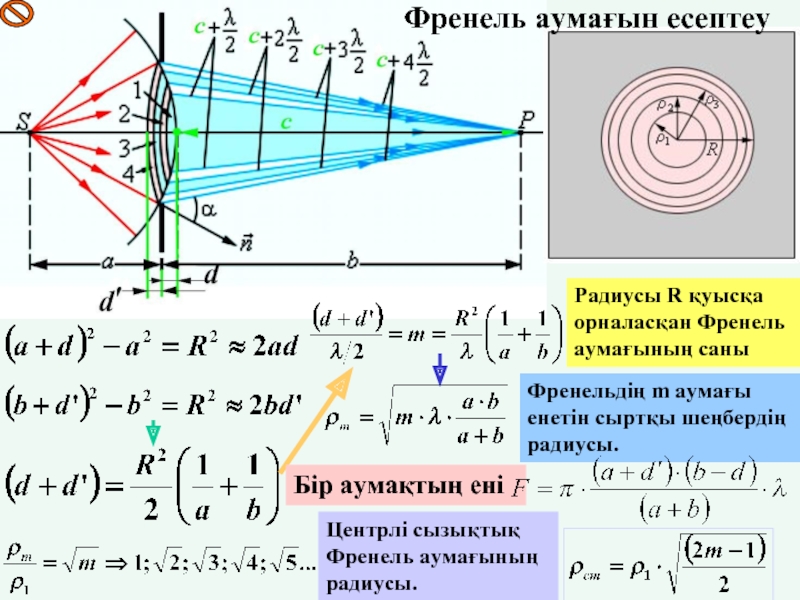
Слайд 22Радиусы R қуысқа орналасқан Френель аумағының саны
Френельдің m аумағы енетін сыртқы
Бір аумақтың ені
Френель аумағын есептеу
Центрлі сызықтық Френель аумағының радиусы.
Слайд 23Пуассон дағы
D және L мәніне тәуелсіз диск көлеңкесінің центрінде интенсивтіліктің максимумы
Слайд 24
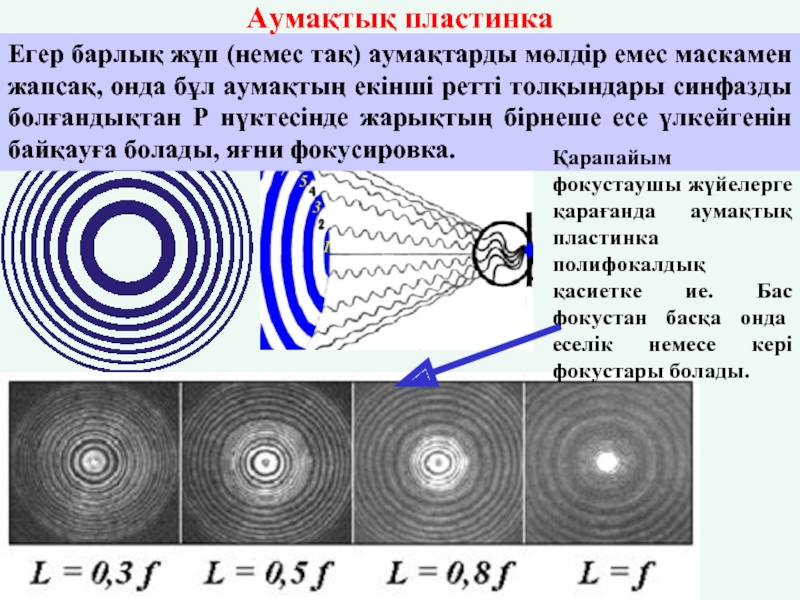
Егер барлық жұп (немес тақ) аумақтарды мөлдір емес маскамен жапсақ, онда
Қарапайым фокустаушы жүйелерге қарағанда аумақтық пластинка полифокалдық қасиетке ие. Бас фокустан басқа онда еселік немесе кері фокустары болады.
Аумақтық пластинка
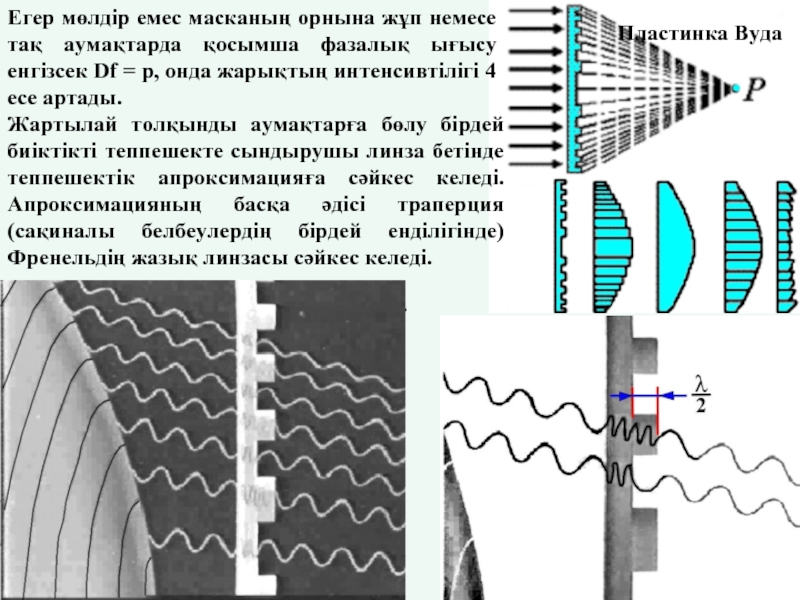
Слайд 25Пластинка Вуда
Егер мөлдір емес масканың орнына жұп немесе тақ аумақтарда қосымша
Жартылай толқынды аумақтарға бөлу бірдей биіктікті теппешекте сындырушы линза бетінде теппешектік апроксимацияға сәйкес келеді. Апроксимацияның басқа әдісі траперция (сақиналы белбеулердің бірдей енділігінде) Френельдің жазық линзасы сәйкес келеді.
Слайд 26λ/2
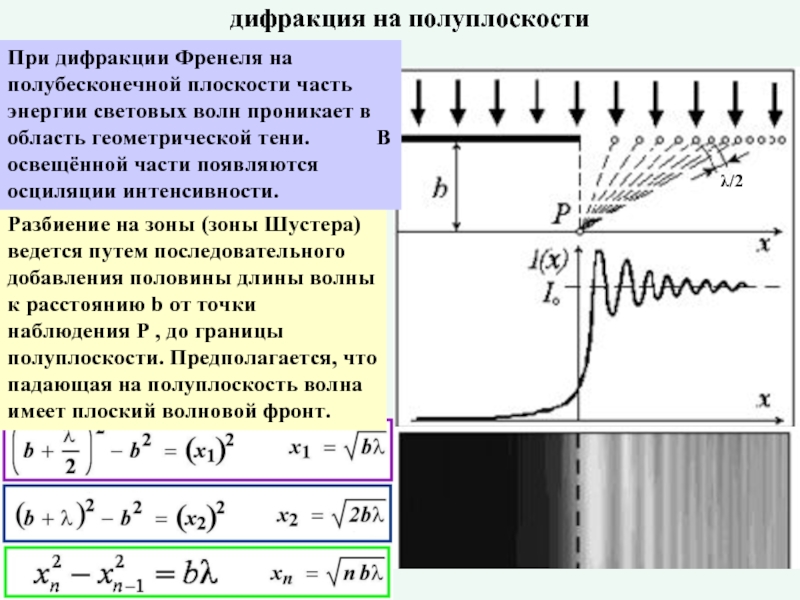
Разбиение на зоны (зоны Шустера) ведется путем последовательного добавления половины длины
При дифракции Френеля на полубесконечной плоскости часть энергии световых волн проникает в область геометрической тени. В освещённой части появляются осциляции интенсивности.
дифракция на полуплоскости
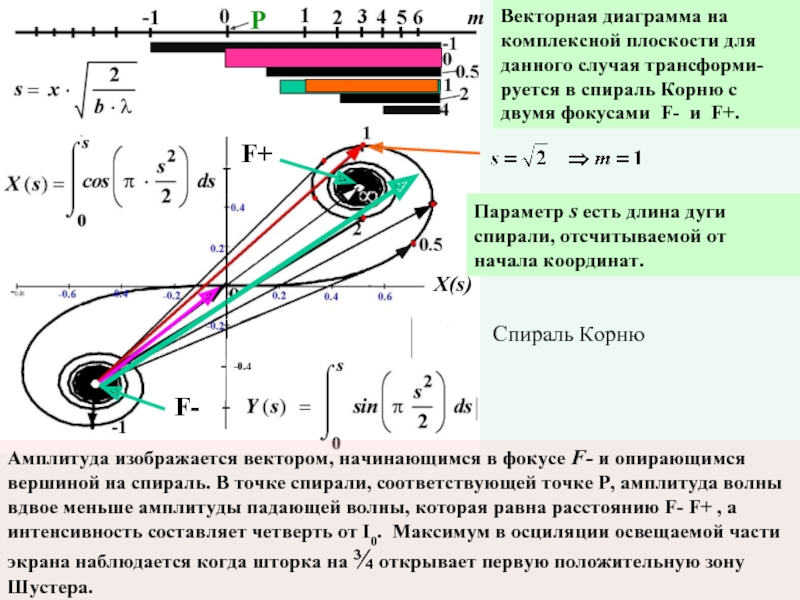
Слайд 27Векторная диаграмма на комплексной плоскости для данного случая трансформи-руется в спираль
F-
F+
Амплитуда изображается вектором, начинающимся в фокусе F- и опирающимся вершиной на спираль. В точке спирали, соответствующей точке Р, амплитуда волны вдвое меньше амплитуды падающей волны, которая равна расстоянию F- F+ , а интенсивность составляет четверть от I0. Максимум в осциляции освещаемой части экрана наблюдается когда шторка на ¾ открывает первую положительную зону Шустера.
т
Х(s)
Параметр s есть длина дуги спирали, отсчитываемой от начала координат.
Спираль Корню
Р
-0.4
Слайд 28
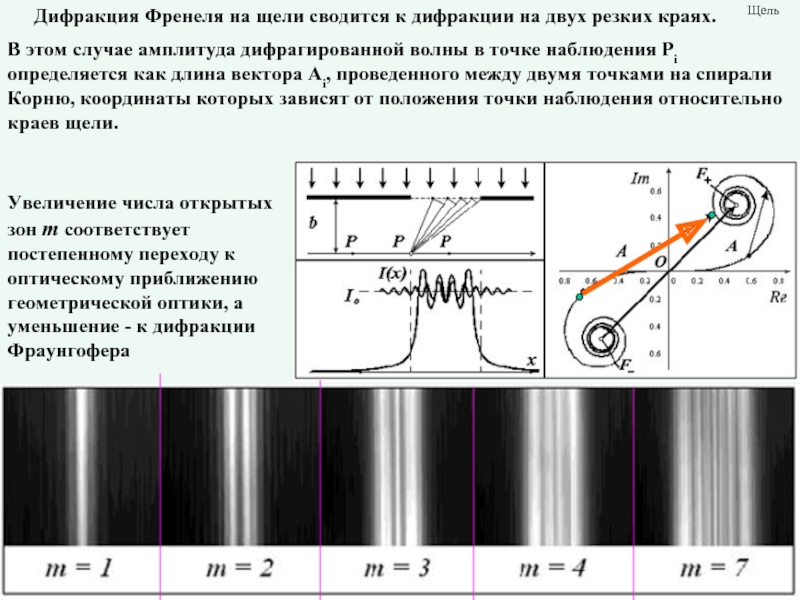
Дифракция Френеля на щели сводится к дифракции на двух резких краях.
Увеличение числа открытых зон m соответствует постепенному переходу к оптическому приближению геометрической оптики, а уменьшение - к дифракции Фраунгофера
В этом случае амплитуда дифрагированной волны в точке наблюдения Pi определяется как длина вектора Ai, проведенного между двумя точками на спирали Корню, координаты которых зависят от положения точки наблюдения относительно краев щели.
Щель