струмом
Взаємодія струмів
Закон повного струму, магнітне поле соленоїда. Вихровий характер магнітного поля.
Робота при переміщенні провідника зі струмом в магнітному полі. Енергія провідника зі струмом.
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Закони магнітостатики. Магнітне поле прямого та колового провідників зі струмом. (Лекція 13) презентация
Содержание
- 1. Закони магнітостатики. Магнітне поле прямого та колового провідників зі струмом. (Лекція 13)
- 2. 1. Магнітне поле прямого та колового провідників
- 3. Французький астроном, мате-матик і фізик П. Лаплас
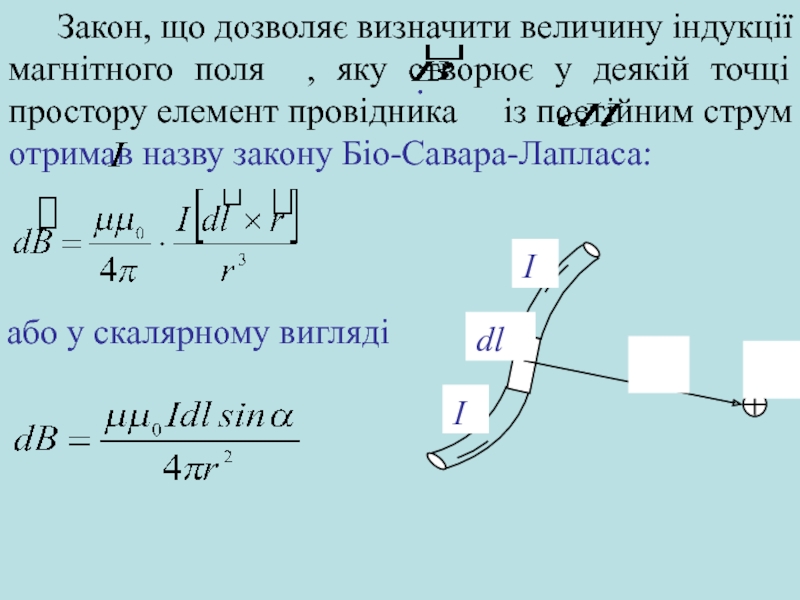
- 4. Закон, що дозволяє визначити величину індукції магнітного
- 5. – радіус-вектор, що з’єднує елемент
- 6. Цей закон дозволяє розрахувати індукцію магнітного поля
- 7. Для розрахунку індукції маг-нітного поля провідників зі
- 8. Розглянемо приклади застосування закону Біо-Савара-Лапласа для розрахунку
- 9. враховуючи, що усі ділянки про-відника у центрі
- 10. Отже, Винесемо незалежні величини за
- 11. Індукція магнітного поля на відстані а від
- 12. Щоб визначити індукцію магнітного поля провідника зі
- 13. відстань замінимо елементом дуги радіуса
- 14. Винесемо сталі величини за знак інтегралу та
- 15. Провідники по яким проходять електричні струми взаємодіють
- 16. На елемент струму
- 17. Застосовуючи закон Ампера для двох нескінченно довгих
- 18. Величину
- 19. Знайдемо циркуляцію вектора індукції магніт-ного поля прямого
- 20. Сформулюємо закон повного струму або теорему про
- 21. Отже, робота при перенесенні пробного одиничного елемента
- 22. При застосуванні закону повного струму необхідно враховувати
- 23. Закон повного струму і закон Біo-Савара-Лапласа використовують
- 24. Прикладом застосування закону повного струму є розрахунок
- 25. Циркуляцію вектора по замкненому контуру можна подати
- 26. тоді індукція магнітного поля на осі довгого
- 27. Явище виникнення магнітного поля навколо провідників зі
- 28. Звичайно електромагніт складається з обмотки і феромагнітного
- 29. у пристроях техніки зв’язку (телефон, телеграф, радіо),
- 30. Широкого застосування електромагніти набули в електромагнітних механізмах,
- 31. 4. Робота при переміщенні провідника зі струмом
- 32. Енергію магнітного поля визначають за формулою
- 33. А об’ємна густина енергії магнітного поля в
- 34. Лекція № 13. Закон Біо-Савара- Лапласа.
1. Магнітне поле прямого та колового провідників зі струмом. Досліджуючи магнітне поле провідників зі струмом заданої конфігурації, французькі вчені Ж. Біо і Ф. Савар експериментально встановили, що індукція магнітного
Слайд 21. Магнітне поле прямого та колового провідників зі струмом.
Досліджуючи магнітне
поле провідників зі струмом заданої конфігурації, французькі вчені Ж. Біо і Ф. Савар експериментально встановили, що індукція магнітного поля складним чином залежить від розмірів і конфігурації провідника, завжди пропорційна силі струму , що протікає у ньому та зменшується при віддаленні точки спостереження від провідника (~ )
Слайд 3Французький астроном, мате-матик і фізик П. Лаплас теоретично узагальнив ці експе-риментальні
факти і отримав математичні формули, розра-хунки за якими завжди збігалися з емпіричними вимірюваннями індукції магнітного поля .
Слайд 4Закон, що дозволяє визначити величину індукції магнітного поля , яку створює
у деякій точці простору елемент провідника із постійним струм отримав назву закону Біо-Савара-Лапласа:
або у скалярному вигляді
.
Слайд 5 – радіус-вектор, що з’єднує елемент провідника довжиною
із точкою простору, у якій визначається індукція магнітного поля;
α – кут між векторами і ;
μ0 – магнітна стала, ;
μ – магнітна проникність середовища, яка показує, у скільки разів індукція магнітного поля у середовищі більша, ніж у вакуумі.
α – кут між векторами і ;
μ0 – магнітна стала, ;
μ – магнітна проникність середовища, яка показує, у скільки разів індукція магнітного поля у середовищі більша, ніж у вакуумі.
Слайд 6Цей закон дозволяє розрахувати індукцію магнітного поля провідника зі струмом довільної
конфігурації при застосуванні принципу суперпозиції магнітних полів – вектор індукції магнітного поля , створений провідником у вибраній точці простору, дорівнює векторній сумі індукцій, що створюються окремими елементами цього струму в даній точці.
інтегрування здійснюється вздовж усієї довжини провідника.
Слайд 7Для розрахунку індукції маг-нітного поля провідників зі стру-мом різних конфігурацій у
довіль-них точках простору використо-вують формулу, що об’єднує закон Біо-Савара-Лапласа та принцип суперпозиції магнітних полів:
або
або
де – напруженість магнітного поля – характерис-тика, що не залежить від магнітних влас-тивостей середовища, в якому знаходиться провідник:
Одиницею вимірювання напруженості магніт-ного поля є 1 А/м.
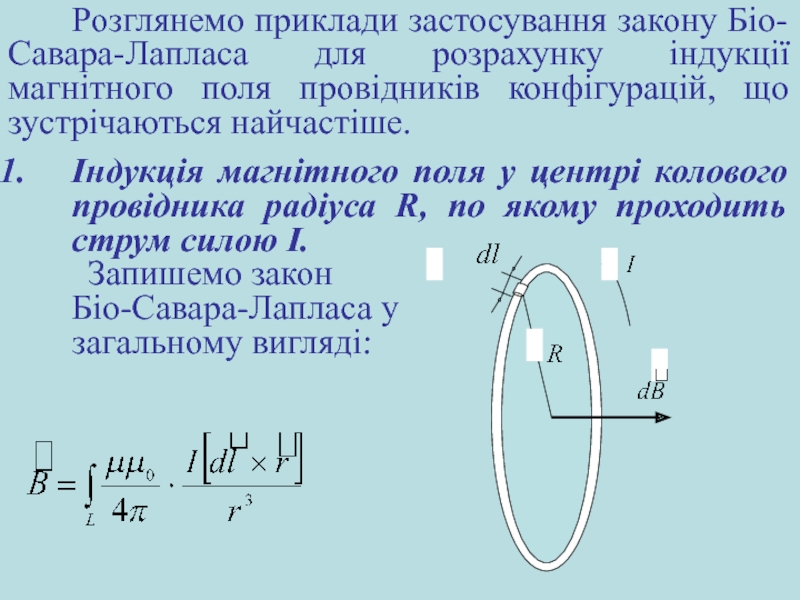
Слайд 8Розглянемо приклади застосування закону Біо-Савара-Лапласа для розрахунку індукції магнітного поля провідників
конфігурацій, що зустрічаються найчастіше.
Індукція магнітного поля у центрі колового провідника радіуса R, по якому проходить струм силою I.
Запишемо закон
Біо-Савара-Лапласа у
загальному вигляді:
Індукція магнітного поля у центрі колового провідника радіуса R, по якому проходить струм силою I.
Запишемо закон
Біо-Савара-Лапласа у
загальному вигляді:
Слайд 9враховуючи, що усі ділянки про-відника у центрі колового витка створюватимуть елементарні
значення індукції магнітного поля одного напрямку, перепишемо закон Біо-Савара-Лапласа у скалярному вигляді:
де – довільно обраний елемент провідника зі стру-мом силою І,
– відстань від елементу провідника до точки визначення індукції магнітного поля, дорівнює радіусу кола ,
L – довжина колового витка;
– кут між елементом провідника і радіусом кола;
тому , а .
Слайд 11Індукція магнітного поля на відстані а від прямолінійного провідника, по якому
тече струм силою І.
Запишемо закон
Біо-Савара-Лапласа у
загальному вигляді:
Запишемо закон
Біо-Савара-Лапласа у
загальному вигляді:
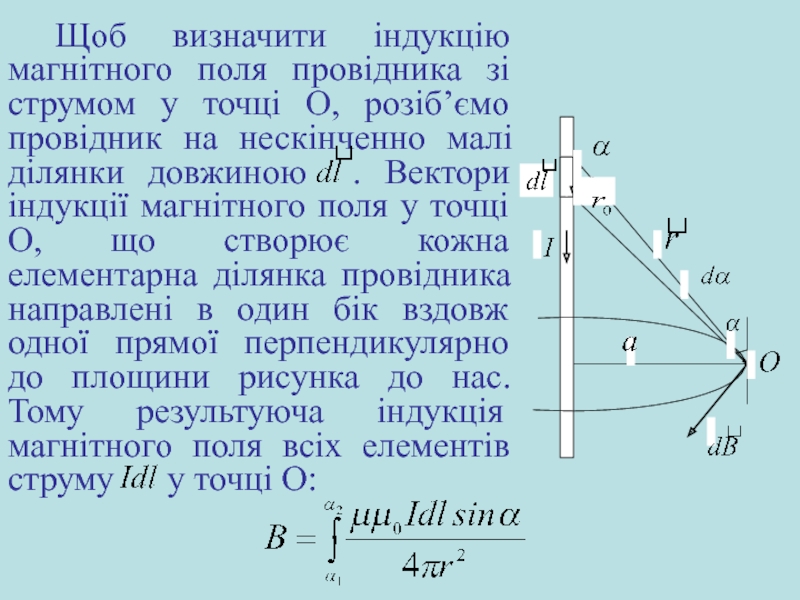
Слайд 12Щоб визначити індукцію магнітного поля провідника зі струмом у точці О,
розіб’ємо провідник на нескінченно малі ділянки довжиною . Вектори індукції магнітного поля у точці О, що створює кожна елементарна ділянка провідника направлені в один бік вздовж одної прямої перпендикулярно до площини рисунка до нас. Тому результуюча індукція магнітного поля всіх елементів струму у точці О:
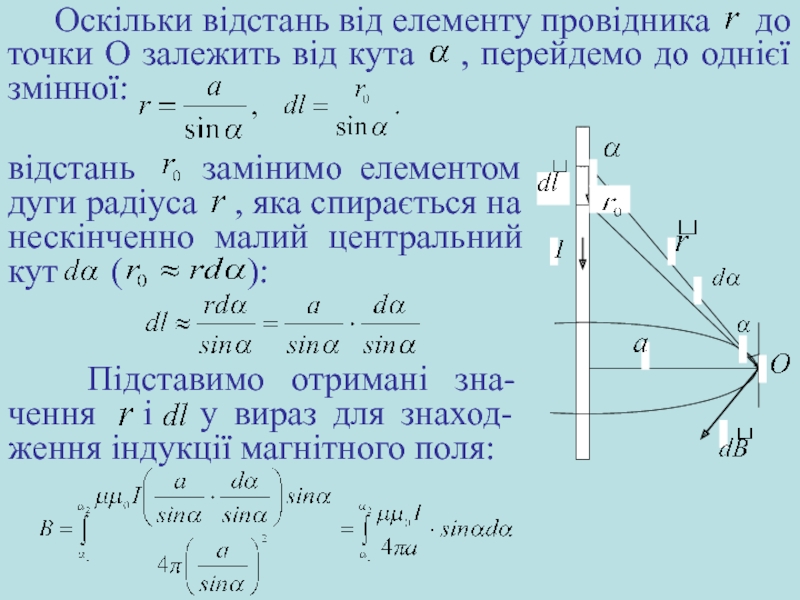
Слайд 13відстань замінимо елементом дуги радіуса , яка спирається на
нескінченно малий центральний кут ( ):
Оскільки відстань від елементу провідника до точки О залежить від кута , перейдемо до однієї змінної:
Підставимо отримані зна-чення і у вираз для знаход-ження індукції магнітного поля:
Слайд 14Винесемо сталі величини за знак інтегралу та здійснимо інтегрування:
Індукція магнітного
поля прямолінійного провідника скінченної довжини:
Якщо провідник нескінченно довгий, а . , то індукція магнітного поля нескінченно довгого прямолінійного провідника:
Якщо провідник нескінченно довгий, а . , то індукція магнітного поля нескінченно довгого прямолінійного провідника:
Слайд 15 Провідники по яким проходять електричні струми взаємодіють один з одним через
власні магнітні поля. Цю силу взаємодії можна визначити поєднуючи закон Біо-Савара-Лапласа із законом Ампера. За законом Біо-Савара-Лапласа елемент струму у точці О, що знаходиться на відстані . створює магнітне поле індукцією
2. Взаємодія струмів
Слайд 16 На елемент струму , поміщений у точку
О, за законом Ампера, діятиме сила з боку магнітного поля, що створюється елементом струму
підставивши значення індукції магнітного поля у точці О в закон Біо-Савара-Лапласа, отримаємо загальний закон Ампера:
підставивши значення індукції магнітного поля у точці О в закон Біо-Савара-Лапласа, отримаємо загальний закон Ампера:
Слайд 17Застосовуючи закон Ампера для двох нескінченно довгих прямолінійних паралельних провідників, можна
отримати силу взаємодії, що припадає на одиницю їх довжини:
де – відстань між провідниками.
де – відстань між провідниками.
Використовуючи правило свердлика та правило лівої руки, можна визначити, що провідники з однаковим напрямом струмів взаємно притягу-ються, а з різним – відштовхуються.
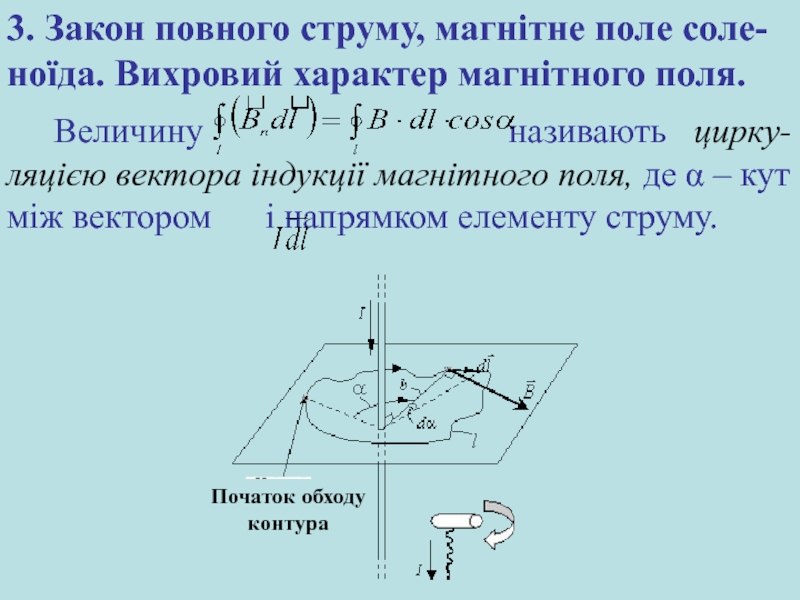
Слайд 18Величину називають цирку-ляцією
вектора індукції магнітного поля, де α – кут між вектором і напрямком елементу струму.
3. Закон повного струму, магнітне поле соле-ноїда. Вихровий характер магнітного поля.
Початок обходу контура
Слайд 19Знайдемо циркуляцію вектора індукції магніт-ного поля прямого провідника зі струмом. Індукція
магнітного поля прямого нескінченого провідника із струмом дорівнює:
де R – відстань від провідника до точки, в якій визначається В.
Охопимо провідник колом радіуса R. Тоді
де R – відстань від провідника до точки, в якій визначається В.
Охопимо провідник колом радіуса R. Тоді
Так як І, μ, μ0 і R величини сталі, маємо:
або
і
Слайд 20Сформулюємо закон повного струму або теорему про циркуляцію вектора індукції магнітного
поля в загальному вигляді, циркуляція вектора індукції магнітного поля постійних струмів по довільному замкненому контуру дорівнює алгебраїчній сумі сил струмів, які охоплюються цим контуром, помноженій на магнітну сталу і магнітну проникність середовища:
де – сума струмів, які охоплюються контуром.
Слайд 21Отже, робота при перенесенні пробного одиничного елемента струму в магнітному полі
в загальному випадку не дорівнює нулеві, тому його називають непотенціальним або вихровим. Характерною ознакою вихрового поля є замкненість його силових ліній.
Слайд 22При застосуванні закону повного струму необхідно враховувати правило знаків: якщо напрямок
обходу контуру співпадає з напрямом обертального руху свердлика (правого гвинта), то охоплені контуром струми, напрями яких співпадають із напрямом поступального руху свердлика, записують із знаком «+», а ті, що не співпадають – із знаком «–».
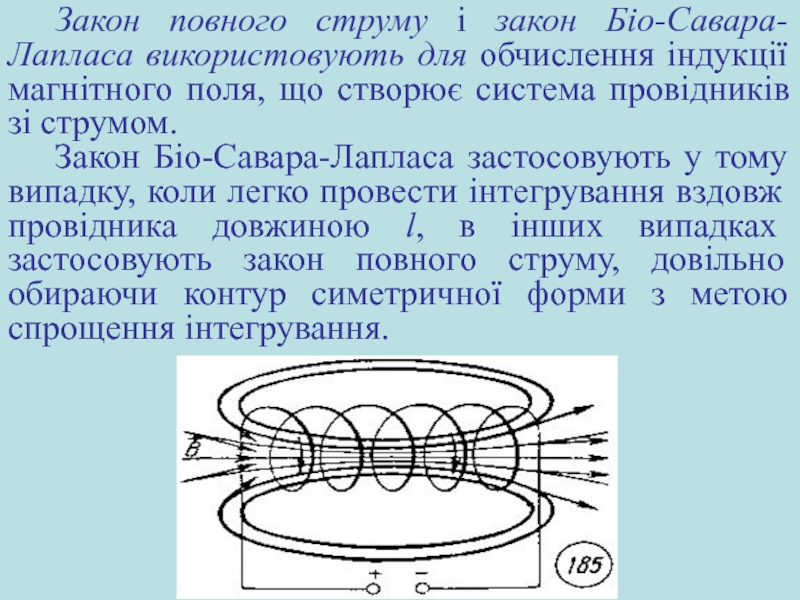
Слайд 23Закон повного струму і закон Біo-Савара-Лапласа використовують для обчислення індукції магнітного
поля, що створює система провідників зі струмом.
Закон Біо-Савара-Лапласа застосовують у тому випадку, коли легко провести інтегрування вздовж провідника довжиною l, в інших випадках застосовують закон повного струму, довільно обираючи контур симетричної форми з метою спрощення інтегрування.
Закон Біо-Савара-Лапласа застосовують у тому випадку, коли легко провести інтегрування вздовж провідника довжиною l, в інших випадках застосовують закон повного струму, довільно обираючи контур симетричної форми з метою спрощення інтегрування.
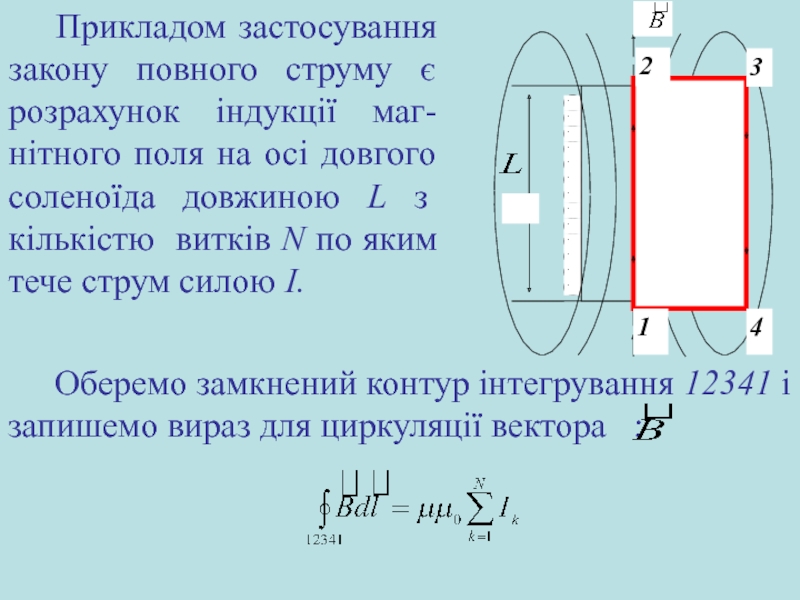
Слайд 24Прикладом застосування закону повного струму є розрахунок індукції маг-нітного поля на
осі довгого соленоїда довжиною L з кількістю витків N по яким тече струм силою I.
Оберемо замкнений контур інтегрування 12341 і запишемо вираз для циркуляції вектора :
Слайд 25Циркуляцію вектора по замкненому контуру можна подати у вигляді чотирьох доданків
Оскільки
обраний контур охоплює N витків по кожному з яких тече струм силою I, то
Підставляючи у закон повного струму отримані вирази циркуляції вектора і суми сил струмів матимемо:
Підставляючи у закон повного струму отримані вирази циркуляції вектора і суми сил струмів матимемо:
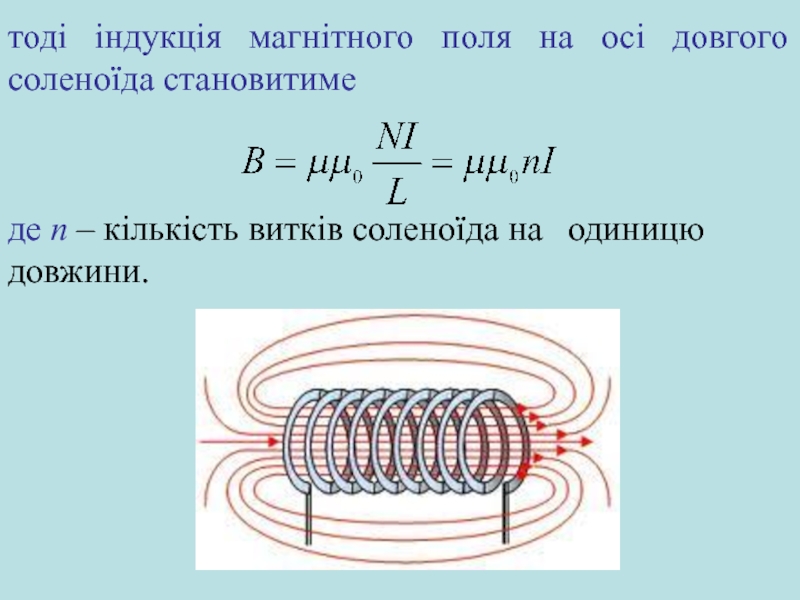
Слайд 26тоді індукція магнітного поля на осі довгого соленоїда становитиме
де n –
кількість витків соленоїда на одиницю довжини.
Слайд 27Явище виникнення магнітного поля навколо провідників зі струмом використовують для виготовлення
електромагнітів – пристроїв, здатних створювати власні магнітні поля при про-ходженні електричного струму у витках обмотки.
Слайд 28Звичайно електромагніт складається з обмотки і феромагнітного осердя, який набуває властивостей
магніту при проходженні по обмотці струму (на рисунку наведено найпростіший електромагніт – електропровід в ізоляції намотаний навколо феромаг-нітного осердя).
Електромагніти використо-вуються там, де необхідне маг-нітне поле, яке можна швидко і легко змінити, наприклад у побутових приладах (телевізор, магнітофон, електробритва),
Електромагніти використо-вуються там, де необхідне маг-нітне поле, яке можна швидко і легко змінити, наприклад у побутових приладах (телевізор, магнітофон, електробритва),
Слайд 29у пристроях техніки зв’язку (телефон, телеграф, радіо), в електричних машинах (елек-трогенератори
та електро-двигуни), у пристроях промислової автоматики (пускачі, перемикачі, реле та інше), в електромагнітних сепараторах для очищення механічних сумішей від магнітних предметів.
Слайд 30Широкого застосування електромагніти набули в електромагнітних механізмах, що здійснюють поступально-поворотні рухи
чи гальмувальні процеси – вантажопідйомні електромагніти (див. рис.), металорізальні верстати, магнітні замки, релейні та пускові пристрої, механізми автоматичного вимикання, гальмові пристрої тощо.
Слайд 314. Робота при переміщенні провідника зі струмом в магнітному полі. Енергія
провідника зі струмом.
При переміщенні провідника зі струмом в магнітному полі виконується робота
Енергія магнітного поля замкненого провід-ного контуру зі струмом І та індуктивністю L
Слайд 32Енергію магнітного поля визначають за формулою
Якщо врахувати формулу зв’язку вектора індукції
магнітного поля і вектора напруженості магнітного поля
то енергія магнітного поля у даній точці дорівнюватиме
то енергія магнітного поля у даній точці дорівнюватиме
Слайд 33А об’ємна густина енергії магнітного поля в околі кожної точки простору
визначатиметься значеннями векторних характеристик поля:
Слайд 34Лекція № 13.
Закон Біо-Савара- Лапласа.
Магнітне поле прямого та колового
провідників зі струмом.
Взаємодія струмів.
Закон повного струму, магнітне поле соленоїда. Вихровий характер магнітного поля.
Робота при переміщенні провідника зі струмом в магнітному полі. Енергія провідника зі струмом.
Взаємодія струмів.
Закон повного струму, магнітне поле соленоїда. Вихровий характер магнітного поля.
Робота при переміщенні провідника зі струмом в магнітному полі. Енергія провідника зі струмом.
