- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
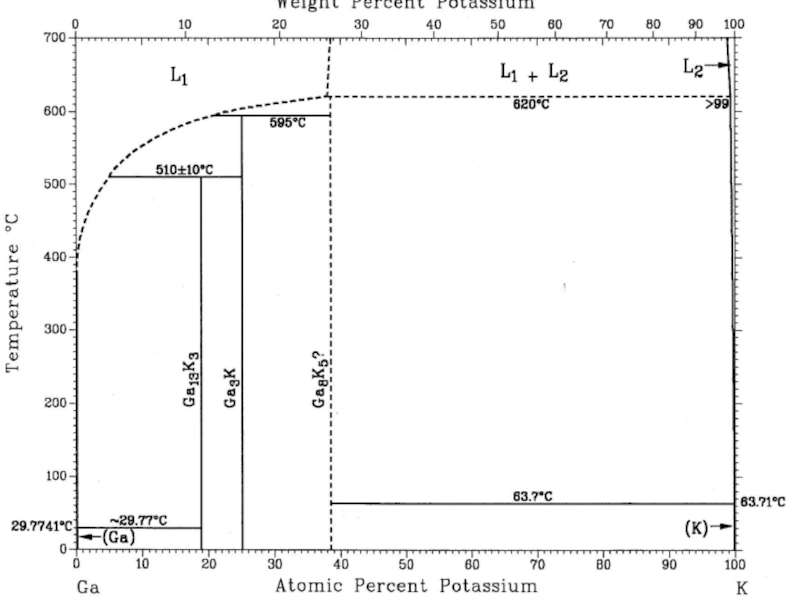
Вырожденные фазовые равновесия на экспериментальных t-x диаграммах презентация
Содержание
- 10. ВЫРОЖДЕННЫЕ ФАЗОВЫЕ РАВНОВЕСИЯ НА ЭКСПЕРИМЕНТАЛЬНЫХ T-X ДИАГРАММАХ
- 12. Двухкомпонентная система, n = 2, P
- 13. Двухкомпонентная система, n = 2, P
- 14. 2) Вблизи чистого компонента у двухфазной области,
- 15. Равновесие двух растворов (1) и (2)
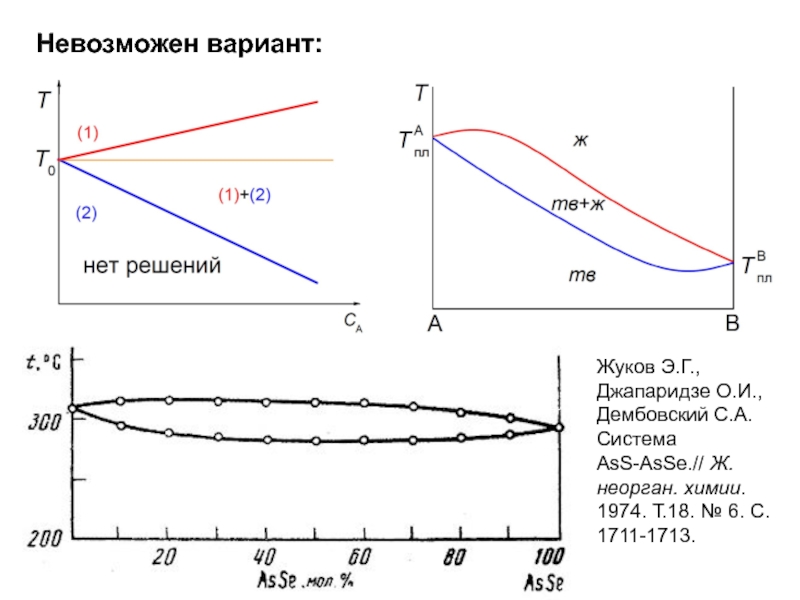
- 16. Невозможен вариант: Жуков Э.Г., Джапаридзе
- 17. 3) Правило фаз Райнза в модифицированном варианте:
- 18. Лев Самойлович Палатник, Александр Исаакович
- 19. Правило фаз Райнза является частным случаем правила
- 20. В T-P координатах, переходы в однокомпонентных системах
- 21. Правило Палатника и, соответственно, правило Райнза могут
- 22. 3а) Однофазные области не могут иметь общей
- 23. 3б) При изменении температуры двухфазная область может
- 25. 4) Правило тройных стыков: Пусть на двумерной
- 26. На T-x диаграммах бинарных систем правило тройных
- 27. Тройная точка правилом Райнза запрещена, хотя и
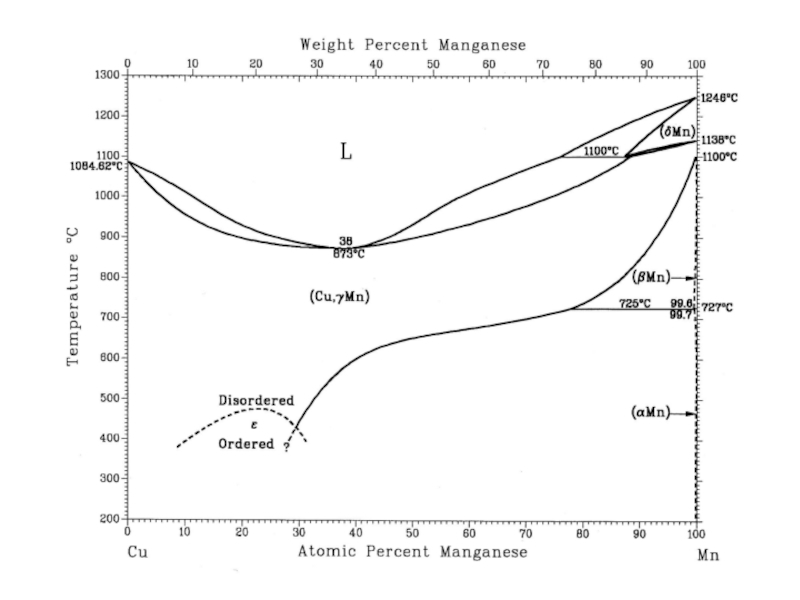
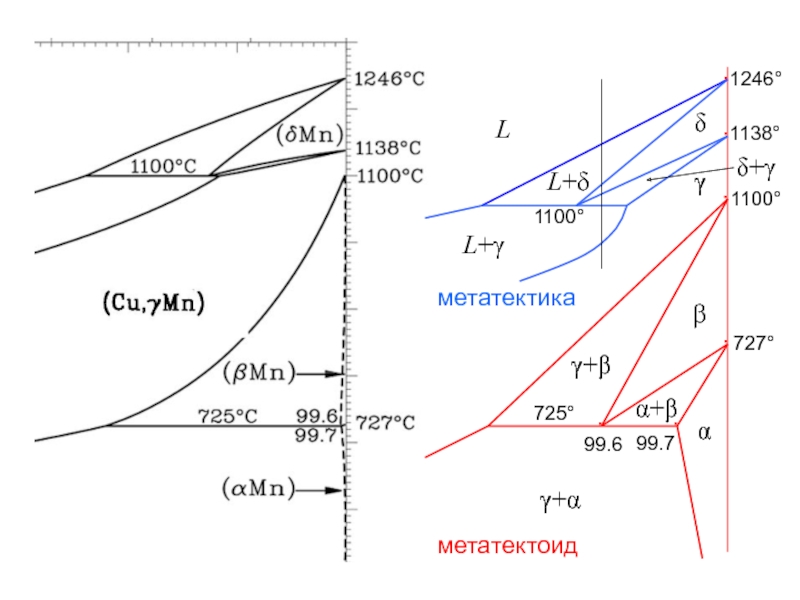
- 30. 99.7 99.6 727° 725° 1100° γ β
- 32. ∙ ∙ ∙ ∙
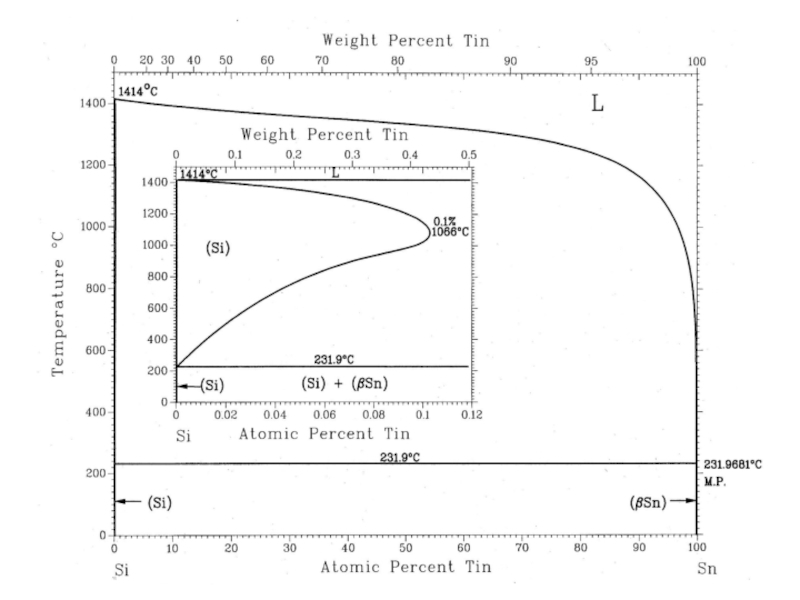
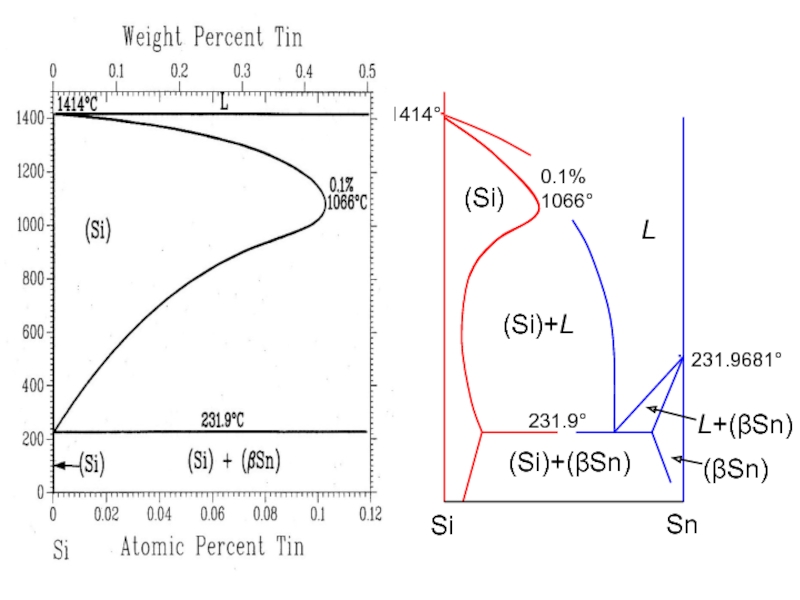
- 34. ∙ 231.9681° 1414° ∙ 0.1% 1066°
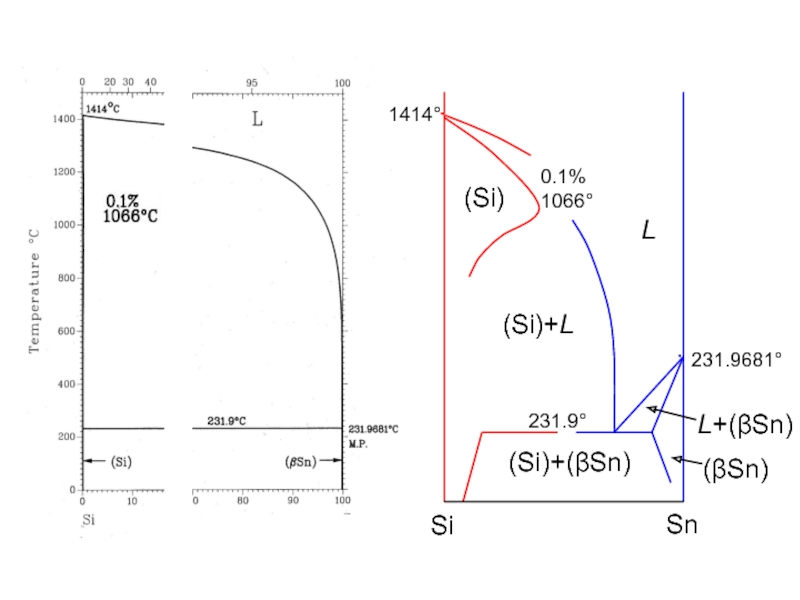
- 35. ∙ 231.9681° 231.9° 1414° ∙ 0.1% 1066°
- 37. ∙
- 38. ∙ ∙ ∙ ∙ 912° 1538° 1394°
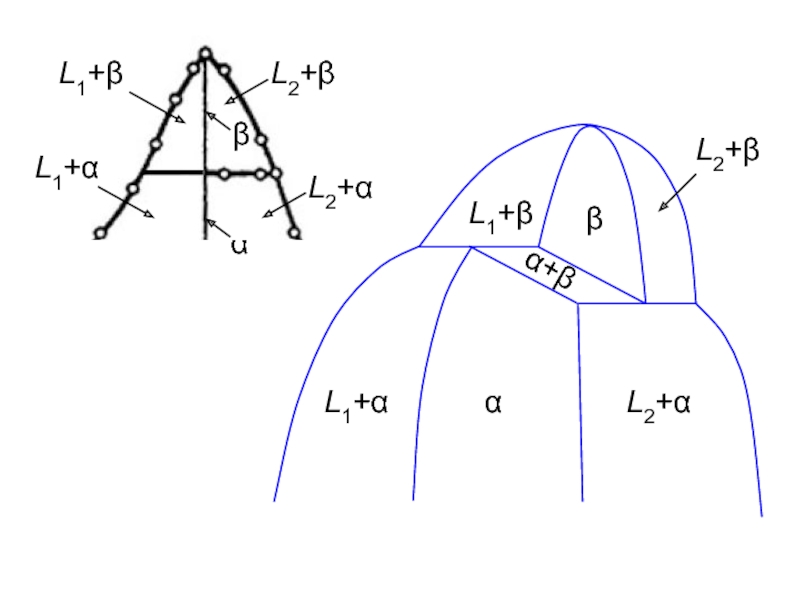
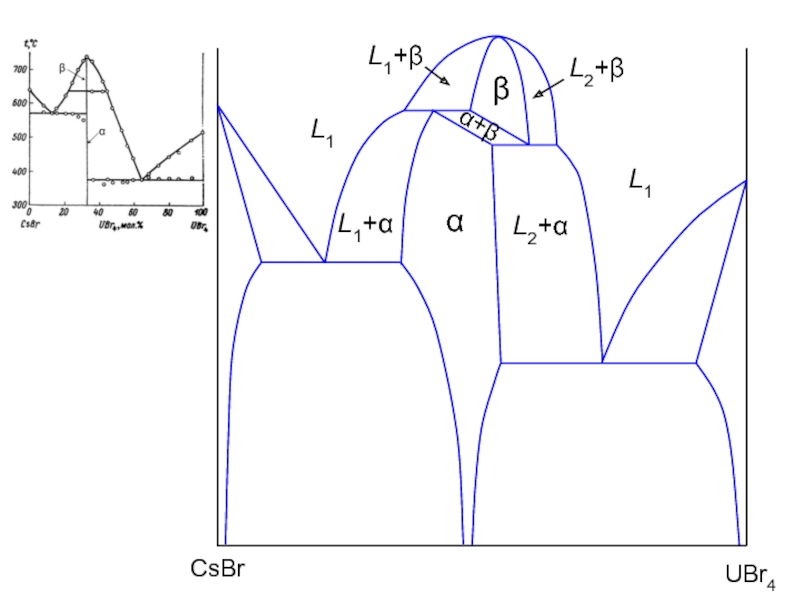
- 39. L2 L1
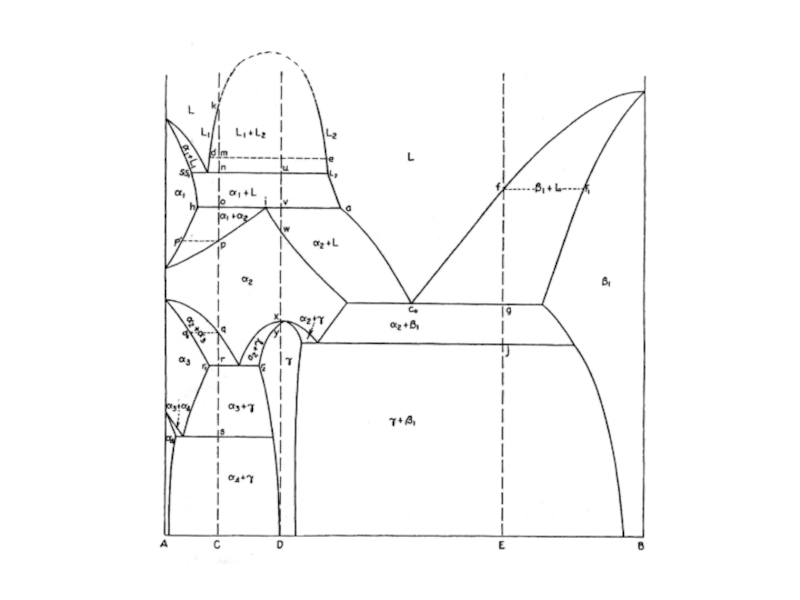
- 40. β α L1+β L1+α L2+α L2+β α+β
- 41. β α
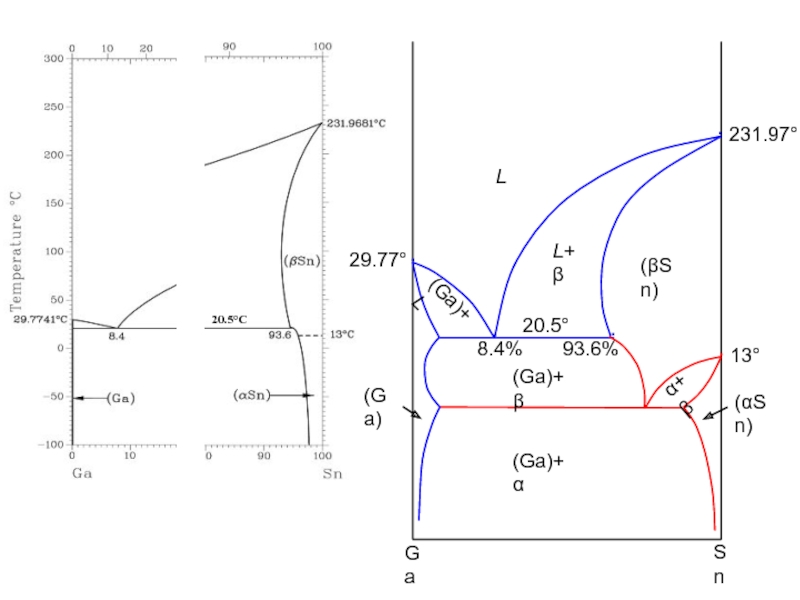
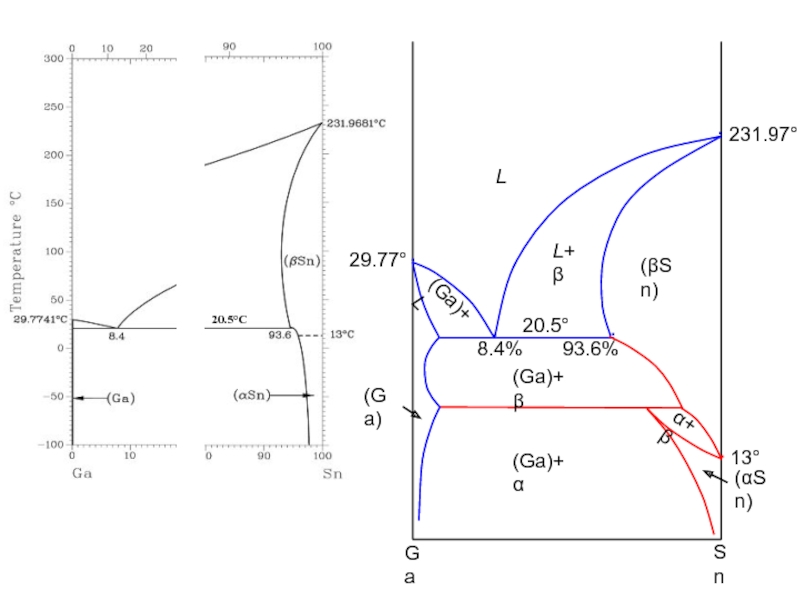
- 43. 20.5°C 20.5°
- 44. 20.5°C 20.5°
- 45. 1) Горизонтали на T-x диаграмме соединяют составы
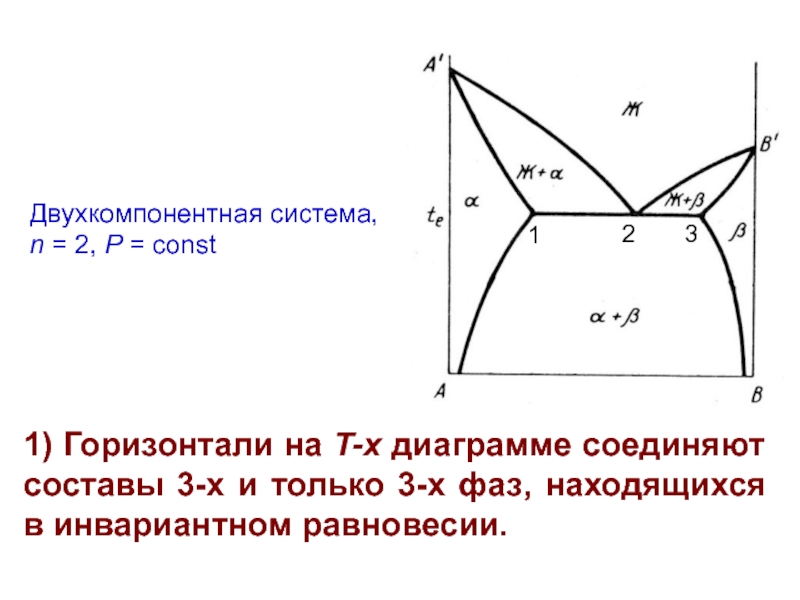
Слайд 12Двухкомпонентная система,
n = 2, P = const
1) Горизонтали на
Слайд 13Двухкомпонентная система,
n = 2, P = const
f = n
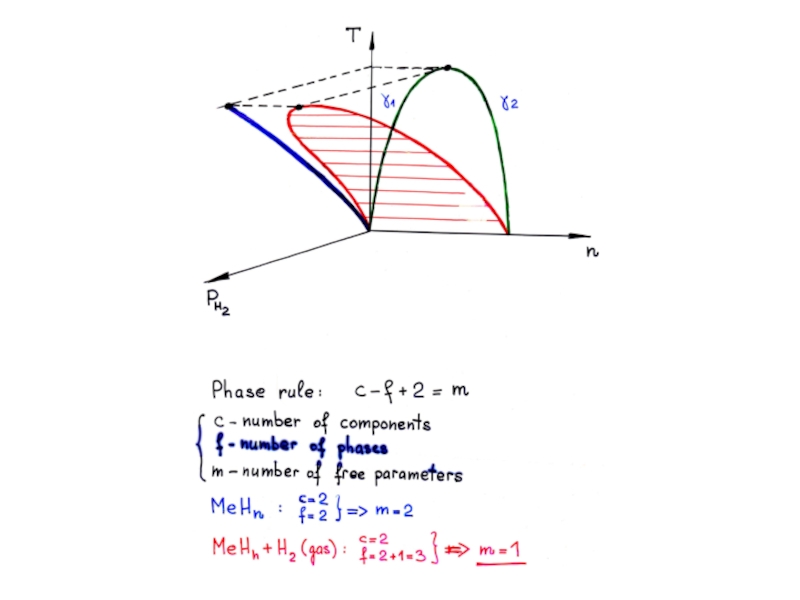
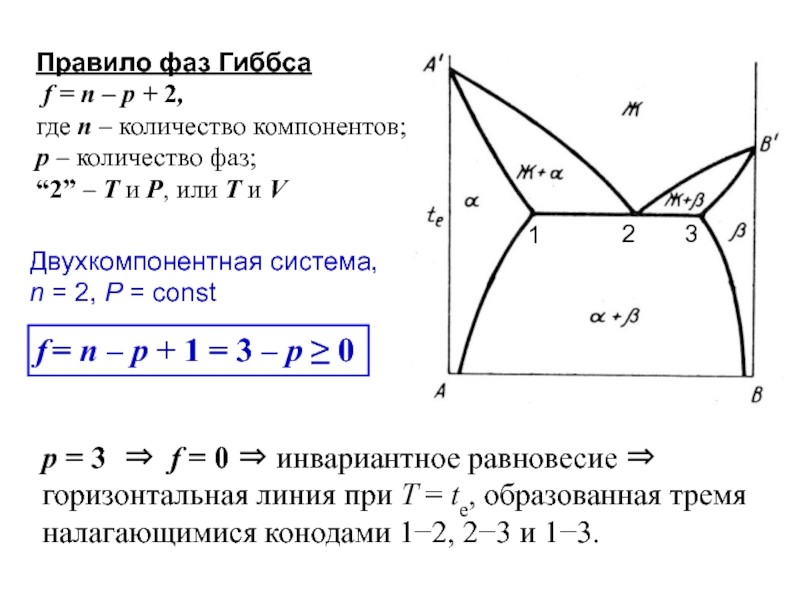
Правило фаз Гиббса
f = n – p + 2,
где n – количество компонентов;
p – количество фаз;
“2” – Т и P, или T и V
p = 3 ⇒ f = 0 ⇒ инвариантное равновесие ⇒
горизонтальная линия при T = te, образованная тремя налагающимися конодами 1−2, 2−3 и 1−3.
Слайд 142) Вблизи чистого компонента у двухфазной области, порождаемой фазовым переходом в
[1] Л.Д. Ландау,
Е.М. Лифшиц, Статистическая физика, т. 5, М., Физматлит, 1995,
стр. 328
μ׳ = kTlnc + ψ(P,T)
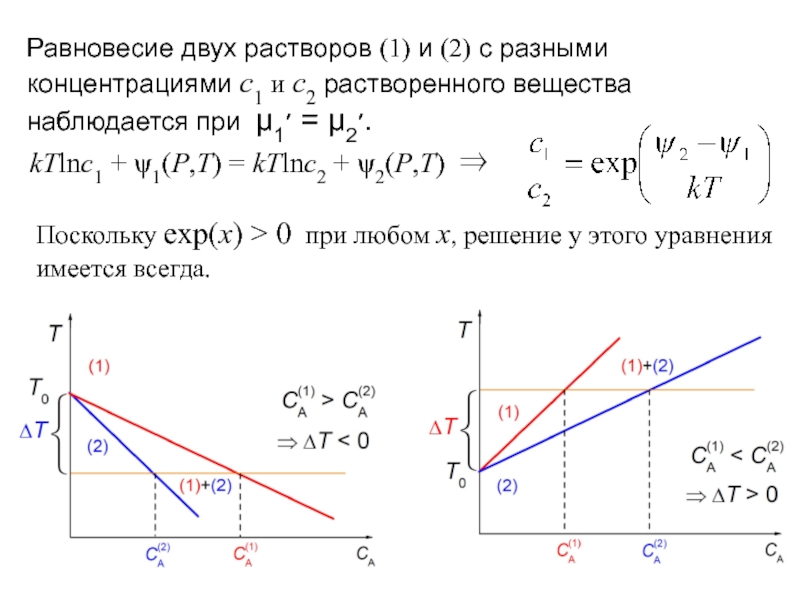
Слайд 15
Равновесие двух растворов (1) и (2) с разными концентрациями c1 и
kTlnc1 + ψ1(P,T) = kTlnc2 + ψ2(P,T) ⇒
Поскольку exp(x) > 0 при любом х, решение у этого уравнения имеется всегда.
Слайд 16
Невозможен вариант:
Жуков Э.Г., Джапаридзе О.И., Дембовский С.А. Система AsS-AsSe.// Ж. неорган.
Слайд 173) Правило фаз Райнза в модифицированном варианте:
Фазовые составы областей, соприкасающихся
α
β+γ
Правило фаз Райнза (общепринятное): Область диаграммы фазового равновесия, представляющая равновесие между n фазами, может граничить только с областями, представляющими равновесие между n-1 или n+1 фазой [1].
[1] Ф. Райнз “Диаграммы фазового равновесия в металлургии”,
М., Металлургиздат, 1960, c. 239.
α+γ
Слайд 18
Лев Самойлович Палатник, Александр Исаакович Ландау.
Фазовые равновесия в многокомпонентных системах,
изд. Харьковского
Пусть при переходе через фазовую границу D0 фаз
не изменяются, D– исчезают и D+ появляются.
Тогда выполняется правило:
R1 = R – (D– + D+) ≥ 0,
где R – размерность фазовой диаграммы или ее сечения,
а R1 – размерность границы между (D0 + D–) и (D0 + D+)
областями этой диаграммы или сечения.
Правило соприкосновения фазовых пространств
(правило Палатника):
Граница выделяется условием:
Слайд 19Правило фаз Райнза является частным случаем правила Палатника R1 = R
(D– + D+) = R – R1 = R – (R – 1) = 1
Поскольку D– ≥ 0 и D+ ≥ 0, то возможны лишь варианты:
D– = 0; D+ = 1 ⇒ n→n+1
D– = 1; D+ = 0 ⇒ n→n–1
Правило Райнза (как и правило Палатника) не выполняется для граничных линий, при пересечении которых содержание хотя бы одной фазы в системе изменяется скачком. Причина − граница выделяется условием:
Требуется, по крайней мере, чтобы количество каждой из этих фаз на границе было определено.
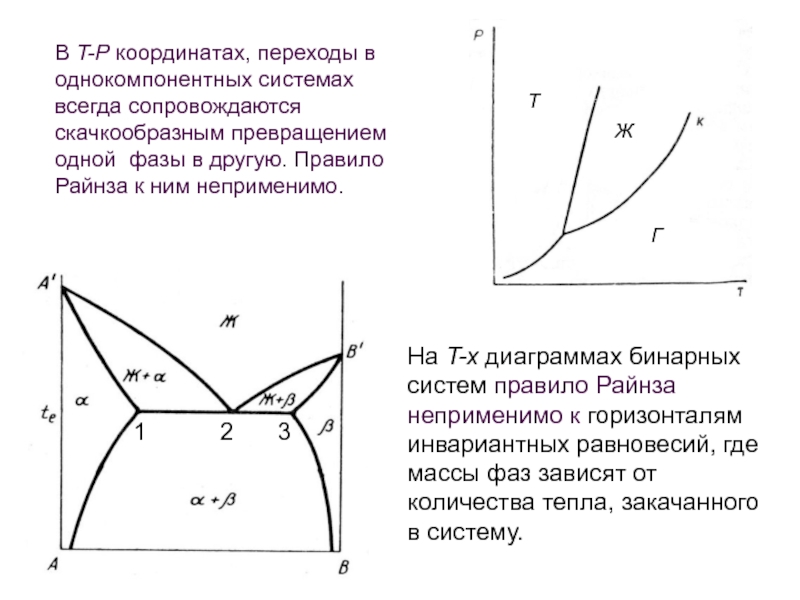
Слайд 20В T-P координатах, переходы в однокомпонентных системах
всегда сопровождаются скачкообразным превращением одной
На T-x диаграммах бинарных систем правило Райнза неприменимо к горизонталям инвариантных равновесий, где массы фаз зависят от количества тепла, закачанного в систему.
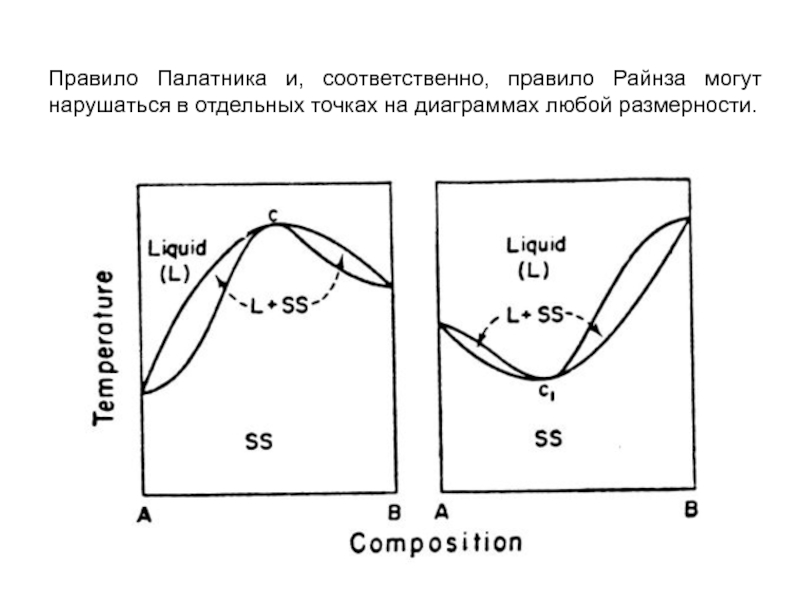
Слайд 21Правило Палатника и, соответственно, правило Райнза могут нарушаться в отдельных точках
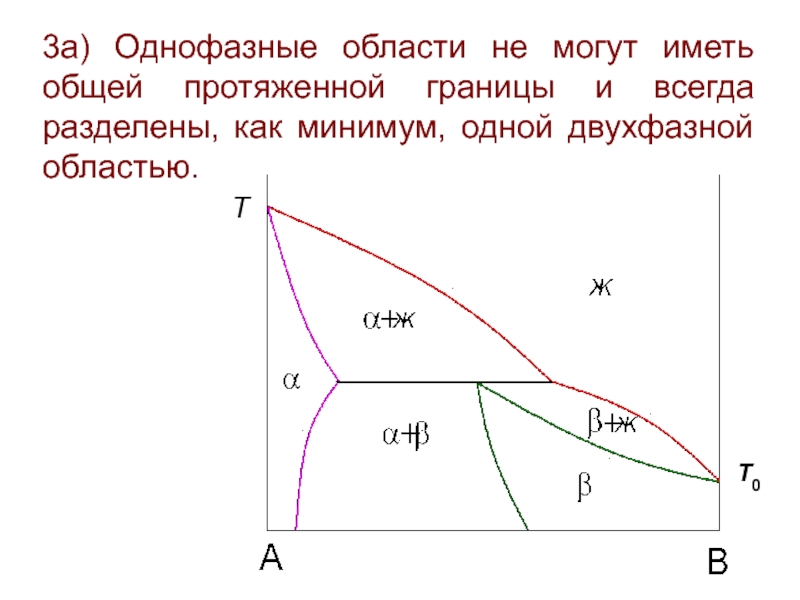
Слайд 223а) Однофазные области не могут иметь общей протяженной границы и всегда
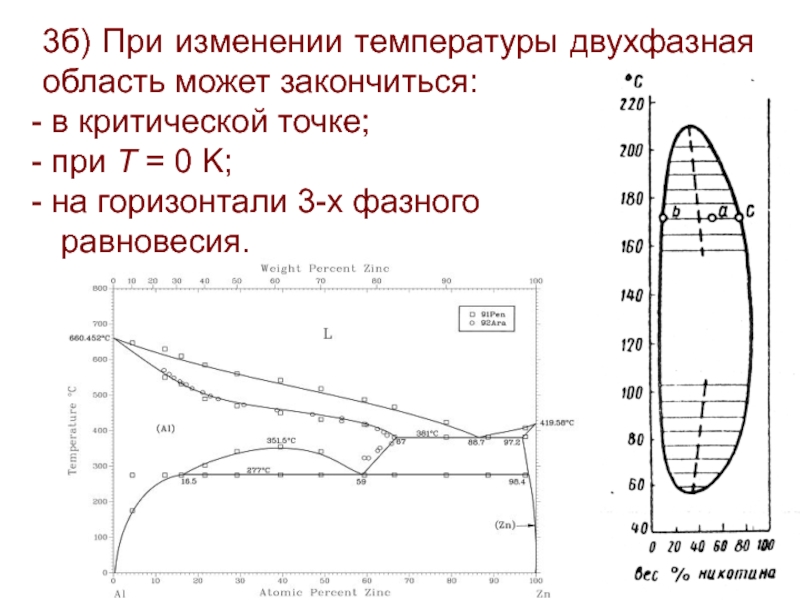
Слайд 233б) При изменении температуры двухфазная область может закончиться:
в критической точке;
на горизонтали 3-х фазного
равновесия.
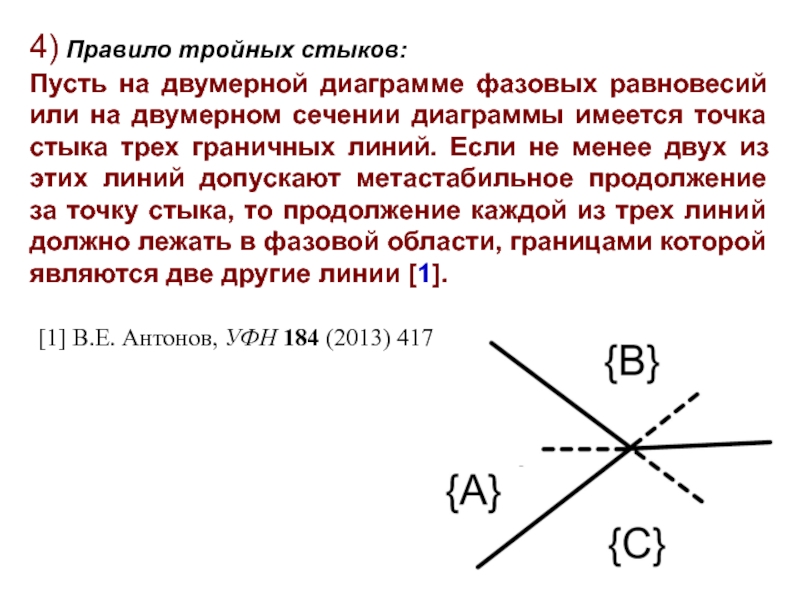
Слайд 254) Правило тройных стыков:
Пусть на двумерной диаграмме фазовых равновесий или на
[1] В.Е. Антонов, УФН 184 (2013) 417
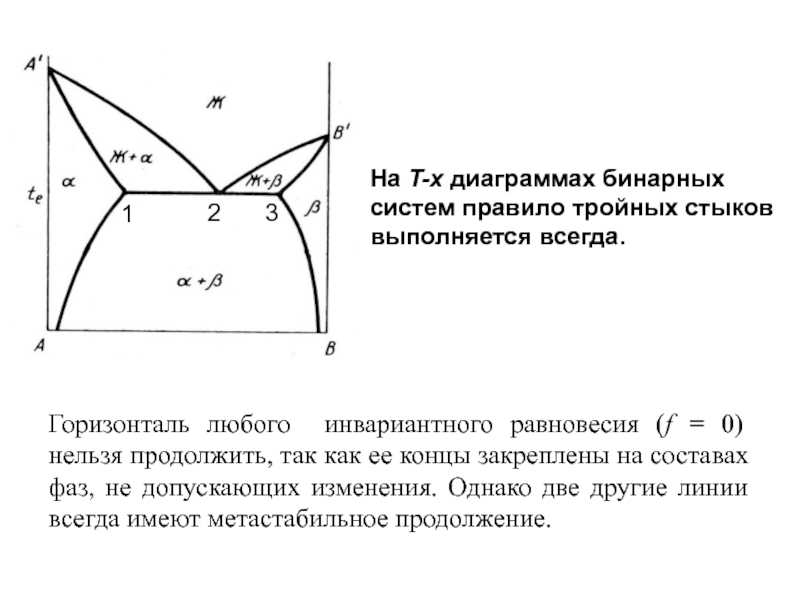
Слайд 26На T-x диаграммах бинарных систем правило тройных стыков выполняется всегда.
Горизонталь
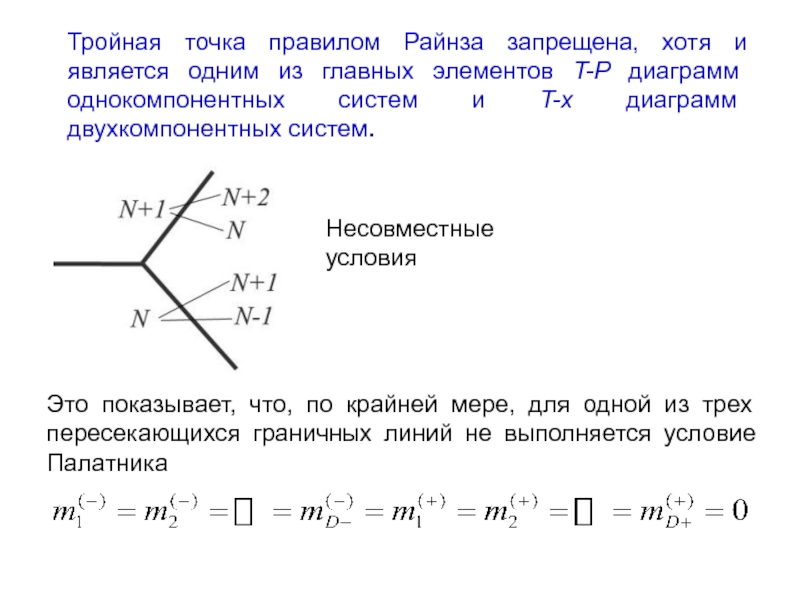
Слайд 27Тройная точка правилом Райнза запрещена, хотя и является одним из главных
Несовместные
условия
Это показывает, что, по крайней мере, для одной из трех пересекающихся граничных линий не выполняется условие Палатника
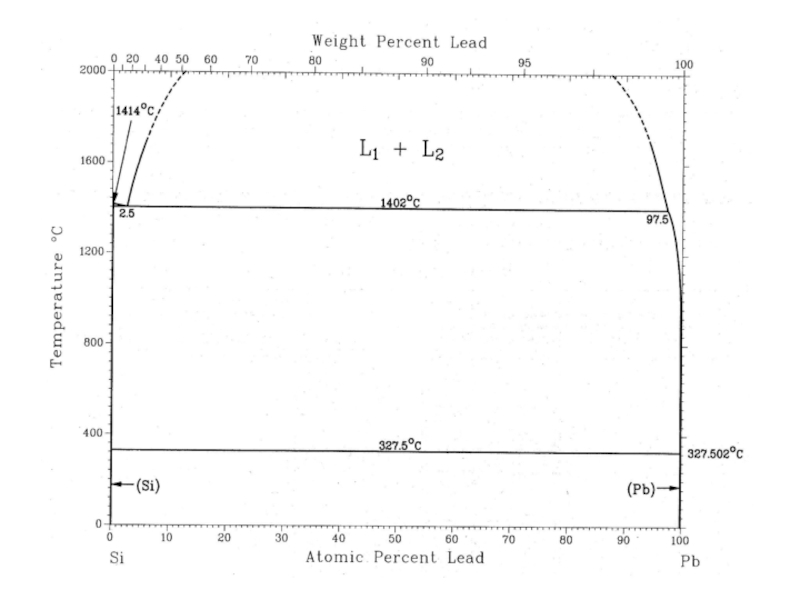
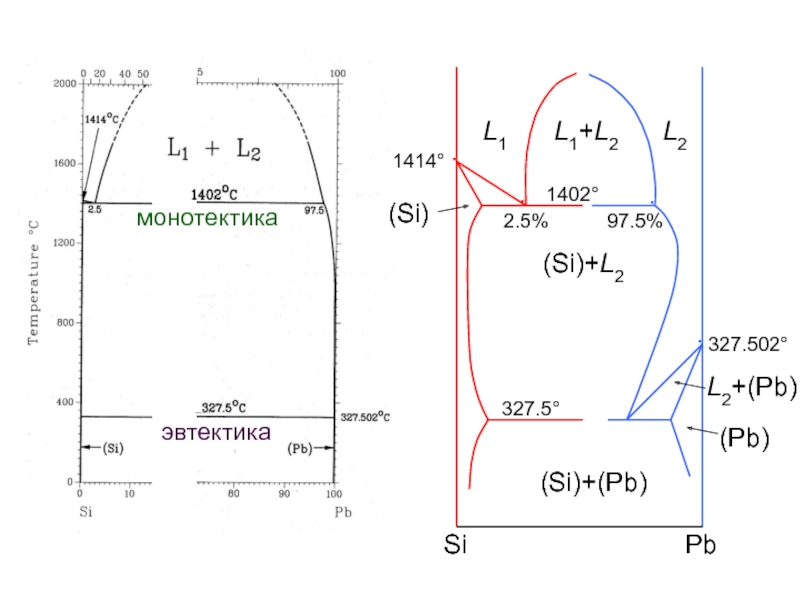
Слайд 32∙
∙
∙
∙
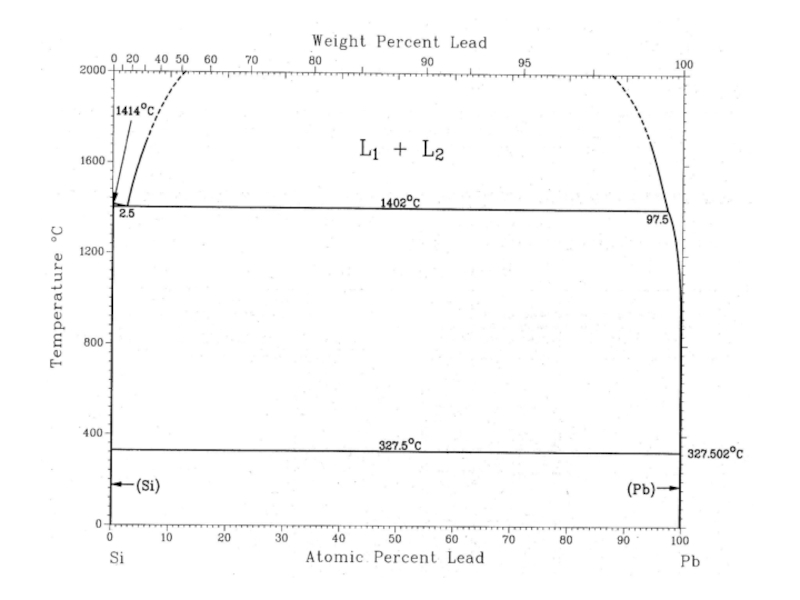
327.502°
327.5°
1402°
2.5%
97.5%
L1+L2
L1
L2
(Si)+L2
(Si)+(Pb)
1414°
(Pb)
(Si)
L2+(Pb)
Si
Pb
эвтектика
монотектика
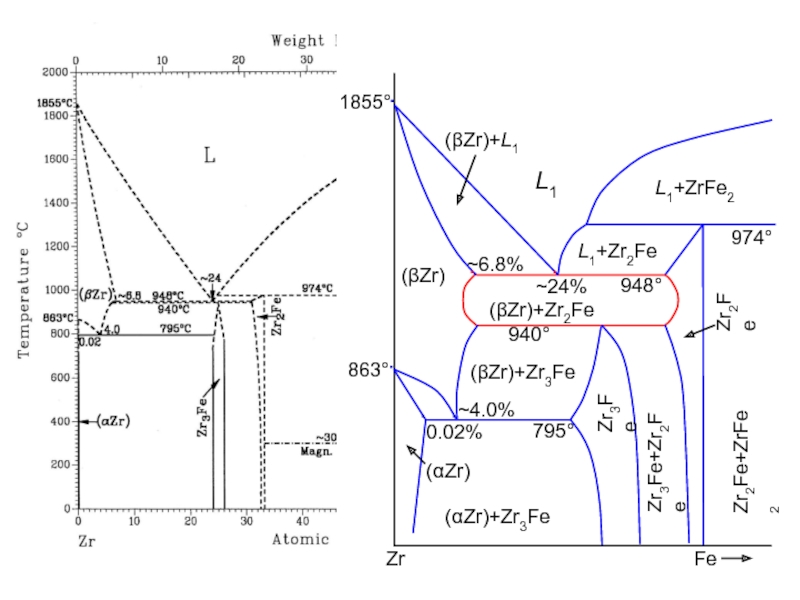
Слайд 37
∙
1855°
∙
863°
∙
∙
795°
940°
948°
~6.8%
~24%
~4.0%
0.02%
∙
∙
(βZr)
(αZr)
Zr3Fe
Zr2Fe
L1
L1+Zr2Fe
L1+ZrFe2
974°
Zr3Fe+Zr2Fe
(βZr)+Zr3Fe
(αZr)+Zr3Fe
(βZr)+Zr2Fe
(βZr)+L1
Zr2Fe+ZrFe2
Zr
Fe
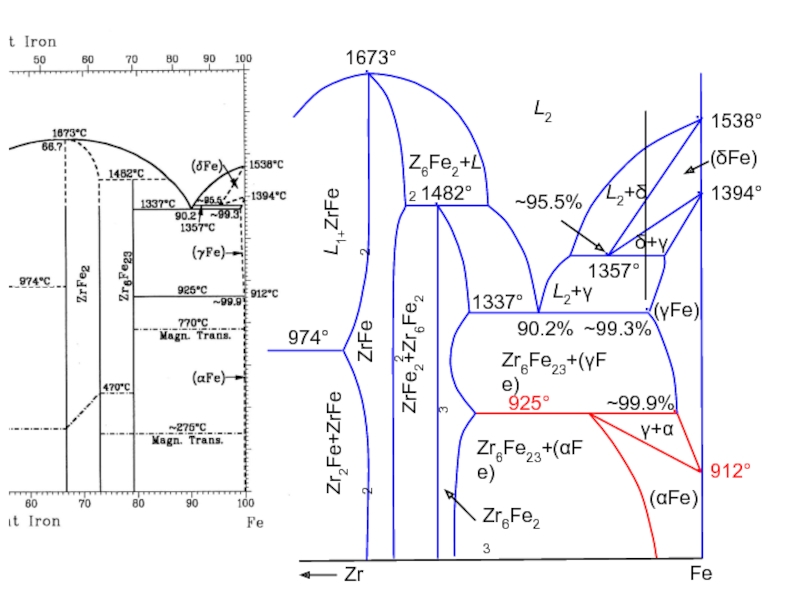
Слайд 38∙
∙
∙
∙
912°
1538°
1394°
925°
974°
1337°
1482°
1673°
1357°
~99.9%
~99.3%
90.2%
∙
∙
~95.5%
∙
∙
(γFe)
(δFe)
(αFe)
L2
ZrFe2+Zr6Fe23
ZrFe2
γ+α
Zr6Fe23+(αFe)
Zr6Fe23+(γFe)
Zr6Fe23
δ+γ
L2+δ
L2+γ
Z6Fe2+L2
L1+ZrFe2
Zr2Fe+ZrFe2
Fe
Zr
Слайд 451) Горизонтали на T-x диаграмме соединяют составы 3-х и только 3-х
2) Вблизи чистого компонента у двухфазной области, порождаемой фазовым переходом в этом компоненте при температуре T0, обе границы направлены либо вверх, либо вниз от T0.
3) Правило фаз Райнза: Фазовые составы областей, соприкасающихся вдоль линии на двумерном сечении фазовой диаграммы, отличаются на одну фазу, которая появляется или исчезает при пересечении линии.
3а) Однофазные области не могут иметь общей протяженной границы и всегда разделены, как минимум, одной двухфазной областью.
3б) При изменении температуры двухфазная область может закончиться i) в критической точке; ii) при T = 0 K; iii) на горизонтали 3-х фазного равновесия.
4) Правило тройных стыков: Пусть на двумерной диаграмме фазовых равновесий или на двумерном сечении диаграммы имеется точка стыка трех граничных линий. Если не менее двух из этих линий допускают метастабильное продолжение за точку стыка, то продолжение каждой из трех линий должно лежать в фазовой области, границами которой являются две другие линии.