- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Тепломассообмен. Теплопроводность презентация
Содержание
- 1. Тепломассообмен. Теплопроводность
- 2. Кафедра Теплогазоснабжения и вентиляции ТЕПЛОМАССООБМЕН Курс лекций
- 3. ООО «Меди»
- 4. ООО «Меди»
- 5. ПРОЦЕССЫ ПЕРЕДАЧИ ТЕПЛОТЫ ТЕПЛОПРОВОДНОСТЬЮ Теплопроводность – молекулярный
- 6. ООО «Меди»
- 7. ТЕМПЕРАТУРНОЕ ПОЛЕ - в векторной форме: Температурное
- 8. ООО «Меди»
- 9. ООО «Меди»
- 10. ООО «Меди»
- 11. ООО «Меди»
- 12. ООО «Меди»
- 13. ООО «Меди»
- 14. ООО «Меди»
- 15. ООО «Меди»
- 16. ООО «Меди»
- 17. 3. Температуры тела: Вт/(м⋅К)
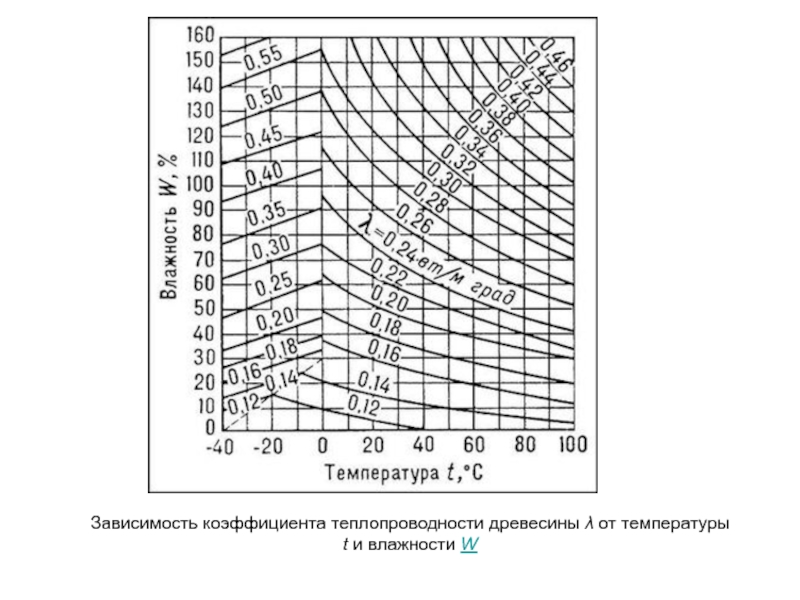
- 18. Зависимость коэффициента теплопроводности древесины λ от температуры t и влажности W
- 19. 5. Структуры материала. Это относится к материалам,
- 20. Уравнение теплопроводности Наиболее последовательная и законченная
- 21. Количество теплоты, затраченное на изменение температуры: Количество теплоты, уходящее через поверхность: По теореме Гаусса-Остроградского:
- 22. Исходя из уравнения: или с учетом получим:
- 23. и после сокращения на После преобразований Окончательно получим:
- 24. Выражение называется коэффициентом температуропроводности Коэффициент температуропроводности
- 25. Частные случаи уравнения: 1. При W=0
- 26. Из уравнения Фурье следует, что скорость распространения
- 27. Из формулы следует, что время релаксации увеличивается
- 28. 2). Граничные условия II -го рода –
- 29. Уравнение является аналитическим выражением граничного условия III
- 30. 4). Граничные условия сопряжения (IY -го рода)
- 31. Теплопроводность при стационарном режиме Теплопроводность однослойной и
- 32. В направлении Оy и Оz температура будет
- 33. Откуда следует, что если коэффициент теплопроводности стенки
- 34. Для определения плотности теплового потока применим закон
- 35. На практике часто применяют безразмерные величины
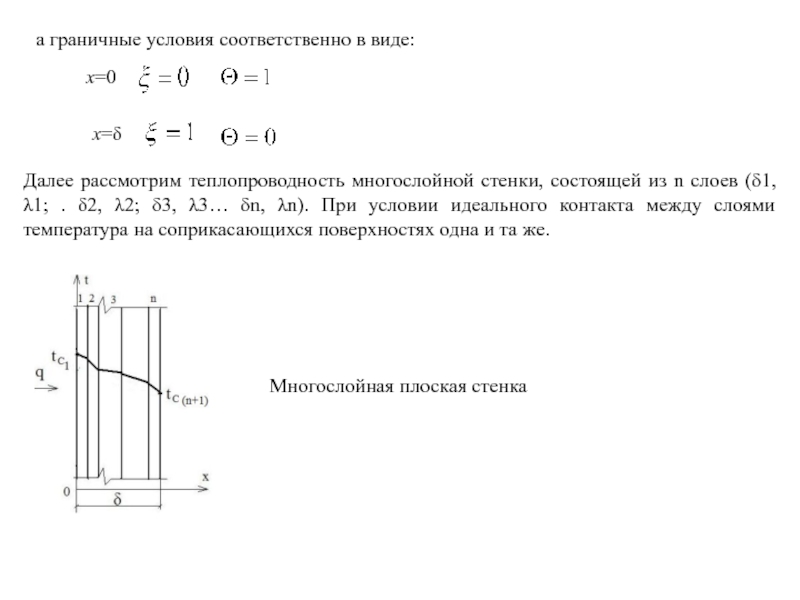
- 36. а граничные условия соответственно в виде: x=0
- 37. Тепловой поток через каждый слой …………………….
- 38. после преобразований получаем: ……………………. Сложив почленно левые и правые части уравнений, имеем:
- 39. Отсюда можно найти плотность теплового потока в
- 40. ……………………. Для многослойной стенки температурная кривая представляет собой ломаную линию Теплопередача через плоскую стенку
- 41. Переход теплоты из одной среды к другой
- 42. Тот же поток передается от второй стенки
- 43. Обозначая знаменатель уравнения через k Величина
- 44. Отсюда плотность теплового потока определяется по формуле
- 45. не может быть меньше самого малого значения
- 46. Теплопроводность цилиндрических стенок Рассмотрим стационарный
- 47. Уравнение теплопроводности для данной задачи записывается в
- 48. Граничные условия имеют вид: Введем переменную
- 49. Учитывая получаем: или После интегрирования имеем
- 50. Подставляя в уравнение для t, получаем: Подставим
- 51. Иногда тепловой поток относят к единице длины:
- 52. Теплопередача через цилиндрическую стенку Искомыми величинами будут:
- 53. Тот же поток передается от второй стенки
- 54. Введем величину линейного коэффициента теплопередачи: Линейное термическое
- 55. Для выбора рациональной толщины изоляции трубы рассмотрим
- 56. Исследуем как функцию , для чего
- 57. Теплопроводность тел сложной формы Пусть имеется
- 58. Обозначим тогда уравнение
- 59. Из граничных условий находим: Тогда постоянные интегрирования:
- 60. Подставляя в это уравнение значение градиента температуры,
- 61. Отсюда следует, что тепловой поток: коэффициент теплопередачи шаровой стенки. термическое сопротивление шаровой стенки:
- 62. Анализируя выражение , можно сделать вывод, что,
- 63. Принимаем, что размеры поперечного сечения стержня существенно
- 64. Из закона Фурье: Отсюда тепловой поток, отдаваемый
- 65. Дифференцируя , получаем: и Подставляя в имеем:
- 66. Анализ формул показывает, что при оребрении необходимо
- 67. Учитывая равенство количества теплоты, подведенного к торцу
- 68. После преобразований имеем: Учитывая, что – гиперболический
- 69. Определим градиент температуры: где th(ml) – гиперболический
- 70. Учитывая, что для ребра , тогда
- 71. Окончательно уравнение для теплового потока с поверхности
- 72. Система уравнений теплопередачи через ребристую стенку может
- 73. Для расчета теплового потока тел различной формы
- 74. Теплопроводность плоской стенки при наличии внутренних источников
- 75. Постоянные интегрирования определяются из граничных условий: Таким
- 76. Рассмотрим процесс теплопроводности в круглом сплошном стержне
- 77. Учитывая, что величины в знаменателе не равны
- 78. Рассмотрим стационарный процесс теплопроводности полого цилиндра
- 79. Температура в этом случае изменяется только в
- 80. При Т.к. , то
- 81. Плотность теплового потока на этой поверхности: Температуру
- 82. Для второго случая граничные условия при
- 83. Для третьего случая очевидно, что внутри стенки
- 84. Для определения координаты изотермической поверхности с
Слайд 1
Кафедра Теплогазоснабжения и вентиляции
ФГБОУ ВПО «Санкт-Петербургский государственный архитектурно-строительный университет»
Слайд 3 ООО «Меди»
ОБЩИЕ ПОЛОЖЕНИЯ
Тепломассообмен – необратимый самопроизвольный процесс распространения в пространстве теплоты или массы одного из компонентов вещества относительно другого.
Существуют три механизма передачи теплоты - «простой» теплообмен:
- теплопроводность (Т) или кондукция,
- конвекцию (К),
тепловое излучение (Л) или радиация.
Теплопроводность характерна для твердых тел, конвекция – для жидких и газообразных, излучение – для поверхностей, разделенных лучепрозрачной средой. Если в теплообмене участвует более чем одна составляющая, то такой теплообмен называется «сложным», например, теплопроводность и конвекция; конвекция и излучение; теплопроводность, конвекция и излучение.
Слайд 4 ООО «Меди»
Перенос массы происходит следующими способами:
- диффузией,
- конвекцией.
В реальных процессах процессы теплообмена и массообмена обычно сопутствуют друг другу. Теплопроводность и конвекция всегда связаны с переносом массы примеси (диффузией), т.е. имеет место сложный тепломассообмен.
Значительный вклад в создание и развитие теоретических и практических основ тепломассообмена внесли такие известные Российские ученые как М.В. Кирпичев, М.А. Михеев, А.А. Гухман, А.В. Лыков, Г.М. Кондратьев, С.С. Кутателадзе, С.Н. Шорин, Л.С. Эйгенсон, В.Н. Богословский и др. Благодаря их трудам сформировалась отечественная школа тепломассообмена.
Слайд 5ПРОЦЕССЫ ПЕРЕДАЧИ ТЕПЛОТЫ ТЕПЛОПРОВОДНОСТЬЮ
Теплопроводность – молекулярный перенос, обусловленный неоднородностью распределения температуры
в твердых телах (диэлектриках) – за счет упругих колебаний кристаллических решеток (упругих волн);
в твердых телах (электрических проводниках) – основным «носителем» тепловой энергии являются свободные электроны, а роль упругих колебаний кристаллических решеток - второстепенна;
в жидкостях – за счет упругих колебаний молекул около равновесного состояния;
в газах – за счет обмена энергией путем диффузии при соударении между элементарными частицами (молекулами, атомами) вещества.
Теплопроводность протекает на уровне элементарных частиц и зависит от неравномерности распределения температур в теле. В «чистом» виде теплопроводность имеет место в твердых телах.
Слайд 6 ООО «Меди»
ТЕМПЕРАТУРНОЕ ПОЛЕ
В общем случае процесс передачи теплоты теплопроводностью сопровождается изменением температуры в пространстве и во времени. Для описания пространственно-временного распределения температуры вводится понятие температурного поля. Температурным полем называется совокупность мгновенных значений температур во всех точках рассматриваемого объема. Общий вид температурного поля в декартовой системе координат:
в цилиндрических координатах:
- в сферических координатах:
Слайд 7ТЕМПЕРАТУРНОЕ ПОЛЕ
- в векторной форме:
Температурное поле в таком виде называется трехмерным
.
Если
и
, то получаем двумерное уравнение:
Слайд 8 ООО «Меди»
Наиболее простым случаем является одномерное (линейное) стационарное температурное поле при условии: и
Температура является скалярной величиной, таким образом, температурное поле – есть скалярное поле.
Непрерывное поле – такое поле, в котором бесконечно малому приращению координат соответствует бесконечно малое приращение температуры, т.е. производные будут конечны.
Разрывное поле - поле, в котором бесконечно малому приращению координат соответствует конечное приращение температуры.
Слайд 9 ООО «Меди»
ДИФФЕРЕНЦИАЛЬНЫЕ ОПЕРАТОРЫ
Градиент поля – вектор, определенный в каждой точке поля, имеющий направление нормали к поверхности уровня в сторону возрастания величины и численно равный частной производной по нормали
Градиент поля обозначается – grad U или
(набла, оператор Гамильтона).
- единичный вектор, перпендикулярный к поверхности уровня
- орты декартовой системы координат (ортогональные единичные векторы, ориентированные в пространстве).
Слайд 10 ООО «Меди»
Модуль градиента:
Правила вычисления градиента:
(C=const)
Слайд 11 ООО «Меди»
Дивергенция вектора V:
В цилиндрических координатах:
(C=const)
Правила вычисления дивергенции (U- скаляр, V-вектор):
Слайд 12 ООО «Меди»
Оператор Лапласа обозначается –
или
В цилиндрических координатах:
Теорема Гаусса-Остроградского (переход от двойного интеграла к тройному):
Скалярный поток вектора V через замкнутую поверхность s равен интегралу от divV, распространенному по объему v, заключенному внутри поверхности s.
Слайд 13 ООО «Меди»
Всегда найдется такая вторая точка, в которой температура будет равна начальной t1 = t2, далее будет третья точка - t1 = t2 = t3 и т.д. В конечном итоге можно получить некоторую замкнутую кривую, в которой t = const.
Совокупность точек пространства, имеющих одинаковую температуру, образуют изотермическую поверхность. Изотермические поверхности в пространстве не пересекаются, поскольку одна и та же точка не может иметь в данный момент разные температуры.
Изменение температуры наблюдается только в направлениях, пересекающих изотермические поверхности. Максимальное изменение температуры имеет место в направлении нормали к изотермическим поверхностям.
Градиент температуры - вектор, направленный по нормали к изотермической поверхности в сторону возрастания температуры:
К/м, (град/м)
Слайд 14 ООО «Меди»
Изотермические поверхности Градиент температуры
Нетрудно видеть, что во всех направлениях, отличных от нормали, grad t будет меньше. Например, проекция вектора grad t на ось координат х:
Слайд 15 ООО «Меди»
ТЕПЛОВОЙ ПОТОК
В любом теле при отсутствии полного теплового равновесия возникает тепловой поток. Для математического описания вводится вектор теплового потока в соответствии с гипотезой Фурье: количество теплоты, проходящее через элемент изотермической поверхности dF за промежуток времени dτ, пропорционально температурному градиенту:
ПЛОТНОСТЬ ТЕПЛОВОГО ПОТОКА:
, Дж
λ – коэффициент теплопроводности, Вт/м∙К.
Вт/м2
Слайд 16 ООО «Меди»
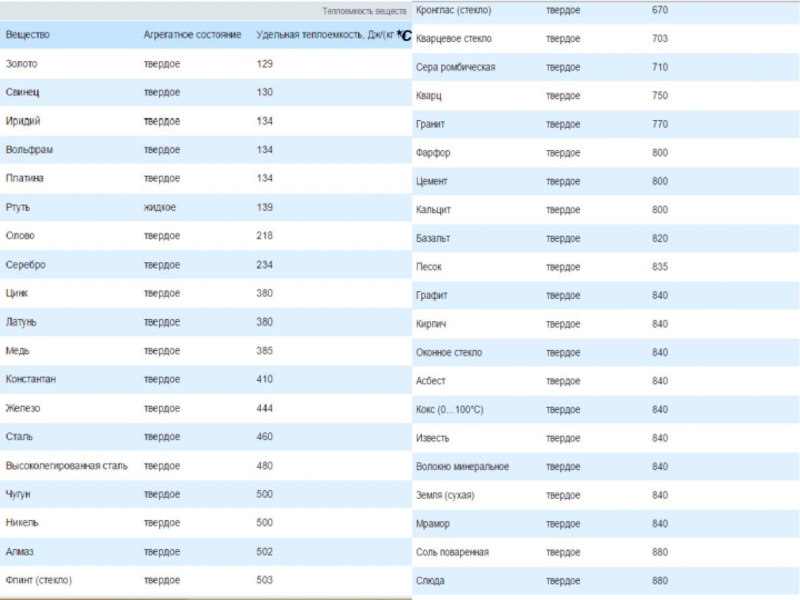
Коэффициент теплопроводности
Коэффициент теплопроводности λ - физическая характеристика данного вещества, которая показывает интенсивность переноса теплоты через данное вещество, т.е. представляет собой плотность теплового потока при grad t=1К/м.
Коэффициент теплопроводности зависит от следующих факторов:
Физических свойств вещества. Максимальное значение имеют металлы (электрические проводники) - λ>35Вт/(м⋅К); минимальное – газы, например, воздух: λ ≈ 0,03Вт/(м⋅К)
2. Плотности данного материала, которая зависит от его пористости, т.е. наличия воздушных включений (приведенное ниже уравнение справедливо только для одного и того же материала):
Вт/(м⋅К)
Объясняется это тем, что в сухом состоянии поры вещества заполнены воздухом, имеющим минимальный коэффициент теплопроводности.
Слайд 173. Температуры тела:
Вт/(м⋅К)
где - коэффициент
β - коэффициент температурного расширения, К-1.
Известно, что температурный коэффициент β имеет отрицательное значение для металлов и положительное для диэлектриков, т.е. с увеличением температуры коэффициент теплопроводности диэлектриков возрастает, а металлов – уменьшается. Для большинства строительных материалов коэффициент теплопроводности λ увеличивается с повышением температуры.
4. Влажности материала, с увеличением которой коэффициент теплопроводности растет за счет заполнения пор более теплопроводным, чем воздух, веществом – водой ( ) и конвективного переноса теплоты, связанного
с капиллярным движением воды внутри пористого материала. Зависимость λ от относительной влажности материала W обычно представляется в графической форме (рис.1.4).
Слайд 195. Структуры материала. Это относится к материалам, имеющим неоднородное (анизотропное) строение
Слайд 20Уравнение теплопроводности
Наиболее последовательная и законченная теория, позволяющая аналитически определить коэффициент
Для вывода уравнения теплопроводности принимаются следующие допущения:
1. Теплопроводное тело является гомогенным.
2. Рассматривается изотропное тело.
3. Все теплофизические характеристики тела – величины постоянные и не зависят от температуры.
4. Интенсивность процесса теплообмена достаточно мала.
Пусть имеется тело произвольной формы с элементарным объемом dV. Внутри этого тела имеются источники теплоты мощностью W. Количество теплоты, затраченное на изменение внутренней энергии тела и передаваемое окружающей среде, определяется:
Слайд 21Количество теплоты, затраченное на изменение температуры:
Количество теплоты, уходящее через поверхность:
По теореме
Слайд 24Выражение
называется коэффициентом температуропроводности
Коэффициент температуропроводности а [м2/с] – физическая характеристика данного
~
а
Анализируя уравнение
– частных производных;
– II-го порядка;
– линейное, т.е. температура входит в 1-ой степени;
– параболического типа.
можно сделать следующие выводы, что это уравнение:
Слайд 25Частные случаи уравнения:
1. При W=0 получаем уравнение Фурье:
2. Стационарный процесс
–
3. При и – уравнение Лапласа:
W=0
Слайд 26Из уравнения Фурье следует, что скорость распространения теплоты в теле бесконечно
Для высокоинтенсивных нестационарных процессов [4] это условие не соблюдается, т.е. скорость распространения теплоты конечна. При резком изменении теплового потока на поверхности тела вследствие тепловой инерции перестройка температурного поля и изменение градиента температуры могут запаздывать во времени по сравнению с условиями, когда распространение теплоты происходит при
Время запаздывания называется временем релаксации. Связь между скоростью распространения теплоты и временем релаксации можно выразить следующим соотношением:
~
где τP – время релаксации, т.е. равновесия между плотностью теплового потока (q) и gradt.
Слайд 27Из формулы следует, что время релаксации увеличивается с увеличением тепловой инерции
а уравнение Фурье соответственно примет вид уравнения гиперболического типа:
Условия однозначности – условия, которые однозначно определяют конкретный тип задачи, включают в себя:
1). Геометрические условия, характеризующие форму и размер тела;
2). Физические условия, характеризующие свойства среды и тела;
3). Временные или начальные условия, характеризующие распределение температуры в начальный момент времени;
4). Граничные условия, которые необходимо задать по всей поверхности тела.
Граничные условия принято подразделять на ряд типов:
1). Граничные условия I-го рода – такие граничные условия, при которых в любой момент времени задается распределение температуры на поверхности тела:
Частный случай –
.
Слайд 282). Граничные условия II -го рода – такие граничные условия, при
Частный случай –
Такие условия теплообмена могут создаваться при нагревании тел высокотемпературными источниками теплоты, когда теплообмен происходит главным образом по закону Стефана-Больцмана, если при этом собственная температура тела существенно меньше температуры излучающей поверхности.
3). Граничные условия III -го рода – такие граничные условия, при которых в любой момент времени задается температура окружающей среды и закон теплообмена между поверхностью тела и окружающей средой. В случае нагрева (охлаждения):
где α – коэффициент теплоотдачи, Вт/(м2∙К);
Tокр ,Tс – температура окружающей среды и поверхности (стенки) тела.
Коэффициент теплоотдачи характеризует интенсивность теплового воздействия среды заданной Tокр на поверхность тела. В нестационарных процессах температура окружающей среды в общем случае изменяется во времени. Уравнение выражает закон Ньютона. Плотность потока, подводимая (отводимая) за счет теплопроводности к (от) поверхности тела, определяется по закону Фурье. Таким образом, на основании закона сохранения энергии с учетом получаем:
Слайд 29Уравнение является аналитическим выражением граничного условия III -го рода, которое широко
В отличие от λ коэффициент теплоотдачи (теплообмена) не является физической постоянной, характерной для того или иного вещества. В общем случае он отражает совместное действие конвекции, теплопроводности и зависит от многих факторов, например геометрической формы и размеров тела, физических свойств обтекающего потока, направления и скорости потока, температурных условий.
Из граничных условий III -го рода можно получить граничные условия I и II -го рода.
– граничные условия I -го рода,
- граничные условия II -го рода.
Слайд 304). Граничные условия сопряжения (IY -го рода) соответствуют теплообмену тела с
Задачи с граничными условиями IY рода ставятся, например, при расчетах многослойных теплоизоляционных покрытий.
выражает условие непрерывности температурного поля
закон сохранения энергии на поверхности двух соприкасающихся тел (условия идеального теплового контакта).
Слайд 31Теплопроводность при стационарном режиме
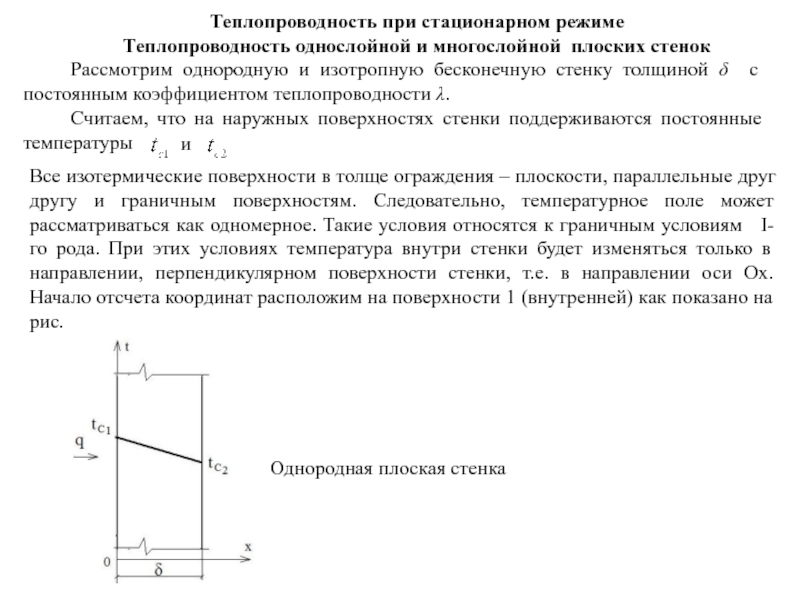
Теплопроводность однослойной и многослойной плоских стенок
Рассмотрим однородную
Считаем, что на наружных поверхностях стенки поддерживаются постоянные температуры
Все изотермические поверхности в толще ограждения – плоскости, параллельные друг другу и граничным поверхностям. Следовательно, температурное поле может рассматриваться как одномерное. Такие условия относятся к граничным условиям I-го рода. При этих условиях температура внутри стенки будет изменяться только в направлении, перпендикулярном поверхности стенки, т.е. в направлении оси Ох. Начало отсчета координат расположим на поверхности 1 (внутренней) как показано на рис.
и
Однородная плоская стенка
Слайд 32В направлении Оy и Оz температура будет неизменной:
и
Таким образом,
Из уравнения следует, что:
Интегрируя уравнение, получаем:
или
Слайд 33Откуда следует, что если коэффициент теплопроводности стенки – величина постоянная, то
при x=0
при x=δ
Тогда при первом граничном условии:
Из второго следует соответственно
и с учетом выражения для
Отсюда находим:
или
Подставляя полученные выражения, находим закон распределения температуры в плоской стенке:
Слайд 34Для определения плотности теплового потока применим закон Фурье:
Т.к.
получаем:
Откуда можно
и обратно пропорционально толщине стенки δ.
называется температурным напором.
называется тепловой проводимостью стенки, Вт/(м2 К)
называется термическим сопротивлением стенки, (м2 К)/Вт.
Слайд 35На практике часто применяют безразмерные величины
текущую избыточную температуру
максимальную избыточную
то можно перейти к безразмерной избыточной температуре:
Используя безразмерную координату
уравнение
можно представить следующим образом:
Слайд 36а граничные условия соответственно в виде:
x=0
x=δ
Далее рассмотрим
Многослойная плоская стенка
Слайд 37Тепловой поток через каждый слой
…………………….
Исходя из закона сохранения энергии при
Слайд 38после преобразований получаем:
…………………….
Сложив почленно левые и правые части уравнений, имеем:
Слайд 39Отсюда можно найти плотность теплового потока в виде:
называется суммарным внутренним
Температура на границе слоев определяется следующим образом:
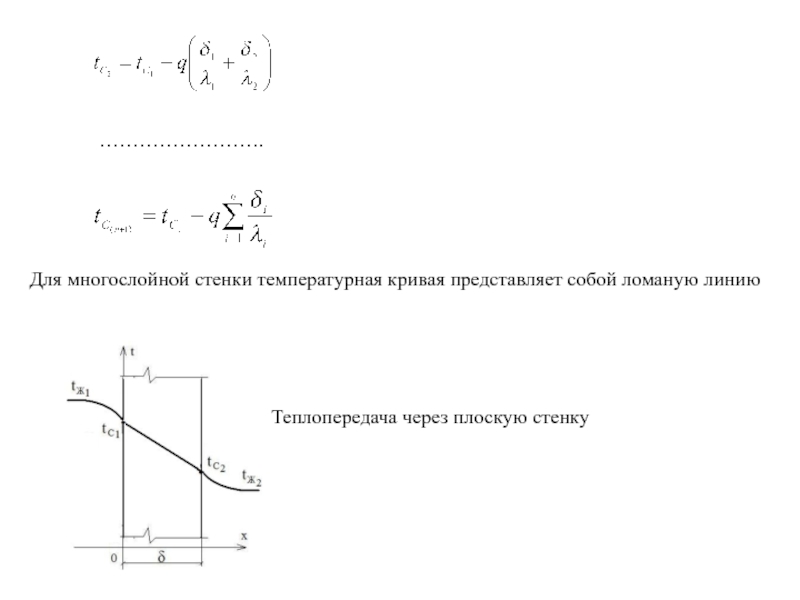
Слайд 40…………………….
Для многослойной стенки температурная кривая представляет собой ломаную линию
Теплопередача через
Слайд 41Переход теплоты из одной среды к другой через разделяющую их стенку
Допустим, что имеется плоская стенка с толщиной δ. Считаем, что известны температуры окружающей среды
Коэффициент теплопроводности стенки λ. Предполагаем стационарный режим. Считаем также заданными коэффициенты теплоотдачи α1 и α2.
Такие условия называется граничными условиями третьего рода. Это позволяет рассматривать одномерную задачу: изменение температуры стенки и среды будет происходить только по нормали к стенке. Искомыми величинами будут: температуры на поверхности стенки и тепловой поток от горячей к холодной жидкости.
Исходя из закона Ньютона, плотность теплового потока от жидкости к стенке определяется уравнением:
Плотность теплового потока через стенку:
Слайд 42Тот же поток передается от второй стенки к холодной жидкости посредством
После преобразований:
Сложив почленно левые и правые части этих уравнений, получим следующее уравнение:
или
Слайд 43Обозначая знаменатель уравнения через k
Величина k называется коэффициентом теплопередачи, Вт/(м2K).
Часто в расчетах используется понятие суммарного термического сопротивления теплопередачи. Это величина, обратная коэффициенту теплопередачи
Для многослойной стенки с разными величинами толщины δi и коэффициента теплопроводности λi термическое сопротивление определяется:
Слайд 44Отсюда плотность теплового потока определяется по формуле
И, соответственно, тепловой поток можно
где F – площадь поверхности стенки, м2.
Для исследования интенсификации процесса теплопередачи в теплообменниках проанализируем уравнение. Допустим заданы значения
Учитывая, что для металлических конструкций отношение
мало, коэффициент теплопередачи можно записать в виде:
Слайд 45не может быть меньше самого малого значения
то увеличение
практически не
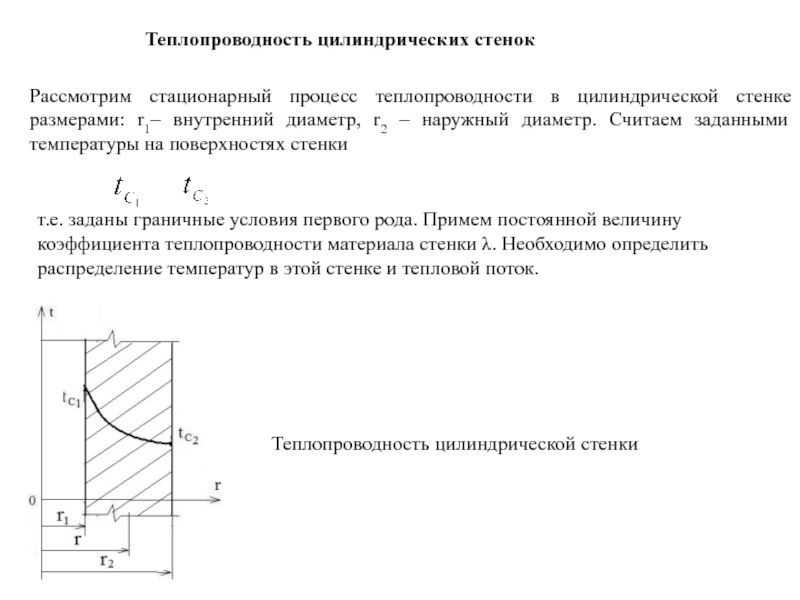
Слайд 46Теплопроводность цилиндрических стенок
Рассмотрим стационарный процесс теплопроводности в цилиндрической стенке размерами:
т.е. заданы граничные условия первого рода. Примем постоянной величину коэффициента теплопроводности материала стенки λ. Необходимо определить распределение температур в этой стенке и тепловой поток.
Теплопроводность цилиндрической стенки
Слайд 47Уравнение теплопроводности для данной задачи записывается в цилиндрических координатах
Температура изменяется
Т.к. труба симметрична, то и поле температур будет коаксиально-симметричным:
Тогда уравнение запишем в виде:
Слайд 48Граничные условия имеют вид:
Введем переменную
Уравнение
Решая данное обыкновенное дифференциальное уравнение с разделяющимися переменными, получим:
Слайд 49Учитывая
получаем:
или
После интегрирования имеем уравнение логарифмической кривой:
определяем из граничных условий.
Решение
Слайд 50Подставляя в уравнение для t, получаем:
Подставим в закон Фурье значение градиента
Плотность теплового потока на внутренней поверхности имеет вид:
Соответственно для наружной поверхности
Слайд 51Иногда тепловой поток относят к единице длины:
Величина
Для случая многослойной цилиндрической
называется линейной плотностью теплового потока
Рассмотрим граничные условия третьего рода. Пусть заданы температуры окружающей среды
Коэффициент теплопроводности стенки λ. Предполагаем стационарный режим. Считаем также заданными коэффициенты теплоотдачи α1 и α2. Считаем, что длина трубы значительно превышает толщину стенки. Тогда потерями теплоты на концах трубы можно пренебречь.
Слайд 52Теплопередача через цилиндрическую стенку
Искомыми величинами будут: температуры на поверхности стенки и
Плотность теплового потока через стенку:
Слайд 53Тот же поток передается от второй стенки к холодной жидкости посредством
Или:
Суммируя уравнения, получим температурный напор:
Тогда:
Слайд 54Введем величину линейного коэффициента теплопередачи:
Линейное термическое сопротивление теплопередачи определяется по формуле:
Для
Слайд 55Для выбора рациональной толщины изоляции трубы рассмотрим влияние толщины изоляции на
Многослойная цилиндрическая стенка (труба с тепловой изоляцией)
Запишем уравнение для трубы с изоляцией:
два первых члена постоянны
Величина третьего члена
увеличивается при увеличении
а четвертый
–
Уменьшается при увеличении
Слайд 56Исследуем
как функцию
, для чего возьмем производную
по
и приравняем ее к
и критический внешний диаметр трубы с изоляцией
соответствующий минимальному сопротивлению теплопередачи, определяется из выражения:
Критическая толщина тепловой изоляции трубы
значение второй производной функции
по
будет минимальным. Таким образом, для эффективной работы изоляции должно быть выполнено условие:
Слайд 57Теплопроводность тел сложной формы
Пусть имеется полый шар с радиусами
Теплопроводность
постоянным коэффициентом теплопроводности
и с заданными температурами поверхностей
(граничные условия первого рода).
Поскольку в данном случае температура изменяется только в направлении радиуса шара, то уравнение теплопроводности запишем в сферических координатах с учетом осевой симметрии
:
Граничные условия:
Слайд 58Обозначим
тогда уравнение
или
Интегрируя, получаем:
или
или
Обозначим
тогда
или
Отсюда
или
Интегрируя второй раз, имеем:
или
или
или
Слайд 59Из граничных условий находим:
Тогда постоянные интегрирования:
Имея выражения для постоянных интегрирования, получаем
Используя закон Фурье, определим количество теплоты, проходящее через шаровую поверхность
в единицу времени:
Слайд 60Подставляя в это уравнение значение градиента температуры, получаем:
Для многослойной стенки:
При граничных
и
известны температуры окружающей среды
коэффициенты
Причем все вышеуказанные величины являются постоянными. Поскольку процесс стационарный, то тепловой поток определим следующим образом, переходя от радиусов к соответствующим диаметрам:
Слайд 61Отсюда следует, что тепловой поток:
коэффициент теплопередачи шаровой стенки.
термическое сопротивление шаровой стенки:
Слайд 62Анализируя выражение , можно сделать вывод, что, если значение
мало, то
При использовании метода оребрения необходимо иметь в виду следующее правило:
оребрять поверхность со стороны
до достижения равенства
Дальнейшее увеличение малоэффективно.
Ребра в поперечном сечении могут иметь разный профиль. Это может быть прямоугольник, треугольник, круг и т.д.
Рассмотрим задачу о теплопроводности в ребре постоянного поперечного сечения
Пусть
– площадь поперечного сечения ребра,
- его периметр. Ребро (стержень) находится в среде с
коэффициент теплоотдачи от поверхности к среде
.
Слайд 63Принимаем, что размеры поперечного сечения стержня существенно меньше его длины, поэтому
Введем избыточную температуру
– текущая температура стержня. Если известна температура основания стержня
то
На расстоянии
от основания выделим элемент стержня
Уравнение теплового баланса для выделенного элемент:
.
Перенос теплоты через стержень
Слайд 64Из закона Фурье:
Отсюда тепловой поток, отдаваемый элементом в окружающую среду:
Согласно закону
тогда
Приравнивая, получаем
или
постоянные, тогда и
Найдем решение уравнения в виде:
искомая постоянная.
Слайд 65Дифференцируя , получаем:
и
Подставляя в
имеем:
или
и
Общее решение будет иметь вид:
или
Для определения значений
и
рассмотрим ребро бесконечной длины.
В начальном сечении ребра при
При
Подставляя граничные условия в уравнение , имеем:
Это возможно только при
отсюда
и окончательно получаем:
Слайд 66Анализ формул показывает, что при оребрении необходимо выбирать материал с большим
Ребра , имеющие профиль с меньшими
более эффективны.
Определим количество теплоты, отданное стержнем в окружающую среду, которое равно количеству теплоты, проходящему через основание ребра:
Поскольку
получаем:
Для ребра конечной длины дифференциальное уравнение и его решение имеют вид
, но иными будут граничные условия:
при
при
или
- температура и коэффициент теплоотдачи с торца ребра.
Слайд 67Учитывая равенство количества теплоты, подведенного к торцу за счет теплопроводности и
при
при
совместно эти уравнения относительно
и
, получаем:
Подставляя эти выражения в , получаем:
Слайд 68После преобразований имеем:
Учитывая, что
– гиперболический косинус, а
- гиперболический синус, уравнение
Если
на конце ребра малая величина, а коэффициент
достаточно большой, то можно пренебречь теплоотдачей с конца ребра, чем практически всегда пользуются в инженерной практике. Тогда уравнение примет вид:
Слайд 69Определим градиент температуры:
где th(ml) – гиперболический тангенс.
Учитывая, что тепловой поток, отдаваемый
потоку, подводимому к основанию ребра :
То
Подставляя значение
, получаем:
Если длина ребра велика, то
, а
, тогда:
и
Рассмотрим тепловой поток через плоскую ребристую стенку безграничных размеров, причем стенка имеет оребрение со стороны меньшего коэффициента теплоотдачи (рис.). В данном случае тепловой поток будет не только через ребра, но и через стенку. Принимаем заданными значениями коэффициенты теплоотдачи на неоребренной поверхности
, гладкой части оребренной поверхности
и на поверхности ребер
, геометрические размеры ребер и температуры теплоносителей
и
Слайд 70Учитывая, что для ребра
, тогда периметр поперечного сечения ребра
,
Теплопередача через ребристую стенку
Подставив выражение для
В , умножив и разделив на
получим:
Число Био представляет собой отношение внутреннего термического сопротивления к внешнему сопротивлению теплоотдачи:
- безразмерный комплекс, число Био.
Слайд 71Окончательно уравнение для теплового потока с поверхности ребра можно представить в
Введем обозначение:
коэффициент эффективности ребра и изменяется от 0 до 1. Тогда
Тепловой поток с гладкой части оребренной поверхности
Oбщий тепловой поток:
или
– приведенный коэффициент теплоотдачи:
Слайд 72Система уравнений теплопередачи через ребристую стенку может быть записана в виде:
и
(
– толщина гладкой части оребренной стенки.
Решая их, получаем:
или
- коэффициент теплоотдачи для ребристой поверхности (Вт/К):
Слайд 73Для расчета теплового потока тел различной формы использованы термические сопротивления тела
Теплопроводность при наличии внутренних источников теплоты
Рассмотрим процессы теплопроводности, когда кроме внешних источников теплоты имеются и внутренние, распределенные по объему. Для строительства одним из подобных процессов является процесс затвердения бетона, что приводит к увеличению внутренних напряжений и в дальнейшем к образованию продольных трещин.
При стационарном процессе в однородной стенке с постоянными значениями коэффициентов
, температуры окружающей среды
и равномерным распределением температуры в стенке (рис.) дифференциальное уравнение теплопроводности можно записать в виде:
- мощность внутренних источников теплоты.
Для круглой трубы с наружным оребрением:
Слайд 74Теплопроводность плоской стенки при наличии внутренних источников теплоты
В этом случае
будет изменяться только вдоль оси
нормально поверхности тела, т.е. задача одномерная.
, направленной
Поскольку граничные условия на обеих поверхностях одинаковые, то температурное поле симметрично относительно плоскости
В этом случае рассматриваем только одну половину стенки и запишем для нее граничные условия:
при
Интегрируя уравнение , получаем:
Слайд 75Постоянные интегрирования определяются из граничных условий:
Таким образом, уравнение для температурного поля
Зависимость
от
квадратичная, т.е. распределение температуры соответствует
параболическому закону. Если
, то
и полученное уравнение представляет температурное поле для граничных условий первого рода. Отсюда следует:
Температура в центре стенки
Плотность теплового потока изменяется только вдоль оси
, т.е.
При
а при
плотность теплового потока будет максимальная
Слайд 76Рассмотрим процесс теплопроводности в круглом сплошном стержне - цилиндре (рис.). Радиус
Теплопроводность цилиндра при наличии внутренних источников теплоты
Примем равномерное распределение внутренних источников теплоты,
и
. При этом температура
будет везде одинаковой, т.е. задача также будет одномерной. Запишем уравнение теплопроводности в цилиндрических координатах:
Граничные условия:
при
Произведем замену переменной
и проинтегрируем уравнение (1)
(1)
Слайд 77Учитывая, что величины в знаменателе не равны 0, то получим однородное
или
или
Тогда:
Из граничных условий:
Окончательно уравнение температурного поля любой точки сплошного цилиндрического тела примет вид:
При
и соответственно
условиям первого рода. При этом на внешней поверхности цилиндра имеет место максимальная плотность теплового потока
.
получаем решение, отвечающее граничным
Слайд 78Рассмотрим стационарный процесс
теплопроводности полого цилиндра (трубы) с внутренним радиусом
наружным
Внутри стенки цилиндра имеются равномерно распределенные источники теплоты мощностью
(рис.)
а) б) в)
К расчету теплопроводности цилиндрической стенки при наличии внутренних источников теплоты
Возможны три случая:
1. Теплота отводится только через наружную поверхность трубы (рис.а);
2. Теплота отводится только через внутреннюю поверхность трубы (рис.б);
3. Теплота отводится только через наружную и внутреннюю поверхность трубы (рис.в).
Слайд 79Температура в этом случае изменяется только в направлении радиуса (одномерная задача)
Для первого случая считаем, что заданы граничные условия третьего рода, т.е.
и
со стороны наружной поверхности трубы.
Решение этого уравнения было записано ранее
Постоянные интегрирования:
При
Тогда из уравнения
При
или
Слайд 80При
Т.к.
, то
и окончательно:
Приравнивая , получаем уравнение относительно
получим
Температура на наружной поверхности трубы
Слайд 81Плотность теплового потока на этой поверхности:
Температуру на внутренней поверхности трубы находим
Температурный перепад в стенке определяется по формуле:
Слайд 82Для второго случая граничные условия при
и
имеют вид:
при
После
Общий температурный перепад в стенке получаем в виде:
Слайд 83Для третьего случая очевидно, что внутри стенки должен существовать максимум температуры.
и
Для решения этой задачи можно использовать результаты двух предыдущих случаев. перепады температур в наружном и внутреннем слоях:
получаем перепад температур между стенками:
Слайд 84Для определения координаты изотермической поверхности с
уравнение решаем относительно
:
Значение
. В случае, если
Если
и
неизвестны, а известны
,
,
и
, то для определения
требуется совместное решение уравнений:
где





















![Выражение называется коэффициентом температуропроводностиКоэффициент температуропроводности а [м2/с] – физическая характеристика данного вещества, которая играет существенную](/img/tmb/3/203521/e37bc8ed35498ce9e8b5527c810281ce-800x.jpg)