свободы
Курбацкий Евгений Николаевич
профессор кафедры “Мосты и тоннели”,
д.т.н.
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Вынужденные колебания системы с одной степенью свободы презентация
Содержание
- 1. Вынужденные колебания системы с одной степенью свободы
- 2. Вынужденные гармонические колебания системы с одной степенью
- 3. Принятые обозначения
- 4. Некоторые сведения из краткого курса математического анализа
- 5. Общее решение однородного и неоднородного дифференциального уравнения
- 6. Определение констант А и В однородного дифференциального
- 7. Определение констант С и D решения неоднородного
- 8. Для определение констант С и D приравняем
- 9. Общее решение дифференциального уравнения колебаний системы
- 10. Колебания с частотой вынуждающей силы
- 11. Вынужденные колебания системы с одной степенью свободы
- 12. Вынужденные колебания системы с одной степенью свободы
- 13. Вынужденные колебания системы с одной степенью свободы
- 14. Зависимость амплитуд вынужденных колебаний от отношения частоты собственных колебаний к частоте вынуждающей силы
- 15. Заключение При частоте
- 16. Реакция системы с одной степенью свободы на импульс
- 17. Дифференциальное уравнение системы при импульсивном воздействии можно
- 18. Реакция системы с одной степенью свободы на
- 19. Реакция системы с одной степенью свободы на
- 20. Если на массу в момент времени
- 21. При таких начальных условиях уравнение
- 22. При действии произвольной силы необходимо проинтегрировать
- 23. Некоторые начальные сведения теории интегрального преобразования Фурье
- 24. Некоторые начальные сведения теории преобразования Фурье (продолжение)
- 25. Некоторые начальные сведения теории преобразования Фурье (продолжение)
- 26. Пример использования преобразования Фурье Дифференциальное уравнение
- 27. Пример использования преобразования Фурье (продолжение)
- 28. Для определения функции
- 29. Сдвиг во времени Воздействие на разные
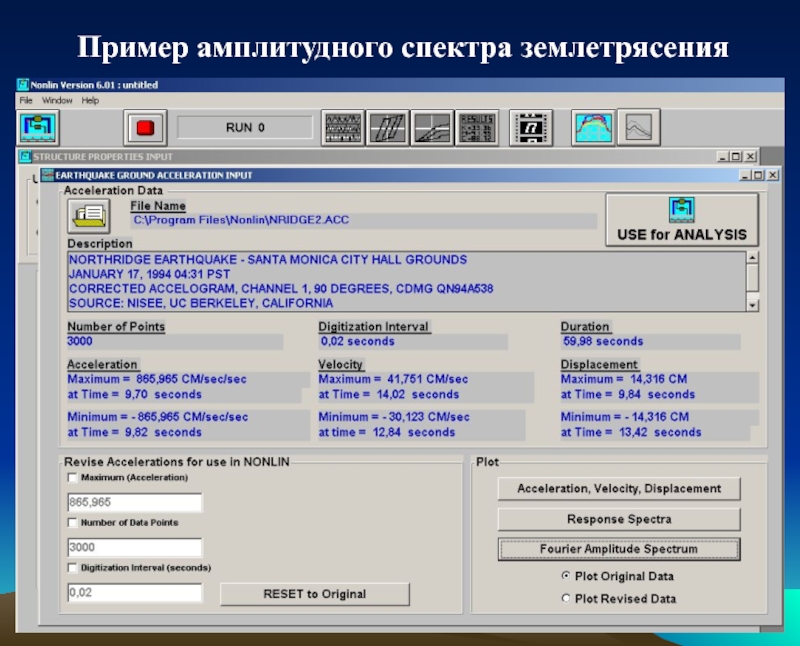
- 30. Пример амплитудного спектра землетрясения
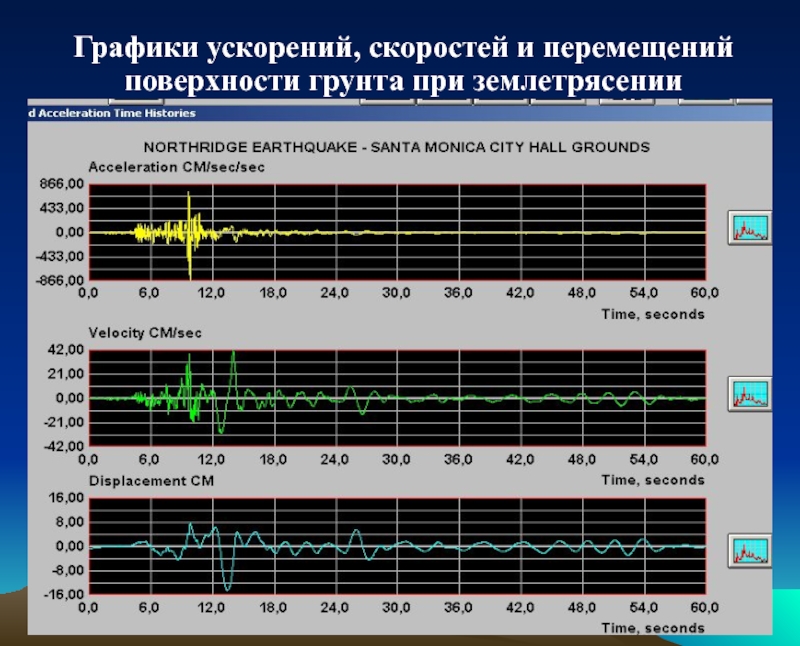
- 31. Графики ускорений, скоростей и перемещений поверхности грунта при землетрясении
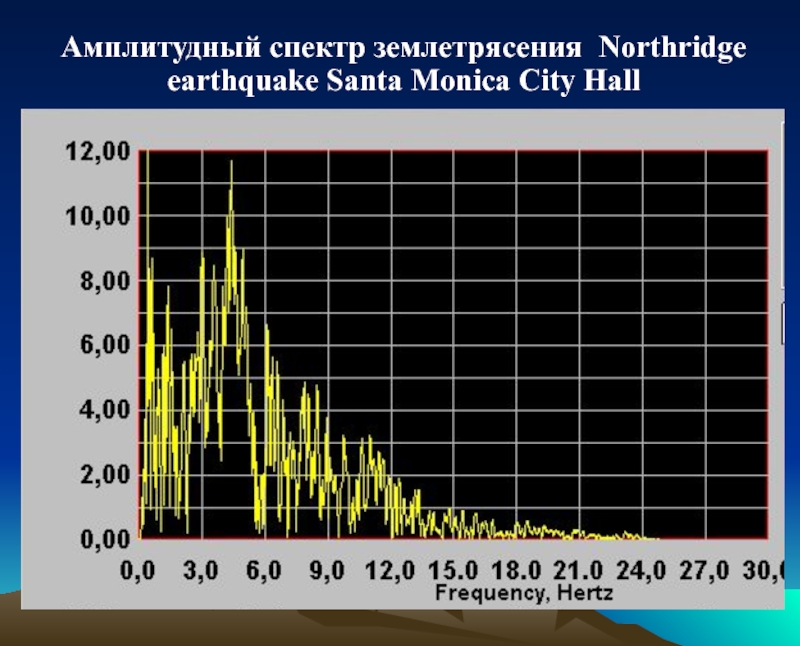
- 32. Амплитудный спектр землетрясения Northridge earthquake Santa Monica City Hall
- 33. СВОБОДНЫЕ КОЛЕБАНИЯ
- 34. Исходные данные
- 35. Исходные данные
- 36. Исходные данные
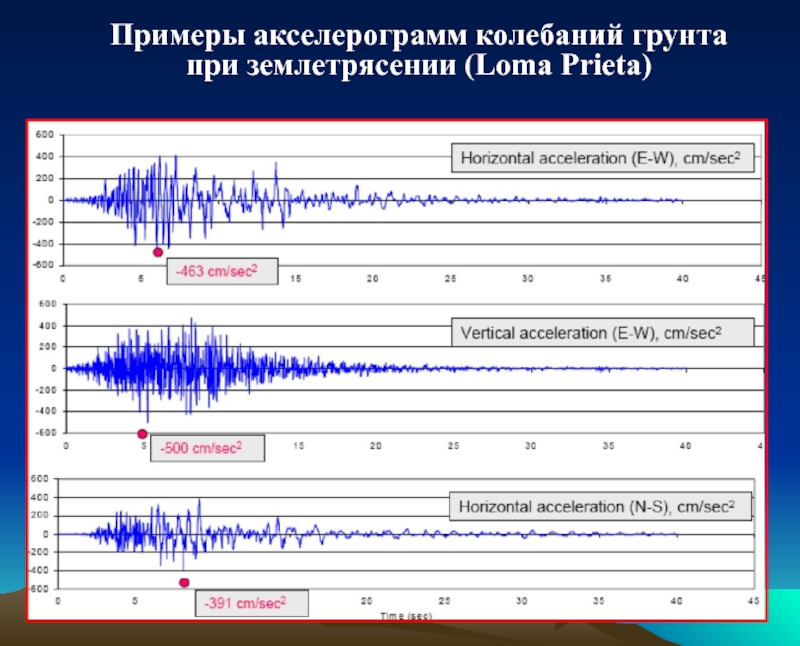
- 37. Примеры акселерограмм колебаний грунта при землетрясении (Loma Prieta)
Вынужденные гармонические колебания системы с одной степенью свободы с учётом вязкого демпфирования
Слайд 1
Московский государственный университет путей сообщения
Вынужденные колебания системы с одной степенью
Слайд 2Вынужденные гармонические колебания системы с одной степенью свободы с учётом вязкого
демпфирования
Слайд 4Некоторые сведения из краткого курса математического анализа
Общее
решение уравнения с правой частью (1) можно составить как сумму общего решения соответствующего уравнению без правой части (2) и какого либо частного решения данного уравнения (1)
Слайд 7Определение констант С и D решения неоднородного дифференциального уравнения
Подставив (а)
в (b), получим
Слайд 8Для определение констант С и D приравняем коэффициенты левой и правой
части уравнения при одинаковых тригонометрических функциях
Получим систему уравнений:
Получим систему уравнений:
Слайд 9Общее решение дифференциального уравнения колебаний системы с одной степенью свободы
при гармоническом воздействии с учётом сил сопротивления пропорциональных скорости
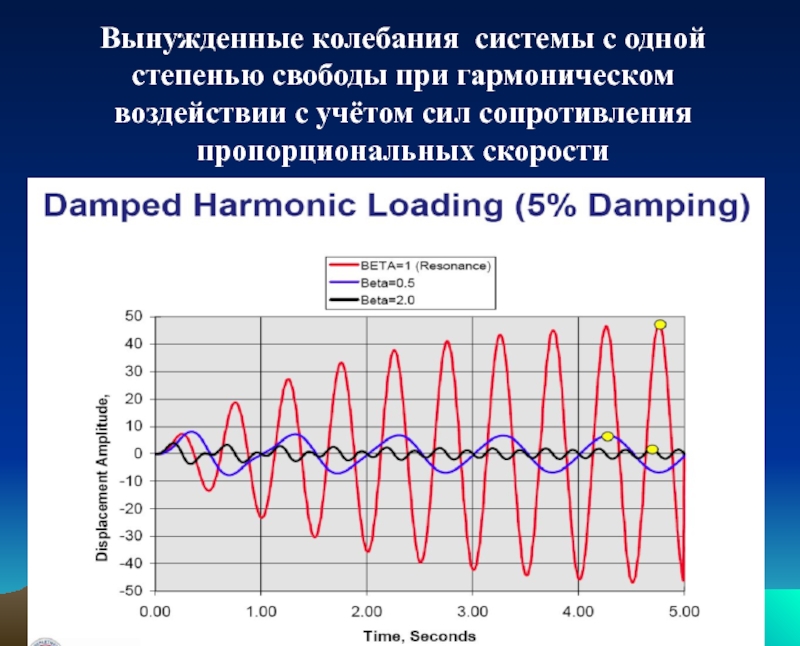
Слайд 11Вынужденные колебания системы с одной степенью свободы при гармоническом воздействии с
учётом сил сопротивления пропорциональных скорости
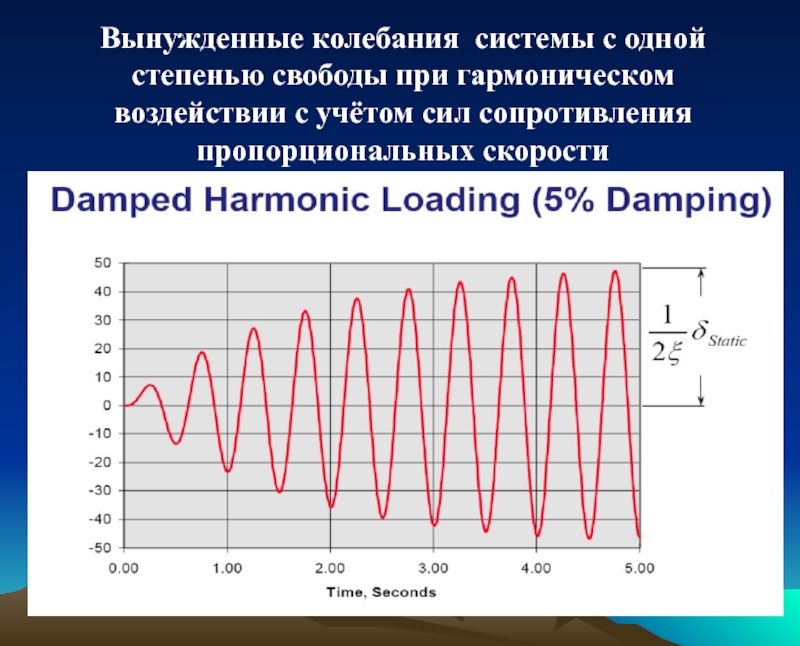
Слайд 12Вынужденные колебания системы с одной степенью свободы при гармоническом воздействии с
учётом сил сопротивления пропорциональных скорости
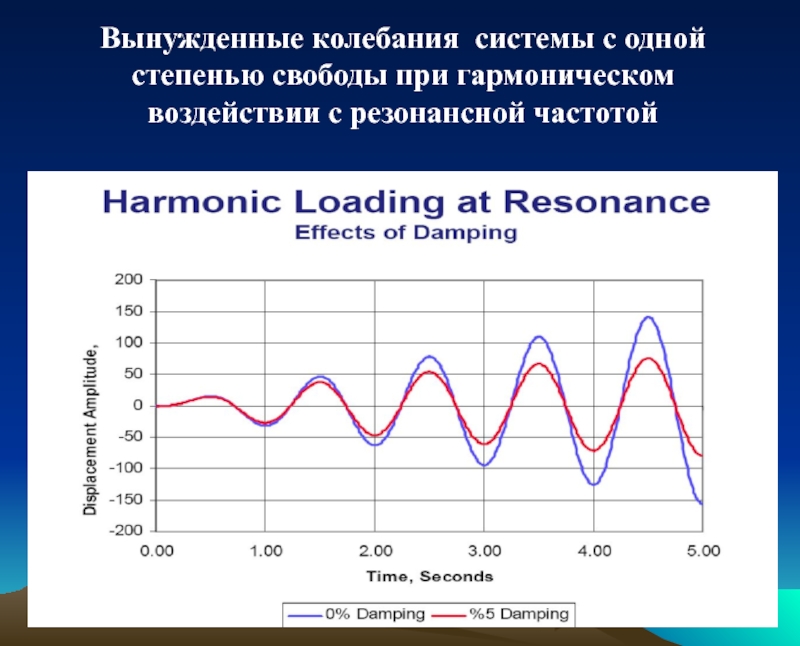
Слайд 13Вынужденные колебания системы с одной степенью свободы при гармоническом воздействии с
резонансной частотой
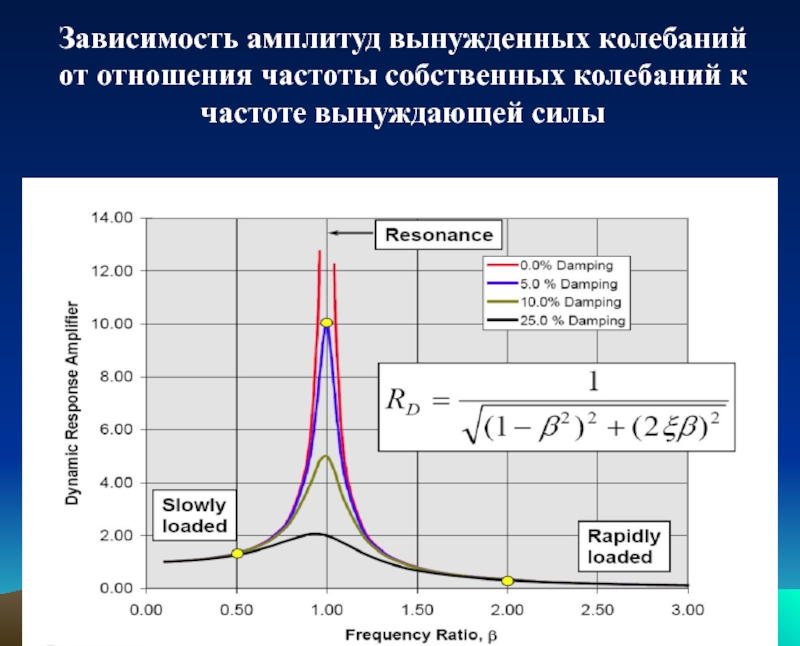
Слайд 14Зависимость амплитуд вынужденных колебаний от отношения частоты собственных колебаний к частоте
вынуждающей силы
Слайд 15Заключение
При частоте возмущающей силы близкой к собственной
частоте амплитуды вынужденных колебаний возрастают и превышают статические.
Такое явление называется резонансом.
В системах с малым коэффициентом демпфирования амплитуды при резонансах могут достигать больших значений.
Демпфируемые системы при резонансе имеют ограниченные амплитуды:
Такое явление называется резонансом.
В системах с малым коэффициентом демпфирования амплитуды при резонансах могут достигать больших значений.
Демпфируемые системы при резонансе имеют ограниченные амплитуды:
Слайд 17Дифференциальное уравнение системы при импульсивном воздействии можно записать, используя обобщённые функции
Слайд 18Реакция системы с одной степенью свободы на произвольное воздействие
Для определения
решения произвольная сила рассматривается как последовательность импуль-сов бесконечно малой продолжительности.
Слайд 19Реакция системы с одной степенью свободы на единичный импульс
Рассмотрим силу,
действующую в момент времени в течении малого интервала времени
При величина силы становится бесконечно большой но интеграл по времени остаётся равным единице. Такую силу называют единичным импульсом.
Смещённая дельта функция Дирака
При величина силы становится бесконечно большой но интеграл по времени остаётся равным единице. Такую силу называют единичным импульсом.
Смещённая дельта функция Дирака
Слайд 20
Если на массу в момент времени в
течении бесконечно малого интервала времени
действует единичный импульс, масса приобретает начальную скорость , определяемую
выражением
При этом ни пружина, ни демпфер не успевают среагировать. Поэтому в момент времени
Можно сформулировать следующие начальные условия:
действует единичный импульс, масса приобретает начальную скорость , определяемую
выражением
При этом ни пружина, ни демпфер не успевают среагировать. Поэтому в момент времени
Можно сформулировать следующие начальные условия:
Слайд 21
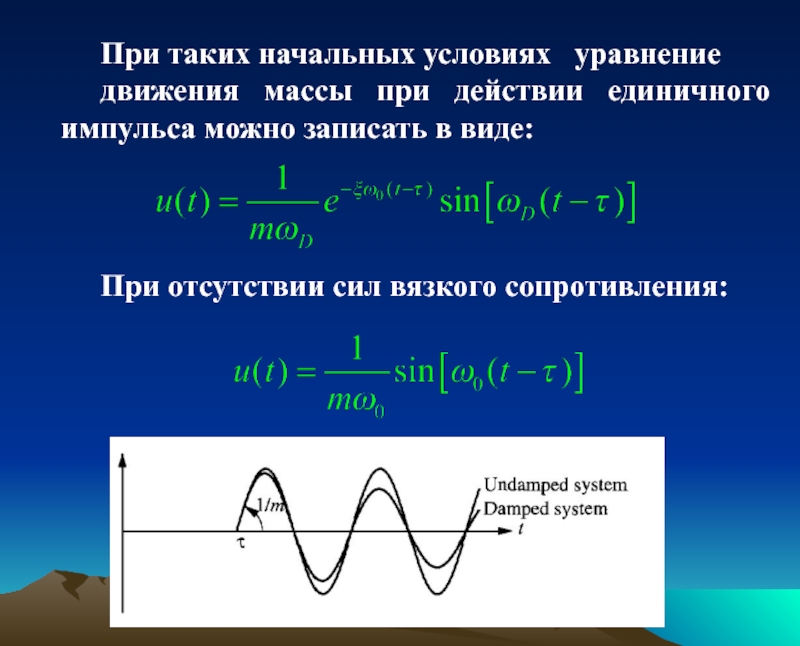
При таких начальных условиях уравнение
движения массы при действии единичного
импульса можно записать в виде:
При отсутствии сил вязкого сопротивления:
При отсутствии сил вязкого сопротивления:
Слайд 22
При действии произвольной силы необходимо проинтегрировать реакции от единичных импуль-сов, увеличенных
на значения силы. Интеграл Дюамеля
При отсутствии сил вязкого сопротивления:
При отсутствии сил вязкого сопротивления:
Слайд 23Некоторые начальные сведения теории интегрального преобразования Фурье
Преобразованием Фурье функции
называется интеграл, определяемый
выражением
При решении динамических задач преобразование Фурье или интеграл Фурье является одним из основных математических аппаратов
Слайд 24Некоторые начальные сведения теории преобразования Фурье (продолжение)
Если функция
является преобразованием
(изображением ) Фурье функции тогда
изображение Фурье производной этой функции по
времени определится выражением:
второй производной выражением:
(изображением ) Фурье функции тогда
изображение Фурье производной этой функции по
времени определится выражением:
второй производной выражением:
Слайд 25Некоторые начальные сведения теории преобразования Фурье (продолжение)
Таким образом
дифференцированию функции во временной области соответствует умножению функции на множитель
Слайд 26Пример использования преобразования Фурье
Дифференциальное уравнение колебаний системы с одной степенью свободы
при сейсмическом воздействии имеет вид
Применим преобразование Фурье к обеим частям уравнения обозначив изображение Фурье неизвестной функции . Получим
Применим преобразование Фурье к обеим частям уравнения обозначив изображение Фурье неизвестной функции . Получим
Слайд 27Пример использования преобразования Фурье (продолжение)
Выполнив необходимые преобразования, получим изображение Фурье искомой
функции
Слайд 28Для определения функции необходимо выполнить обратное
преобразования Фурье
Обратное преобразования Фурье можно получить, используя стандартную программу быстрого преобразования Фурье FFT, или получить аналитическое выражение, используя различные методы интегрирования
Слайд 29Сдвиг во времени
Воздействие на разные опоры сооружения может отличаться во времени
из за более позднего прихода сейсмических волн
Преобразование Фурье позволяет довольно просто учитывать это явление. Так как сдвигу функции во временной области соответствует умножение на экспоненту в области изображений.
Преобразование Фурье позволяет довольно просто учитывать это явление. Так как сдвигу функции во временной области соответствует умножение на экспоненту в области изображений.
