- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Вычисление скорости точки при вращении тела. (Лекция 2) презентация
Содержание
- 1. Вычисление скорости точки при вращении тела. (Лекция 2)
- 2. Вычисление скорости точки при вращении тела.
- 3. 2.3. Плоскопараллельное движение твердого тела Определение.
- 4. Теорема. Любое перемещение плоской фигуры можно заменить
- 5. Скорость точки плоской фигуры через скорость полюса.
- 6. Мгновенный центр скоростей. Способы его нахождения.
- 7. 3. Сложное движение МТ Основные понятия и
- 8. Определение. Движение точки относительно подвижной системы отсчета
- 9. Абсолютная скорость и абсолютное ускорение точки. Определение.
- 10. 4. Ускорение Кориолиса. Правило Жуковского. Определение. Ускорение
- 11. Правило Жуковского. 1. Строим плоскость, перпендикулярную вектору
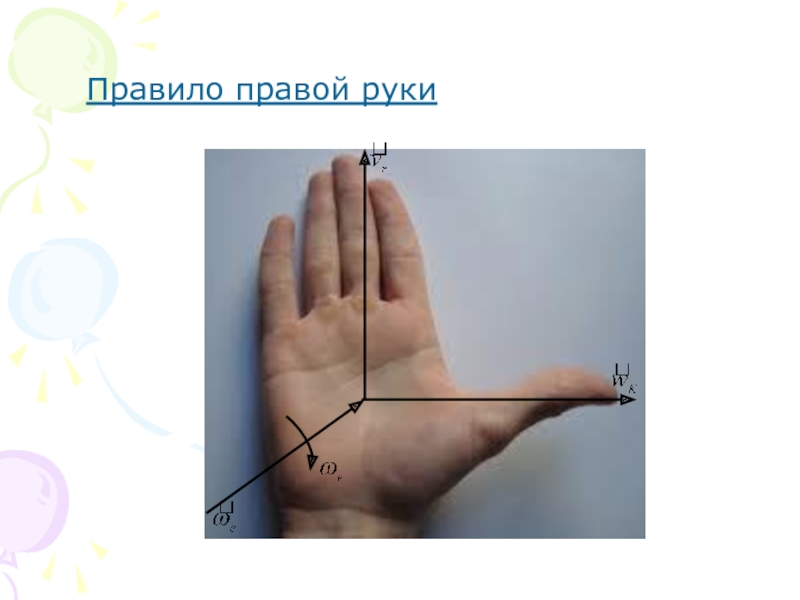
- 12. Правило правой руки
- 13. Кинетика Изучает движение тел с учетом причин, вызвавших это движение
- 14. 1. Динамика материальной точки 1.1. Основные аксиомы
- 15. 2. Основной закон динамики.
- 16. 3. Аксиома действия и противодействия.
- 17. Аксиома независимости действия сил. Результат
- 18. 5. Аксиома связи. Определение. Связью называют
- 19. Все задачи на динамику МТ делятся на
- 20. 1.2. Движение точки по гладкой поверхности Определение.
- 21. Определение. Поверхность называется шероховатой, если реакция поверхности
- 22. 2. Теория моментов 2.1. Алгебраический момент силы
- 24. Свойства: От переноса силы вдоль линии действия
Слайд 2Вычисление скорости точки при вращении тела.
Тогда скорость:
Ускорение:
Нормальное ускорение направлено по кратчайшему расстоянию к оси вращения.
Тогда полное ускорение: .
Угол - угол между полным ускорением и перпендикуляром, опущенным на ось вращения:
Слайд 32.3. Плоскопараллельное движение твердого тела
Определение. Движение твердого тела, при котором
Слайд 4Теорема. Любое перемещение плоской фигуры можно заменить совокупностью 2 движений:
2) вращательное движение относительно полюса.
Характеристики плоскопараллельного движения:
При этом третье уравнение не зависит от выбора полюса.
Угловая скорость и ускорение определяется также, как и при вращательном движении, за исключением того, что вектор имеет начало в точке, являющейся полюсом.
Слайд 5Скорость точки плоской фигуры через скорость полюса.
Пусть т. А - полюс,
где и
Слайд 6Мгновенный центр скоростей. Способы его нахождения.
Определение. Точка плоской фигуры, скорость которой
Для любого тела, совершающего плоское движение справедлива формула:
Способы нахождения МЦС.
Слайд 73. Сложное движение МТ
Основные понятия и определения.
Определение. Движение точки, при котором
Определение. Движение точки
относительно неподвижной
системы отсчета называется
абсолютным ( ).
Слайд 8Определение. Движение точки относительно подвижной системы отсчета называется относительным (
Определение. Движение подвижной системы отсчета относительно неподвижной называется переносным ( ) и обозначается индексом (entraner (лат) – увлекать за собой).
Слайд 9Абсолютная скорость и абсолютное ускорение точки.
Определение. Абсолютной скоростью (ускорением) т. М,
Скорость:
Теорема Кориолиса. Абсолютное ускорение точки складывается из относительного, переносного ускорения, а также ускорения Кориолиса:
Слайд 104. Ускорение Кориолиса. Правило Жуковского.
Определение. Ускорение Кориолиса – это вектор, равный
Длина вектора определяется по формуле:
Слайд 11Правило Жуковского.
1. Строим плоскость, перпендикулярную вектору угловой скорости:
2. Проецируем на эту плоскость вектор относительной плоскости: .
3. Поворачиваем полученный вектор на угол 90 градусов в сторону вращения угловой скорости:
.
4. Полученный вектор восстанавливаем при помощи параллельного переноса до точки М. Получим вектор ускорения Кориолиса:
Слайд 141. Динамика материальной точки
1.1. Основные аксиомы динамики.
1. Аксиома инерции.
Существуют такие инерциальные
Слайд 152. Основной закон динамики.
Ускорение любой свободной МТ прямо пропорционально действующей силе
Слайд 163. Аксиома действия и противодействия.
Сила действия 1-ой МТ на вторую вызывает
Слайд 17Аксиома независимости действия сил.
Результат действия некоторой системы сил на МТ не
Слайд 185. Аксиома связи.
Определение. Связью называют тело, ограничивающее свободу перемещения заданного тела.
Любую связь можно отбросить, заменив ее действие силой, которую называют реакцией связи.
Слайд 19Все задачи на динамику МТ делятся на два типа:
Первая задача динамики
Вторая задача динамики (обратная). По заданной массе и силе определить кинематические характеристики, если заданы начальные условия.
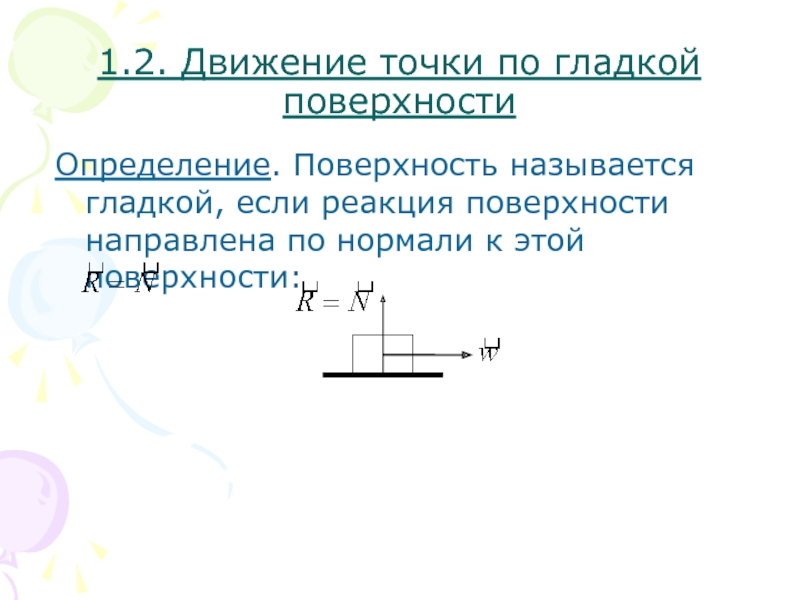
Слайд 201.2. Движение точки по гладкой поверхности
Определение. Поверхность называется гладкой, если реакция
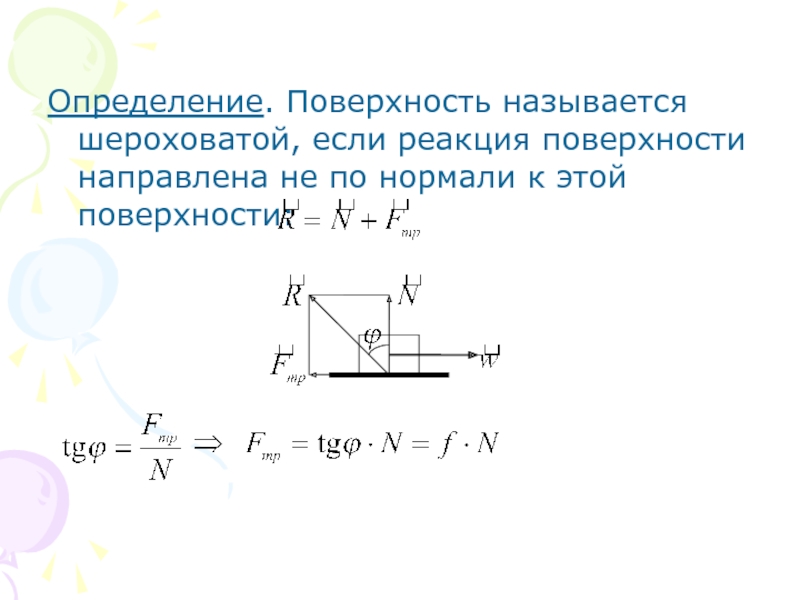
Слайд 21Определение. Поверхность называется шероховатой, если реакция поверхности направлена не по нормали
Слайд 222. Теория моментов
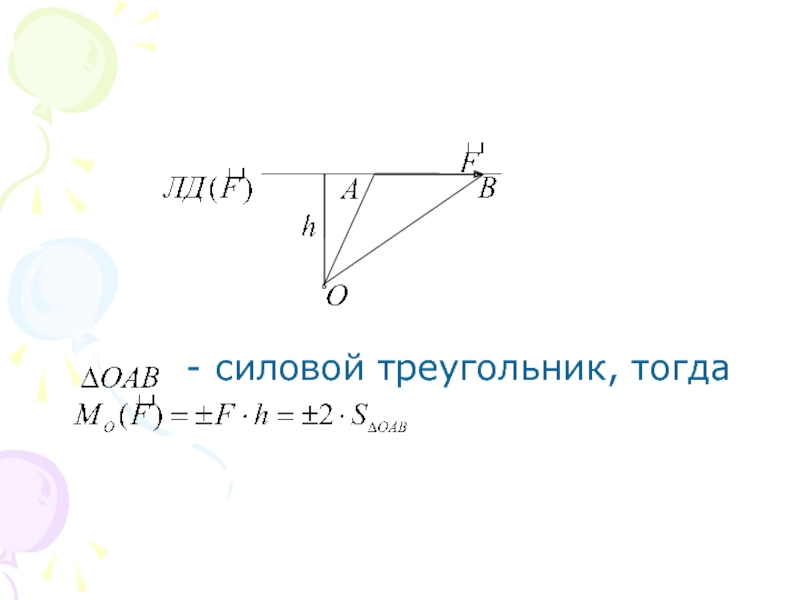
2.1. Алгебраический момент силы относительно точки.
Определение. Алгебраическим моментом силы
, где плечо – кратчайшее расстояние от моментной точки до линии действия силы
Слайд 24Свойства:
От переноса силы вдоль линии действия алгебраический момент не меняется.
Если моментная
.
.