- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Введение в физику. (Лекция 1) презентация
Содержание
- 1. Введение в физику. (Лекция 1)
- 2. Лекции по физике Лектор – Леонид Константинович
- 3. Катунь-Еландинский порог
- 4. Лекции по физике Программа Курса в
- 5. Лекции по физике Формы проверки знаний Одно
- 6. Литература - учебники Л.А. Лукьянчиков. Механика. Молекулярная
- 7. Литература - задачники Задачи по общей физике
- 8. Линия старта
- 9. Лекция 1. Введение Слово «физика» (φύσις )
- 10. Физика и математика Математика предоставляет аппарат, с
- 11. Физика и геология Проблемы геологии, теснейшим образом
- 12. Необходимая математика-Дифференцирование Определение производной Геометрический
- 13. Необходимая математика-Дифференцирование Правила Дифференцирования
- 14. Необходимая математика-Дифференцирование Примеры производных
- 15. Необходимая математика-Интегрирование Определение интеграла
- 16. Необходимая математика-Интегрирование Вычисление определенного интеграла Таблица неопределенных интегралов
- 17. Необходимая математика-Вектора Сложение векторов r3
- 18. Необходимая математика-Вектора Для векторов создана векторная алгебра.
- 19. Необходимая математика-Вектора Направление векторного произведения – правило правой руки
- 20. Механика как раздел физики Механика есть наука о движении и равновесии тел и частиц.
- 21. Исаак Ньютон – основоположник механики Принципы классической
- 22. Ограничения классической механики Законы классической механики могут
- 23. Кинематика Кинема́тика - раздел механики, изучающий математическое
- 24. Свойства пространства Пространство однородно. Все точки в нем равноправны
- 25. Свойства пространства Пространство изотропно. Все направления в нем равноправны
- 26. Свойства пространства Пространство Евклидово. Параллельные прямые не пересекаются, сумма углов всегда треугольника равна π
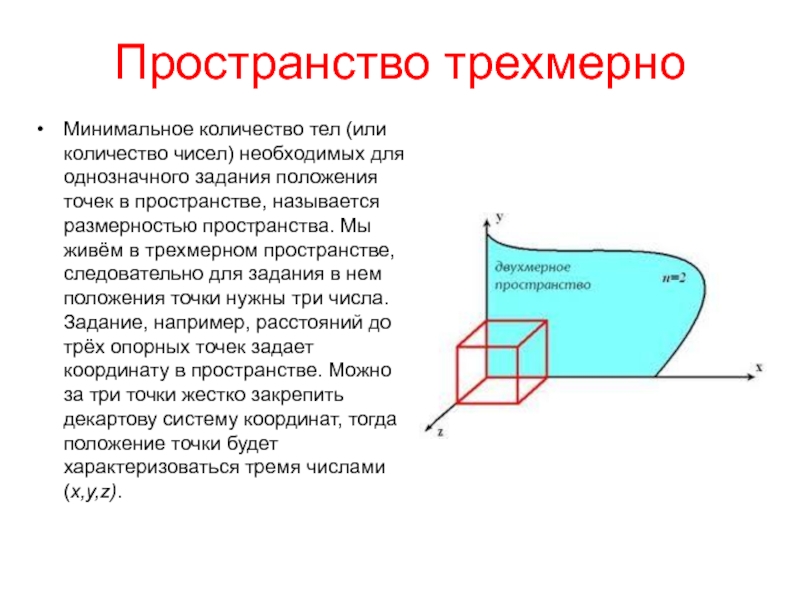
- 27. Пространство трехмерно Минимальное количество тел (или количество
- 28. Экспериментальная геометрия В 19 веке Гаусс и
- 29. Свойства Времени Во всем пространстве можно ввести единое время, текущее равномерно и одинаково
- 30. Эталоны времени и длины Секунда – 1/86164
- 31. Система отсчета Система координат, снабженная часами, называется
- 32. Системы координат- декартова и полярная Переход от
- 33. Сферическая система координат Положение точки задается радиусом
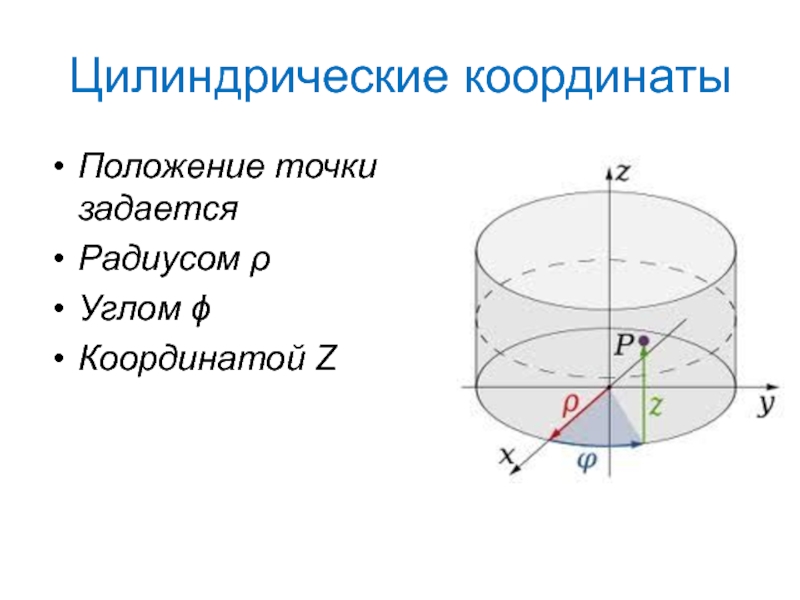
- 34. Цилиндрические координаты Положение точки задается Радиусом ρ Углом ϕ Координатой Z
- 35. Скорость и ускорение Средняя скорость за время
- 36. Примеры расчета скорости и ускорения
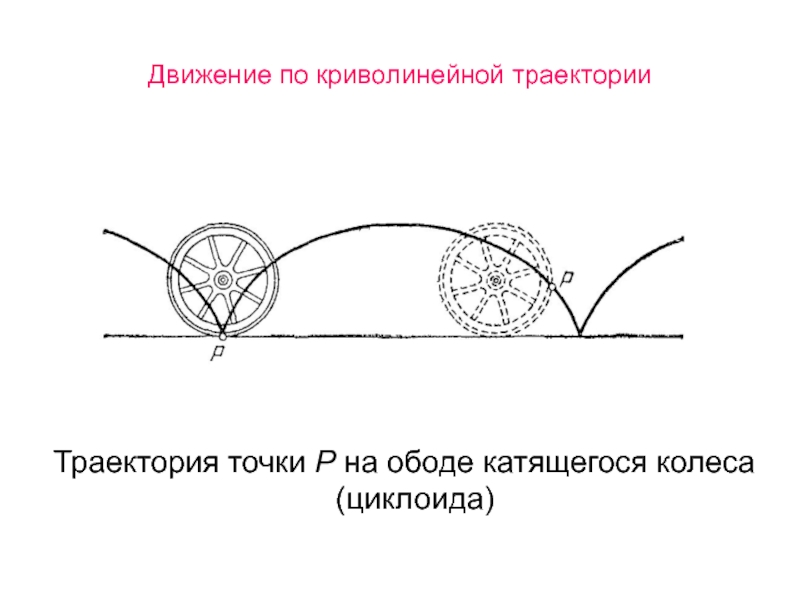
- 37. Движение по криволинейной траектории Траекторией Материальной
- 38. Движение по криволинейной траектории Траектория точки Р на ободе катящегося колеса (циклоида)
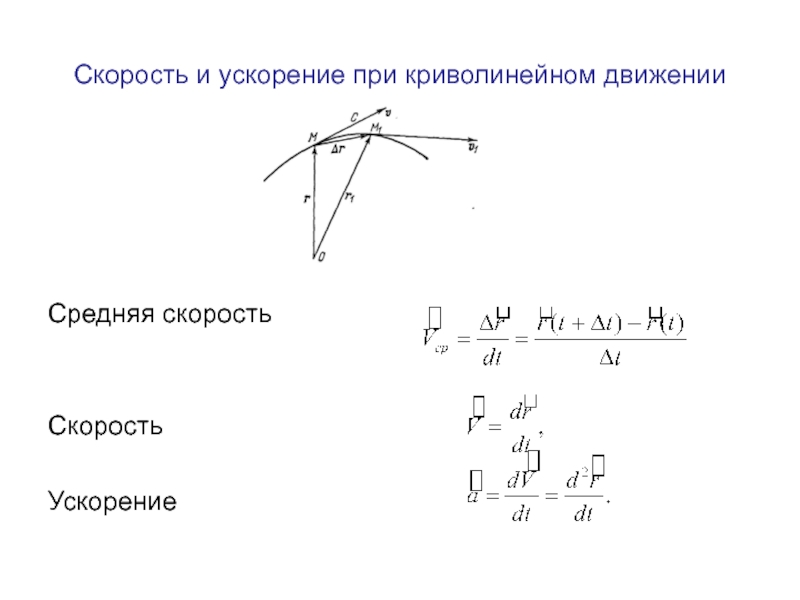
- 39. Скорость и ускорение при криволинейном движении Средняя скорость Скорость Ускорение
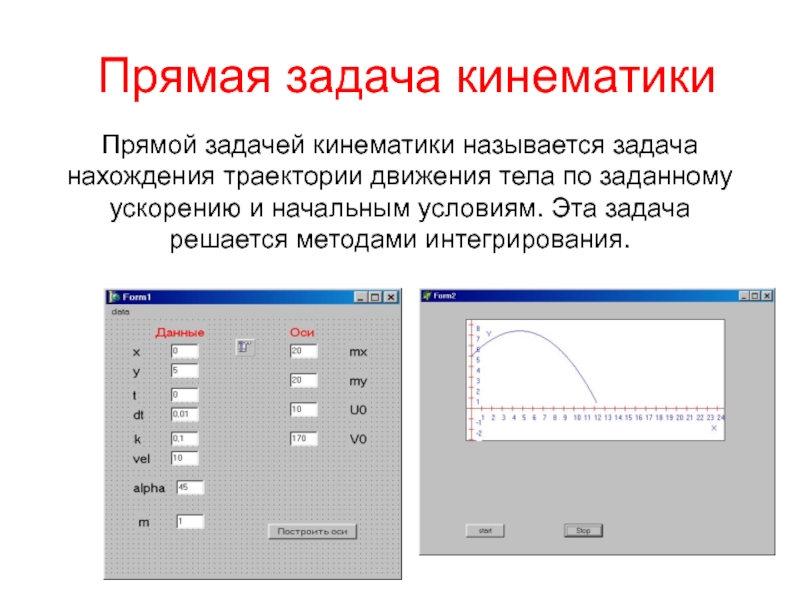
- 40. Прямая задача кинематики Прямой задачей кинематики
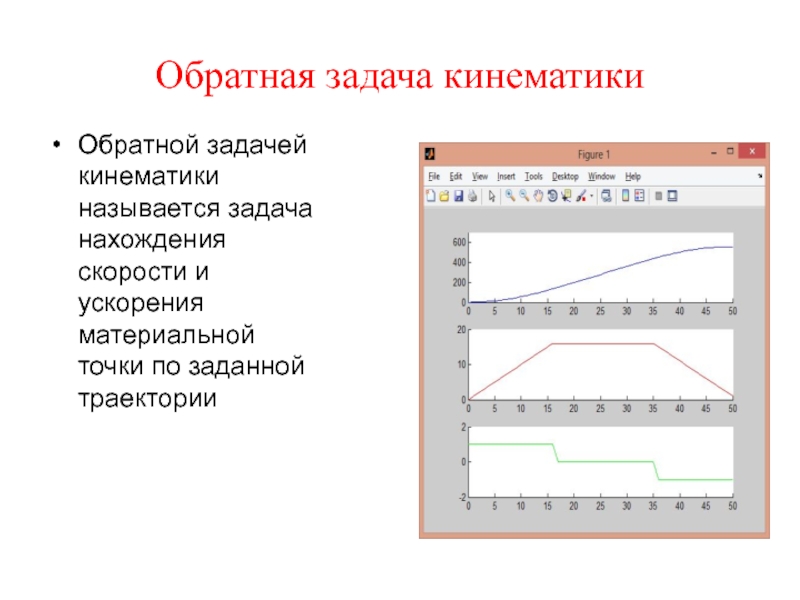
- 41. Обратная задача кинематики Обратной задачей кинематики называется
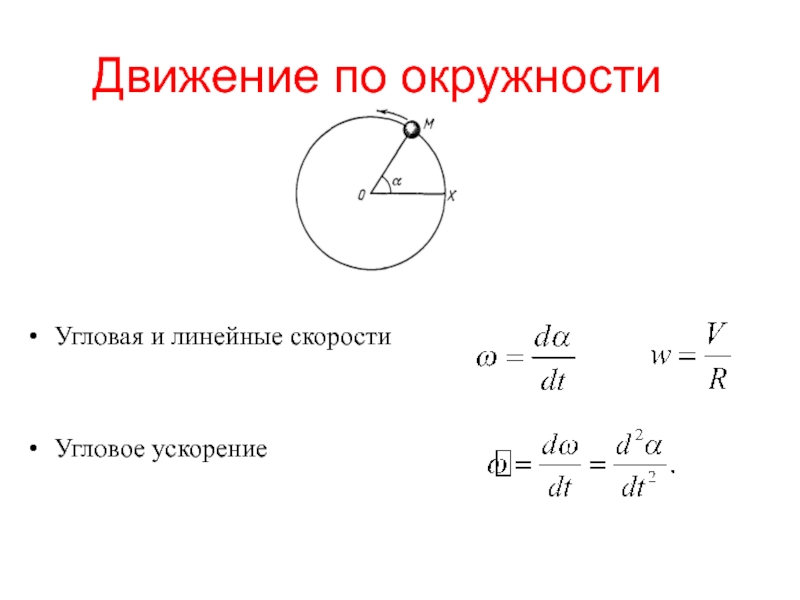
- 42. Движение по окружности Угловая и линейные скорости Угловое ускорение
- 43. Движение по окружности – декартовы координаты Ускорение при равномерном движении направлено к центру окружности.
- 44. Движение по окружности – полярные координаты
- 45. Тангенциальное и нормальное ускорения при движении по
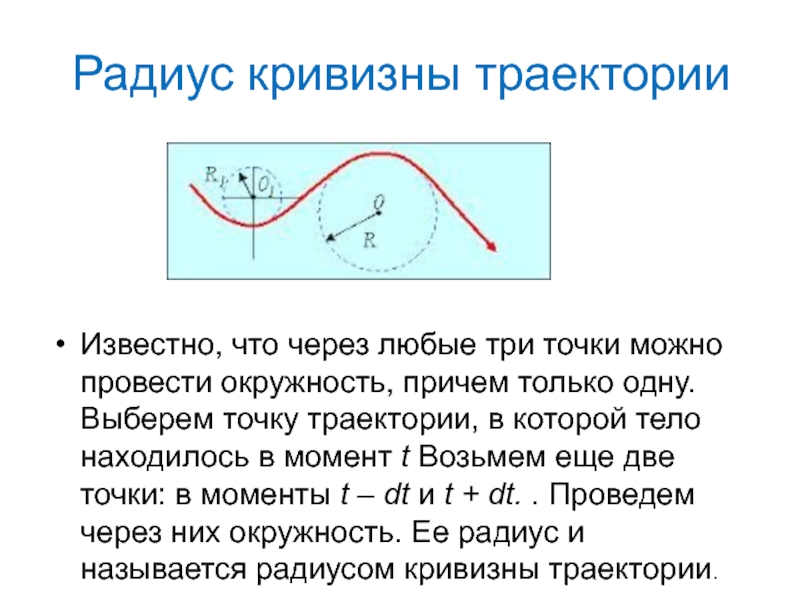
- 46. Радиус кривизны траектории Известно, что через любые
- 47. Радиус кривизны траектории
- 48. Радиус кривизны траектории
- 49. Пример: тело брошенное горизонтально
- 50. Пример: тело брошенное горизонтально
- 51. До встречи через неделю! Республика Алтай. Катунь. Ильгуменский порог.
Лекции по физике Лектор – Леонид Константинович Попов Электронный адрес: lkpopov@ngs.ru Расписание: Аудитории 3113, 2120 Четверг - 9-00, Пятница (знаменатель)- 12-40 Семинары: 3 семинара в 2 недели
Слайд 2Лекции по физике
Лектор – Леонид Константинович Попов
Электронный адрес: lkpopov@ngs.ru
Расписание: Аудитории 3113,
2120
Четверг - 9-00,
Пятница (знаменатель)- 12-40
Семинары: 3 семинара в 2 недели
Четверг - 9-00,
Пятница (знаменатель)- 12-40
Семинары: 3 семинара в 2 недели
Слайд 4Лекции по физике
Программа Курса в текущем семестре:
Основы классической механики –
12
лекций –февраль-март.
2. Термодинамика и молекулярная физика –
12 лекций апрель-май.
2. Термодинамика и молекулярная физика –
12 лекций апрель-май.
Слайд 5Лекции по физике
Формы проверки знаний
Одно семестровое задание, состоящее из двух частей.
Две
контрольных работы.
Экзамен.
Экзамен.
Слайд 6Литература - учебники
Л.А. Лукьянчиков. Механика. Молекулярная физика. НГУ, 2007 г.
Д.В. Сивухин.
Курс общей физики. Т. 1. Механика. М., «Наука» 1989 г.
Д.В. Сивухин. Курс общей физики. Т. 2. Термодинамика и молекулярная физика. 1990 г.
И.Е. Иродов. Механика. Основные законы. М. Высшая школа. 1985 г.
Д.В. Сивухин. Курс общей физики. Т. 2. Термодинамика и молекулярная физика. 1990 г.
И.Е. Иродов. Механика. Основные законы. М. Высшая школа. 1985 г.
Слайд 7Литература - задачники
Задачи по общей физике для геологов. НГУ 2000 г.
С.П.
Стрелков, Д.В. Сивухин, В.А. Угаров, И.А. Яковлев. Сборник задач по общему курсу физики. М. 1977 г.
Д.В.Сивухин. Сборник задач по общему курсу физики. Термодинамика и молекулярная физика. М., «Наука» 1976 г.
И.Е. Иродов. Задачи по общей физике. М., «Наука» 1979 г.
В.С. Волькенштейн. Сборник задач по общему курсу физики. М., «Наука» 1985 г.
Д.В.Сивухин. Сборник задач по общему курсу физики. Термодинамика и молекулярная физика. М., «Наука» 1976 г.
И.Е. Иродов. Задачи по общей физике. М., «Наука» 1979 г.
В.С. Волькенштейн. Сборник задач по общему курсу физики. М., «Наука» 1985 г.
Слайд 9Лекция 1. Введение
Слово «физика» (φύσις ) в греческом языке означает «природа».
Этот термин впервые ввел Аристотель (384-322 гг. до н.э). Его учение пользовалось незыблемым авторитетом более 1500 лет.
Предметом физики и является материяПредметом физики и является материя (в виде веществаПредметом физики и является материя (в виде вещества и полейПредметом физики и является материя (в виде вещества и полей) и наиболее общие формы её движения, а также фундаментальные взаимодействия, управляющие движением материи.
Предметом физики и является материяПредметом физики и является материя (в виде веществаПредметом физики и является материя (в виде вещества и полейПредметом физики и является материя (в виде вещества и полей) и наиболее общие формы её движения, а также фундаментальные взаимодействия, управляющие движением материи.
Слайд 10Физика и математика
Математика предоставляет аппарат, с помощью которого физические законы могут
быть точно сформулированы.
Физические теории почти всегда формулируются в виде математических выражений.
Развитие математики стимулировалось потребностями физических теорий.
Физические теории почти всегда формулируются в виде математических выражений.
Развитие математики стимулировалось потребностями физических теорий.
Слайд 11Физика и геология
Проблемы геологии, теснейшим образом связанные с физикой:
происхождение Земли
и других планет;
строение и состав различных геосфер;
возраст Земли и датирование этапов её развития;
термическая история Земли;
разработка теории разрушения горных пород;
прогноз геодинамических процессов (землетрясения, горные удары, внезапные выбросы газов и др.).
строение и состав различных геосфер;
возраст Земли и датирование этапов её развития;
термическая история Земли;
разработка теории разрушения горных пород;
прогноз геодинамических процессов (землетрясения, горные удары, внезапные выбросы газов и др.).
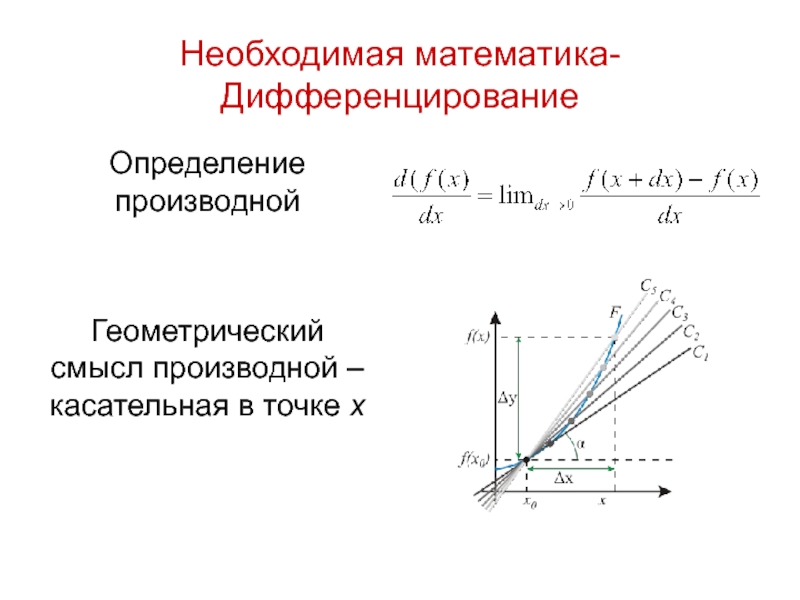
Слайд 12Необходимая математика-Дифференцирование
Определение производной
Геометрический смысл производной – касательная в точке x
Слайд 13Необходимая математика-Дифференцирование
Правила Дифференцирования
Дифференцирование дроби функций
Дифференцирование произведения функций
Дифференцирование сложных
функций
Слайд 15Необходимая математика-Интегрирование
Определение интеграла
Определенный интеграл как площадь под кривой
Слайд 16Необходимая математика-Интегрирование
Вычисление определенного интеграла
Таблица неопределенных интегралов
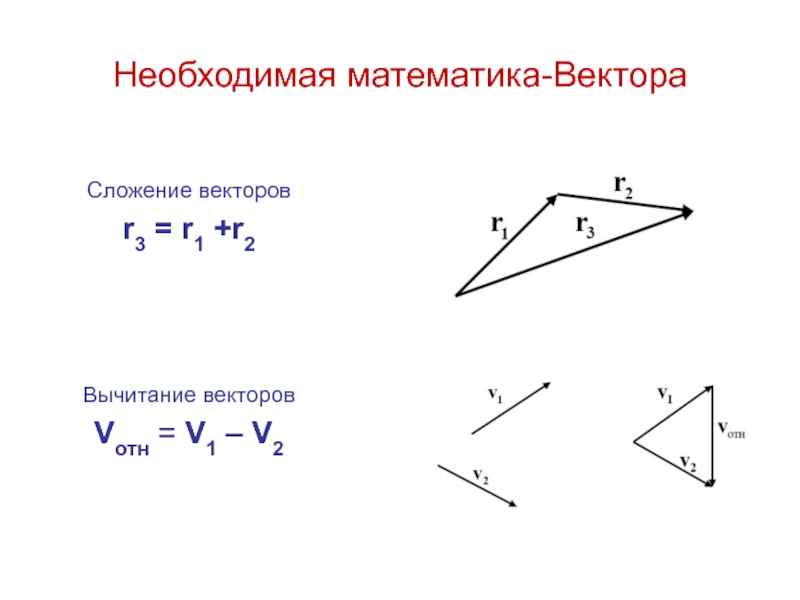
Слайд 17Необходимая математика-Вектора
Сложение векторов
r3 = r1 +r2
Вычитание векторов
Vотн = V1
– V2
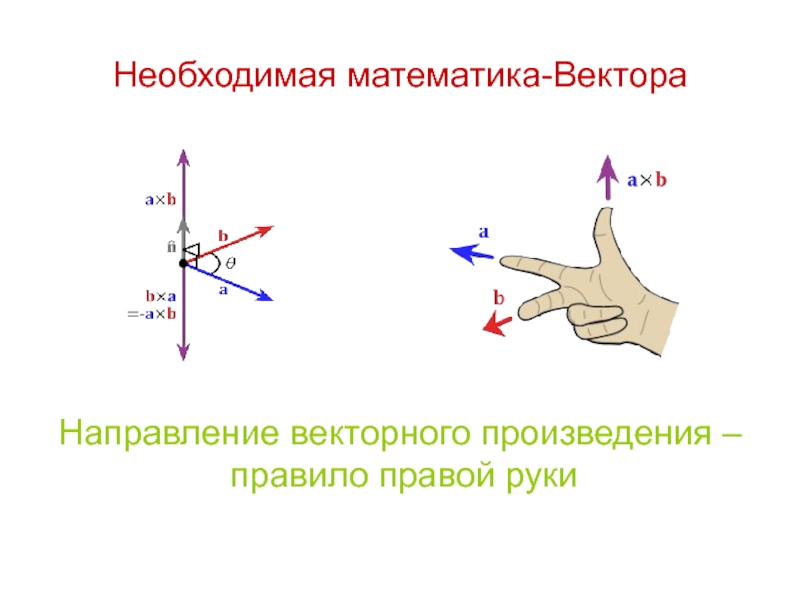
Слайд 18Необходимая математика-Вектора
Для векторов создана векторная алгебра.
b = c a- умножение на
число
c = a+b – сложение;
с =a -b – вычитание;
c =(ab)= |a||b|cosϕ - скалярное умножение (с - скаляр, т.е. число, ϕ - угол между направлениями векторов).
С=[ab]=a×b = - векторное умножение С=|a||b|sin(ϕ)
c = a+b – сложение;
с =a -b – вычитание;
c =(ab)= |a||b|cosϕ - скалярное умножение (с - скаляр, т.е. число, ϕ - угол между направлениями векторов).
С=[ab]=a×b = - векторное умножение С=|a||b|sin(ϕ)
Слайд 21Исаак Ньютон – основоположник механики
Принципы классической механики впервые были сформулированы Ньютоном
(1642-1727) в его основном сочинении «Математические начала натуральной философии», первое издание которого вышло 1687 году.
До начала двадцатого века эти принципы практически не изменялись.
До начала двадцатого века эти принципы практически не изменялись.
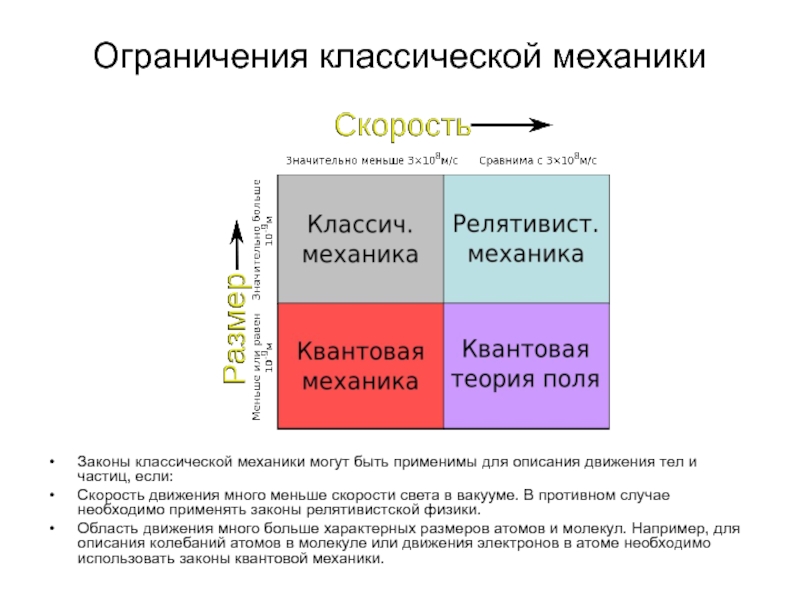
Слайд 22Ограничения классической механики
Законы классической механики могут быть применимы для описания движения
тел и частиц, если:
Скорость движения много меньше скорости света в вакууме. В противном случае необходимо применять законы релятивистской физики.
Область движения много больше характерных размеров атомов и молекул. Например, для описания колебаний атомов в молекуле или движения электронов в атоме необходимо использовать законы квантовой механики.
Скорость движения много меньше скорости света в вакууме. В противном случае необходимо применять законы релятивистской физики.
Область движения много больше характерных размеров атомов и молекул. Например, для описания колебаний атомов в молекуле или движения электронов в атоме необходимо использовать законы квантовой механики.
Слайд 23Кинематика
Кинема́тика - раздел механики, изучающий математическое описание движения идеализированных объектов без
рассмотрения причин движения.
Исходные понятия кинематики - пространствоИсходные понятия кинематики - пространство и время.
Исходные понятия кинематики - пространствоИсходные понятия кинематики - пространство и время.
Слайд 26Свойства пространства
Пространство Евклидово. Параллельные прямые не пересекаются, сумма углов всегда треугольника
равна π
Слайд 27Пространство трехмерно
Минимальное количество тел (или количество чисел) необходимых для однозначного задания
положения точек в пространстве, называется размерностью пространства. Мы живём в трехмерном пространстве, следовательно для задания в нем положения точки нужны три числа. Задание, например, расстояний до трёх опорных точек задает координату в пространстве. Можно за три точки жестко закрепить декартову систему координат, тогда положение точки будет характеризоваться тремя числами (x,y,z).
Слайд 28Экспериментальная геометрия
В 19 веке Гаусс и Лобачевский усомнились в справедливости постулатов
Евклида превратив геометрию из аксиоматической в экспериментальную науку.
Слайд 29Свойства Времени
Во всем пространстве можно ввести единое время, текущее равномерно и
одинаково
Слайд 30Эталоны времени и длины
Секунда – 1/86164 доля земных суток.
Длина – изначально
одна сорокамиллионная парижского меридиана.
В настоящее время- длина пути, которую свет проходит за
1/2999792458 сек.
В настоящее время- длина пути, которую свет проходит за
1/2999792458 сек.
Слайд 31Система отсчета
Система координат, снабженная часами, называется системой отсчета. Существует два вида
декартовых систем координат – правая и левая. Положение каждой точки в избранной системе отсчета можно задавать тремя числами: координатами точки x,y,z. Три координаты можно объединить в один направленный отрезок или радиус-вектор r, проведенный из начала координат в рассматриваемую точку. Координаты x,y,z являются его проекциями на координатные оси.
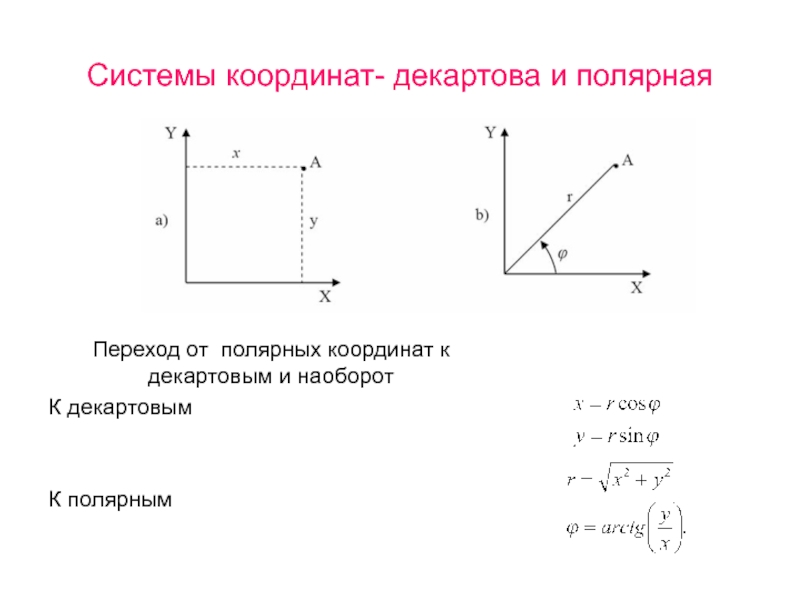
Слайд 32Системы координат- декартова и полярная
Переход от полярных координат к декартовым и
наоборот
К декартовым
К полярным
К декартовым
К полярным
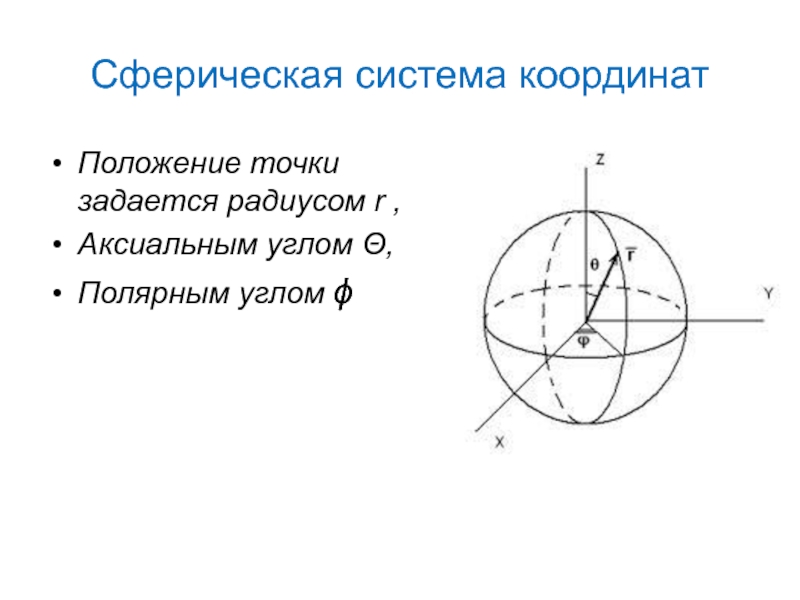
Слайд 33Сферическая система координат
Положение точки задается радиусом r ,
Аксиальным углом Θ,
Полярным
углом ϕ
Слайд 37Движение по криволинейной траектории
Траекторией Материальной точки называется линия в пространстве,
представляющая собой множество точек, в которых находилась, находится или будет находиться материальная точка при своём перемещении в пространстве относительно выбранной системы отсчета.
Слайд 38Движение по криволинейной траектории
Траектория точки Р на ободе катящегося колеса (циклоида)
Слайд 40 Прямая задача кинематики
Прямой задачей кинематики называется задача нахождения траектории движения
тела по заданному ускорению и начальным условиям. Эта задача решается методами интегрирования.
Слайд 41Обратная задача кинематики
Обратной задачей кинематики называется задача нахождения скорости и ускорения
материальной точки по заданной траектории
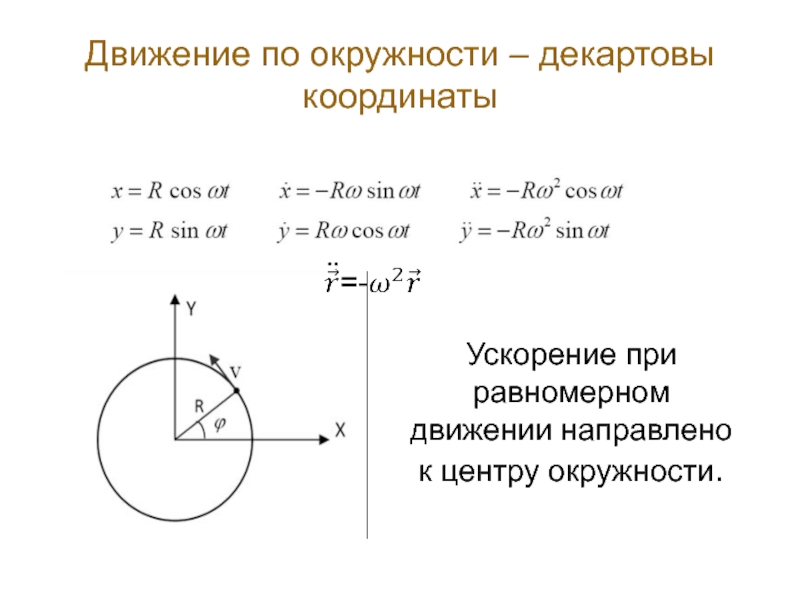
Слайд 43Движение по окружности – декартовы координаты
Ускорение при равномерном движении направлено к
центру окружности.
Слайд 44Движение по окружности – полярные координаты
Рассмотрим эту же задачу в полярных
системах координат. При смещении точки на угол dϕ вектор скорости поворачивается на тот же угол . Изменение скорости по модулю находим CD находим по формуле
Вектор разности скоростей направлен к центру окружности.
вектор единичной длины, направленный вдоль радиус-вектора
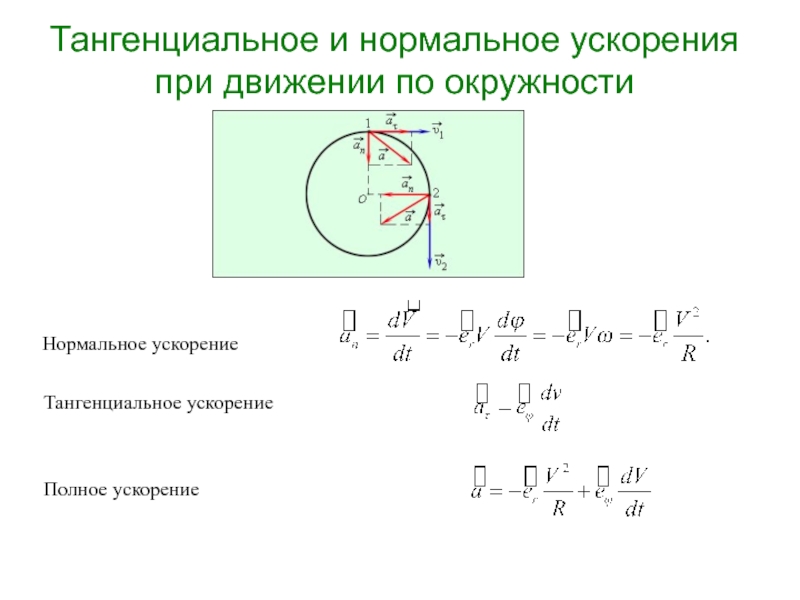
Слайд 45Тангенциальное и нормальное ускорения при движении по окружности
Нормальное ускорение
Тангенциальное ускорение
Тангенциальное
ускорение
Полное ускорение
Слайд 46Радиус кривизны траектории
Известно, что через любые три точки можно провести окружность,
причем только одну. Выберем точку траектории, в которой тело находилось в момент t Возьмем еще две точки: в моменты t – dt и t + dt. . Проведем через них окружность. Ее радиус и называется радиусом кривизны траектории.
