- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Поток энергии. Поток импульса. Сила сопротивления при потенциальном обтекании презентация
Содержание
- 1. Поток энергии. Поток импульса. Сила сопротивления при потенциальном обтекании
- 2. 1. Поток энергии. Оценка скорости изменения
- 3. Из термодинамического определения энтальпии
- 4. Так как по определению
- 5. Закон сохранения энергии в локальной форме
- 6. Учитывая, что имеем Плотность потока энергии
- 7. 2. Поток импульса. Импульс единицы объема ρv
- 8. Величина представляет собой симметричный тензор 2-го
- 9. В произвольном направлении, задаваемом единичным вектором n,
- 10. 3. Сила сопротивления при потенциальном обтекании. 1)
- 11. 3) Общие замечания относительно решения
- 12. 4) Оценка кинетической энергии W жидкости, индуцированной
- 13. 5) Тензор присоединенных масс и полный импульс
- 14. 6) Выводы если тело в
Слайд 1Лекция 3
«Гидродинамика идеальной жидкость»
Содержание
Поток энергии.
Поток импульса.
Сила сопротивления при потенциальном обтекании.
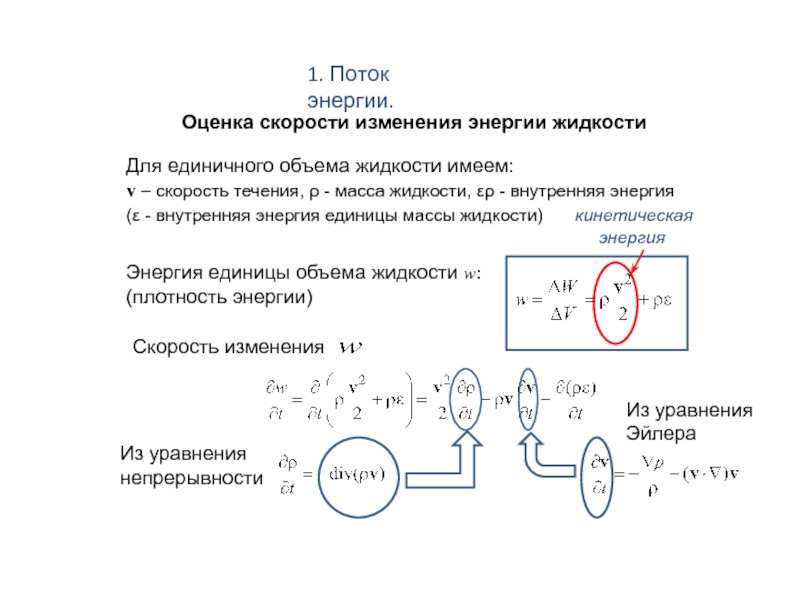
Слайд 21. Поток энергии.
Оценка скорости изменения энергии жидкости
Для единичного объема жидкости
v – скорость течения, ρ - масса жидкости, ερ - внутренняя энергия
(ε - внутренняя энергия единицы массы жидкости) кинетическая
энергия
Энергия единицы объема жидкости w:
(плотность энергии)
Cкорость изменения
Из уравнения
непрерывности
Из уравнения
Эйлера
Слайд 3 Из термодинамического
определения энтальпии
Из I начала
термодинамики
и т.к.
массы, то здесь V=1/ρ и
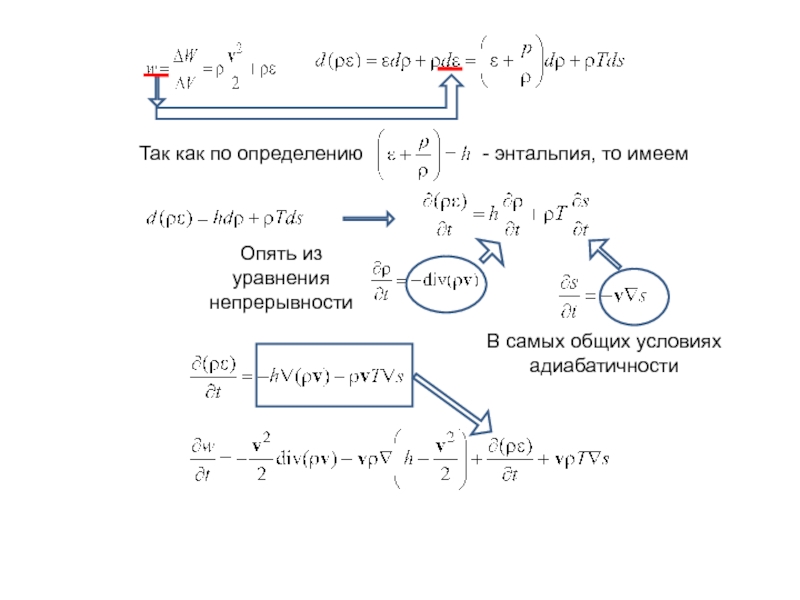
Слайд 4
Так как по определению
- энтальпия, то имеем
Опять из уравнения
непрерывности
В самых
адиабатичности
Слайд 5
Закон сохранения энергии
в локальной форме
V
j
Уменьшение физической величины
q в
существованием соответствующего
ей потока j: ∂q/∂t=−∇j
вектор плотности потока
энергии (вектор Умова)
Слайд 6Учитывая, что
имеем
Плотность потока энергии определяется из собственно
переноса энергии текущей жидкостью
вклада в поток, вносимого работой сил давления p над
жидкостью pv
В случае стационарных течений
Из закона сохранения энергии имеем
т.е.
Для несжимаемой жидкости имеем дополнительно
и т.к. v≠0
При ε=gh
(однородное поле тяготения)
получаем закон Бернулли
в его классическом виде
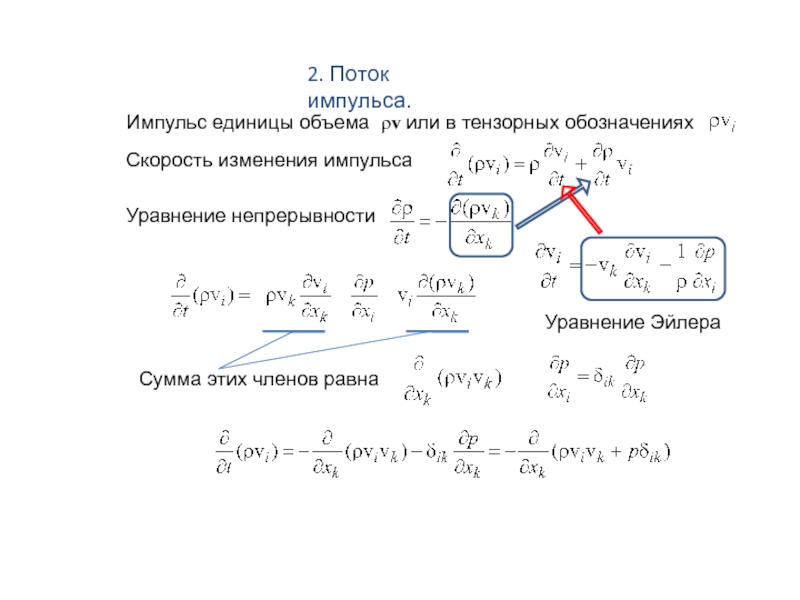
Слайд 72. Поток импульса.
Импульс единицы объема ρv или в тензорных обозначениях
Скорость изменения импульса
Уравнение непрерывности
Уравнение Эйлера
Сумма этих членов равна
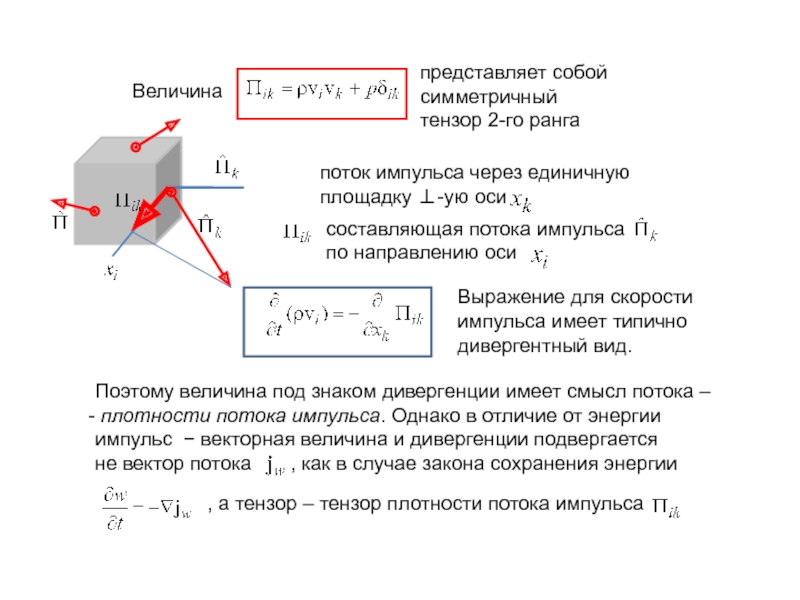
Слайд 8Величина
представляет собой
симметричный
тензор 2-го ранга
поток импульса через единичную
площадку ⊥-ую оси
составляющая потока импульса
по направлению оси
Выражение для скорости
импульса имеет типично
дивергентный вид.
Поэтому величина под знаком дивергенции имеет смысл потока –
плотности потока импульса. Однако в отличие от энергии
импульс − векторная величина и дивергенции подвергается
не вектор потока , как в случае закона сохранения энергии
, а тензор – тензор плотности потока импульса
Слайд 9В произвольном направлении, задаваемом единичным вектором
n, величина тензора
Данная величина является вектором и может быть записана
в явном виде
Характеристическая поверхность тензора
получается
сверткой
и является эллипсоидом
вращения вокруг направления вектора скорости.
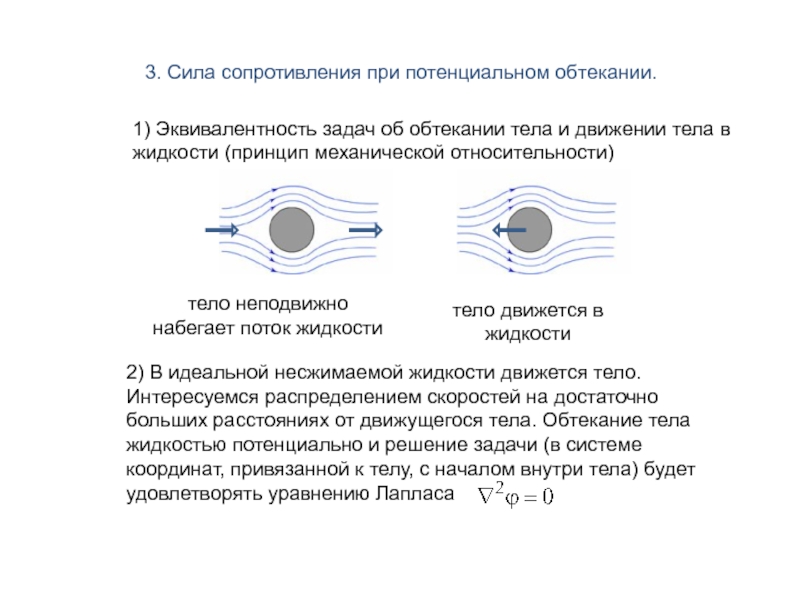
Слайд 103. Сила сопротивления при потенциальном обтекании.
1) Эквивалентность задач об обтекании тела
жидкости (принцип механической относительности)
тело неподвижно
набегает поток жидкости
тело движется в
жидкости
2) В идеальной несжимаемой жидкости движется тело.
Интересуемся распределением скоростей на достаточно
больших расстояниях от движущегося тела. Обтекание тела
жидкостью потенциально и решение задачи (в системе
координат, привязанной к телу, с началом внутри тела) будет
удовлетворять уравнению Лапласа
Слайд 113) Общие замечания относительно решения
на большом (бесконечном) удалении от тела
математически задача аналогична электростатической задаче для внешней области и потенциал представляется мультипольным разложением вида
a должно быть ≡0 иначе существует радиальный поток
через замкнутую поверхность, охватывающую тело, что
противоречит условию несжимаемости жидкости
на больших расстояниях r достаточно ограничиться дипольным
приближением
Здесь n - единичный вектор в направлении радиус-вектора.
Слайд 124) Оценка кинетической энергии W жидкости, индуцированной
движением тела
По определению v=∇ϕ имеем
(A
u − скорость движения тела, V − объем жидкости
После преобразований имеем
Вектор A определяется размерами и формой тела.
Для этого нужно построить решение граничной задачи.
Однако общий характер связи A с u можно установить,
не прибегая к решению граничной задачи.
Слайд 135) Тензор присоединенных масс и полный импульс жидкости.
Вследствие линейности связи A
условий и в общем случае можно принять
- тензор присоединенных масс
При бесконечно малых изменениях энергия W и импульс
жидкости P связаны между собой равенством
Отсюда вытекает, что
Передаваемый за ед. времени от тела жидкости импульс по
3 закону Ньютона равен с изменением знака силе реакции
со стороны жидкости на тело, т.е.
Слайд 146) Выводы
если тело в процессе движения не меняет свою форму
ориентацию, то и сила реакции отсутствует,
если движение тела равномерное (парадокс Даламбера)
определение импульса через посредство коэффициентов
присоединенных масс приводит к уравнению движения тела
в жидкости под действием внешней силы f вида
Видно, что тело в жидкости, как бы увеличивает свою массу
M на величину , что и явилось поводом для введения
термина «присоединенная масса».