- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Второе начало термодинамики презентация
Содержание
- 1. Второе начало термодинамики
- 2. Вопросы к зачёту 13. Определение второго начала
- 3. Вопросы к зачёту 19. Открытые системы и
- 4. Первое начало термодинамики или закон сохранения энергии ΔQ = ΔU + ΔA
- 5. Формулировка второго начала термодинамики Тепло само
- 6. Замкнутая система Система не обменивающаяся с внешней средой ни энергией, ни веществом, ни информацией.
- 7. Формулировка второго начала термодинамики Второе начало термодинамики
- 8. Формулировка второго начала термодинамики Постулат Клаузиуса: «Невозможен
- 9. Необратимые процессы Необратимым называется процесс называется
- 10. Деградация энергии “Высококачественная” световая энергия превращается в
- 11. Энтропия Энтропи́я (от греч. ἐντροπία — поворот, превращение) —
- 12. Принцип двойственности систем Все системы состоят из
- 13. Энтропи́я Энтропи́я – мера деградации энергии, мера неупорядоченности, неопределённости, нестабильности.
- 14. Свойства замкнутой системы Энергия замкнутой системы остается постоянной. Энтропия замкнутой системы возрастает
- 15. Формула Больцмана S = k lnW Людвиг Больцман
- 16. Демон Максвелла Демон Максвелла — мысленный экспериментмысленный эксперимент
- 17. Суть парадокса Мысленный экспериментМысленный эксперимент состоит в
- 18. Суть парадокса Таким образом, получается, что демон
- 19. Демон Максвелла и информация Получена она в
- 20. Наименьшее количество информации 1бит – соответствует
- 21. Открытые системы Лекция 6
- 22. Открытые системы – системы, обменивающиеся с
- 23. Автотрофы (др.-греч. αὐτός — сам и τροφή —
- 24. Диссипативные структуры Диссипативная система (или диссипативная структура,
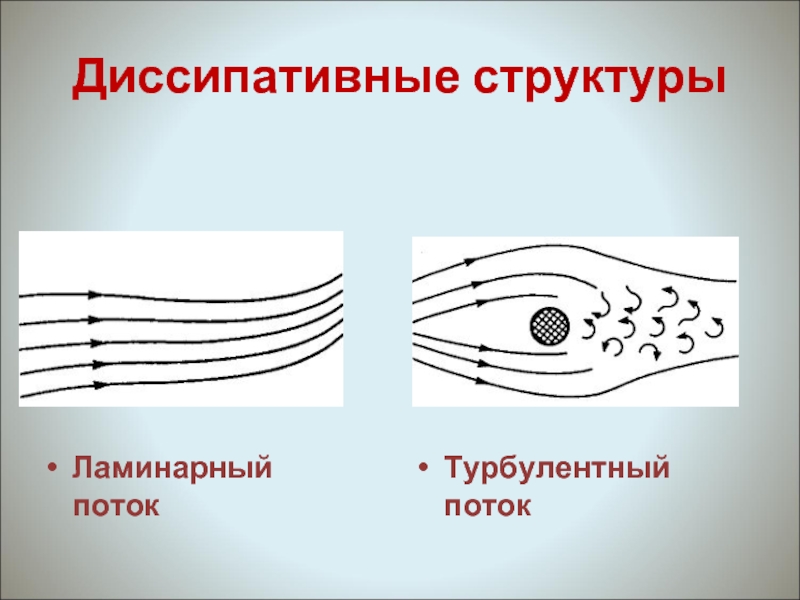
- 25. Диссипативные структуры Ламинарный поток Турбулентный поток
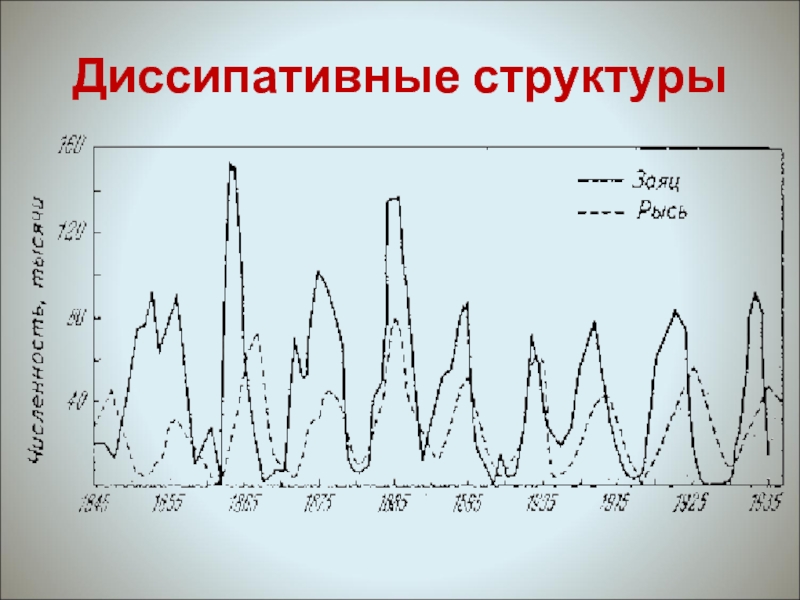
- 26. Диссипативные структуры Диссипативные структуры в экологии связаны
- 27. Диссипативные структуры
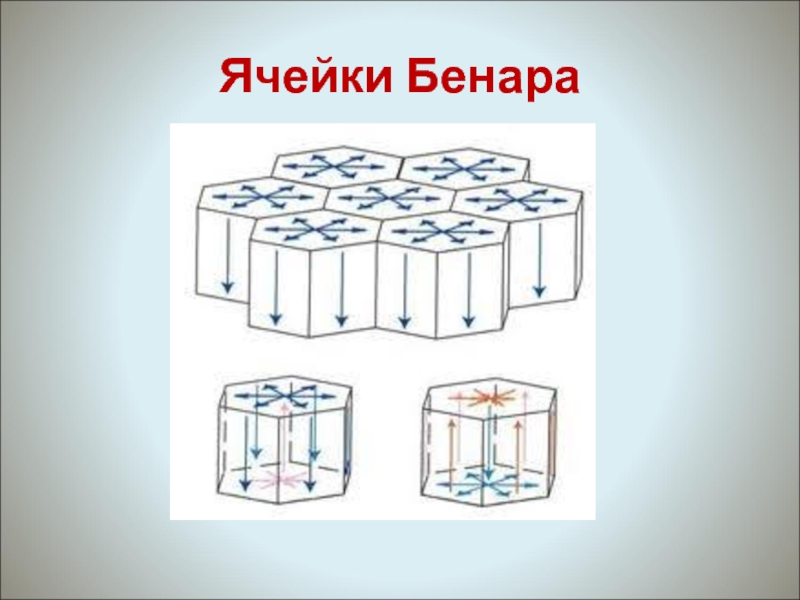
- 28. Ячейки Бенара
- 29. Ячейки Бенара
- 30. Ячейки Бенара
- 31. Ячейки Бенара
- 32. Ячейки Бенара
- 33. Реакция Белоусова Жаботинского
- 34. Необходимые свойства самоорганизующихся систем Система должна быть открытой; Наличие управляющих параметров; Наличие внутрисистемных связей.
- 35. Схема процесса самоорганизации внешнее воздействие на систему;
- 36. Теория Дарвина и самоорганизация или от простого к сложному
- 37. Дарвин против Больцмана? Больцман против космоса?
- 38. Синергетика Синергетический подход означает эквивалентность рассмотрения процессов
- 39. Хаос и порядок Порядок из хаоса или хаос из порядка
Слайд 2Вопросы к зачёту
13. Определение второго начала термодинамики.
14. Понятие замкнутой системы.
15. Понятие
16. Принцип двойственности систем.
17. Определение энтропии системы. Формула Больцмана.
18. Свойства замкнутой системы.
Слайд 3Вопросы к зачёту
19. Открытые системы и их свойства.
20. Понятие диссипативных структур.
21. Понятие самоорганизации. Примеры.
22. Как «работают» ячейки Бенара.
23. Суть синергетического подхода.
Слайд 5Формулировка второго начала термодинамики
Тепло само собой всегда переходит от более нагретого
Или
невозможен самопроизвольный переход тепла от тела, менее нагретого, к телу, более нагретому.
Слайд 6Замкнутая система
Система не обменивающаяся с внешней средой
ни энергией,
ни веществом,
ни информацией.
Слайд 7Формулировка второго начала термодинамики
Второе начало термодинамики запрещает так называемые вечные двигатели
Второе начало термодинамики является постулатомВторое начало термодинамики является постулатом, не доказываемым в рамках термодинамики. Оно было создано на осно -ве обобщения опытных фактов и получило многочисленные экспериментальные подтверждения.
Слайд 8Формулировка второго начала термодинамики
Постулат Клаузиуса: «Невозможен процесс, единственным результатом которого являлась
Постулат Томсона: «Невозможен круговой процесс, единственным результатом которого было бы производство работы за счет охлаждения теплового резервуара» (такой процесс называется процессом Томсона).
Слайд 9Необратимые процессы
Необратимым называется процесс называется процесс, который нельзя провести в
Слайд 10Деградация энергии
“Высококачественная” световая энергия превращается в энергию химических связей тканей растений,
Деградация энергии – переход от высокоупорядоченной энергии к энергии хаотического движения (т.е.тепловой энергии)
Слайд 11 Энтропия
Энтропи́я (от греч. ἐντροπία — поворот, превращение) — мера беспорядка системы или мера
Энтропия впервые введена Клаузиусом в термодинамике в 1865 году для определения меры необратимого рассеивания энергии, меры отклонения реального процесса от идеального. Она является функцией состояния и остаётся постоянной в обратимых процессах в обратимых процессах. В необратимых процессах энтропия увеличивается.
Рудольф Клаузиус
Слайд 12Принцип двойственности систем
Все системы состоят из двух составляющих:
хаотической
Соотношение этих составляющих меняется при всех изменениях системы.
Слайд 13Энтропи́я
Энтропи́я – мера деградации энергии, мера неупорядоченности,
неопределённости,
нестабильности.
Слайд 14Свойства замкнутой системы
Энергия замкнутой системы остается постоянной.
Энтропия замкнутой системы возрастает
Слайд 16Демон Максвелла
Демон Максвелла — мысленный экспериментмысленный эксперимент 1867 года, а также его
Джеймс Максвелл
Слайд 17Суть парадокса
Мысленный экспериментМысленный эксперимент состоит в следующем: предположим, сосуд с газомМысленный
Слайд 18Суть парадокса
Таким образом, получается, что демон Максвелла позволяет нагреть правую часть
Слайд 19Демон Максвелла и информация
Получена она в 1928 г. американским инженером Р.
x=log2N.
В информатике используется формула Хартли:
Слайд 20
Наименьшее количество информации 1бит – соответствует выбору одного из двух значений
Две цифры – два бита и т.д. I цифр – соответствует количеству информации в битах, равному I.
Слайд 22
Открытые системы – системы, обменивающиеся с окружающей средой веществом, энергией и
Энтропия открытой системы может как увеличиваться (в случае регресса и увеличения хаоса), так и уменьшаться (в случае развития и упорядочения).
Слайд 23
Автотрофы (др.-греч. αὐτός — сам и τροφή — пища) — живые организмы, синтезирующие органические
Автотрофы составляют первый ярус в пищевой пирамидеАвтотрофы составляют первый ярус в пищевой пирамиде (первые звенья пищевых цепей). Именно они являются первичными продуцентамиАвтотрофы составляют первый ярус в пищевой пирамиде (первые звенья пищевых цепей). Именно они являются первичными продуцентами органического вещества в биосфереАвтотрофы составляют первый ярус в пищевой пирамиде (первые звенья пищевых цепей). Именно они являются первичными продуцентами органического вещества в биосфере, обеспечивая пищей гетеротрофов. Следует отметить, что иногда резкой границы между автотрофами и гетеротрофами провести не удается. Например, одноклеточ- ная эвглена на свету является автотрофом, а в темноте — гетеротрофом.
Слайд 24Диссипативные структуры
Диссипативная система (или диссипативная структура, от лат. dissipatio — «рассеиваю, разрушаю») — это
Слайд 26Диссипативные структуры
Диссипативные структуры в экологии связаны в первую очередь с системами
Слайд 34Необходимые свойства самоорганизующихся систем
Система должна быть открытой;
Наличие управляющих параметров;
Наличие внутрисистемных связей.
Слайд 35Схема процесса самоорганизации
внешнее воздействие на систему;
изменение управляющего параметра;
изменение эффективности прежних или
образование диссипативных структур, усложнение системы.