существуют такие функции от координат и скоростей частиц, которые не изменяют свои значения при их движении. Таких функций, называемых интегралами движения, имеется три:
1) энергия
2) импульс
3) момент импульса
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Динамика. Закон сохранения импульса презентация
Содержание
Динамика Закон сохранения импульса + = 0 по 3 закону Ньютона – импульс системы – результирующая внешних сил
Слайд 1Динамика
Закон сохранения импульса
Силы
внутренние
внешние
В случае замкнутых (изолированных) систем
внешние силы отсутствуют
Для замкнутых систем
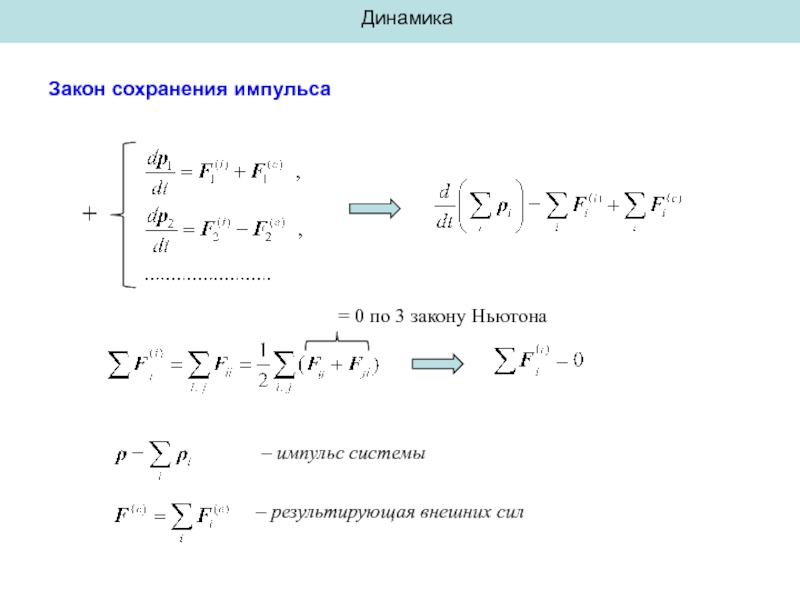
Слайд 2Динамика
Закон сохранения импульса
+
= 0 по 3 закону Ньютона
– импульс системы
– результирующая
внешних сил
Слайд 3
Динамика
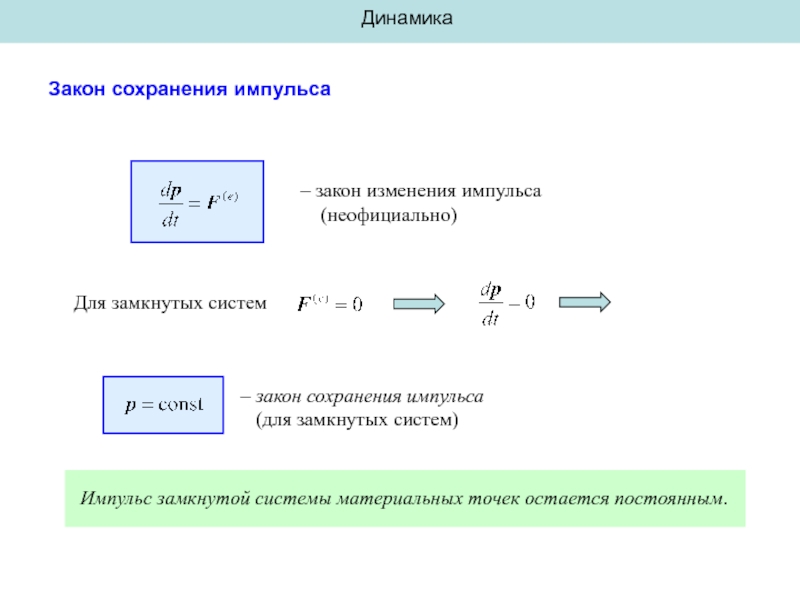
Закон сохранения импульса
– закон изменения импульса
(неофициально)
Для замкнутых систем
Импульс замкнутой
системы материальных точек остается постоянным.
– закон сохранения импульса
(для замкнутых систем)
Слайд 4
Динамика
Закон сохранения импульса
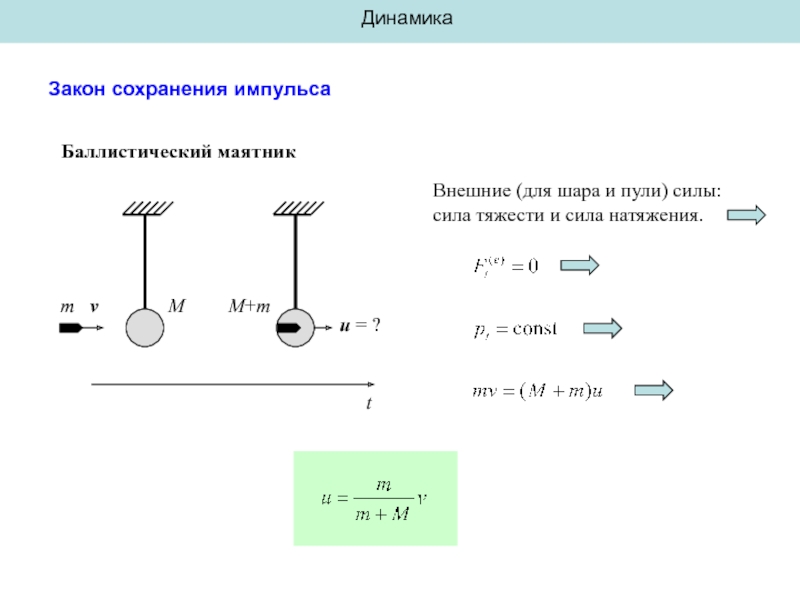
Баллистический маятник
M
m v
M+m
u = ?
t
Внешние (для шара и
пули) силы:
сила тяжести и сила натяжения.
Слайд 5
Динамика
Теорема о движении центра масс
– центр масс
Центр масс системы движется
как материальная точка, масса которой равна массе системы, а действующая сила – результирующей внешних сил, действующих на систему.
– теорема о движении центра масс
Слайд 6
Динамика
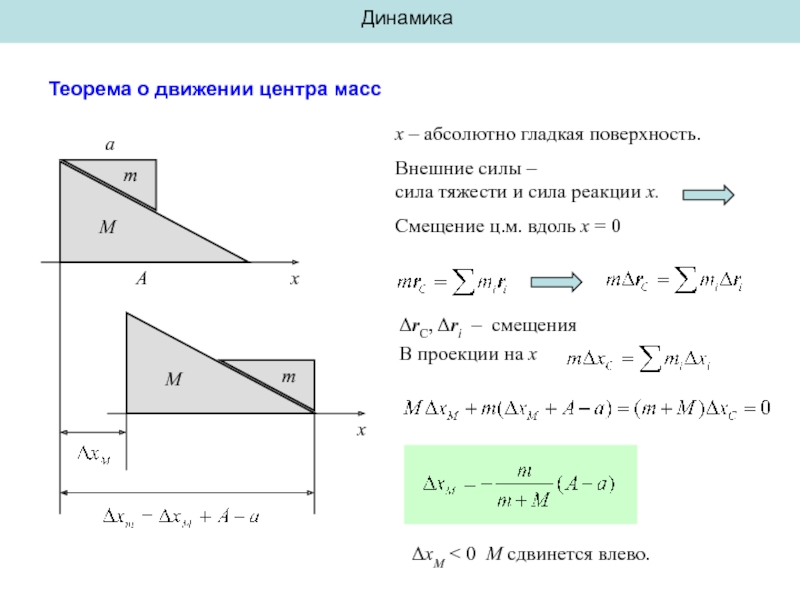
Теорема о движении центра масс
x
M
A
m
a
x
M
m
x – абсолютно гладкая поверхность.
Внешние силы –
сила
тяжести и сила реакции x.
Смещение ц.м. вдоль x = 0
Смещение ц.м. вдоль x = 0
ΔrC, Δri – смещения
В проекции на x
ΔxM < 0 M сдвинется влево.
Слайд 7Динамика
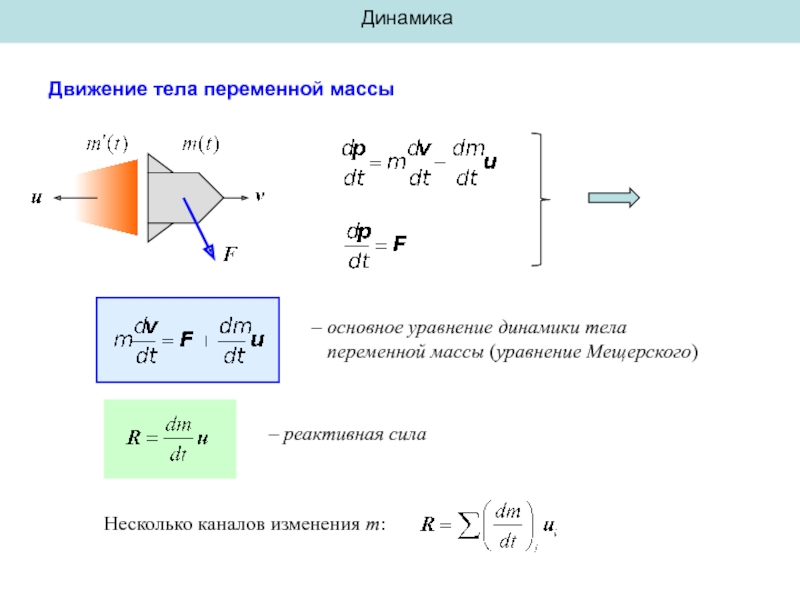
Движение тела переменной массы
v – скорость ракеты (основной массы),
u – скорость
газов (убывающей массы)
относительно ракеты,
F – внешняя сила.
– импульс ракеты
– импульс ракеты и газов
Слайд 8
Динамика
Движение тела переменной массы
– основное уравнение динамики тела
переменной массы
(уравнение Мещерского)
– реактивная сила
Несколько каналов изменения m:
Слайд 9
Динамика
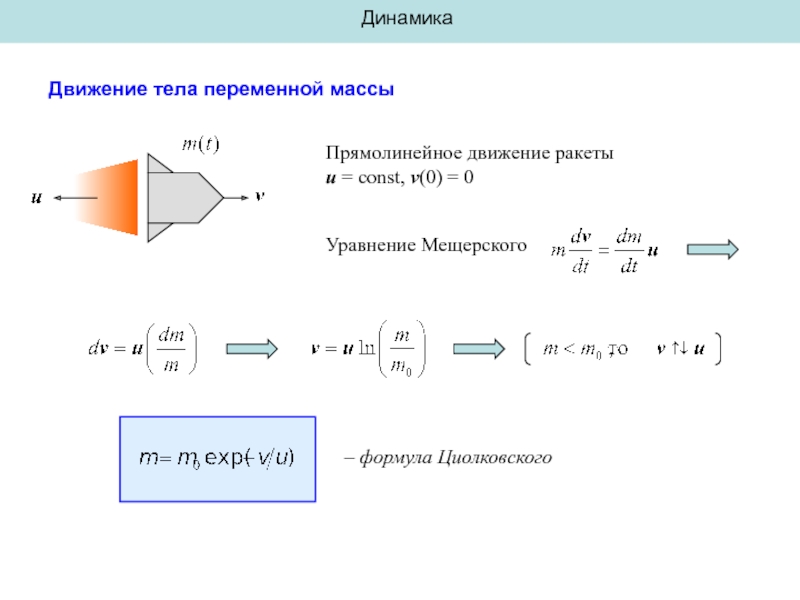
Движение тела переменной массы
Прямолинейное движение ракеты
u = const, v(0) = 0
Уравнение
Мещерского
– формула Циолковского
Слайд 10
Динамика
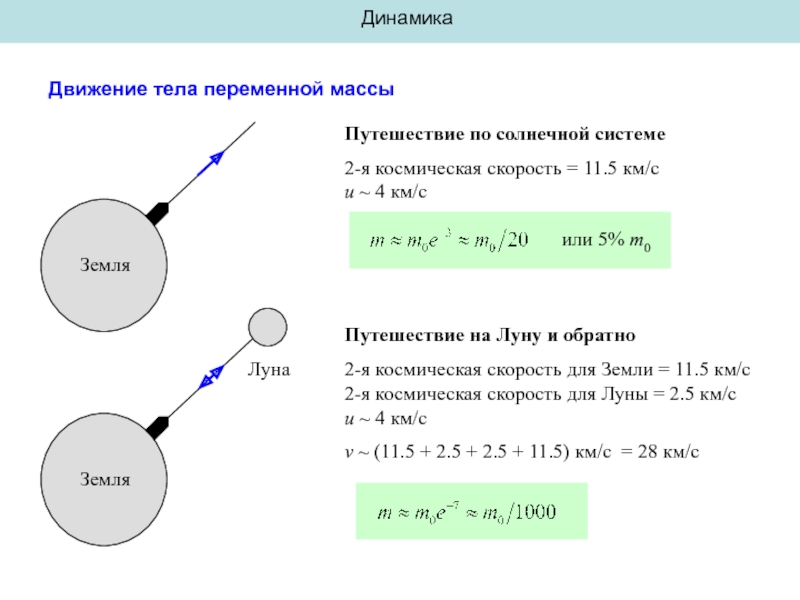
Движение тела переменной массы
Земля
Земля
Луна
Путешествие по солнечной системе
2-я космическая скорость = 11.5
км/с
u ~ 4 км/с
или 5% m0
Путешествие на Луну и обратно
2-я космическая скорость для Земли = 11.5 км/с
2-я космическая скорость для Луны = 2.5 км/с
u ~ 4 км/с
v ~ (11.5 + 2.5 + 2.5 + 11.5) км/с = 28 км/с
Слайд 11
Динамика
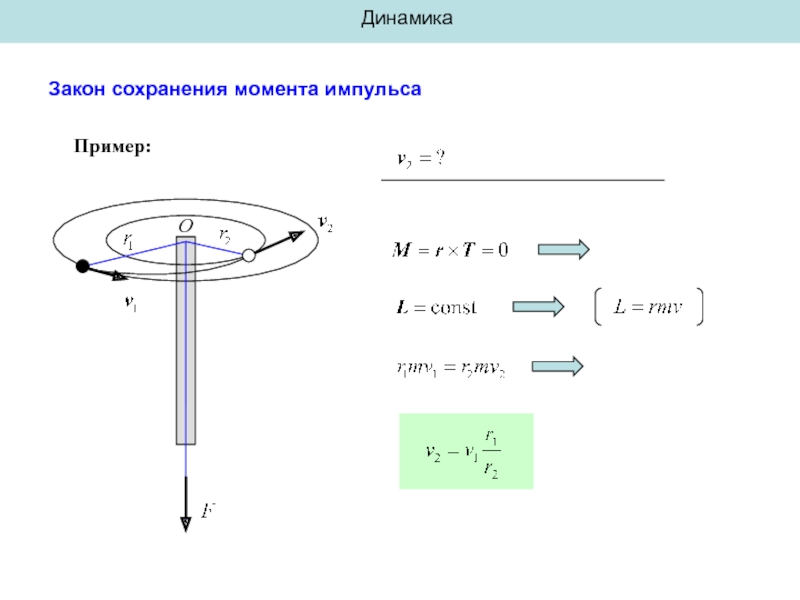
Закон сохранения момента импульса
O
r
F
p = mv
Определения:
– момент импульса
– момент силы
– уравнение моментов
Слайд 12
Динамика
Закон сохранения момента импульса
i
O
Для системы материальных точек
– момент импульса системы
– момент
силы, действующей на систему
= 0 по 3-му закону Ньютона
Слайд 13
Динамика
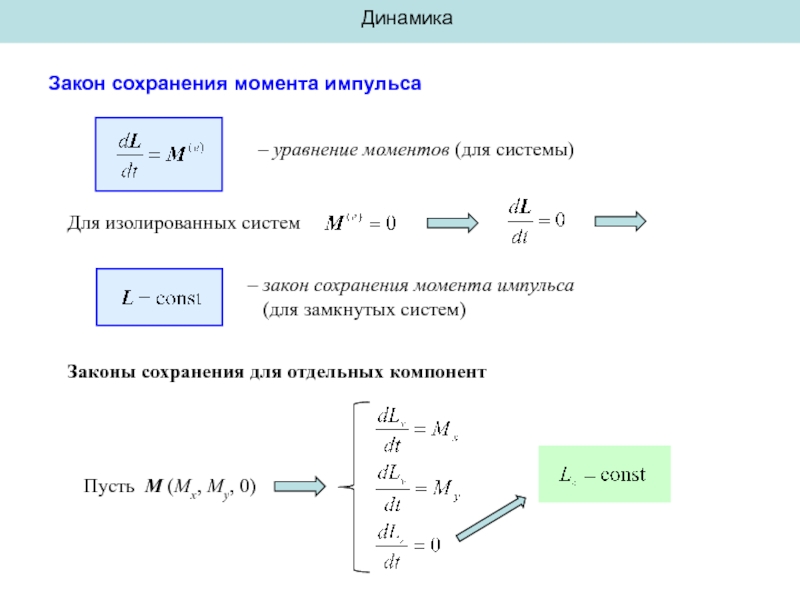
Закон сохранения момента импульса
– уравнение моментов (для системы)
Для изолированных систем
–
закон сохранения момента импульса
(для замкнутых систем)
Законы сохранения для отдельных компонент
Пусть M (Mx, My, 0)
Слайд 15
Динамика
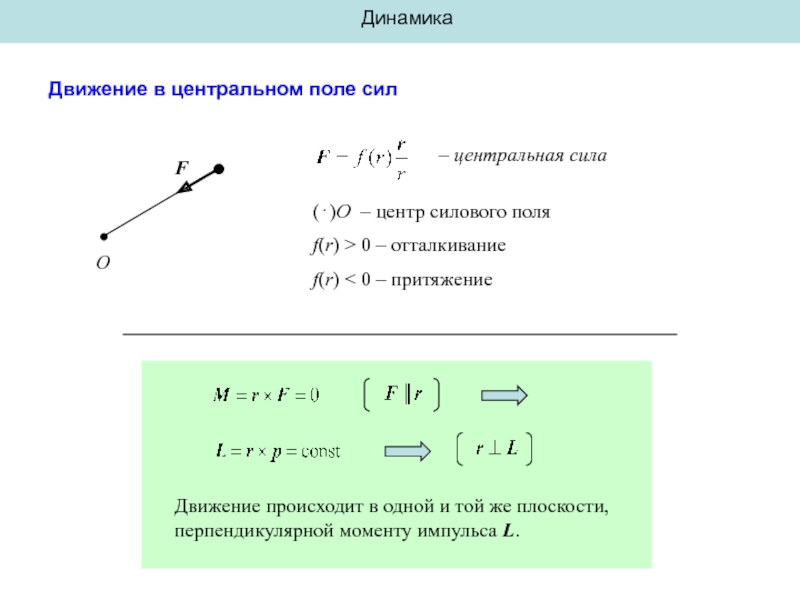
Движение в центральном поле сил
O
– центральная сила
F
(⋅)O – центр силового поля
f(r)
> 0 – отталкивание
f(r) < 0 – притяжение
f(r) < 0 – притяжение
Движение происходит в одной и той же плоскости, перпендикулярной моменту импульса L.
Слайд 16
Динамика
Движение в центральном поле сил
O
vdt
r
– векторный элемент площади
– площадь Δ
dS
⊥ площади Δ
1)
2)
– секториальная скорость
Так как
– закон площадей
За равные промежутки времени радиус-вектор материальной точки описывает одинаковые по величине площади.
Слайд 17Динамика
Законы Кеплера и закон всемирного тяготения
1. Каждая планета движется по эллипсу, в
одном из фокусов
которого находится Солнце;
2. Радиус-вектор планеты за равные промежутки времени описывает равные площади ;
3. Квадраты времен обращения планет относятся как кубы больших полуосей эллиптических орбит, по которым они движутся вокруг Солнца .
2. Радиус-вектор планеты за равные промежутки времени описывает равные площади ;
3. Квадраты времен обращения планет относятся как кубы больших полуосей эллиптических орбит, по которым они движутся вокруг Солнца .
2a
a – большая полуось
Слайд 18
Динамика
Законы Кеплера и закон всемирного тяготения
Пусть планета движется по окружности, тогда
(движение
равномерное)
Согласно 3-му закону Кеплера
Солнце и планета в их взаимодействии выступают как равноправные тела
– закон всемирного тяготения
γ – гравитационная постоянная
