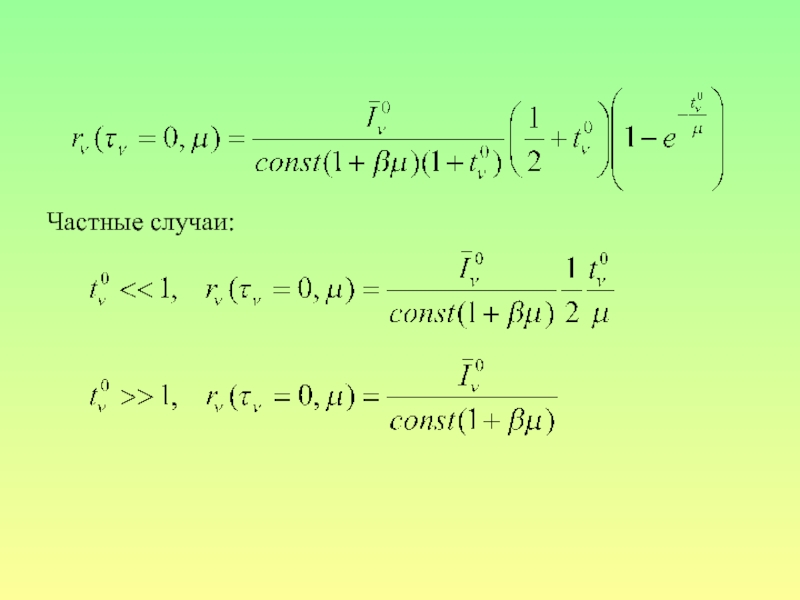- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Уравнение переноса излучения с учетом поглощения в линиях. (Тема 13) презентация
Содержание
- 1. Уравнение переноса излучения с учетом поглощения в линиях. (Тема 13)
- 2. Уравнение переноса излучения с учетом поглощения в
- 3. Функция источника для линий при ЛТР Чтобы
- 4. Линии при ЛТР Для непрерывного спектра
- 5. Для интегрирования (а) положим, что Тогда:
- 6. Сравнение с наблюдениями (для Солнца) при θ
- 7. Линии поглощения при рассеянии
- 8. Условие монохроматического лучистого равновесия функция источника полностью определяется полем излучения
- 9. Модель Шварцшильда-Шустера «обращающий» слой (атмосфера) фотосфера УП:
- 10. Обозначим: Получим систему: Сумма уравнений Разность уравнений
- 11. Граничные условия: Вычисляем потоки:
- 12. Для непрерывного спектра взят обычный (линейный) закон потемнения.
- 13. Частные случаи:
- 14. Вычисляем остаточную интенсивность: «число поглощающих
- 15. Модель Милна-Эддингтона В этой модели нет разделения
- 16. Решение методом Милна=Эддингтона Умножаем на
- 17. Перепишем Это возможно, если функция
- 18. 7) Граничные условия: 8) Из (2) имеем: (3) (4)
- 19. Из (1) имеем: 10) Из (3-5) имеем: (5)
- 20. 11) Теперь (5) будет иметь вид: 12)
- 21. 13) Окончательно для профиля линии (остаточной
- 22. 15) Сравнение с наблюдениями
Уравнение переноса излучения с учетом поглощения в линиях Теперь общий коэффициент поглощения равен сумме коэффициентов поглощения в континууме и в линиях Соответственно и оптическая
Слайд 2Уравнение переноса излучения с учетом поглощения в линиях
Теперь общий коэффициент поглощения
равен сумме коэффициентов поглощения в континууме и в линиях
Соответственно и оптическая глубина будет определяться как:
Функция источника также будет иметь следующий
вид:
Уравнение переноса будет формально иметь обычный вид:
Соответственно и оптическая глубина будет определяться как:
Функция источника также будет иметь следующий
вид:
Уравнение переноса будет формально иметь обычный вид:
Слайд 3Функция источника для линий при ЛТР
Чтобы решить уравнение переноса, надо знать
функции источника для континуума и линии.
Проблема с : она зависит от населенностей уровней, которые сами зависят от поля излучения в континууме и от функции
Эта взаимосвязь сильно усложняет решение уравнения переноса с учетом линий.
Простейший случай - ЛТР:
Что это означает физически?
- населенности уровней зависят только от температуры и не зависят от поля излучения,
- это приближение хорошо работает только в том случае, когда населенности уровней определяются только столкновениями, а не полем излучения.
Проблема с : она зависит от населенностей уровней, которые сами зависят от поля излучения в континууме и от функции
Эта взаимосвязь сильно усложняет решение уравнения переноса с учетом линий.
Простейший случай - ЛТР:
Что это означает физически?
- населенности уровней зависят только от температуры и не зависят от поля излучения,
- это приближение хорошо работает только в том случае, когда населенности уровней определяются только столкновениями, а не полем излучения.
Слайд 4Линии при ЛТР
Для непрерывного спектра
Для непрерывного спектра и линии
Решение:
Профиль линии
(остаточная интенсивность)
(только
для Солнца)
(для звезд)
(а)
Слайд 6Сравнение с наблюдениями (для Солнца)
при θ
900
(на краю лимба) линия исчезает: rν
1
Теория:
Наблюдения:
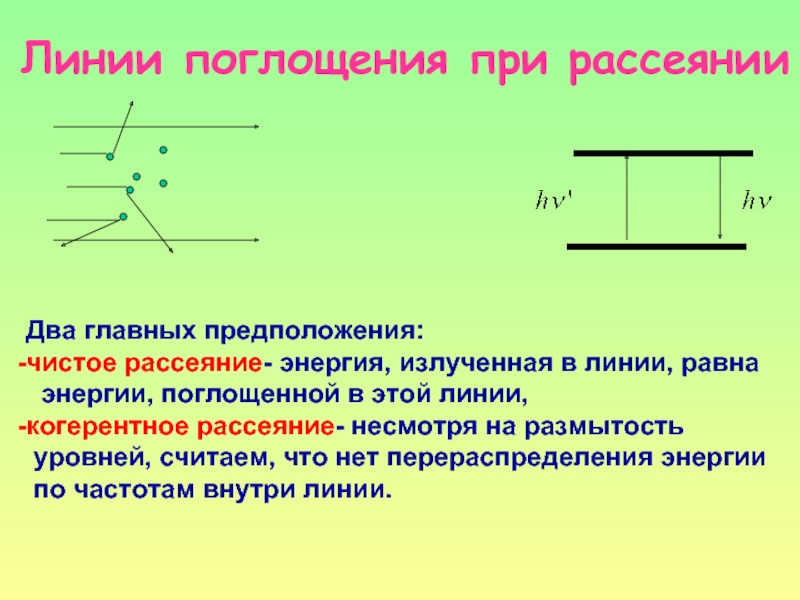
Слайд 7Линии поглощения при рассеянии
Два главных предположения:
чистое рассеяние- энергия, излученная в линии,
равна
энергии, поглощенной в этой линии,
когерентное рассеяние- несмотря на размытость
уровней, считаем, что нет перераспределения энергии
по частотам внутри линии.
энергии, поглощенной в этой линии,
когерентное рассеяние- несмотря на размытость
уровней, считаем, что нет перераспределения энергии
по частотам внутри линии.
Слайд 8Условие монохроматического лучистого равновесия
функция источника полностью
определяется полем
излучения
Слайд 9Модель Шварцшильда-Шустера
«обращающий» слой
(атмосфера)
фотосфера
УП:
:
Решим эту систему методом Шварцшильда-Шустера
Напоминание: метод Шварцшильда-Шустера основан на
усреднении интенсивностей по нижней и верхней полу – сферам и на выносе из под интеграла среднего значения
Слайд 14Вычисляем остаточную интенсивность:
«число поглощающих атомов»-
число атомов, производящих
линию и находящихся в
столбце
сечением в 1 см2 и протяжен-
ностью, равной протяженности
«обращающего слоя».
сечением в 1 см2 и протяжен-
ностью, равной протяженности
«обращающего слоя».
Слайд 15Модель Милна-Эддингтона
В этой модели нет разделения на слои: в каждой точке
атмос-
феры имеется поглощение и излучение как в континууме, так
и в линии.
Полагаем, что
феры имеется поглощение и излучение как в континууме, так
и в линии.
Полагаем, что
Для континуума
считаем, что
выполняется ЛТР
(это оправдано)
Для получения аналитического решения необходимо сделать основное предположение: величина является постоянной, т.е. не зависит от глубины.
Из условия
монохроматического
лучистого
равновесия
Слайд 16
Решение методом Милна=Эддингтона
Умножаем на и интегрируем по
всем направлениям:
Умножаем на и интегрируем по направлениям:
(1)
3) В итоге:
Умножаем на и интегрируем по направлениям:
(1)
3) В итоге:
Слайд 17Перепишем
Это возможно, если функция Планка является линейной по оптической глубине
Решение:
(2)
Слайд 2113) Окончательно для профиля линии (остаточной
интенсивности) имеем:
14) Оценим глубину профиля
линии (остаточной
интенсивности) для центральной частоты линии. В этом
случае
интенсивности) для центральной частоты линии. В этом
случае
Тогда из (6) имеем
~1
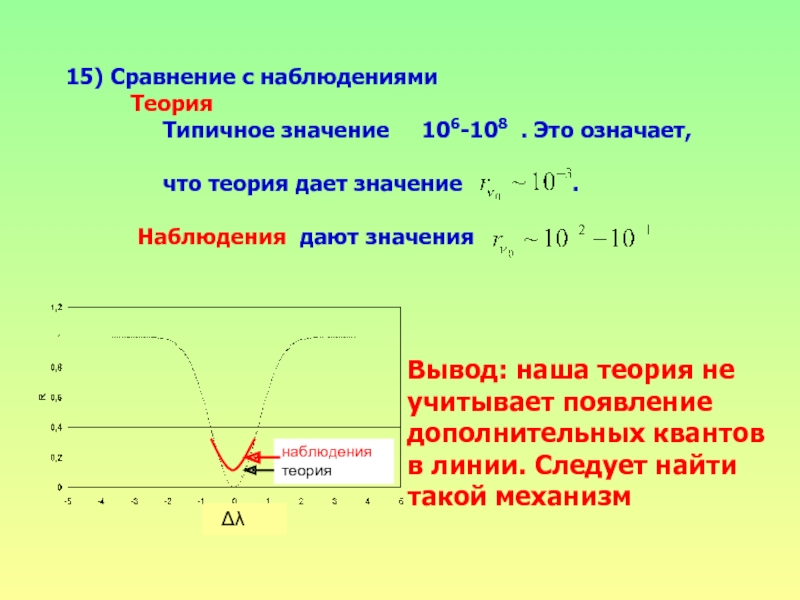
Слайд 2215) Сравнение с наблюдениями
Теория
Типичное значение 106-108 . Это означает,
что теория дает значение .
Наблюдения дают значения
что теория дает значение .
Наблюдения дают значения
наблюдения
теория
Вывод: наша теория не
учитывает появление
дополнительных квантов
в линии. Следует найти
такой механизм
Δλ
