- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Динамика вращательного движения презентация
Содержание
- 1. Динамика вращательного движения
- 2. Лекцию читает Кандидат физико-математических наук, доцент Кузьмин Юрий Ильич
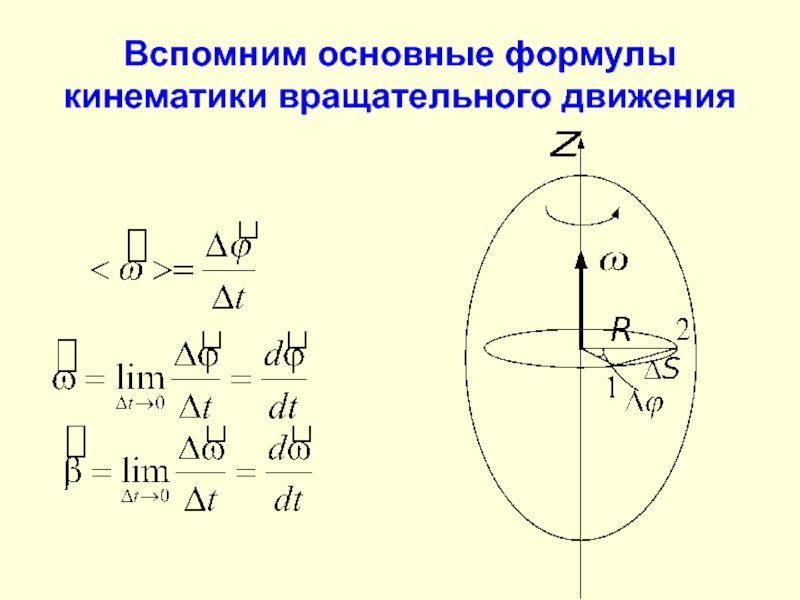
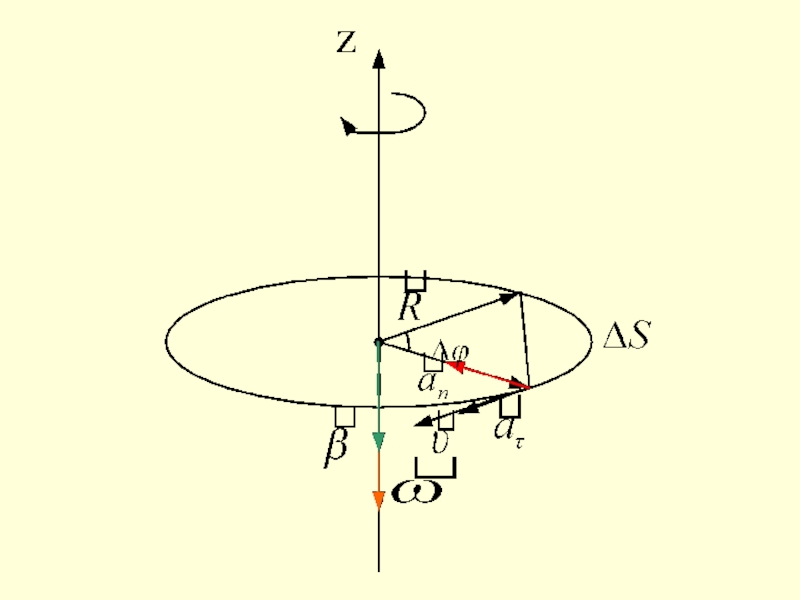
- 3. Вспомним основные формулы кинематики вращательного движения
- 5. 1. МОМЕНТЫ СИЛЫ Определим момент
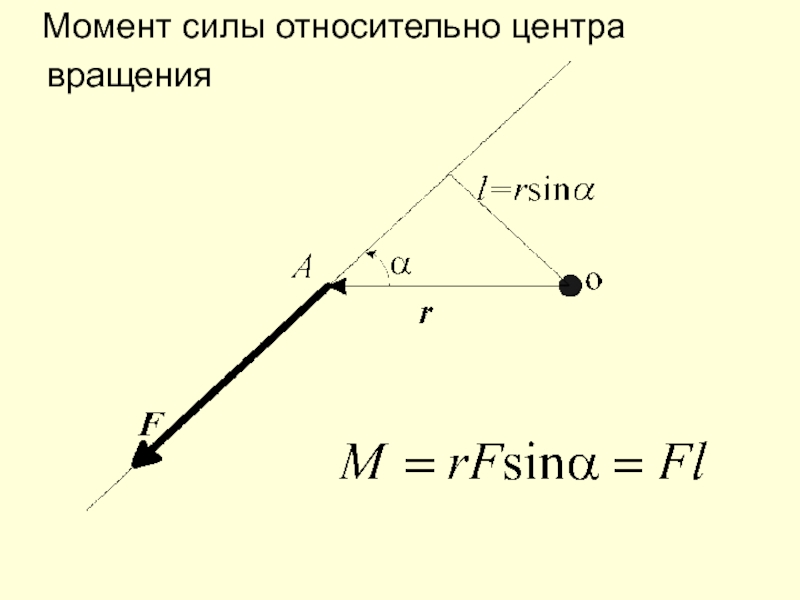
- 6. Момент силы относительно центра
- 7. Вначале определим момент силы
- 9. Разложим на две составляющие.
- 10. 2. МОМЕНТ ИНЕРЦИИ. МОМЕНТ ИМПУЛЬСА. Определение
- 11. Так как абсолютно твердое тело недеформируемо, то
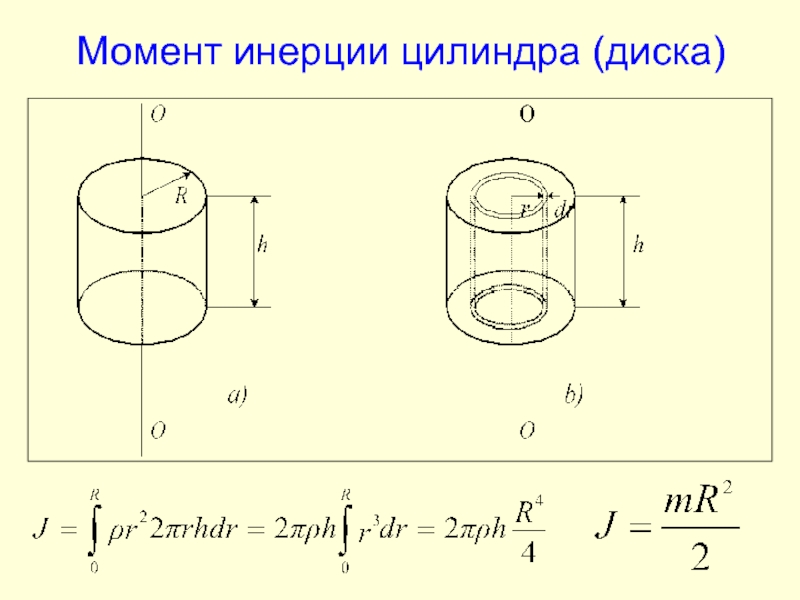
- 12. Момент инерции цилиндра (диска)
- 13. Момент инерции стержня относительно оси, проходящей через центр масс
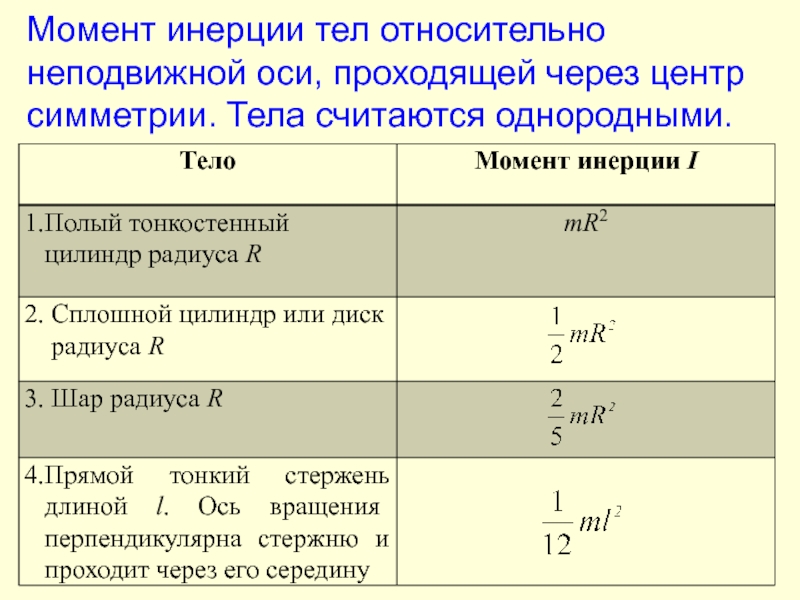
- 14. Момент инерции тел относительно неподвижной оси,
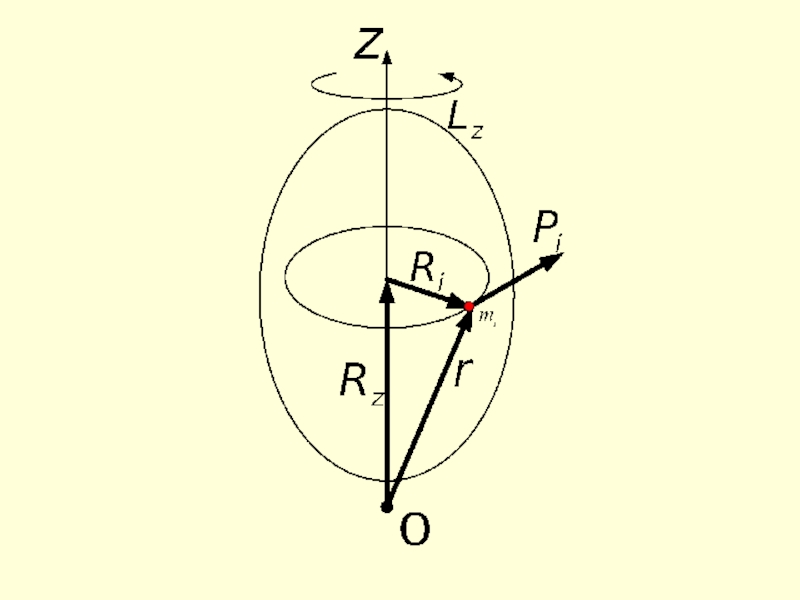
- 15. Момент импульса твердого тела Вначале определяем момент
- 17. Затем, просуммировав по всем элементарным объемам,
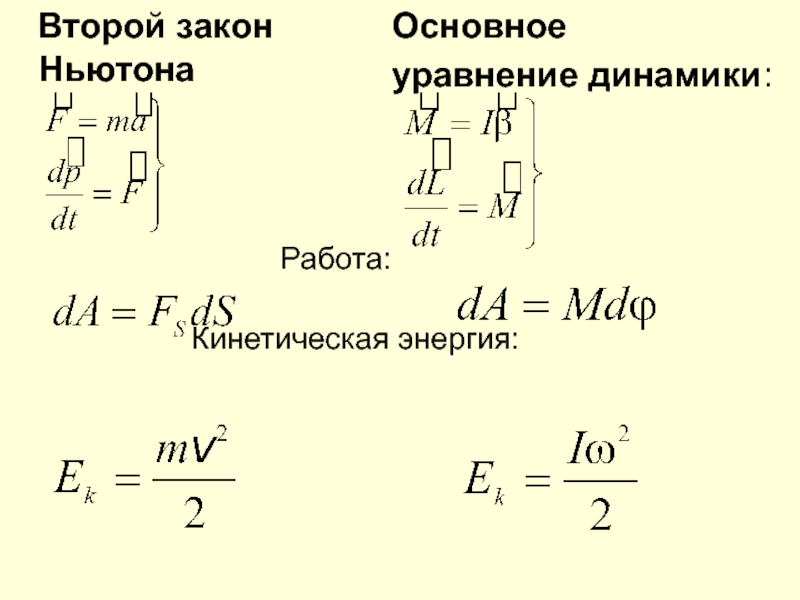
- 18. Для кинетической энергии вращательного движения твёрдого тела
- 19. Основное уравнение динамики вращательного Запишем второй
- 20. Где
- 21. Получим другую форму закона основного уравнения динамики,
- 22. Формулировка: Производная момента импульса твердого тела по
- 23. Формулировка: Момент импульса системы сохраняется, т.е. не
- 24. Таблица аналогий величин и законов поступательного и
- 25. Второй закон
- 26. ЗАДАЧА К ободу диска радиусом 0,2
- 27. Дано:
- 28. Решение 1. Основное уравнение динамики вращательного движения
- 29. Задача На скамье Жуковского стоит человек и
- 30. Дано:
- 31. Решение Закон сохранения момента импульса
Слайд 5
1. МОМЕНТЫ СИЛЫ
Определим момент силы относительно
центра вращения О
(1)
M – векторная величина, определяемая
векторным произведением радиус-
вектора на силу
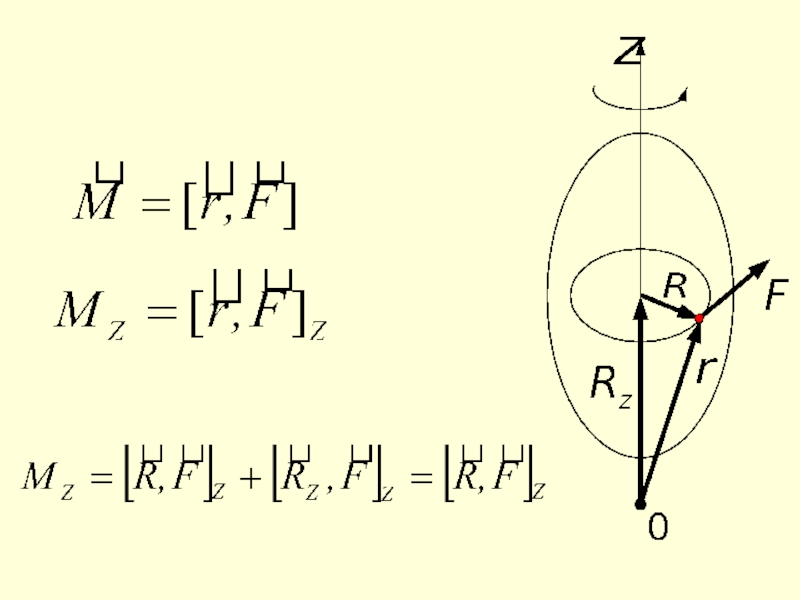
Слайд 7 Вначале определим момент силы
относительно точки (О):
величина определяемая векторным произведением радиус-вектора на силу.
(1)
Направление определяется правилом буравчика. Момент силы относительно оси вращения - это скалярная величина, равная проекции на эту ось вектора
(2)
Слайд 9Разложим на две составляющие.
Подставив (3) в выражение (2), получим
(4)
т.к. второй член в выражении (4) равен нулю.
Слайд 102. МОМЕНТ ИНЕРЦИИ.
МОМЕНТ ИМПУЛЬСА.
Определение момента инерции элементарного объема относительно оси
(1)
Слайд 11Так как абсолютно твердое тело недеформируемо, то момент инерции твердого тела
(2)
Слайд 14 Момент инерции тел относительно неподвижной оси, проходящей через центр симметрии. Тела
Слайд 15Момент импульса твердого тела
Вначале определяем момент импульса элементарного объема относительно оси
(3)
где – импульс элементарного объема.
Слайд 17
Затем, просуммировав по всем элементарным объемам, получим выражение для момента импульса
где I – момент инерции твердого тела.
Слайд 18Для кинетической энергии вращательного движения твёрдого тела
где Ic – момент инерции тела относительно оси вращения, проходящей через центр масс;
– скорость центра масс тела.
Слайд 19Основное уравнение динамики вращательного
Запишем второй закон Ньютона для каждого элементарного
(1)
где – касательная составляющая силы,
– тангенциальное ускорение.
Подставим выражение для в формулу (1) и
умножим обе части полученного выражения на Ri.
Тогда: (2)
Слайд 20Где
– момент силы относительно оси
вращения.
Момент можно представить как сумму моментов всех внутренних и внешних сил, действующих на точку.
Просуммировав выражение (2) по всем элементарным объемам получим основное уравнение динамики вращательного движения:
(3)
Слайд 21Получим другую форму закона основного уравнения динамики, используя понятие момента импульса
Перепишем выражение (3):
(4)
Слайд 22Формулировка: Производная момента импульса твердого тела по времени равна результирующему моменту
вращение тела.
При , ,т.е.
(5)
Это математическая запись закона сохранения момента импульса.
Слайд 23Формулировка: Момент импульса системы сохраняется, т.е. не изменяется с течением времени,
Из закона следует, что так как сохраняется постоянным произведение , то увеличение момента инерции приводит к пропорциональному уменьшению частоты вращения и наоборот.
Слайд 24Таблица аналогий величин и законов поступательного и вращательного движения
Поступательное
Масса m Момент инерции I
Скорость Угловая скорость
Ускорение Угловое ускорение
Сила Момент силы
Импульс Момент импульса
Слайд 26ЗАДАЧА
К ободу диска радиусом 0,2 м приложена постоянная касательная сила
Слайд 28Решение
1. Основное уравнение динамики вращательного движения твердого тела:
– момент инерции диска.
(2)
М – результирующий момент всех внешних сил. После подстановки (2) в (1) с учетом (1) получим
(3)
откуда