- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Тепломассообмен. Теплопроводность через плоские и цилиндрические стенки презентация
Содержание
- 1. Тепломассообмен. Теплопроводность через плоские и цилиндрические стенки
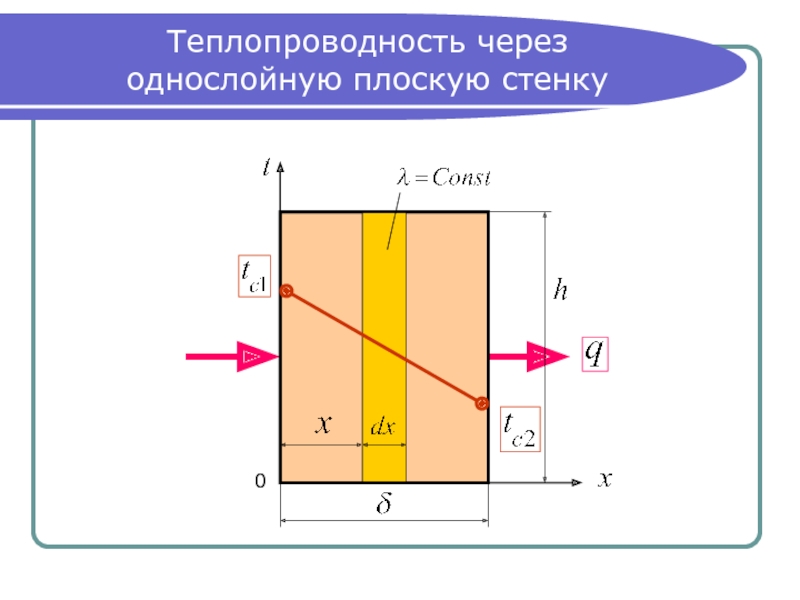
- 2. Теплопроводность через однослойную плоскую стенку 0
- 3. Дифференциальное уравнение теплопроводности (частный случай)
- 4. Условия однозначности Для
- 5. Удельный тепловой поток После 2-го
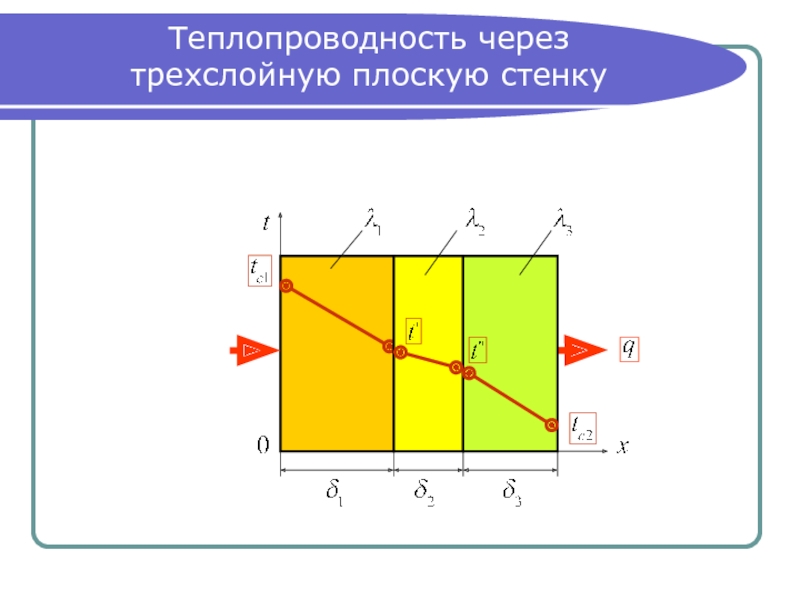
- 6. Теплопроводность через трехслойную плоскую стенку
- 7. Термическое сопротивление тепло-проводности 3-слойной плоской стенки Для
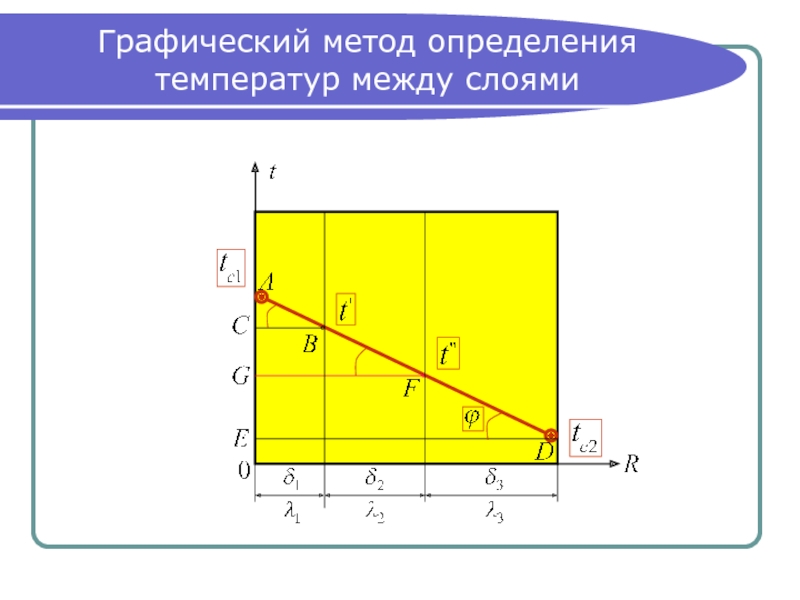
- 8. Графический метод определения температур между слоями
- 9. Определение температур между слоями
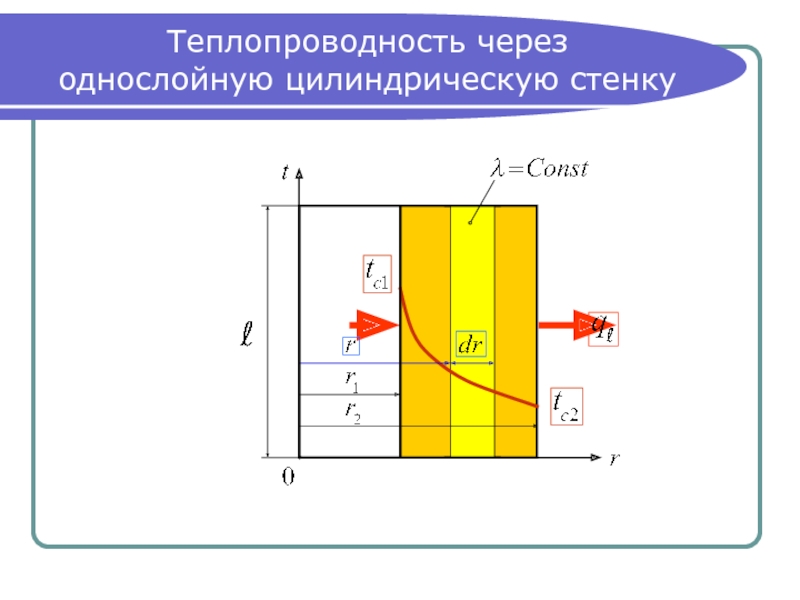
- 10. Теплопроводность через однослойную цилиндрическую стенку
- 11. Дифференциальное уравнение тепло-проводности для цилиндрической стенки
- 12. Условия однозначности Добавляем условия однозначности:
- 13. Преобразование дифференциального уравнения
- 14. Интегрирование После первого
- 15. Определение констант интегрирования
- 16. Тепловой поток Подставляем (8) в (7):
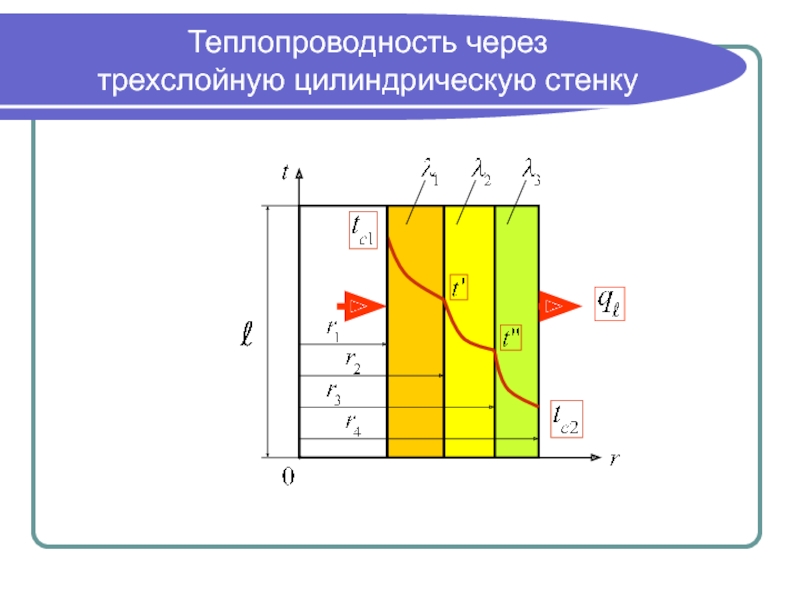
- 17. Теплопроводность через трехслойную цилиндрическую стенку
- 18. Линейное термическое сопротивление теплопроводности Для всех
Слайд 3Дифференциальное уравнение теплопроводности (частный случай)
Ранее мы получили общий вид
дифференциального уравнения
теплопроводности: .
В частном случае, для стационарного процесса ;
при отсутствии внутренних источников теплоты
из (1) при следует:
или развернутое выражение
оператора Лапласа: . (2)
Для бесконечной пластины: , то есть:
.
Дифференциальное уравнение
теплопроводности запишется в виде: . (3)
Слайд 4Условия однозначности
Для рассматриваемого случая добавляем
условия однозначности:
● Геометрические:
● Физические:
● Начальные: для стационарного процесса не требуются,
● Граничные условия I рода: при
при (4)
Найти:
После первого интегрирования
дифференциального уравнения (3) имеем: (5)
После разделения переменных в (5): (6)
Слайд 5Удельный тепловой поток
После 2-го интегрирования: (7)
Для определения констант интегрирования
подставляем (4) в (7): при
при (8)
откуда с учетом (5) имеем: (9)
По закону Фурье: откуда градиент (10)
Подставляя (10) в (9), получим: откуда:
или в форме закона Ома: (11)
Слайд 7Термическое сопротивление тепло-проводности 3-слойной плоской стенки
Для стационарного теплового режима
в первом
во втором слое
в третьем слое
Сложив правые и левые части этих трех выражений, получим:
или в форме закона Ома –
где термическое сопротивление теплопроводности
трехслойной плоской стенки, (м2К)/Вт : .
Слайд 9Определение температур
между слоями
Треугольники АBC и ADE подобны между
трех углов. Из их подобия следует:
или:
то есть , откуда находится температура .
Аналогично, из подобия треугольников AFG и ADE:
Отсюда находится температура .
Слайд 11Дифференциальное уравнение тепло-проводности для цилиндрической стенки
Общее выражение дифференциального уравнения
теплопроводности: (1)
Для стационарного процесса
при отсутствии внутренних источников теплоты
с учетом этих условий уравнение (1) примет вид .
Но , тогда частный вид дифференциального уравнения
теплопроводности:
Или через развернутое выражение оператора Лапласа:
. (2)
Слайд 12Условия однозначности
Добавляем условия однозначности:
● Геометрические условия:
● Физические условия:
● Начальные условия: для стационарного процесса не требуются;
● Граничные условия I рода:
при
(3)
при
Слайд 13Преобразование
дифференциального уравнения
В соответствии с геометрическими условиями однозначности,
в бесконечной цилиндрической
ется по координатам z и , тогда уравнение (2) примет вид:
(4). Найти:
Представим дифференциальное уравнение (4) в виде:
Умножим его на: и получим
окончательно
Слайд 14Интегрирование
После первого интегрирования имеем:
Или:
После потенцирования: (5)
Разделяем переменные в (5):
- это логарифмическая зависимость .
Слайд 15Определение констант интегрирования
Подставляем граничные условия (3) в (6):
при
Получим:
Находим отсюда константу интегрирования, которая
с учетом (5): (7)
По закону Фурье: или (8)
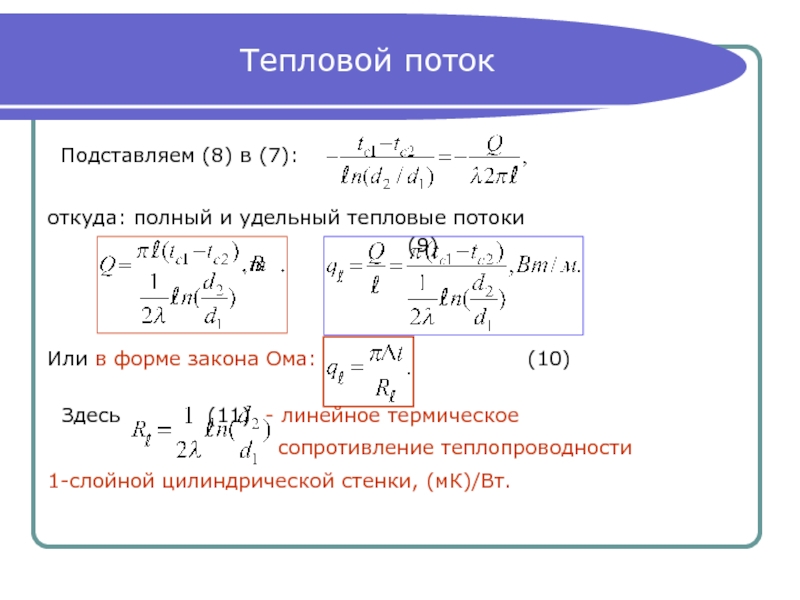
Слайд 16Тепловой поток
Подставляем (8) в (7):
откуда: полный и удельный тепловые
(9)
Или в форме закона Ома: (10)
Здесь (11) - линейное термическое
сопротивление теплопроводности
1-слойной цилиндрической стенки, (мК)/Вт.
Слайд 18Линейное термическое
сопротивление теплопроводности
Для всех слоев при стационарном тепловом режиме:
Тогда падения температур в каждом слое:
Сложив левые и правые части этих уравнений, получим:
тогда линейное термическое сопротивление
трехслойной цилиндрической стенки, (мК)/Вт
и температуры между слоями °С:
;