- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Тепломассообмен. Сложный теплообмен презентация
Содержание
- 1. Тепломассообмен. Сложный теплообмен
- 2. План 1. Критический диаметр изоляции. 2.
- 3. 1. Критический диаметр изоляции Тепловой изоляцией называют
- 4. Для тепловой изоляции используют любые материалы с
- 5. При неправильном выборе материала изоляции тепловые потери
- 6. Рассмотрим условие, при котором материал, используемый для
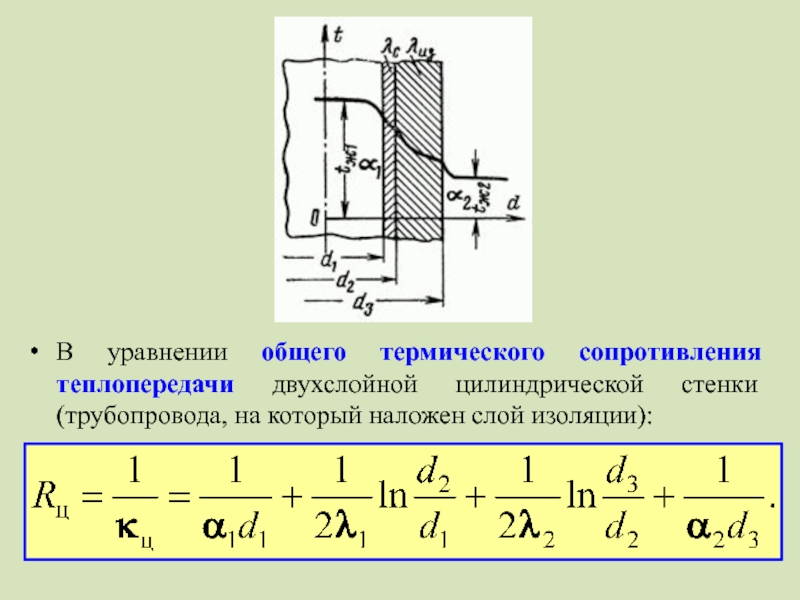
- 7. В уравнении общего термического сопротивления теплопередачи двухслойной цилиндрической стенки (трубопровода, на который наложен слой изоляции):
- 8. Из формулы следует, что при наложении изоляции
- 9. Возьмем первую производную от правой части уравнения
- 10. Критический диаметр изоляции, отвечающий экстремальной точке кривой
- 11. Критический диаметр тем меньше, чем меньше теплопроводность
- 12. Анализ уравнения показывает, что если
- 13. При равенстве dиз=dкр получаются максимальные тепловые потери
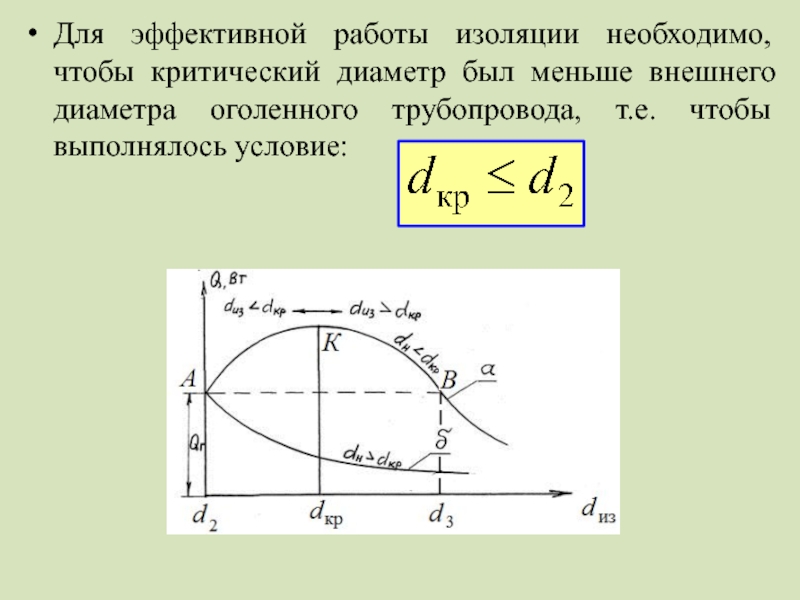
- 14. Для эффективной работы изоляции необходимо, чтобы критический
- 15. Для того чтобы изоляция вызывала уменьшение теплопотерь
- 16. Характер изменения тепловых потерь трубопровода ql в
- 17. Пример Для изоляции трубопровода диаметром d2= 30
- 18. Пример Критический диаметр изоляции
- 19. 2. Теплопередача через плоскую ребристую стенку Ребристые
- 20. Оребрение стенки с большим термическим сопротивлением позволяет:
- 21. Температура ребер изменяется по высоте, если t1>t2.
- 22. Отношение количества теплоты QTр, передаваемой поверхностью ребер
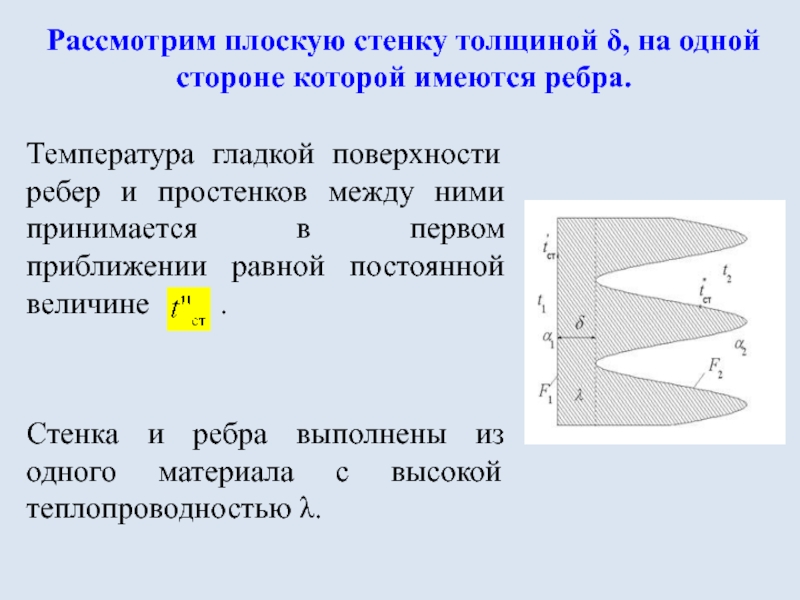
- 23. Температура гладкой поверхности ребер и простенков между
- 24. Коэффициент теплоотдачи на гладкой стороне α1.
- 25. Для стационарного режима можно записать три уравнения теплового потока:
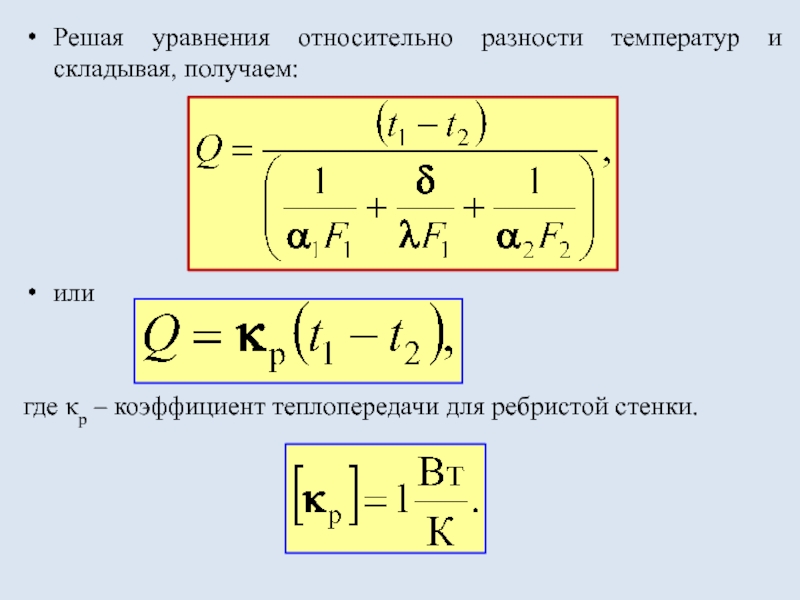
- 26. Решая уравнения относительно разности температур и складывая,
- 27. коэффициент теплопередачи для ребристой стенки
- 28. Тепловой поток отнесеннный к единице гладкой поверхности,
- 29. Для круглой трубы с наружным оребрением:
- 30. Приведенные формулы справедливы для ребер небольшой высоты.
- 31. Пример. Определить количество теплоты, передаваемое через
- 32. Решение. Коэффициент теплопередачи определяем по формуле:
- 33. При гладкой поверхности стенки κ определяем по
- 34. 3. Интенсификации процессов теплопередачи Практика эксплуатации тепловых
- 35. Возможности осуществления требований к интенсификации процессов теплопередачи
- 36. Вопрос о путях интенсификации процесса теплопередачи более
- 37. Если термическим сопротивлением стенки
- 38. Пример 1. В паровом котле коэффициент
- 39. Пример 1. Если для увеличения коэффициента
- 40. Пример 2. Рассмотрим аппараты, в которых
- 41. Пример 2. Данный пример показывает, что при
План 1. Критический диаметр изоляции. 2. Теплопередача через плоскую ребристую стенку. 3. Способы интенсификации процессов теплопередачи.
Слайд 2План
1. Критический диаметр изоляции.
2. Теплопередача через плоскую ребристую стенку.
3. Способы интенсификации
процессов теплопередачи.
Слайд 31. Критический диаметр изоляции
Тепловой изоляцией называют всякое покрытие горячей поверхности, которое
способствует снижению потерь теплоты в окружающую среду.
Слайд 4Для тепловой изоляции используют любые материалы с низкой теплопроводностью – асбест,
пробка, слюда, шлаковая или стеклянная вата, шерсть и др.
Анализ формулы полного линейного термического сопротивления теплопередачи цилиндрической стенки показывает, что тепловые потери изолированных трубопроводов уменьшаются не пропорционально увеличению толщины изоляции.
Анализ формулы полного линейного термического сопротивления теплопередачи цилиндрической стенки показывает, что тепловые потери изолированных трубопроводов уменьшаются не пропорционально увеличению толщины изоляции.
Слайд 5При неправильном выборе материала изоляции тепловые потери возрастут.
Это связано с тем,
что у изолированного трубопровода внешняя поверхность увеличивается и условия теплоотвода улучшаются.
Анализ показывает, что материал выбран правильно, если λиз удовлетворяет неравенству
где d2 – наружный диаметр трубопровода, а α2, и – коэффициент теплоотдачи от внешней поверхности к окружающей среде.
Анализ показывает, что материал выбран правильно, если λиз удовлетворяет неравенству
где d2 – наружный диаметр трубопровода, а α2, и – коэффициент теплоотдачи от внешней поверхности к окружающей среде.
Слайд 6Рассмотрим условие, при котором материал, используемый для изоляции трубы, будет уменьшать
тепловые потери.
Цилиндрическая труба покрыта однослойной изоляцией.
При постоянных α1, α2, d1, d2, λ1, λ2, t1 и t2 рассмотрим, как будет изменяться полное термическое сопротивление при изменении толщины изоляции.
Цилиндрическая труба покрыта однослойной изоляцией.
При постоянных α1, α2, d1, d2, λ1, λ2, t1 и t2 рассмотрим, как будет изменяться полное термическое сопротивление при изменении толщины изоляции.
Слайд 7В уравнении общего термического сопротивления теплопередачи двухслойной цилиндрической стенки (трубопровода, на
который наложен слой изоляции):
Слайд 8Из формулы следует, что при наложении изоляции термическое сопротивление слоя изоляции
возрастает на величину
это способствует снижению потерь теплоты, но одновременно термическое сопротивление теплоотдачи в окружающую среду уменьшается на величину
что связано с увеличением внешней поверхности (d3>d2).
это способствует снижению потерь теплоты, но одновременно термическое сопротивление теплоотдачи в окружающую среду уменьшается на величину
что связано с увеличением внешней поверхности (d3>d2).
Слайд 9Возьмем первую производную от правой части уравнения по d3 и приравнивая
ее к нулю, получаем:
Слайд 10Критический диаметр изоляции, отвечающий экстремальной точке кривой
определяется формулой:
Из формулы следует: критический
диаметр изоляции не зависит от размеров трубопровода.
Слайд 11Критический диаметр тем меньше, чем меньше теплопроводность изоляции и чем больше
теплоотдачи от наружной поверхности изоляции к окружающей среде.
Если вторая производная от Rц больше нуля. Следовательно, критический диаметр соответствует минимуму теплового сопротивления и максимуму теплового потока.
Если вторая производная от Rц больше нуля. Следовательно, критический диаметр соответствует минимуму теплового сопротивления и максимуму теплового потока.
Слайд 12Анализ уравнения
показывает, что если наружный диаметр изоляции dиз увеличивается, но остается
меньше dкр, то тепловые потери возрастают и будут больше тепловых потерь голого трубопровода (кривая АК).
Слайд 13При равенстве dиз=dкр получаются максимальные тепловые потери в окружающую среду (точка
К).
При дальнейшем увеличении наружного диаметра изоляции dиз>dкр теплопотери будут меньше, чем при dиз=dкр (кривая ВК).
Только при dиз=d3 тепловые потери вновь станут такими же, как и для неизолированного трубопровода.
При дальнейшем увеличении наружного диаметра изоляции dиз>dкр теплопотери будут меньше, чем при dиз=dкр (кривая ВК).
Только при dиз=d3 тепловые потери вновь станут такими же, как и для неизолированного трубопровода.
Слайд 14Для эффективной работы изоляции необходимо, чтобы критический диаметр был меньше внешнего
диаметра оголенного трубопровода, т.е. чтобы выполнялось условие:
Слайд 15Для того чтобы изоляция вызывала уменьшение теплопотерь цилиндрической стенки по сравнению
с голым трубопроводом, при данном наружном диаметре трубы d2 и заданным коэффициентом теплоотдачи α2 необходимо, чтобы
Слайд 16Характер изменения тепловых потерь трубопровода ql в зависимости от толщены слоя
при рациональном и неверном подборе материала показан на рисунке
Слайд 17Пример
Для изоляции трубопровода диаметром d2= 30 мм имеется шлаковая вата, теплопроводность
которой λиз= 0,1 Вт/(м·К), коэффициент теплоотдачи α2= 4,0 Вт/(м2·К).
Целесообразно ли применять в данном случае в качестве изоляции шлаковую вату?
Целесообразно ли применять в данном случае в качестве изоляции шлаковую вату?
Слайд 18Пример
Критический диаметр изоляции
Так как dкр>d2, шлаковую вату в рассматриваемом случае применять
нецелесообразно.
Для нашей задачи λиз должна быть меньше
Для нашей задачи λиз должна быть меньше
Слайд 192. Теплопередача через плоскую ребристую стенку
Ребристые поверхности применяются для выравнивания термических
сопротивлений теплоотдачи с обеих сторон стенки, когда одна поверхность омывается капельной жидкостью с большим коэффициентом теплоотдачи, а другая поверхность омывается газом с малым коэффициентом теплоотдачи, создающим большое термическое сопротивление.
Слайд 20Оребрение стенки с большим термическим сопротивлением позволяет:
увеличить ее поверхность соприкосновения с
горячим (или холодным) теплоносителем;
уменьшить общее тепловое сопротивление теплопередачи;
увеличить тепловые потоки.
уменьшить общее тепловое сопротивление теплопередачи;
увеличить тепловые потоки.
Слайд 21Температура ребер изменяется по высоте, если t1>t2.
У основания ребра температура равна
температуре поверхности стенки .
У вершины ребра температура будет значительно меньше и равна .
Участки поверхности ребра у основания передают больше теплоты, чем участки у ребра вершины.
У вершины ребра температура будет значительно меньше и равна .
Участки поверхности ребра у основания передают больше теплоты, чем участки у ребра вершины.
Слайд 22Отношение количества теплоты QTр, передаваемой поверхностью ребер в окружающую среду, к
теплоте QTп.р., которую эта поверхность могла передать при постоянной температуре, равной температуре у основания ребер, называется коэффициентом эффективности ребер:
Коэффициент эффективности ребер всегда меньше единицы.
Для коротких ребер, выполненных из материала с высокой теплопроводностью, коэффициент эффективности близок к единице.
Коэффициент эффективности ребер всегда меньше единицы.
Для коротких ребер, выполненных из материала с высокой теплопроводностью, коэффициент эффективности близок к единице.
Слайд 23Температура гладкой поверхности ребер и простенков между ними принимается в первом
приближении равной постоянной величине .
Стенка и ребра выполнены из одного материала с высокой теплопроводностью λ.
Стенка и ребра выполнены из одного материала с высокой теплопроводностью λ.
Рассмотрим плоскую стенку толщиной δ, на одной стороне которой имеются ребра.
Слайд 24Коэффициент теплоотдачи на гладкой стороне α1.
Коэффициент теплоотдачи ребер α2.
Площадь гладкой поверхности
F1.
Площадь поверхности ребер и промежутков между ними F2.
Температура горячего теплоносителя t1.
Температура холодного теплоносителя t2.
Площадь поверхности ребер и промежутков между ними F2.
Температура горячего теплоносителя t1.
Температура холодного теплоносителя t2.
Слайд 26Решая уравнения относительно разности температур и складывая, получаем:
или
где
κр – коэффициент теплопередачи для ребристой стенки.
Слайд 28Тепловой поток отнесеннный к единице гладкой поверхности, то коэффициент теплопередачи для
ребристой стенки равен
Тепловой поток отнесённый к единице ребристой поверхности, то коэффициент теплопередачи для ребристой стенки равен
Тепловой поток отнесённый к единице ребристой поверхности, то коэффициент теплопередачи для ребристой стенки равен
Слайд 29Для круглой трубы с наружным оребрением:
откуда
где d1 –
внутренний диаметр трубы; d2 – наружный диаметр трубы.
Слайд 30Приведенные формулы справедливы для ребер небольшой высоты.
Отношение оребренной поверхности F2 к
гладкой F1 называется коэффициентом оребрения.
Точное значение коэффициента теплопередачи для ребристых поверхностей может быть определено только экспериментальным путем.
Точное значение коэффициента теплопередачи для ребристых поверхностей может быть определено только экспериментальным путем.
Слайд 31Пример.
Определить количество теплоты, передаваемое через 1 м2 ребристой стенки, коэффициент оребрения
которой F2/F1=12.
Стенка выполнена из чугуна с теплопроводностью λ=63 Вт/(м·К) и толщиной δ=12 мм.
Коэффициент теплоотдачи от рабочего тела к стенке α1=250 Вт/(м2·К) и α2=12 Вт/(м2·К).
Температура рабочего тела t1=117°С, а температура воздуха t2=17°С.
Стенка выполнена из чугуна с теплопроводностью λ=63 Вт/(м·К) и толщиной δ=12 мм.
Коэффициент теплоотдачи от рабочего тела к стенке α1=250 Вт/(м2·К) и α2=12 Вт/(м2·К).
Температура рабочего тела t1=117°С, а температура воздуха t2=17°С.
Слайд 32Решение.
Коэффициент теплопередачи определяем по формуле:
Считаем, что тепловой поток отнесен к гладкой
поверхности.
Плотность теплового потока определяем по уравнению:
Плотность теплового потока определяем по уравнению:
Слайд 33При гладкой поверхности стенки κ определяем по уравнению:
Плотность теплового потока для
гладкой стенки
Оребрение стенки увеличило теплопередачу в 7,9 раза.
В действительности с учетом изменения коэффициента теплоотдачи и температуры вдоль ребра эффект от оребрения может быть значительно меньше.
Оребрение стенки увеличило теплопередачу в 7,9 раза.
В действительности с учетом изменения коэффициента теплоотдачи и температуры вдоль ребра эффект от оребрения может быть значительно меньше.
Слайд 343. Интенсификации процессов теплопередачи
Практика эксплуатации тепловых аппаратов требует наилучших условий передачи
теплоты от горячего теплоносителя к холодному.
При решении практических задач теплопередачи в одних случаях требуется интенсифицировать процесс, в других, наоборот, всячески тормозить.
Слайд 35Возможности осуществления требований к интенсификации процессов теплопередачи вытекают из закономерностей протекания
основных способов передачи теплоты.
Термическое сопротивление стенки можно уменьшить путем уменьшения толщины стенки и увеличения коэффициента теплопроводности материала.
Теплоотдача соприкосновением может быть интенсифицирована путем перемешивания жидкости и увеличения скорости движения.
При тепловом излучении – путем повышения степени черноты и температуры излучающей поверхности.
Слайд 36Вопрос о путях интенсификации процесса теплопередачи более сложный.
Правильное его решение может
быть получено лишь на основе тщательного анализа частных условий теплопередачи.
Пример:
Рассмотрим формулу коэффициента теплопередачи для плоской стенки:
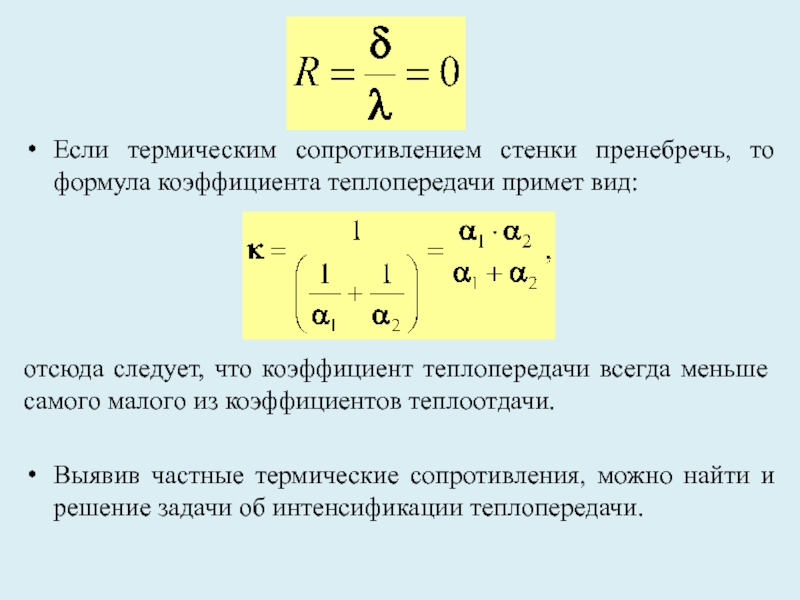
Слайд 37
Если термическим сопротивлением стенки пренебречь, то формула коэффициента теплопередачи примет вид:
отсюда
следует, что коэффициент теплопередачи всегда меньше самого малого из коэффициентов теплоотдачи.
Выявив частные термические сопротивления, можно найти и решение задачи об интенсификации теплопередачи.
Выявив частные термические сопротивления, можно найти и решение задачи об интенсификации теплопередачи.
Слайд 38Пример 1.
В паровом котле коэффициент теплоотдачи от топочных газов к стенке
равен α1=30 Вт/(м2·К), а от стенки к кипящей воде α2=5000 Вт/(м2·К), теплопроводность стальной стенки λ=50 Вт/(м·К), толщина стенки δ=0,02 м. Стенку считаем плоской.
При этих условиях коэффициент теплопередачи κ=29,5 Вт/(м2·К), т.е. он меньше наименьшего α.
При этих условиях коэффициент теплопередачи κ=29,5 Вт/(м2·К), т.е. он меньше наименьшего α.
Слайд 39Пример 1.
Если для увеличения коэффициента теплопередачи κ улучшить условия теплоотдачи от
стенки к воде или применять более тонкую стенку из теплопроводного материала, то этими способами увеличить κ не удается.
Существенно повысить κ можно лишь тогда, когда улучшим передачу теплоты от топочных газов к стенке.
Существенно повысить κ можно лишь тогда, когда улучшим передачу теплоты от топочных газов к стенке.
Слайд 40Пример 2.
Рассмотрим аппараты, в которых коэффициенты α1 и α2 велики.
В водяном
конденсаторе со стороны воды α1=5000 Вт/(м2·К), а со стороны пара α2=10000 Вт/(м2·К).
Если стенку такого конденсатора изготовить из стали толщиной 20 мм, то κ=1428 Вт/(м2·К),
если взять стенку толщиной 3 мм, то κ=2770 Вт/(м2·К),
а если сталь заменить красной медью и взять стенку толщиной 1 мм, то κ=3400 Вт/(м2·К).
Если стенку такого конденсатора изготовить из стали толщиной 20 мм, то κ=1428 Вт/(м2·К),
если взять стенку толщиной 3 мм, то κ=2770 Вт/(м2·К),
а если сталь заменить красной медью и взять стенку толщиной 1 мм, то κ=3400 Вт/(м2·К).
Слайд 41Пример 2.
Данный пример показывает, что при больших значениях коэффициентов теплоотдачи коэффициент
теплопередачи в значительной степени зависит от теплопроводности стенки.
При изучении условий передачи теплоты в тепловых аппаратах для интенсификации теплопередачи необходимо стремиться уменьшить наибольшее сопротивление.
При изучении условий передачи теплоты в тепловых аппаратах для интенсификации теплопередачи необходимо стремиться уменьшить наибольшее сопротивление.
