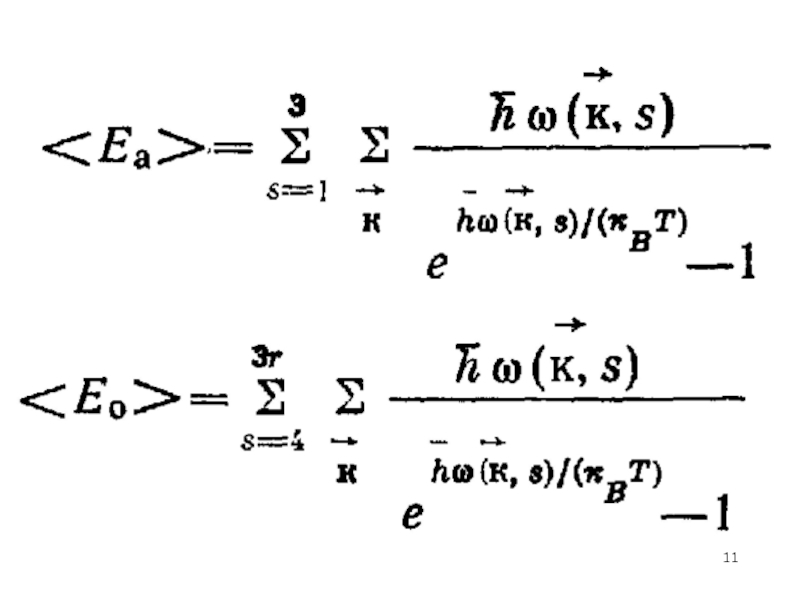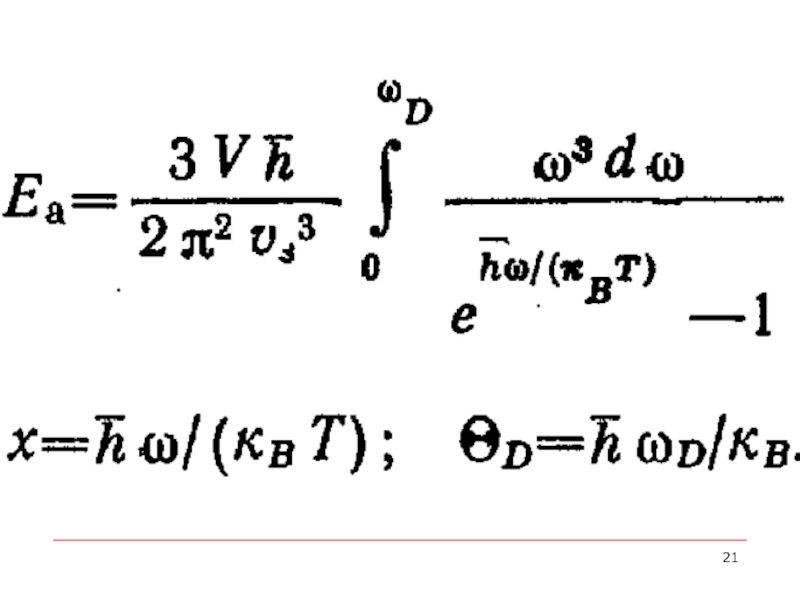- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Теплоемкость. Модель Дебая. Закон Дебая. Экспериментальные методы исследований фононного спектра презентация
Содержание
- 1. Теплоемкость. Модель Дебая. Закон Дебая. Экспериментальные методы исследований фононного спектра
- 4. При фиксированном m производящей функцией последовательности является
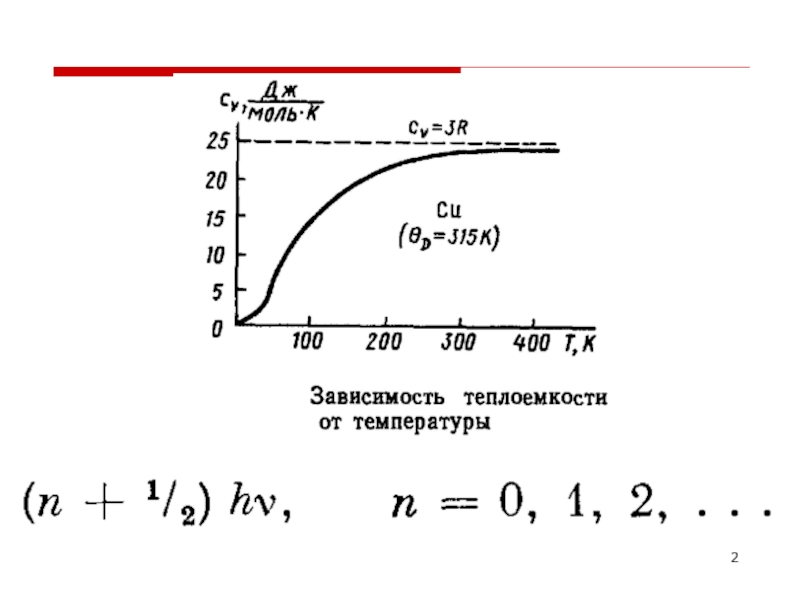
- 6. ТЕПЛОЕМКОСТЬ ПРИ ВЫСОКИХ ТЕМПЕРАТУРАХ
- 7. ТЕПЛОЕМКОСТЬ ПРИ НИЗКИХ ТЕМПЕРАТУРАХ
- 8. Θ- характеристическая температура Эйнштейна
- 9. МОДЕЛь ДЕБАЯ ИНТЕРПОЛЯЦИОННАЯ СХЕМА ДЕБАЯ В
- 10. 3rN-3 3
- 12. кристалла dN –число нормальных колебаний в интервале
- 15. Спектральная функция распределения частот Число нормальных колебаний в интервале ω − ω+dω
- 16. Усреднение по всем направлениям и типам колебаний
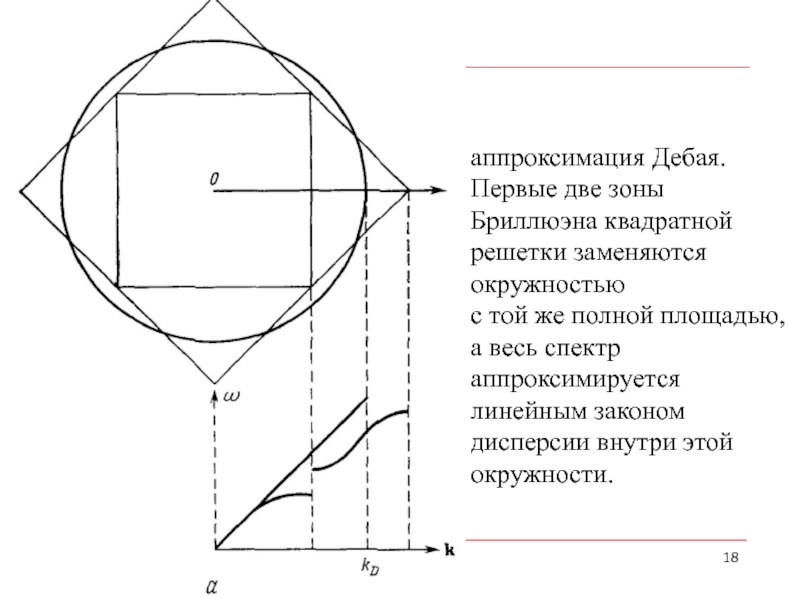
- 18. аппроксимация Дебая. Первые две зоны Бриллюэна квадратной
- 22. Интерполяционная формула Дебая
- 23. Функция Дебая ΘD/T максимальный квант энергии
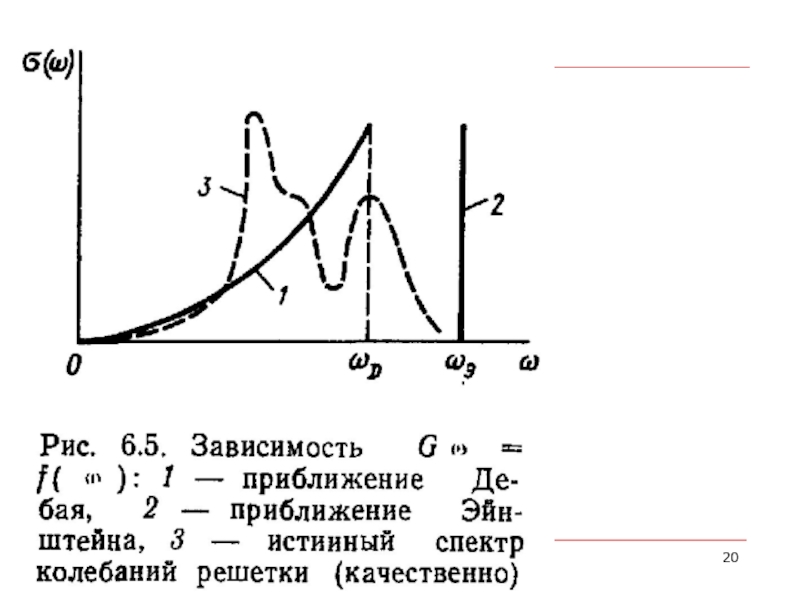
- 29. МОДЕЛЬ ЭЙНШТЕЙНА (еще раз)
- 30. При очень низких температурах моды с частотами
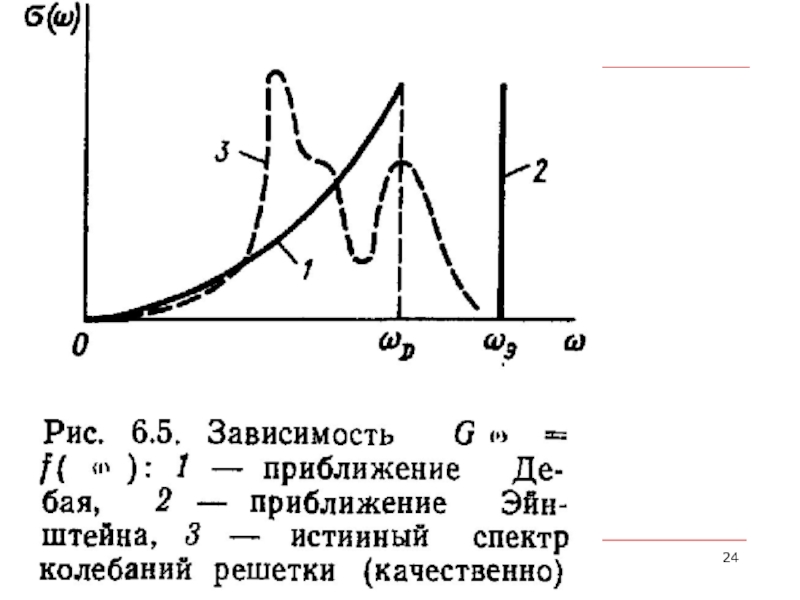
- 32. аппроксимация Дебая. Первые две зоны Бриллюэна квадратной
- 33. аппроксимация Дебая для акустической ветви и аппроксимация
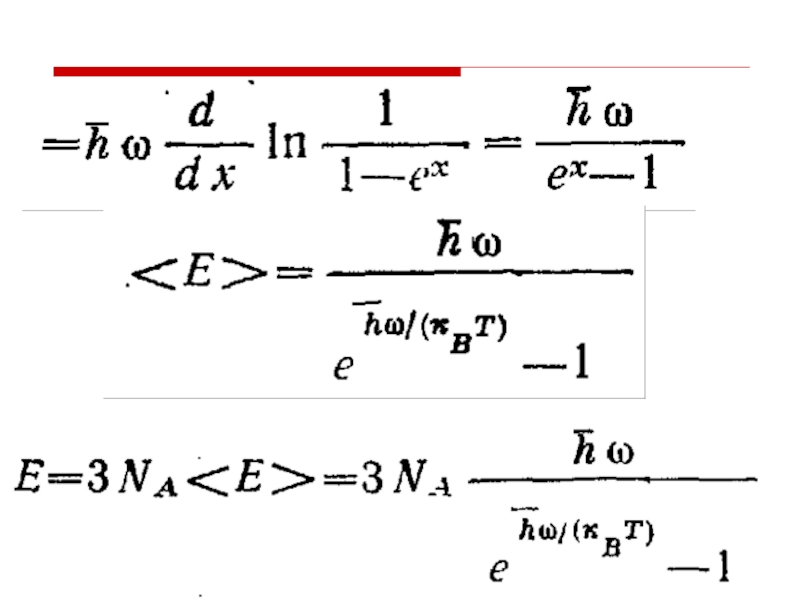
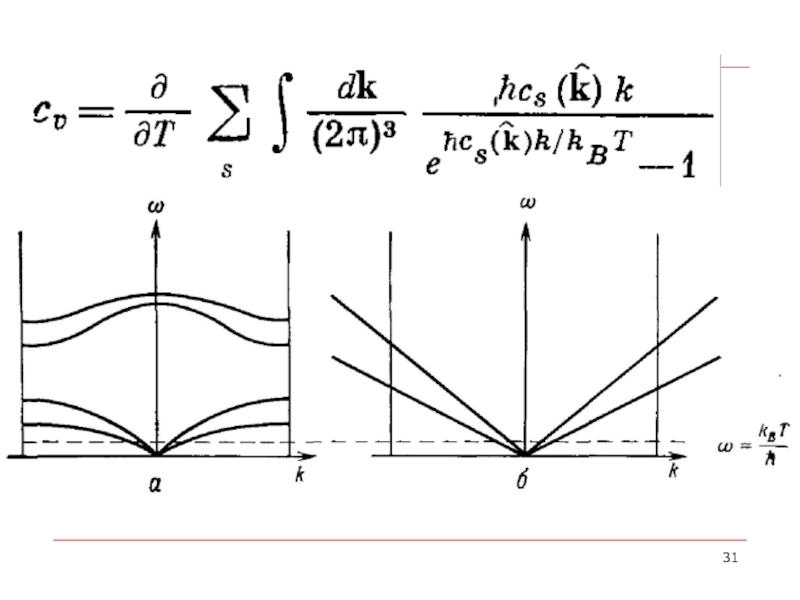
- 34. КВАНТОВАЯ ТЕОРИЯ ГАРМОНИЧЕСКОГО КРИСТАЛЛА Вывод формулы для теплоемкости, основанный на представлении о фононах
- 36. для плотности энергии гармонического кристалла
- 37. 2
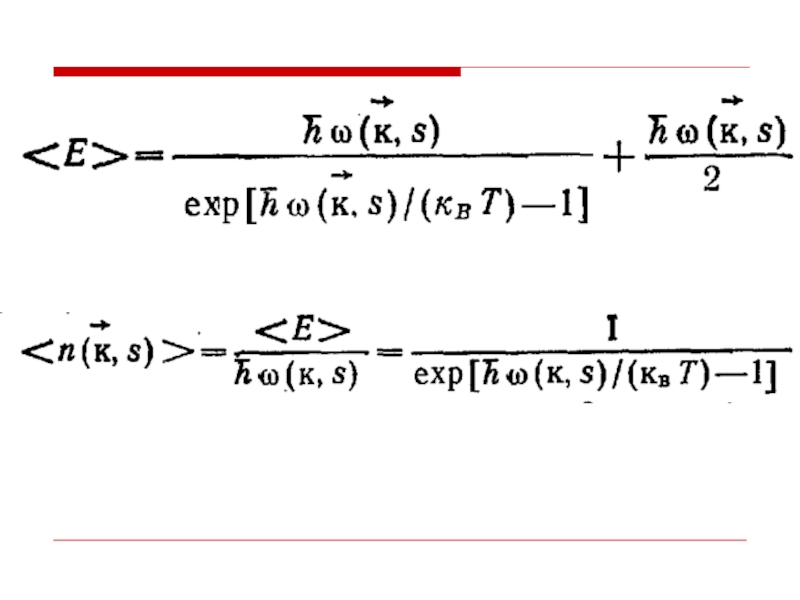
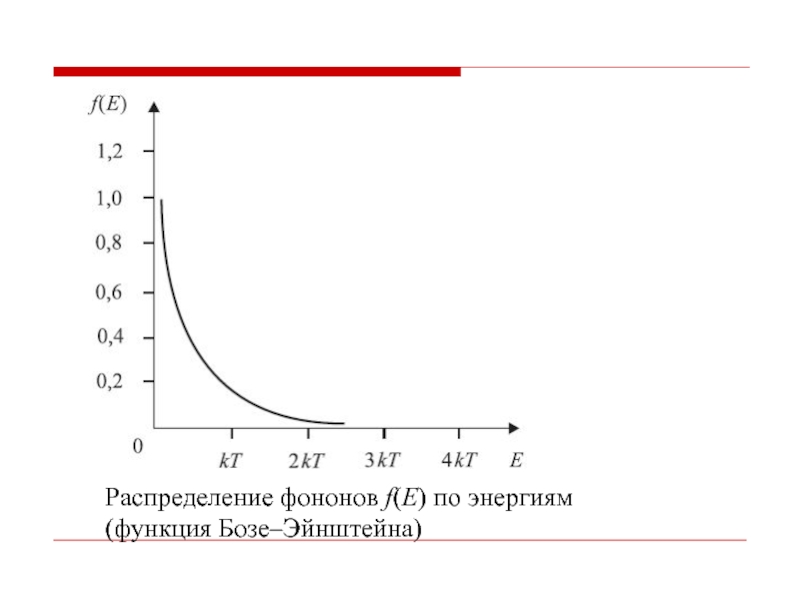
- 41. Распределение фононов f(E) по энергиям (функция Бозе–Эйнштейна)
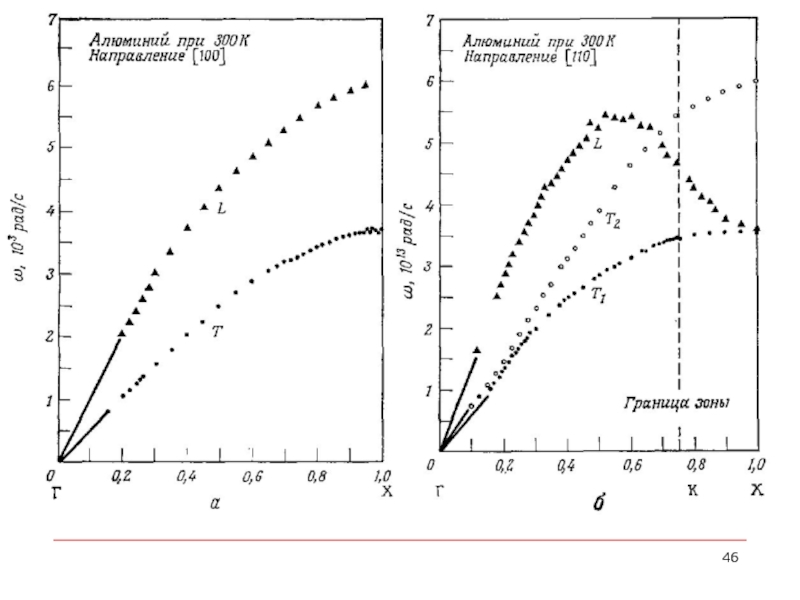
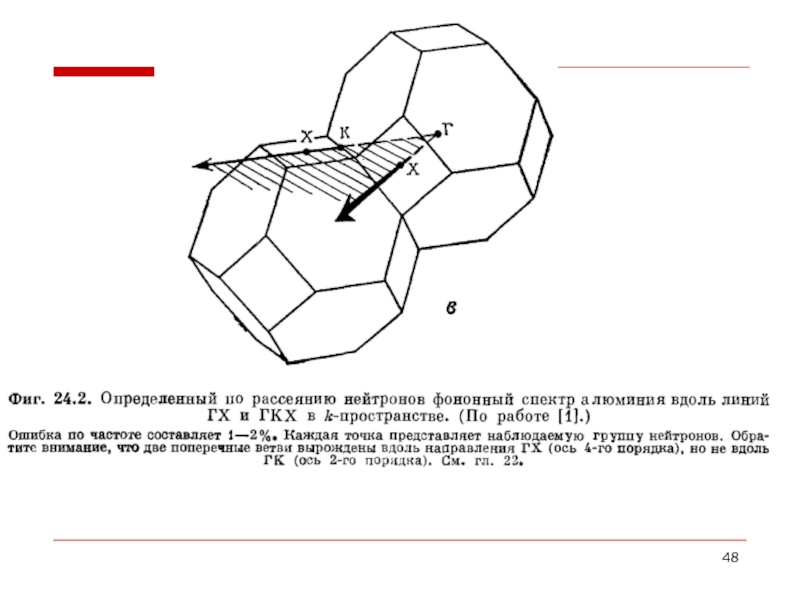
- 42. Исследования рассеяния нейтронов и фотонов представляют собой
- 47. Вид фононного спектра в кристалле кремния (Si)
- 49. 1/с3 — обратная третья степень длинноволновой фазовой
- 50. при очень низких температурах Cυ ≈ f(T3)
При фиксированном m производящей функцией последовательности является
Слайд 1
Тема 3
Теплоемкость. Модель Дебая. Закон Дебая. Экспериментальные методы исследований фононного спектра.
Слайд 9МОДЕЛь ДЕБАЯ
ИНТЕРПОЛЯЦИОННАЯ СХЕМА ДЕБАЯ
В модели Дебая все ветви колебательного спектра
заменяются тремя ветвями с одним и тем же линейным законом дисперсии
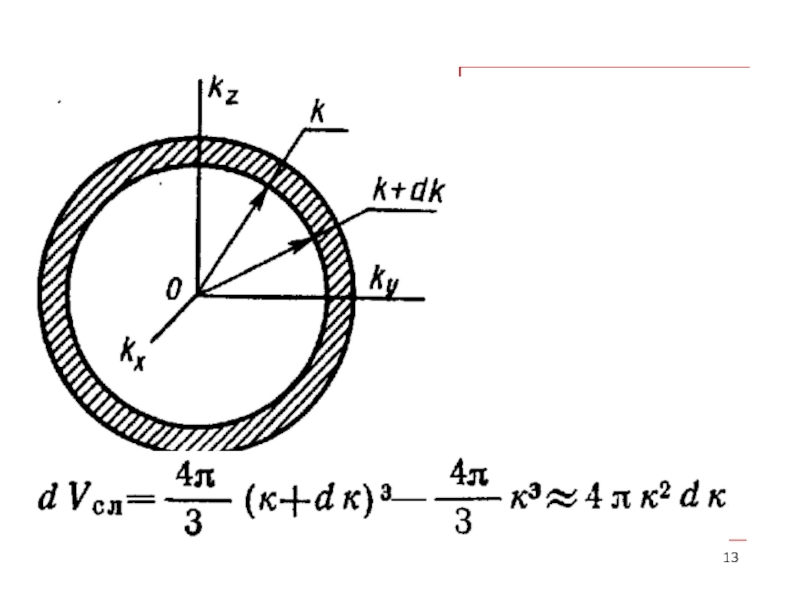
Слайд 12кристалла
dN –число нормальных колебаний в интервале от k до k+dk
Интегрирование
производится по зоне Бриллюэна
Слайд 18аппроксимация Дебая. Первые две зоны Бриллюэна квадратной решетки заменяются окружностью
с
той же полной площадью, а весь спектр аппроксимируется линейным законом дисперсии внутри этой
окружности.
окружности.
Слайд 23Функция Дебая
ΘD/T
максимальный квант энергии , способный возбудить колебания решетки
выражает энергию
= удельную теплоемкость при всех температурах через один эмпирический параметр
Слайд 30При очень низких температурах моды с частотами hωs(k) >> kвТ дают
пренебрежимо малый вклад
1. Даже для кристалла с полиатомным базисом в сумме по s можно не
учитывать оптические моды, поскольку их частоты ограничены снизу
2. Закон дисперсии трех акустических ветвей ω = ωs(k) -? предельной формой для больших длин волн ω = cs(k) k.
3. Интегрирование по первой зоне Бриллюэна в k-пространстве можно заменить интегрированием по всему k-пространству
Слайд 32аппроксимация Дебая. Первые две зоны Бриллюэна квадратной решетки заменяются окружностью
с
той же полной площадью, а весь спектр аппроксимируется линейным законом дисперсии внутри этой
окружности.
окружности.
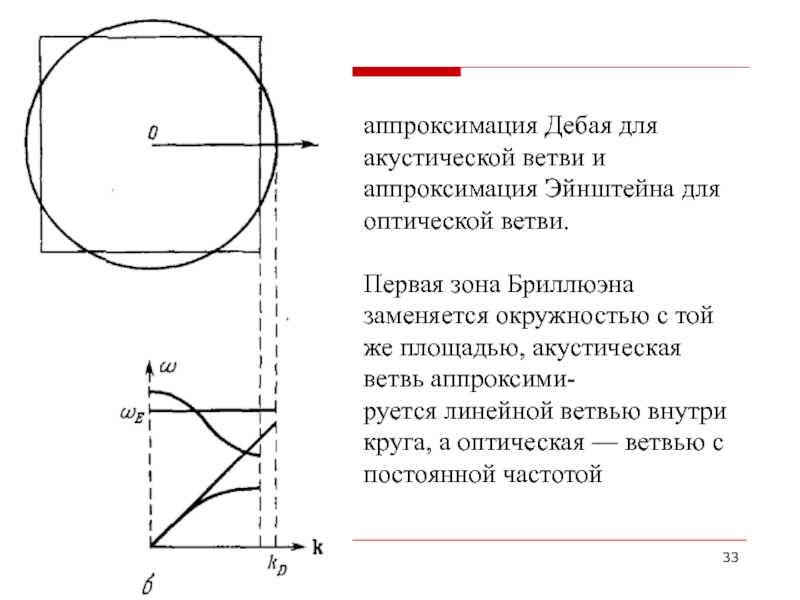
Слайд 33аппроксимация Дебая для акустической ветви и аппроксимация Эйнштейна для оптической ветви.
Первая зона Бриллюэна заменяется окружностью с той же площадью, акустическая ветвь аппроксими-
руется линейной ветвью внутри круга, а оптическая — ветвью с постоянной частотой
Слайд 34КВАНТОВАЯ ТЕОРИЯ ГАРМОНИЧЕСКОГО КРИСТАЛЛА
Вывод формулы для теплоемкости, основанный на представлении о
фононах
Слайд 42Исследования рассеяния нейтронов и фотонов представляют собой различные способы анализа фононного
спектра - они характеризуются совершенно разными соотношениями между энергией и импульсом
Слайд 47Вид фононного спектра в кристалле кремния (Si)
Знание фононных спектров необходимо
для анализа и расчета многих физических свойств твердых тел − оптических, тепловых, электрических и т. д. В экспериментах определяют дисперсионные кривые продольных и поперечных волн в направлениях высокой симметрии. Затем эта информация используется для численного расчета плотности состояний . При интерпретации спектров колебаний очень важным этапом является анализ критических точек.
Слайд 491/с3 — обратная третья степень длинноволновой фазовой скорости, усредненной по телесному
углу и трем акустическим модам
