- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Теорія псевдопотенціалів презентация
Содержание
- 1. Теорія псевдопотенціалів
- 2. Зміст Для чого потрібні псевдопотенціали
- 3. Для чого потрібні псевдопотенціали ? Теорія
- 4. Теорема Блоха: при трансляційній інваріантності на вектор
- 5. Різниця між реальними потенціалами і псевдопотенціалами
- 6. Псевдопотенціали з перших принципів
- 7. ОПХ-псевдопотенціали з перших принципів
- 8. Формалізм повністю ортогоналізованих плоских хвиль
- 9. Переваги формалізму повністю ортогоналізованих плоских
- 10. Умови, що накладаються на “вибрані”
- 11. Недоліки формалізму ПОПХ
- 12. Модельний підхід у теорії псевдопотенціалів
- 13. Використання теорії збурень по псевдопотенціалу Повна
- 14. Псевдопотенціал Краско-Гурського Г.Л.Краско, З.А.Гурский.
- 15. Псевдопотенціал Краско-Гурського Умови на
- 16. Прогрес у теорії псевдопотенціалів
- 17. Різниця між реальними потенціалами і зберігаючими
- 18. Зберігаючі норму псевдопотенціалами Умова збереження заряду
- 19. Алгоритм генерування зберігаючих норму псевдопотенціалів Числовий
- 20. Алгоритм генерування зберігаючих норму псевдопотенціалів Знаходження
- 21. Аналітичне задання псевдофункцій Умови: Аналітичне представлення:
- 22. Аналітичне задання псевдофункцій Як правило береться лише 3-4 члени в розкладі: максимальне
- 23. Факторизація псевдопотенціалів Така процедура потрібна для
- 24. Резюме для ЗН псевдопотенціалів На даний
- 25. Дві енергії відліку для побудови
- 26. Не-зберігаючі норму псевдопотенціалами ЗН ПП Ультрам’які ПП
- 27. Не-зберігаючі норму псевдопотенціалами Необхідно врахувати відмінність у нормі при r
Слайд 1Теорія псевдопотенціалів
Тарас Брик
Інститут фізики
конденсованих систем НАН України
Львів, 6 травня 2009р.
Слайд 2
Зміст
Для чого потрібні псевдопотенціали (ПП)?
Модельні ПП
Зберігаючі норму ПП
Перші ab initio псевдопотенціали та їхні проблеми
PAW-потенціали
Слайд 3
Для чого потрібні псевдопотенціали ?
Теорія псевдопотенціалів є ефективним підходом для знаходження
Основна мета введення псевдопотенціалів:
для
Стани валентних електронів відповідають найнижчим по енергіях розв’язкам рівняння для псевдохвильових функцій з
Рівняння Кона-Шема для валентного електрона в кристалі:
Розклад по плоских хвилях є
неефективним через кулонівську асимптотику для .
Слайд 4Теорема Блоха: при трансляційній інваріантності на вектор τ одноелектронна функція дістає
Можна ввести періодичну функцію
Тоді
Фур’є-розклади густини
потенціалу
На практиці береться скінчене число плоских хвиль
Розклади хвильових функцій по плоским хвилям
Слайд 5
Різниця між реальними потенціалами і псевдопотенціалами
Реальні потенціали у рівнянні КШ будуть
Типи псевдопотенціалів (ПП):
Зберігаючі норму (норма псевдохвильових та хвильових функцій ідентична)
Ультрам’які (не-зберігаючі норму)
Точні ПП
Слайд 6
Псевдопотенціали з перших принципів
J.Phillips, L.Kleinman (1959) – псевдопотенціали, побудовані
Сильнолокалізовані функції іонного кістяка 1s, 2s, … вважаються власними функціями гамільтоніана кристалу:
Ортогоналізовані до остовних станів плоскі хвилі:
Хвильова функція валентних електронів:
Слайд 7
ОПХ-псевдопотенціали з перших принципів
Основні недоліки ОПХ-псевдопотенціалів:
Залежність від шуканої
Переповненість базисного набору ОПХ
Слайд 8
Формалізм повністю ортогоналізованих плоских хвиль
M.D.Girardeau // J.Math.Phys., 1971, v.12,
Б.О.Гурський, З.О.Гурський // УФЖ, 1976, т.21, с.1603-1608
Основна ідея формалізму ПОПХ:
Для кристалів:
Повністю ортогоналізовані плоскі хвилі:
Слайд 9
Переваги формалізму повністю ортогоналізованих плоских хвиль
Унітарне перетворення між
ПОПХ –псевдопотенціал не залежить від шуканої енергії.
Існує строге співвідношення між хвильовими функціями та псевдофункціями. Знаючи псевдогустину завжди можна відтворити електронну густину системи.
Перерозподіл електронної густини викликаний ортогоналізаційними ефектами задовольняє правилу сум.
Слайд 10
Умови, що накладаються на “вибрані” вектори зворотньої гратки Gα
T.Bryk,
Слайд 11
Недоліки формалізму ПОПХ
Необхідність співставлення блохівським функціям
Наявність лінійних по блохівських функціях членів у операторі L приводить до залежності ПОПХ-псевдопотенціалів від фази функцій , що вимагає додаткової оптимізації псевдопотенціалів.
Слайд 12
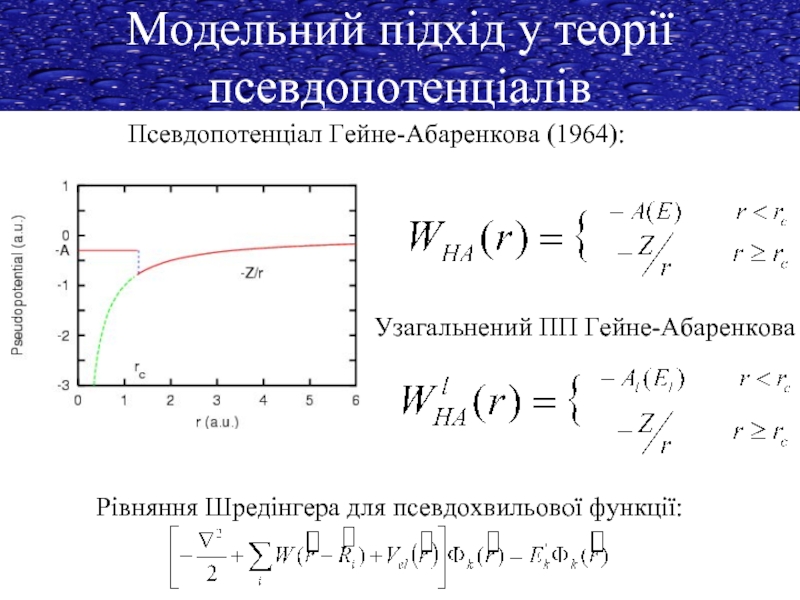
Модельний підхід у теорії псевдопотенціалів
Псевдопотенціал Гейне-Абаренкова (1964):
Узагальнений ПП Гейне-Абаренкова
Рівняння Шредінгера
Слайд 13
Використання теорії збурень по псевдопотенціалу
Повна енергія електрон-іонної системи:
Енергія зонної структури:
Слайд 14
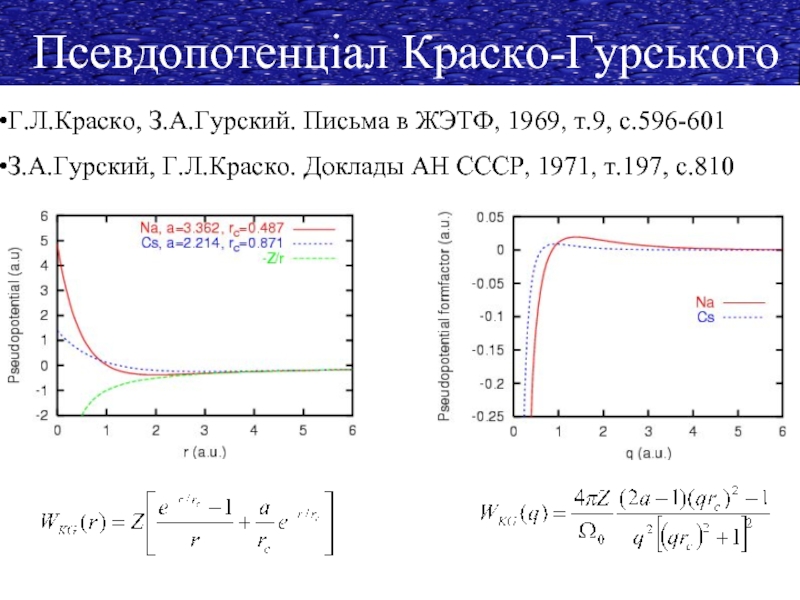
Псевдопотенціал Краско-Гурського
Г.Л.Краско, З.А.Гурский. Письма в ЖЭТФ, 1969, т.9, с.596-601
З.А.Гурский,
Слайд 15
Псевдопотенціал Краско-Гурського
Умови на знаходження параматрів та
Безвузловій псевдохвильовій функції відповідає те ж значення енергії, що і для хвильової функції валентного електрона.
Наявність мінімум повної енергії при експериментально спостережувальній сталій гратки:
Слайд 16
Прогрес у теорії псевдопотенціалів
після формалізму ПОПХ
L.Kleinman, D.M. Bylander: Exact
P.Blochl: Formalism of Projector-augmented waves (PAW), 1994
D.Hamann, M. Schluter, C.Chiang: Norm-conserving pseudopotentials (1979):
D.Vanderbilt: Ultrasoft non-norm-conserving pseudopotentials (1990):
Слайд 17
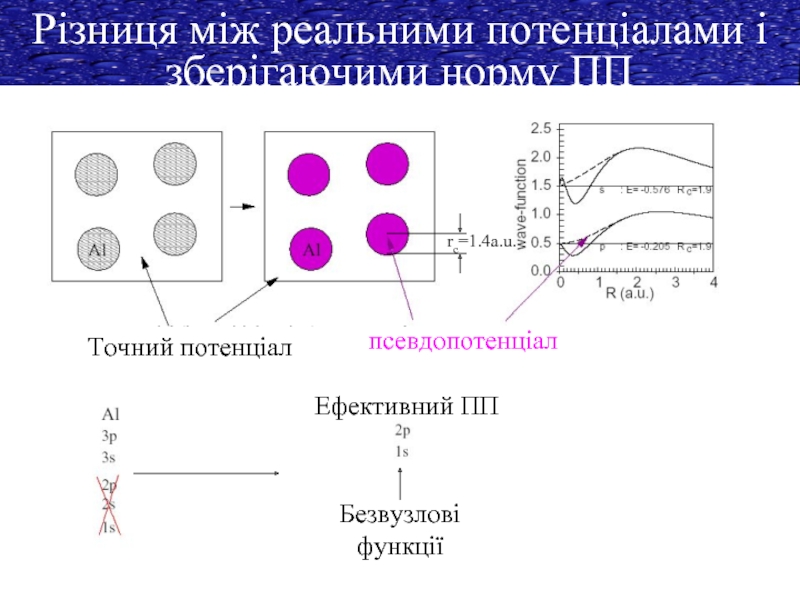
Різниця між реальними потенціалами і зберігаючими норму ПП
псевдопотенціал
Точний потенціал
rc=1.4a.u.
Ефективний ПП
Безвузлові функції
Слайд 18
Зберігаючі норму псевдопотенціалами
Умова збереження заряду
Важливий наслідок ЗНПП:
–справжня хвильова функція
– псевдохвильова функція
В
Слайд 19
Алгоритм генерування зберігаючих норму псевдопотенціалів
Числовий розв’язок рівняння КШ для атома (Al,Si,…)
Вибирається енергія для якої буде генеруватись псевдофункція;
Заміна атомної хвильової функції на безвузлову функцію для r
умова збереження норми
Знаходження ПП через псевдохвильову функцію
“Розекранування” ПП
Слайд 20
Алгоритм генерування зберігаючих норму псевдопотенціалів
Знаходження ПП через псевдохвильову функцію – для
“Розекранування” ПП - від атомного псевдопотенціалу віднімаються кулонівський та обмінно-кореляційний потенціали, породжені валентними електронами. Мета – отримати ПП голого іону, який буде занурений у електронну густину.
l=0,1,2,3,…
s,p,d,f,…
Слайд 21
Аналітичне задання псевдофункцій
Умови:
Аналітичне представлення:
поліноміальна функція (Troullier and Martins)
сферичні функції
, q’I з умови
Слайд 23
Факторизація псевдопотенціалів
Така процедура потрібна для пришвидшення розрахунків.
Вибрати локальний потенціал відліку
Зконструювати проектор, такий що
Факторизований гамільтоніан задається виразом
де
Легко можна перевірити, що
Слайд 24
Резюме для ЗН псевдопотенціалів
На даний момент знаємо, що:
Точна атомна хвильова
Для енергії та є ідентичними поза радіусом кістяка
Точна функція та псевдофункція мають ідентичну норму для r
Слайд 25
Дві енергії відліку для побудови
ЗН псевдопотенціалів
Побудова псевдофункцій при двох енергіях
Будуються два проектори
Факторизований гамільтоніан
Легко переконатись
Слайд 27
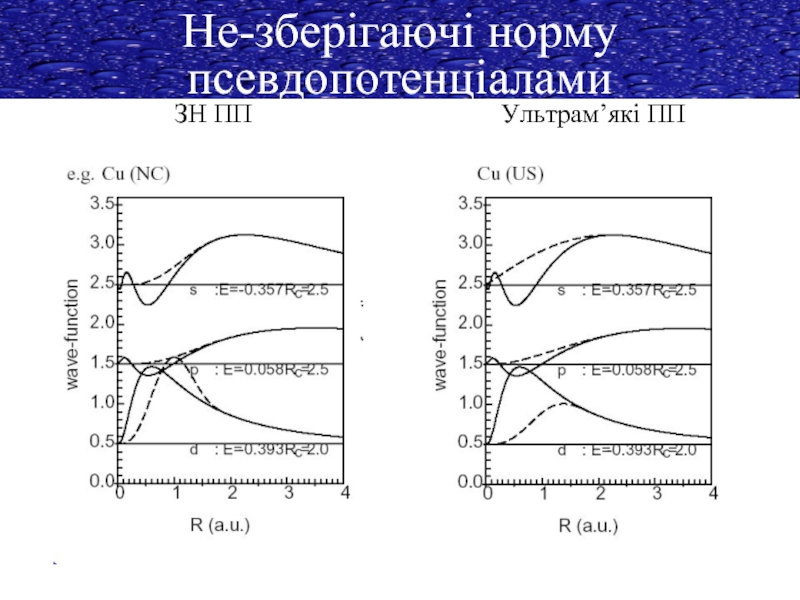
Не-зберігаючі норму псевдопотенціалами
Необхідно врахувати відмінність у нормі при r
Будуються два проектори
Факторизований гамільтоніан
Оператор перекриття
Можна показати, що