- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Теоретическая механика. (Лекция 1) презентация
Содержание
- 1. Теоретическая механика. (Лекция 1)
- 2. Введение
- 3. Теоретическая механика является наукой, в которой
- 4. Кинематика Кинематика изучает движения тел без
- 5. Кинематика материальной точки. Способы задания движения точки
- 6. Скоростью точки называется вектор, равный первой
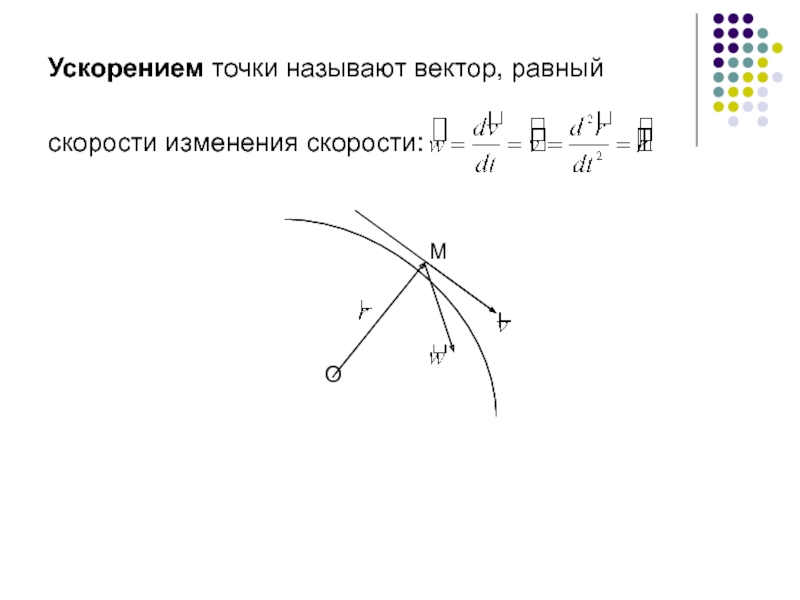
- 7. Ускорением точки называют вектор, равный
- 8. Введем правую тройку векторов (естественную ось координат),
- 9. 2. Координатный способ задания движения точки. Свяжем
- 10. Скорость:
- 11. Полное ускорение: Где
- 12. Касательное ускорение: Нормальное ускорение:
- 13. 3. Естественный способ задания движения точки
- 14. Скорость:
- 15. Частные случаи: Движение точки называется равномерным, если
- 16. Кинематика твердого тела Теорема о проекциях
- 17. 1. Поступательное движение твердого тела Определение. Движение
- 18. 2. Вращательное движение твердого тела. 2.1. Основные
- 19. Положительное направление оси вращения при
- 20. 2.2. Угловая скорость и ускорение. Определение. Алгебраическим
- 21. Определение. Алгебраическим значением углового ускорения
- 22. Частные случаи: ВД считается равномерным, если
Слайд 3 Теоретическая механика является наукой, в которой изучаются механические взаимодействия тел.
Основные
Механическое движение.
Механическое взаимодействие.
Материальная точка (МТ).
Механическая система (МС).
Абсолютно твердое тело (АТТ).
Теоретическая механика делится на 3 основных раздела: кинематика, статика и динамика.
Слайд 4Кинематика
Кинематика изучает движения тел без учета причин, вызвавших это движение.
Основные темы:
Кинематика МТ.
Кинематика твердого тела.
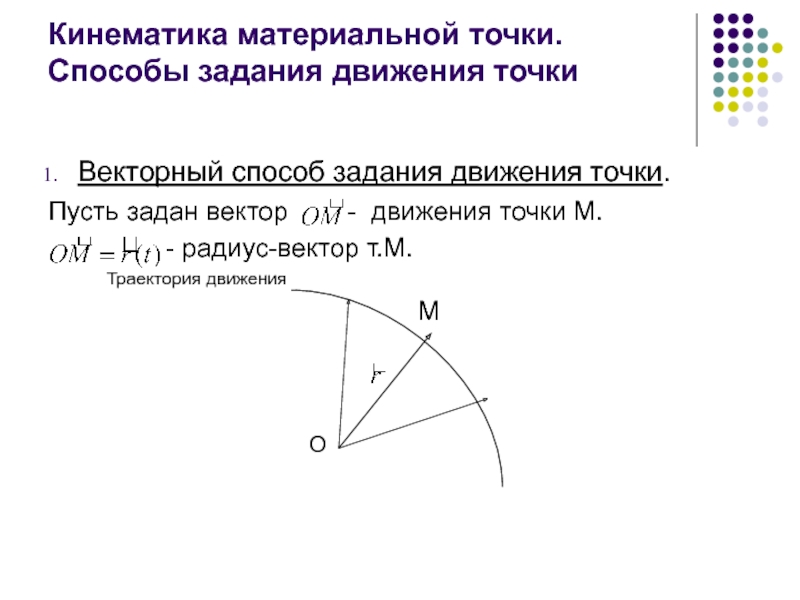
Слайд 5Кинематика материальной точки. Способы задания движения точки
Векторный способ задания движения точки.
Пусть
- радиус-вектор т.М.
Траектория движения
М
О
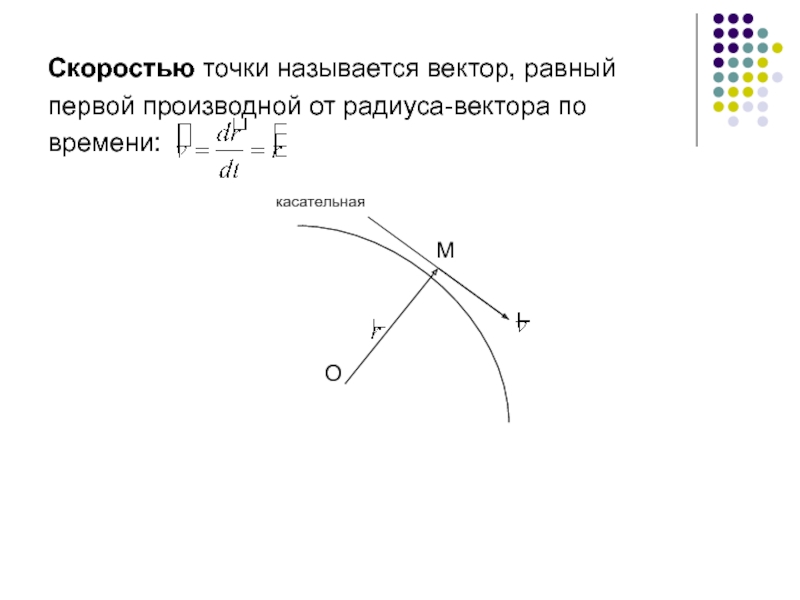
Слайд 6Скоростью точки называется вектор, равный
первой производной от радиуса-вектора по
времени:
М
О
Слайд 8Введем правую тройку векторов (естественную ось координат), начало которых лежит в
Тогда ускорение: ,
где
М
Итак, окончательно, полное ускорение:
Слайд 92. Координатный способ задания движения точки.
Свяжем с точкой О декартову прямоугольную
М(x,y,z)
z
О y
x
Тогда радиус-вектор можно представить в виде:
Слайд 11Полное ускорение:
Где
оси координат.
Длина вектора полного ускорения:
Слайд 12Касательное ускорение:
Нормальное ускорение:
, где
движения.
Полное ускорение:
Слайд 133. Естественный способ задания движения точки
Слайд 14Скорость:
- алгебраическое значение скорости
(длина
Ускорение:
- касательное ускорение
- нормальное ускорение
Слайд 15Частные случаи:
Движение точки называется равномерным, если
Движение точки называется равнопеременным, если .
Тогда
- формула Галлея.
Слайд 16Кинематика твердого тела
Теорема о проекциях скоростей 2 точек твердого тела.
Проекция
Или
Слайд 171. Поступательное движение твердого тела
Определение. Движение твердого тела, при котором любая
Теорема: При поступательном движении твердого тела траектории, скорость и ускорение двух точек совпадают.
Вывод:
Слайд 182. Вращательное движение твердого тела.
2.1. Основные понятия и определения.
Определение. Движение твердого
Определение. Прямая, с заданным положительным направлением, называется осью вращения.
За положительное направление оси вращения принято считать направление, с конца которого вращение видно против часовой стрелки.
Слайд 19 Положительное направление оси
вращения при помощи правила
правой руки.
Характеристикой вращательного
Если задано количество оборотов , то
Размерность:
Слайд 202.2. Угловая скорость и ускорение.
Определение. Алгебраическим значением угловой
скорости называют величину,
Вектором угловой скорости называют скользящий вектор, лежащий на оси вращения, положительное направление которого определяется также как и направление оси вращения.
Размерность:
Слайд 21Определение. Алгебраическим значением углового
ускорения называют величину, равную
Вектором углового ускорения называют скользящий вектор, лежащий на оси вращения, положительное направление которого определяется также как и направление оси вращения.
Размерность:
Слайд 22Частные случаи:
ВД считается равномерным, если
Тогда .
2. ВД считается равнопеременным, если .
Тогда