(поля напряжений)
вокруг дислокаций. Энергия
дислокаций.
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Теория упругости сплошных сред. Упругие поля (поля напряжений) вокруг дислокаций. Энергия дислокаций презентация
Содержание
- 1. Теория упругости сплошных сред. Упругие поля (поля напряжений) вокруг дислокаций. Энергия дислокаций
- 2. Типы дислокаций: Краевые дислокации -
- 3. Ядро дислокации (??) сильные искажения решетки,
- 4. Свойства вектора Бюргерса Finish-start/ right hand
- 5. Свойства дислокаций Дислокационная линия не может закончиться
- 7. Сетка Франка Дислокационная петля в fcc кристале Примеры дислокационных петель и узлов в кристаллах
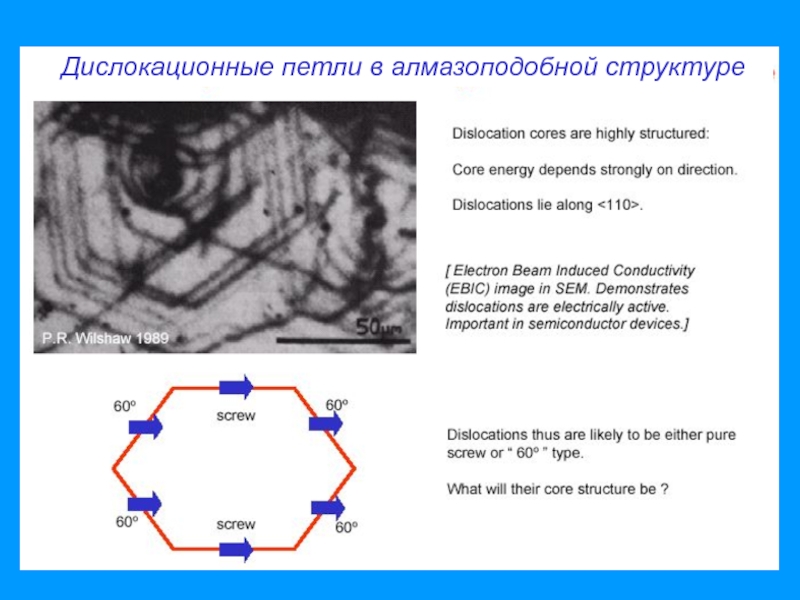
- 8. Дислокационные петли в алмазоподобной структуре
- 9. ρ -1/2 Плотность дислокаций Определение плотности дислокаций
- 10. Элементы теории упругости сплошных сред
- 11. Закон Гука, модуль Юнга Y ≡ E Брусок из однородного изотропного материала
- 12. Коэффициент Пуассона В кристаллах: σ ij = Cijkl εkl
- 13. Брусок под действием гидростатического давления
- 15. Объемный модуль упругости
- 16. Однородный сдвиг (1) клей
- 17. Однородный сдвиг (2) ∑Fi = 0 ∑Mi = 0
- 18. Однородный сдвиг (3) сдвиге
- 19. -1 < σ < 1/2 Однородный сдвиг (4)
- 20. Элементы теории упругости кристаллов
- 22. σij = dFi /dAj
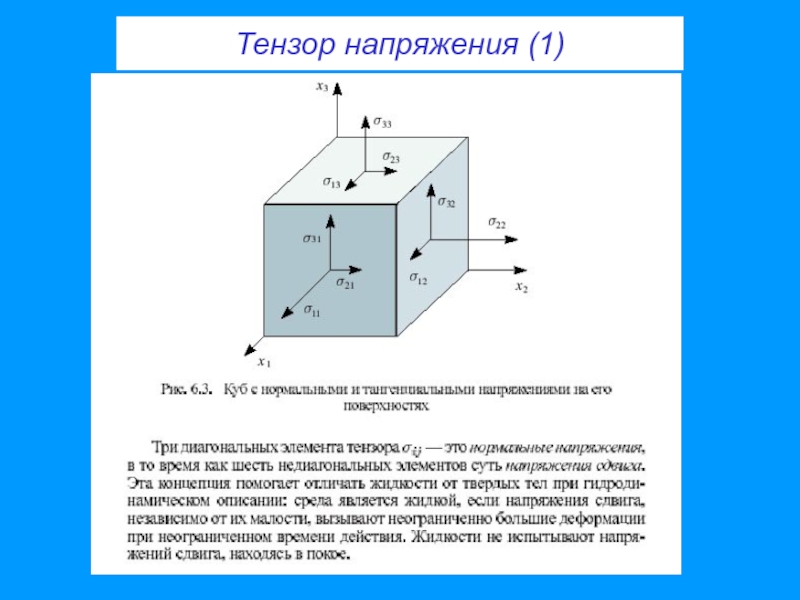
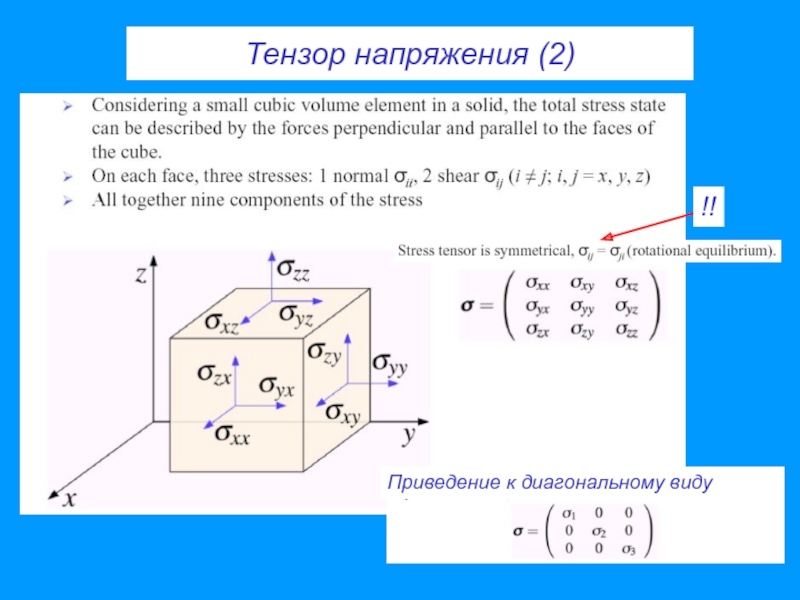
- 24. Тензор напряжения (1)
- 25. Тензор напряжения (2) Приведение к диагональному виду !!
- 26. σij Симметрия тензора напряжения σij
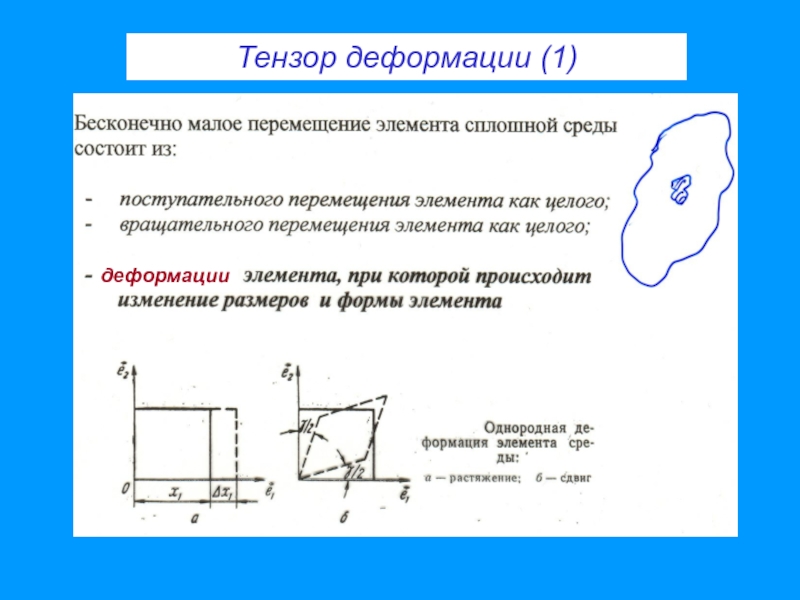
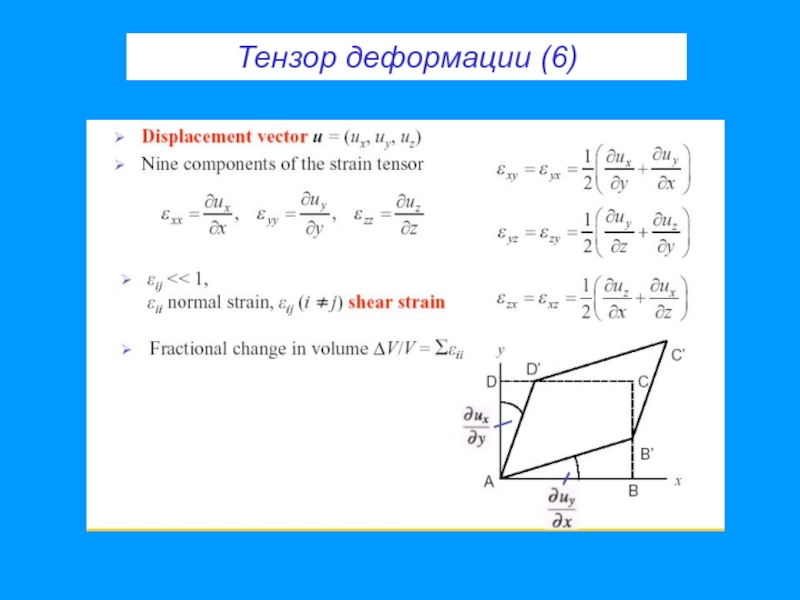
- 27. Тензор деформации (1) деформации
- 28. Тензор деформации (2) u - смещение
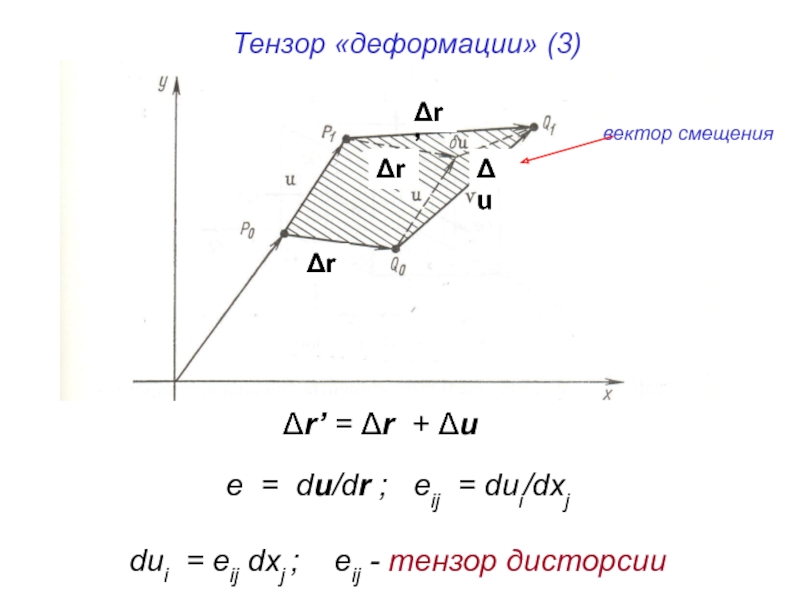
- 29. Тензор «деформации» (3) Δr’ Δr Δr Δu
- 30. Тензор дисторсии (1)
- 31. В общем случае: Δ r’
- 32. Тензор дисторсии (2) 2
- 33. Определение тензора деформации - Тензор деформации - Чистые повороты
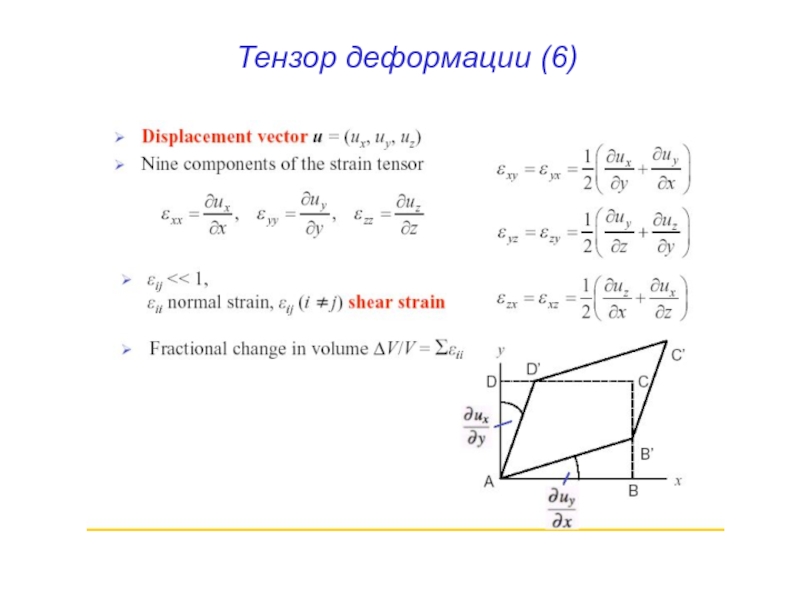
- 34. Тензор деформации (6)
- 35. Δr’ = Δr + Δu (Δr’)2 =
- 36. Δr Δr’ Δu = ω x Δr Акивис, Гольдберг, 1969
- 37. Акивис, Гольдберг, 1969
- 39. Тензор деформации (5)
- 40. Тензор деформации (6)
- 41. Тензор упругости σij σij = Cijkl εkl σij σij
- 42. Роль симметрии В кубических кристаллах достаточно трех упругих констант Кубические кристаллы Ромбическая Тригональная
- 43. Изотропное твердое тело μ ≡ G
- 44. Коэффициенты упругости Кубические кристаллы 1.6х10-12 Оценка величины
- 45. Изотропные тела Дин/см2 = эрг/см3 = 10 -1 дж/м3 = 10 -1 Н/м2 Дин/см2
- 46. Энергия деформируемого кристалла
- 47. В случае однородной деформации: εkl =
- 48. Энергия деформируемого кристалла
- 49. В общем случае если деформация производится обратимо
- 50. Упругие поля и напряжения вокруг дислокаций
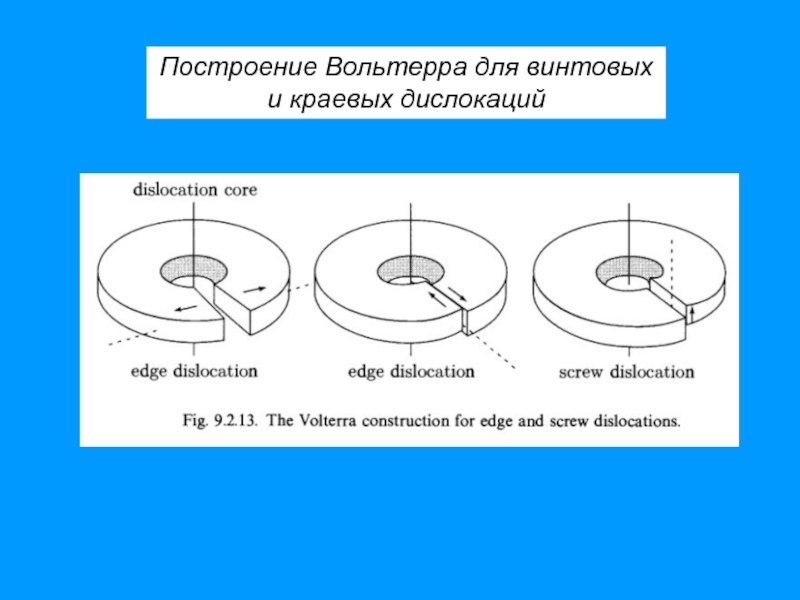
- 51. Дислокации в непрерывной упругой среде Построение Вольтерра
- 52. Образование краевой дислокации в кристалле
- 53. Построение Вольтерра для винтовых и краевых дислокаций
- 54. Поле смещений вокруг винтовой дислокации Цилиндрические координаты:
- 55. Вычисление компонент тензора деформации (1) uz =
- 56. Вычисление компонент тензора деформации (2) Смещения: (1/2)duz/dy
- 57. Вычисление компонент тензора деформации (3) εxx =
- 58. μ ≡ G Вычисление компонент тензора напряжений
- 59. Компоненты тензора напряжений в цилиндрических
- 60. Компоненты тензоров напряжений и деформаций в
- 61. Отличные от нуля компоненты εij и σkl
- 62. Сравнение законов спадания напряжений с расстоянием r,
- 63. в нем имеются внутренние напряжения, источником которых являются дислокации.
- 64. Упругая энергия дислокации Полная энергия
- 65. Оценки упругой энергии дислокации При обычных значениях
- 67. Наименьшей энергией обладают дислокации с наи- !!
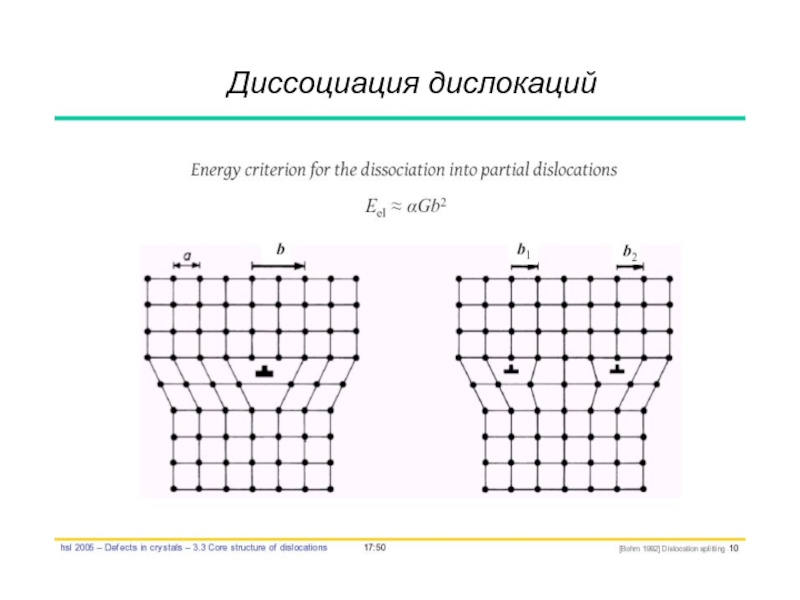
- 68. Диссоциация дислокаций
- 69. Ядро дислокации ядро – неупругие искажения упругие деформации
- 70. Оценки, выполненные на основе различных микроскопических подходов
Типы дислокаций: Краевые дислокации - Edge Dislocation: A portion of
Слайд 1Профессор Б.И.Островский
Физика реального кристалла
ostr@cea.ru
7. Теория упругости сплошных сред.
Упругие поля
Слайд 2Типы дислокаций:
Краевые дислокации - Edge Dislocation:
A portion of an extra plane of atoms
Винтовые дислокации - Screw Dislocation:
Helical atomic displacement around a
line extending through the crystal
Смешанные дислокации - Mixed Dislocation:
Some edge, some screw nature
Винтовые дислокации - Screw Dislocation:
Helical atomic displacement around a
line extending through the crystal
Смешанные дислокации - Mixed Dislocation:
Some edge, some screw nature
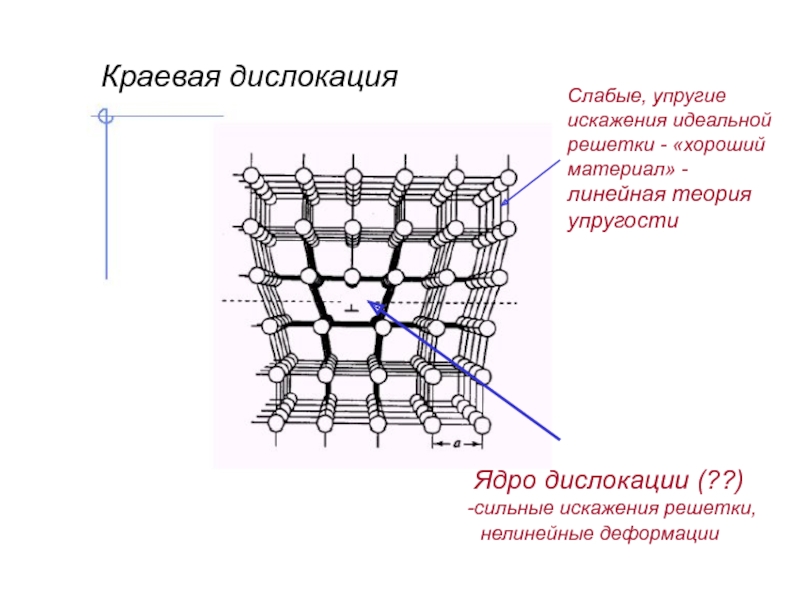
Слайд 3Ядро дислокации (??)
сильные искажения решетки,
нелинейные деформации
Краевая дислокация
Слабые, упругие
искажения идеальной
решетки
- «хороший
материал» -
линейная теория
упругости
материал» -
линейная теория
упругости
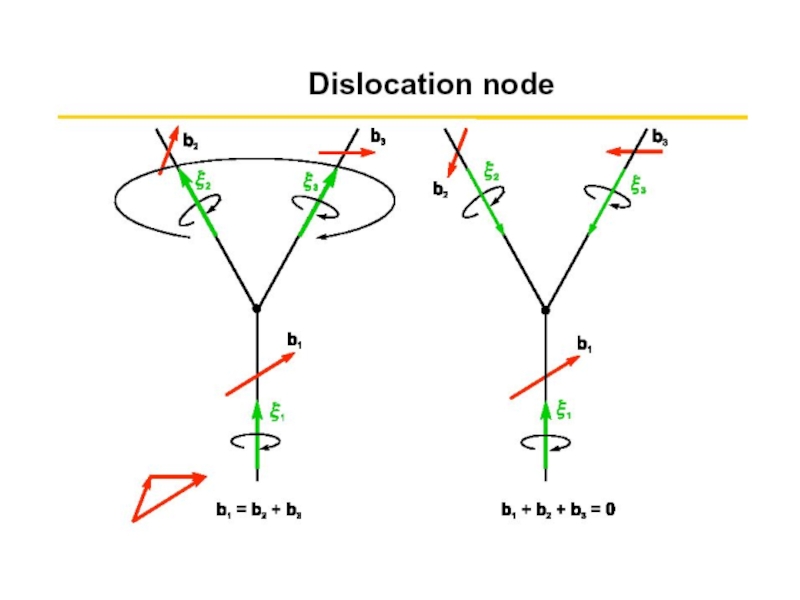
Слайд 5Свойства дислокаций
Дислокационная линия не может закончиться внутри кристалла,
а только
- на его поверхности
- на внутренней границе раздела ( на границах зерен)
- в дислокационном узле
- с образованием дислокационной петли
- на внутренней границе раздела ( на границах зерен)
- в дислокационном узле
- с образованием дислокационной петли
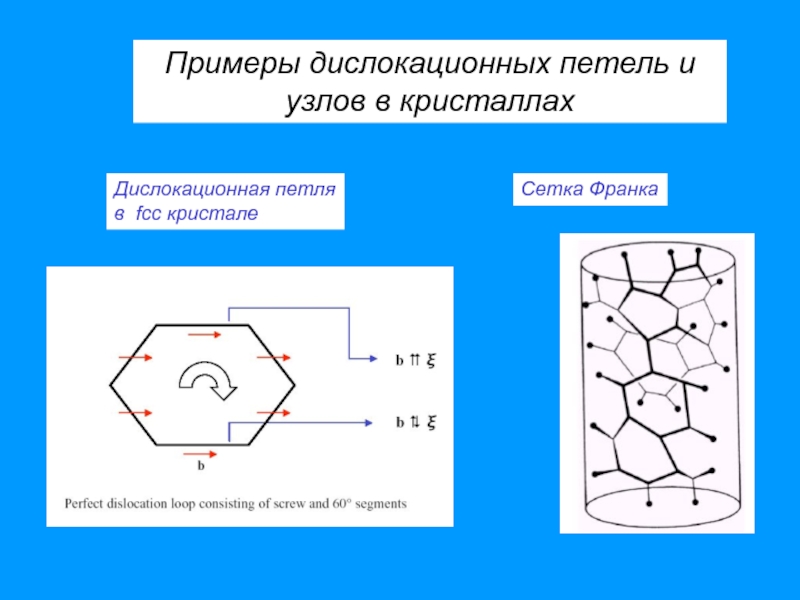
Слайд 7Сетка Франка
Дислокационная петля
в fcc кристале
Примеры дислокационных петель и
узлов в кристаллах
Слайд 9ρ -1/2
Плотность дислокаций
Определение плотности дислокаций
Выражается в единицах, см-2
Типичные значения в отожженных
металлах
В полупроводниках
После пластической деформации
и выше
ρ = L/ V = Nl/ V = Nl/ lS = N/ S
ρ = L/ V
ρ-1 = S/ N
ρ-1/2 = < r >- среднее расстояние
между дислокациями
Слайд 28Тензор деформации (2)
u - смещение
частицы
e = lim (Δ x’
- Δ x)/ Δ x =
= lim Δu/ Δx = du/dx - деформация
= lim Δu/ Δx = du/dx - деформация
Δ x’ = Δ x + u2 - u1
Δ x’ = Δ x + Δu
Δx → 0
Δx → 0
Слайд 29Тензор «деформации» (3)
Δr’
Δr
Δr
Δu
Δr’ = Δr + Δu
e = du/dr ; eij = dui/dxj
dui = eij dxj ; eij - тензор дисторсии
e = du/dr ; eij = dui/dxj
dui = eij dxj ; eij - тензор дисторсии
вектор смещения
Слайд 31В общем случае: Δ r’ = Δ r +
Δ u
e = du/dr ; eij = dui/dxj
dui = eij dxj ; eij - тензор деформации (??)
e = du/dr ; eij = dui/dxj
dui = eij dxj ; eij - тензор деформации (??)
вектор смещения
Легко понять смысл компонент тензора eij :
Δ x = (Δ x1; 0; 0)
Δui = eij Δxj
Слайд 35Δr’ = Δr + Δu
(Δr’)2 = (Δr)2 + 2Δr Δu +
Δu2
(Δr’)2 - (Δr)2 = 2Δr Δu
2Δr Δu =2eijΔxiΔxj
2Δr Δu =2εijΔxiΔxj
Акивис,
Гольдберг,
1969
Таким образом,
в чистую
деформацию
вносит вклад
только тензор ε
Вклад равен 0
Слайд 42Роль симметрии
В кубических кристаллах достаточно трех упругих констант
Кубические кристаллы
Ромбическая
Тригональная
Слайд 43Изотропное твердое тело
μ ≡ G
E = 2G (1+ ν)
ν = λ/2(λ
+G )
Связь с константами упругости
кубического кристалла
Связь с модулем Юнга и
коэффициентом Пуассона
Слайд 44Коэффициенты упругости
Кубические кристаллы
1.6х10-12
Оценка величины коэффициентов упругости
C11
Cijkl
C
C
C12
C44
Дин/см2 = эрг/см3 = 10 -1
дж/м3
C = U/a3
Слайд 47 В случае однородной деформации: εkl = const (r )
Wel полн = (1/2)Cε2 V - одноконстантное приближение
При неоднородной деформации:εkl = εkl (r ) ;
Wel полн = (1/2)∫Cε2(r)d3r
При неоднородной деформации:εkl = εkl (r ) ;
Wel полн = (1/2)∫Cε2(r)d3r
d Wel = σij dεij = Cijkl εkld εij
σij = Cijkl εkl - Закон Гука
Когда единичный элемент объема деформируется на малую величину dεij ,
напряжения совершают над ним работу:
Плотность
энергии!
[эрг/см3]
Полная упругая энергия деформации получается интегрированием
по всему объему кристалла: Wel полн = (1/2)∫Cijkl εijεkl d3r
После интегрирования имеем для плотности энергии:
Wel = (1/2)Cijklεijεkl = (1/2)σijεij
V
Слайд 49В общем случае если деформация производится обратимо и при постоянной температуре,
и если вся работа идет на упругую деформацию, то свободная энергия системы имеет вид:
F = (1/2)∫Cijkl εijεkld3r
Плотность энергии деформации в общем случае записывается в виде:
Wel = Wel (εkl) = (1/2)Cijklεijεkl + (1/6)Cijklтnεijεkl εmn+
+ (1/24)Cijklmnpqεijεkl εmn εpq
F = (1/2)∫Cijkl εijεkld3r
Плотность энергии деформации в общем случае записывается в виде:
Wel = Wel (εkl) = (1/2)Cijklεijεkl + (1/6)Cijklтnεijεkl εmn+
+ (1/24)Cijklmnpqεijεkl εmn εpq
Гармоническое приближение
Ангармонические поправки
∂2Wel / ∂εij ∂εkl
V
Слайд 54Поле смещений вокруг винтовой дислокации
Цилиндрические
координаты:
r, θ, z
x2 + y2 = r2;
tgθ
= y/x
uz = uz(x,y)
arctg (y/x)
Слайд 56Вычисление компонент тензора деформации (2)
Смещения:
(1/2)duz/dy =(b/4π)d[ arctg(y/x)]/dy =
∫dy/(y2 +a2) = (1/a)
arctg(y/a)
arctg (y/x)
Слайд 57Вычисление компонент тензора деформации (3)
εxx = εyy = εzz = εxy
= εyx = 0
εxz = εzx
Цилиндрические
координаты:
r, θ, z; x2 + y2 = r2; tgθ = y/x
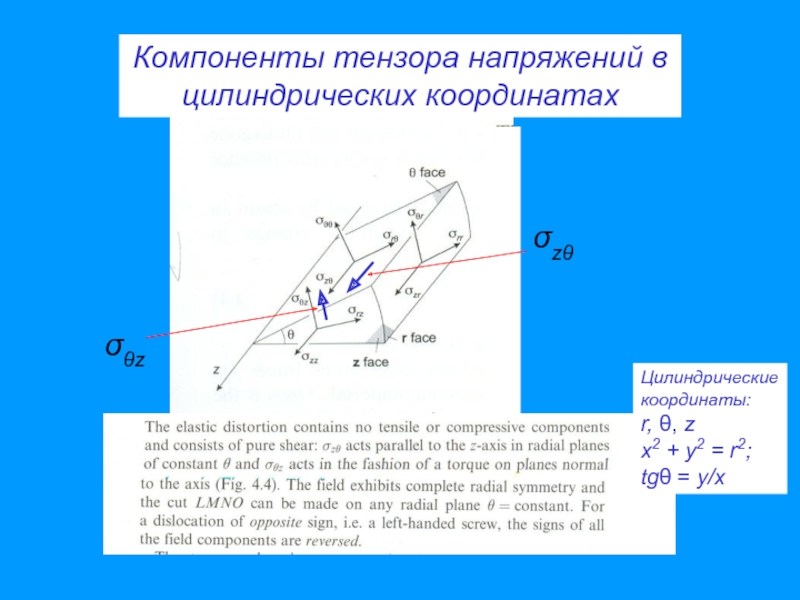
Слайд 59
Компоненты тензора напряжений в
цилиндрических координатах
σθz
σzθ
Цилиндрические
координаты:
r, θ, z
x2 + y2 =
r2;
tgθ = y/x
tgθ = y/x
Слайд 60Компоненты тензоров напряжений и деформаций в
цилиндрических координатах
используя соотношения:
и, аналогичным образом,
для сдвиговых деформаций, получаем:
Слайд 61Отличные от нуля компоненты εij и σkl убывают с
расстоянием от
дислокации как r -1,
ε ~ σ ~ r -1
ε ~ σ ~ r -1
Упругие поля искажений вокруг дислокаций
являются дальнодействующими!
Слайд 62Сравнение законов спадания напряжений с расстоянием r,
для точечных дефектов, дислокаций
и
дислокационных стенок
дислокационных стенок
Слайд 64Упругая энергия дислокации
Полная энергия дислокации состоит из двух частей:
Плотность упругой энергии,
запасенной в дислокации:
2
2
8
Полная энергия, запасенная в полом цилиндре радиуса R и длины L :
= (Gb2/8π2)∫dz ∫dθ ∫rdr/r2 =
0
0
L
2π
R
r0
L
L
Или на единицу длины дислокации:
полн
полн
/L =
полн
=∫
dV
Wel = (1/2) Cijklεijεkl
= (1/2)σijεij
Слайд 65Оценки упругой энергии дислокации
При обычных значениях плотности дислокаций ρ =107 см-2,
среднее
расстояние между ними составляет R ≈ ρ-1/2 ≈ 3.10-4 см, что дает
для
расстояние между ними составляет R ≈ ρ-1/2 ≈ 3.10-4 см, что дает
для
≈ 10
и
полн
/L =
≈
При G ≈ 1012 дин.см-2 и b = 2.10 -8 см имеем:
полн
/L =
≈
4.10 -4 эрг/см
Что в пересчете на одну связь дает:
Ebond = 4.10 -4 эрг/см x 2.10 -8 см = 8.10-12 эрг 5 эв
≈
≈
Ebond ≈ Gb3
Слайд 70Оценки, выполненные на основе различных микроскопических подходов
и результатов компьютерного моделирования
взаимодействий в ядре
дислокаций, показывают, что энергия ядра дислокации не превышает
10-15% полной энергии, т.е. большая часть энергии дислокации
связана с упругими деформациями, распространяющимися далеко
в объеме кристалла.
дислокаций, показывают, что энергия ядра дислокации не превышает
10-15% полной энергии, т.е. большая часть энергии дислокации
связана с упругими деформациями, распространяющимися далеко
в объеме кристалла.
