Теорема Остроградского-Гаусса презентация

Содержание

1. Теорема Остроградского-Гаусса
2. 2.1. Силовые линии электростатического поля Теорема
3. Остроградский Михаил Васильевич (1801 – 1862)
4. Гаусс Карл Фридрих (1777 – 1855) немецкий
5. Основная ценность теоремы Остроградского-Гаусса состоит в том,
6. силовые линии – это линии, касательная к
7. Однородным называется электростатическое поле,
8. В случае точечного заряда поле неоднородно, линии
9. Для системы зарядов, как видим, силовые линии направлены от положительного заряда к отрицательному
11. Густота силовых линий должна быть
12. 2.2. Поток вектора напряженности
13. Таким образом, поток вектора есть скаляр,
14. Для первого рисунка – поверхность А1 окружает
15. 2.3. Теорема Остроградского-Гаусса Итак, по определению,
16. поток вектора напряженности через произвольную элементарную площадку
17. Подсчитаем поток вектора через произвольную замкнутую поверхность
18. Центр сферы совпадает с центром заряда.
19. Тогда поток через S1
20. Подсчитаем поток через сферу S2, имеющую радиус R2:
21. Из непрерывности линии
22. Для любого числа произвольно расположенных зарядов, находящихся
23. Полный поток проходящий через S3, не охватывающую заряд q, равен нулю:
24. Таким образом, для точечного заряда q, полный
25. Электрические заряды могут быть
26. Суммарный заряд объема dV будет равен:
37. 2.5.2. Поле двух равномерно заряженных плоскостей
38. Результирующее поле, находится как суперпозиция полей, создаваемых

2.1. Силовые линии электростатического поля Теорема Остроградского-Гаусса, которую мы докажем и обсудим позже, устанавливает связь между электрическими зарядами и электрическим полем. Она представляет собой более общую и более изящную формулировку

Главная
Физика
Теорема Остроградского-Гаусса

Слайд 1
2.1. Силовые линии электростатического поля
2.2. Поток вектора напряженности
2.3. Теорема Остроградского-Гаусса
2.4. Дифференциальная

форма теоремы2.4. Дифференциальная форма теоремы 2.4. Дифференциальная форма теоремы Остроградского-Гаусса
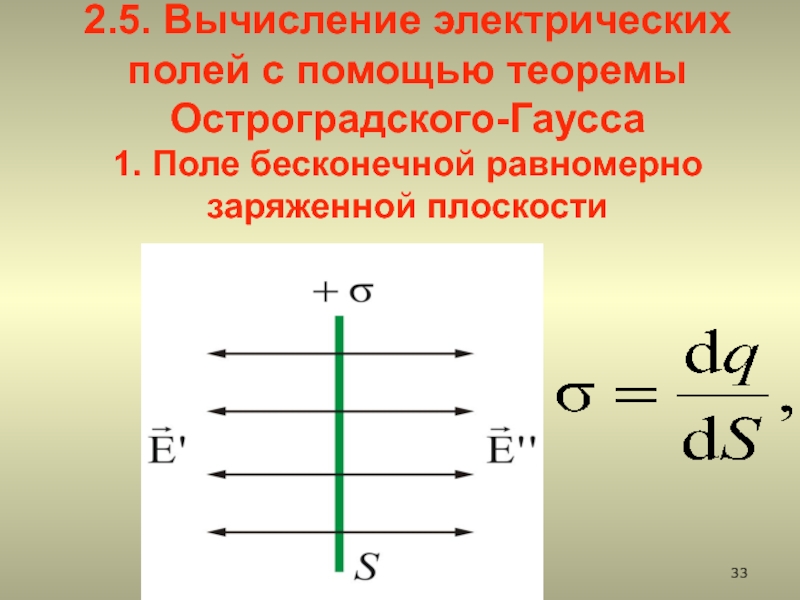
2.5. Вычисление электростатических полей с помощью теоремы Остроградского-Гаусса
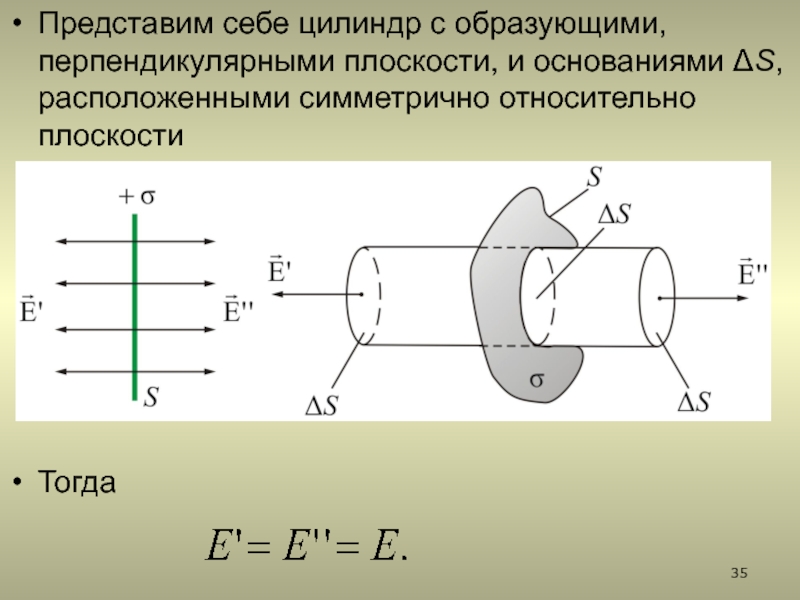
2.5.1. Поле бесконечной однородно заряженной плоскости
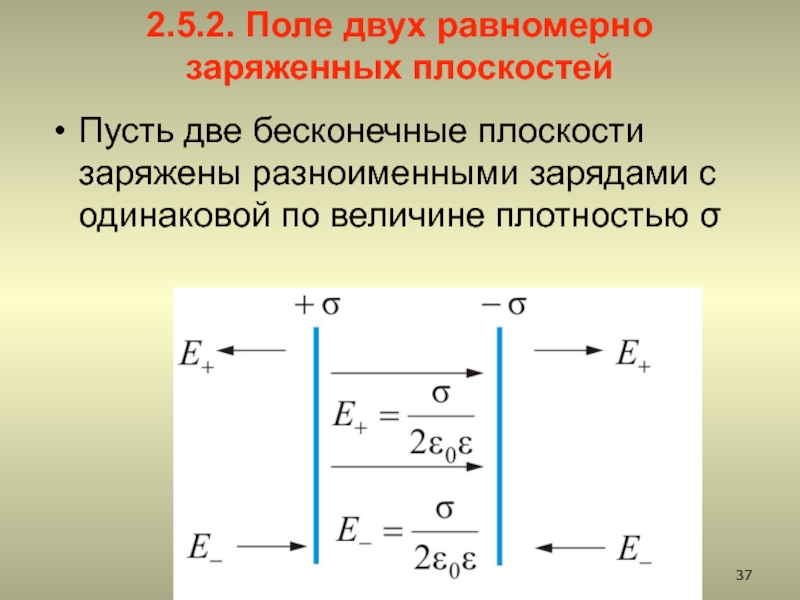
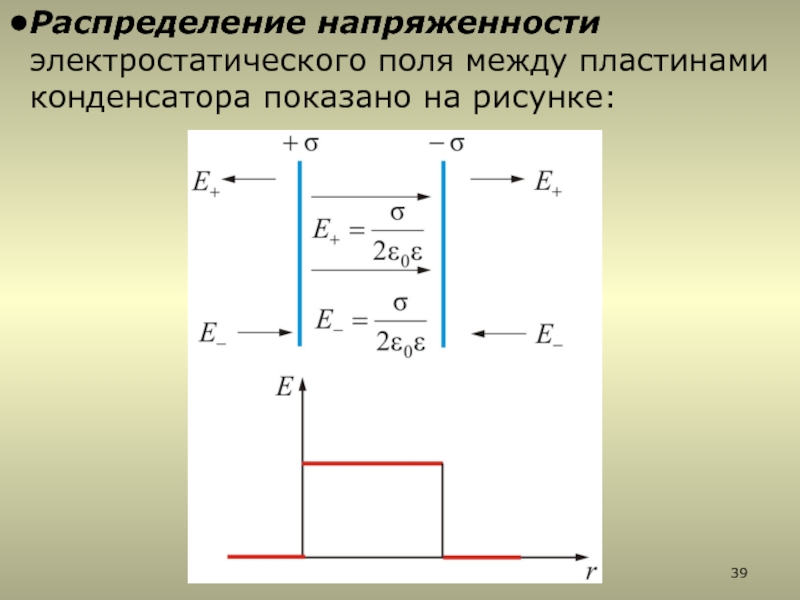
2.5.2. Поле двух равномерно заряженных плоскостей
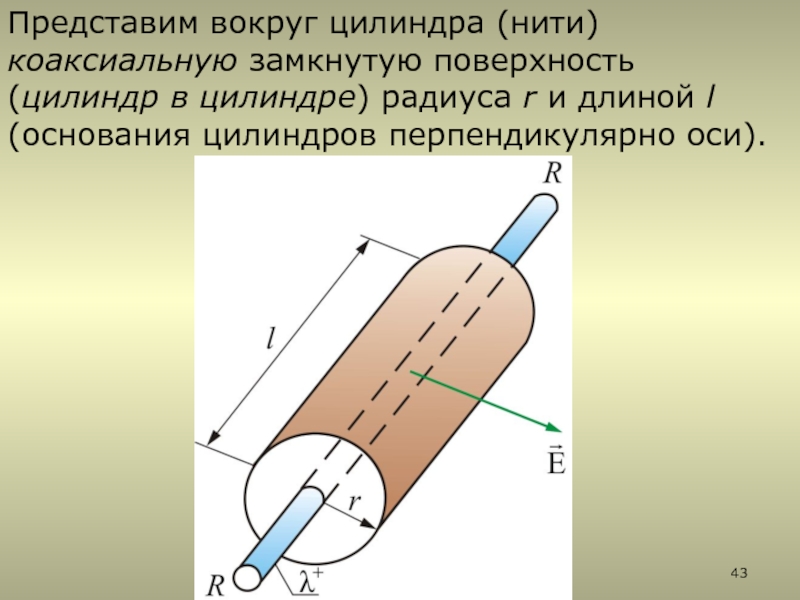
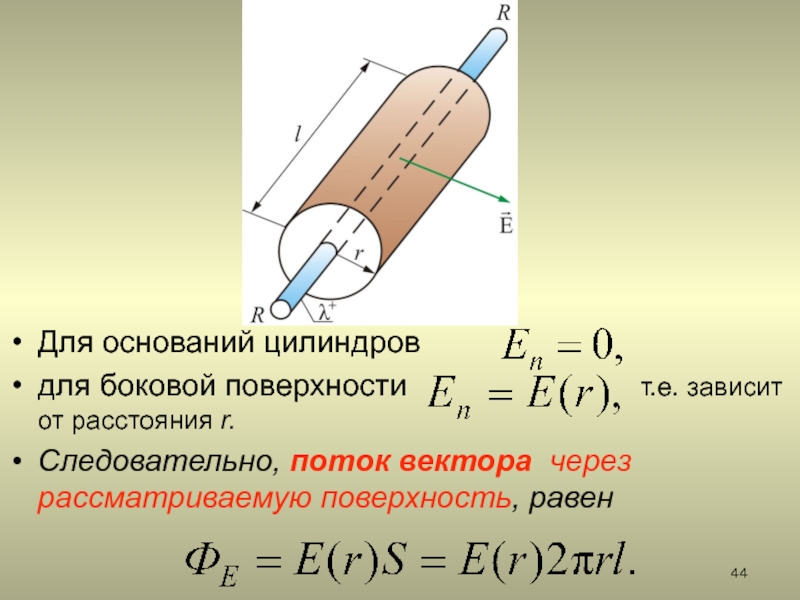
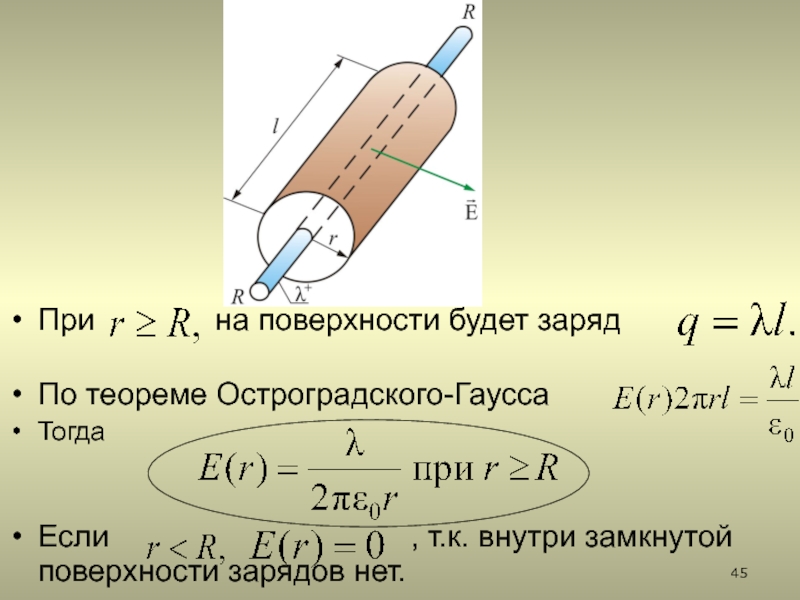
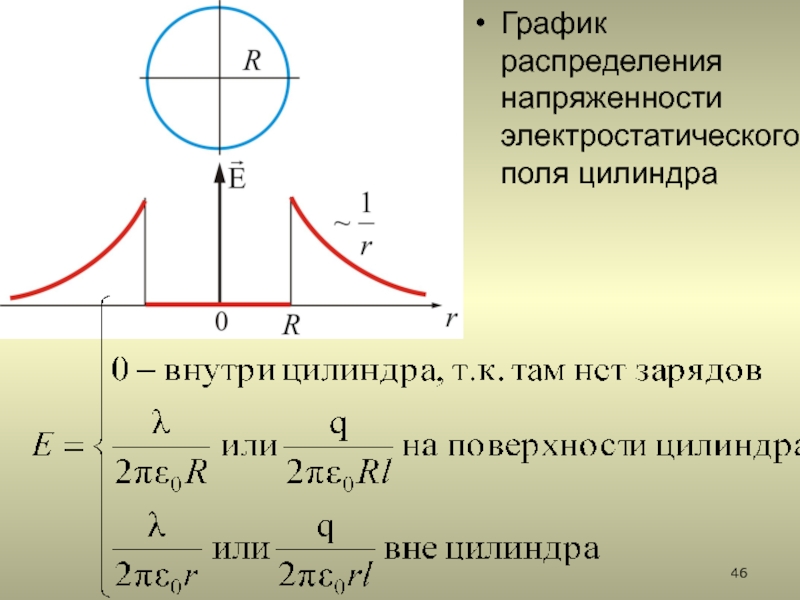
2.5.3. Поле заряженного бесконечного цилиндра (нити)
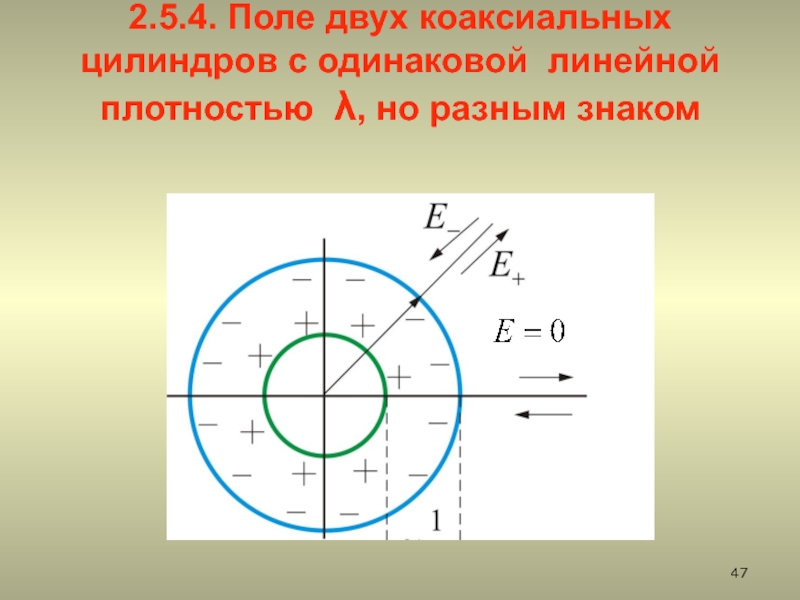
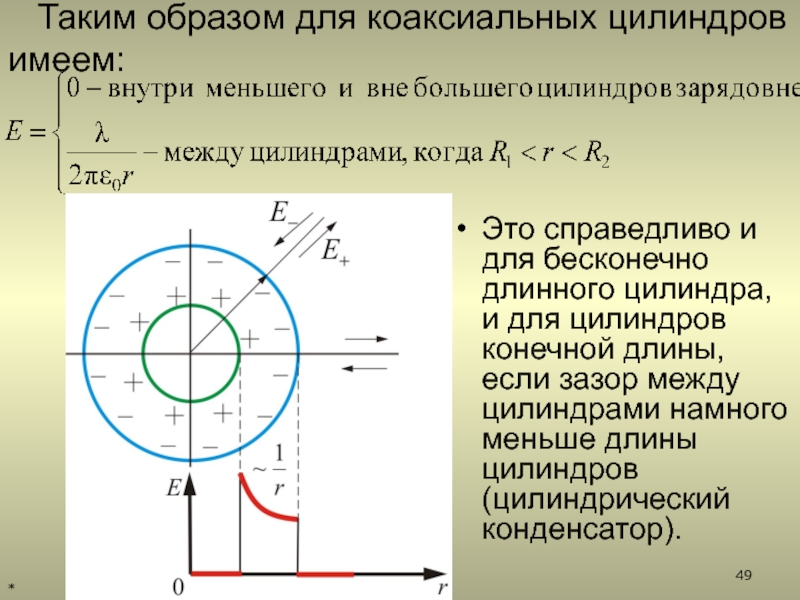
2.5.4. Поле двух коаксиальных цилиндров с одинаковой линейной плотностью заряда, но разным знаком
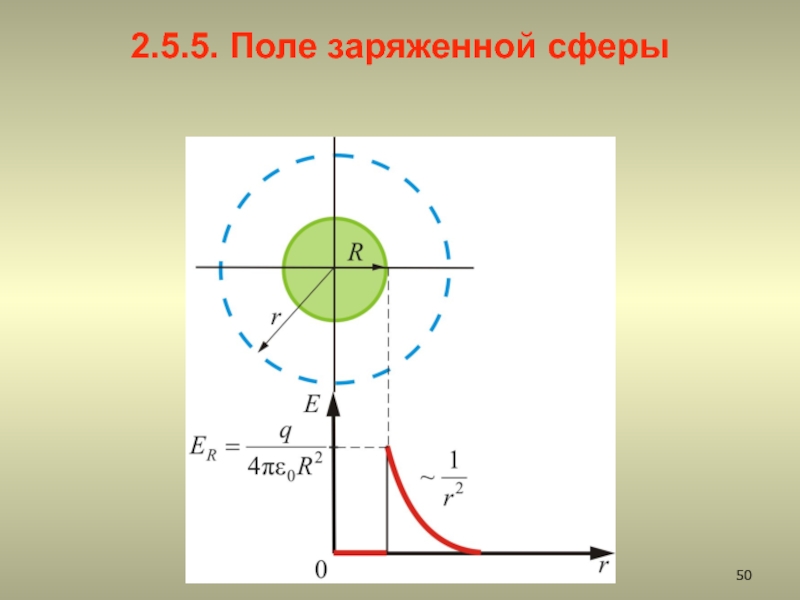
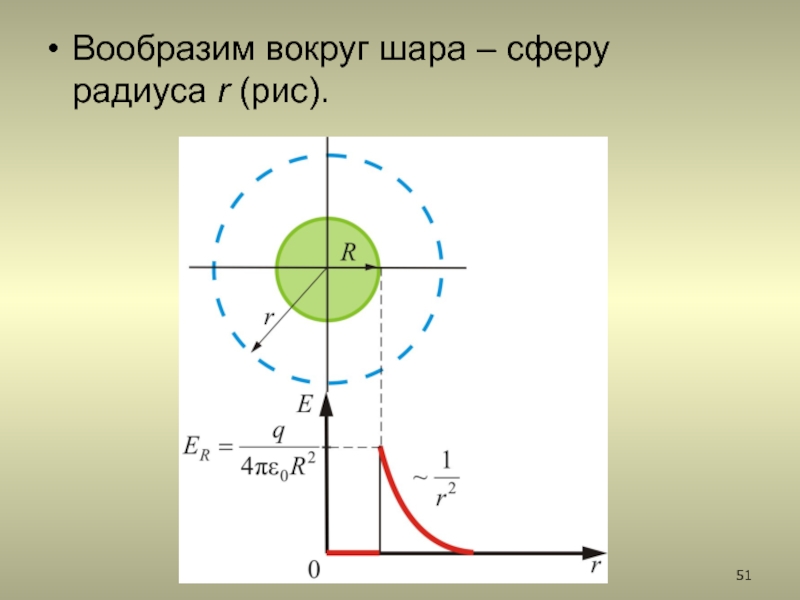
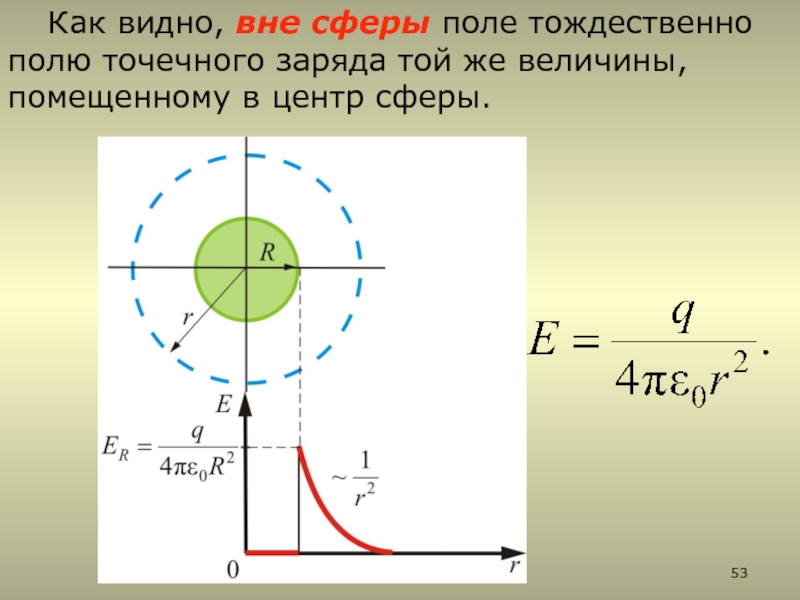
2.5.5. Поле заряженного пустотелого шара
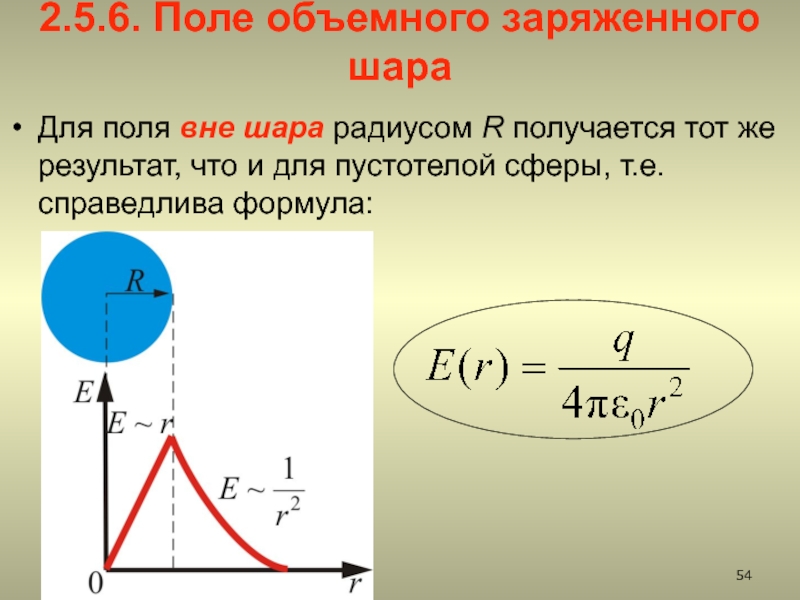
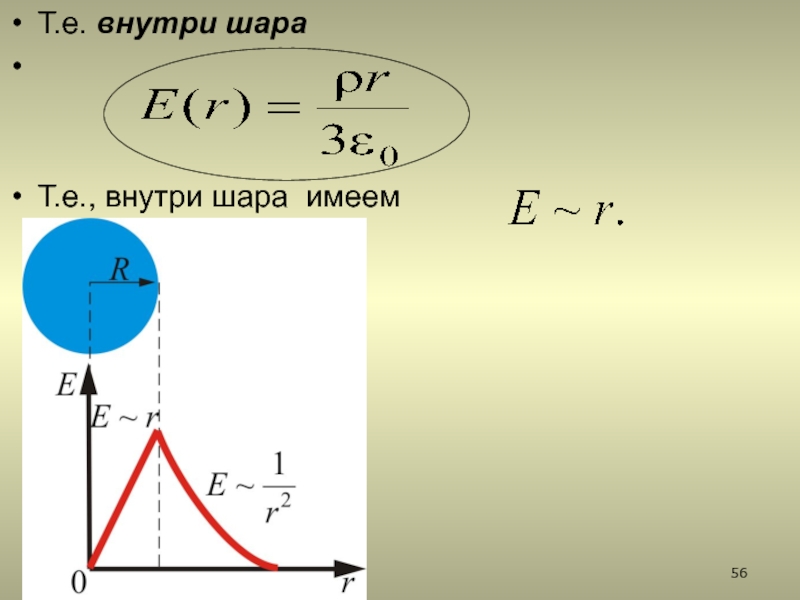
2.5.6. Поле объемного заряженного шара

Тема 2. ТЕОРЕМА ОСТРОГРАДСКОГО-ГАУССА

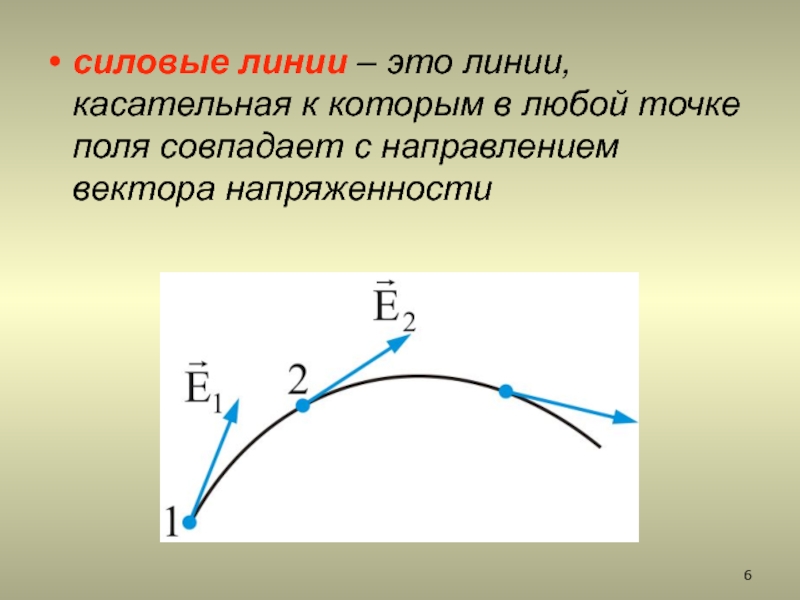
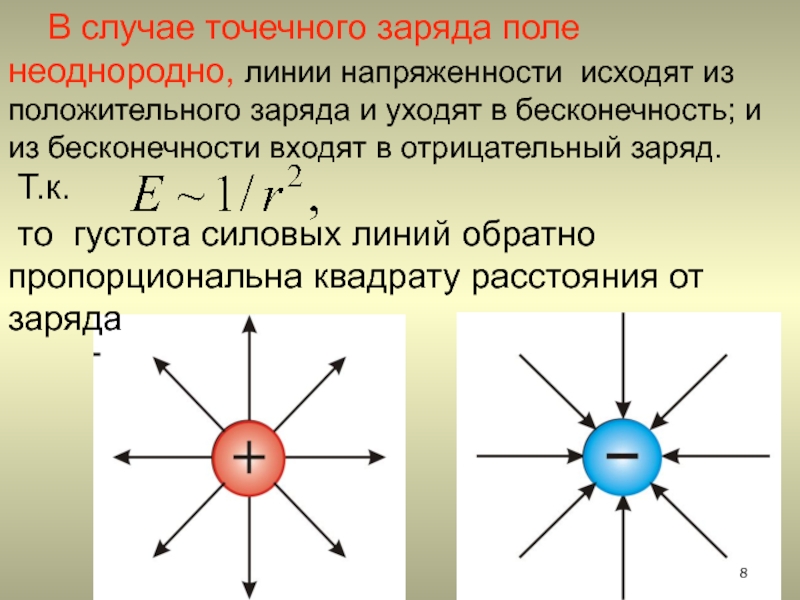
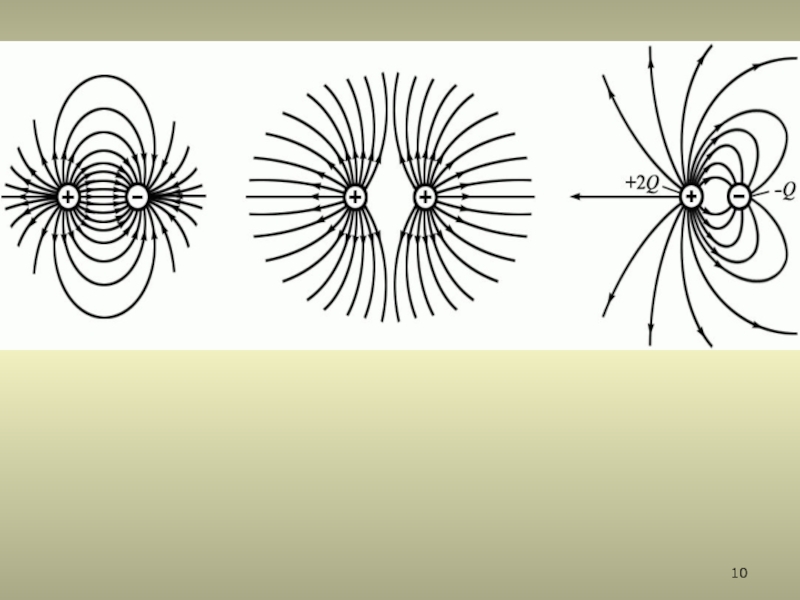
2.1. Силовые линии электростатического поля
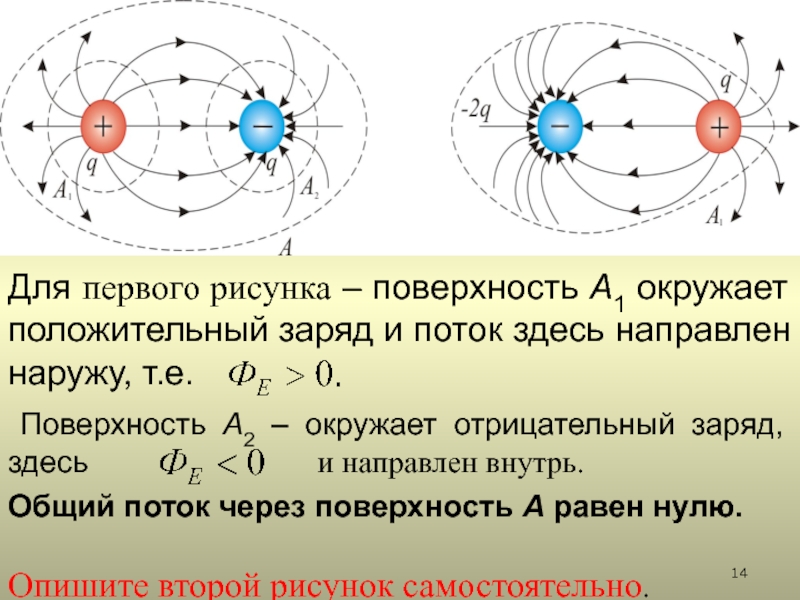
2.2. Поток вектора напряженности
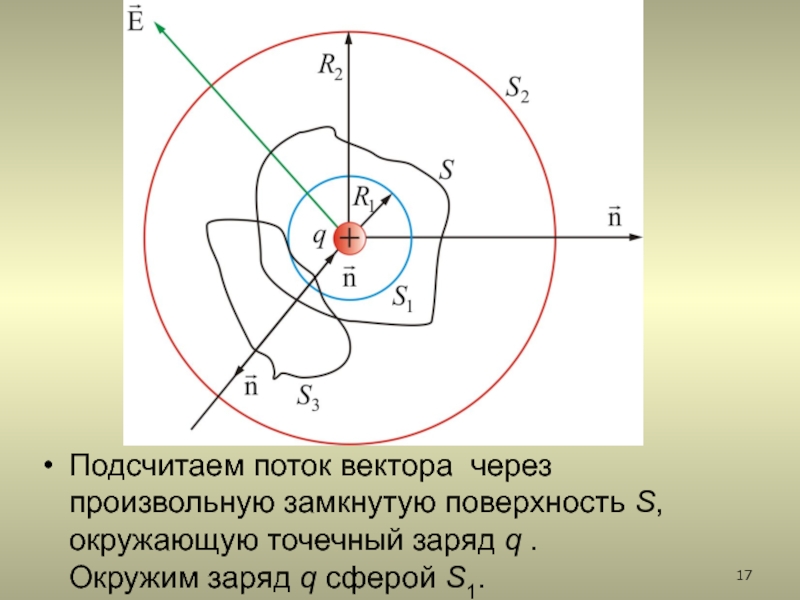
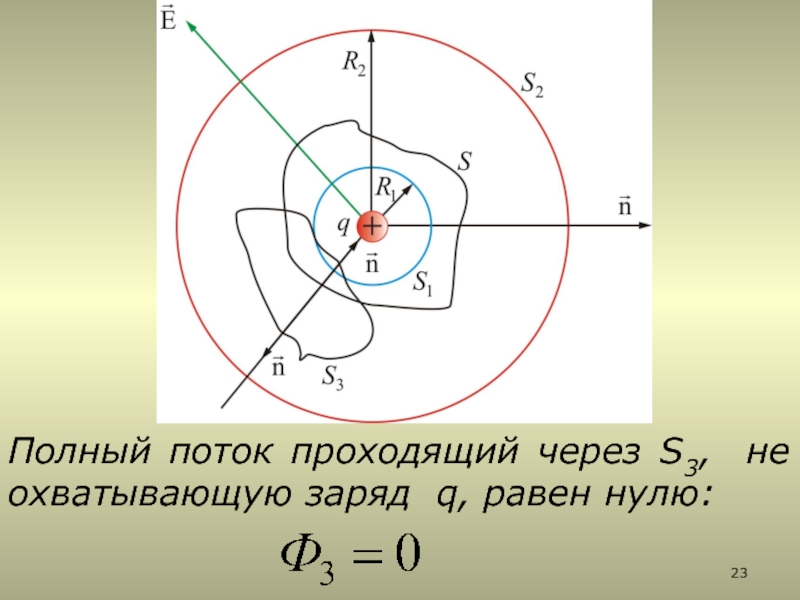
2.3. Теорема Остроградского-Гаусса
2.4. Дифференциальная форма теоремы2.4. Дифференциальная форма теоремы 2.4. Дифференциальная форма теоремы Остроградского-Гаусса
2.5. Вычисление электростатических полей с помощью теоремы Остроградского2.5. Вычисление электростатических полей с помощью теоремы Остроградского 2.5. Вычисление электростатических полей с помощью теоремы Остроградского -2.5. Вычисление электростатических полей с помощью теоремы Остроградского - 2.5. Вычисление электростатических полей с помощью теоремы Остроградского - Гаусса
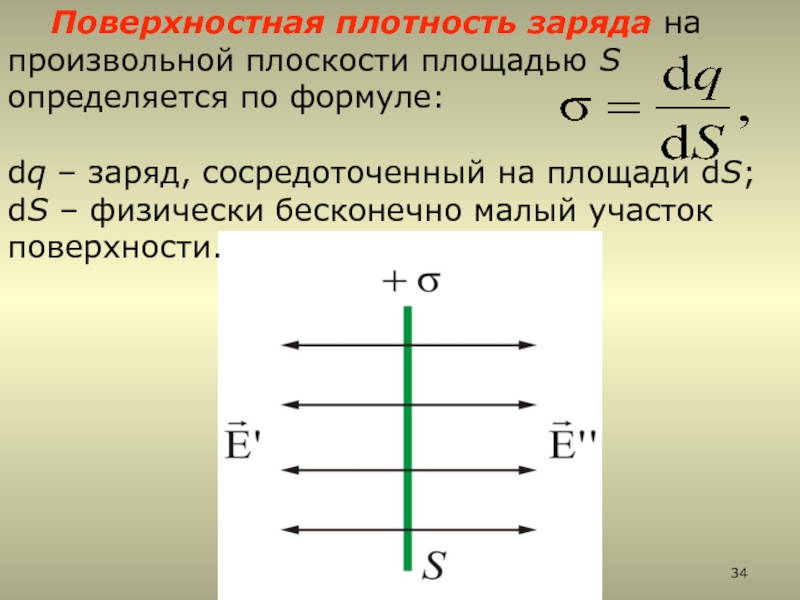
2.5.1. Поле бесконечной равномерно заряженной плоскости
2.5.2. Поле двух бесконечных равномерно заряженных параллельных плоскостей
2.5.3. Поле бесконечно длинного равномерно заряженного2.5.3. Поле бесконечно длинного равномерно заряженного прямого кругового цилиндра (нити)
2.5.4. Поле двух коаксиальных цилиндров с одинаковой линейной плотностью заряда, но разным знаком
2.5.5. Поле равномерно заряженной сферы.
2.5.6. Поле объемного заряженного шара

Слайд 22.1. Силовые линии электростатического поля
Теорема Остроградского-Гаусса, которую мы докажем и обсудим

позже, устанавливает связь между электрическими зарядами и электрическим полем. Она представляет собой более общую и более изящную формулировку закона Кулона.

Слайд 3Остроградский Михаил Васильевич (1801 – 1862)
отечественный математик и механик. Учился

в Харьковском ун-те (1816 – 1820), совершенствовал знания в Париже (1822 – 1827).
Основные работы в области математического анализа, математической физики, теоретической механики. Решил ряд важных задач гидродинамики, теории теплоты, упругости, баллистики, электростатики, в частности задачу распространения волн на поверхности жидкости (1826 г.). Получил дифференциальное уравнение распространения тепла в твердых телах и жидкостях. Известен теоремой Остроградского-Гаусса в электростатике (1828 г.).

Слайд 4Гаусс Карл Фридрих (1777 – 1855) немецкий математик, астроном и физик.

Исследования посвящены многим разделам физики.
В 1832 г. создал абсолютную систему мер (СГС), введя три основных единицы: единицу времени – 1 с, единицу длины – 1 мм, единицу массы – 1 мг.
В 1833 г. совместно с В. Вебером построил первый в Германии электромагнитный телеграф.
Еще в 1845 г. пришел к мысли о конечной скорости распространения электромагнитных взаимодействий. Изучал земной магнетизм, изобрел в 1837 г. униполярный магнитометр, в 1838 г. – бифилярный. В 1829 г.
Сформулировал принцип наименьшего принуждения (принцип Гаусса).
Один из первых высказал в 1818 г. предположение о возможности существования неевклидовой геометрии.

Слайд 5Основная ценность теоремы Остроградского-Гаусса состоит в том, что она позволяет

глубже понять природу электростатического поля и устанавливает более общую связь между зарядом и полем.

Слайд 6силовые линии – это линии, касательная к которым в любой точке

поля совпадает с направлением вектора напряженности

Слайд 7 Однородным называется электростатическое поле, во всех точках которого

напряженность одинакова по величине и направлению.
Однородное электростатическое поле изображается параллельными силовыми линиями на равном расстоянии друг от друга

Слайд 8 В случае точечного заряда поле неоднородно, линии напряженности исходят из положительного

заряда и уходят в бесконечность; и из бесконечности входят в отрицательный заряд.
Т.к.

то густота силовых линий обратно пропорциональна квадрату расстояния от заряда

Слайд 9 Для системы зарядов, как видим, силовые линии направлены от

положительного заряда к отрицательному

Слайд 10

Слайд 11 Густота силовых линий должна быть такой, чтобы единичную площадку,

нормальную к вектору напряженности пересекало такое их число, которое равно модулю вектора напряженности, т.е. :

Слайд 122.2. Поток вектора напряженности
Полное число силовых линий, проходящих через

поверхность S называется потоком вектора напряженности Ф через эту поверхность
В векторной форме можно записать

– скалярное произведение двух векторов, где вектор .

Слайд 13 Таким образом, поток вектора есть скаляр, который в зависимости от

величины угла α может быть как положительным, так и отрицательным.

Слайд 14Для первого рисунка – поверхность А1 окружает положительный заряд и поток

здесь направлен наружу, т.е.

Поверхность А2 – окружает отрицательный заряд, здесь и направлен внутрь.

Общий поток через поверхность А равен нулю.

Опишите второй рисунок самостоятельно.

Слайд 152.3. Теорема Остроградского-Гаусса
Итак, по определению, поток вектора напряженности электрического поля равен

числу линий напряженности, пересекающих поверхность S.

Слайд 16поток вектора напряженности через произвольную элементарную площадку dS будет равен:

Т.е. в

однородном поле
В произвольном электрическом поле

Слайд 17Подсчитаем поток вектора через произвольную замкнутую поверхность S, окружающую точечный заряд

q . Окружим заряд q сферой S1.

Слайд 18
Центр сферы совпадает с центром заряда. Радиус сферы S1 равен R1.

В каждой точке поверхности S1проекция Е на направление
внешней нормали
одинакова и равна

Слайд 19Тогда поток через S1

Слайд 20

Подсчитаем поток через сферу S2, имеющую радиус R2:

Слайд 21Из непрерывности линии следует, что поток и

через любую произвольную поверхность S будет равен этой же величине:

– теорема Гаусса для одного заряда.

Слайд 22Для любого числа произвольно расположенных зарядов, находящихся внутри поверхности:

– теорема Гаусса

для нескольких зарядов:
Поток вектора напряженности электрического поля через замкнутую поверхность в вакууме равен алгебраической сумме всех зарядов, расположенных внутри поверхности, деленной на ε0.

Слайд 23Полный поток проходящий через S3, не охватывающую заряд q, равен нулю:

Слайд 24Таким образом, для точечного заряда q, полный поток через любую замкнутую

поверхность S будет равен:

– если заряд расположен внутри замкнутой поверхности;
– если заряд расположен вне замкнутой поверхности;
этот результат не зависит от формы поверхности, и знак потока совпадает со знаком заряда.

Слайд 25 Электрические заряды могут быть «размазаны» с некоторой объемной

плотностью различной в разных местах пространства:

Здесь dV – физически бесконечно малый объем, под которым следует понимать такой объем, который с одной стороны достаточно мал, чтобы в пределах его плотность заряда считать одинаковой, а с другой – достаточно велик, чтобы не могла проявиться дискретность заряда, т.е. то, что любой заряд кратен целому числу элементарных зарядов электрона или протона .

Слайд 26Суммарный заряд объема dV будет равен:

Тогда из теоремы Гаусса можно получить:

–

это ещё одна форма записи теоремы Остроградского-Гаусса, если заряд неравномерно распределен по объему.

Слайд 27

Слайд 28

Слайд 29

Слайд 30

Слайд 31

Слайд 32

Слайд 33

Слайд 34

Слайд 35

Слайд 36

Слайд 372.5.2. Поле двух равномерно заряженных плоскостей
Пусть две бесконечные плоскости заряжены разноименными

зарядами с одинаковой по величине плотностью σ

Слайд 38Результирующее поле, находится как суперпозиция полей, создаваемых каждой из плоскостей.
Тогда

внутри плоскостей

Вне плоскостей напряженность поля

Полученный результат справедлив и для плоскостей конечных размеров, если расстояние между плоскостями гораздо меньше линейных размеров плоскостей (плоский конденсатор).

Теорема Остроградского-Гаусса презентация

Содержание

Слайд 12.1. Силовые линии электростатического поля2.2. Поток вектора напряженности2.3. Теорема Остроградского-Гаусса2.4. Дифференциальная

Слайд 22.1. Силовые линии электростатического поля Теорема Остроградского-Гаусса, которую мы докажем и обсудим

Слайд 3Остроградский Михаил Васильевич (1801 – 1862) отечественный математик и механик. Учился

Слайд 4Гаусс Карл Фридрих (1777 – 1855) немецкий математик, астроном и физик.

Слайд 5Основная ценность теоремы Остроградского-Гаусса состоит в том, что она позволяет

Слайд 6силовые линии – это линии, касательная к которым в любой точке

Слайд 7 Однородным называется электростатическое поле, во всех точках которого

Слайд 8 В случае точечного заряда поле неоднородно, линии напряженности исходят из положительного

Слайд 9 Для системы зарядов, как видим, силовые линии направлены от

Слайд 11 Густота силовых линий должна быть такой, чтобы единичную площадку,

Слайд 122.2. Поток вектора напряженности Полное число силовых линий, проходящих через

Слайд 13 Таким образом, поток вектора есть скаляр, который в зависимости от

Слайд 14Для первого рисунка – поверхность А1 окружает положительный заряд и поток

Слайд 152.3. Теорема Остроградского-Гаусса Итак, по определению, поток вектора напряженности электрического поля равен

Слайд 16поток вектора напряженности через произвольную элементарную площадку dS будет равен:Т.е. в

Слайд 17Подсчитаем поток вектора через произвольную замкнутую поверхность S, окружающую точечный заряд

Слайд 18Центр сферы совпадает с центром заряда. Радиус сферы S1 равен R1.

Слайд 19Тогда поток через S1

Слайд 20Подсчитаем поток через сферу S2, имеющую радиус R2:

Слайд 21Из непрерывности линии следует, что поток и

Слайд 22Для любого числа произвольно расположенных зарядов, находящихся внутри поверхности:– теорема Гаусса