трех непараллельных сил, лежащих в одной плоскости, то линии действия этих сил пересекаются в одной точке.
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Теорема о трех силах. (Лекция 2) презентация
Содержание
- 1. Теорема о трех силах. (Лекция 2)
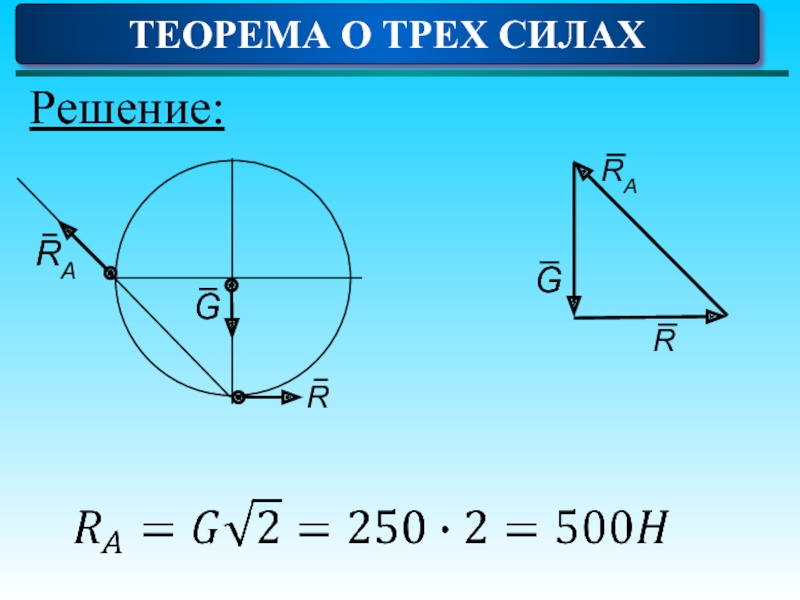
- 2. Вес диска реакция шарнира RA=… H. ТЕОРЕМА О ТРЕХ СИЛАХ
- 3. Решение: ТЕОРЕМА О ТРЕХ СИЛАХ
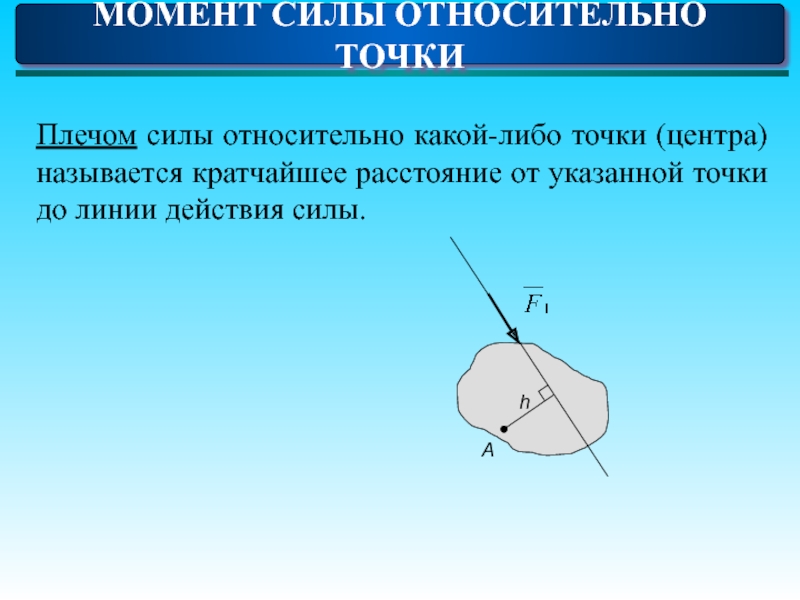
- 4. Плечом силы относительно какой-либо точки (центра) называется
- 5. МОМЕНТ СИЛЫ ОТНОСИТЕЛЬНО ТОЧКИ Момент силы
- 6. МОМЕНТ СИЛЫ ОТНОСИТЕЛЬНО ТОЧКИ Алгебраический момент
- 7. Пара сил - совокупность двух параллельных, равных
- 8. ПАРА СИЛ Момент пары сил -
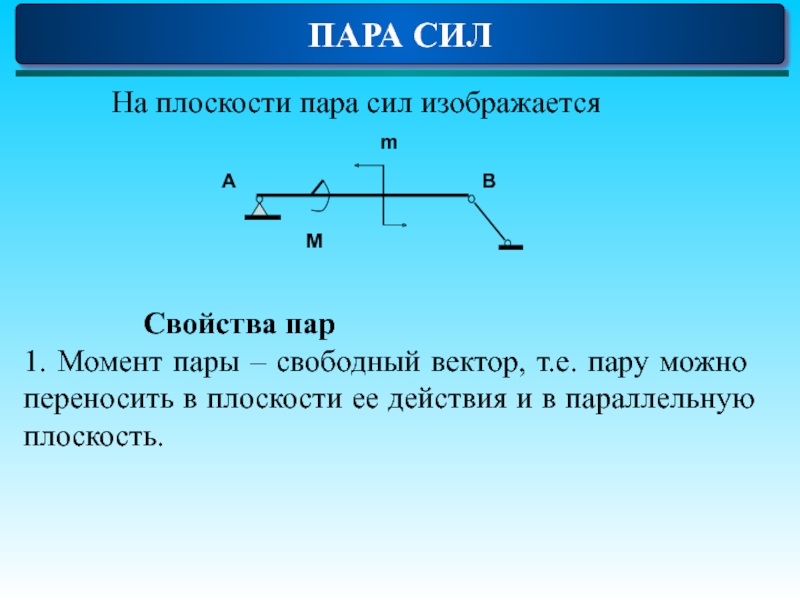
- 9. ПАРА СИЛ На плоскости пара сил
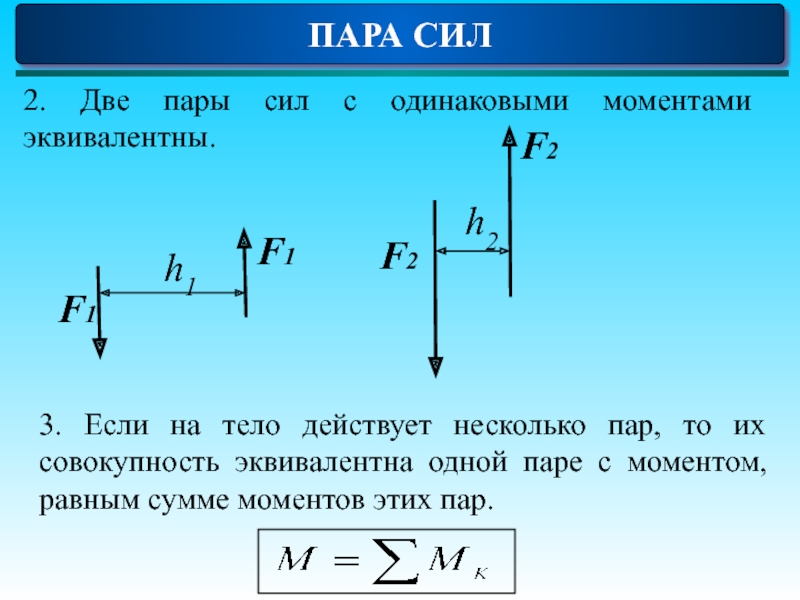
- 10. ПАРА СИЛ 2. Две пары сил
- 11. ТЕОРЕМА О ПАРАЛЛЕЛЬНОМ ПЕРЕНОСЕ СИЛЫ Силу,
- 12. ОСНОВНАЯ ТЕОРЕМА СТАТИКИ Главным вектором системы
- 13. ОСНОВНАЯ ТЕОРЕМА СТАТИКИ Теорема Пуансо
- 14. ОСНОВНАЯ ТЕОРЕМА СТАТИКИ А
- 15. УСЛОВИЯ РАВНОВЕСИЯ СИСТЕМЫ СИЛ Для равновесия
- 16. РАВНОВЕСИЕ ПЛОСКОЙ СИСТЕМЫ СИЛ Плоской называется
- 17. РАВНОВЕСИЕ ПЛОСКОЙ СИСТЕМЫ СИЛ Вторая форма:
- 18. РАВНОВЕСИЕ ПЛОСКОЙ СИСТЕМЫ СИЛ Третья форма:
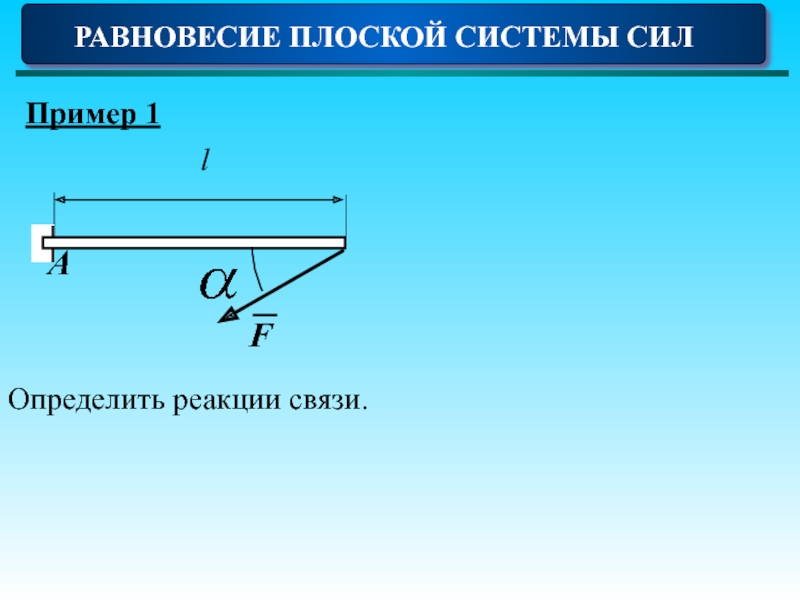
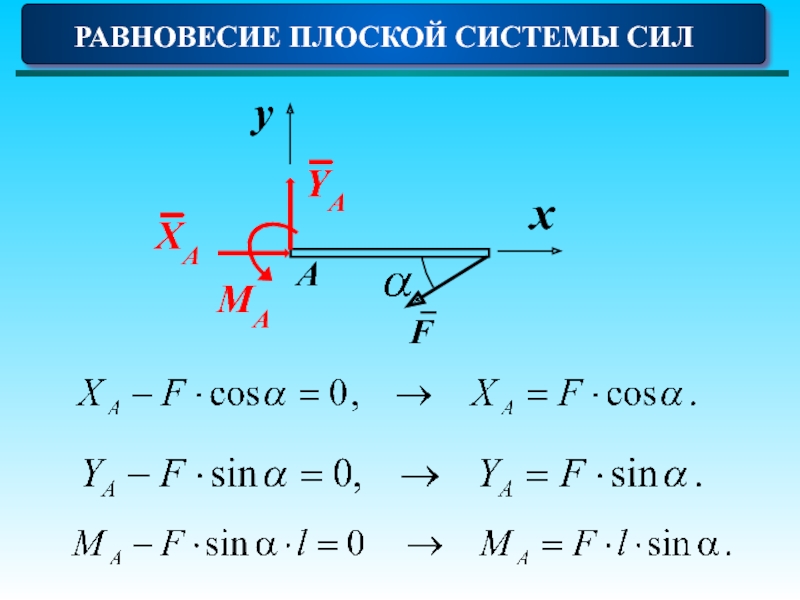
- 19. РАВНОВЕСИЕ ПЛОСКОЙ СИСТЕМЫ СИЛ Пример 1 F Определить реакции связи.
- 20. РАВНОВЕСИЕ ПЛОСКОЙ СИСТЕМЫ СИЛ
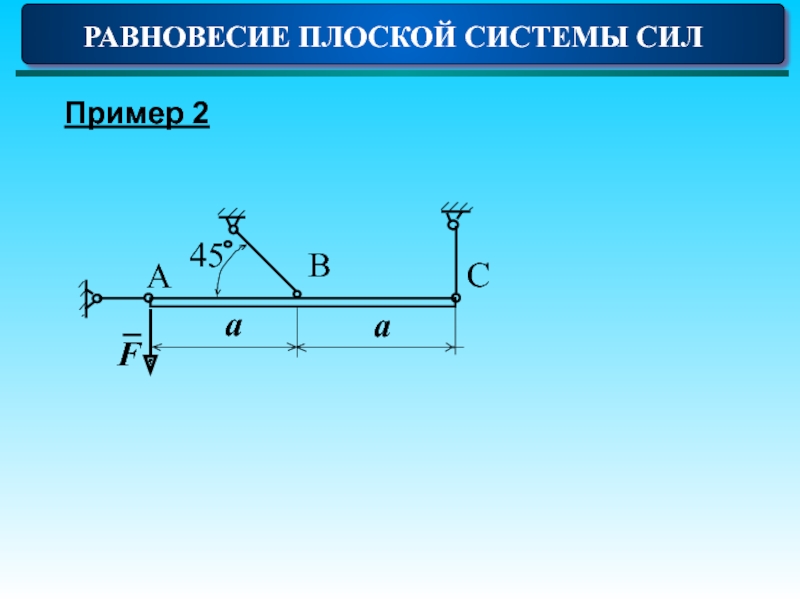
- 21. РАВНОВЕСИЕ ПЛОСКОЙ СИСТЕМЫ СИЛ Пример 2
- 22. РАВНОВЕСИЕ ПЛОСКОЙ СИСТЕМЫ СИЛ Вторая форма:
- 23. РАВНОВЕСИЕ ПЛОСКОЙ СИСТЕМЫ СИЛ
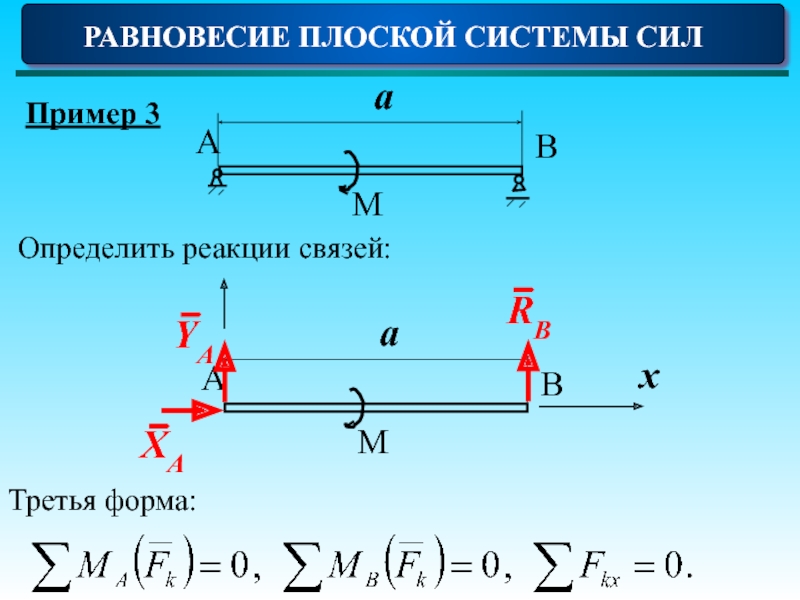
- 24. РАВНОВЕСИЕ ПЛОСКОЙ СИСТЕМЫ СИЛ Пример 3 x Третья форма: Определить реакции связей:
- 25. РАВНОВЕСИЕ ПЛОСКОЙ СИСТЕМЫ СИЛ
Вес диска реакция шарнира RA=… H. ТЕОРЕМА О ТРЕХ СИЛАХ
Слайд 4Плечом силы относительно какой-либо точки (центра) называется кратчайшее расстояние от указанной
точки до линии действия силы.
МОМЕНТ СИЛЫ ОТНОСИТЕЛЬНО ТОЧКИ
Слайд 5
МОМЕНТ СИЛЫ ОТНОСИТЕЛЬНО ТОЧКИ
Момент силы относительно центра это вектор, численно равный
произведению модуля силы на плечо и направленный перпендикулярно плоскости, проходящей через выбранную точку и вектор силы, в ту сторону, откуда “вращение” силы вокруг точки направлено против хода часовой стрелки.
Слайд 6
МОМЕНТ СИЛЫ ОТНОСИТЕЛЬНО ТОЧКИ
Алгебраический момент силы
Алгебраический момент силы F относительно центра
О равен взятому с соответствующим знаком произведению модуля силы на ее плечо
Правило знаков: момент считается положительным, когда сила стремится повернуть тело вокруг центра О по ходу часовой стрелки
Слайд 7Пара сил - совокупность двух параллельных, равных по модулю, противоположно направленных
сил.
ПАРА СИЛ
Плечо пары - это кратчайшее расстояние между линиями действия сил, составляющих пару.
Слайд 8
ПАРА СИЛ
Момент пары сил - это вектор, численно равный произведению модуля
силы на плечо пары; направлен перпендикулярно плоскости, в которой лежит пара, в ту сторону, откуда поворот пары виден происходящим против хода часовой стрелки.
Оказалось, что момент пары не зависит от выбора
центра О.
Алгебраический момент пары равен:
h
Слайд 9
ПАРА СИЛ
На плоскости пара сил изображается
Свойства пар
1. Момент пары – свободный
вектор, т.е. пару можно переносить в плоскости ее действия и в параллельную плоскость.
Слайд 10
ПАРА СИЛ
2. Две пары сил с одинаковыми моментами эквивалентны.
3. Если на
тело действует несколько пар, то их совокупность эквивалентна одной паре с моментом, равным сумме моментов этих пар.
Слайд 11
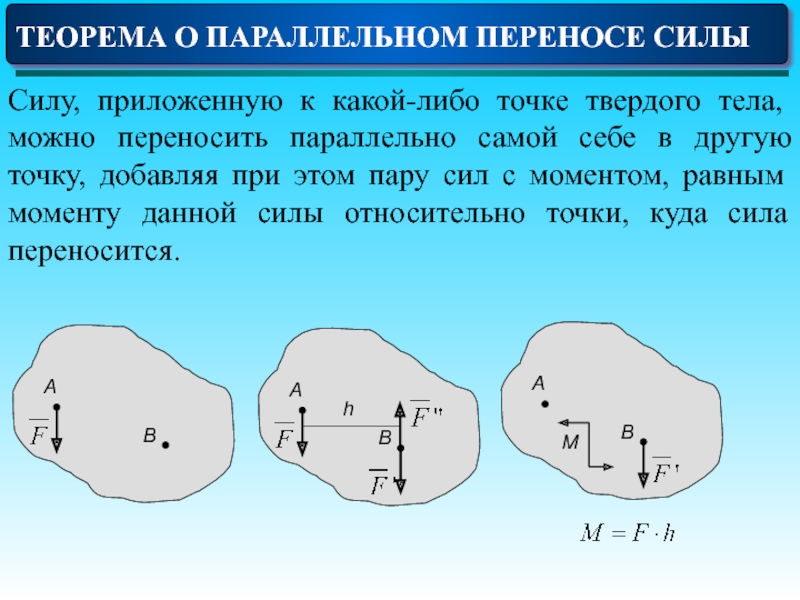
ТЕОРЕМА О ПАРАЛЛЕЛЬНОМ ПЕРЕНОСЕ СИЛЫ
Силу, приложенную к какой-либо точке твердого тела,
можно переносить параллельно самой себе в другую точку, добавляя при этом пару сил с моментом, равным моменту данной силы относительно точки, куда сила переносится.
А
А
В
В
А
В
h
M
Слайд 12
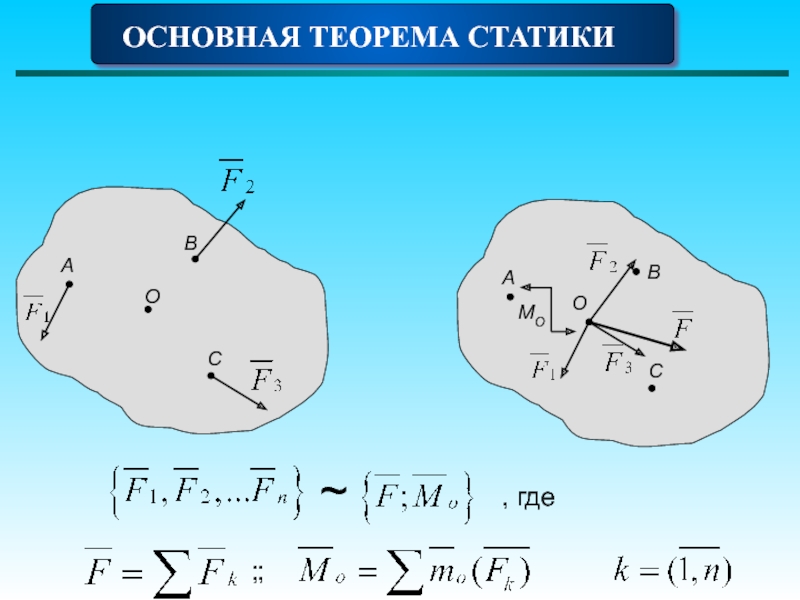
ОСНОВНАЯ ТЕОРЕМА СТАТИКИ
Главным вектором системы сил называется геометрическая сумма всех сил
системы
Главным моментом системы сил относительно центра О называется геометрическая сумма моментов всех сил относительно этого центра
Слайд 13
ОСНОВНАЯ ТЕОРЕМА СТАТИКИ
Теорема Пуансо
Всякую пространственную систему сил можно заменить эквивалентной системой,
состоящей из силы, приложенной в выбранном центре и равной главному вектору, и пары сил, момент которой равен главному моменту всех сил относительно выбранного центра.
Слайд 15
УСЛОВИЯ РАВНОВЕСИЯ СИСТЕМЫ СИЛ
Для равновесия любой системы сил необходимо и достаточно,
чтобы главный вектор этой системы сил и ее главный момент относительно любого центра были равны нулю
Слайд 16
РАВНОВЕСИЕ ПЛОСКОЙ СИСТЕМЫ СИЛ
Плоской называется система сил, как угодно расположенных в
одной плоскости.
Первая (основная) форма уравнений равновесия:
Для равновесия плоской системы сил необходимо и достаточно, чтобы алгебраические суммы проекций всех сил на две координатные оси и алгебраическая сумма моментов всех сил относительно произвольной точки равнялись нулю.
Слайд 17
РАВНОВЕСИЕ ПЛОСКОЙ СИСТЕМЫ СИЛ
Вторая форма:
Для равновесия плоской системы сил необходимо и
достаточно, чтобы суммы моментов всех сил относительно любых трех точек, не лежащих на одной прямой, были равны нулю.
Слайд 18
РАВНОВЕСИЕ ПЛОСКОЙ СИСТЕМЫ СИЛ
Третья форма:
Для равновесия плоской системы сил необходимо и
достаточно, чтобы суммы моментов всех сил относительно любых двух точек А и В и сумма проекций сил на ось Оx, не перпендикулярную прямой АВ, были равны нулю.
